Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2019 Aug 1.
Published in final edited form as: Curr Dir Psychol Sci. 2018 Jul 11;27(4):232–240. doi: 10.1177/0963721417746743

Collective Motion in Human Crowds

William H Warren 1,1
PMCID: PMC6121818  NIHMSID: NIHMS921296  PMID: 30197472

Abstract

The balletic motion of bird flocks, fish schools, and human crowds is believed to emerge from local interactions between individuals, in a process of self-organization. The key to explaining such collective behavior thus lies in understanding these local interactions. After decades of theoretical modeling, experiments using virtual crowds and analysis of real crowd data are enabling us to decipher the ‘rules’ governing these interactions. Based on such results, we build a dynamical model of how a pedestrian aligns their motion with that of a neighbor, and how these binary interactions are combined within a neighborhood in a crowd. Computer simulations of the model generate coherent motion at the global level and reproduce individual trajectories at the local level. This approach yields the first experiment-driven, bottom-up model of collective motion, providing a basis for understanding more complex patterns of crowd behavior in both everyday and emergency situations.

Keywords: Crowd behavior, pedestrian dynamics, flocking, collective behavior, self-organization

The spectacle of a murmuration of starlings careening in near-perfect synchrony, or a school of herring smoothly circling in a ‘mill’ formation, are prime examples of collective behavior in biological systems. Humans exhibit such collective motion as well, when a crowd of pedestrians adopts a common motion on the way to a train platform, or forms opposing lanes of traffic in a shopping mall. Collective behavior can also go tragically awry, such as a stampede in a stadium or collective motion to one exit in a burning nightclub. How do many individuals spontaneously coalesce into a coherently moving body? After decades of theoretical modeling, research has now advanced to the point that experimentally-grounded models of collective motion are possible.

THE SELF-ORGANIZATION OF BEHAVIOR

Beyond its intrinsic fascination, collective motion is a paradigmatic case of self-organized behavior. There is a growing recognition among biologists, psychologists, and cognitive scientists that general principles of self-organization hold promise for explaining the organization of human and animal behavior at multiple levels, avoiding appeals to a prioi neural or cognitive structure (Camazine et al., 2001; Goldstone & Gureckis, 2009; Kelso, 1995).

The ingredients of self-organization have been identified in systems ranging from lasers to ant trails (Haken, 1983): (a) an open system that dissipates energy, (b) composed of many interacting components, (c) which are locally coupled by physical or information fields; (d) a fluctuation that nudges the system away from disorder;2 and (e) a positive feedback that amplifies this initial fluctuation, capturing more components, (f) to yield an emergent spatial or temporal pattern.

One can see this process at work in fish schooling. A shoal of foraging fish (dissipative components), locally coupled by sensory information, is randomly oriented (disorder). The approach of a predator triggers nearby fish to escape by swimming in a similar direction, which progressively recruits neighboring fish into the emerging pattern (positive feedback), to form a coherently moving school. Collective motion has become a test bed for self-organized behavior because these mechanisms are observable and amenable to experimental study.

MODELING COLLECTIVE MOTION

If collective behavior emerges from local interactions between individuals, then the crux of the problem is understanding the nature of these interactions. This insight has motivated a raft of ‘microscopic’ or agent-based models, focused on the local level of individual behavior. They are complementary to ‘macroscopic’ models, which treat huge crowds as a fluid and focus on global properties such as density and mean velocity (Cristiani, Piccoli, & Tosin, 2014).

The Attraction-Repulsion Framework

The dominant class of microscopic models is the attraction-repulsion framework, derived from early research on fish schooling (Schellinck & White, 2011). It assumes three basic rules (Figure 1): (a) attraction – move toward neighbors in a far zone, (b) repulsion – move away from neighbors in a near zone, and (c) alignment – match the velocity (speed and heading direction) of neighbors in an intermediate zone. By adjusting the radii of these zones, the model can generate unaligned aggregation (shoaling), strongly aligned translation (schooling), and rotational motion (mills) (Couzin, Krause, James, Ruxton, & Franks, 2002). Craig Reynolds (1987) famously applied this model to computer animation, producing the wildebeest stampede in The Lion King and the bat swarms in Batman.

Figure 1.

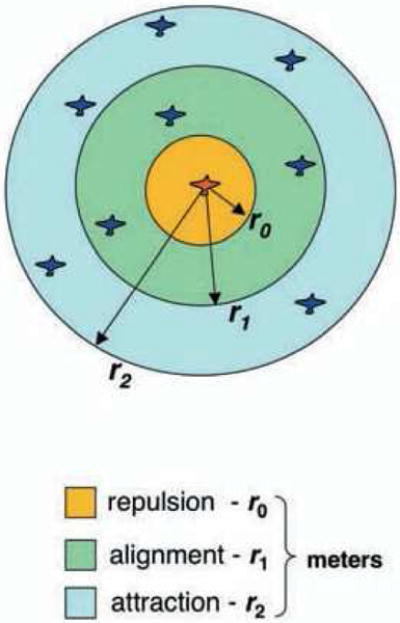
Figure 1

Open in a new tab

The attraction-repulsion framework: An individual is repelled from neighbors in the near zone (orange), aligns their velocity with neighbors in the intermediate zone (green), and is attracted to neighbors in the far zone (blue). Each zone has a constant coupling strength with a hard metric radius r. Reprinted from Giardina (2008).

The stripped-down self-propelled particle model (Czirók & Vicsek, 2000) subsequently showed that a velocity-based alignment rule alone can generate translational motion, as well as transitions from incoherent to coherent motion. Conversely, the social force model (Helbing & Molnár, 1995) was predicated on position-based attraction and repulsion rules. It, too, generates plausible patterns of global motion, but individual trajectories do not resemble human locomotion at the local level (Pelechano, Allbeck, & Badler, 2007). More recently, vision-based models proposed that local interactions are driven by visual or cognitive heuristics (Moussaïd, Helbing, & Theraulaz, 2011; Ondrej, Pettré, Olivier, & Donikian, 2010).

With recent advances in 3D motion tracking of animals and humans, researchers are starting to compare such theoretical models with observational data, yielding many tantalizing insights (Cavagna et al., 2010; Charalambous, Karamouzas, Guy, & Chrysanthou, 2014; Hildenbrandt, Carere, & Hemelrijk, 2010; Lukeman, Li, & Edelstein-Keshet, 2010; Moussaïd et al., 2012; Wolinski et al., 2014; Zhang, Klingsch, Schadschneider, & Seyfried, 2012). Computer simulations of observational data are, however, insufficient to test local rules. It has recently been recognized that the same motion pattern can be generated by different local rules (Vicsek & Zafeiris, 2012; Weitz et al., 2012), an example of degeneracy in complex systems. Deciphering the rules and the perceptual information that actually govern local interactions thus requires experimental manipulation of individual behavior at the local level (Gautrais et al., 2012; Sumpter, Mann, & Perna, 2012).

BEHAVIORAL DYNAMICS

My students and I are pursuing just such an experiment-driven, bottom-up model of human crowd behavior (for a similar approach in fish, see Gautrais et al., 2012; Zienkiewicz, Barton, Porfiri, & Di Bernardo, 2015). In the behavioral dynamics approach (Warren, 2006), we first study each basic behavior and model it as a dynamical system. Related experiments determine the visual information that controls that behavior (Gibson, 1979; Warren, 1998). The resulting control laws are analogous to local ‘rules’ but emphasize their continuous dynamical rather than logical cognitive form.

Building a Pedestrian Model

We began by building a pedestrian model that captures how people walk through an environment of goals, obstacles, and moving objects (Fajen & Warren, 2003; Warren & Fajen, 2008). We tested participants walking in virtual reality (VR), making it possible to manipulate the visual environment, and modeled their locomotor trajectories. To get an intuition for the model, imagine that a pedestrian’s heading direction is attached to the goal direction by a damped spring (Figure 2a). As the pedestrian walks forward, their heading is pulled into alignment with the goal (an attractor); conversely, another spring pushes their heading away from the direction of an obstacle (a repeller). The path of locomotion is the result of all such ‘spring forces’ acting on the pedestrian as they move through the environment. This simple attractor/repeller dynamics successfully models the emergence of locomotor paths and predicts paths in more complex environments.

Figure 2.

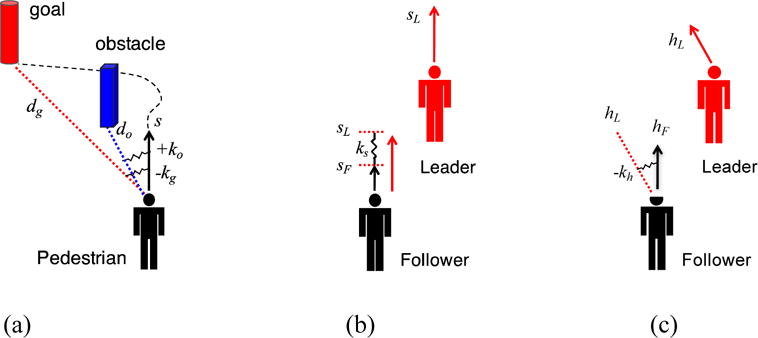
Figure 2

Open in a new tab

Pedestrian model and velocity alignment dynamics. (a) Goals and obstacles: As pedestrian walks with speed s, their heading direction is attracted to the goal direction by a damped spring with negative stiffness (−kg), and repelled from the obstacle direction by a damped spring with positive stiffness (+ko); stiffness decays exponentially with distance (dg and do). The current heading is the resultant of all spring forces, which evolve over time, yielding an emergent locomotor path. (b) Following: speed matching. Follower is attracted to leader’s speed by spring with stiffness ks. (c) Following: heading matching. Follower is attracted to leader’s heading direction by spring with stiffness −kh.

Alignment Dynamics

To scale up to crowds, we next studied binary interactions between two pedestrians – in particular, how one person follows another (Dachner & Warren, 2014; Rio, Rhea, & Warren, 2014). Rather than keeping a constant distance from the leader, we found that the follower matches the leader’s velocity – similar to an alignment rule. The results allowed us to formulate a simple model of alignment dynamics, in which the follower linearly accelerates to match the leader’s speed (Figure 2b), and angularly accelerates to match the leader’s heading (Figure 2c). By manipulating the visual information for the leader in VR, we have determined that the follower does this by jointly canceling the leader’s optical expansion and change in bearing direction, yielding a visual control law for following that decays with distance (Dachner & Warren, 2017). We believe these alignment dynamics form the basis of collective motion.

A PEDESTRIAN’S NEIGHBORHOOD

In a crowd, however, each pedestrian is influenced by multiple neighbors, so the key to collective motion is a pedestrian’s zone of influence or neighborhood. We thus set out to determine how the influences of multiple neighbors are combined within a neighborhood. To probe these interactions experimentally, we created a novel VR paradigm in which a participant is asked to “walk with” a virtual crowd, allowing us to manipulate the speed and heading of neighbors and measure the participant’s response. We compared the results to motion-capture data on a human ‘swarm’, in which a group of 16–20 participants walked together about a large hall, veering randomly left and right. What we discovered enabled us to formulate the first bottom-up model of collective motion.

Superposition and Coupling Strength

Nearly all models of collective motion assume that binary interactions between a pedestrian and each neighbor are linearly combined, a principle known as superposition. To test this basic assumption, we perturbed the speed or heading of a subset of the 12 virtual neighbors (Figure 3a) and measured the participant’s change in speed or heading (Rio, Dachner, & Warren, 2017). We found that the mean response increased linearly with the number of perturbed neighbors, supporting superposition (the correlation coefficient, a measure of agreement that varies between 0 and 1, was r=.99). This proportional response was observed on individual trials.

Figure 3.

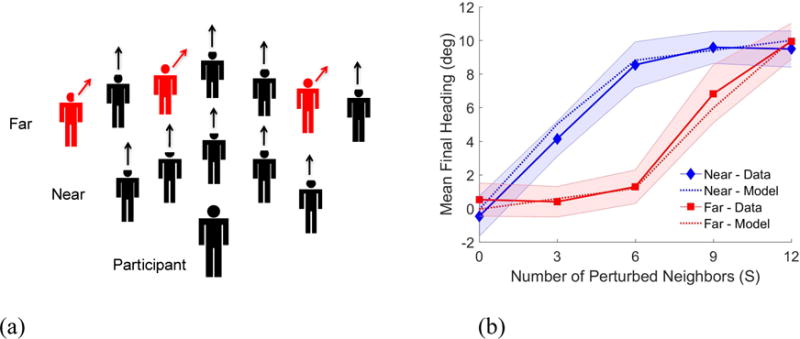
Figure 3

Open in a new tab

A participant walks with a virtual crowd of 12 neighbors. (a) The heading direction (or speed) of a subset of neighbors (S=0, 3, 6, 9, 12, red), in a near zone or a far zone, is perturbed midway through a 12s trial. (b) Participant’s mean final heading in the last 2s (solid curves) increases linearly with the number of perturbed neighbors, but the response is greater to near (blue) than far (red) neighbors. Simulations of the crowd model (dotted curves) are nearly identical, within the 95% confidence interval of the human data (shaded regions). Modified from Rio, Dachner, & Warren (2017).

However, we also found that the response to near neighbors (~1.8m) was significantly greater than to far neighbors (~3.5m) (Figure 3b). Most ‘zonal’ models assume a constant coupling strength with a hard radius (Figure 1), but analysis of the human ‘swarm’ data (Figure 4) confirmed that coupling strength decreases exponentially with distance, going to zero at about 4m. Such a ‘soft’ radius is advantageous for collective motion (Cucker & Smale, 2007). We thus modeled the neighborhood as a weighted average of neighbors, where the weight decays exponentially with distance. This might have a visual basis, for a neighbor’s visual angle and optical velocity decrease with distance due to the laws of perspective, and farther neighbors are progressively occluded by nearer neighbors in a crowd.

Figure 4.

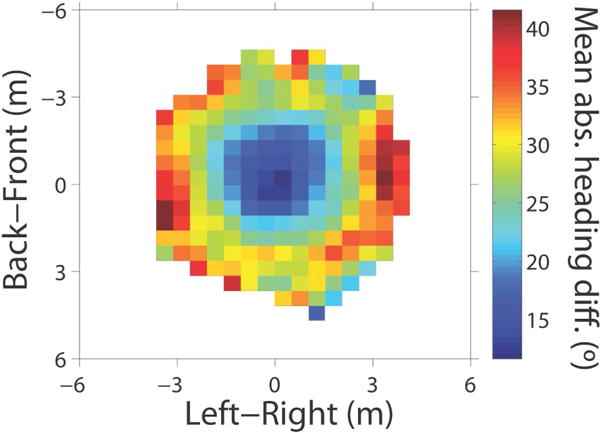
Figure 4

Open in a new tab

Data from the human ‘swarm’: Heat map of mean absolute heading difference (deg) between the central participant nearest the center of the swarm (at [0,0], heading upward) and each neighbor, averaged over 6 min of data (three 2-min trials, initial interpersonal distance of 2m) (cell=0.5×0.5m). Reprinted from Rio, et al. (2017)

On the other hand, coupling strength did not consistently depend on a neighbor’s eccentricity (lateral position). This result suggests that the human neighborhood is circular, which is borne out by the swarm data (Figure 4). Yet coupling strength obviously drops to zero at the edges of the field of view. Prey species often have nearly panoramic vision, implying that flocks and schools are bi-directionally coupled (but see Nagy, Akros, Biro, & Vicsek, 2010). In contrast, humans have an approximately 180° visual field, which implies that crowds are uni-directionally coupled, so a pedestrian only responds to neighbors in front of them. This suspicion is confirmed by analysis of time delays in the swarm data, which shows that a pedestrian turns after neighbors ahead, followed by neighbors behind. The observation has important implications for causal networks in crowds, how crowds steer and make decisions.

Metric or Topological?

Most microscopic models assume that a zone or neighborhood (Figure 5) is defined by metric distance, such that an individual is influenced by all neighbors within a fixed radius (e.g. 4m). In contrast, evidence suggests that starlings have neighborhoods defined by topological distance, or a fixed number of nearest neighbors (e.g. 7) regardless of their absolute distance (Ballerini et al., 2008; but see Evangelista, Ray, Raja, & Hedrick, 2017). This adaptation would insure cohesive flocking despite large variation in the density of a swooping murmuration and prevent birds drifting away from the flock.

Figure 5.

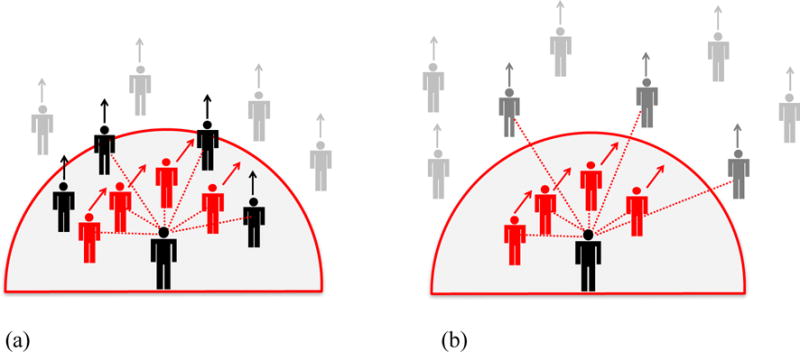
Figure 5

Open in a new tab

Metric and topological neighborhoods. On the metric hypothesis, the participant is influenced by all neighbors within a fixed radius (shaded region); on the topological hypothesis, the participant is influenced by a fixed number of nearest neighbors (dotted red lines). (a) High density condition: Both metric and topological neighborhoods contain perturbed (red) and unperturbed (black) neighbors. (b) Low density condition: The metric neighborhood contains fewer unperturbed neighbors (gray) than before, so the metric hypothesis predicts a greater response to the perturbed neighbors (red). But the nearest neighbors remain the same, so the topological hypothesis predicts the same response to the perturbed neighbors.

We tested these hypotheses in humans by manipulating the density of a virtual crowd of 12 neighbors. In the critical experiment (Wirth & Warren, 2016), we perturbed the heading of the nearest 2–4 neighbors, who always appeared at constant distances, while unperturbed neighbors varied in distance (Figure 5). The topological hypothesis predicts that density should have no effect on the response. In contrast, the metric hypothesis predicts that responses should be greater in the low-density condition, when fewer unperturbed neighbors appear in the neighborhood, than in the high-density condition. That is precisely what we found, consistent with the metric hypothesis.

Double Decay

However, it seemed unlikely that a group of neighbors outside a metric radius of 4m would be completely ignored. To check, we varied the distance of the entire virtual crowd up to 8m – and found that the participant still responded to heading perturbations. The response decreased with distance again, but at a much more gradual rate than before. This result raised the prospect of a flexible neighborhood with two decay rates: a slow decay to the nearest neighbors in the crowd, possibly due to the laws of perspective, and a faster decay within the crowd, perhaps due to added occlusion.

To test the double-decay hypothesis, we varied the distance of the whole crowd and selectively perturbed the near, middle, or far row of neighbors. As expected, we observed a gradual decay to the nearest neighbor, which went to zero at about 11m, followed by a more rapid decay within the crowd, which went to zero 4m from the nearest neighbor. Such a flexible neighborhood would allow pedestrians to coordinate their motion with a group up to 11m away, so they don’t drift away from the ‘flock’.

A Neighborhood Model

Taken together, the experimental results enabled us to formalize a model of a pedestrian’s neighborhood (Figure 6) as (a) circularly symmetric, (b) with a uni-directional coupling to neighbors within ±90° of the heading direction, (c) whose influences are combined as a weighted average, (d) with weights that decay exponentially with metric distance (e) at two decay rates.

Figure 6.

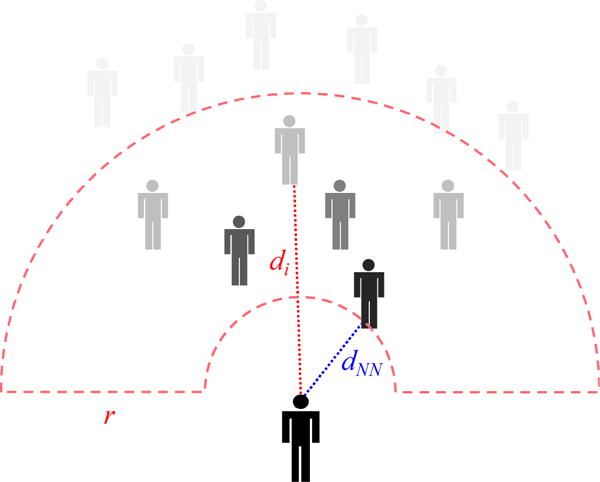
Figure 6

Open in a new tab

Neighborhood model. The participant’s response is a weighted average of neighbors i, where the weight decays gradually with distance to the nearest neighbor (dNN) up to 11m, and more rapidly within the crowd (di-dNN), creating a flexible neighborhood with a soft radius (r=4m).

CROWD DYNAMICS

Combining the neighborhood model (Figure 6) with the alignment dynamics (Figure 2) gives us a model of the local interactions underlying collective motion. Specifically, a pedestrian’s linear (or angular) acceleration is a weighted average of the difference between their current speed (or heading) and that of each neighbor, where the weight decays exponentially with distance. We tested this model against human data at the global and local levels.

Global Motion

First, to demonstrate that the model generates globally coherent motion, we performed multi-agent simulations of ten 10s segments of the ‘swarm’ data. The model agents were assigned the initial positions and velocities of the participants and then ‘let go’, simulating the trajectories of all interacting agents. The model indeed generated patterns of collective motion, with a mean ‘dispersion’ of 21° (mean pairwise difference in heading over a 3s traveling window), comparable to the human mean of 24°. The model thus reproduces the basic phenomenon of common motion with a coherence comparable to human crowds.

Local Trajectories

We cannot expect to simulate individual trajectories this way, however – akin to predicting the motions of individual molecules in a gas. Instead, we simulated each participant in the swarm one at a time, treating the positions and velocities of their neighbors as input (Figure 7) (Rio et al., 2017). The mean correlation between model and human trajectories for the ten segments was r=.95 for heading and r=.70 for speed (a bit lower because there was little speed variation in the swarm).

Figure 7.

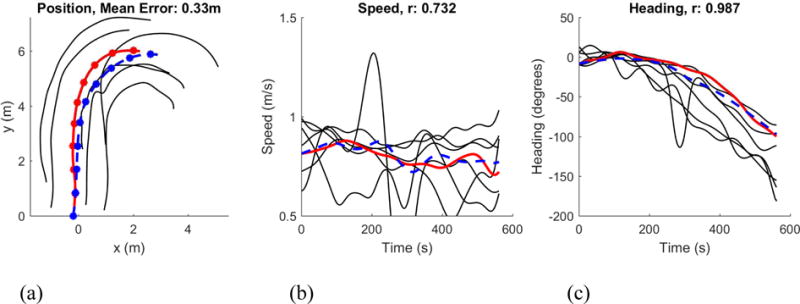
Figure 7

Open in a new tab

Simulation of a sample trajectory from the human ‘swarm’. (a) Path in space (dots at 1s intervals). (b) Time series of speed. (c) Time series of heading. Solid red curve corresponds to participant, dashed blue curve to model agent, black curves to neighbors in the neighborhood that were input to model. Simulations were performed on ten 10s segments of swarm data that had continuous tracking of ≥8 neighbors.

We also simulated the trajectories of participants walking in the virtual crowd experiment, when the neighbors’ speed or heading was perturbed. The model closely reproduced human trajectories (mean r=0.89 for changes in heading, mean r=0.82 for changes in speed). Moreover, the model’s final heading and speed were virtually identical with the mean human data in each condition (Figure 3). The model thus reproduces pedestrian motion at the local as well as global level.

The Neighborhood as a Mechanism of Self-Organization

Essential to self-organization is a positive feedback mechanism that progressively recruits more individuals into the emerging pattern. In collective motion, this role is played by the local neighborhood. Each individual is visually coupled to multiple neighbors ahead, and influences others behind. As neighbors begin to align, they increasingly influence the neighborhoods that contain them, drawing more individuals into alignment. In this manner, a pattern of coherent motion propagates through the crowd.

Conclusion

Thanks to experiments with virtual crowds and motion-capture data on real crowds, we are beginning to decipher the local interactions that underlie collective crowd behavior. This approach has yielded the first experiment-driven, bottom-up model of collective motion, accounting for both globally coherent motion and local trajectories. Challenges ahead include building a full vision-based model, explaining more complex patterns of crowd behavior, formally linking the microscopic and macroscopic levels of description (Cristiani et al., 2014; Degond, Appert-Rolland, Moussaïd, Pettré, & Theraulaz, 2013), understanding the causes of crowd disasters and improving evacuation planning (Helbing, Buzna, Johansson, & Werner, 2005; Schadschneider, Klingsch, Klüpfel, Rogsch, & Seyfried, 2008).

Acknowledgments

This research was supported by National Institutes of Health grant R01EY010923 and National Science Foundation grant BCS-1431406. The author would like to thank Kevin Rio, Greg Dachner, Trent Wirth, Stéphane Bonneaud, Max Kinateder, Emily Richmond, Arturo Cardenas, Michael Fitzgerald, and the team who helped collect and process data from the Sayles Swarm.

Footnotes

2

Technically this is known as ‘symmetry-breaking’ because the pattern of components is no longer symmetric (invariant) under transformations such as translation and rotation.

References

  1. Ballerini M, Cabibbo N, Candelier R, Cavagna A, Cisbani E, Giardina I, Zdravkovic V. Interaction ruling animal collective behavior depends on topological rather than metric distance: Evidence from a field study. Proceedings of the National Academy of Sciences. 2008;105(4):1232–1237. doi: 10.1073/pnas.0711437105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Camazine S, Deneubourg JL, Franks NR, Sneyd J, Theraulaz G, Bonabeau E. Self-organization in biological systems. Princeton, NJ: Princeton University Press; 2001. An accessible introduction to principles of self-organization and their application to many types of animal behavior. [Google Scholar]
  3. Cavagna A, Cimarelli A, Giardina I, Parisi G, Santagati R, Stefanini F. Scalefree correlations in starling flocks. Proceedings of the National Academy of Sciences. 2010;107(26):11865–11870. doi: 10.1073/pnas.1005766107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Charalambous P, Karamouzas I, Guy SJ, Chrysanthou Y. A Data-driven framework for visual crowd analysis. Computer Graphics Forum. 2014;33(7):41–50. doi: 10.1111/cgf.12472. [DOI] [Google Scholar]
  5. Couzin ID, Krause J, James R, Ruxton GD, Franks NR. Collective memory and spatial sorting in animal groups. Journal of Theoretical Biology. 2002;218:1–11. doi: 10.1006/jtbi.2002.3065. [DOI] [PubMed] [Google Scholar]
  6. Cristiani E, Piccoli B, Tosin A. Multiscale modeling of pedestrian dynamics. Vol. 12. Heidelberg: Springer; 2014. A current review and introduction to mathematical models of pedestrian and crowd behavior. [Google Scholar]
  7. Cucker F, Smale S. Emergent behavior in flocks. IEEE Transactions on Automatic Control. 2007;52(5):852–862. [Google Scholar]
  8. Czirók A, Vicsek T. Collective behavior of interacting self-propelled particles. Physica A. 2000;281:17–29. [Google Scholar]
  9. Dachner G, Warren WH. Behavioral dynamics of heading alignment in pedestrian following. Transportation Research Procedia. 2014;2:69–76. [Google Scholar]
  10. Dachner G, Warren WH. A vision-based model for the joint control of speed and heading in pedestrian following. Journal of Vision. 2017;17(10):716. [Google Scholar]
  11. Degond P, Appert-Rolland C, Moussaïd M, Pettré J, Theraulaz G. A hierarchy of heuristic-based models of crowd dynamics. Journal of Statistical Physics. 2013;152:1033–1068. [Google Scholar]
  12. Evangelista DJ, Ray DD, Raja SK, Hedrick TL. Three-dimensional trajectories and network analyses of group behaviour within chimney swift flocks during approaches to the roost. Proc R Soc B. 2017;257(1849):20162602. doi: 10.1098/rspb.2016.2602. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Fajen BR, Warren WH. Behavioral dynamics of steering, obstacle avoidance, and route selection. Journal of Experimental Psychology: Human Perception and Performance. 2003;29:343–362. doi: 10.1037/0096-1523.29.2.343. [DOI] [PubMed] [Google Scholar]
  14. Gautrais J, Ginelli F, Fournier R, Blanco S, Soria M, Chaté H, Theraulaz G. Deciphering interactions in moving animal groups. PLoS Comput Biology. 2012;5(9):e1002678. doi: 10.1371/journal.pcbi.1002678. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Gibson JJ. The ecological approach to visual perception. Boston: Houghton Mifflin; 1979. [Google Scholar]
  16. Goldstone RL, Gureckis TM. Collective behavior. Topics in Cognitive Science. 2009;1(3):412–438. doi: 10.1111/j.1756-8765.2009.01038.x. [DOI] [PubMed] [Google Scholar]
  17. Haken H. Synergetics, an introduction: Nonequilibrium phase transitions and self-organization in physics, chemistry, and biology. 3rd. New York: Springer-Verlag; 1983. [Google Scholar]
  18. Helbing D, Buzna L, Johansson A, Werner T. Self-organized pedestrian crowd dynamics: Experiments, simulations, and design solutions. Transportation science. 2005;39(1):1–24. [Google Scholar]
  19. Helbing D, Molnár P. Social force model of pedestrian dynamics. Physical Review E. 1995;51:4282–4286. doi: 10.1103/physreve.51.4282. [DOI] [PubMed] [Google Scholar]
  20. Hildenbrandt H, Carere C, Hemelrijk CK. Self-organized aerial displays of thousands of starlings: A model. Behavioral Ecology. 2010;21(6):1349–1359. [Google Scholar]
  21. Kelso JAS. Dynamic patterns: The self-organization of brain and behavior. Cambridge, MA: MIT Press; 1995. [Google Scholar]
  22. Lukeman R, Li YX, Edelstein-Keshet L. Inferring individual rules from collective behavior. Proceedings of the National Academy of Sciences. 2010;107(28):12576–12580. doi: 10.1073/pnas.1001763107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Moussaïd M, Guillot EG, Moreau M, Fehrenbach J, Chabiron O, Lemercier S, Theraulaz G. Traffic instabilities in self-organized pedestrian crowds. PLoS Comput Biology. 2012;8(3):e1002442. doi: 10.1371/journal.pcbi.1002442. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Moussaïd M, Helbing D, Theraulaz G. How simple rules determine pedestrian behavior and crowd disasters. Proceedings of the National Academy of Sciences. 2011;108(17):6884–6888. doi: 10.1073/pnas.1016507108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Nagy M, Akros Z, Biro D, Vicsek T. Hierarchical group dynamics in pigeon flocks. Nature. 2010;464:890–893. doi: 10.1038/nature08891. [DOI] [PubMed] [Google Scholar]
  26. Ondrej J, Pettré J, Olivier AH, Donikian S. A synthetic-vision based steering approach for crowd simulation. ACM Transactions on Graphics. 2010;29(4):121–129. 123. [Google Scholar]
  27. Pelechano N, Allbeck JM, Badler NI. Controlling individual agents in high-density crowd simulation. Proceedings of the 2007 ACM SIGGRAPH/Eurographics Symposium on Computer Animation. 2007:99–108. [Google Scholar]
  28. Reynolds CW. Flocks, herds, and schools: a distributed behavioral model. Computer Graphics. 1987;21:25–34. [Google Scholar]
  29. Rio K, Dachner G, Warren WH. Local interactions underlying collective motion in human crowds. 2017 doi: 10.1098/rspb.2018.0611. Submitted for publication. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Rio K, Rhea C, Warren WH. Follow the leader: Visual control of speed in pedestrian following. Journal of Vision. 2014;14(2):1–16. doi: 10.1167/14.2.4. 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Schadschneider A, Klingsch W, Klüpfel H, Rogsch C, Seyfried A. Evacuation dynamics: empirical results, modeling and applications. In: Meyers B, editor. Encyclopedia of Complex and Systems Science. Berlin: Springer; 2008. pp. 1–57. [Google Scholar]
  32. Schellinck J, White T. A review of attraction and repulsion models of aggregation: Methods, findings and a discussion of model validation. Ecological Modeling. 2011;222:1897–1911. [Google Scholar]
  33. Sumpter DJT, Mann RP, Perna A. The modelling cycle for collective animal behaviour. Interface Focus. 2012;2(6):764–773. doi: 10.1098/rsfs.2012.0031. An insigntful discussion of how to study and model collective behavior at local and global levels. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Vicsek T, Zafeiris A. Collective motion. Physics Reports. 2012;517:71–140. [Google Scholar]
  35. Warren WH. Visually controlled locomotion: 40 years later. Ecological Psychology. 1998;10:177–219. [Google Scholar]
  36. Warren WH. The dynamics of perception and action. Psychological Review. 2006;113:358–389. doi: 10.1037/0033-295X.113.2.358. The author’s behavioral dynamics manifesto, introducing concepts of dynamical systems and applications to modeling human behavior. [DOI] [PubMed] [Google Scholar]
  37. Warren WH, Fajen BR. Behavioral dynamics of visually-guided locomotion. In: Fuchs A, Jirsa V, editors. Coordination: Neural, behavioral, and social dynamics. Heidelberg: Springer; 2008. [Google Scholar]
  38. Weitz S, Blanco S, Fournier R, Gautrais J, Jost C, Theraulaz G. Modeling collective animal behavior with a cognitive perspective: A methodological framework. PLoS One. 2012;7(6):e38588. doi: 10.1371/journal.pone.0038588. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Wirth T, Warren WH. The visual neighborhood in human crowds: Metric vs. topological hypotheses. Journal of Vision. 2016;15(12):1332. [Google Scholar]
  40. Wolinski DJ, Guy S, Olivier AH, Lin M, Manocha D, Pettré J. Parameter estimation and comparative evaluation of crowd simulations. Computer Graphics Forum. 2014;33(2):303–312. doi: 10.1111/cgf.12328. [DOI] [Google Scholar]
  41. Zhang J, Klingsch W, Schadschneider A, Seyfried A. Ordering in bidirectional pedestrian flows and its influence on the fundamental diagram. Journal of Statistical Mechanics: Theory and Experiment. 2012:02002. [Google Scholar]
  42. Zienkiewicz A, Barton DA, Porfiri M, Di Bernardo M. Data-driven stochastic modelling of zebrafish locomotion. Journal of Mathematical Biology. 2015;71(5):1081–1105. doi: 10.1007/s00285-014-0843-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Giardina I. Collective behavior in animal groups: theoretical models and empirical studies. HFSP Journal. 2008;2(4):205–219. doi: 10.2976/1.2961038. A readable introduction to microscopic and macroscopic models of collective animal motion. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES