Abstract
A user ready, portable, documented software package, NFTsim, is presented to facilitate numerical simulations of a wide range of brain systems using continuum neural field modeling. NFTsim enables users to simulate key aspects of brain activity at multiple scales. At the microscopic scale, it incorporates characteristics of local interactions between cells, neurotransmitter effects, synaptodendritic delays and feedbacks. At the mesoscopic scale, it incorporates information about medium to large scale axonal ranges of fibers, which are essential to model dissipative wave transmission and to produce synchronous oscillations and associated cross-correlation patterns as observed in local field potential recordings of active tissue. At the scale of the whole brain, NFTsim allows for the inclusion of long range pathways, such as thalamocortical projections, when generating macroscopic activity fields. The multiscale nature of the neural activity produced by NFTsim has the potential to enable the modeling of resulting quantities measurable via various neuroimaging techniques. In this work, we give a comprehensive description of the design and implementation of the software. Due to its modularity and flexibility, NFTsim enables the systematic study of an unlimited number of neural systems with multiple neural populations under a unified framework and allows for direct comparison with analytic and experimental predictions. The code is written in C++ and bundled with Matlab routines for a rapid quantitative analysis and visualization of the outputs. The output of NFTsim is stored in plain text file enabling users to select from a broad range of tools for offline analysis. This software enables a wide and convenient use of powerful physiologically-based neural field approaches to brain modeling. NFTsim is distributed under the Apache 2.0 license.
This is a PLoS Computational Biology Software paper.
Introduction
The brain is a multiscale physical system, with structures ranging from the size of ion channels to the whole brain, and timescales running from sub-millisecond to multi-year durations. When modeling brain structure and dynamics, it is thus necessary to choose models that are appropriate to the scales of the phenomena involved. These range from microscale models of individual neurons and their substructures, through network-level models of discrete neurons, to population-level mesoscale and macroscale neural mass and neural field models that average over microstructure and apply from local brain areas up to the whole brain. Many useful results can be obtained analytically from models at various scales, either generally or when applied to specific brain systems and phenomena. However, in order to minimize approximations and make realistic predictions in complex situations, numerical simulations are usually necessary. The purpose of this paper is to present a neural field software package, NFTsim, that can simulate scales from a few tenths of a millimeter and a few milliseconds upward, thereby making contact with experiments [1–6] and other classes of simulations over this range [7, 8].
No one type of brain model is optimal at all scales. For example, single neuron models abound in neuroscience, and can include a large number of biophysical effects with relatively few approximations. Many such models have also been used to study networks of interconnected neurons with varying degrees of idealization, thereby revealing a huge number of insights [9–11]. However, several key problems arise as network size grows: (i) the computational resources required become prohibitive, meaning that simulations can often only be carried out in physiologically unrealistic scenarios, typically with idealized neurons, which may be quantitatively and/or qualitatively inappropriate for the real brain; (ii) it is increasingly difficult to measure and assign biophysical parameters to the individual neurons—e.g., individual connectivities, synaptic strengths, or morphological features, so large groups of neurons are typically assigned identical parameters, thereby partly removing the specificity of such simulations; (iii) analysis and interpretation of results, such as large collections of timeseries of individual soma voltages, becomes increasingly difficult and demanding on storage and postprocessing; (iv) emergence of collective network-level phenomena can be difficult to recognize; (v) the scales of these simulations are well suited to relate to single-neuron measurements, and microscopic pieces of brain tissue, but are distant from those of noninvasive imaging modalities such as functional magnetic resonance imaging (fMRI), electroencephalography (EEG), and magnetoencephalography (MEG) [12–14], which detect signals that result from the aggregate activity of large numbers of neurons; and (vi), inputs from other parts of the brain are neglected, meaning that such models tend to represent isolated pieces of neural tissue.
At the level of neurons and neuronal networks [15, 16], software is abundant, including BRIAN, NEURON, GENESIS, and NeoCortical Simulator [17–22]. A detailed review of tools and implementation strategies for spiking neural network simulations can be found in [9].
At the largest scales, neural mass models average the properties of huge numbers of neurons into those of a single population, without taking account of its spatial aspects. This enables the temporal dynamics of whole neural populations to be approximated, but information on individual neurons and spatial dynamics and patterns is not tracked. This scale can be used to study whole-brain phenomena such as generalized seizures, if time delays within each mass can be neglected. This approach has been used to treat relatively coarse-grained networks of interacting cortical brain regions, each modeled as a neural mass. However, it is rare to see careful attention paid to the need for these representations to approach the continuum limit, in which the cortex is treated as a continuous sheet of neural tissue, as the size of the regions decreases [10, 23–25], thereby throwing some such discretizations into question. Of course, neural structure is not truly continuous, but its granularity is at a far finer scale than that of the discretizations just mentioned.
Above the single-neuron scale and extending to encompass the neural-mass limit as a special case, neural field approaches retain spatial information in a continuum limit in which properties such as firing rate and soma voltage are viewed as local averages over many neurons, and can vary from point to point, and as functions of time; when correctly discretized, neural mass models are a limiting case of the more general neural fields and should not be viewed as a separate category. Neural fields approximate rate-based models of single neurons from the small scale, while retaining relative timings between neural inputs and outputs. Simultaneously, they self-consistently add spatial structure that is neglected in neural mass models. Hybrid models with features of both neural fields and spiking neurons have also been developed and used to clarify the relationship between these approaches [3], or to enable single-neuron dynamics to be influenced by average neural fields [26], but we do not discuss these classes of models further here.
The issues discussed in the preceding paragraphs are closely analogous to ones that arise in other branches of physics. Specifically, no single model can cover all scales at once. Rather, a hierarchy of models is needed, from the microscale to the macroscale, each relating predictions to measurements at its operational scale. This yields tractable models that can be interpreted in terms of concepts and measurements that apply at the appropriate scales for a given phenomenon. Importantly, each model needs to be related to the ones at nearby scales, especially by making complementary predictions at overlapping scales of common applicability. By analogy, molecular dynamics approaches and statistical mechanics (akin to single neuron approaches) are widely used to track molecules at the microscopic scale, but large-scale theories like thermodynamics and fluid mechanics (akin to neural mass and neural field methods) are more useful and tractable for macroscopic phenomena, and their predictions can be more easily interpreted. At intermediate scales, nonequilibrium thermodynamics and fluctuation theory meet with statistical mechanics and molecular approaches to make complementary predictions of the same phenomena; so that consistency of the various approaches in their common domain can be established. Although molecular-level and spiking-neuron approaches are more fundamental, they are not practical at large scales, and yield results that have to be reinterpreted in terms of larger-scale observables in any case. Conversely, thermodynamic and neural-field approaches fail at spatial and temporal scales that are too short to justify the relevant averaging over a system’s microscopic constituents.
Neural field theory (NFT) incorporates multiple scales such as neurotransmitter effects, synaptodendritic dynamics at the microscale; an average of medium to long-range corticocortical axonal ranges which are essential to model dissipative wave transmission and to produce synchronous oscillations at the mesoscopic scale; and, long-range time delays at the macroscopic scale of the whole brain. Thus, NFT both provides useful macroscopic predictions and can reach down to mesoscopic scales that now overlap with those that can be simulated with neuron-level methods. This provides a range of common applicability on scales of around 1 mm, or slightly less, where complementary predictions can be made and tested—an overlap that will increase as microscopic simulations increase in scale. Equally significantly, quantitative neural field predictions can readily be made of quantities observable by EEG, MEG, fMRI, electrocorticography (ECoG), and other imaging technologies, by adding the biophysics of these signals, measurement procedures, and postprocessing [27–30]. This enables predictions of a single brain model to be tested against multiple phenomena in order to better determine the relevant physiological parameters.
As an illustration of the versatility of NFT approaches, we note that the particular NFT on which the present NFTsim software is based has been extensively applied and quantitatively tested against experiments, including EEG, evoked response potentials (ERPs), ECoG, age-related changes to the physiology of the brain, sleep and arousal dynamics, seizures, Parkinson’s disease, and other disorders, transcranial magnetic stimulation (TMS), synaptic plasticity phenomena [1, 6, 27–39]. Indeed, one of the major strengths of this NFT is its versatility: within the same framework we can express different models to study purely cortical phenomena, the corticothalamic system, basal ganglia, sleep dynamics, or the visual cortex, among an essentially unlimited number of other applications [1, 27–29, 31, 33, 35–38, 40–43]. This NFT has also been clearly linked to hybrid spiking-field approaches [3, 26], and to network and connection-matrix representations of spatial structure in the brain [44], usually obtained via fMRI.
We stress that the NFT embodied in NFTsim is not the only possibility. Other NFTs have been developed and applied by numerous authors [45–53], each of which has been applied to one or more physical situations in these and subsequent publications. This list is not exhaustive, since the present work is not intended as a review, but more examples can be found in [10, 25], and [54]. Notably, most of these NFTs can be expressed in the notation of the present paper, and can thus be simulated with the NFTsim software described below. Some of these previous neural field models leave out physical effects that are included in NFTsim, while others include additional features that remain to be incorporated in a future version of the code.
A few software packages are available to model neural masses and neural fields: [7] developed a neuroinformatics platform for large-scale brain modeling in terms of a network of linked neural masses with anatomically specified cortical geometry [54], long-range connectivity, and local short-range connectivity that approximates the continuum limit when it is Gaussian and homogeneous [24]. While the mathematical framework described in [54] allows for neural field models to be treated using realistic geometry on nonregular grids, a user-ready implementation is not currently available. Similarly, the Brain Dynamics Toolbox [55] provides tools for network-based and continuum models of brain dynamics. The most recent simulation tool for spatiotemporal neural dynamics is the Neural Field Simulator [8], which allows for study of a range of 2D neural field models on a square grid. However, this software does not allow for either the simulation of neural field models with heterogeneous parameters or with multiple populations.
To address the need for research-ready NFT simulation tools with direct application to the study of large-scale brain phenomena, this paper introduces and describes NFTsim, a software package that solves neural field equations expressed in differential form for simulating spatially extended systems containing arbitrary numbers of neural populations. The examples of dynamics provided in this work represent perturbations around a fixed point to follow what has been done in previous analytic work. However, NFTsim is not limited to the simulation of such dynamics and can produce a range of oscillatory [6, 56], chaotic [57] and bursting dynamics [58].
Neural field theory
Neural field theory (NFT) treats multiscale brain activity by averaging neural quantities such as firing rate, soma voltage, and incoming and outgoing activity over multiple neurons. The scales over which neural field models average must be sufficient to represent large numbers of neurons and spikes, but can still be small enough to resolve quite fine structure in the brain and its activity. NFTsim allows an arbitrary number p of spatially extended populations of neurons to be simulated. Each of these can be distinguished by its location (e.g., belonging to the cortex or a particular nucleus) and its neural type (e.g., pyramidal excitatory, interneuron). To model a particular system, we must specify the neural populations and the connections between them, including self-connections within a population. If we introduce position and time coordinates r and t, the main macroscopic variables that describe the activity of neural populations a and their interaction with other populations b are: the incoming, axonal spike-rate fields ϕab(r, t) arriving at population a at (r, t) from population b, the dendritic potentials Vab(r, t), the mean soma potential Va(r, t), the mean firing rate Qa(r, t), and the axonal fields ϕca(r, t) propagating to other populations c from population a. Fig 1 illustrates the interactions of these quantities: (i) synaptodendritic dynamics involving the incoming axonal fields ϕab(r, t) to yield the potentials Vab(r, t); (ii) dendritic summation and soma charging processes to yield the soma potential Va(r, t); (iii) generation of pulses Qa(r, t) at the axonal hillock, and (iv) axonal propagation of pulses ϕca(r, t) within and between neural populations [1]. The following subsections present a review of the equations describing these physiological processes, while Table 1 summarizes the quantities and symbols used in NFT and their SI units. Note that neural field models can be expressed in integrodifferential form [53]. However, in that form, there is always a convolution that is either difficult to handle analytically or numerically [8, 59]. For that reason, all the equations in this NFT [2] and NFTsim are expressed and implemented in differential form, respectively.
Fig 1. Schematic of the dynamical processes that occur within and between neural populations.
Gray circles are quantities associated with interactions between populations (i.e., a and b), while white circles are quantities associated with a population (i.e., a or b). Spike-rate fields ϕab arriving at neurons of type a from ones of type b are modulated by the synaptic dynamics, and undergo dendritic dynamics to produce postsynaptic subpotentials Vab. These contributions are linearly summed in the dendritic tree, eventually resulting in charging currents at the soma that give rise to the soma potential Va, after allowing for capacitive effects and leakage. Action potentials generated at the axonal hillock are averaged over a population of neurons. Then, when the mean soma voltage exceeds a threshold, the mean firing rate Qa of the population is obtained via a nonlinear response function. Finally, the pulses propagate away across the axonal tree and the dendrites of the receiving population c as the set of average spike-rate fields ϕca. Note that self-connections with b = a or c = a are included.
Table 1. NFT quantities and associated SI units.
| Symbol | Description | Units |
|---|---|---|
| Maximum firing rate | s−1 | |
| γab | Damping rate | s−1 |
| vab | Wave velocity | m s−1 |
| rab | Mean axonal range | m |
| θa | Mean neural firing threshold | V |
| Standard deviation of the firing threshold | V | |
| αab | Mean dendritic response decay rate | s−1 |
| βab | Mean dendritic response rise rate | s−1 |
| νab | Synaptic coupling strength | V s |
| τab | Long range time delay | s |
| ϕab | Axonal field | s−1 |
| Qa | Mean firing rate | s−1 |
| Vab | Subpotential | V |
| Va | Mean soma potential | V |
Symbols used in NFT, associated physical quantities and their SI units. Double subscripts ab mean that the target population is a and the source population is b.
Synaptodendritic dynamics and the soma potential
When spikes arrive at synapses on neurons of population a from a neural population b, they initiate neurotransmitter release and consequent synaptic dynamics, like transmembrane potential changes, followed by dendritic propagation of currents that result in soma charging and consequent modifications of the soma potential. Each of these processes involves its own dynamics and time delays and results in low pass filtering and temporal smoothing of the original spike until the soma response is spread over a time interval that is typically tens of ms, exhibiting a fast rise and an approximately exponential decay [3, 60].
If the overall synaptodendritic and soma responses are linear, which is the most common approximation in the literature [2, 31, 61], the total soma potential Va is the sum of subpotential contributions Vab, which are components of perturbation to the dendritic transmembrane potential, arriving at each type of dendritic synapse ab. The subscript a denotes the receiving population and b denotes the neural population from which the incoming spikes originate, distinguished by its source and the neurotransmitter type. The subpotentials Vab at a particular location comprise contributions from both the wave fields ϕab from other internal populations b and inputs ϕax from external populations x [62]; the external inputs are often split into a uniform mean nonspecific excitation and a specific excitation due to structured stimuli. Thus we write the total mean cell body potential as the sum of postsynaptic subpotentials
| (1) |
where the subscript b distinguishes the different combinations of afferent neural type and synaptic receptor and all the potentials are measured relative to resting [2].
The overall effect of synaptodendritic dynamics and soma charging in response to an incoming weighted pulse-rate field ϕab are well described by an impulse response kernel Lab(t − t′)
| (2) |
| (3) |
where ϕab is the average rate of spikes arriving at a from population b; the time delay τab is nonzero when a and b are in anatomical structures that are separated by a nonzero distance [2]. In Eq (3), Nab is the mean number of connections of mean time-integrated synaptic strength sab to a cell of type a from cells of type b. In [2], Lab is a nonnegative response kernel with
| (4) |
and Lab(r, u) = 0 for u < 0 to express causality. Note that τab are not the only time delays in the system. Propagation delays within a single structure, such as the cortex, are handled by accounting for axonal propagation, as described in section Propagation of axonal pulse-rate fields. In NFTsim Lab(r, t) is defined as
| (5) |
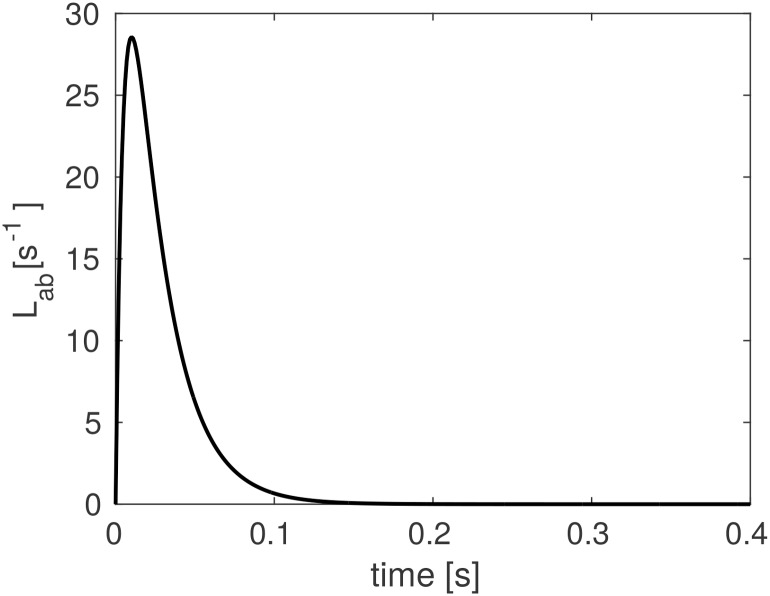
for t ≥ 0, with Lab(r, t) = 0 for t < 0 and the r-dependence of the positive constants α and β has been omitted for compactness. These quantities parametrize the decay rate and rise rate of the soma response, respectively, and β ≥ α is assumed without loss of generality. The temporal profile of the dendritic response function is illustrated in Fig 2. This function peaks at t = ln(β/α)/(β − α) for α ≠ β; if α = β, the peak is at t = 1/α. In addition, there are two special cases of Eq (5): (i) if either α → ∞ or β → ∞, then Lab becomes a single exponential function in which only one of the characteristic timescales dominates; and, (ii) if α = β = ∞, then the kernel reduces to the impulse Lab(r, t) = δ(r, t).
Fig 2. Dendritic response function.
The response to a delta-function input, via Lab as defined in Eq (5), for decay rate parameter αab = 45 s−1 and rise rate parameter βab = 185 s−1. This function peaks at t = ln(β/α)/(β − α) for α ≠ β.
The convolution in Eq (2) can be re-expressed as
| (6) |
where the differential operator Dab is given by
| (7) |
In some previous work [60] a special approximation has been used where αab and βab are independent of b and are thus treated as effective values, representing an average over different receptor time constants. Under this approximation Eq (6) becomes
| (8) |
All the aforementioned cases and forms of the operators (differential and integral) are implemented in NFTsim.
Generation of pulses
Pulses (i.e., spikes or action potentials) are produced at the axonal hillock when the soma potential exceeds a threshold potential θa(r, t). When we consider the mean response of a population of neurons to a mean soma potential we must bear in mind that each neuron has slightly different morphology and environment. Hence, they respond slightly differently in the same mean environment. This has the effect of blurring the firing threshold and the resulting overall population response function is widely approximated by the nonlinear form [48]
| (9) |
where θa is the mean threshold potential of population a and Sa is a function that increases monotonically from zero at large negative Va to a maximum firing rate at large positive Va, with the steepest increase concentrated around the mean threshold θa. NFTsim employs by default the nonlinear sigmoid response function
| (10) |
where is the population standard deviation of the soma voltage relative to the threshold. If the function in Eq (10) is linearized to consider small perturbations around a steady state of the system [2, 32], one finds the linear response function
| (11) |
where and are the relevant steady-state values and ρa = dQa/dVa, is the slope of the sigmoid function, evaluated at [2]. This linear population response function is also implemented in NFTsim and other functional forms can be defined as well.
Propagation of axonal pulse-rate fields
The propagation of the pulses Qb(r, t) in each population b generates an outgoing mean field ϕab that propagates via axons to the population a at other locations. In general, this propagation can depend on both the initial and final populations, and can incorporate arbitrary nonuniformities and a range of propagation velocities via propagator methods, for example [59, 63]. However, considerable theoretical and experimental work has shown that, to a good approximation, the mean field of axonal signals in a smoothly structured neural population propagates approximately as if governed by an isotropic damped wave equation [2, 47, 49, 52, 53, 64–69]. In NFTsim we implement the widely used equation
| (12) |
with
| (13) |
where γab = vab/rab is a temporal damping coefficient, rab is the spatial effective axonal range, vab is the axonal velocity [2, 53, 65–69], and ∇2 is the Laplacian operator. Eqs (12) and (13) constitute the two-dimensional generalization of the telegrapher’s equation [2, 53, 70]. More generally, γab, rab, and vab can be functions of position. If the special case of spatially uniform activity is considered, the Laplacian operator has no effect and can be omitted from (13). This special case results in the harmonic operator
| (14) |
We stress that this is not the same as using a local neural mass model because the damping parameter γab depends on spatial propagation. To obtain the neural mass limit, one also needs to set the spatial ranges rab = 0 so γab becomes infinite and
| (15) |
This yields
| (16) |
which is termed the local interaction approximation [2, 50].
The parameter rab in the propagators in Eqs (13) and (14) encompasses divergence of axons traveling to the target population a from the source population b and the extent of dendritic arborization of the target population a, and thus rab ≠ rba in general [71].
Design and implementation of NFTsim
This section presents a comprehensive description of NFTsim. The subsection General workflow gives an overview of the typical usage workflow of NFTsim. The subsection Classes and their interactions describes the main NFTsim classes, which represent the biophysical processes and quantities introduced in Neural field theory. Next, subsection Input-output illustrates with examples how to specify a model in the input configuration file to NFTsim and how to interpret the output file. In addition, subsection Numerical methods, considerations, and constraints elaborates on the numerical approaches and constraints used to correctly solve the equations of neural field models while attaining numerical accuracy and stability. Table 2 summarizes the configuration parameters relevant to these methods. Lastly, subsection Analysis and visualization presents a simple example of how to run a simulation, and analyze and visualize the results using the auxiliary Matlab module +nf. A list of the available functions in this module is presented in Table 3.
Table 2. Symbols, configuration parameters and units.
| Symbol | Parameter name in configuration file |
Units | Parameter exposure |
|---|---|---|---|
| N | Nodes | - | required |
| Nx | Longside nodes | - | optional () |
| Lx | Length | m | required |
| Δx | - | m | none (Lx/Nx) |
| Δy | - | m | none (Δx) |
| Ny | - | - | none (N/Nx) |
| Ly | - | m | none (NyΔy) |
First column: symbols used in this work to identify the parameters specified in a configuration file. Second column: parameter names used in configuration files to determine the physical size and spatial resolution of the 2D sheets for each population. The symbol - means the parameter is not specified directly in a configuration file. Third column: SI units of each parameter. Here, the symbol - means the parameter is dimensionless. Fourth column: shows whether the exposure [79] of each parameter in the configuration file is (i) required, (ii) optional (with its default value); or, (iii) not required (none). In the latter case, the parameter is derived internally in the code and we provide the equation used to calculate its value).
Table 3. Auxiliary functions available in the module +nf.
| Function | Description |
|---|---|
| extract | extracts time-series from an output structure |
| get_frequencies | returns the spatial frequencies |
| grid | reshapes output into a 3D array of shape (Lout, Nx, Ny) |
| movie | generates a movie from a 3D array produced by nf.grid |
| plot_timeseries | plots vertically spaced timeseries of specific traces and nodes |
| read | reads an output file and returns a structure |
| report | prints information about a structure |
| run | runs a simulation from a configuration file |
| spatial_spectrum | computes spatiotemporal spectrum |
| spectrum | computes temporal spectrum |
| wavelet_spectrogram | computes wavelet spectrogram using a Morlet wavelet |
First column: names of the available Matlab functions. Second column: brief descriptions of what each function does. The variable Lout is the number of time points in the output file.
The typographic conventions used in the remainder of this text are that: (i) all computer code is typeset in a typewriter font; and (ii) code snippets are framed by horizontal lines with line numbers on the left.
General workflow
A typical NFTsim workflow consists of three broad phases: configuration; simulation; and postprocessing. The first phase involves writing a configuration file that specifies the neural field model as well as other parameters required to run a simulation. This file is a human readable plain text file with the extension .conf. Once a configuration is specified the simulation can be launched by invoking the nftsim executable, either directly via a shell (bash) terminal
1 user@host$ nftsim -i <my-model.conf> -o <my-model.output>
or indirectly via the nf.run Matlab function. In the simulation phase, NFTsim reads the configuration file, specified after the flag -i, builds the objects of the specified model, runs the simulation and writes the output file, which contains the timeseries of the neural quantities requested in the configuration file. The name of the output file can be specified using the flag -o and must have the extension .output. In the absence of an output file name, NFTsim uses the input file name with the extension .output. For autogenerated output file names, the flag -t can be used to append a string to the output file name of the form _YYYY-MM-DDTHHMMSS, which follows the standard ISO 8601 [72] to represent date and time. In the postprocessing phase, the simulation results can be analyzed offline and visualized with the functions provided in the Matlab module +nf.
Code architecture
Neural field models can be decomposed into a small number of objects, that represent their various parts. Each object has intrinsic properties that, in turn, can be well represented as classes, each of which is a set of elements having common attributes different from other sets, using object oriented programming. NFTsim classes have been implemented in C++ (C++11 standard) [73, 74].
The most prominent components of neural field models are populations, synaptic connections, and propagators. Each of these components (or objects) is described by a main base class with properties specific to a group of objects. Derived classes are defined via the mechanism of class inheritance which allows for: (i) the definition of class in terms of another class; (ii) the customization of different parts of the system being modeled; and (iii) the extension of the functionalities of the library. For instance, a base class describing propagators has properties such as axonal range and axonal velocity. These properties are common to different propagators (derived classes) such as the wave propagator in Eq (13) or the harmonic propagator in Eq (14), and are inherited from the base class. However, the optimal method to solve each form of propagation may vary and thus each propagator-derived class can have its own solver. Furthermore, there are auxiliary base classes that define additional properties of the main classes described above. These auxiliary classes embody processes like dendritic dynamics, soma charging, firing response, external stimuli, and anatomical time delays.
Thanks to this modular architecture, NFTsim allows for the specification of models with (i) an arbitrary number of neural populations, of different types and with different parameter sets; (ii) different types of connections between pairs of populations; and (iii) different types of activity propagation, with or without propagation time delays between and within neural populations.
Classes and their interactions
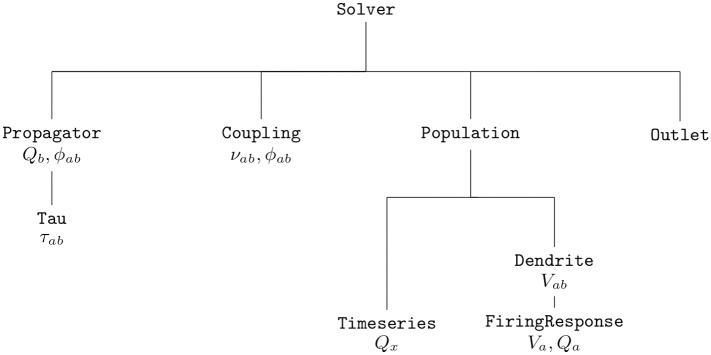
An overview of NFTsim’s calling interactions between classes, is illustrated in Fig 3. In this diagram main and auxiliary base classes are positioned so that, in a simulation, their position corresponds to being initialized and stepped forward in time from top to bottom and from left to right within each row. In the first row, we see the high-level class Solver which coordinates how the other classes interact during a simulation. In the second row, the main base class Propagator computes each of the axonal pulse-rate fields ϕab generated by the firing rate Qb. In any given neural field model there are as many Propagator objects as there are connections. These can be any of three derived Propagator classes (Wave, Harmonic, Map) implemented to accommodate the operators defined in Eqs (13), (14) or (15), respectively. The Wave class uses an explicit time stepping method based on second order central difference schemes in space and time (see Explicit difference method and boundary conditions for the 2D wave equation). The Harmonic class implements Eq (14), where for spatially homogeneous models the Laplacian term is zero and one finds a damped oscillator response. This class uses a standard fourth-order Runge-Kutta (RK4) explicit forward time stepping method with a fixed time step [75]. Lastly, the Map class, where the propagator is simply a direct mapping as in Eq (15). Below Propagator, there is the auxiliary class Tau, which handles the activity history and retrieves the appropriate delayed activity when the discrete time delay τab is nonzero. This class actually stores time delayed activity between every pair of populations, for every spatial location, and makes it available to the numerical solvers. Then, to the right of Propagator, the Coupling class handles synaptic connections and their dynamics. The base Coupling class assumes that the synaptic strengths are constant over space and time. Thus, the output signal is a product of incoming activity and synaptic weights. Other derived Coupling classes implement temporally varying synaptic strengths as in [36], or modulation by pre- or postsynaptic activity, as in [40]. To the right of Coupling, the Population class describes neural population activity and its parameters define the type.
Fig 3. Simplified diagram of NFTsim’s call graph.
The execution of a simulation is controlled by the class Solver. Initial conditions are given in terms of firing rates Qb which are then propagated to other populations via Propagator. Synaptic connections are handled via Coupling. The incoming activity to postsynaptic Population undergoes dendritic dynamics via Dendrite. The sum of individual contributions Vab and the resulting firing response are handled by FiringResponse. The class Timeseries is used to represent external inputs Qx from a stimulus Population. Lastly, the class Outlet stores the variables that are written to the output file.
In the third and fourth rows, below Population, we see that each Population uses two subsidiary classes: an array of Dendrite objects (one for every population connected via a Coupling); and, a FiringResponse. The signal from a Coupling object is passed to a corresponding Dendrite object which implements the synaptodendritic effects defined in Eq (6). The contributions Vab are then summed to yield the soma potential Va of the population. Then, the population’s FiringResponse object implements Eq (9) to calculate the resulting population firing rate Qa. Different forms of the activation function are specified within the base FiringResponse class. Other types of activation function that involve modulation of parameters due to presynaptic or postsynaptic activity are implemented in classes derived from the FiringResponse class. Such is the case of BurstingResponse that implements modulation of firing threshold θa [58]. External or stimulus populations are also objects of the Population class. However, their activity is a predefined spatiotemporal profile of firing rate Qx, that represents a chosen input and is contained in an object of the class Timeseries. In NFTsim the external inputs may include noisy and/or coherent components which may or may not be spatially localized (e.g., afferent to the visual thalamus in response to a visual stimulus). Currently, NFTsim supports a number of different external driving signals (ϕax) to stimulate any population a of a system. These signals include: a constant value equivalent to applying DC voltage; sine waves; square pulse trains; and, Gaussian white noise to simulate random perturbations. These basic functions can be combined additively to generate more complex stimulation signals.
Lastly, to the right of Population, the class Outlet, stores the variables that are written to the output file.
In summary, a compact representation of the neural field equations with the label of the associated NFTsim classes is
| (17) |
| (18) |
| (19) |
| (20) |
where the auxiliary variable Pab in Eq (18) is only defined inside the Coupling class and assigned the presynaptic inputs weighted by the local synaptic coupling strength. Fig 4, which is analogous to the diagram presented in Fig 1, illustrates the input and output variables of each class and the direction in which they flow within a simulation.
Fig 4. NFTsim classes associated with biophysical processes.
This diagram illustrates the relationship of the classes in the library and the biophysical transformations they represent. Input variables are on the left, while output variables are on the right. Gray boxes are classes associated with interactions between populations, while white boxes are classes associated with internal mechanisms of a population.
Input-output
The main routine of NFTsim takes a plain text configuration file as input, where all the model description and simulation parameters are specified, and writes the simulation result to an output file. Both the configuration file and output file are plain text files, so launching simulations and reading the results with other programming languages is also possible. Note that all the parameters in the configuration and output files are specified directly in SI units without prefixes (e.g., s, s−1, V); e.g., a value of 1 mV is written as 1e-3 (where V is implicit).
Configuration and output files
The following listing shows an exemplar configuration file, named e-erps.conf, which is included with other examples in the configs/ directory of NFTsim. This file specifies a neural field model with a single cortical excitatory population that receives inputs from an external population which is the source of a stimulus to the cortex. In this example, parameters were taken from [33], with the exception of the axonal propagation parameters, which are tuned to emphasize wave propagation properties (i.e., by decreasing the damping rate γab). We emphasize that this an illustrative example, and that while it emulates the scenario of evoked responses due to a stimulus (e.g. a flash of light) it does not represent any specific experiment.
The cortical population is initially in a steady state of low firing rate around 10 s−1 and is driven by two pulses applied toward the center of the grid. The first pulse occurs at t ≈ 32 ms and has a positive amplitude of s−1. The onset of the second pulse is t ≈ 60 ms and has a negative amplitude of s−1.
 |
The above file starts with a brief description of the model to be simulated. This comment is optional and can span multiple lines. In lines 4-5, global parameters for the simulation are defined: simulation duration (Time), time step size (Deltat), and the total number of nodes in the two dimensional grid (Nodes).
The aforementioned parameters are followed by the specification of a square connection matrix in lines 7-10, where the rows are the target populations and columns indicate the source populations. In this matrix, a positive integer indicates there is a connection between two populations and it also serves as an identifier of that connection. In the case presented above, there are only two nonzero connections, connection 1 to Population 1 from itself and connection 2 to Population 1 from Population 2. The couplings, dendrites and propagators are labeled by these consecutive positive integers. The two populations of this example are defined in lines 12-25. Each population in the model is specified separately, indicating its type (e.g., excitatory, inhibitory, or external), the physical size of its longest side (Length), its initial condition in terms of firing rate Q, and its type of dendritic and firing responses. The next step, in lines 27-28, is to define the type of propagation and coupling between each pair of connected populations. In line 27, the axonal propagation of the excitatory-excitatory connection follows a damped wave equation, with zero long-range time delay (Tau), characteristic spatial range of 0.2 m (Range) and a damping coefficient of 30 s-1 (gamma). Finally, at the end of the configuration file, from line 33 onwards in this example, we specify which timeseries are written to the output file.
There are three global output parameters: Node which specifies the labels of the grid nodes whose activity will be written to the output file; Start, sets the time (in seconds) from which the output timeseries will be written, and cannot be larger than the total simulation duration Time; and, Interval is the sampling interval between points in the output timeseries. The Interval should be chosen as an integer multiple of Deltat, that is, the ratio Interval/Deltat should be an integer number K, because NFTsim does not perform interpolation or averaging when users request downsampled output. The timeseries written to disk is simply a subsampled version of the original, where only every K-th sample is kept. In lines 34 and 36 we see that NFTsim has to write the firing rate (Q) of Population 2, and the axonal field phi of Propagator 1, respectively. NFTsim first writes the configuration file at the top of the output file to ensure full reproducibility of the results, then it writes a line filled with the symbol =, and finally, it writes the requested timeseries. Below we show an excerpt of the output file e-erps.output.
 |
Here, the first column is the time vector. The values are expressed in seconds. The second column is the firing rate Q of the second population at node 2000. The third column is the excitatory field of Propagator 1 from Population 1 to itself at node 2000. Line 3 provides the label of each timeseries, while line 4 shows the node index.
Numerical methods, considerations, and constraints
This section focuses on considerations and constraints regarding the numerical methods implemented in NFTsim. In Initial conditions. we give a general overview and strategies to set initial conditions for neural field simulations. Furthermore, Discretization of the spatial domain. and Courant condition. describe the way space is discretized in NFTsim and the maximum grid ratio for correctly solving the 2D damped wave equation, respectively. In Explicit difference method and boundary conditions for the 2D wave equation we explain the stepping method used to solve the wave equation on a finite grid. Lastly, in Time delays, we briefly explain how time delays are handled in NFTsim.
Initial conditions
Neural field equations are partial delay differential equations (PDDEs), thus at the start of a simulation activity from previous times is required for initialization. NFTsim assumes the system is initialized at a stable fixed point and then fills a history array, which stores the past activity of the system, with the values of firing rate at equilibrium. A more detailed explanation on how time delays are handled is given in a subsequent section.
In a steady state all the temporal derivatives can be set to zero. Furthermore, NFTsim currently also assumes that the initial activity is uniform spatially, so the spatial derivatives are also set to zero. Under these assumptions, if the initial conditions are not exaclty a stable state of the system, one can expect to see transient activity until the system settles into the closest stable attractor (either a fixed point or another manifold).
In NFT, the number of stable steady-state equilibria strongly depends on the number of populations and connections between them [76], thus providing a general method to find the steady-state solutions is beyond the scope of NFTsim’s functionality.
Nevertheless, there are four main strategies that users may adopt to set initial conditions:
-
(i)
Finding the steady-state solutions analytically. This method is successful for simple neural field models with a couple to a few populations such as a purely cortical model [32], and that do not include a nonlinearity in their firing response.
-
(ii)
Finding steady-state solutions numerically. If one uses the NFT equations which include a nonlinear firing response, then the steady-state equation is a transcendental function of either firing rate or voltage, and its roots cannot be calculated analytically. Fixed points can be identified by evaluating the steady state equation of the system between consecutive test values of one of the fields or voltages (e.g., or , and detecting the zero crossings. This is the method that has been used extensively to find the roots of the corticothalamic model for different parameter ranges [6, 29, 30, 39, 76]. A standard root finding algorithm (e.g., Newton-Raphson) can then be used to refine the roots. If the steady-state equation of the neural field model depends on more than one variable [56] then a root finding algorithm like Broyden’s method is required. Note that the strategy described here does not identify the stability of the fixed points.
-
(iii)
Running auxiliary simulations. This approach is best suited for scenarios in which one already has an initial estimate of the initial stable state of the system; and for nonuniform situations [77, 78], in which case the auxiliary simulations are run for the uniform case and the nonuniformities in the parameters are introduced in the main simulations. Auxiliary simulations should be long enough to give the system enough time to reach a stable state. The end state of this auxiliary simulation can then be used to provide the initial conditions for other simulations.
-
(iv)
Using Monte Carlo methods to run numerous simulations in NFTsim with randomly sampled initial conditions in order to find the stable states. This approach is more general than the previous one and does not require any a priori knowledge of the initial conditions. This approach is best suited for neural field models with several populations and for which finding the steady states of the system following (i) or (ii) is not possible or is too cumbersome. If multiple stable steady states are found [47, 76], users must decide which one is to be used for the main simulations. In NFT, the linearly stable fixed point that represents the lowest firing rates is usually selected as the initial condition on the basis that represents a normal brain state [2, 29].
Discretization of the spatial domain
Each population is modeled as a 2D rectangular sheet. In NFTsim, the physical spatial domain of each population, whatever its extent, is divided into a finite number N of uniform grid cells (or nodes), which remain invariant throughout the simulations for all times. Note that in this work grid cells refer to smallest surface area units used to discretize a continuous and spatially extended domain such as the cortex, and not to the homonymous biological cells in the enthorinal cortex.
In a configuration file, the parameter Length corresponds to the physical length of the x-axis. By default, the domains are assumed to be square with Lx = Ly. In this case, the value of the parameter Nodes must be a perfect square so that the spatial resolutions
| (21) |
and
| (22) |
are the same.
To define a rectangular domain, in addition to the parameter Nodes (N), in the configuration file one can specify the number of nodes along the x-axis via the parameter Longside nodes (Nx). In this case, the number of nodes along the x and y axes are different, but the spacing remains the same for both axes (i.e., Δx = Δy)
| (23) |
The number of nodes and physical length of the y-axis can be obtained as Ny = N/Nx and Ly = NyΔy, respectively. Table 2 summarizes the symbols and configuration length and size parameters used in this section and in the remainder of the text.
As an example, we show part of a configuration file for a neural field model with two populations. The physical length of the first population is larger than the length of second population .
 |
In the above file the two internal populations are modeled as rectangular grids with a total of 12 nodes or grid cells, and with the number of nodes of the longest side specified by Longside nodes. The resulting 2D grid has a size of 4× 3 nodes as shown in the schematic of Fig 5. For illustrative purposes, the parameter values used in this configuration file have been exaggerated so the link between the input parameters and the discretization of the space shown in the schematic is clear. However, this configuration file will not produce accurate results because the spatial resolution is too coarse.
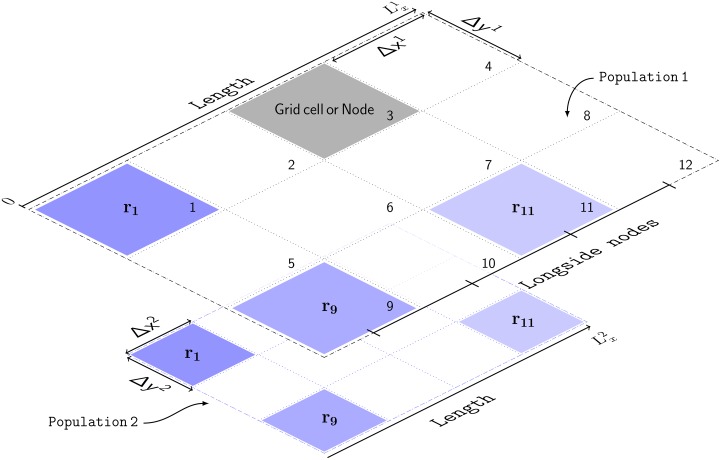
Fig 5. Schematic of the discretized spatial domain.
The model has two populations: Population 1 and Population 2. Geometrically, each population is represented by a grid of 12 nodes, which are labeled with integers. The grid is rectangular with dimensions 4 × 3 nodes. The number of nodes of the longest side is specified by Longside nodes. The physical size, Lx, of each population is different. Thus, each node in Population 1 has a linear size of Δx1, and of Δx2 in Population 2. Each spatial point (e.g., r1, r9, r11) is at the center of a grid cell. The subscript denotes the node index on this grid. Also, rn denotes the actual position in the largest population; in the smallest population rn denotes a rescaled physical dimension. Lastly, the borders of the grid are depicted with dashed lines to denote periodic boundary conditions (PBCs), which represent structures with planar geometry and toroidal topology.
Fig 5 illustrates that NFTsim populations are linked via a primary topographic one-to-one map, which implies that all the populations must have the same number of grid points N, even if they have different physical spatial dimensions. We assign the same map coordinate rn to homologous grid cells in different populations. In this example, r1 is assumed to be the actual physical position in Population 1, but in Population 2, r1 denotes a rescaled physical dimension. Also, any physical position rn, for n = 1, …, N is assumed to be at the center of a grid cell, which is also labeled with integers n = 1, …, N. For instance, in Population 1, r1 corresponds to position (Δx1/2, Δy1/2) = (0.1, 0.1) m; and, in Population 2, r1 corresponds to position (Δx2/2, Δy2/2) = (0.01, 0.01) m.
Courant condition
The interval Δx is used to evaluate whether the current parameters satisfy the Courant condition, a necessary condition for obtaining stable solutions when solving hyperbolic partial differential equations on a regular discrete grid. For the wave equation in 1D the dimensionless number
| (24) |
is called the Courant number [80]; Δt is the integration time step size and vab = γab rab is the magnitude of the wave velocity. In the continuum wave equation, activity propagates at maximum speed vab and the method is stable when Δx/Δt ≥ vab. Unstable schemes arise when Δx/Δt < vab because waves propagate more than one grid spacing in a period Δt. However, for the 2D case one finds the stability criterion to be [75]
| (25) |
so, because Δx = Δy
| (26) |
| (27) |
Hence, considering all wave-type propagators, the maximum value of the Courant number pmax must satisfy
| (28) |
This condition is checked internally by NFTsim and if it is not satisfied, an error message is returned. Note that, in practice, one usually imposes a stricter condition to ensure the system has a margin of stability; e.g., in [2], the grid ratio was chosen so that pmax = 0.1.
Explicit difference method and boundary conditions for the 2D wave equation
NFTsim uses an explicit central difference method [81] to solve Eq (13), which represents axonal propagation of activity through the cortex or other structures with a significant spatial extent. Here, we present the explicit time stepping formula currently implemented to compute the next value of ϕab from past values of ϕab and Qb. The full derivation is in the Supporting Information.
Eq (13) is the inhomogeneous damped wave equation, which can be simplified by making the substitutions
| (29) |
| (30) |
We then obtain the undamped wave equation
| (31) |
Note that this simplification only works for small values of Δt because the exponential factors introduced in Eqs (29) and (30) diverge as Δt → ∞.
Then, the final time-stepping formula using an explicit central difference method for the 2D wave equation is
| (32) |
where the superscript n indexes time step; the first and second subscripts index space along the orthogonal x and y directions, respectively, except for the subscripts on γab; and p is the Courant number. In the Eq (32), the positive exponential factors introduced in Eqs (29) and (30) are cancelled out and the algorithm actually evaluates negative exponential factors e−γabΔt and e−2γabΔt.
Note that in Eq (32), only five spatial points are required: the central point m, l; its horizontal neighbors m + 1, l and m − 1, l; and, its vertical neighbors m, l + 1 and m, l − 1. This pattern is often referred to as a five-point stencil. There are alternative finite difference methods that use higher-order terms to approximate the derivatives and would require larger stencils (e.g., more neighboring points) [82]. It is usually better to increase the spatial resolution rather than the stencil complexity to obtain higher accuracy.
The finite difference scheme presented above is second-order accurate in space and time. This means that the rate at which the error between the discretized approximation and the exact continuum solution decreases to zero is . For instance, halving Δx, Δy, or Δt, subject to Eq (28) leads to a decrease of the error by a factor of four.
When solving partial differential equations on a finite spatial domain, one must specify boundary conditions for the simulations. NFTsim uses periodic boundary conditions (PBCs). This type of condition avoids boundary effects stemming from the finite size of a grid and avoids the perturbing influence of an artificial boundary like a reflective wall. In PBCs, opposite boundaries are treated as if they were physically connected, that is, the top of the grid is wrapped on to the bottom and the left of the grid on to the right.
The class Stencil has two main functions: (i) retrieving the five-point stencil pattern for every node in the grid; and, (ii) correctly copying the activity close to the boundaries of the domain at every time step to implement periodicity. To achieve this, Stencil operates on a grid of size (Nx + 2) × (Ny + 2). The additional ghost cells are used to store copies of the top and bottom rows and left and right columns of the grid.
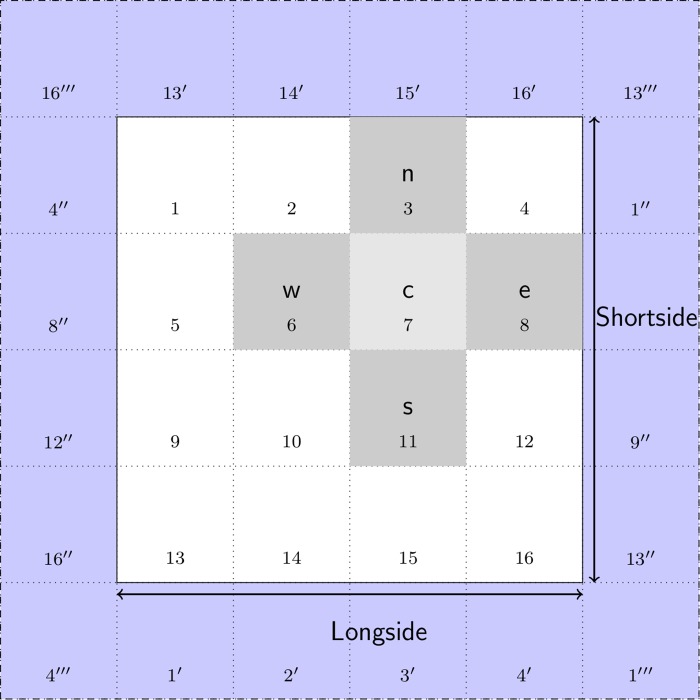
Fig 6 illustrates a 4 × 4 grid with the additional ghost cells shaded in light blue and five-point stencil pattern consisting of a central grid point c and its 4 neighbors labeled as n, s, e, w (i.e., north, south, east, west). The number in each grid cell represents its linear index—because the class Stencil accesses the elements of the two dimensional grid using a single subscript instead of two. The grid cells with prime, double-prime, and triple-prime indices are copies of the original cells with the same indices. These copies are used to implement PBCs along the vertical, horizontal, and diagonal directions, respectively. For instance, the cell 1′ is the vertical copy of cell 1; cell 1″ is the horizontal copy, and cell 1‴ is the diagonal copy. The diagonal copies are not used by the 5-point stencil, but would be used by a 9-point stencil [82].
Fig 6. Schematic of the grid used by the class Stencil.
This class retrieves the four nearest neighbors (labeled n, s, e, w) of a central point c. These five points define the pattern known as a five-point stencil. The cells in light blue are the ghost cells required to implement periodic boundary conditions. The prime, double-prime and triple prime indices represent copies of the corresponding indices in the vertical, horizontal and diagonal directions, respectively.
Time delays
For systems with time delays, NFTsim creates one history array of size N × Da per population, where N is the number of nodes as defined in previous sections. The delay depth Da of a history array is expressed as a number of integration steps.
To determine the exact value of Da, NFTsim checks every Propagator originating from a. Thus, the final delay depth for a given population a is
where P is the number of populations in the system; and, in the case that the parameter Tau represents spatially nonuniform time delays, NFTsim first selects the largest time delay over space
This produces history arrays with the minimum necessary delay depth for each population and thus is memory efficient.
Each Propagator stores an integer array with indices used to access the appropriate past activity of its origin population.
Analysis and visualization
NFTsim includes a Matlab module which provides ancillary tools to assist with running, analyzing and visualizing models. This package folder is called +nf. The available functions and a description of their functionality are summarized in Table 3.
The code snippet below uses some basic nf functions as an example of how users can interact with NFTsim directly from Matlab. The model is the same as the one specified in the configuration file e-erps.conf presented earlier, except that the timeseries of all the nodes in the grid are written to the output file. The simulation is executed via nf.run(). Once the output file is available nf.read() loads the simulated data into a Matlab structure.
Spatial patterns of activity and propagation of waves of activity across space can be visualized using the function nf.movie()
1 nf_struct = nf.run('configs/e-erps-all-nodes.conf')
2 nf.movie(nf_struct, 'Propagator.1.phi', 1)
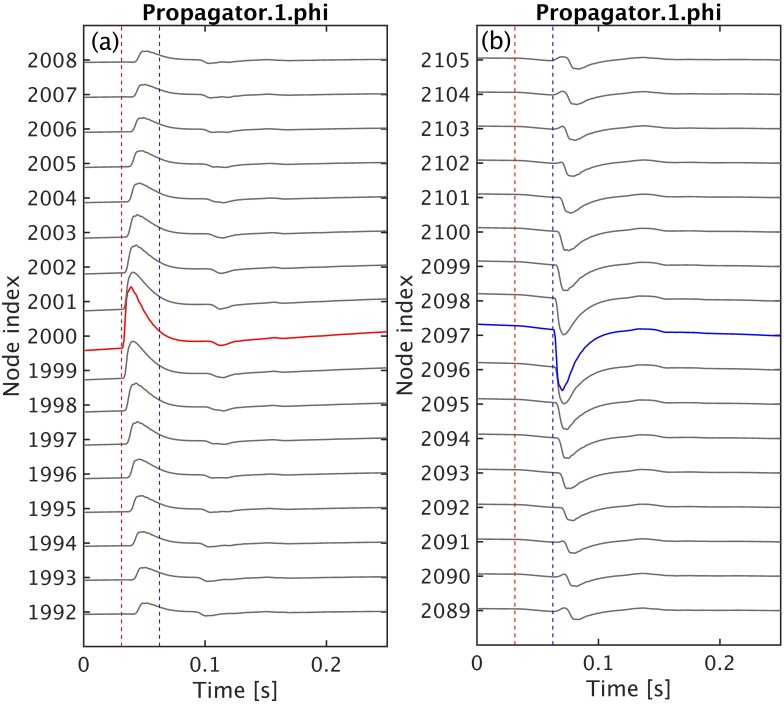
Representative frames from the movie of waves propagating from stimulation sites are shown in Fig 7(a) to 7(f). In each panel the mean spatial value of ϕee(x, y, t) at time t has been subtracted, so red and blue reflect positive and negative deviations, respectively, from the mean. The effects of PBCs can be appreciated from Fig 7(c) onwards. In particular, in Fig 7(c) the positive wave front propagating towards the left on the inset (x → 0) reappears at the right (x ≈ Lx). In a similar way, Fig 7(e), shows that the positive wavefront propagating along the y-axis results in a slight increase of the ϕee close to the boundaries.
Fig 7. Neural activity of the model described in e-erps.conf.
The cortical population is driven by two square pulses. The first pulse is positive, while the second pulse is negative. For illustrative purposes, in each panel the mean spatial value of ϕee(x, y, t) has been subtracted, so the color reflects deviations from the mean at that specific time. Each panel shows a surface plot of s−1 propagating radially outwards from the stimulation sites, and an inset with a planar view of the same quantity, at different times: (a) 42 ms; (b) 52 ms; (c) 62 ms; (d) 77 ms; (e) 86 ms; (f) 104 ms.
The file used in this example is included in NFTsim and is also available in the Supporting Information.
Furthermore, extracting and plotting the timeseries of a few nodes enable users to directly inspect the type of activity (e.g., healthy neural activity, evoked responses, or seizures). In this example, nf.extract() is used internally by nf.plot_timeseries() to select the timeseries Propagator.1.phi.
1 these_nodes = {[1992:2008],[2089:2105]};
2 these_traces = {'Propagator.1.phi', 'Propagator.1.phi'};
3 nf.plot_timeseries(nf_struct, these_traces, these_nodes, true)
Fig 8 shows the resulting plots generated with the code shown above. Each set of timeseries is centered around one of the stimulation sites. In Fig 8(a) the red curve is the axonal field at the site that received positive stimulation; and, in Fig 8(b), the blue line is the axonal field at the site that received negative inputs. The timeseries in gray above and below the colored curves are the axonal fields from neighboring sites along the x-direction. In these plots, the distance between the stimulation sites and neighboring sites increases vertically from the center to the top and bottom edges. The vertical dashed lines are not automatically produced by nf.plot_timseries, but have been added to mark the onset time of the positive (red dashed) and negative (blue dashed) inputs, respectively.
Fig 8. Timeseries of neural activity of the model described in e-erps.conf.
The cortical population is driven by two temporal square pulses applied at the center of the grid as shown in Fig 7. Here, we illustrate the timeseries of ϕee from a few nodes close to the vicinity of (gray lines) and at the stimulation sites. The vertical dashed lines mark the onset time of the positive (red dashed) and negative (blue dashed) stimulation inputs, respectively. (a) the axonal field at the site receiving the positive stimulus is highlighted in red while the time evolution of the same axonal field at neighbouring locations is shown as gray lines. (b) the axonal field at the site receiving the negative input is highlighted in blue.
Another important step is the calculation of the temporal power spectrum for a range of frequencies (in Hz), which is often compared to the power spectrum of experimental data. The power spectrum may also include multiple spatial modes for a range wave numbers (in m−1) and incorporate volume conduction or hemodynamic effects [83, 84] on measurement. A comparison between the linear analytic power spectrum and the numerical nonlinear power spectrum calculated with nf.spatial_spectrum() is given as an example in Standard tests and reproducibility.
Results and applications
In this section we first present four exemplar systems that can be simulated using NFTsim and that have been previously studied in detail. Then, section Observables and diagnostics briefly discusses the main observables that can be currently computed in NFTsim and how these have been used to predict a range of brain phenomena and compare to experimental results. In section Standard tests and reproducibility,, we discuss how NFTsim could be used as a validation tool for neural field models and neural field simulators. Lastly, section Benchmarks presents performance metrics and practical information for users regarding average run times, memory usage, and storage required for typical simulations based on a neural field model of the corticothalamic system [29].
Exemplar systems
The versatility of neural field theory and its concomitant implementation in NFTsim allow for the investigation of an unlimited variety of specific models and parameter sets. In this section we present a few illustrative cases, which have been thoroughly described elsewhere, along with some of their applications [1, 2, 6, 27–31, 33–39, 58]. Their respective configuration files are included in NFTsim.
The most general corticothalamic model considered here includes populations with long-, mid-, and short-range connections in the cortex, the specific and reticular nuclei in the thalamus, and external inputs. We indicate how components of this model can be successively deleted to obtain a family of models suited to simpler applications in corticothalamic and cortical systems. In what follows we label specific models according to the internal populations they include. The first system, called EMIRS, includes five different populations of neurons: cortical excitatory pyramidal (e), excitatory mid-range (m) and inhibitory (i) populations; internal thalamic reticular nucleus (r), relay specific nucleus (s), whereas the simplest case is of a system with a single excitatory population (e). There is also always at least one external population that provides inputs (often labeled either x or n). NFTsim provides a number of external input types such as sinusoids (in space and time), pulses, and Gaussian white noise. For instance, these inputs could be from excitatory neurons of the auditory pathway, which transmit signals from the cochlea to the thalamus [85]; or, they could be artificial external stimulation like Transcranial Magnetic Stimulation [38].
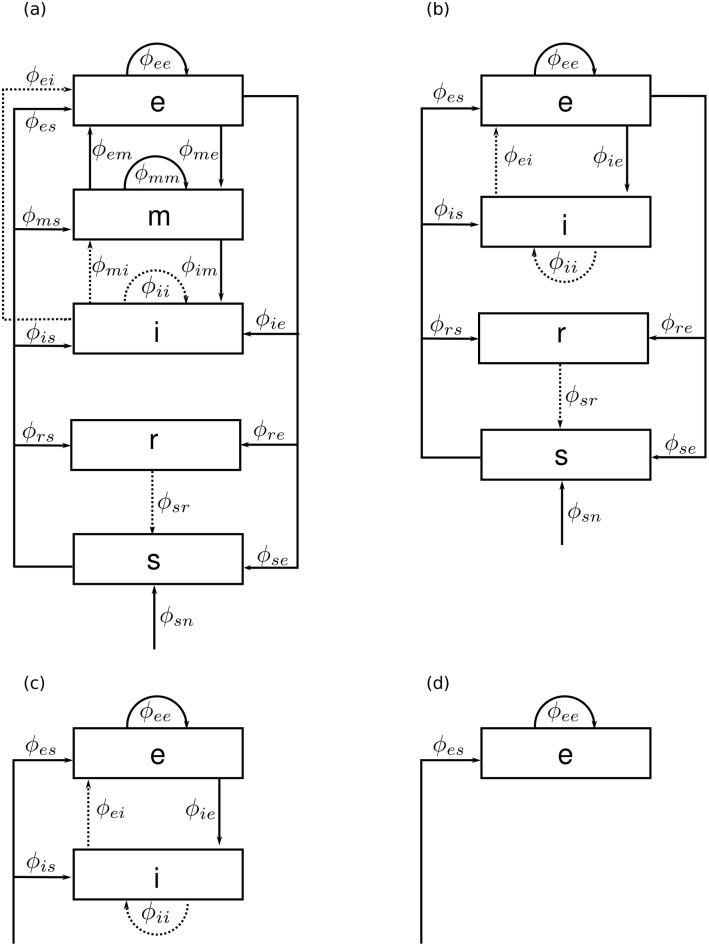
Fig 9 shows schematics of the illustrative neural field models described here. The EMIRS corticothalamic model displayed in Fig 9(a) includes three cortical populations (e, m, and i) and two thalamic populations (r and s), with intracortical, intrathalamic, and corticothalamic connections.
Fig 9. Schematic of four representative neural field models.
The quantities ϕab are the fields propagating to population a from population b. Dashed lines represent inhibitory connections. (a) Corticothalamic model including excitatory (e), mid-range (m), inhibitory (i), reticular (r), specific relay (s) and external non-specific (n) populations. (b) Corticothalamic model including excitatory (e), inhibitory (i), reticular (r), specific relay (s), and external (n) populations. (c) Cortical model comprising excitatory (e) and inhibitory (i) cortical populations plus an external input field from a subcortical population (s). (d) Purely excitatory (e) cortical model with input from a subcortical population (s).
The EIRS corticothalamic model is obtained by deleting the population m from Fig 9(a) to obtain Fig 9(b). Physically, this deletion corresponds to describing the effects of the mid- range population, whose axonal range is of the order of a few millimeters, as part of the short-range i population [1]. In this case, the excitatory effect partly cancels inhibition to give a weaker, net effect from this compound population, which includes the effects of both short-range excitatory and inhibitory interneurons. This model has been successfully applied to investigate a wide range of phenomena [31, 43, 86] (see Introduction). The model has five distinct populations of neurons: four internal and one external.
In the purely cortical EI model of Fig 9(c), thalamic dynamics are deleted and ϕes = ϕis is assumed to replace ϕsn as the external input to an isolated cortex. The basic EI model includes external inputs to two cortical populations (e and i), and both intracortical and corticocortical feedback are represented. This model is a starting point for understanding more elaborate neural fields models of the cortex (e.g., modeling distinct layers within the gray matter [35, 85]). Delays in the propagation of signals within neurons are due to synaptodendritic, soma, and axonal dynamics. However, in this model there are no long-range delays like those from the thalamus to the cortex. An extensive description and analysis of this model are given elsewhere [2, 32, 87], including emergence of gamma rhythm [86] and integration of cholinergic modulation [88]. Finally, the excitatory-only E model in Fig 9(d) omits cortical inhibitory effects. This neural field model is the simplest system we consider that can be simulated in NFTsim and has been used as the central example throughout this work.
Observables and diagnostics
Brain phenomena including the alpha rhythm [31, 34], age-related changes to the physiology of the brain [27], evoked response potentials [28, 35, 85], and seizure dynamics [1, 5, 36, 58], can be measured noninvasively via EEG. In these studies, the fields of activity of the excitatory cortical population ϕee have been used to approximate EEG signals measured from the surface of the scalp [49, 89] and constitute one of the main biophysical observables comparable to experimental EEG data.
For the reasons mentioned above, the neural activity produced by NFTsim closely resembles the electrical activity measured by EEG and ECoG up to a dimensional constant (i.e., translate units of rate (s−1) into voltages).
Another tool traditionally used to detect various waking and sleep stages [6, 29] is the EEG power spectrum [49]. In calculating scalp EEG spectra (rather than intracranial ones), one must consider filtering due to volume conduction by the cerebrospinal fluid, skull, and scalp [49, 89]. The calculation of the power spectrum including volume conduction filtering is implemented as a spatial filter in nf.spatial_spectrum. The smoothed EEG timeseries can be obtained by inverse Fourier transforming the filtered power spectrum. In the case of ECoG, the spatial filtering due to volume conduction should not be applied.
It is important to notice, though, that the neural activity of different cortical and subcortical populations can be used to predict other relevant electrical signals such as local field potentials (LFPs), and stereoencephalography (SEEG); magnetic signals such as MEG; metabolic-related signals like fMRI [90] or indirect fluorescence signals like those recorded via voltage sensitive dyes imaging (VSDI) [91]. Note that conversion of NFTsim outputs to the desired neuroimaging modality signals still requires additional modeling steps, including a description of the causal relationship and physiological couplings between the sources (i.e., the spatiotemporal fields of neural activity stemming from multiple populations) and the effective biophysical quantity measured in experiments [83, 84, 92–95].
Standard tests and reproducibility
Standard tests are a set of benchmarks used evaluate and compare disparate numerical implementations of similar neurobiological models [96]. There are very few such tests in computational neuroscience [97] and the ones currently available are only for single-cell models. To the best of the authors’ knowledge, there are no published standard tests for mesoscopic models such as neural fields. Thus, there is a huge void regarding quality assessment of scientific software for continuum models of brain dynamics.
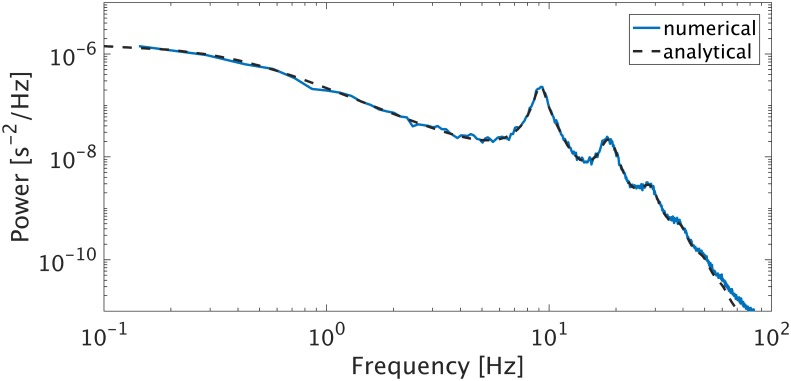
NFTsim provides a reference framework for standard tests for implementations of neural field models because its methods have been verified with analytic results; and, the linear analytic closed form solutions upon which the code is based have been extensively validated with experiments, as discussed in the Introduction. For example, in Fig 10 we reproduce the results presented in Fig. 2 from [6]. This plot shows a comparison between the linear analytic power spectrum (dashed line) and the spectrum computed from NFTsim simulations. Both spectra agree within the range of 0.1-45 Hz with a root-mean-square error of approximately 6 × 10−20. NFTsim’s default eirs-corticothalamic.conf is used with the parameters from [6], which we do not repeat here because the original configuration files are also included as part of the library package. The power spectrum is calculated using the nf.spatial_spectrum() function.
Fig 10. Comparison of analytic and numeric EEG power spectra in the corticothalamic system.
The dynamics of the EIRS model were simulated using the wake parameters from [6] for their Figure 2. The linear analytic spectrum (black dashed solid) is compared against the spectra computed from simulations (solid line).
Furthermore, the NFTsim’s methods and implementation have also been directly validated by experimental data for nonlinear dynamics, notably neural activity corresponding to seizures [36] and sleep spindles [6].
Benchmarks
NFTsim provides a tool for semi-automated benchmarking. Timing and configuration information for simulation runs are stored in a comma-separated value (csv) file that can be processed at a later stage.
Invoking the script
1 nf_benchmarks
without any arguments will run all the configuration files in the benchmarks/ directory once. We provide ten default configuration files that run in a total of under 700 s on a desktop computer. Example results for specific hardware are given below. These files are based on the corticothalamic model and are representative of typical simulation scenarios. With nf_benchmarks users can also:
-
(i)
benchmark a specific configuration file
1 nf_benchmarks <config_filename>
-
(ii)
benchmark a specific configuration file multiple times (e.g., 8 times in this example)
1 nf_benchmarks --num-trials 8 <config_filename>
-
(iii)
benchmark a specific configuration file with output written to memory instead of disk (this only works under Linux)
1 nf_benchmarks --to-mem <config_filename>
-
(iv)
benchmark a specific configuration file using a non-default compiler
1 nf_benchmarks --clang <config_filename>
In NFTsim propagating fields are followed via partial differential equations, so the main contributions to the runtime T are (i) the number of grid cells N; (ii) advancing a maximum of P2 fields, between P populations, on the N cells; (iii) the length of the simulation in integration steps L = Tsim/Δt; and, (iv) the size of the output O written to file. So,
| (33) |
where the coefficients ksim and kout depend on the hardware architecture. The output size O depends on the product of the total number of variables (W), the number of grid cells (Nout) and the total output time points [Lout = (Tsim − Tstart)/Δtout] requested in the configuration file.
For large O, the runtime is dominated by writing operations. This overhead is expected for two reasons: (i) a simulated data sample is written to disk every Δtout, which takes additional time; and, (ii) writing the output to a text file requires conversion of numbers to text. Despite the runtime overhead this last point entails, text files are a convenient format to store the output because they are easier to debug than binary files.
The required memory, M, used by a NFTsim process is dominated by the number of grid points N and the history arrays of P internal populations with delay depth Da, which is the number of integration steps for a signal to propagate to the target population from the source population. So,
| (34) |
Table 4 summarizes the simulation parameters that determine runtime and memory usage of a NFTsim process, including those which are not directly specified in a configuration file.
Table 4. NFTsim simulation and output size parameters, and runtime and memory usage symbols.
| Symbol | Description | Parameter in configuration file | Units |
|---|---|---|---|
| Tsim | Simulation length | Time | s |
| Δt | Integration time step | Deltat | s |
| L | Number of time steps | - | - |
| P | Number of populations | - | - |
| D | Delay depth | - | - |
| O | Output size | - | - |
| Nout | Number of output nodes | Node | - |
| Δtout | Output sampling period | Interval | s |
| Tstart | Output start time | Start | s |
| W | Number of output variables | - | - |
| Lout | Number of output time points | - | - |
| M | Memory used | - | byte |
| T | Runtime | - | s |
First column: symbols used in this work to identify either the parameters specified in a configuration file, or variables associated with runtime and memory usage. Second column: description of the variable or parameter. Third column: parameter names used in configuration files. The symbol - means the parameter is not specified directly in a configuration file. Fourth column: SI units. Here, the symbol - means the quantity is dimensionless.
To assess NFTsim’s performance, we select the corticothalamic model presented in earlier sections, with the parameters taken from previously published work [6] and thus considered a typical simulation use case.
The simulation length and integration time step are held constant at 16 s and Δt = 2−14 s ≈ 10−4 s, respectively. So, the only varying parameter that affects the runtime and storage is Nodes (N). The choice of this integration time step size is such that is sufficiently small to resolve high frequency oscillations and to satisfy the Courant condition for numerical stability for a range of discretization values between 3 mm < Δx < 50 mm. The Courant number ranges between 0.014 < p < 0.15 for a fixed velocity vab = 10 m s−1.
Two groups of simulations were run. The first group, Gno, runs the simulation and only writes a copy of the configuration file to the output file. The subscript no means no output. In this case the runtime represents the effective time spent executing a simulation without the time overhead due to writing operations. From Eq (33), the group Gno has kout ≈ 0. The second group of simulations Gwo consists of identical simulations to those of Gno, except that all the model variables (firing rate, voltages, fields, coupling strengths), for all the nodes, sampled at 512 Hz, are written to a file in the hard disk.
Approximate runtimes and memory usage are measured using tools available on Linux systems. The computer used for the benchmarks has Red Hat Enterprise Linux (RHEL) 6.9 as operating system, GNU Compiler collection (gcc) 4.9.2 as the default compiler, a 3.50 GHz Intel i5-4690 processor and 8GB of RAM.
Table 5 presents the benchmark results for different grid sizes and shows that the runtimes scale linearly as a function of the number of nodes with ksim ≈ 0.15 s for the simulation group Gno and and ksim ≈ kout ≈ 0.15 s for group Gwo. From these results, we conclude that in order to produce one minute worth of data sampled at a rate typically used in clinical EEG recordings, NFTsim takes about four minutes to run the simulation and write the output to disk. Thus, NFTsim’s simulation length to real-time data length ratio (Tsim/Treal) for EEG-compatible outputs is approximately 4. To reduce this ratio users can decrease the size of the output O, by writing only a few relevant variables to disk.
Table 5. Benchmarks for different grid sizes using NFTsim v.0.1.5.
| Nodes | Storage [GB] | Memory [MB] | Runtime Gno [s] | Runtime Gwo [s] |
|---|---|---|---|---|
| 144 | 1.1 | 5 | 24 | 44 |
| 256 | 1.9 | 6 | 40 | 79 |
| 1024 | 7.3 | 16 | 161 | 302 |
| 4096 | 29 | 51 | 646 | 1208 |
| 16384 | 116 | 200 | 2601 | 4908 |
The value of Nodes is reported on the first column. The second column informs the storage size of the output file with all the model variables for each node (firing rate, voltages, fields, coupling strengths) sampled at 1/Δtout = 512 Hz for the group of simulations Gwo. The third column presents the total memory usage of the process. Reported runtimes on the fourth column and fifth columns are the time elapsed in seconds. The values on the fourth column correspond to simulations with no output (no) written to the output file. The fifth column corresponds to the running times of simulations for which all the model variables for every node of the grid are written to the output file (wo). The same corticothalamic model is used in every simulation with Tsim = 16 s, and Δt = 2−14 s.
While these benchmarks offer a narrow view of NFTsim’s performance, they are a valuable practical tool for users and provide: (i) estimates of resources required to run simulations; and, (ii) a guide to make informed decisions between the execution runtimes and accuracy (i.e., decreasing the spatial resolution and/or the time step).
Conclusions, availability, and future directions
We have introduced NFTsim, a user-ready, extensible and portable suite for numerical simulations of neural activity based on neural field models expressed in differential form. NFTsim is based on the well established framework of neural field theory [2] and has been validated with both analytic solutions and experimental data. Thus, when working with new models and simulations users can use analytic solutions as a way to validate their results.
Written in C++, NFTsim has been tested on a range of Linux distributions (RHEL 6.9, RHEL 7.4, OpenSUSE 13.2, OpenSUSE 42.2). Current users have reported compatibility with OS X 10.11 and mac OS 10.12 in conjunction with the CLANG compiler, provided that the C++11 standard is supported. NFTsim has not been tested under Microsoft Windows.
The output of NFTsim is written to a plain text file and ancillary modules written in Matlab contain functions to assist in simulation execution, quick analysis and visualization of the results. NFTsim thus provides an efficient solution to simulating various continuum spatiotemporal models including spatially uniform (homogeneous) and nonuniform (inhomogeneous) neural field models [77]; systems with heterogeneous time delays between populations [34]; and, the selected format for data storage is simple enough that enables users to choose from a broad selection of tools to perform further analysis and visualization. The development of NFTsim follows essential practices of modern open-source scientific software development [97] such as:
The code is licensed under the Apache 2.0 license.
Our code sources are hosted on Github: https://github.com/BrainDynamicsUSYD/nftsim.
We use pull requests to review new features and bug fixes.
Our users can open issues reporting bugs and/or other problems they encounter.
A separate manual is provided for end-users.
Releases are tagged, so users can refer to and download continuously improved versions of the code that are considered stable and tested. For instance, for this paper, we have used v1.1.0.
Most notably, the activity from neural populations can be used to calculate biophysical signals such as LFP, ECoG, or EEG signals, the latter being the most commonly found in previous studies. Other forms of biophysical observables, such as fMRI and VSDI may also be implemented, but require additional modeling work to define how the electrical activity relates to the corresponding measurements (e.g., oxygen consumption, blood flow changes or fluorescence). Further physical effects can be implemented as a part of postprocessing modules like +nf.
Due to its flexibility and generality, NFTsim allows for a systematic study of both healthy and unhealthy brain function. For instance, in [6] the authors used simulations of a full nonlinear EIRS model for parameter values representing typical sleep spindle oscillations. They found that the numerical nonlinear power spectrum had an additional harmonic peak that was neither present in the linear EIRS model nor it was predicted by the analytic linearized power spectrum. This study clearly demonstrated that NFTsim’s flexibility allowed for the investigation of nonlinearities, introducing them one at the time in different neural populations. This enabled the authors to determine which anatomical structures and physiological mechanisms were responsible for the dynamics observed in experiments.
Due to its modularity, NFTsim is extensible and can accommodate new features presented in theoretical work on neural fields. In fact, a tool like NFTsim is essential for the study of nonlinearities and connectivities configurations that do not necessarily follow the random connectivity approximation [2, 50, 99] or are not spatially homogeneous or constant over time. For instance, [58] explored the mechanisms of seizures by incorporating slow currents modulating the bursting behavior of the reticular nucleus in the corticothalamic (EIRS) model; while [38] incorporated a model of synaptic plasticity to the purely excitatory subsystem. These two mechanisms are already implemented in the current version of NFTsim. However, further investigation and development work is required before implementing a general mechanism of parameter modulation, which would allow for the study different types and functional forms of neural feedbacks [62, 100].
We remind potential users that NFTsim, as any scientific software, should not be used blindly. As a minimal requirement, users should check that:
-
(i)
The integration time step is small enough to resolve the simulated dynamics correctly, especially if the system exhibits chaotic and bursting dynamics;
-
(ii)
The parameter Interval, which effectively subsamples the timeseries written to disk, is an integer multiple of the time step; and, is small enough so as to avoid temporal aliasing if there are signals with high-frequency content (e.g., the effective sampling frequency of the signal written to disk (1/Interval) is sufficient to respect Nyquist’s sampling theorem.
-
(iii)
The integration time step is small enough to respect the Courant conditions. If this condition is not met the code throws an error. A way to select an appropriate value of Deltat would by running the simulation with increased or decreased time steps to check for stability and convergence of the solutions to a limiting case.
-
(iv)
Setting parameters such as Deltat, Interval and Nodes as multiples or submultiples of powers of two (NFTsim’s default values), minimizes numerical errors due to the inherent limitations of representing floating point numbers on a computer. In addition, other advantages of using powers of two are (i) achieving optimal performance of FFT algorithms when applied to the output timeseries (1 second of data will have a power-of-two number of samples); and, (ii) avoiding zero-padding which is a frequent default behavior of FFT algorithms. However, users are not obliged to use NFTsim’s default values. They can select any value and simulations will be executed.
-
(v)
Artifacts of periodicity introduced by PBCs as illustrated in Fig 7 are avoided. This can be achieved by setting the grid’s area larger than that of the actual physical system under consideration. In this scenario, waves propagating from the region of interest towards the right edge of the grid would die off before being reintroduced on the left edge. This approximation would be close to the solution in the absence of artificial boundaries in which the region of interest has infinite size; or to absorbing boundary conditions (ABCs).
Note that PBCs may be preferable over absorbing BCs in scenarios when one is interested in studying wave-wave interactions. However, in neural field models that approximate a small patch of cortex such as the primary visual cortex V1, in which waves of activity propagate away from a source point of stimulation [94], then absorbing BCs would likely be more appropriate.
In the present work we have concentrated mainly on a high-level description of the software and presented examples for which model parameters are assumed to be spatially uniform. NFTsim already accepts spatial variations in many parameters, although more development work needs to be done to provide general mechanisms of parameter variation.
Note that NFTsim solves differential equations. It does not solve integrodifferential equations like those of Nichols and Hutt’s Neural Field Simulator [8]. It is important to notice that not all neural field expressed in integrodifferential form can be expressed in differential form. On the other hand, neural fields expressed in differential form can be expressed in integrodiffrential form and can be solved in NFTsim.
As mentioned in Classes and their interactions, NFTsim currently has Gaussian white noise in its collection of external driving signals because in the literature [1, 2, 4, 8, 28–31, 39, 65, 101–104] neural field models are typically either initialized or driven by a signal with a flat (white) power spectrum. These inputs correspond to the activity of other brain structures that are not explicitly modeled in the equations. In the case of the corticothalamic system, these inputs may represent background activity from the brain stem. In the case of a purely cortical model, these inputs could represent the combined activity from the thalamus and other structures. It is important to notice that external inputs with a broad white spectrum enter the NFT differential equations in exactly the same way as more coherent stimulus such as a sine wave would, as such, standard numerical methods (RK4) are employed.
However, there are several limitations that make this type of signal a poor choice. The first limitation is that idealized continuous noise is not physically realistic because it has an infinite bandwidth and infinite power. The second limitation is that in computer simulations, where continuous models are inevitably discretized, the bandwidth of a white noise signal depends on the size of the discretization. This dependence implies that if either the time step or the spatial step are reduced, the bandwidth increases and as a result a white noise signal has additional modes (i.e., frequency components). One can use a scaling parameter to adjust the overall power of the discretized driving signal [6, 81]. This scaling has no effect on the resulting spectral shape that is often compared to EEG [6]. For these reasons, it is necessary to incorporate a new type of stimuli that has a white spectrum but that is differentiable in time and space; and its spectral profile does not change under changes of the discretization.
Future work will extend NFTsim scientific features by including (i) a new bandlimited noise generation to render the inputs even more biologically realistic; (ii) generalized mechanisms of spatiotemporal variations for different model parameters and variables; (iii) generalized mechanisms of neuromodulation; (iv) absorbing boundary conditions; and, (v) spherical topology. In addition, a number of technical enhancements will be made such as (i) implement support for output binary files; and (ii) extend and automate unit test coverage to ensure that new additions to the code do not break previous functionality.
Supporting information
(PDF)
(PDF)
Acknowledgments
The authors thank B. Fulcher, M. Prodanovic, J. A. Roberts and R. G. Townsend for useful discussions and feedback.
Data Availability
All relevant data are within the paper and its Supporting Information files. In addition, all configuration files used in the paper are available from the public repository: https://github.com/BrainDynamicsUSYD/nftsim.
Funding Statement
This work was supported by an Australian Research Council (www.arc.gov.au) Laureate Fellowship (grant number FL1401000025) and the Australian Research Council Center of Excellence for Integrative Brain Function (grant number CE140100007). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Robinson PA, Rennie CJ, Rowe DL, O’Connor SC, Gordon E. Multiscale brain modelling. Phil Trans R Soc B. 2005;360(1457):1043–1050. 10.1098/rstb.2005.1638 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Robinson PA, Rennie CJ, Wright JJ. Propagation and stability of waves of electrical activity in the cortex. Phys Rev E. 1997;56:826–840. 10.1103/PhysRevE.56.826 [DOI] [Google Scholar]
- 3. Robinson PA, Kim JW. Spike, rate, field, and hybrid methods for treating neuronal dynamics and interactions. Comp Neurosci. 2012;205:283–294. [DOI] [PubMed] [Google Scholar]
- 4. Roberts JA, Robinson PA. Quantitative theory of driven nonlinear brain dynamics. Neuroimage. 2012;62(3):1947–1955. 10.1016/j.neuroimage.2012.05.054 [DOI] [PubMed] [Google Scholar]
- 5. Roberts JA, Robinson PA. Modeling absence seizure dynamics: implications for basic mechanisms and measurement of thalamocortical and corticothalamic latencies. J Theor Biol. 2008;253(1):189–201. 10.1016/j.jtbi.2008.03.005 [DOI] [PubMed] [Google Scholar]
- 6. Abeysuriya RG, Rennie CJ, Robinson PA. Prediction and verification of nonlinear sleep spindle harmonic oscillations. J Theor Biol. 2014;344:70–77. 10.1016/j.jtbi.2013.11.013 [DOI] [PubMed] [Google Scholar]
- 7. Sanz-Leon P, Knock SA, Woodman MM, Domide L, Mersmann J, McIntosh AR, et al. The Virtual Brain: A simulator of primate brain network dynamics. Front Neuroinform. 2013;7(10). 10.3389/fninf.2013.00010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Nichols EJ, Hutt A. Neural Field Simulator: Two-dimensional spatio-temporal dynamics involving finite transmission speed. Front Neuroinf. 2015;9(25). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Brette R, Rudolph M, Carnevale T, Hines M, Beeman D, Bower JM, et al. Simulation of networks of spiking neurons: A review of tools and strategies. J Comput Neurosci. 2007;23(3):349–398. 10.1007/s10827-007-0038-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Deco G, Jirsa VK, Robinson PA, Breakspear M, Friston KJ. The dynamic brain: from spiking neurons to neural masses and cortical fields. PLoS Comput Biol. 2008;4(8):e1000092 10.1371/journal.pcbi.1000092 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Wu H, Robinson PA, Kim JW. Firing responses of bursting neurons with delayed feedback. J Comput Neurosci. 2011;31(1):61–71. 10.1007/s10827-010-0302-z [DOI] [PubMed] [Google Scholar]
- 12. Hämäläinen MS, Sarvas J. Realistic conductivity geometry model of the human head for interpretation of neuromagnetic data. IEEE Trans Biomed Eng. 1989;36(2):165–171. 10.1109/10.16463 [DOI] [PubMed] [Google Scholar]
- 13. Hämäläinen MS. Magnetoencephalography: A tool for functional brain imaging. Brain Topogr. 1992;5(2):95–102. 10.1007/BF01129036 [DOI] [PubMed] [Google Scholar]
- 14. Hämäläinen MS, Hari R, Ilmoniemi RJ, Knuutila J, Lounasmaa OV. Magnetoencephalography-theory, instrumentation, and applications to noninvasive studies of the working human brain. Rev Mod Phys. 1993;65(2):413–497. 10.1103/RevModPhys.65.413 [DOI] [Google Scholar]
- 15. Gerstner W, Kistler WM. Spiking neuron models Single neurons, populations, plasticity. Cambridge: Cambridge U. Press; 2002. [Google Scholar]
- 16. Izhikevich EM. Simple model of spiking neurons. IEEE Trans Neural Netw. 2003;14(6):1569–1572. 10.1109/TNN.2003.820440 [DOI] [PubMed] [Google Scholar]
- 17. Goodman DFM, Brette R. Brian: A simulator for spiking neural networks in python. Front Neuroinform. 2008;2:5 10.3389/neuro.11.005.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Brette R, Goodman DFM. Vectorized algorithms for spiking neural network simulation. Neural Comput. 2011;23(6):1503–1535. 10.1162/NECO_a_00123 [DOI] [PubMed] [Google Scholar]
- 19. Hines ML, Davison AP, Muller E. NEURON and Python. Front Neuroinf. 2009;3(1). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Gewaltig M, Diesmann M. NEST (Neural Simulation Tool). Scholarpedia. 2007;2(4):1430 10.4249/scholarpedia.1430 [DOI] [Google Scholar]
- 21. Pecevski D, Natschläger T, Schuch K. PCSIM: A Parallel Simulation Environment for Neural Circuits Fully Integrated with Python. Front Neuroinform. 2009;3:11 10.3389/neuro.11.011.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Hoang RV, Tanna D, Jayet Bray LC, Dascalu SM, Harris FC Jr. A novel CPU/GPU simulation environment for large-scale biologically realistic neural modeling. Front Neuroinf. 2013;7:19 10.3389/fninf.2013.00019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Zalesky A, Fornito A, Harding IH, Cocchi L, Yücel M, Pantelis C, Bullmore ET. Whole-brain anatomical networks: does the choice of nodes matter? Neuroimage. 2010;5(3):970–983. 10.1016/j.neuroimage.2009.12.027 [DOI] [PubMed] [Google Scholar]
- 24. Spiegler A, Jirsa VK. Systematic approximations of neural fields through networks of neural masses in the virtual brain. Neuroimage. 2013;83C:704–725. 10.1016/j.neuroimage.2013.06.018 [DOI] [PubMed] [Google Scholar]
- 25. Breakspear M. Dynamic models of large-scale brain activity. Nature Rev Neurosci. 2017;20(3):340–352. 10.1038/nn.4497 [DOI] [PubMed] [Google Scholar]
- 26. Kerr CC, Van Albada SJ, Neymotin SA, Chadderdon GL, Robinson PA, Lytton WW. Cortical information flow in Parkinson’s disease: A composite network/field model. Front Comput Neurosci. 2013;7:39 10.3389/fncom.2013.00039 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. van Albada SJ, Kerr CC, Chiang AKI, Rennie CJ, Robinson PA. Neurophysiological changes with age probed by inverse modeling of EEG spectra. Clin Neurophysiol. 2010;121(1):21–38. 10.1016/j.clinph.2009.09.021 [DOI] [PubMed] [Google Scholar]
- 28. Rennie CJ, Robinson PA, Wright JJ. Unified neurophysical model of EEG spectra and evoked potentials. Biol Cybern. 2002;86(6):457–471. 10.1007/s00422-002-0310-9 [DOI] [PubMed] [Google Scholar]
- 29. Robinson PA, Rennie CJ, Rowe DL. Dynamics of large-scale brain activity in normal arousal states and epileptic seizures. Phys Rev E. 2002;65:041924 10.1103/PhysRevE.65.041924 [DOI] [PubMed] [Google Scholar]
- 30. Abeysuriya RG, Rennie CJ, Robinson PA, Kim JW. Experimental observation of a theoretically predicted nonlinear sleep spindle harmonic in human EEG. J Clin Neurophysiol. 2014;125(10):2016–2023. 10.1016/j.clinph.2014.01.025 [DOI] [PubMed] [Google Scholar]
- 31. Rowe DL, Robinson PA, Rennie CJ. Estimation of neurophysiological parameters from the waking EEG using a biophysical model of brain dynamics. J Theor Biol. 2004;231(3):413–433. 10.1016/j.jtbi.2004.07.004 [DOI] [PubMed] [Google Scholar]
- 32. Robinson PA, Rennie CJ, Wright JJ, Bourke PD. Steady states and global dynamics of electrical activity in the cerebral cortex. Phys Rev E. 1998;58:3557–3571. 10.1103/PhysRevE.58.3557 [DOI] [Google Scholar]
- 33. Robinson PA, Rennie CJ, Rowe DL, O’Connor SC. Estimation of multiscale neurophysiologic parameters by electroencephalographic means. Hum Brain Mapp. 2004;23(1):53–72. 10.1002/hbm.20032 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Robinson PA, Whitehouse RW, Rennie CJ. Nonuniform corticothalamic continuum model of electroencephalographic spectra with application to split-alpha peaks. Phys Rev E. 2003;68:021922 10.1103/PhysRevE.68.021922 [DOI] [PubMed] [Google Scholar]
- 35. Kerr CC, Rennie CJ, Robinson PA. Model-based analysis and quantification of age trends in auditory evoked potentials. Clin Neurophysiol. 2011;122:134–147. 10.1016/j.clinph.2010.05.030 [DOI] [PubMed] [Google Scholar]
- 36. Breakspear M, Roberts JA, Terry JR, Rodrigues S, Mahant N, Robinson PA. A unifying explanation of primary generalized seizures through nonlinear brain modeling and bifurcation analysis. Cereb Cortex. 2006;16(9):1296–1313. 10.1093/cercor/bhj072 [DOI] [PubMed] [Google Scholar]
- 37. Fung PK, Robinson PA. Neural field theory of calcium dependent plasticity with applications to transcranial magnetic stimulation. J Theor Biol. 2013;324:72–83. 10.1016/j.jtbi.2013.01.013 [DOI] [PubMed] [Google Scholar]
- 38. Fung PK, Robinson PA. Neural field theory of synaptic metaplasticity with applications to theta burst stimulation. J Theor Biol. 2014;340(7):164–176. 10.1016/j.jtbi.2013.09.021 [DOI] [PubMed] [Google Scholar]
- 39. Abeysuriya RG, Rennie CJ, Robinson PA. Physiologically based arousal state estimation and dynamics. J Neurosci Meth. 2015;253:55–69. 10.1016/j.jneumeth.2015.06.002 [DOI] [PubMed] [Google Scholar]
- 40. Fung PK, Haber AL, Robinson PA. Neural field theory of large-scale synaptic plasticity in the cerebral cortex. J Theor Biol. 2013;318:44–57. 10.1016/j.jtbi.2012.09.030 [DOI] [PubMed] [Google Scholar]
- 41. Robinson PA. Neural Field Theory of Synaptic Plasticity. J Theor Biol. 2011;285:156–163. 10.1016/j.jtbi.2011.06.023 [DOI] [PubMed] [Google Scholar]
- 42. Wilson MT, Goodwin DP, Brownjohn PW, Shemmell J, Reynolds JNJ. Numerical modelling of plasticity induced by transcranial magnetic stimulation. J Comp Neurosci. 2013;36(3):499–514. 10.1007/s10827-013-0485-1 [DOI] [PubMed] [Google Scholar]
- 43. Robinson PA, Loxley PN, O’Connor SC, Rennie CJ. Modal analysis of corticothalamic dynamics, electroencephalographic spectra, and evoked potentials. Phys Rev E. 2001;63:041909 10.1103/PhysRevE.63.041909 [DOI] [PubMed] [Google Scholar]
- 44. Robinson PA, Sarkar S, Pandejee GM, Henderson JA. Determination of effective brain connectivity from functional connectivity with application to resting state connectivities. Phys Rev E. 2014;90(1):012707 10.1103/PhysRevE.90.012707 [DOI] [PubMed] [Google Scholar]
- 45. Amari S. Homogeneous nets of neuron-like elements. Biol Cybern. 1975;17:211–220. 10.1007/BF00339367 [DOI] [PubMed] [Google Scholar]
- 46. Amari S. Dynamics of pattern formation in lateral inhibition type neural fields. Biol Cybern. 1977;27:77–87. 10.1007/BF00337259 [DOI] [PubMed] [Google Scholar]
- 47. Wilson HR, Cowan JD. A mathematical theory of the functional dynamics of cortical and thalamic nervous tissue. Kybernetik. 1973;13:55–80. 10.1007/BF00288786 [DOI] [PubMed] [Google Scholar]
- 48. Freeman WJ. Mass Action in the Nervous System. New York: Academic; 1975. [Google Scholar]
- 49. Nunez PL. Neocortical Dynamics and Human EEG Rhythms. Oxford: Oxford University Press; 1995. [Google Scholar]
- 50. Wright JJ, Liley DTJ. Dynamics of the brain at global and microscopic scales: Neural networks and the EEG. Behav Brain Sci. 1996;19:285–320. 10.1017/S0140525X00042679 [DOI] [Google Scholar]
- 51. Lopes da Silva FH, Hoeks A, Smits H, Zetterberg LH. Model of brain rhythmic activity. The alpha-rhythm of the thalamus. Kybernetik. 1974;15:27–37. 10.1007/BF00270757 [DOI] [PubMed] [Google Scholar]
- 52. Ermentrout B. Neural networks as spatio-temporal pattern-forming systems. Rep Prog Phys. 1998;61(4):353 10.1088/0034-4885/61/4/002 [DOI] [Google Scholar]
- 53. Jirsa VK, Haken H. Field Theory of Electromagnetic Brain Activity. Phys Rev Lett. 1996;77:960–963. 10.1103/PhysRevLett.77.960 [DOI] [PubMed] [Google Scholar]
- 54. Sanz-Leon P, Knock SA, Spiegler A, Jirsa VK. Mathematical framework for large-scale brain network modeling in The Virtual Brain. Neuroimage. 2015;111:385–430. 10.1016/j.neuroimage.2015.01.002 [DOI] [PubMed] [Google Scholar]
- 55. Heitmann S, Breakspear M. Handbook for the Brain Dynamics Toolbox. 1st ed Brisbane: QIMR Berghofer Medical Research Institute; 2017. [Google Scholar]
- 56. Müller EJ, van Albada SJ, Kim JW, Robinson PA. Unified neural field theory of brain dynamics underlying oscillations in Parkinson’s disease and generalized epilepsies. J Theor Biol. 2017;428:132–146. 10.1016/j.jtbi.2017.06.016 [DOI] [PubMed] [Google Scholar]
- 57. Yang DP, Robinson PA. Critical dynamics of Hopf bifurcations in the corticothalamic system: Transitions from normal arousal states to epileptic seizures. Phys Rev E. 2017;95(4):042410 10.1103/PhysRevE.95.042410 [DOI] [PubMed] [Google Scholar]
- 58. Zhao X, Robinson PA. Generalized seizures in a neural field model with bursting dynamics. J Comput Neurosci. 2015;39(2):197–216. 10.1007/s10827-015-0571-7 [DOI] [PubMed] [Google Scholar]
- 59. Bojak I, Liley DTJ. Axonal velocity distributions in neural field equations. PLoS Comput Biol. 2010;6(1):e1000653 10.1371/journal.pcbi.1000653 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Robinson PA, Rennie CJ, Rowe DL, O’Connor SC. Estimation of multiscale neurophysiologic parameters by electroencephalographic means. Hum Brain Mapp. 2004;23:53–72. 10.1002/hbm.20032 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. O’Connor SC, Robinson PA, Chiang AKI. Wave-number spectrum of electroencephalographic signals. Phys Rev E. 2002;66(6):1–12. [DOI] [PubMed] [Google Scholar]
- 62. Robinson PA, Roy N. Neural field theory of nonlinear wave-wave and wave-neuron processes. Phys Rev E. 2015;91(6-1):062719 10.1103/PhysRevE.91.062719 [DOI] [PubMed] [Google Scholar]
- 63. Roberts JA, Robinson PA. Modeling distributed axonal delays in mean-field brain dynamics. Phys Rev E. 2008;78:051901 10.1103/PhysRevE.78.051901 [DOI] [PubMed] [Google Scholar]
- 64. Nunez PL. Wavelike properties of the alpha rhythm. IEEE Trans Biomed Eng. 1974;21:473–482. 10.1109/TBME.1974.324336 [DOI] [Google Scholar]
- 65. Steyn-Ross ML, Steyn-Ross DA, Sligh JW, Liley DTJ. Theoretical electroencephalogram stationary spectrum for a white-noise-driven cortex: Evidence for a general anesthetic-induced phase transition. Phys Rev E. 1999;60:7299–7311. 10.1103/PhysRevE.60.7299 [DOI] [PubMed] [Google Scholar]
- 66. Kandel ER, Schwartz JH, Jessell TM. Principles of Neural Science. 4th ed New York: McGraw-Hill; 2000. [Google Scholar]
- 67. Rubino D, Robbins KA, Hatsopoulos NG. Propagating waves mediate information transfer in the motor cortex. Nat Neurosci. 2006;9:1549–1557. 10.1038/nn1802 [DOI] [PubMed] [Google Scholar]
- 68. Xu W, Huang X, Takagaki K, Wu JY. Compression and reflection of visually evoked cortical waves. Neuron. 2007;55:119–129. 10.1016/j.neuron.2007.06.016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69. Schiff SJ, Huang X, Wu JY. Dynamical evolution of spatiotemporal patterns in mammalian middle cortex. Phys Rev Lett. 2007;98:178102 10.1103/PhysRevLett.98.178102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70. Beurle RL. Properties of a Mass of Cells Capable of Regenerating Pulses. Phil Trans R Soc B. 1956;240:55–94. 10.1098/rstb.1956.0012 [DOI] [Google Scholar]
- 71. Robinson PA. Propagator theory of brain dynamics. Phys Rev E. 2005;72:011904-1–011904-13. 10.1103/PhysRevE.72.011904 [DOI] [PubMed] [Google Scholar]
- 72. International Organization for Standardization. ISO International Standard 8601—Date and time format. 2nd ed Geneva: ISO;2004. Available from: https://www.iso.org/iso-8601-date-and-time-format.html. [Google Scholar]
- 73. International Organization for Standardization. International Standard ISO/IEC 14882:2011—Information Technology—Programming Languages—C++. 3rd ed Geneva: ISO/IEC; 2011. Available from: https://webstore.iec.ch/publication/21240. [Google Scholar]
- 74. Meyers S. Overview of the new C++ (C++11/14). 1st ed Walnut Creek: Aritm; 2015. [Google Scholar]
- 75. Press WH, Teukolsky SA, Vetterling WT, Flannery BP. Numerical Recipes in C: The Art of Scientific Computing. 2nd ed New York: Cambridge University Press; 1992. [Google Scholar]
- 76. Sanz-Leon P, Robinson PA. Multistability in the corticothalamic system. J Theor Biol. 2017; 432:141–156 10.1016/j.jtbi.2017.07.015 [DOI] [PubMed] [Google Scholar]
- 77. O’Connor SC, Robinson PA. Spatially uniform and nonuniform analyses of electroencephalographic dynamics, with application to the topography of the alpha rhythm. Phys Rev E. 2004;70:110–119. [DOI] [PubMed] [Google Scholar]
- 78. O’Connor SC and Robinson PA. Unifying and interpreting the spectral wavenumber content of EEGs, ECoGs, and ERPs. J Theor Biol. 2004;231:386–412. [DOI] [PubMed] [Google Scholar]
- 79. List M, Ebert P, Albrecht F. Ten Simple Rules for Developing Usable Software in Computational Biology. PLoS Comput Biol. 2017;13(1):1–5. 10.1371/journal.pcbi.1005265 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80. Courant R, Friedrichs K, Lewy H. On the Partial Difference Equations of Mathematical Physics. IBM J Res Dev. 1967;11(2):215–234. 10.1147/rd.112.0215 [DOI] [Google Scholar]
- 81.Rennie C. Modeling the large-scale electrical activity of the brain. Ph.D. Thesis. The University of Sydney. 2001. Available from: http://www.brain-dynamics.net/~chris_rennie/thesis/thesis.pdf.
- 82.Hamilton B, Bilbao S. On finite difference schemes for the 3D wave equation using non-cartesian grids. In: Proceedings of Stockholm Musical Acoustics Conference/Sound and Music Computing Conference; 2013. pp.592–599.
- 83. Drysdale PM, Huber JP, Robinson PA, Aquino KM. Spatiotemporal BOLD dynamics from a poroelastic hemodynamic model. J Theor Biol. 2010;265:524–534. 10.1016/j.jtbi.2010.05.026 [DOI] [PubMed] [Google Scholar]
- 84. Aquino KM, Schira MM, Robinson PA, Drysdale PM, Breakspear M. Hemodynamic traveling waves in human visual cortex. PLoS Comput Biol. 2012;8(3):e1002435 10.1371/journal.pcbi.1002435 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85. Kerr CC, Rennie CJ, Robinson PA. Physiology-based modeling of cortical auditory evoked potentials. Biol Cybern. 2008;98(2):171–184. 10.1007/s00422-007-0201-1 [DOI] [PubMed] [Google Scholar]
- 86. Rennie CJ, Wright JJ, Robinson PA. Mechanisms of cortical electrical activity and emergence of gamma rhythm. J Theor Biol. 2000;205:17–35. 10.1006/jtbi.2000.2040 [DOI] [PubMed] [Google Scholar]
- 87. Rennie CJ, Robinson PA, Wright JJ. Effects of local feedback on dispersion of electrical waves in the cerebral cortex. Phys Rev E. 1999;59:3320–3329. 10.1103/PhysRevE.59.3320 [DOI] [Google Scholar]
- 88. Clearwater JM, Rennie CJ, Robinson PA. Mean field model of acetylcholine mediated dynamics in the thalamocortical system. J Theor Biol. 2008;255:287–298. 10.1016/j.jtbi.2008.08.010 [DOI] [PubMed] [Google Scholar]
- 89. Srinivasan R, Nunez PL, Silberstein RB. Spatial Filtering and Neocortical Dynamics: Estimates of EEG coherence. IEEE Trans Biomed Eng. 1998;45(7):814–826. 10.1109/10.686789 [DOI] [PubMed] [Google Scholar]
- 90. Ogawa S, Lee TM. Magnetic resonance imaging of blood vessels at high fields: in vivo and in vitro measurements and image simulation. Magn Reson Med. 1990;16(1):9–18. 10.1002/mrm.1910160103 [DOI] [PubMed] [Google Scholar]
- 91. Grinvald A, Hildesheim R. VSDI: A new era in functional imaging of cortical dynamics. Nat Rev Neurosci. 2004;5(11):874–875. 10.1038/nrn1536 [DOI] [PubMed] [Google Scholar]
- 92. Chemla S, Chavane F. A biophysical cortical column model to study the multi-component origin of the VSDI signal. NeuroImage. 2010;53(2):420–438. 10.1016/j.neuroimage.2010.06.026 [DOI] [PubMed] [Google Scholar]
- 93. Erhardt EB, Allen EA, Yonghua W, Eichele T. StimTB, a simulation toolbox for fMRI data under a model of spatiotemporal separability. NeuroImage. 2010;59(4):4160–4167. 10.1016/j.neuroimage.2011.11.088 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94. Rankin J, Chavane F. Neural field model to reconcile structure with function in primary visual cortex. PLoS Comput Biol. 2017;13(10):1–30. 10.1371/journal.pcbi.1005821 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95. Friston KJ, Mechelli A, Turner R, Price CJ. Nonlinear responses in fMRI: The Balloon model, Volterra kernels, and other hemodynamics. NeuroImage. 2000;12(4):466–477. 10.1006/nimg.2000.0630 [DOI] [PubMed] [Google Scholar]
- 96. Bhalla US, Bilitch DH, Bower JM. Rallpacks: A set of benchmarks for neuronal simulators. In: Computation and Neural Systems; 1993. pp. 133–140. 10.1007/978-1-4615-3254-5_21 [DOI] [PubMed] [Google Scholar]
- 97. Gewaltig MO, Cannon R. Current practice in software development for computational neuroscience and how to improve it. PLoS Comput Biol. 2014;10(1):e1003376 10.1371/journal.pcbi.1003376 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.van Heesch, Dimitri. Doxygen Qt-interest Archive. 1997. Available from: http://www.stack.nl/~dimitri/doxygen/.
- 99. Braitenberg V, Schüz A. In:. Springer, Berlin, Heidelberg Cortex: Statistics and Geometry of Neuronal Connectivity. Berlin: Springer; 1998. [Google Scholar]
- 100. Roy N, Sanz-Leon P, Robinson PA. Spectral signatures of local neural feedback in the corticothalamic system. Phys Rev E. 2017. October 26:Forthcoming. 10.1103/PhysRevE.96.052310 [DOI] [PubMed] [Google Scholar]
- 101. Kilpatrick ZP, Ermentrout B. Wandering bumps in stochastic neural fields. SIAM J Appl Dyn Syst. 2013;12:61–94. 10.1137/120877106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102. Faugeras O, Inglis J. Stochastic neural field equations: a rigorous footing. J Math Biol. 2015;71:259–300. 10.1007/s00285-014-0807-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103. Thul R, Coombes S, Laing CR. Neural Field Models with Threshold Noise J Math Neurosci. 2016;6(1). 10.1186/s13408-016-0035-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104. Bressloff PC, Webber MA. Front propagation in stochastic neural fields. SIAM J Appl Dyn Syst. 2012;11(2):708–740. 10.1137/110851031 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(PDF)
(PDF)
Data Availability Statement
All relevant data are within the paper and its Supporting Information files. In addition, all configuration files used in the paper are available from the public repository: https://github.com/BrainDynamicsUSYD/nftsim.