Auto-contouring via Automatic Anatomy Recognition of Organs at Risk in Head and Neck Cancer on CT images

Abstract

Contouring of the organs at risk is a vital part of routine radiation therapy planning. For the head and neck (H&N) region, this is more challenging due to the complexity of anatomy, the presence of streak artifacts, and the variations of object appearance. In this paper, we describe the latest advances in our Automatic Anatomy Recognition (AAR) approach, which aims to automatically contour multiple objects in the head and neck region on planning CT images. Our method has three major steps: model building, object recognition, and object delineation. First, the better-quality images from our cohort of H&N CT studies are used to build fuzzy models and find the optimal hierarchy for arranging objects based on the relationship between objects. Then, the object recognition step exploits the rich prior anatomic information encoded in the hierarchy to derive the location and pose for each object, which leads to generalizable and robust methods and mitigation of object localization challenges. Finally, the delineation algorithms employ local features to contour the boundary based on object recognition results. We make several improvements within the AAR framework, including finding recognition-error-driven optimal hierarchy, modeling boundary relationships, combining texture and intensity, and evaluating object quality. Experiments were conducted on the largest ensemble of clinical data sets reported to date, including 216 planning CT studies and over 2,600 object samples. The preliminary results show that on data sets with minimal (<4 slices) streak artifacts and other deviations, overall recognition accuracy reaches 2 voxels, with overall delineation Dice coefficient close to 0.8 and Hausdorff Distance within 1 voxel.

1. INTRODUCTION

Planning radiation therapy (RT) for the treatment of head and neck (H&N) cancer requires precise delineation of the organs at risk (OARs) in this body region on planning computed tomography (CT) images. In clinical practice, this delineation is done mostly manually by dosimetrists and radiation oncologists, which is time-consuming and suffers from intra- and inter- observer variations as well as protocol variability [1] from center to center. As an alternative, auto-contouring is a useful tool that could bring substantial time reduction even if post hoc manual editing is required [2].

Various auto-contouring methods have been proposed for the H&N OARs. Atlas-based methods seem to be quite popular in this application due to their robustness and requirement of small training samples [3–4]. Recent research using neural networks shows promising accuracy with longer training time [5] and often much larger training sample sizes. In this paper, a different method is proposed that inspects the geographic relationship among objects to locate each object, followed by a low-level process to contour the boundaries. This research is an extension of our Automatic Anatomy Recognition (AAR) framework [6], which has been successfully applied to different modalities and body regions. In this adaptation of AAR to H&N CT images, we made several improvements to the basic methodology itself: 1) A data-driven optimal hierarchy algorithm directly formulated to reduce recognition error is employed instead of the previous one defined by prior knowledge; 2) The boundary information is incorporated to refine recognized location; 3) Texture information combined with intensity information is utilized in the recognition and delineation processes; And 4) A voxel-classification approach is proposed for delineation and finally an optimal boundary fit from the fuzzy model is performed to output the final delineation.

2. METHODS

Object Definition, Data Collection, and Quality Evaluation

This retrospective study was conducted following approval from the Institutional Review Board at the Hospital of the University of Pennsylvania along with a Health Insurance Portability and Accountability Act (HIPAA) waiver. We analyzed image and contour data sets for 216 H&N cancer patients from the Department of Radiation Oncology, University of Pennsylvania. The voxel size ranges from 0.93×0.93×1.5 mm³ to 1.6×1.6×3 mm³. The contour data for the cases were previously created by the dosimetrists in the process of routine RT planning of these patients. Following published guidelines [1, 7] for H&N anatomic object definitions, we formulated detailed and precise computational definitions for specifying each object and for delineating its boundaries on axial CT slices and mended the contours to fit these strict definitions as much as possible.

Image quality typically attained in a body region plays an important role in the performance of any auto-contouring method. To investigate its influence on the performance, we developed a method [9] to derive an object quality score (OQS) to the image appearance of each object in each image and an image quality score (IQS) for each image based on a set of 9 criteria: neck posture deviation, mouth position, other types of body posture deviations, image noise, beam hardening (streak) artifacts, shape distortion, presence of pathology, object intensity deviation, and object contrast. Based on the quality scores, we found that about 17% (36 cases - 20 male and 16 female) of the cases are model worthy (meaning that these studies had contours for all OARs considered and the OARs were all near normal with good quality) within the cohort of 216 cases gathered, which are then used for building the AAR fuzzy models. Object samples derived from 5 of these data sets are shown in Figure 1. Streak artifacts arising from tooth fillings are ubiquitous in H&N CT images, which pose the greatest challenge to auto-contouring methods in H&N. Object samples were divided into good-quality and poor-quality groups, where objects in the “good” groups had OQS in the upper end of the score scale and did not have more than 3 slices containing streak artifacts or other major deviations.

Figure 1.

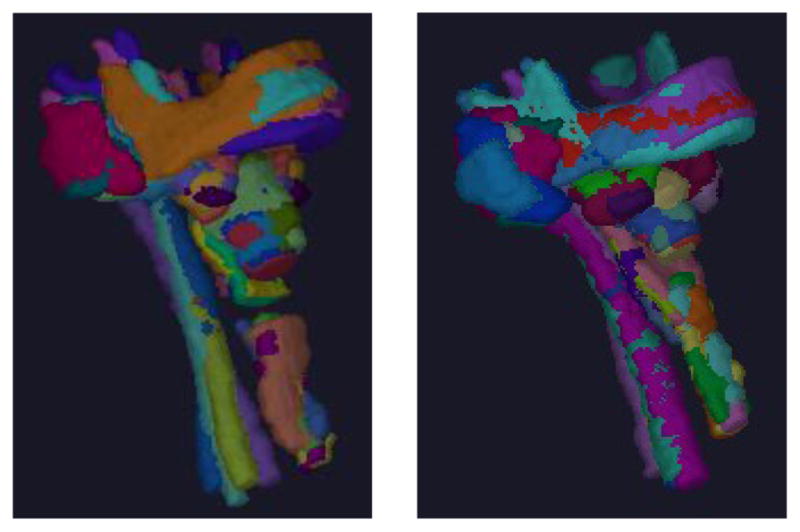
An illustration of five object samples from 5 model-worthy data sets for each of 9 objects: Male (left), Female (right). Different colors indicate 45 different object samples in each panel.

Building Population Fuzzy Anatomy Models

In our research, the anatomic objects (i.e., OARs) considered were: skin outer boundary (SB), left and right parotid glands (LPG, RPG), left and right submandibular glands (LSG, RSG), cervical esophagus (ES), supraglottic and glottic larynx (LX), cervical spinal canal (SC), mandible (MD), and orohypopharynx constrictor muscle (OHP). We further subdivided object SB into an inferior portion below the neck (SBi) and a superior portion (SBs) in the neck. The reason was that SBs has far less subject-to-subject variation than SBi due to the different extent to which the upper extremities were included/excluded in different subjects in their CT images.

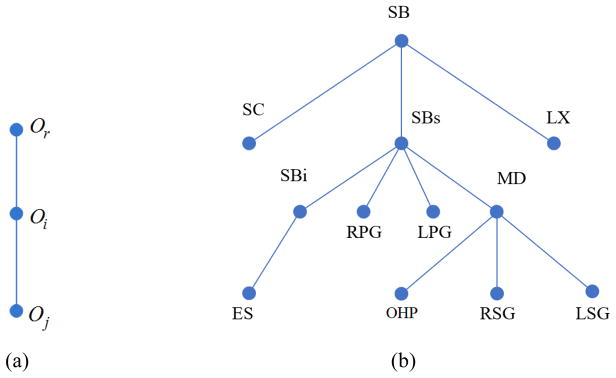
The Fuzzy Anatomy Model of the H&N body region B for a group G, FAM(B, G) = (H, M, ρ, γ, η) was then built from the binary and gray images following mostly the methodology in [6] except for changes as described below. Note that H denotes a hierarchical arrangement of the objects; M is a set of fuzzy models with one model for each object; ρ represents the parent to offspring spatial relationship; γ is a set of scale ranges; and η includes a host of parameters representing object properties such as the range of variation of size, image intensity, etc. of each object. We created two anatomy models FAM(B, G_M) and FAM(B, G_F) for the male and female group, respectively, by using the model-worthy data sets mentioned above. The tree structure for H is determined by finding an optimal hierarchy using a novel strategy which is more advanced than the one described in [6]. In this strategy, we first run recognition for each pair of objects, e.g., object O_i and object O_j in the target OARs, following a mini hierarchy as shown in Figure 2(a). Then the corresponding location error LE_i(O_j) of the recognized O_j from its ground-truth is calculated as its cost c_ij from parent O_i, which is arranged as the corresponding element in the cost matrix C_n for all the n objects. We set SB as the root object O_r for initial recognition. If we regard the cost matrix C_n as a weighted complete connected graph with n nodes where every node is connected to every other node, then the optimal hierarchy arrangement Ĥ can be derived by calculating the optimal spanning tree with SB as the starting point:

$$\widehat{H}=arg{min}_H(\sum _{i=1}^n\sum _{j=1}^{n_i}L{E}_i(O_j))$$ (1)

where n_i is the number of children for the object O_i in H. The optimal hierarchy Ĥ ensures the minimum global cost when each object is recognized by this order. The derived optimal hierarchy is shown in Figure 2(b). The same hierarchy is used for building the model for the female group.

Figure 2.

An illustration of the optimal hierarchy structure. (a) Mini-hierarchy for training. (b) The learned optimal hierarchy for the head and neck region.

Object recognition/localization and delineation

The object at the root of the tree H is localized first. Other objects are then recognized following the tree, making use of the parent-to-child relationship encoded in FAM(B, G). A fine-tuning around the initial location is conducted by scaling and translation of the fuzzy model M. As an improvement on [6], we combined the intensity with texture calculated by Gray-level Co-occurrence Matrix (GLCM) to derive a binary template for fine-tuning, and the recognition is finished when the false positive and false negative between the fuzzy model M and binary template are minimized. Furthermore, we added a refinement step after recognition, in which the distance between the boundaries of all objects is modeled by a Bayesian Network, and the prior knowledge from anatomy definition is adopted for initializing. When each object is recognized, the boundaries for all related objects are predicted, which is then fused with their recognized boundaries to rescale the fuzzy model. We describe some aspects of the recognition algorithm in [7].

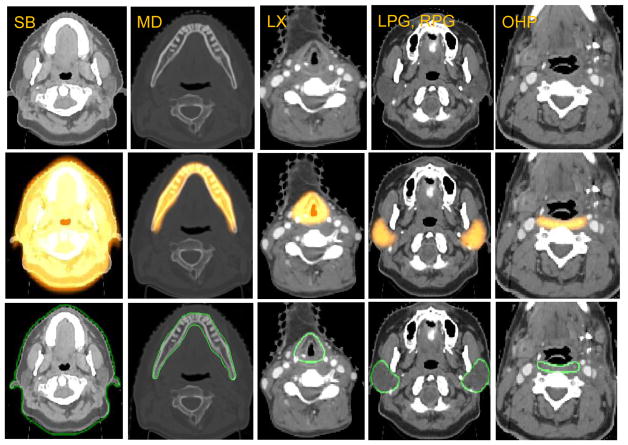
The recognition step aims to use the high-level information to overlay the fuzzy model on the object, while delineation relies on the low-level information to obtain the clear boundary proceeding from the recognition result. We use two delineation methods for different objects, which is different from [6]. For skin, we use Iterative Relative Fuzzy Connectedness (IRFC) [10]. For all other objects, we initially use a k-NN voxel-wise classifier to find the foreground voxels by the intensity and texture features, and then we fit optimally the fuzzy model to the foreground by finding the best iso-membership surface derived from the fuzzy model. Sample recognition and delineation results are demonstrated in Figure 3 for different OARs.

Figure 3.

Sample results for different objects on representative H&N CT images. Rows 1: Original CT image. Row 2: Overlay with recognition result. Rows 3: Overlay with delineation result.

3. RESULTS

As preliminary result, we demonstrate our experiment on five objects for the male group, the results are shown in Table 1. The recognition performance is evaluated by location error (LE, mm), and delineation by Dice coefficient (DC) and Hausdorff distance (HD). We conducted experiments on the good-quality and poor-quality datasets separately.

Table 1.

Location error in mm (LE) for recognition, Dice Coefficient (DC) and Hausdorff Distance (HD) for delineation in experiments E1–E4. Mean and SD values over tested samples are listed.

Object		SB	LX	LPG	RPG	MD	OHP	All
Good Image Quality	LE	4.86	3.23	4.27	4.24	4.47	3.79	4.14
		0.82	2.04	1.73	1.62	1.03	1.36	1.43
	DC	0.98	0.75	0.77	0.76	0.89	0.58	0.79
		0.01	0.04	0.05	0.06	0.03	0.04	0.04
	HD	1.81	4.47	3.25	3.23	1.61	2.57	2.82
		0.33	0.71	0.55	0.52	0.26	0.32	0.45
Poor Image Quality	LE	9.25	16.93	18.25	14.44	9.90	14.80	13.93
		3.07	8.05	10.16	5.22	2.95	7.28	6.12
	DC	0.96	0.49	0.46	0.54	0.79	0.42	0.61
		0.03	0.13	0.16	0.12	0.07	0.12	0.11
	HD	2.98	7.71	7.06	5.68	2.32	4.43	5.03
		1.33	2.59	2.96	1.71	0.55	2.02	1.86

As mentioned earlier, streak artifacts pose serious challenges to H&N object recognition and delineation. Overall, the accuracy of recognition (object localization) for good-quality groups in these experiments, is about 2 voxels, and the accuracy in delineation is close to 0.8 for Dice coefficient and around 1 voxel for Hausdorff distance. The results on poor-quality group shows that when the objects have significant artifacts, the results are much worse, around 5 voxels for recognition, 0.6 for Dice coefficient and around 2 voxels for Hausdorff distance.

We also compare our results with related research works. The statistical results will be influenced by multiple factors, such as patient group, image quality, image resolution, object definition, manual ground-truth quality, etc., so a fair comparison is hard to achieve but could still give a rough idea about the performances. We listed our results on the good-quality group for a fair comparison. In the literature we did not find mention of artifacts or even their illustration qualitatively as to how they affect results. Furthermore, the number of studies and object samples on which results are illustrated is substantially lower than the number of samples we used. Also, train-test data set division ratio used in the literature is much higher that what we have employed.

For MD, the following results are reported in literature (DC and HD are listed by range or mean value, if available): 0.86–0.94 and 1.3–3.8mm [11], 0.77–0.96 and 3.1–5.6mm [12], 0.75–0.93 and 1.8–5.6mm [13], 0.92–0.94 and 0.9–2.6mm [14], 0.9–0.96 and 1.3–2.9mm [15] and 0.89 [5]. Our proposed methods reach an average DC of 0.89 and HD of 1.6 mm on much more realistic and larger data cohort.

For LPG and RPG, reported results are: 0.74–0.84 and 3.8–8.8mm [11], 0.56–0.79 and 5–10.7mm [12], 0.73–0.88 and 3.1–8.7mm [13], 0.74–0.89 and 2.8–8.5mm [14], 0.68–0.85 and 3.2–9.4mm [15], 0.77 [5], 0.74–0.83 and 1.6–3.3mm [16], 0.65 and 4.5mm [18]. Our method got 0.74 and 3.2mm on LPG, and 0.75 and 3.2mm on LPG on much more realistic and larger data cohort.

For LX, reported results are 0.86 [5], 0.5–0.62 and 2.0–6.0mm [16], 0.73 [17]. Our results are 0.74 and 4.0mm. The definition of LX could be quite variable, regarding whether to include the central trachea region and other components. Therefore, the reported performance on different dataset is quite different. This emphasizes the importance of a consistent and standardized OAR definition.

For OHP, reported results are 0.4–0.6 and 1–1.25mm [16], 0.64 [17] and our results are 0.58 and 2.6mm. This object is very challenging due to lack of contrast with surrounding muscles. Our results are much more realistic in actual clinical setting because of larger cohort and consideration of object quality dependent variations etc.

One advantage of our method is its steadiness. Indeed, on every object the performance is above average standard in the scope of comparing references, which implies the robustness of the proposed method on the variation of different size, shape and appearance. This is mainly because of the recognition step which could overlay the fuzzy model to the object within a location error of 2 voxels. Surprisingly in many instances, even when the image/object quality is poor, recognition was accurate. However, in these instances delineation may go awry due to artifacts and misleading intensity information.

4. CONCLUSIONS

1. When data sets are nearly streak-artifact-free (<4 slices), our methods yield recognition accuracy within 2 voxels and delineation boundary distance HD around 1 voxel. This is within the variability observed among dosimetrists in manual contouring (result not shown here). Tooth fillings and dental implants cast streak artifacts that are much brighter or much darker than the actual tissue intensity on CT images and affect almost all H&N structures, which in turn seriously influence accuracy. To make an impact on H&N RT planning by way of improving contouring efficiency, productivity for handling cases, and accuracy needed for adaptive RT planning, the challenge of streak artifacts must be addressed.

2. Understanding object and image quality and how they influence performance is crucial for devising effective object recognition and delineation algorithms. This becomes eminently important for comparing methods in a meaningful manner. The recognition operation is much more robust than delineation. We often observed that even when the models were placed very close (within 2 voxels) to the actual object with strong streak artifacts, delineation failed to retain that accuracy.

3. Individual object quality expressed by OQS seems to be much more important than the overall image quality expressed by IQS in determining accuracy.