Abstract
CT is routinely used for radiotherapy planning with organs and regions of interest being segmented for diagnostic evaluation and parameter optimization. For cardiac segmentation, many methods have been proposed for left ventricular segmentation, but few for simultaneous segmentation of the entire heart. In this work, we present a convolutional neural networks (CNN)-based cardiac chamber segmentation method for 3D CT with 5 classes: left ventricle, right ventricle, left atrium, right atrium, and background. We achieved an overall accuracy of 87.2% ± 3.3% and an overall chamber accuracy of 85.6 ± 6.1%. The deep learning based segmentation method may provide an automatic tool for cardiac segmentation on CT images.
Keywords: Cardiac imaging, Image segmentation, Deep Learning, Whole heart segmentation, CT imaging, Convolutional neural networks, Heart chamber segmentation
1. INTRODUCTION
Computed tomography (CT) is routinely used for diagnosing conditions, treatment planning, and procedure guidance1-4. In the field of radiation oncology, the heart can be segmented from CT volumes when planning a radiotherapy treatment plan when the dose is applied near the heart 5. Cardiologists and surgeons use CT images for planning procedures to correct septum defects and diagnosing congenital heart disease6, 7. Precise chamber-specific segmentation can also be used to assess cardiac function using metrics such as chamber volume, ejection fraction, and myocardial mass8.
The processes of segmentation can be time consuming for a radiologist. A quick and accurate segmentation method capable of locating individual heart chambers is desirable. Other groups have segmented the four heart chambers on CT previously, but the methods required the deformation of a prior model or atlas9,10. In most cardiac cases, this would require a non-rigid deformation, which can introduce additional errors into segmentation, due to natural differences between patient anatomy 11. This is further compounded when 4D atlas-based segmentation is considered12, 13. Other methods depend on computed tomography angiography data for atlas segmentation14, 15. However, this procedure is time-consuming and exposes the patient to more radiation than a traditional CT.
A convolutional neural network (CNN) segmentation method offers a valuable alternative to atlas-based approaches. A key advantage of using a CNN is that there is no need to perform deformable registration. Many different heart sizes and conditions could be included in the training data to create the model, which removes the need for a generalized physical representation of the heart. In addition, a CNN could be easily integrated into imaging software to provide automatic estimations for measurements such as heart size and surface-to-volume ratios during CT scans. In this study, we explore how a CNN could be used to segment the four chambers of the heart using patches from 3D CT images.
2. METHODS
2.1. Data Acquisition and Processing
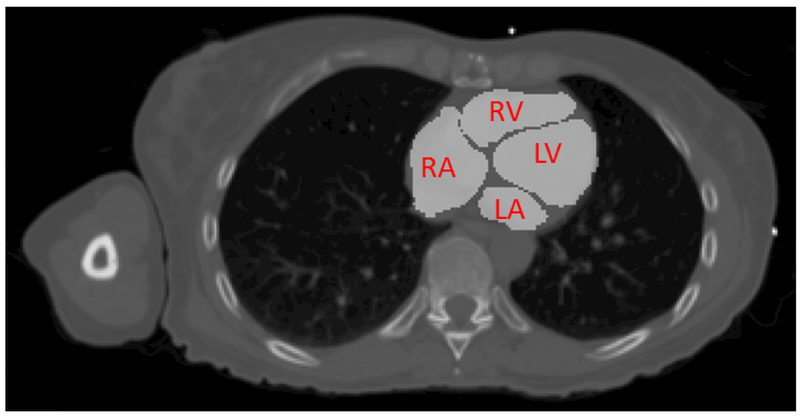
Chest CT images were acquired for 11 patients at baseline prior to radiotherapy. Each CT had a slice thickness of 2.5 mm, with the total number of slices ranging from 78 to 154. The in-plane resolution varied from 0.979 × 0.979 mm2 to 1.270 × 1.270 mm22, with an image size of 512 × 512 pixels. After imaging, an atlas was deformed to each patient heart and verified by a radiologist to create a gold standard for the left ventricle, right ventricle, left atrium, and right atrium. An example is shown in Figure 1. The CT volumes and radiologist-verified segmentations were loaded into MATLAB (MathWorks, Inc., Natick, MA, USA) to make 31 × 31 pixel patches. The patches were placed into one of five classes: left ventricle (LV), right ventricle (RV), left atrium (LA), right atrium (RA), and background. The background is any area inside the patient body but not part of the four classes. From these patch lists, 2500 patches from each class for each patient were chosen for CNN training and validation.
Figure 1.
Gold standard segmentation provided by a trained radiologist. The left ventricle (LV), right ventricle (RV), left atrium (LA), and right atrium (RA) are visible on this slice.
2.2. Convolutional Neural Network Fabrication
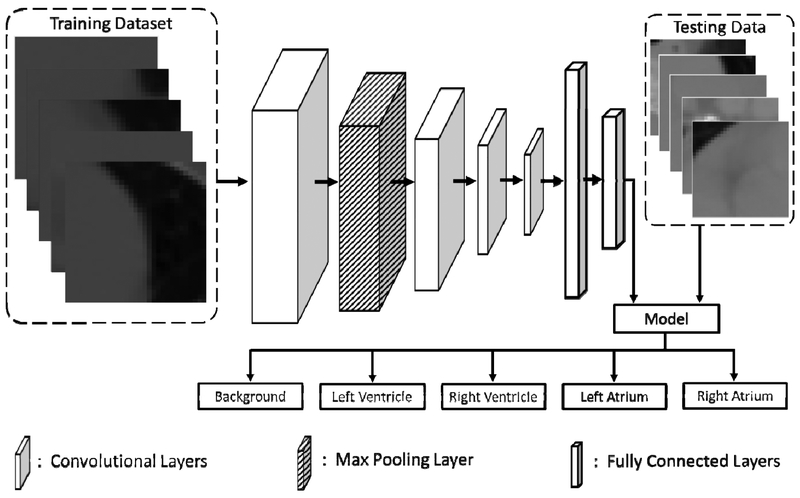
The diagram of the TensorFlow16 CNN is shown in Figure 2, which used the AdaDelta17 optimizer. The CNN had four convolution layers with an additional max pooling layer between the first and second convolution layers. All layers used the ‘Valid’ specification, as outlined in the TensorFlow documentation. The kernel size and stride for the max pooling layer were both 2 × 2. These layers were followed by two fully connected layers, after which a model would be created to classify the testing data. Each patch from the testing data could be one of five classes: background, left ventricle, right ventricle, left atrium, or right atrium.
Figure 2.
The workflow for the convolutional neural network used to segment the heart on 3D CT. The training patches from the 3D CT volumes of 10 patients are fed into four convolutional layers and a max pooling layer. These are followed by two fully connected layers and the final model. Testing data is then assigned a label of background, left ventricle, right ventricle, left atrium, or right atrium by the model.
The sizes of the convolutional layer filters and the number of neurons in the fully connected layers were adjusted to optimize the neural network, along with the learning rate, drop-out value, AdaDelta parameters ρ and ε, and the bias initialization constant were adjusted to optimize the results. The convolutional kernel size was set to 3 × 3. Various convolutional kernel sizes were investigated, with the first two convolutional layers using the same filter size and the last two using the same filter size. The number of neurons in the fully connected layers were also investigated and allowed to differ. Training was allowed to ran for 40 epochs with a batch size of 25. Model evaluation was performed at the end of each epoch.
2.3. Validation
The results were validated by calculating the overall accuracy of the classification of each class, with accuracy defined as the number of correctly labeled patches over the total number of patches for the testing dataset. The highest accuracy for each patient is averaged to give a final average accuracy for the parameters used. In addition to the overall accuracy, individual class accuracies were also calculated for each heart.
3. RESULTS
The optimal learning rate was found to be 0.005, with values from 0.1 to 0.0001 being tested. Drop-out values from 0.6 to 1.0 were also tested, with 1.0 producing the highest average accuracy. The bias initialization constant was set to 0.10 and the optimal values were 0.95 and 1 × 10−9 for AdaDelta parameters ρ and ε. Fully connected layer neuron numbers were set to 256 and 128. Various values for the convolutional layer filter sizes were tested, with the optimal results shown in Table 1. Increasing the convolutional filter sizes caused a steady increase in overall accuracy and a decrease in standard deviation. Using sizes of 500, 500, 1000, and 1000 for the convolutional filters, an average accuracy of 87.2% ± 3.3% was obtained. Average accuracies for each chamber were over 80%, while the average accuracy for the background patches was 93.7% ± 2.4%.
Table I.
Effect of convolutional filter size on classification results. Results shown represent the average accuracy for all patients. The values for the other parameters are shown below the table. Accuracies are in percentage.
| CFS 1 &2 |
CFS 3 & 4 |
Background | LV | RV | LA | RA | Overall |
|---|---|---|---|---|---|---|---|
| 150 | 75 | 88.4 ± 4.9 | 78.1 ± 9.1 | 73.3 ± 9.0 | 69.2 ± 11.2 | 66.0 ± 8.5 | 75.0 ± 5.7 |
| 200 | 100 | 88.7 ± 4.4 | 78.4 ± 14.2 | 73.9 ± 9.1 | 71.1 ± 5.8 | 69.3 ± 7.7 | 76.3 ± 5.3 |
| 100 | 200 | 88.9 ± 4.2 | 82.9 ± 7.9 | 74.6 ± 9.3 | 70.9 ± 10.1 | 71.3 ± 7.1 | 77.7 ± 4.8 |
| 200 | 400 | 91.6 ± 3.2 | 79.6 ± 7.1 | 78.9 ± 9.7 | 82.0 ± 6.6 | 77.9 ± 6.4 | 82.0 ± 4.3 |
| 300 | 600 | 92.6 ± 2.9 | 85.4 ± 6.4 | 80.5 ± 8.8 | 83.1 ± 7.6 | 80.6 ± 4.2 | 84.8 ± 4.2 |
| 400 | 800 | 93.1 ± 2.8 | 86.6 ± 5.8 | 81.6 ± 7.7 | 85.9 ± 5.7 | 82.9 ± 6.2 | 86.0 ± 3.7 |
| 500 | 1000 | 93.7 ± 2.4 | 87.8 ± 5.6 | 82.9 ± 6.2 | 88.6 ± 3.5 | 83.0 ± 6.2 | 87.2 ± 3.3 |
Learning Rate: 0.005, Drop-out Value: 1.0, Bias Initialization Constant: 0.10, ρ: 0.95, ε: 1 × 10−9, Fully Connected Layer Neuron Counts: 256 and 128. CFS: Convolution Filter Size
Individual patient performance using the optimal CNN parameters with convolutional filter sizes of 500, 500, 1000, and 1000 are shown in Table II. The overall accuracy for each patient was greater than 80%, with values ranging from 80.8% to 92.9%. All individual class accuracies were 73.0% or greater. Among the four chamber classes used, the performance for each patient for each chamber differed. For instance, Patients 1 and 2 had lower accuracies in the left atrium, while Patients 3 and 4 had their lowest accuracies in the right ventricle.
Table II.
Individual patient performance using the optimal CNN parameters with convolution filter sizes of 500, 500, 1000, and 1000. Accuracies are in percentage.
| Patient# | Background | LV | RV | LA | RA | Overall |
|---|---|---|---|---|---|---|
| 1 | 95.7 | 91.9 | 97.8 | 86.2 | 93.1 | 92.9 |
| 2 | 96.4 | 90.3 | 86.4 | 84.7 | 86.0 | 88.8 |
| 3 | 95.0 | 90.0 | 78.2 | 87.6 | 82.1 | 86.6 |
| 4 | 97.2 | 88.4 | 76.4 | 89.6 | 82.0 | 86.7 |
| 5 | 94.0 | 91.8 | 86.0 | 95.9 | 90.3 | 91.6 |
| 6 | 94.4 | 93.5 | 83.2 | 92.2 | 77.4 | 88.2 |
| 7 | 90.4 | 84.2 | 86.6 | 89.1 | 73.0 | 84.7 |
| 8 | 92.9 | 92.0 | 78.2 | 90.4 | 88.9 | 88.5 |
| 9 | 93.5 | 87.7 | 84.7 | 90.2 | 80.3 | 87.3 |
| 10 | 88.4 | 82.7 | 74.6 | 84.8 | 86.2 | 83.3 |
| 11 | 92.7 | 73.1 | 80.2 | 83.7 | 74.1 | 80.8 |
| Average | 93.7 ± 2.4 | 87.8 ± 5.6 | 82.9 ± 6.2 | 88.6 ± 3.5 | 83.0 ± 6.2 | 87.2 ± 3.3 |
4. DISCUSSION
Overall, the average classification accuracies increased with increasing convolution filter sizes, as shown in Table I. This indicated the number of features needed to accurately classify the patches was relatively large. The large patch size helped by providing enough information for the CNN to extract the variety of features needed. Background patches had the highest accuracy, which was not unexpected since the anatomy outside the heart was easily distinguishable from cardiac anatomy. The left and right atrium patches saw the largest improvements with increasing convolutional filter sizes. Standard deviations for the average accuracies also decreased, showing more consistency between patients during leave-one-out cross-validation training.
The individual patient performances in Table II show only three patients with an overall accuracy below 85%: Patients 7, 10, and 11. Patient 7 had the lowest right atrium accuracy of all 11 patients. Patient 10 had the lowest right ventricle accuracy. Patient 11 had the lowest overall accuracy, with relatively poor performances for the left ventricle and right atrium. Left atrium classification accuracy was high for all patients, with the lowest being 83.7% and four patients having accuracies over 90%. This suggests some uniformity between patient left atriums which may not exist in the other chambers. For example, even though the left ventricle classification accuracy was also high, Patient 11 performed poorly, suggesting some dissimilarity exists between the left ventricle of Patient 11 and the other patients.
A limitation of the study was the small number of patients included. By using more hearts in the training dataset, the classification accuracy of each patient and the average accuracies for each class should become more uniform. In particular, the average accuracies for the right ventricle and atrium could approach that of the left ventricle and atrium, increasing the overall accuracy of the method. Including more data would also decrease the risk of dissimilar patients.
5. CONCLUSIONS
We developed a patch-based, entirely autonomous convolutional neural network-based method to segment the four heart chambers from a conventional CT scan with high accuracy. This approach required no atlas and no prior registration between patients, reducing possible sources of error. Data pre-processing was limited to only patch creation, which is easily performed independently of the user. The results from the method can then be used for patient treatment planning or to automatically calculate cardiac function metrics. Future work will extend the CNN to four-dimensional (4D) CT and to explore the use of 3D patches to further improve the results.
ACKNOWLEDGEMENTS
This research is supported in part by NIH grants (CA176684, CA156775, and CA204254) and by the National Cancer Institute (NCI) via NRG Oncology, a member of the NCI National Clinical Trials Network with Federal funds from the Department of Health and Human Services under Grant Number U10 CA37422. The contents of this publication do not necessarily reflect the views or policies of the Department of Health and Human Services, nor does it imply endorsement by the U.S. Government.
REFERENCES
- [1].Boland GW, Lee MI, Gazelle GS, Halpern EF, McNicholas ΜM, and Mueller PR, “Characterization of adrenal masses using unenhanced CT: an analysis of the CT literature,” American Journal of Roentgenology, 171(1), 201–204 (1998). [DOI] [PubMed] [Google Scholar]
- [2].Balter JM, Lam KL, McGinn CJ, Lawrence TS, and Ten Haken RK, “Improvement of CT-based treatment-planning models of abdominal targets using static exhale imaging,” International Journal of Radiation Oncology*Biology*Physics, 41(4), 939–943 (1998). [DOI] [PubMed] [Google Scholar]
- [3].Daly B, and Templeton PA, “Real-time CT Fluoroscopy: Evolution of an Interventional Tool,” Radiology, 211(2), 309–315 (1999). [DOI] [PubMed] [Google Scholar]
- [4].Lee T, Tsai IC, Fu Y-C, Jan S-L, Wang C-C, Chang Y, and Chen M-C, “Using multidetector-row CT in neonates with complex congenital heart disease to replace diagnostic cardiac catheterization for anatomical investigation: initial experiences in technical and clinical feasibility,” Pediatric Radiology, 36(12), 1273–1282 (2006). [DOI] [PubMed] [Google Scholar]
- [5].Zaidi H, and El Naqa I, “PET-guided delineation of radiation therapy treatment volumes: a survey of image segmentation techniques,” European Journal of Nuclear Medicine and Molecular Imaging 37(11), 2165–2187 (2010). [DOI] [PubMed] [Google Scholar]
- [6].Ecabert O, Peters J, Weese J, Lorenz C, Von Berg J, Walker M, Olszewski M, Vembar M, and Cardiac C, “Automatic heart segmentation in CT: current and future applications,” Medicamundi, 50(3), 308–313 (2006). [Google Scholar]
- [7].Goo HW, Park I-S, Ko JK, Kim YH, Seo D-M, Yun T-J, Park J-J, and Yoon CH, “CT of Congenital Heart Disease: Normal Anatomy and Typical Pathologic Conditions,” RadioGraphics, 23(suppl_1), S147–S165 (2003). [DOI] [PubMed] [Google Scholar]
- [8].Peng P, Lekadir K, Gooya A, Shao L, Petersen SE, and Frangi AF, “A review of heart chamber segmentation for structural and functional analysis using cardiac magnetic resonance imaging,” Magnetic Resonance Materials in Physics Biology and Medicine, 29(2), 155–195 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Ecabert O, Peters J, Schramm H, Lorenz C, von Berg J, Walker MJ, Vembar M, Olszewski ME, Subramanyan K, Lavi G, and Weese J, “Automatic model-based segmentation of the heart in CT images,” Ieee Transactions on Medical Imaging, 27(9), 1189–1201 (2008). [DOI] [PubMed] [Google Scholar]
- [10].Zheng Y, Barbu A, Georgescu B, M., S., and D., C., “Four-Chamber Heart Modeling and Automatic Segmentation for 3-D Cardiac CT Volumes Using Marginal Space Learning and Steerable Features,” IEEE Transactions on Medical Imaging, 27(11), 1668–1681 (2008). [DOI] [PubMed] [Google Scholar]
- [11].van Rikxoort EM, Isgum I, Arzhaeva Y, Staring M, Klein S, Viergever MA, Pluim JPW, and van Ginneken B, “Adaptive local multi-atlas segmentation: Application to the heart and the caudate nucleus,” Medical Image Analysis, 14(1), 39–49 (2010). [DOI] [PubMed] [Google Scholar]
- [12].Lorenzo-Valdés M, Sanchez-Ortiz GI, Elkington AG, Mohiaddin RH, and Rueckert D, “Segmentation of 4D cardiac MR images using a probabilistic atlas and the EM algorithm,” Medical Image Analysis, 8(3), 255–265 (2004). [DOI] [PubMed] [Google Scholar]
- [13].Montagnat J, and Delingette H, “4D deformable models with temporal constraints: application to 4D cardiac image segmentation,” Medical Image Analysis, 9(1), 87–100 (2005). [DOI] [PubMed] [Google Scholar]
- [14].Kiri§li HA, Schaap M, Klein S, Papadopoulou SL, Bonardi M, Chen CH, Weustink AC, Mollet NR, Vonken EJ, van der Geest RJ, van Walsum T, and Niessen WJ, “Evaluation of a multi-atlas based method for segmentation of cardiac CTA data: a large-scale, multicenter, and multivendor study,” Medical Physics, 37(12), 6279–6291 (2010). [DOI] [PubMed] [Google Scholar]
- [15].Zuluaga MA, Cardoso MJ, Modat M, and Ourselin S, [Multi-atlas Propagation Whole Heart Segmentation from MRI and CTA Using a Local Normalised Correlation Coefficient Criterion] Springer Berlin Heidelberg, Berlin, Heidelberg: (2013). [Google Scholar]
- [16].Abadi M, Agarwal A, Barham P, Brevdo E, Chen Z, Citro C, Corrado GS, Davis A, Dean J, Devin M, Ghemawat S, Goodfellow I, Harp A, Irving G, Isard M, Jia Y, Jozefowicz R, Kaiser L, Kudlur M, Levenberg J, Mane D, Monga R, Moore S, Murray D, Olah C, Schuster M, Shlens J, Steiner B, Sutskever I, Talwar K, Tucker P, Vanhoucke V, Vasudevan V, Viegas F, Vinyals O, Warden P, Wattenberg M, Wicke M, Yu Y, and Zheng X, “Tensorflow: Large-scale machine learning on heterogeneous distributed systems,” arXiv preprint arXiv:1603.04467, (2015). [Google Scholar]
- [17].Zeiler MD, “ADADELTA: an adaptive learning rate method,” arXiv preprint arXiv:1212.5701, (2012). [Google Scholar]