From random to regular: neural constraints on the emergence of isochronous rhythm during cultural transmission

Abstract

A core design feature of human communication systems and expressive behaviours is their temporal organization. The cultural evolutionary origins of this feature remain unclear. Here, we test the hypothesis that regularities in the temporal organization of signalling sequences arise in the course of cultural transmission as adaptations to aspects of cortical function. We conducted two experiments on the transmission of rhythms associated with affective meanings, focusing on one of the most widespread forms of regularity in language and music: isochronicity. In the first experiment, we investigated how isochronous rhythmic regularities emerge and change in multigenerational signalling games, where the receiver (learner) in a game becomes the sender (transmitter) in the next game. We show that signalling sequences tend to become rhythmically more isochronous as they are transmitted across generations. In the second experiment, we combined electroencephalography (EEG) and two-player signalling games over 2 successive days. We show that rhythmic regularization of sequences can be predicted based on the latencies of the mismatch negativity response in a temporal oddball paradigm. These results suggest that forms of isochronicity in communication systems originate in neural constraints on information processing, which may be expressed and amplified in the course of cultural transmission.

Introduction

Temporal regularity is a key principle of human communication and expressive systems (Patel, 2010). For example, music tends to be organized in motivic patterns of one or few duration categories (Savage et al., 2015), and it often shows a significant proportion of metronomical (‘isochronous’) sequences. Isochronicity aids perception and memory of musical phrases and becomes important in contexts where multiple individuals must coordinate their perceptions and actions in time, in dance or in a music ensemble (Laland et al., 2016). But how did this property originate?

Recent theories regard universal properties of cultural systems, such as language and music, as shaped by human cortical function (Christiansen and Chater, 2008; Merker et al., 2015). These systems, as they are introduced in human cultures, might ‘invade’ evolutionarily older neural circuits, thus inheriting their computational capacities and constraints (Dehaene and Cohen, 2007). This process is amplified while cultural systems are being transmitted across multiple brains, so that structure in those systems increasingly reflects properties of cortical function. Over time, cultural systems ‘fit’ the relevant processing systems, becoming more regular and compressed and easier to acquire and reproduce. Experiments on language (Kirby et al., 2008), music (Ravignani et al., 2016; Lumaca and Baggio, 2017), reading and arithmetics (Dehaene et al., 2015; Hannagan et al., 2015) support this hypothesis.

Likewise, we may hypothesise that forms of temporal regularity in cultural systems originate from adaptations of rhythm patterns to constraints imposed by temporal information processing (Drake and Bertrand, 2001) over millennia of perception, imitation and transmission (Morley, 2013). This view is now supported by behavioural laboratory experiments (Ravignani et al., 2016), but neural evidence is still missing. Here, we aim to provide such evidence, using musical rhythm as a model for studying the emergence of the most widespread form of temporal regularity: isochronicity. We devised two experiments. In the first, we reproduced the cultural evolution of isochronicity in the laboratory. We show that an artificial rhythmic system, when it is transmitted across individuals in ‘diffusion chains’ (Bartlett, 1932), progressively develops a metronomic structure. In the second experiment, we investigated the relation between isochronicity and neural function. We measured neurophysiological responses from each participant to establish whether those could affect learning, transmission and, most importantly, regularization of rhythms differently across participants.

Our study involves transmission across individuals of an artificial set of five rhythms referring to emotions (a ‘code’), through multigenerational signalling games (MGSGs) (Moreno and Baggio, 2015; Nowak and Baggio, 2016; Lumaca and Baggio, 2017). MGSGs are an iterated version of classical two-player signalling games (Lewis, 1969; Skyrms, 2010), where two players repeatedly interact to agree on a common code (here, a shared set of rhythm-emotion mappings). The capacity of music to convey emotions is one of the reasons why it is maintained over time. In this regard, previous studies suggest that rhythmic structures can bear affective content (Balkwill and Thompson, 1999; Eerola et al., 2006) that can be socially learned and transmitted. The use of an interactive music transmission model involves a basic assumption: that music transmission, like language communication, requires alignment between the agents involved, at various levels of musical structure, including syntactic and affective levels (Vuust and Roepstorff, 2008; Vuust and Kringelbach, 2010; Bharucha et al., 2011; Schober and Spiro, 2016). For the communication process to be successful, a mutual understanding is needed between performers and listeners on how structures, and their mappings to meanings, are recoverable from the surface structures of the signals in use (Temperley, 2004), possibly through repeated listening (Margulis, 2014). A lack of alignment between the internal states of producers and listeners may hinder the communicative process and threaten the continued transmission of the music item.

Table 1 provides an overview of the study. In the first experiment, a rhythmic code was used to initialise each diffusion chain (the seed or starting material) (Whiten et al., 2007). The intergenerational transmission of the code in signalling games occurs via interactions between a sender (generation n) and a receiver (generation n+1) (Figure 1A). Over repeated rounds, the receiver learns five rhythms (4-sound sequences) and relative mappings to simple (peace, joy and sadness) and compound emotions (peace x joy and peace x sadness) portrayed by facial expressions (Fritz et al., 2009; Palmer et al., 2013) (details in Materials and Methods). In the subsequent game, the player switches his role from receiver to sender and is asked to transmit what he has learned to a naive individual (a new receiver, generation n+2) (Figure 1B). Memory for rhythmic patterns is rarely flawless: errors are introduced during transmission. Because this procedure is iterated multiple times, we can test how regularity of rhythms changes over experimental generations. Regularization is the process by which entropy, the information content of a sequence, is reduced or eliminated. We computed intergenerational changes in the regularity of rhythms, or patterns of time intervals, by using an information-theoretic measure of entropy (Shannon, 1949). Rhythmic patterns, from speech to musical phrases, can be described formally as inter-onset interval (IOI) time series or probability distributions (Cohen, 1962; Toussaint, 2013; Ravignani and Norton, 2017). Entropy is zero in isochronous sequences, and it takes low values in sequences with a few duration categories. Conversely, this quantity is large in rhythms that lack a temporal structure, i.e. with several interval durations of distinct values. We expected that non-random errors, introduced by neural constraints on temporal processing and memory, accrued during cultural transmission of rhythm sequences, would minimise the entropy of the artificial rhythmic systems, leading to a statistical structural universal of music and beyond: isochronicity (Savage et al., 2015). In addition, we addressed the hypothesis that participants would gradually reorganize rhythmic signals to express their meanings more efficiently. To this end, we quantified to what degree signals and meanings were systematically related, using measures of compositionality (Kirby et al., 2008).

Table 1.

Illustration of the study design. In Experiment 1 we used MGSGs in which two-player signalling games (Figure 1A) are played iteratively in diffusion chains. Each game, played by a sender and a receiver, corresponds to one generation (G). In each game, players must converge on a mapping of signals (equitone rhythmic patterns) to states (simple and compound emotions). The receiver in one game then becomes the sender in the next game, playing a new game with a new participant (the receiver) (Figure 1B). This process is repeated until the end of each chain (eight generations). We monitored changes in isochronicity across generations. In Experiment 2 each individual participated in two experiments, on 2 successive days: on day 1, we tested the temporal processing capabilities of individuals, using event-related potentials in a temporal oddball paradigm. There, each individual was presented with standard and deviant rhythmic patterns of different complexity (high, low and isochronous), while brain activity was recorded. On day 2, the same individual participated in a reduced version of MGSGs, consisting of two signalling games: the first as receiver, the second as sender. We tested whether MMN parameters (latency and amplitude), recorded on day 1, could predict learning, transmission and regularization of the rhythmic symbolic systems on day 2.

Experiment	Methods	Procedure	Hypothesis
1 Multigenerational signalling games	Diffusion chains, behavioural (full)	Systems of rhythmic tone sequences are transmitted along diffusion chains; two-player signalling games are played in each transmission step (Figure 1).	Increase of isochronicity of rhythm sequences along diffusion chains.
2 Neural predictors of signalling behaviour	Day 1: EEG/ERP	Oddball paradigm: the MMN is recorded from each participant in a temporal oddball paradigm (Figure 3).	The MMN recorded from participants on day 1 predicts behaviour in signalling games on day 2.
	Day 2: diffusion chains, behavioural (reduced)	Diffusion chain: the participant plays two signalling games, the first as receiver and the second as sender.

Fig. 1.

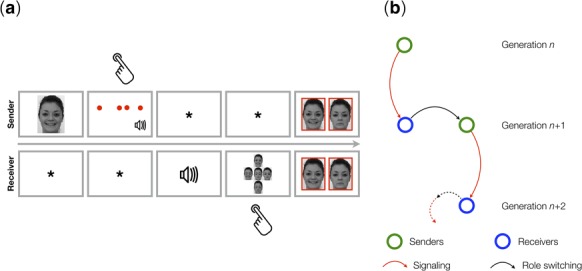
(a) Example of a trial from the signalling games played by participants in Experiments 1 and 2. The top and bottom rows show what senders and receivers saw on their screens, respectively. The task for the sender was to compose a four-tone rhythm sequence to be used as a signal for the simple or compound emotion expressed by the face presented on the screen at the start of the trial. For the receiver, the task was to respond to that signal by choosing the face the sender may have seen. The sender and the receiver converged over several trials on a shared mapping of signals (monotone rhythm sequences) to meanings (emotions). Hand symbols indicate when the sender or the receiver had to produce a response. Feedback was provided to both players simultaneously, displaying the face seen by the sender and the face selected by the receiver in a green frame (matching faces, correct) or in a red frame (mismatching faces, incorrect). Time is indicated by the arrow and flows from left to right. (b) Structure of MGSGs. The receiver in one game (generation n) is the sender in the next game (generation n + 1).

In the second experiment, we tested whether a relationship exists between the emergence of isochronicity in music transmission and neural processing constraints. We conducted the experiment on 2 successive days. On day 1, participants participated in an auditory temporal oddball task using rhythmical patterns (Figure 3). We recorded event-related brain potentials (ERPs) and derived the mismatch negativity (MMN) from them. The MMN is a negative fronto-centrally distributed ERP component, elicited pre-attentively, peaking between 100 and 220 ms in response to a sequence mismatch (Näätänen et al., 1978). This component is a reliable neural marker of temporal information processing (Takegata and Morotomi, 1999; Kujala et al., 2001). On day 2, the same participants played a reduced version of the MGSG: the first game as receivers (learners) and the second as senders (transmitters). We assessed quantitatively to what extent each participant would learn, retransmit and regularize the material received. We expected individuals’ MMN characteristics measured on day 1 to predict regularization behaviour in signalling games played on day 2.

Fig. 3.

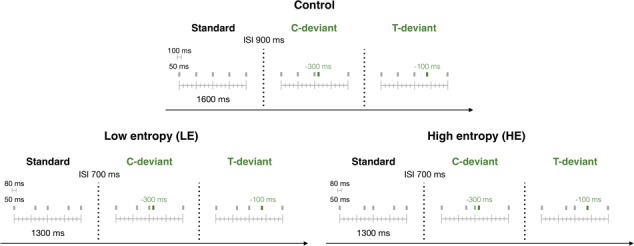
Schematic illustration of the rhythm sequences presented to participants during day 1 of Experiment 2. The EEG was recorded while participants listened to these rhythm sequences. Sequences of different complexity were used in three separate sessions (blocked design): control (isochronous) sequences, LE and HE entropy sequences. For each condition, 80% of the stimuli were standard sequences, and the remaining 20% were deviant stimuli violating the rhythmic contour of the sequences (10%, C-deviants) or not (10%, T-deviants).

Our study establishes a first link between the origin of near-universal aspects of musical systems, here isochronicity (Experiment 1), and human brain function properties (Experiment 2). Our results suggest that brain function differences across individuals can be a source of variation in cultural systems.

Materials and Methods

Experiment 1

Participants

Sixty-five subjects (one confederate) participated in Experiment 1 (33 females, mean age: 24.94). All subjects reported normal hearing and no formal musical training (besides typical school education). Upon arrival, participants received written instructions on the task (Supplementary Information 1.1) and signed an informed consent form. Participants were organized in eight diffusion chains with nine generations each (the confederate played as first sender in all chains).

Stimuli

The states in signalling games were five emotions: three basic (joy, peace and sadness), two compound (peace + joy and peace + sadness), shown as facial expressions. Compound emotions were then constructed by combining basic component categories (upper face of peace with lower face of joy/sadness) (Ekman and Friesen, 2003). The use of facial expressions as affective meanings was driven by the link between music-evoked emotions and facial expressions shown by neural and behavioural research (Hsieh et al., 2012; Kamiyama et al., 2013; Palmer et al., 2013; Lense et al., 2014). The signals were 4-sounds rhythms of 2 s duration, each denoting a different state. Each sound was a drum timbre of 100 ms duration (5 ms fade in–out) to be produced by participants tapping on one numeric key of the computer keyboard. To aid the perception of an underlying meter, the signal was presented twice to the receiver (4 s). In both presentations, the first sound of the signal was increased in volume (30%). Stimuli were delivered through stereo headphones at 80 dB.

Procedure

Figure 1A shows the structure of a trial. The sender is privately shown a facial expression (2 s) and sends a rhythmic signal denoting that emotion to the receiver, composing a 4-note sequence by tapping on a numeric key of the computer keyboard (with the exception of the first sender of a chain; see below). Unheard by the receiver, the sender could try a combination of sounds at will, listening to the final sound sequence played twice (eight sounds; 4 s) via headphones. The signal was delivered to the receiver, who listened to it via headphones (repeated twice: 4 s). The receiver responded by selecting among the five facial expressions presented on the screen the one the sender might have seen. The order of facial expressions was randomized across trials. Feedback (2 s) was then shown simultaneously to the players, showing the face the sender had seen and the one the receiver had chosen. A trial was correct if the two expressions matched. The game ended at 70 trials. Each facial expression was randomly presented 14 times in each game, twice every 10 trials. At the end of a game, the receiver (generation n) became the sender and played with a new receiver (generation n+1) (Figure 1B). The sender was now instructed to transmit as faithfully as possible the code learned in the previous game. Thus, a diffusion chain of nine generations (eight games) was constructed.

We designed four signal sets to initialize the eight diffusion chains (or seeding material). Regularity was matched across sets (mean Shannon entropy = 1.5, range 0:2). For additional information on the seeding material see Supplementary Information 1.2. Tempo was always 120 beat per min (bpm). A confederate (generation 1; first sender in each chain) was instructed to deliver these rhythmic stimuli to the partner (receiver; generation 2).

Data analysis

First, we aimed to describe the evolution of rhythmic regularity in the course of transmission within diffusion chains. The main dependent variable was regularity (measured by entropy) in linear mixed-effects regression models (Winter and Wieling, 2016) in R Studio (2015) and lme4 (Bates et al., 2013). We tested changes over time in regularity by using likelihood ratio tests for the fixed effect included in the model against a null model (fixed effect excluded). A baseline measure of change was also included by shuffling the IOI of the entire dataset and reflecting how codes would evolve by chance (dotted line in the figures).

Second, we examined the effects of the semantic (affective) space on the structural organization of rhythms. We hypothesised that rhythms would change, in the course of transmission, from holistic (one-to-one signal-to-meaning mappings) to compositional, morse-like signals (with few interval durations systematically recombined to produce the whole meaning space) (Kirby et al., 2008). We first measured compositionality in the rhythmic code using the information-theoretic tool RegMap (Tamariz, 2013; Supplementary Information 1.3). Then, we constructed a linear mixed-effects model to test the changes of ‘compositionality’ over generations [model: compositionality ∼ generation + (1|chain) + (0+t|chain)].

All signals produced were normalized to a tempo of 120 bpm and quantized on the best-fitting metrical grid [duple, triple or irregular; (Supplementary Information 1.4)]. Changes in the regularity of signals were measured using the Shannon Entropy (Shannon, 1949) on time intervals, using the following equation:

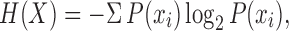where X is the time series of interval durations in a rhythm and P(x_i) is the probability that the element i occurs in that sequence (given the alphabet of interval durations in use and their relative frequency). Lower scores are associated with more isochronous signals.

Indexes of model efficiency

One key property of cultural transmission is information flow from one individual (or generation) to the next. We tested this property in our model using two measures: accuracy in transmission (also related to learnability) and direction of information flow (asymmetry). Changes in accuracy were computed using a similarity index (range 0:1): the inverse of the normalized edit distance (the number of elements in common between two strings of equal length). The elements compared were four time intervals (time similarity) or the relative contour profile (contour similarity; ‘larger’, ‘constant’ or ‘smaller’) of rhythmic patterns denoting corresponding states. Based on these two measures, we computed three indexes of efficiency: transmission, innovation and coordination. Transmission measures the similarity of the rhythms of adjacent senders (or generations; between-players measure). Innovation was computed as the distance between rhythms heard in one game as receivers and transmitted in the next game as senders (within-player measure). Coordination is a measure of the similarity between rhythms, the two players used for corresponding emotions. An asymmetry index (A = S − R/S + R) was also computed as the normalized difference in the number of remappings done on the emotion-to-signal link in the set by sender (S) and receiver (R) (range, 1:1). When coordination and transmission are large (i.e. most of the code is shared and accurately transmitted from one generation to the next), asymmetry is negative (the receiver changes his code more often than the sender does), and all are statistically different from 0 (one sample Wilcoxon test), information flows vertically from senders to receivers, i.e. from the first to the last generation of the diffusion chains.

Experiment 2

Participants

Seventeen new volunteers were recruited for the second study (11 females, mean age = 25.9 y, s.d.= 5.6; five additional individuals were excluded due to excessive electroencephalographic (EEG) artefacts). All participants were naive about Experiment 1 and non-musicians to avoid effects of musical training on auditory processing. All participants signed an informed consent form (Supplementary Information 2.1).

Design

Each subject participated in two experimental sessions on 2 successive days (24 h apart). On day 1 the EEG session took place. The EEG was recorded in three blocks with rhythmic patterns at three different levels of rhythmic entropy (see EEG stimuli) delivered by loudspeakers (80 dB). Meanwhile, the subject was watching a subtitled silent movie centered on the screen (8 ⨉ 11 frame). On day 2, the subject played two signalling games with a confederate, the first as receiver, the second as sender. In game 1 the participant was instructed to learn a signalling system from a confederate. In game 2, the participant (now sender) was instructed to retransmit the signalling system to the confederate (now the receiver) as they best remembered it.

Day 1. Electroencephalogram (EEG)

Stimuli

Stimuli were sine-waves equitone rhythms of five tones, presented in three recording sessions. The order of sessions [high entropy (HE), H = 2, low entropy (LE), H = 1 and control or isochronous, H = 0] was counterbalanced across participants. Each session consisted of four blocks with 100 stimuli each. Figure 3 shows the three stimuli types used in each session: one standard and two deviants. In each block, 80% were standard stimuli and 20% were deviants. On 10% of the deviants, the fourth tone was shifted 300 ms earlier (onset-to-onset), following the third tone by 100 ms and altering the rhythmic contour (contour deviant). The rhythmic contour is the profile of changing timing patterns (longer, shorter and same) in a rhythm, without regard to the exact interval durations (Dowling et al., 1999). On the remaining 10% of the deviants, the fourth tone occurred 100 ms earlier, following the third tone by 300 ms and producing a deviant preserving the original rhythmic contour profile (timing deviant). To maintain the same setting across all entropy conditions, control (isochronous) stimuli were designed longer (1600 ms long, 900 ms of inter-sequence interval or ISI) than high- and low-entropic stimuli (1300 ms long, 700 ms of ISI). If not, ISIs would not be sufficiently long to produce a contour deviant (1300 ms/4 = 325 ms IOIs). Sinusoidal tones were 50 ms long. Standards and deviants were presented in pseudorandom order (two deviants were never presented twice in a row). The equitone rhythms within each block were randomly transposed at three different fundamental frequencies (315 Hz, 397 Hz and 500 Hz).

EEG recording and processing

EEG data were recorded at a sampling rate of 1000 Hz from an EEG actiCap (Brain Products) with 64 Ag-AgCl electrodes arranged in the international 10–20 system and referenced to FCz. EEG data were downsampled offline to 500 Hz, bandpass filtered between 0.1 and 30 Hz (roll-off = 12 dB/octave) using the Matlab toolboxes ERPlab (Lopez-Calderon and Luck, 2014) and EEGlab (Delorme and Makeig, 2004). The EEG was re-referenced offline to the average of the mastoid channels and then segmented into 700 ms epochs, i.e. -100 (baseline) to 600 ms relative to the onset of the fourth tone. EEG responses exceeding ±70 μV (peak-to-peak, moving window = 200 ms) in any epoch were considered artefacts and excluded from the average. The presence of eye-movement-related artefacts was further determined by additional visual inspection in EEGlab.

ERP data analysis

The remaining epochs were averaged separately for each condition (standard and deviant), and deviant-standard difference waves were computed for each participant by subtracting standard from deviant ERPs. This procedure isolates the MMN component (Alain et al., 1999; Tervaniemi et al., 1999; Kujala et al., 2001; Vuust et al., 2005; Vuust et al., 2012).

First, we tested the presence of an MMN using a three-way analysis of variance (ANOVA) with mean MMN amplitude as dependent variable in each of the three conditions and three factors: stimulus type (standard or deviant), temporal window (three levels) and quadrant (three levels). Nine electrodes were selected from each of the three scalp quadrants: anterior (AF3, AF4, Fz, F1, F2, F3, F4, FC1 and FC2), centro-parietal left (C5, C3, C1, CP5, CP3, CP1, P5, P3 and P1) and centro-parietal right (C2, C4, C6, CP2, CP4, CP6, P2, P4 and P6). Studies have found the scalp distribution of the MMN to be maximal at midline fronto-central scalp locations (including Fz and neighbouring channels). Three 80 ms time windows (80–160 ms, 160–240 ms and 240–320 ms) were selected according to the timing characteristics of the MMN. The Huynh–Feldt correction was applied to all P-values. Two-tailed t-tests were used in post-hoc analyses.

We then tested whether the MMN recorded on day 1 could predict learning, transmission and reorganization of signalling systems on day 2. To this purpose, we correlated individual peak latencies or amplitudes of MMN difference waves obtained in each time window/quadrant with different measures of behaviour in signalling games (see below). We expected that ERPs with the timing and topographical characteristics of the MMN would be predictive of behavioural measures.

Day 2. Signalling games

Stimuli

Signals and states were the same as in Experiment 1. In each set, stimuli varied in regularity: two rhythms were high-entropic (H = 2), two low-entropic (H = 1) and one isochronous (H = 0). Sounds were produced as sine waves at a fundamental frequency of 500 Hz. Three sets of stimuli with these properties were produced and counterbalanced across participants as starting material in game 1.

Procedure

The trial design was the same as in Experiment 1.

Data analysis

We tested whether MMN amplitudes or latencies predicted individual learning, transmission and regularization of signalling systems. The same procedures (tempo normalization and quantization) and and formal measures used in Experiment 1 (coordination, innovation, transmission, asymmetry and regularity) were applied to the set of signals in Experiment 2. We also calculated a consistency index (consistency within a participant in sending the same signal, for a given emotion, across trials). We computed Pearson product-moment correlations (r) between behaviour (coordination, transmission, innovation and consistency) and structural changes across games (regularity of time intervals) and MMN parameters. All P-values were Bonferroni corrected for multiple comparisons (α = 0.05/12 = 0.004).

Results

The first experiment showed that rhythmic systems, when transmitted along a diffusion chain, exhibit increasing regularity or isochronicity of signals across generations, while maintaining one-to-one mappings to meanings. The second experiment demonstrated that the latency of the auditory MMN can predict the individual’s learning, transmission and regularization of rhythmic signaling systems.

Results of Experiment 1.

Figure 2 shows entropy changes across generations. A likelihood ratio test of the reduced model against the null model revealed a significant trend of decreasing entropy (linear mixed-effect: χ²(1) = 9.45, P = 0.002). This is supported by a significant difference in entropy between the first and the last generations (Wilcoxon signed-rank test: P = 0.01). This indicates that the initial rhythmic material was regularized over time. Moreover, a significant difference in entropy was observed between the last generation and median baseline levels (P = 0.005). This suggests that changes in entropy are not random but driven by directed pressures. Regardless of the adopted partition of signals (3 + 1 IOIs, 2 + 2 IOIs and 1 + 3 IOIs), we did not observe a significant predictive effect of generation for measures of compositionality (Supplementary Figure 1.3.1) (3 + 1 IOIs: χ²(1) = 0.009, P = 0.92; 2 + 2 IOIs: χ²(1) = 0.10, P = 0.74; 1 + 3 IOIs: χ²(1) = 0.002, P = 0.95).

Fig. 2.

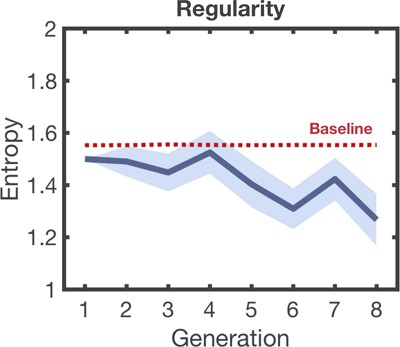
Evolution of rhythmic regularity across generations in Experiment 1. The thick blue line shows the mean rhythmic entropy for each generation across chains. The shaded blue area represents standard errors of the mean.

Next, to test how efficient signalling games were for modeling music transmission we used indexes of information flow direction (‘asymmetry’) and learning or recall (‘coordination’, ‘transmission’ and ‘innovation’) (see Material and Methods). Asymmetry was negative and significantly different from zero (one-sample Wilcoxon: median = −0.13, n = 64, Z = −6.957, P < 0.001); receivers adjusted their mappings more often than senders during coordination. Coordination (on rhythmic contours) was also different from zero (median = 0.51, n = 64, Z = −6.955, P < 0.001); most of the code was shared between players at the end of each session. No significant changes over generations were found for contour transmission and innovation (transmission, 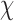²(1) = 0.005, P = 0.93; innovation, 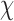²(1) = 0.62, P = 0.42). The high values of transmission observed in generation 2 (M = 0.66, s.d. = 0.11) were maintained throughout the diffusion chain until the last game (M = 0.67, s.d. = 0.19). We observed similar results for the low values of innovation (G2, M = 0.45 and s.d. = 0.20). These results suggest that most of the code was transmitted from one generation to the next in a diffusion chain.

Results of Experiment 2

Signalling games

Results were similar to those in Study 1. Asymmetry during game 2 was negative and different from zero (median = −0.05, n = 17, Z = −3.18, P < 0.001). Coordination was also different from zero (median = 0.91, n = 17, Z = 4.01, P < 0.001). These data indicate that the confederates (receivers) adjusted their mappings more often than the participants (senders) and that learning of the codes occurred during game 1. Transmission of rhythms was high and different from zero (taken on rhythm contours; median = 0.7, n = 17, Z = 3.62, P < 0.001) with scarce innovation (median = 0.2, n = 17, Z = 3.34, P = 0.001). Finally, we observed a reorganization of the structure of the signalling systems by the participants. The entropy of rhythms significantly decreased between the two games (median = 0.25, Z = −3.496, P < 0.001).

Mismatch negativity

The timing and topographical distribution of the neural responses elicited by deviants are consistent with the MMN (Figures 4 and 5 and Supplementary Figure 2.3.2). The ANOVA results and post-hoc analyses on interaction effects showed a large response in the central left quadrant between 160 and 240 ms in all conditions (Table 2). We further examined whether ERPs recorded on day 1 predicted participant behaviour in signalling games on day 2. To this purpose we correlated the MMN amplitudes and latencies with signalling measures and changes in the regularity of signals between the two games, as reported above. We focused on the central left quadrant at 160–240 ms from the deviant onset, which showed a strong effect in the previous analysis.

Fig. 4.

Grand average ERPs from a left central site (C1) in response to the onset of the fourth tone in standard and T-deviant stimuli in control, LE and HE sequences. Difference waves between T-deviants and standards are also shown. Waveforms were low-pass filtered at 30 Hz. See Supplementary Figure 2.3.1 for an account on the near-flat grand average response in HE.

Fig. 5.

Topographic isovoltage maps of grand average ERP difference waves between T-deviants and standards in control, LE and HE sequences. The MMN corresponds to the topographic maps shown at 160–240 ms; 0 ms is the onset of the fourth tone in a sequence.

Table 2.

Repeated measures ANOVA for grand average data. Results of ANOVA statistics on mean MMN amplitude values in the HE, LE and control conditions (CTRL).

Main effect	Condition	F	d	d err.	p*	η p 2
Stimulus type	HE	0.21	1	16	0.64	0.01
	LE	10.16	1	16	0.006	0.38
	CTRL	11.60	1	16	0.004	0.42
Temporal window	HE	4.08	1.45	23.27	0.04	0.20
	LE	4.97	1.66	26.69	0.01	0.23
	CTRL	0.92	1.61	25.83	0.38	0.05
Quadrant	HE	5.12	1.34	21.55	0.02	0.24
	LE	4.57	1.47	23.51	0.03	0.22
	CTRL	0.32	2	32	0.72	0.02
Two-way interactions
Stimulus type × temporal window	HE	8.18	2	32	0.001	0.33
	LE	14.55	1.60	23.77	<0.0001	0.47
	CTRL	11.86	1.70	27.21	<0.0001	0.42
Stimulus type × quadrant	HE	1.66	1.95	31.31	0.20	0.09
	LE	2.85	2	32	0.07	0.15
	CTRL	13.28	1.86	29.77	<0.0001	0.45
Three-way interactions
Stimulus type × temporal window × quadrant	HE	2.34	2.87	46.02	0.08	0.12
	LE	2.67	3.48	55.71	0.04	0.14
	CTRL	14.89	4	64	<0.0001	0.48

^* P-values are Huynh–Feldt corrected.

Neural predictors

Figure 6 shows correlations between the MMN peak latencies (160–240 ms) recorded from the central left quadrant in the HE condition with behavioural measures (coordination, transmission, innovation and consistency) and structural measures (regularity) (Supplmentary Tables 2.4.1 and 2.4.2). The MMN peak latency was negatively correlated with coordination (r = −0.63, P = 0.006), transmission (r = −0.73, P < 0.001) and consistency (r = −0.64, P = 0.005) and positively correlated with innovation (r = 0.62, P = 0.007); players with shorter MMN peak latencies tended to learn and retransmit the signalling system more efficiently than players with longer peak latencies.

Fig. 6.

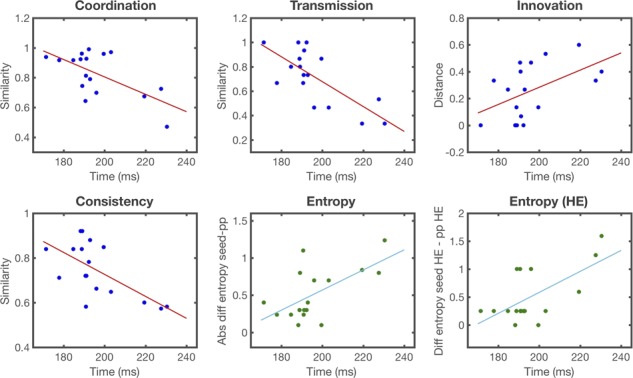
Pearson product-moment correlations (r) between MMN peak latencies relative to the onset of the deviant tone (0 ms) in HE sequences from the left hemispheric scalp quadrant on day 1 (x-axis) and behavioural (blue, red) and structural (green, light blue) measures in signalling games on day 2 (y-axis). Behavioural measures were defined as the extent of the code learned by a participant in game 1 (coordination) that was faithfully recalled and transmitted in game 2 (consistency and transmission) and reorganized between the two games (innovation). The structural measure (entropy) was obtained as the absolute difference between mean code entropy values in games 1 and 2. All MMN peaks fall within the 160–240 ms window. See Methods for further details on the measures, and Supplementary Tables 2.4.1 and 2.4.2. for Pearson product-moment correlations (r) values. Each point on a scatterplot is one participant.

Changes in the regularity of signalling systems were also predicted by MMN peak latencies. Positive correlations for MMN peak latencies were found with mean absolute changes in the entropy of signalling systems (r = 0.62, P = 0.007) and mean changes of high-entropic signals (r = 0.63, P = 0.005). These data reflect a general regularization of the code, mainly introduced by individuals with longer MMN peak latencies. The same individuals were found to be most responsible for the regularization of highly irregular signals. No significant correlations were found in other conditions, time windows and quadrants or using MMN amplitudes (Supplementary Tables 2.4.3–2.4.12). Similarly, no significant correlations were found for contour deviants (Supplmentary Tables 2.4.13–2.4.24).

Discussion

We investigated the relations between interindividual variation in brain signals and the evolution of isochronicity. We demonstrate that near-periodic rhythm patterns arise in signalling systems when these are transmitted across generation of learners via iterated signalling rounds. In addition, we showed that learning, transmission and temporal regularization of similar rhythm sequences by single individuals relate to individual pre-attentive information processing capabilities. We discuss the implication of the neural findings on the broader context of cultural evolution.

Cultural evolution of temporal regularity in the laboratory

Rhythmic structure implies the regularity and predictability of temporal events. Diffusion chains studies have shown that regularity in cultural systems may reflect universal principles of cognition and perception (Kirby et al., 2008). In this regard, constraints on temporal processing and encoding might be responsible for the origins of temporal regularity in human symbolic systems such as music (Trehub, 2015). The progressive decrease of rhythmic entropy found in the first study is consistent with this prediction. Here we showed that equitone rhythmic sequences increase in temporal regularity when transmitted across generations of participants.

The tendency of subjects to equalise, within a tone sequence, the interval durations, as shown in our results, and by behavioural and neurophysiological works (Povel, 1981; Jacoby and McDermott, 2017), could explain this result. When this process iterates, cultural information is progressively transformed or distorted towards rhythmic sets of fewer (one or two) durational categories, i.e. more regular rhythmic set.

In contrast, we did not observe significant changes in the degree of compositionality of rhythmic sets. Compositionality provides the most parsimonious encoding of complex meanings and is likely to emerge in communication systems as an adaptive response to the synergetic effect of learning and communicative pressures (Kirby et al., 2015). Our result stands in contrast with previous iterated learning work, showing an increase in the compositionality of linguistic and non-linguistic systems over generations (Kirby et al., 2008; Theisen-White et al., 2011). We show that rhythmic signals, in the course of transmission, are reorganized to maximize redundancy (learnability), partly losing their expressive power (but see Ravignani and Madison 2017 for a possible communicative function of isochrony). Constraints on temporal perception and encoding, rather than principles of information compression, could be the driving force behind the evolution of musical rhythms.

Similar findings were obtained by Ravignani et al., (2016) using a different cultural transmission model, iterated learning (Kirby et al., 2008), in the absence of an affective meaning space. The conceptual reproducibility of this result supports the view that temporal regularity in music may have arisen by principles of processing economy or simplicity (Chater and Vitányi, 2003), most likely different from the principles at play in the evolution of language (Lumaca and Baggio, 2018; Ravignani and Verhoef, 2018). Cognitive limits on cultural transmission might drive the emergence of temporal regularity in many musical systems.

A neurophysiological index of individual-level constraints on temporal processing

The auditory MMN reflects the brain’s automatic detection of deviations from regularity representations and how accurately these representations are encoded in memory (Winkler, 2007; Näätänen et al.,2010). The MMN found here provides further evidence that temporal structure is one of the elements encoded in auditory predictive models (Winkler et al., 2009; Vuust and Witek, 2014). Can the MMN be used as an individual marker of (auditory) temporal processing efficiency? Interindividual variability in brain structure and function has been shown to affect auditory processing mechanisms (Zatorre, 2013). Previous studies reported correlations between MMN characteristics and discrimination accuracy on sound deviations for complex spectro-temporal patterns (Näätänen et al., 1993; Tiitinen et al., 1994). Similar findings were reported in the temporal domain; larger amplitude and earlier latencies reflect a better and faster detection of temporal deviations from standard sequences (Kujala et al., 2001). Together, these suggest a neural disposition by individuals for processing complex spectro-temporal patterns.

ERP latencies seem to reflect learning or maturational states of the relevant neural networks; the myelination degree of white matter connectivity between cortical generators (Cardenas et al., 2005) while ERP amplitudes seem to rely on the neuronal population size of cortical generators and the extent of active tissue (Rasser et al., 2011). Myelination and functional connectivity between the relevant cortical generators may contribute to how fast auditory temporal mechanisms are at processing incoming information rapidly and at detecting standard–deviant differences (Bishop, 2007). The evidence presented in this section suggests that intersubject variability in MMN latency, as found in this study, likely reflects differences in automatic information processing rather than global or contextual, non-functional factors (i.e. unrelated to the psychological or neural processes of interest). Early sensory memory mechanisms may then account for the individual behaviour performance in signalling games.

Sequence complexity, MMN and behavioural prediction

The encoding of complex rules has been found to co-vary with individual differences in auditory sensory memory capacity (Näätänen et al., 1989). In this regard, temporal regularity optimizes temporal integration mechanisms (Tavano et al., 2014). Small temporal deviations are more easily detected in isochronous than irregular temporal patterns. Irregular temporal patterns may increasingly tax the auditory system, reducing the quality of memory templates. In turn, this would be echoed by slower and weaker responses from the automatic change-detection system. In support of this view, previous studies have reported a weaker MMN effect and an increased offset response latency (Costa-Faidella et al.,2011; Schwartze et al., 2013; Tavano et al.,2014; Andreou et al.,2015) to violations of random versus isochronous auditory stimuli. This effect mirrors the individual’s behaviour in deviance detection tasks, showing faster response times and increased accuracy for isochronous vs random stimuli (Andreou et al.,2015). These results are consistent with predictive coding (PC) (Friston, 2005) and with the view that the MMN is a neural signature of prediction error. One prediction put forward by PC is that the more uncertain the rhythm is, the less salient is the prediction error generated by a pattern violation (Vuust et al., 2018). Our results support this view, showing the weakest MMN response for the high-entropic stimuli.

Noticeably, only the MMN latency generated by these stimuli was consistently predictive of behavioural performance (see Brattico et al., 2001 for similar results on musicians). In line with our previous work (Lumaca and Baggio, 2016), we propose that more demanding auditory tasks may be necessary for the emergence of inter-subject variability in behaviour. If as noted before, high-entropic stimuli require more sensitive auditory processing mechanisms, even small differences in processing capabilities across individuals, as reflected by the MMN, would manifest in behaviour. This difference would be minimal for control and low-entropic stimuli, where temporal information is highly predictable. Complexity appears to be a critical ingredient to investigate individual information processing capacities.

Neural predictors of cultural behaviour

Faithful transmission is one property of cumulative cultural evolution (Tomasello, 1999). This may depend on the difficulty of the cultural repertoire to be transmitted and the learning skills of the receiver. An inaccurate learner will be an unreliable transmitter in the future. Here, we show that the ‘timing’ of specific brain processes can distinguish good from bad learners and accurate from inaccurate transmitters. In line with Lumaca and Baggio (2016), we found longer MMN latencies for less accurate learners: the ones showing low coordination and inaccurate transmission within (low consistency) and between games (low transmission and high innovation). Changes in MMN amplitude and latency have been shown to predict variations in reaction times and hit rates on auditory discrimination tasks (Tiitinen et al., 1994; Kraus et al., 1996; Tervaniemi et al., 1997). Here, we showed that early sensory mechanisms can also drive more complex reproduction tasks. This result further contributes to the theory of the involvement of memory processes in eliciting the MMN.

Perhaps more interesting is that ‘timing’ of early brain processes predicted the temporal regularization of the signalling system. Major properties of human cultural systems can be understood as adaptations to ‘information bottlenecks’ of the human brain. The size of the information bottleneck determines the symbolic system's properties transmitted therein. Previous works show that the tighter the bottleneck (i.e. the smaller the size of the data available to the learner), the more regular the system in time (Kirby et al., 2007). In previous simulation work, agents had no memory limits or learning constraints of any type. Here we provide evidence that similar results are obtained with a tighter ‘memory’ bottleneck: the less efficient the information processing capabilities of individuals, the greater the pressures for learnability and regularization (Newport, 1990; Kempe et al., 2015). Individual noise in perception and cognition determines the magnitude of adaptation by cultural material.

Individual processing constraints, cultural evolution and diversity

Cultural transmission is a powerful regularizer of symbolic systems. Regularities emerge consequence of adaptation to the structure and function of human cognition (Boyd and Richerson, 1988; Christiansen and Chater, 2008). Empirical work on language evolution supports this view (Kirby, 2001; Kirby et al., 2007; Kirby et al., 2008). However, these studies have so far only focused on general patterns of changes, and the sources of these changes were only inferred at the population level. Individual variability was treated as noise and removed by simple arithmetical procedures. Here we show that this variability, instead of representing random noise, may reflect the information processing capabilities of individuals. Critically, this work shows a direct, visible trace of the relation between cultural adaptation and neural processes, up to now only assumed by cultural transmission research.

How does individual neural variability manifest itself at the population level, and through what mechanisms? Dediu and Ladd (2007) point to cultural transmission as one potential mechanism. They proposed that neural variability is related to phenotypic differences in the acquisition and production of linguistic tones. This variability is amplified by cultural transmission leading to variation in linguistic patterns observed among world cultures or, if processing constraints produce the same trajectory of change, graded universality. Here, we support the latter view combining an experimental model of cultural transmission with electrophysiology. We showed that (possibly) small and different individual regularity biases on temporal processing (whose traces were isolated in Study 2) are amplified during cultural transmission in a diffusion chain and are reflected into a design feature of musical rhythm: isochronicity.

Classification scheme methods constituted up until now the main approaches to explaining cultural variation. Changes over time in the frequency of cultural variants may produce peculiar population-pattern phenomena, with a rich variability within the same culture (Rzeszutek et al., 2012). However, the source of the initial variability is often vague and assumed a priori. We propose that neurocognitive variation is a non-negligible source of cultural variation. In the present context, it may have contributed to some forms of variation observed for temporal regularity over time and across cultures (Levitin et al., 2012).