Evaluation of the postural stability of elderly persons using time domain signal analysis

Abstract

A force platform is widely used in the evaluation of postural stability in man. Although an abundance of parameters are typically retrieved from force platform data, no uniform analysis of the data has been carried out. In general, the signal analysis does not analyze the underlying postural event, i.e., whether the signal consists of several small corrections or large excursions. In the present work, we studied the postural stability of 4589 elderly persons from Iceland on a force platform under visual and non-visual conditions during stance on a solid surface. We analyzed the internal relationship between frequently used time domain variables. In addition, we conducted a factor analysis using a subset of selected variables. Factor analysis yielded three components that can be considered different strategies for maintaining posture. In one control strategy, long swaying amplitues were pronounced, allowing the person to react when postural confidence limits are reached. In a second strategy, a high oscillation rate about the stationary point was the dominant characteristic of maintaining postural control. The third strategy appears to involve a short critical time period during which an open loop control changes into a closed loop that very rapidly controls excessive postural oscillations. The findings suggest that conventional parameters such as swaying velocity and amplitude alone do not provide sufficient information regarding a person’s ability to maintain an upright stance.

1. Introduction

The study of human postural control under non-visual conditions can be simplified by regarding the standing human as a system consisting of an inverted pendulum in the gravitational field [23]. The stabilization of this system can be controlled by sensory information from the sole of the foot, the proprioceptors of the calf muscles [10] and the inner ear [22]. Receptor systems in each of these areas can detect positional, velocity or acceleration information that can be used for the control of posture [20]. For example, the sole of the foot contains four distinct populations of receptors that respond slowly or quickly to changes in static pressure, tension of the skin and dynamic changes of pressure. Anesthesia of these receptors leads to deteriorated postural control [14]. The interaction between the otolith and semicircular canal systems of the vestibular system provides information regarding the linear and angular acceleration of a head movement, and the muscle spindle system provides data on the tension, length and changes in the length (velocity) of leg muscles [19]. The central postural system uses such information selectively in the context of postural control to execute corrective reflexes. Acceleration perceived by the vestibular system seems to be dominant in postural control [19]. However, because the sensory control systems for the maintenance of posture overlap, the quantification of postural derangement is challenging, especially because compensation and adaptation constantly alter the output and result in context-dependent postural reactions.

For rapid screening of postural stability in humans, the force platform has become increasingly popular [7,15]. When used without external stimulation, the force platform quantifies body sway during quiet stance using an inverted pendulum model, although the different segments of the body continue to oscillate around their optimal position. Although the force platform technique is widely used due to its simplicity, no generally approved method of analyzing the signal is available [3]. A recent literature survey [9] found 163 different parameters that have been used to describe human posture. The large number of parameters used suggests that no single parameter describes postural efforts adequately in individual cases. There are likely several reasons for this. First, the control strategy is likely to be context-dependent [11] Second, the control strategy changes with age [12]. Third, the control strategy may be individually selected based on experience [8]; fourth, it may depend on the general health of the subject [21]. In addition, the selected control strategy may work properly for most normal tasks, but the system may fail under the stringent demands of testing. Palmieri et al. [17] evaluated the parameters used in 67 reports in the literature and concluded that the literature in this field has failed to identify parameters that reliably describe changes in the postural control system.

The number of parameters that can be calculated from a posturography signal is enormous in relation to the simplicity of force platform measurement. This suggests that there must be an abundance of parameters associated with the measurement that contain redundant information. Thus, reduction of the number of parameters is key for understanding the results of force platform measurements and defining the clinical implications of the posturography method.

The purpose of this work was to calculate a set of intuitive and commonly used time domain variables from the posturography signals of elderly persons and to study the efficacy of these variables in describing postural stability. To reduce the redundant information provided by the parameters calculated from posturography signals and to select parameters by means of which changes in postural control can be determined, we searched for the correlation structure of variables and sought to neglect variables that contain redundant information. Finally, we performed a factor analysis, the results of which suggested that three different controlling strategies consisting of (1) torque control, (2) positional control and (3) anticipatory control of the center point of force (CPF) are used in the maintenance of postural stability. The basic statistics of the data will be published elsewhere.

2. Materials and methods

2.1. Subjects

We measured postural stability in 4589 elderly persons from Iceland in connection with a larger study (Age Gene/Environment Susceptibility Reykjavik Study; AGES-Reykjavik) We studied 2664 females and 1925 males; the mean age of the subjects was 76.2 years (SD ± 5.4 years). This study has been funded by NIH contract N01-AG-1–2100, the NIA Intramural Research Program, Hjartavernd (the Icelandic Heart Association), and the Althingi (the Icelandic Parliament). The study is approved by the Icelandic National Bioethics Committee, VSN: 00–063. The Reykjavik Study cohort originally comprised a random sample of 30,795 men and women born in 1907–1935 and living in Reykjavik in 1967. A total of 19,381 people attended, resulting in 71% recruitment rate. The study sample was divided into six groups by birth year and birth date within month. One group was designated for longitudinal follow up and was examined in all stages. One group was designated a control group and was not included in examinations until 1991. Other groups were invited to participate in specific stages of the study. Between 2002 and 2006, the Age Gene/Environment Susceptibility Reykjavik Study (AGES-Reykjavik study) re-examined 5764 survivors of the original cohort who had participated before in the Reykjavik Study. All participants were invited to take part in the balance test except blind people and people in wheel chairs who were excluded. In addition, people who needed assistance in standing up in the chair rise test were excluded from the stance test.

2.2. Device

We used a static force platform to measure posture. A force platform can be considered a scale that can measure both the mass of a subject standing on it and the location of the vertical force acting on it in two dimensions. The weight of a subject is recorded within the location information.

2.3. Test setup

The analysis of the data in the present work focused on stance on the rigid platform surface over a period of 30 seconds. Thereafter, the subject was asked to close his or her eyes, and the test was repeated. During the test, the subject was instructed to keep his or her hands on the chest, lock the knee joints, and stand as stably as possible. Participants were instructed to stand on the force platform with their feet separated from each other forming a V (the exact position of the V feet placement was marked on the platform, heels 5 cm apart, big toes 10 cm apart). The participants always faced the same direction. For the parameter analysis, we analyzed the data in the eyes-closed condition. We rejected 15 seconds from the beginning of the measurement in order to give time to the subjects to settle down on the force platform. For calculation of the Romberg quotient, we also selected one parameter from the eyes-open test. Romberg quotient was calculated as the ratio of the lengths of swaying traces with eyes closed and eyes open. This variable effectively describes the use of visual information in maintaining posture.

2.4. Raw data

The sampling frequency of the force platform was 50 Hz. The outcome signal from the force platform is a three-dimensional time series called a stabilogram. Two of the signal components of the stabilogram give the location of the force reaction under the subject’s feet in the mediolateral (x) and anterior-posterior (y) directions at every sampling instant t. The third component of the stabilogram provides the magnitude of the force reaction acting on the force platform at each respective sampling instant. The latter signal contains the subject’s weight. Although the subject’s mass remains constant, his or her measured weight changes due to postural controlling efforts. The resulting signals are usually contaminated with electrical noise, biological noise and movement artifacts. The noise comes from the electrical characteristics of the voltage sensors of the force platform [1] and its mechanical structure, from the segmental oscillation of the body, and from biological noise, such as the subject’s heartbeat and other internal bodily motions.

2.5. Filtering

We used a finite impulse response (FIR) low-pass filter to suppress high-frequency noise. The pass band of the filter used ended at 17 Hz, and the stop band started at 21 Hz. Maximum ripple at the pass band was 1 dB; the attenuation in the stop band was 80 dB. The order of the filter was 42, which caused a transition error at the beginning of the filtered signal. To remove the effect of the transition error, we removed 150 samples from the beginning of the filtered stabilograms. After preprocessing the lengths of the stabilograms, 600 samples remained, corresponding to the 12 seconds during which the subject stood on the force platform. Before further processing, we removed the mean values of the stabilogram’s positional components. The weight signals centered, altering the mean to 0. However, in the moment calculations presented later, we used the filtered weight signal without centering.

3. Evaluation of posturography signal

In the evaluation of posturography signal we provide formulas for variables only in such situations that are considered to give the reader new information. All other variables are considered to be known.

3.1. Position

Using positional information, we calculated the peak to peak sway amplitudes in the mediolateral and anterior-posterior directions and the confidence limits that contain 95% of the stabilogram samples. The data describe the projections of the stabilogram components in the respective directions. In the mediolateral direction, the sway amplitudes were X, and the confidence limits were C(X); in the anterior-posterior direction, these parameters were Y and C(Y ), respectively.

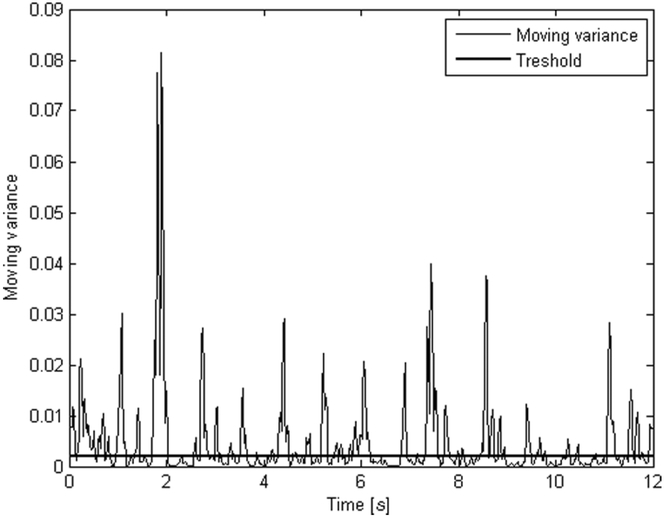
Next, we calculated the sway amplitudes during low variation of the weight signal. In this work, the threshold of low variation was 0.002 corresponding to the upper limit of the lowest quartile of mean value of variance of weight signal over all subjects. This value was compared to the value of the moving variance. If the moving variance was less than or equal to 0.002, the respective sample in the centered weight signal was designated as belonging to a ‘low variation’ period. The length of the moving variance window was 5 samples. Shorter window tend to follow individual controlling efforts while longer window smooth them out. Figure 1 shows the low variation periods under the threshold line during which the parameters Low(X) in the mediolateral direction and Low(Y) in the anterior-posterior direction were calculated. A “spiky” period after a low variance period may suggest that a subject has corrected his posture close to the instability limit. Typically, the correction movement comes late during swaying, and its magnitude is overestimated. A weight signal point p_i was classified as belonging to a low variation period if the following relationship held:

$$test(pi)=\frac{1}{4}{\displaystyle \sum _{j=i-2}^{j=i+2}{\left(wj-\overline{w}\right)}^2}\le 0.002$$ (1)

In formula (1), the testing window is centered at point p_i. The local variation is calculated using the two preceding and the two following weight signal samples. The window ultimately moves over the entire weight signal.

Fig. 1.

Weight signal can reveal postural controlling efforts by the means of increased local variation. Low variation periods are below the threshold line.

3.1.1. Velocity

We calculated component-wise velocities in the mediolateral and anterior-posterior directions. In velocity calculations, we used a similar concept to that was used to determine amplitudes. The velocity in the mediolateral direction was denoted as VX, and its 95% confidence limit as C(VX). In the anterior-posterior direction, the velocity and its 95% confidence interval were VY and C(VY), respectively.

3.1.2. Moment

The moment reactions of ankles and hip that occur when a correction is initiated will modify the stabilogram. We calculated the following moment-related variables about the mediolateral (x-axis): the kurtosis of the moment K(MY), the mean of the absolute values on the moment M(MY) and the standard deviation of the moment STD(MY). The respective variables on the anterior-posterior (y-axis) were K(MX), M(MX) and STD(MX).

3.1.3. Plane interpretation

In the plane interpretation of a stabilogram, we calculated variables on the xy-plane and considered the signal atwo dimensional. These variables included the length of an entire swaying trace (LEN), the area of an ellipse containing all stabilogram samples (EA), the area of a confidence ellipse that contains 95% of the stabilogram samples (CEA), the total time during which the variation of a weight signal is low Low(T) and the number of time periods during which the variation of a weight signal is low Low(N). We also calculated the mean squared moment error about the mediolateral and anterior-posterior directions and summed them into one variable, MERR. A moment error signal about an axis was calculated by selecting from a stabilogram the four-second period during which the local variance of the weight signal was the smallest. Using the four-second stabilogram data, we fitted a line

$$\text{M}=\text{Fx},$$ (2)

to the data. Vector M contains 200 moment values calculated on the basis of the stabilogram in the mediolateral or anterior-posterior component direction on the axis about which the moment is being calculated and its respective weight signal. The vertical force acting on the force platform’s surface was calculated with solving Eq. (2) using standard pseudoinverse.

$$\text{F}={\left({\text{x}}^{\text{T}}\text{x}\right)}^{-1}{\text{x}}^{\text{T}}\text{M}.$$ (3)

The actual mean squared error about the anteriorposterior direction was calculated as the sum of squared differences with the fitted model and the values calculated based on the stabilogram, as follows:

$$MER{R}_y=\frac{1}{600}{\displaystyle \sum _{i=1}^{600}{\left(M_i-F{x}_i\right)}^2}.$$ (4)

The total mean squared error was MERR = MERR_x +MERR_y. In this case, our model predicted the moment value at the same locations (x_i, y_i) as the actual sampled points. Moment error MERR gets large values when there are large corrections in posture. If there were a static weight on the force platform the moment error would be close to zero. The only origin for the error would in that case be the electrical noise from the force platform’s electrical characteristics.

3.1.4. Activity

As an activity measure, we calculated how many times the center point of force crosses the x-axis ZCR(X) and y-axis ZCR(Y). We also calculated how many times the velocity changes direction in the mediolateral direction ZCR(VX) and in the anterior-posterior direction ZCR(VY). Additionally, the activity measure was calculated for the weight signal ZCR(W). The nature of the zero crossing rate of a weight signal STD(WT) measures the standard deviation of times between successive zero crossings of a weight signal. Large values of zero crossings indicate that a person’s swaying amplitudes are small and they occur around a point that remains sufficiently stationary. On contrary, in small zero crossing situations there are long swaying amplitudes or many points around which the swaying occur.

3.1.5. Conventional variables

In addition to the variables mentioned above, we calculated the Romberg quotient ROMB and the critical time at which an open loop control changes into a closed loop control, CRI(T) [4]. Critical time CRI(T) was calculated on the basis of the work of Collins and Luca [4]. An illustration of diffusion plot that includes the critical time is presented in Fig. 2.

Fig. 2.

Example of stabilogram diffusion plot. CRI(T) gives the time when open loop control changes into a closed loop control.

Evaluation of the posturography signal yielded 30 time-domain variables. From these,the moment-related variables were divided by a subject’s mass to remove its contribution.

4. Results

Table 1 presents the correlation coefficients between the pairwise correlations of the variables that characterize mediolateral aspects of postural control.

Table 1.

Sway variables in the mediolateral direction

	Low(X)	C(X)	X	C(VX)	VX	K(MY)	M(MY)	STD(MY)	ZCR(X)	ZCR(VX)
LOW(X)	1.00	0.83	0.83	0.83	0.83	0.08	0.68	0.70	0.09	-0.15
C(X)	0.83	1.00	1.00	1.00	1.00	0.03	0.62	0.63	0.34	0.17
X	0.83	1.00	1.00	1.00	1.00	0.03	0.62	0.63	0.34	0.17
C(VX)	0.83	1.00	1.00	1.00	1.00	0.03	0.62	0.63	0.34	0.17
VX	0.83	1.00	1.00	1.00	1.00	0.03	0.62	0.63	0.34	0.17
K(MY)	0.08	0.03	0.03	0.03	0.03	1.00	-0.07	0.01	0.06	-0.03
M(MY)	0.68	0.62	0.62	0.62	0.62	-0.07	1.00	0.99	-0.30	-0.35
STD(MY)	0.70	0.63	0.63	0.63	0.63	0.01	0.99	1.00	-0.30	-0.36
ZCR(X)	0.09	0.34	0.34	0.34	0.34	0.06	-0.30	-0.30	1.00	0.62
ZCR(VX)	-0.15	0.17	0.17	0.17	0.17	-0.03	-0.35	-0.36	0.62	1.00

All amplitude-related variables were highly intercorrelated, indicating that they measure essentially the same phenomenon.We selected the amplitude of medio lateral peak to peak amplitude X for further analysis, because it is commonly used. From the moment-related variables, we selected the mean of absolute moment M(MY) because this provides information about the ranges of a subject’s ability to maintain balance. Both X and M(MY) describe the dynamic ranges of postural control. Because the activity-related variables ZCR(X) and ZCR(VX) showed lower correlation with the other variables (less than 0.8), we included them in further analysis. Also, because kurtosis of the moment about anterior-posterior axis K(MY) does not correlate with other variables, we concluded that it contains valuable information and included it in further analysis. Kurtosis provides information about the nature of swaying. High kurtosis results from steady swaying with a low number of large excursions, while low kurtosis is a sign of increased swaying.

Table 3 shows variable selection in the anterior posterior (AP) direction. For further analysis, we selected the peak to peak swaying amplitude Y the mean of absolute moment M(MX), the zero crossing rates of position ZCR(Y) and the velocity ZCR(VY). The kurtosis of the moment about the ML-axis K(MX) was also included in further analysis.

Table 3.

Sway variables in the anterior-posterior direction.

	Low(Y)	C(Y)	Y	C(VY)	VY	K(MX)	M(MX)	STD(MX)	ZCR(Y)	ZCR(VY)
Low(Y)	1.00	0.88	0.88	0.88	0.88	0.09	0.60	0.62	0.28	-0.19
C(Y)	0.88	1.00	1.00	1.00	1.00	0.05	0.60	0.62	0.43	0.02
Y	0.88	1.00	1.00	1.00	1.00	0.05	0.60	0.62	0.43	0.02
C(VY)	0.88	1.00	1.00	1.00	1.00	0.05	0.60	0.62	0.43	0.02
VY	0.88	1.00	1.00	1.00	1.00	0.05	0.60	0.62	0.43	0.02
K(MX)	0.09	0.05	0.05	0.05	0.05	1.00	-0.08	0.03	0.11	-0.04
M(MX)	0.60	0.60	0.60	0.60	0.60	-0.08	1.00	0.99	-0.18	-0.29
STD(MX)	0.62	0.62	0.62	0.62	0.62	0.03	0.99	1.00	-0.17	-0.29
ZCR(Y)	0.28	0.43	0.43	0.43	0.43	0.11	-0.18	-0.17	1.00	0.41
ZCR(VY)	-0.19	0.02	0.02	0.02	0.02	-0.04	-0.29	-0.29	0.41	1.00

Table 5 shows the correlation structure of variables that depict the plane interpretation of posturography. Only the area variables were highly correlated. We therefore excluded the area of a 95% confidence ellipse CEA from further analysis, because the whole area EA contains more information about swaying.

Table 5.

Sway variables in plane interpretation

	Low(T)	Low(N)	MERR	LEN	EA	CEA	CRI(T)	ZCR(W)	STD(WT)	ROMB
Low(T)	1.00	-0.63	0.13	-0.16	0.11	0.09	-0.01	-0.44	0.37	0.05
Low(N)	-0.63	1.00	-0.05	0.11	0.10	0.12	-0.06	-0.23	-0.03	0.12
MERR	0.13	-0.05	1.00	0.47	0.58	0.49	-0.10	-0.13	0.03	0.27
LEN	-0.16	0.11	0.47	1.00	0.74	0.68	-0.31	0.08	-0.08	0.53
EA	0.11	0.10	0.58	0.74	1.00	0.96	-0.12	-0.24	0.06	0.54
CEA	0.09	0.12	0.49	0.68	0.96	1.00	-0.04	-0.24	0.07	0.51
CRI(T)	-0.01	-0.06	-0.10	-0.31	-0.12	-0.04	1.00	0.10	0.04	-0.26
ZCR(W)	-0.44	-0.23	-0.13	0.08	-0.24	-0.24	0.10	1.00	-0.40	-0.33
STD(WT)	0.37	-0.03	0.03	-0.08	0.06	0.07	0.04	-0.40	1.00	0.03
ROMB	0.05	0.12	0.27	0.53	0.54	0.51	-0.26	-0.33	0.03	1.00

The variable LEN is the total length of the swaying path. Other variable names and abbreviations are given in Table 8.

Table 8.

Selected swaying variables

Variable abbreviation	Variable name
Low(T)	Time spent in low variation periods
Low(N)	Number of low variation periods
X	Peak to peak amplitude of ML-swaying line
Y	Peak to peak amplitude of AP-swaying line
MERR	Total squared moment error
M(MX)	Mean absolute moment about ML-axis
M(MY)	Mean absolute moment about AP-axis
EA	Area of an ellipse that encloses all stabilogram samples
ZCR(X)	Zero crossing rate over ML-axis
ZCR(Y)	Zero crossing rate over AP-axis
ZCR(VX)	Zero crossing rate of ML-velocity
ZCR(VY)	Zero crossing rate of AP-velocity
ZCR(W)	Zero crossing rate of weight
K(MX)	Kurtosis of moment about ML-axis
K(MY)	Kurtosis of moment about AP-axis
CRI(T)	Critical time when control type changes
ROMB	Romberg’s quotient

In Table 6, the correlations of the selected mediolateral and anterior-posterior direction variables are shown. The zero crossing rates of the velocities in the anterior-posterior ZCR(VY) and mediolateral ZCR(VX) directions are highly correlated. However, we include both variables for further analysis, because these measure conceptionally different aspects of swaying.

Table 6.

Variable selection in the mediolateral and anterior-posterior directions

	X	Y	K(MX)	K(MY)	M(MX)	M(MY)	ZCR(X)	ZCR(Y)	ZCR(VX)	ZCR(VY)
X	1.00	0.76	0.04	0.03	0.47	0.63	0.34	0.41	0.17	0.33
Y	0.76	1.00	0.05	0.03	0.62	0.58	0.11	0.43	-0.03	0.02
K(MX)	0.04	0.05	1.00	0.12	0.03	0.08	-0.03	0.11	-0.06	-0.04
K(MY)	0.03	0.03	0.12	1.00	0.01	0.01	0.06	0.02	-0.03	-0.02
STD(MX)	0.47	0.62	0.03	0.01	1.00	0.67	-0.22	-0.17	-0.28	-0.29
STD(MY)	0.63	0.58	0.08	0.01	0.67	1.00	-0.30	0.00	-0.36	-0.23
ZCR(X)	0.34	0.11	-0.03	0.06	-0.22	-0.30	1.00	0.46	0.62	0.65
ZCR(Y)	0.41	0.43	0.11	0.02	-0.17	0.00	0.46	1.00	0.33	0.41
ZCR(VX)	0.17	-0.03	-0.06	-0.03	-0.28	-0.36	0.62	0.33	1.00	0.88
ZCR(VY)	0.33	0.02	-0.04	-0.02	-0.29	-0.23	0.65	0.41	0.88	1.00

For abbreviations and explanations of the variables see Tables 2 and 4.

Table 2.

Variables in the mediolateral (ML) direction and abbreviations for the variable names in Table 1

Variable abbreviation	Variable name
Low(X)	Amplitude of ML-swaying during low variation
C(X)	Amplitude of 95% ML-swaying line
X	Amplitude of ML-swaying line
C(VX)	Mean velocity along C(X)
VX	Mean velocity along ML-swaying line
K(MY)	Kurtosis of moment about AP-axis
M(MY)	Mean moment about AP-axis
STD(MY)	Standard deviation of moment about AP-axis
ZCR(X)	Zero crossing rate over ML-axis
ZCR(VX)	Zero crossing rate of ML-velocity

Table 4.

Variables of anterior-posterior (AP) direction and abbreviations for variable names in Table 3

Variable abbreviation	Variable name
Low(Y)	Amplitude of AP-swaying during low variation
C(Y)	Amplitude of 95% AP-swaying line
Y	Amplitude of AP-swaying line
C(VY)	Mean velocity along C(Y)
VY	Mean velocity along AP-swaying line
K(MX)	Kurtosis of moment about ML-axis
M(MX)	Mean moment about ML-axis
STD(MX)	Standard deviation of moment about ML-axis
ZCR(Y)	Zero crossing rate over AP-axis
ZCR(VY)	Zero crossing rate of AP-velocity

Table 7 shows the correlation of sway path length and amplitudes in the mediolateral and anterior-posterior directions. The length of a swaying path is highly correlated with the anterior-posterior Y and mediolateral X direction amplitudes (Table 4). We reject the swaying trace length LEN from further analysis because the variables are intercorrelated and the amplitudes of the individual direction components X and Y contain more information than the swaying path length alone.

Table 7.

Variable selection of swaying amplitudes

	X	Y	LEN	ZCR(X)	ZCR(Y)	ZCR(W)	STD(WT)
X	1.00	0.76	0.91	0.34	0.41	0.25	-0.09
Y	0.76	1.00	0.96	0.11	0.43	-0.04	-0.07
LEN	0.91	0.96	1.00	0.21	0.45	0.08	-0.08
ZCR(X)	0.34	0.11	0.21	1.00	0.46	0.56	-0.15
ZCR(Y)	0.41	0.43	0.45	0.46	1.00	0.28	-0.16
ZCR(W)	0.25	-0.04	0.08	0.56	0.28	1.00	-0.40
STD(WT)	-0.09	-0.07	-0.08	-0.15	-0.16	-0.40	1.00

As a result of the correlation analysis, the information contained in the 30 genuine time-domain variables can be expressed with 17 variables without significant information loss. These variables are listed in Table 8. We considered the possibility that the number of variables can be reduced further with principal component analysis (PCA); however, if that is done, we risk losing the intuitive meaning of the variables.

With the selected sway variables, we conducted a factor analysis. We excluded variables from analysis that were associated with only modest loading on all factors. The threshold for the exclusion was 0.1. We also excluded variables with correlations over 0.7 and selected variables that are commonly used. In addition to the commonly used variables we included variables that we calculated and considered important. The results of the analysis suggest that three different strategies (factors) are used to maintain an upright stance (Table 9). With respect to factor 1, the variables that measure swaying extents and torque received high loadings. With respect to factor 2, the variables that measure the activity around stationary points are pronounced. For factor 3, activity in the anterior-posterior direction showed high loading. In addition, the critical time at which open loop control changes to closed loop control showed sufficiently high negative loading, indicating poor adaptation (changes in) postural control by vestibular influx as the system had to “recalibrate” the postural control repeatedly. The three selected factors accounted for 63% of the variance in our selected variable set. We suggest that the factors can be characterized as follows: factor 1 is a torque control, factor 2 a positional control and factor 3 an anticipatory control.

Table 9.

Factors

Variable	Factor 1	Factor 2	Factor 3
Low(T)	-0.54	-0.45	-0.25
X	0.73	0.38	0.41
Y	0.75	0.10	0.48
MERR	0.45	-0.06	0.20
M(MY)	0.81	-0.16	-0.20
M(MX)	0.84	-0.19	-0.03
ZCR(X)	-0.11	0.66	0.34
ZCR(Y)	0.08	0.42	0.69
CRI(T)	-0.09	0.02	-0.55
ZCR(W)	-0.10	0.88	0.07

5. Discussion

Assessment of the value of posturography in clinical use has faced fundamental problems because parameters, measuring techniques and perturbation methods have not been unified and agreed upon. Although a recent consensus meeting did recommend parameters for use in posturography, the recommended parameters were considered to be insufficient for the assessment of balance in several clinical conditions [13]. Much of the uncertainty related to the use of the technique depends on the problem of identifying the clinically relevant outcome variables among those obtained from the posturography signal. In this work, we demonstrated that several of the time domain variables obtained by posturography measure the same aspect of human postural control. For instance, velocity- and amplitude-related variables have a close relationship, as do moment and swaying area variables. All of these variables measure the positional extents of human swaying and are strongly intercorrelated. However, they do not take into account the corrective activity reflected in the sta bilogram. For instance, one large leaning in an otherwise stationary stance may result in large sway amplitudes and area. Therefore, we propose that the activity-related variables should also be used in the evaluation of stabilograms. In particular, the zero crossing rate of the weight signal, ZCR(W), and the standard deviation of the times between successive zero crossings, STD(WT), can provide insight into the structure of a given stabilogram signal. As an example, a long time between successive zero crossings in weight signal may indicate a specific leaning strategy involving knee or hip bending; if a subject slowly bends his or her knees, the time difference in the zero crossing rate of the weight signal ZCR(W) becomes large.

Bigelow and Berne [3] evaluated posturography parameters and related them to habitual falling. The authors concluded that limiting to the conventional eight time domain force platform parameters described by Prieto et al. [18] was not satisfactory but that the inclusion of fractal measures and personal characteristics could predict the fallers. In the assessment of wakefulness of persons using posturography, Forsman et al. [6] evaluated several parameters. A combination of conventional and fractal parameters seemed to predict wakefulness time most efficiently. Interestingly, a detailed analysis of time domain parameters has not been performed earlier, and in several research studies, strongly intercorrelated variables have been used to describe postural stability.

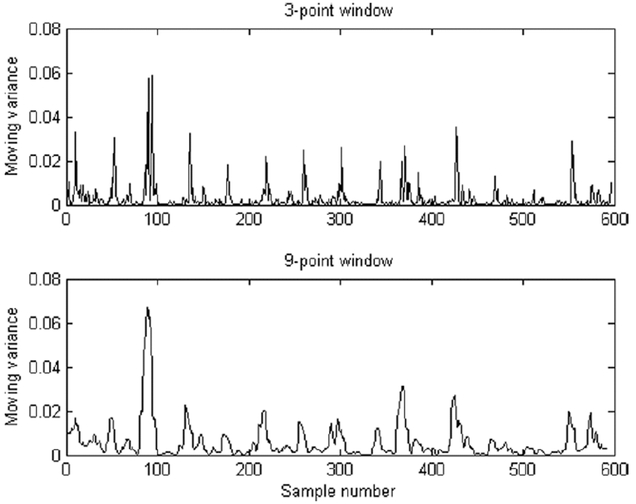
In the present work, the processing of the data and selection of the length of low variation windows of the subject’s weight are important in explaining the outcome of the variables. A short window yields an erratic approximation of local weight variation, while a long window provides a much smoother approximation of local weight variation. However, because all signals in the present study were treated in the same manner, a valid comparison of the number of low variation periods is possible. In Fig. 3 an illustration of window lengths of 3 and 9 is presented. The upper and lower parts are mirrored about x-axis for clarity. Records that show only a few low variance periods indicate that the subject either stood quietly or swayed considerably during the measurement period. On the contrary, records with many low variance periods tend also to have many “spiky” periods, which are indicators of large corrections in posture.

Fig. 3.

Short moving variance window gives us an erratic approximation of local variation while long window suppresses the effect of individual postural controlling actions by averaging.

Moment and zero crossing variables have certain drawbacks when applied to the stabilogram as a whole. The standard deviation of moment, for instance, can be used to reduce possible transients in a signal. The pres ence of transients can be detected using the kurtosis of the moment signal or the total moment error, but the nature of the transients must be studied with individual signals. For zero crossing variables, a possible trend in either the anterior-posterior or mediolateral direction can make the variable useless. This problem can be avoided either by removing the trend in a component of the stabilogram in question or with the zero crossing rate of the respective velocity signal. By using the zero crossing rate of a weight signal, it is possible to detect the transients in a stabilogram signal. Usually, the time delay between two zero crossings is small and quite constant, while during the transients, the time delay is greater. Zero crossing rates have also been used in other studies [18]. In the time domain, the zero crossing rate varies during a measurement due to postural controlling actions.

Variation in zero crossing rates indicates that the components of postural control occur apparently randomly. For this reason, the application of frequency domain analysis might result in the loss of informative aspects of human swaying. The analysis of the frequency-domain behavior of posturography signals will be addressed in our next work.

In the effort of studying the force platform outcome variables authors have commonly used sway position, swaying velocity, and swaying area [2,5,7]. In addition swaying moments have been used [16,24]. Romberg’s quotient is the most common variable and it correlates well (over 0.5) with trace length and swaying areas. However, it also has low correlation (less than 0.35) with all other variables presented in this work. This suggests that it contains information that the other variables can’t provide. On the basis of the results of our factor analysis we propose that several variables should be combined in order to reveal different aspects of human swaying process. For instance, zero crossing rates and critical time provide information about how a stabilogram is produced. In order to verify the results of factor analysis we ran it also on ten random subsets of our data and they yielded similar results. In verification test each subset contained variables from1000 subjects.

6. Conclusion

Table 9 lists the selected variables that are intuitive and that were retained following the correlation analysis. Using our variable set of swaying data obtained with elderly people, these variables delineate three different factors. We consider these factors to represent different postural control strategies in which the variables that characterize human swaying are weighted in different ways. One person may sway over a large area, while another may oscillate only slightly around a stationary point. Other persons characteristically have a short critical time for changing the control type from an open loop to a closed loop. In this case the movements occur in a small interval in anterior posterior direction. On the basis of our findings we conclude that we have to study human balance with variables that describe different aspects of swaying.