Highlights
-
•
The cortical dynamics during the mental calculating processes was clarified by using a whole-scalp magnetoencephalography.
-
•
The inferior parietal area (IPA) and superior temporal area (STA) of each hemisphere were activated with the strongest activation in the left STA.
-
•
The left IPA activated the earliest, and was followed by the activation of the left STA, the right IPA and the right STA.
Keywords: Calculation, Magnetoencephalography, Time course, Inferior parietal area, Superior temporal area
Abstract
Objective
We elucidated active cortical areas and their time courses during simple calculation by using whole-scalp magnetoencephalography.
Methods
Twelve healthy volunteers were asked to view meaningless figures (figure viewing) or digits (digit viewing) and add single digits (calculation). The magnetic signals of the brain were measured using a helmet-shaped 122-channel neuromagnetometer during the three tasks.
Results
The occipital, inferior posterior temporal, and middle temporal areas of each hemisphere and the left superior temporal area (STA) were activated during all tasks (approximately 250 ms after the stimulus onset). The calculation-related sources were located in the left inferior parietal area (IPA) in 8 subjects, right IPA in 5, left STA in 3, right STA in 5, right inferior frontal area in 2, and left inferior frontal area in 1. The IPA and STA of the left hemisphere were activated more strongly and significantly earlier than those of the right hemisphere: the left IPA was activated first (mean activation timing: 301 ms), followed by activations of the left STA (369 ms), right IPA (419 ms), and right STA (483 ms).
Conclusions
Simple digit addition is executed mainly in the left IPA and left STA, followed by the recognition processes of results in the right IPA and right STA.
Significance
This study clarified the cortical process during simple calculation, with excellent temporal and spatial resolution; the IPA and STA of the left hemisphere were activated more strongly and earlier than the corresponding areas of the right hemisphere.
1. Introduction
Calculation is a human intellectual ability that includes recognition, computation, solution of numbers, and arithmetical signs. Acalculia, described first by Henschen (1919), is the pathology of losing the acquired calculating ability, which can exist with or without general intellectual deficits involving aphasia, alexia, agraphia, and visuospatial agnosia (Benson and Weir, 1972, Grafman et al., 1982, Hécaen et al., 1961, Henschen, 1919, Takayama et al., 1994, Warrington, 1982). Many clinical case studies showed that acalculia can occur not only with the occurrence of parieto-occipital lesions in the left hemisphere (Benson and Weir, 1972, Grafman et al., 1982, Hécaen et al., 1961, Takayama et al., 1994, Warrington, 1982) but also with the development of medial frontal and prefrontal lesions in the left hemisphere (Lucchelli and De Renzi, 1993, Tohgi et al., 1995). A large number of studies on patients suggest that many brain areas contribute to the calculation processes, but it has been difficult to elucidate which area would play a crucial role in these processes.
Recently, meta-analyses of studies by functional MRI (fMRI) showed the calculation-related areas are located in the parietal, prefrontal, premotor, posterior temporal, and subcortical areas, which differed depending on the calculation tasks (Arsalidou and Taylor, 2011). Previous electroencephalographical studies using an event-related paradigm showed that negative components from 200 to 300 ms or positive slow components from 400 to 800 ms might be associated with the calculation processes (Dehaene et al., 1999, Iguchi and Hashimoto, 2000, Pauli et al., 1994, Ruchkin et al., 1991). In addition, the theta activities in the insular cortex; hippocampus cingulate cortex; and superior temporal, superior parietal, and frontal areas (FAs) were enhanced by mental arithmetic-induced workload (Sammer et al., 2007). Studies using magnetoencephalography (MEG) revealed that theta bursts appeared in the frontal cortices of both hemispheres (Sasaki et al., 1994), frontal midline theta was generated in the medial prefrontal and the dorsal anterior cingulate cortices (Ishii et al., 2014), and frequency components below 12 Hz in the hippocampus increased during continuous mental calculation (Tesche, 1997). These previous studies using neuroimaging, EEG, and MEG showed the time course of activation but could not accurately indicate the activated areas.
We elucidated the cortical activation areas and their time course by whole-scalp MEG during the calculation processes. We used simple addition to reduce the retrieval of working memory and adapted an event-related method to evaluate the pure arithmetic process. We hypothesized that if each area related to calculation plays a specific role, the activation timing of sources would be different and source strengths in essential areas would be strong during each processing.
2. Methods
Data acquisition and analysis in this study were performed in the same manner as that in the previous study by the co-author Nishitani (Nishitani et al., 1999).
2.1. Subjects
Twelve healthy Japanese volunteers (five males and seven females; ages 23–37 years, mean ± S.D.: 26.0 ± 4.4 years) participated in this study. All subjects were right-handed as assessed by the Edinburgh Inventory (Oldfield, 1971), and their education level was over 16 years. None of them had a previous history of neurological or visual disorders, and they did not know Russian or Greek letters. Informed consent was obtained from each subject after full explanation of the study. This research was performed in accordance with the guidelines of the Committee of Medical Ethics, National Rehabilitation Center for the Disabled.
2.2. Experimental paradigm
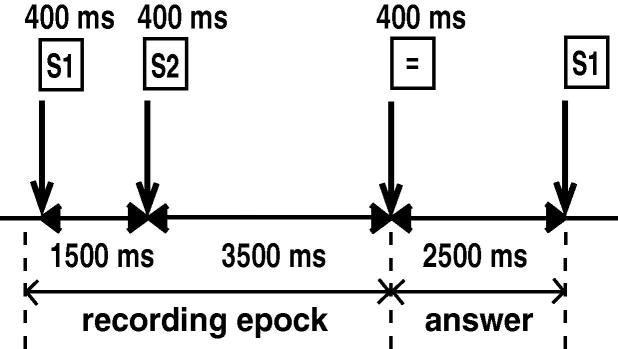
The subject was seated in a magnetically shielded room. The head was positioned in a helmet-shaped dewar and tightly attached against its inner vault. The visual stimuli, produced using MultiStimu Software running on a NEC PC-98 computer, consisted of 41 digits (1–49 except 10, 11, 20, 22, 30, 33, 40, and 44), 7 Cyrillic letters (Russian), 2 Greek letters, and 5 meaningless figures composed of Cyrillic or Greek letters. The stimuli were randomly presented in yellow script on a black screen placed 1 m in front of the subject through a projector (VistaGRAPHX2500, ELECTROHOME) that was positioned outside the magnetically shielded room. The size of the projected stimuli on the screen was 4.5 × 6.0 cm (height × width), and the stimuli were presented for 400 ms. The subjects were asked to (i) view letters or figures (figure viewing), (ii) view digits (digit viewing), and (iii) mentally add the single digits (calculation). In digit viewing, single and double digits were combined to exclude automatic calculation. During calculation, the subjects were instructed to add the second digit (S2) to the first digit (S1) mentally and tell the examiner the result through an interphone after the third stimulus [S3 (‘=’)]. The examiner checked whether each answer was correct. S1 and S2 were different figures or digits in every stimulus epoch in all tasks. Interstimulus intervals S1–S2, S2–S3, and S3–S1 were 1500, 3500, and 2500 ms, respectively (Fig. 1). During the measurements, the subjects were asked to view the visual stimuli and avoid blinking or body movement as much as possible.
Fig. 1.
Stimulus epoch. The subjects were asked to mentally add the second digit (S2) to the first digit (S1) and tell the result to the examiner just after S3 (‘=’). S1: the first stimulus, S2: the second stimulus, S3: the third stimulus.
2.3. MEG recordings and data acquisition
The magnetic signals of the brain were measured using a helmet-shaped 122-channel neuromagnetometer (Neuromag Ltd., Helsinki, Finland), which employs 61 pairs of orthogonally arranged planar first-order gradiometers (Ahonen et al., 1993). This device measures the two orthogonal derivatives of the radial magnetic field component and detects the typically largest signal just above the local cerebral current source. The exact head position with respect to the sensor array was measured using head position indicator coils placed on the scalp at three defined sites at the beginning of each session. To allow the alignment of the MEG and magnetic resonance imaging (MRI) coordinate systems, the locations of coils with respect to anatomical landmarks on the head were measured using a three-dimensional (3D) digitizer (Isotrak 3S1002; Polhemns Navigation Sciences, Colchester, VT). Head MRIs were obtained using a 1.5-tesla Siemens Magnetom Plus (Siemens Medical Systems). To monitor eye movements and blinks, bipolar horizontal and vertical electro-oculograms (EOGs) were recorded from electrodes placed below and above the right eye and bilaterally on the outer canthi. The recording bandpass was 0.03–100 Hz for MEG and 0.05–3000 Hz for EOG. The sampling rate for digital conversion was 403 Hz. Epochs containing signals exceeding 1500 fT/cm in MEG or 150 μV in EOG were automatically rejected. Forty artifact-free epochs were recorded for each session. At least two sessions were repeated to confirm the signal reproducibility for each task. The order of the three tasks was counterbalanced across subjects.
2.4. Data analysis
The MEG waveforms of each subject were digitally low-pass filtered at 20 Hz and high-pass filtered at 0.5 Hz. The signals of each session were averaged time-locked to S2 from 200 ms before to 3000 ms after S2 stimulus with a 200 ms pre-stimulus. Moreover, the waveforms obtained in the two sessions of each task were averaged offline.
To elucidate specific areas of the calculation processes, we analyzed the sources of magnetic fields after S2 according to an approach described previously (Hämäläinen et al., 1993, Nishitani et al., 1999, Nishitani and Hari, 2000). Sources of magnetic fields were modeled as ECDs whose 3D locations, orientations, and current strengths were estimated from the measured signals. A spherical head model was adopted on the basis of the subjects’ MRIs (Hämäläinen et al., 1993). The ECDs that best explained the most dominant signals were calculated for every 1-ms segment over a time period of 50 ms containing the local maximum signal and determined by a least-squares search based on the data of 16–20 channels at areas including the local maximum signal. We accepted only ECDs accounting for at least 80% of the field variance at the selected periods of time for each subset of channels and with confidence volume of <1 cm3. ECDs with the highest goodness-of-fit (g) value and the smallest confidence volume were accepted for further analysis. The analysis periods and channels were extended to the entire measurement time and to all channels by using a multi-dipole model where the strengths of the previously found ECDs were allowed to change as a function of time while their locations and orientations were kept fixed (Hämäläinen et al., 1993). The validity of predicted waveforms by the multi-dipole model was evaluated by comparing measured signals with the response predicted by the model using single-space projection (Uusitalo and Ilmoniemi, 1996). If signals were left unexplained by the model at any channel, a new ECD was identified on the residual field pattern and re-evaluated for a more accurate estimation of generator areas. The goodness of fit of the model was calculated over all 122 channels and over the entire time period. This approach has been explained in detail by Hämäläinen et al. (1993) and has been successfully applied in our previous studies (Nishitani et al., 1999, Nishitani and Hari, 2000).
Finally, the estimated dipoles were superimposed on the subject’s own MRI according to the alignment of the MRI and MEG coordinate systems (Hämäläinen et al., 1993). The source locations on the 3D MRI of each subject were transposed onto the Talairach’s standard brain space (Talairach and Tournoux, 1988) with spatial normalization by using the following coordinate system; x-axis perpendicular to the other two axes through the anterior commissure, y-axis passing through the anterior and posterior commissure, and z-axis perpendicular to the y-axis through the anterior commissure at the middle plane of the brain (Nishitani et al., 1999). The x (left/right), y (anterior/posterior), and z (superior/inferior) coordinates were expressed as millimeters from the anterior commissure at the midline of the atlas of the Talairach’s standard brain space. Calculation-specific source locations were determined in all subjects, with comparison between source locations during calculation and those during digit viewing.
2.5. Statistical analysis
The peak latencies and the source strengths were compared with the results of student’s unpaired t-test between tasks and between locations because the number of sources in the STA was small.
3. Results
3.1. Behavioral performance
All subjects answered correctly, calculating the results with an accuracy of 100% during calculation.
3.2. MEG waveforms
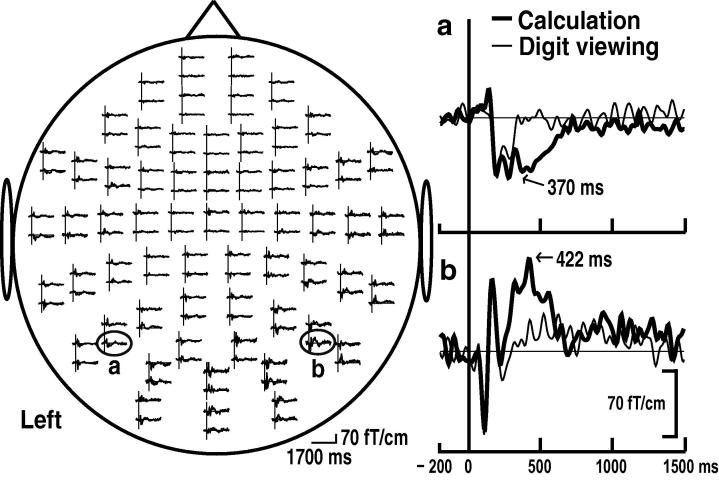
We estimated the reproducibility of the MEG waveforms and analyzed these MEG signals. During the figure and digit viewing tasks, magnetic responses were observed bilaterally from 102 to 257 ms after the S2 stimulus at the posterior channels. The left column of Fig. 2 shows typical MEG signals at whole channels, time-locked to S2 during the calculation task from Subject 1. The superimposed waveforms with MEG signals from the bilateral posterior channels during the calculation and digit viewing tasks were magnified and are shown in the right column of Fig. 2. Although both waveforms were congruent from 0 to 250 ms, differences of waveforms between the two tasks appeared during 250–600 ms, with major peaks at 370 and 422 ms (Fig. 2, right a and b). The waveforms after 1500 ms did not show any peaks during any of the three tasks.
Fig. 2.
Whole-scalp magnetic responses time-locked to S2 during calculation from subject 1. Responses of paired coils in 64 sites are shown as the upper and lower trace in each pair, which are the responses along the latitudinal and the longitudinal derivation of the magnetic field perpendicular to the measurement site (left). Responses from the left posterior channel (a) and right posterior channel (b) are magnified in the right column, superimposed with responses to calculation and digit viewing (right).
3.3. Source distributions
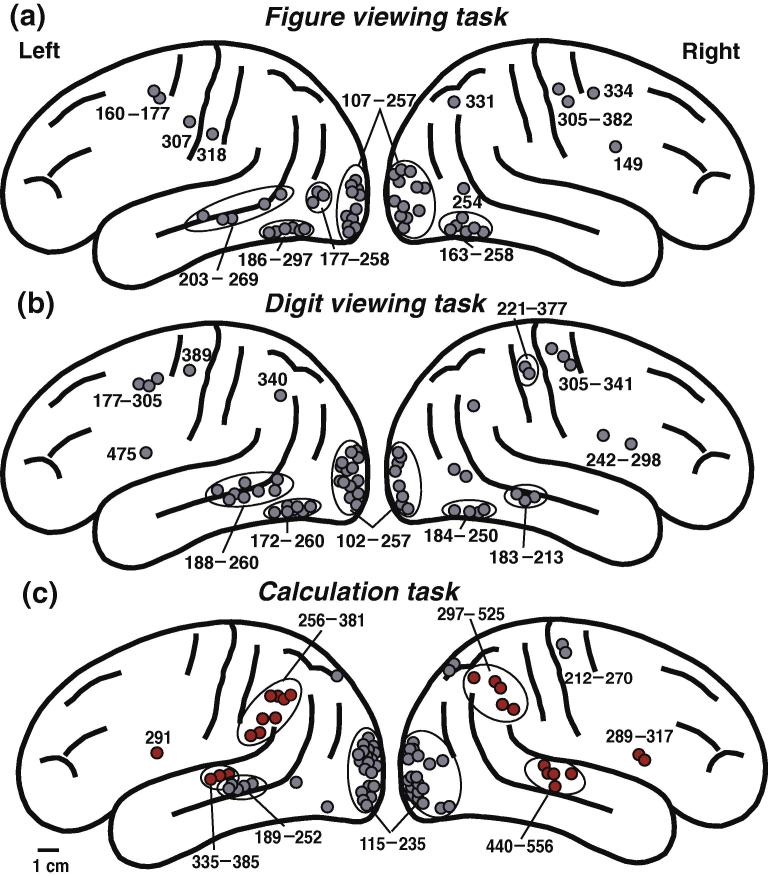
The 3D source locations of each subject were projected onto a schematic brain according to Talairach’s standard brain (1988) (Fig. 3). There was interindividual difference in the number of dipoles. During the figure viewing task, the ECDs were obtained in the occipital and inferoposterior temporal areas (ITA) of each hemisphere and the left middle temporal area (MTA). Other sources were found in the dorsolateral FA and the precentral areas of each hemisphere, the postcentral area of the left hemisphere, and in the right parietal area (Fig.3a). During the digit viewing task, additional ECDs were observed in the right MTA (Fig.3b). During the calculation task, ECD in the occipital area was located first, followed by ECDs in the ITA, the superior temporal area (STA) of each hemisphere, and MTA in the left hemisphere during 250 ms after the stimulus onset (Fig.3C, gray circle). The order of ECDs after 250 ms depended on the subject (Fig.3C, red circle). Fig. 4 shows the MEG signals, isocontour maps, and the ECD locations in the inferior parietal area (IPA) of each hemisphere from subject 2 superimposed on his own MRI during calculation. Table 1 and red circles in Fig.3C show the calculation-related ECD locations and their peak latencies in the bilateral IPA, STA, and FA compared with those observed during digit viewing in all subjects.
Fig. 3.
Source locations for magnetic responses from all subjects during (a) the figure viewing task, (b) digit viewing task, and (c) calculation task on a schematic brain according to Talairach’ s human atlas (1988). Red circles in the calculation task (C) were calculation-related source locations. The source locations on the 3D MRI of each subject were projected onto the schematic brain. The numbers indicate the peak latencies (ms) of the activations. Interindividual difference was observed in the number of dipoles. Each black circle indicates the assumed dipole location during each task from all subjects.
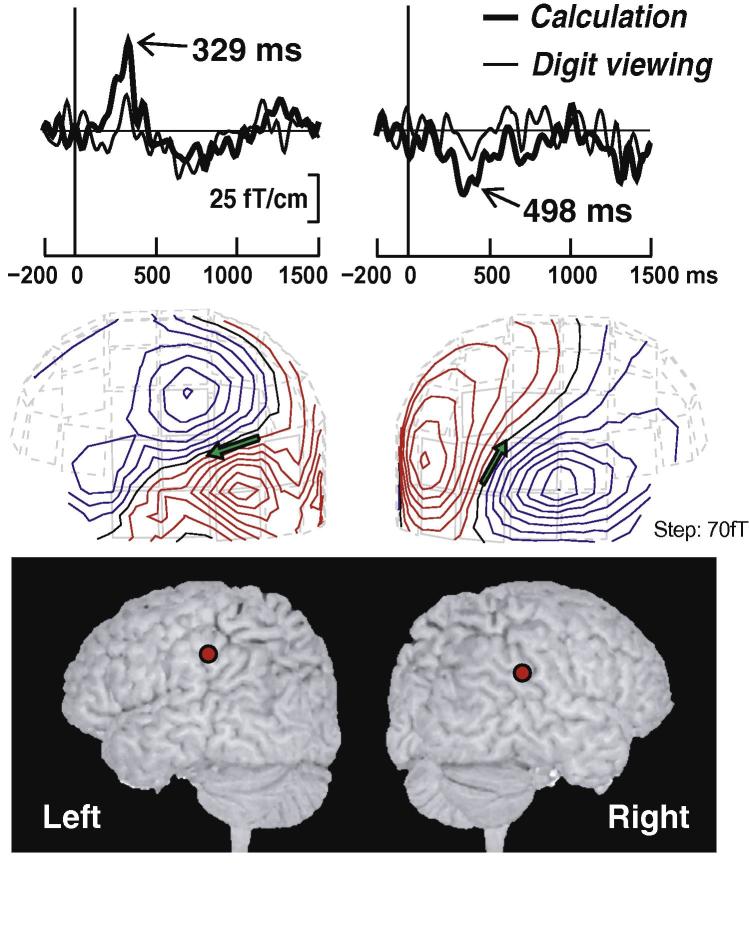
Fig. 4.
Top: Magnetic responses from the left and right middle channels of subject 2 during calculation. Middle: Magnetic field patterns of the responses peaks during calculation. The sensor array is viewed from the right and left. The arrows indicate the dipoles. The isocontours are separated by 15 fT. The areas with red lines indicate magnetic flux emerging from the head, and the areas with blue lines indicate the flux into the head. Bottom: The locations in the inferior parietal area of each hemisphere of one subject during calculation, superimposed on the subject’s own 3D MRI. Left and right figures show the brain surface viewed from the left and right sides, respectively.
Table 1.
Calculation-related equivalent current dipole locations and their peak latencies.
| Left hemisphere |
Right hemisphere |
|||||
|---|---|---|---|---|---|---|
| IPA | STA | IFA | IPA | STA | IFA | |
| Peak latency (ms) | ||||||
| Subject 1 | 262.7 | – | – | – | 497.7 | – |
| 2 | 328.8 | – | – | 498.1 | – | – |
| 3 | 381.1 | – | – | 525.1 | – | – |
| 4 | – | 335.2 | – | – | 467.0 | – |
| 5 | 315.8 | – | – | 325.4 | – | 289.2 |
| 6 | – | – | 291.5 | 450.4 | – | 317.0 |
| 7 | 256.5 | – | – | – | 439.2 | – |
| 8 | – | 385.2 | – | – | – | – |
| 9 | 276.3 | 385.4 | – | – | 556.7 | – |
| 10 | 291.8 | – | – | – | – | – |
| 11 | 295.5 | – | – | 297.2 | – | – |
| 12 | – | – | – | – | 455.2 | – |
| ECD locations in Talairach coordinates (mean ± SEM; cm) | ||||||
| x | −51.3 ± 7.8 | −54.9 ± 6.0 | −57.0 | 44.6 ± 4.9 | 57.6 ± 7.1 | 54.5 ± 2.1 |
| y | −37.1 ± 13.5 | −14.6 ± 5.0 | 14.8 | −41.8 ± 9.4 | −21.3 ± 6.3 | 15.5 ± 1.5 |
| z | 32.2 ± 12.0 | 1.6 ± 7.8 | 17.0 | 39.1 ± 10.4 | 6.5 ± 4.1 | 16.0 ± 3.1 |
| Brodmann’s Area | 40 | 22 | 44 | 40 | 22 | 44 |
IPA: inferior parietal area; STA: superior temporal area; IFA: inferior frontal area; –: ECD was not determined.
Coordinates x (positive to right), y (positive to anterior), and z (positive to upward) are from the point of origin situated at the anterior commissure.
Fig. 5 (top) shows the peak latencies of source waveforms in the IPA and STA of each hemisphere during three tasks. The activation timing of the left STA during the calculation task was significantly longer than that during the figure or digit viewing task (p < 0.005). During the calculation task, the mean peak latency of the ECD was first in the left IPA (301 ms after the stimulus onset), followed by those in the left STA (369 ms), the right IPA (419 ms), and the right STA (483 ms). The left IPA activation was significantly earlier than that of the right IPA (p < 0.05). However, peak latencies of the right IPA and the right STA were not statistically significantly different.
Fig. 5.
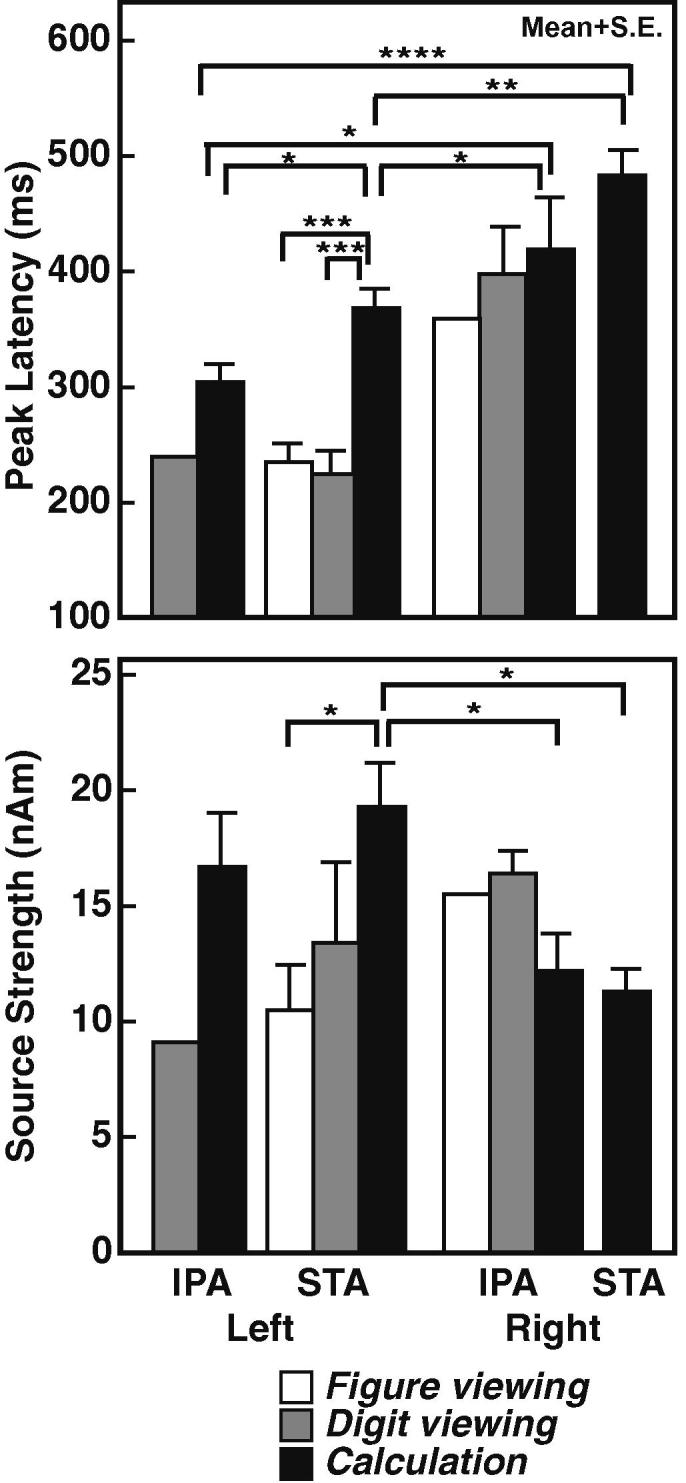
Mean ( + S.E.) peak latencies of source waveforms (top) and source strengths (bottom) in the IPA and STA of both hemispheres in the three tasks. *p < 0.05, **p < 0.01, ***p < 0.005, ****p < 0.001, IPA; the inferior parietal area, STA; the superior temporal area.
Fig. 5 (bottom) shows the source strengths of four areas during the three tasks. During the calculation task, the activation tended to be stronger in the left than in the right hemisphere. The left STA during the calculation task was activated most strongly among all areas and all tasks; the activation was significantly stronger than those of the right STA and the right IPA during the calculation task (p < 0.05) and in the left STA during the figure viewing task (p < 0.05). The source strengths of the right hemisphere did not differ among the tasks.
4. Discussion
Our study showed two prominent aspects without any subtraction between the tasks, unlike previous neuroimaging studies. First, ECDs in the IPA and STA of each hemisphere were obtained during simple addition, with the strong activations in the left IPA and STA. Second, the cortical activations during the simple addition process were elucidated with high temporal resolution.
4.1 Figure viewing and digit viewing
During the figure and digit viewing tasks, activations in the occipital area and the ITA of each hemisphere were obtained in most subjects and the MTA and left STA in several subjects. Activations in the occipital area, ITAs, and MTA during the figure and digit viewing tasks indicated the perception of the visual form of both meaningful and meaningless letters. Pesenti et al. (2000) showed that the bilateral occipito-parietal areas are activated in the recognition processing of Arabic digits. Activation in the MTA was observed in a larger number of subjects during the digit viewing task than during the figure viewing task. This difference could be related to the ability to recognize the stimuli: digits are easily understood and read by the subjects, but figures composed of Russian or Greek letters are not. Activations in the left STA and MTA during the digit viewing task suggest that the subjects recognize Arabic numbers not only as symbols but also meaningful letters and read or silently repeat the numbers (Cowell et al., 2000, Howard et al., 1992, Kamada et al., 1998, Paulesu et al., 1993, Price et al., 1994). Activation in the left STA during the figure viewing task suggests the analysis of detailed properties of meaningless figures (Robertson and Lamb, 1991).
4.2. Calculation
The difference of waveforms between the calculation and the digit viewing tasks from 250 to 800 ms after the S2 onset was observed. This finding suggests that mental addition proceeds after the recognition of digits and silent reading processes during the digit viewing task, because the response time for answers in a simple addition task was 800–1000 ms (Kuo et al., 2008, Menon et al., 2000). This result was in line with those of the previous ERP studies (Dehaene et al., 1999).
4.3. Function associated with the left IPA and STA
The time course of the left STA and left IPA activations was in the order of the left STA in the digit viewing task, the IPA in the calculation task, and then the left STA in the calculation task (Fig. 3, Fig. 5). The strong activations in the left IPA and left STA, which anatomically corresponded to Brodmann’s area (BA) 40 and 22, were observed during the calculation task. Eight of 12 subjects showed activations in the left IPA, which were clarified in the previous imaging studies (Arsalidou and Taylor, 2011, Cowell et al., 2000, Davis et al., 2009, Ischebeck et al., 2009, Kong et al., 2005, Kuo et al., 2008, Pesenti et al., 2000, Rueckert et al., 1996, Stanescu-Cosson et al., 2000, Zago et al., 2008). Lesion in the left IPA shows isolated acalculia (McNeil and Warrington, 1994, Takayama et al., 1994, Warrington, 1982). Two of four subjects, whose ECDs were not clarified in the left IPA, had activations in the left STA, and one of them showed activations in the FA. This result suggests that calculation strategies differ among subjects. The calculation process was not evoked in some subjects, because the simple adding task did not demand enough quality of calculation for them. Instead, the left STA and FA were activated for managing the calculation process. The current model of arithmetic processes assumes that healthy adults solve digit addition problems by not using an actual computation strategy but by retrieving the answer from stored declarative memories (Campbell and Fugelsang, 2001). Three subjects showed activations in the left STA (BA 22). The different activation timing in the left STA between the digit viewing and calculation tasks (Fig. 5 top) suggests that the left STA contributes to the early and late processing steps of mental calculation. The strongest activation in the left STA during the calculation task implies the possibility that some subjects deal with arithmetic operation by using encoded short sentences in verbal semantic memory (e.g., two added to three equals five). This implication was supported by the Dehaene and Cohen’ s model according to which arithmetic processes are transformed into a phonological code and accessed from a phonological store (Dehaene and Cohen, 1995). The left STA, therefore, plays a role not only in the comprehension of digit stimuli but also in arithmetic operation during simple calculation. This suggestion is in line with results of the previous study showing a linear rCBF increase in the left STA from fixation to reading and from reading to calculation (Sakurai et al., 1996). Our results suggested comprehension of digit in the left STA, execution of calculation in the left IPA, and arithmetic operation (silent reading of calculating results) in the left STA.
4.4. Function associated with the right IPA and STA
The right IPA (BA 40) and STA (BA 22) were activated during calculation in our study. Previous neuroimaging studies using fMRI showed the activation of the right IPA (Arsalidou and Taylor, 2011, Chochon et al., 1999, Levin et al., 1996) but not of the right STA. The fMRI studies with subtraction of activation during the control condition from that during the calculation condition may nullify the activation in the STA. Previous studies indicated that the activation of the right STA had a relationship with word repetition and various aspects of semantics and reflected a component of the response to correct matching (Cowell et al., 2000, Howard et al., 1992, Rossell et al., 2001, St George et al., 1999).
The time courses of the right IPA and STA activations were in line with the results of a previous study, indicating that the right IPA and STA play roles in the phonemic and graphemic audiovisual integration of letters (Raji et al., 2001). In our study, there were no significant differences of the source strengths and latencies of the right IPA between during the digit viewing and the calculation tasks. Previous studies with neuroimaging on mental calculation and number processing showed that the right parietal region was not specific to mental calculation (Gruber et al., 2001). Our results suggest that the right IPA and STA are associated with the recognition process of the calculated results rather than with the essential calculation.
4.5. Frontal activations
Frontal activations during the calculation task involved the verbal working memory, which distributes as an executive front-parietal network of the left hemisphere (Arsalidou and Taylor, 2011, Burbaud et al., 1995, Chochon et al., 1999, Cowell et al., 2000, Dehaene et al., 1999, Gruber et al., 2001, Menon et al., 2000, Pesenti et al., 2000, Rickard et al., 2000, Roland and Friberg, 1985, Rueckert et al., 1996, Sakurai et al., 1996). In the present study, because subjects were requested to add single-digit figures, they may not be required to do a complex processing such as a working memory. However, a few subjects showed activation in the FA. The fMRI study also showed activations in the left inferior frontal (BA 44/45) and parietal regions during the single-addition condition (Kuo et al., 2008). Dehaene et al., 1996, Dehaene et al., 1999 reported left-lateralized activations in the inferior frontal lobe and the angular gyrus during exact addition relative to approximation, and they concluded that exact arithmetic was acquired in a language-specific format and that it recruits networks involved in the left inferior frontal circuit in the word association processes. The fMRI study also showed the recruitment of the bilateral fronto-parietal network during the calculation task (Zago et al., 2008). The frontal activation in our study suggested that subjects used verbal rehearsal strategies and linguistic representation for retrieving arithmetic facts.
4.6. Clinical relevance
We showed the process of simple digit addition in normal subjects. First, visual digit stimuli are comprehended in the occipital area and the ITA of both hemispheres. Second, Arabic numbers are transformed into semantic letters by silent reading in the STA of the left hemisphere; the essential calculation is then executed in mainly the left IPA or the arithmetic operation in the STA. Finally, the recognition of calculated results involves the right IPA and STA. These brain regions and their networks are involved in the calculation process. In addition, which brain regions are used during calculation depends on the difficulty of calculation task itself. A complex arithmetic calculation requires the working memory manipulation systems, which are the left inferior fronto-temporal network involved in the retrieval and the fronto-parietal network for attentional and spatial processes (Arsalidou and Taylor, 2011, Burbaud et al., 1995, Chochon et al., 1999, Cowell et al., 2000, Dehaene et al., 1999, Gruber et al., 2001, Menon et al., 2000, Pesenti et al., 2000, Rickard et al., 2000, Roland and Friberg, 1985, Rueckert et al., 1996, Sakurai et al., 1996, Zago et al., 2008). Previous clinical reports showed that patients with acalculia were characterized by many lesions such as the parieto-occipital, medial frontal, and prefrontal lesions in the left hemisphere (Benson and Weir, 1972, Grafman et al., 1982, Hécaen et al., 1961, Takayama et al., 1994, Warrington, 1982, Lucchelli and De Renzi, 1993, Tohgi et al., 1995). The results of our present study and those of the previous imaging studies of arithmetic calculation in normal subjects will be useful to evaluate the lesion of a patient with acalculia in clinical practice.
5. Conclusion
In this study, we elucidated active cortical areas and their time courses during simple calculation by using MEG. The simple digit addition is processed as follows: first, the comprehension of digit stimuli and the transformation of Arabic numbers into semantic letters by silent reading in the STA of the left hemisphere; second, the essential calculation executed in the left IPA or the arithmetic operation in the STA; and finally, the recognition process of the calculated results in the right IPA and STA.
Disclosure
The authors declare that they have no conflicts of interest.
Acknowledgments
This study was supported by the Research Grant for Research on Brain Science H12-Brain-023 from the Japan Ministry of Health, Labour and Welfare. The MRIs were acquired at the Medical Imaging Center of National Rehabilitation Center for the Disabled.
References
- Ahonen A.I., Hämäläinen M.S., Kajola M.J., Knuutila J.E.T., Laine P.P., Lounasmaa O.V., Parkkonen L.T., Simola J.T., Tesche C.D. 122-Channel SQUID instrument for investigating the magnetic signals from the human brain. Phys. Scripta. 1993;49:198–205. [Google Scholar]
- Arsalidou M., Taylor M.J. Is 2 + 2 = ? Meta-analyses of brain areas needed for numbers and calculations. Neuroimage. 2011;54:2382–2393. doi: 10.1016/j.neuroimage.2010.10.009. [DOI] [PubMed] [Google Scholar]
- Benson D.F., Weir W.F. Acalculia: acquired anarithmetia. Cortex. 1972;8:465–472. doi: 10.1016/s0010-9452(72)80008-x. [DOI] [PubMed] [Google Scholar]
- Burbaud P., Degreze P., Lafon P., Franconi J.M., Bouligand B., Bioulac B., Caille J.M., Allard M. Lateralization of prefrontal activation during internal mental calculation: a functional magnetic resonance imaging study. J. Neurophysiol. 1995;74:2194–2200. doi: 10.1152/jn.1995.74.5.2194. [DOI] [PubMed] [Google Scholar]
- Campbell J.I.D., Fugelsang J. Strategy choice for arithmetic verification: effects of numerical surface form. Cognition. 2001;80:21–30. doi: 10.1016/s0010-0277(01)00115-9. [DOI] [PubMed] [Google Scholar]
- Chochon F., Cohen L., van de Moortele P.F., Dehaene S. Differential contribution of left and right inferior parietal lobules to number processing. J. Cogn. Neurosci. 1999;11:617–630. doi: 10.1162/089892999563689. [DOI] [PubMed] [Google Scholar]
- Cowell S.F., Egan G.F., Code C., Harasty J., Watson J.D.G. The functional neuroanatomy of simple calculation and number repetition: a parametric PET activation study. Neuroimage. 2000;12:563–573. doi: 10.1006/nimg.2000.0640. [DOI] [PubMed] [Google Scholar]
- Davis N., Cannistraci C.J., Rogers B.P., Gatenby J.C., Fuchs L.S., Anderson A.W., Gore J.C. The neural correlates of calculation ability in children: an fMRI study. Magn. Reson. Imaging. 2009;27:1187–1197. doi: 10.1016/j.mri.2009.05.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dehaene S., Cohen L. Towards an anatomical and functional model of number processing. Math. Cogn. 1995;1:83–120. [Google Scholar]
- Dehaene S., Tzourio N., Frak V., Raynaud L., Cohen L., Mehler J., Mazoyer B. Cerebral activations during number multiplication and comparison: a PET study. Neuropsychologia. 1996;34:1097–1106. doi: 10.1016/0028-3932(96)00027-9. [DOI] [PubMed] [Google Scholar]
- Dehaene S., Spelke E., Pinel P., Stanescu R., Tsivkin S. Sources of mathematical thinking: Behavioral and brain-imaging evidence. Science. 1999;284:970–974. doi: 10.1126/science.284.5416.970. [DOI] [PubMed] [Google Scholar]
- Grafman J., Passafiume D., Faglioni P., Boller F. Calculation disturbances in adults with focal hemispheric damage. Cortex. 1982;18:37–50. doi: 10.1016/s0010-9452(82)80017-8. [DOI] [PubMed] [Google Scholar]
- Gruber O., Indefrey P., Steinmetz H., Kleinschmidt A. Dissociating neural correlates of cognitive components in mental calculation. Cereb. Cortex. 2001;11:350–359. doi: 10.1093/cercor/11.4.350. [DOI] [PubMed] [Google Scholar]
- Hämäläinen M., Hari R., Ilmoniemi R., Knuutila J., Lounasmaa O.V. Magneto -encephalography: theory, instrumentation, and applications to noninvasive studies of the working human brain. Rev. Mod. Phys. 1993;65:413–497. [Google Scholar]
- Hécaen H., Angelergues R., Houillier S. Les variétés cliniques des acalculies au cours des lésions rétrorolandiques: approche statistique du probleme. Rev. Neurol. 1961;105:85–103. [PubMed] [Google Scholar]
- Henschen S.E. Über Sprach-, Musik-und Rechenmechanismen und ihre Localisation im Grosshirn. Z. Gesamte. Neur. Psychiatr. 1919;52:273–298. [Google Scholar]
- Howard D., Patterson K., Wise R., Brown W.D., Friston K., Weiller C., Frackowiak R. The cortical localization of the lexicons. Brain. 1992;115:1769–1782. doi: 10.1093/brain/115.6.1769. [DOI] [PubMed] [Google Scholar]
- Iguchi Y., Hashimoto I. Squential information processing during a mental arithmetic is reflected in the time course of event-related brain potentials. Clin. Neurophysiol. 2000;111:204–213. doi: 10.1016/s1388-2457(99)00244-8. [DOI] [PubMed] [Google Scholar]
- Ischebeck A., Zamarian L., Schocke M., Delazer M. Flexible transfer of knowledge in mental arithmetic–an fMRI study. Neuroimage. 2009;44:1103–1112. doi: 10.1016/j.neuroimage.2008.10.025. [DOI] [PubMed] [Google Scholar]
- Ishii R., Canuet L., Ishihara T., Aoki Y., Ikeda S., Hata M., Katsimichas T., Gunji A., Takahashi H., Nakahachi T., Iwase M., Takeda M. Frontal midline theta rhythm and gamma power changes during focused attention on mental calculation: an MEG beamformer analysis. Front. Hum. Neurosci. 2014;8:406. doi: 10.3389/fnhum.2014.00406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kamada K., Kober H., Saguer M., Möller M., Kaltenhäuser M., Vieth J. Responses to silent Kanji reading of the native Japanese and German in task subtraction magnetoencephalography. Brain Res. Cogn. Brain Res. 1998;7:89–98. doi: 10.1016/s0926-6410(98)00016-0. [DOI] [PubMed] [Google Scholar]
- Kong J., Wang C., Kwong K., Vangel M., Chua E., Gollub R. The neural substrate of arithmetic operations and procedure complexity. Brain Res. Cogn. Brain Res. 2005;22:397–405. doi: 10.1016/j.cogbrainres.2004.09.011. [DOI] [PubMed] [Google Scholar]
- Kuo B.C., Yeh Y.Y., Chen D.Y., Liang K.C., Chen J.H. The capacity constraint in the prefrotal and parietal regions for coordinating dual arithmetic tasks. Brain Res. 2008;1199:100–110. doi: 10.1016/j.brainres.2007.12.070. [DOI] [PubMed] [Google Scholar]
- Levin H.S., Scheller J., Rickard T., Grahmam J., Martinkowski K., Winslow M.A., Mirvis S. Dyscalcilia and dyslexia after right hemisphere injury in infancy. Arch. Neurol. 1996;53:88–96. doi: 10.1001/archneur.1996.00550010108024. [DOI] [PubMed] [Google Scholar]
- Lucchelli F., De Renzi E. Primary dyscalculia after a medial frontal lesion of the left hemisphere. J. Neurol. Neurosurg. Psychiatry. 1993;56:304–307. doi: 10.1136/jnnp.56.3.304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McNeil J., Warrington E.K. A dissociation between addition and subtraction with written calculation. Neuropsychologia. 1994;32:717–728. doi: 10.1016/0028-3932(94)90031-0. [DOI] [PubMed] [Google Scholar]
- Menon V., Rivera S.M., White C.D., Glover G.H., Reiss A.L. Dissociating prefrontal and parietal cortex activation during arithmetic processing. Neuroimage. 2000;12:357–365. doi: 10.1006/nimg.2000.0613. [DOI] [PubMed] [Google Scholar]
- Nishitani N., Hari R. Temporal dynamics of cortical representation for action. Proc. Natl. Acad. Sci. U.S.A. 2000;97:913–918. doi: 10.1073/pnas.97.2.913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nishitani N., Uutela K., Shibasaki H., Hari R. Cortical visuomotor integration during eye pursuit and eye-finger pursuit. J. Neurosci. 1999;19:2647–2657. doi: 10.1523/JNEUROSCI.19-07-02647.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oldfield R.C. The assessment and analysis of handedness: the Edinburgh inventory. Neuropsychologia. 1971;9:97–113. doi: 10.1016/0028-3932(71)90067-4. [DOI] [PubMed] [Google Scholar]
- Paulesu E., Frith C.D., Frackowiak R.S.J. The neural correlates of the verbal component of working memory. Nature. 1993;362:342–345. doi: 10.1038/362342a0. [DOI] [PubMed] [Google Scholar]
- Pauli P., Lutzenberger W., Rau H., Birbaumer N., Rickard T.C., Yaroush R.A., Bourne L.E., Jr Brain potentials during mental arithmetic: effects of extensive practice and problem difficulty. Brain Res. Cogn. Brain Res. 1994;2:21–29. doi: 10.1016/0926-6410(94)90017-5. [DOI] [PubMed] [Google Scholar]
- Pesenti M., Thioux M., Seron X., De Volder A. Neuroanatomical substrates of arabic number processing, numerical comparison and simple addition: a PET study. J. Cogn. Neurosci. 2000;12:461–479. doi: 10.1162/089892900562273. [DOI] [PubMed] [Google Scholar]
- Price C.J., Wise R.J.S., Watson J.D.G., Patterson K., Howard D., Frackowiak R.S.J. Brain activity during reading the effects of exposure during and task. Brain. 1994;117:1255–1269. doi: 10.1093/brain/117.6.1255. [DOI] [PubMed] [Google Scholar]
- Raji T., Uutela K., Hari R. Audiovisual integration of letters in the human brain. Neuron. 2001;29:617–625. doi: 10.1016/s0896-6273(00)00138-0. [DOI] [PubMed] [Google Scholar]
- Rickard T.C., Romero S.G., Basso G., Wharton C., Flitman S., Grafman J. The calculating brain: an fMRI study. Neuropsychologia. 2000;38:325–335. doi: 10.1016/s0028-3932(99)00068-8. [DOI] [PubMed] [Google Scholar]
- Robertson L.C., Lamb M.R. Neuropsychological contributions to theories of part/whole organization. Cogn. Psychol. 1991;23:299–330. doi: 10.1016/0010-0285(91)90012-d. [DOI] [PubMed] [Google Scholar]
- Roland P.E., Friberg L. Localization of cortical areas activated by thinking. J. Neurophysiol. 1985;53:1219–1243. doi: 10.1152/jn.1985.53.5.1219. [DOI] [PubMed] [Google Scholar]
- Rossell S.L., Bullmore E.T., Williams S.C.R., David A.S. Brain activation during automatic and controlled processing of semantic relations: a priming experiment using lexical-decision. Neuropsychologia. 2001;39:1167–1176. doi: 10.1016/s0028-3932(01)00049-5. [DOI] [PubMed] [Google Scholar]
- Ruchkin D.S., Johnson R., Jr, Canoune H., Ritter W. Event-related potentials during arithmetic and mental rotation. Electroencephalogr. Clin. Neurophysiol. 1991;79:473–487. doi: 10.1016/0013-4694(91)90167-3. [DOI] [PubMed] [Google Scholar]
- Rueckert L., Lange N., Partiot A., Appollonio I., Litvan I., Le Bihan D., Grafman J. Visualizing cortical activation during mental calculation with funtional MRI. Neuroimage. 1996;3:97–103. doi: 10.1006/nimg.1996.0011. [DOI] [PubMed] [Google Scholar]
- Sakurai Y., Momose T., Iwata M., Sasaki Y., Kanazawa I. Activation of prefrontal and posterior superior temporal areas in visual calculation. J. Neurol. Sci. 1996;139:89–94. [PubMed] [Google Scholar]
- Sammer G., Blecker C., Gebhardt H., Bischoff M., Stark R., Morgen K., Vaitl D. Relationship between regional hemodynamic activity and simultaneously recorded EEG-theta associated with mental arithmetic-induced workload. Hum. Brain Map. 2007;28:793–803. doi: 10.1002/hbm.20309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sasaki K., Tsujimoto T., Nambu A., Matsuzaki R., Kyuhou S. Dynamic activities of the frontal association cortex in calculating and thinking. Neurosci. Res. 1994;19:229–233. doi: 10.1016/0168-0102(94)90147-3. [DOI] [PubMed] [Google Scholar]
- St George M., Kutas M., Martinez A., Sereno M.I. Semantic integration in reading: engagement of the right hemisphere during discourse processing. Brain. 1999;122:1317–1325. doi: 10.1093/brain/122.7.1317. [DOI] [PubMed] [Google Scholar]
- Stanescu-Cosson R., Pinel P., van de Moortele P.F., Le Biham D., Cohen L., Dehaene S. Understanding dissociation in dyscalculia: a brain imaging study of the impact of number size on the cerebral networks for exact and approximate calculation. Brain. 2000;123:2240–2255. doi: 10.1093/brain/123.11.2240. [DOI] [PubMed] [Google Scholar]
- Takayama Y., Sugishita M., Akiguchi I., Kimura J. Isolated acalculia due to left parietal lesion. Arch. Neurol. 1994;51:286–291. doi: 10.1001/archneur.1994.00540150084021. [DOI] [PubMed] [Google Scholar]
- Talairach J., Tournoux P. Thieme; Stuttgart: 1988. Co-planar Stereotaxic Atlas of the Human Brain. [Google Scholar]
- Tesche C.D. Non-invasive detection of ongoing neuronal population activity in normal human hippocampus. Brain Res. 1997;749:53–60. doi: 10.1016/s0006-8993(96)01286-3. [DOI] [PubMed] [Google Scholar]
- Tohgi H., Saitoh K., Takahashi S., Takahashi H., Utsugisawa K., Yonezawa H., Hatano K., Sasaki T. Agraphia and acaluculia after a left prefrontal (F1, F2) infarction. J. Neurol. Neurosurg. Psychiatry. 1995;58:629–632. doi: 10.1136/jnnp.58.5.629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uusitalo M.A., Ilmoniemi R.J. The signal-space projection (SSP) methods for separating MEG or EEG into components. Med. Biol. Eng. Comput. 1996;35:135–140. doi: 10.1007/BF02534144. [DOI] [PubMed] [Google Scholar]
- Warrington E.K. The fractionation of arithmetical skills: a single case study. Q. J. Exp. Psychol. 1982;34:31–51. doi: 10.1080/14640748208400856. [DOI] [PubMed] [Google Scholar]
- Zago L., Petit L., Turbelin M., Andersson F., Vigneau M., Tzourio-Mazoyer N. How verbal and spatial manipulation networks contribute to calculation: An fMRI study. Neuropsychologia. 2008;46:2403–2414. doi: 10.1016/j.neuropsychologia.2008.03.001. [DOI] [PubMed] [Google Scholar]