Data and Power Efficient Intelligence with Neuromorphic Learning Machines

Abstract

The success of deep networks and recent industry involvement in brain-inspired computing is igniting a widespread interest in neuromorphic hardware that emulates the biological processes of the brain on an electronic substrate. This review explores interdisciplinary approaches anchored in machine learning theory that enable the applicability of neuromorphic technologies to real-world, human-centric tasks. We find that (1) recent work in binary deep networks and approximate gradient descent learning are strikingly compatible with a neuromorphic substrate; (2) where real-time adaptability and autonomy are necessary, neuromorphic technologies can achieve significant advantages over main-stream ones; and (3) challenges in memory technologies, compounded by a tradition of bottom-up approaches in the field, block the road to major breakthroughs. We suggest that a neuromorphic learning framework, tuned specifically for the spatial and temporal constraints of the neuromorphic substrate, will help guiding hardware algorithm co-design and deploying neuromorphic hardware for proactive learning of real-world data.

Graphical Abstract

Systems Neuroscience; Computer Science; Evolvable Hardware

Introduction

The harnessing of future big data for societal and economical advances demands an unprecedented amount of computing resources. The difficulties in scaling current computing technologies to meet such demands, combined with a looming end of Moore's law, is spurring widespread interest in novel scalable computing paradigms. One such paradigm is neuromorphic engineering, which strives to reproduce in hardware the brain's cognitive and adaptive abilities by mimicking its architectural and dynamical properties (Mead, 1990). The adaptivity, efficiency, and largely unsurpassed performance of the brain at solving complex cognitive tasks has been a continuing inspiration for designing computing systems (von Neumann, 1958). Although the reasons for the extraordinary robustness, efficiency, and adaptivity of brains are puzzling, their style of computation, supported by massively parallel and self-organizing neural architectures that are fundamentally different from that used in conventional computers, is believed to be a key piece of the puzzle (Douglas and Martin, 2004).

The foundational insight of neuromorphic engineering is that the current-voltage dependence in ion channels and transistors operated in the sub-threshold regime are both exponential (Mead, 1990), owing to the same diffusion law governing the transport of their respective carriers. This similarity implies that electronic and biological substrates share constraints on communication, power, and reliability. Thus, neuromorphic hardware designed along these principles has the potential to translate advances in neuroscience research into ultra-low-power computing technologies targeted at producing cognitive function (Indiveri and Liu, 2015). This hardware can in turn be employed as a tool to investigate the organizational principles of the brain by accelerating existing neural simulations (Zenke and Gerstner, 2014) or by analyzing the qualities of the constructed hardware (Cauwenberghs, 2013). Since its inception in the early 1990s, the interest in neuromorphic engineering is rising rapidly (Schuman et al., 2017), and neuromorphic engineering now extends to a wide gamut of software and hardware efforts (Schuman et al., 2017) dedicated at simulating or emulating neural network dynamics.

Efforts in neuromorphic engineering resulted in many successful devices (Indiveri et al., 2011). These range from mixed signal (Benjamin et al., 2014, Chicca et al., 2013, Park et al., 2014, Schemmel et al., 2010) systems that emulate the dynamics of spiking neural network models in very-large-scale integration (VLSI) to digital systems (Merolla et al., 2014, Davies et al., 2018, Furber et al., 2014) dedicated at simulating the dynamics of spiking networks on a dedicated digital architecture. Neuromorphic systems have been successfully demonstrated in pattern recognition, decision-making, and navigation tasks (Qiao et al., 2015, Srinivasa and Cho, 2014, Neftci et al., 2013, Serrano-Gotarredona et al., 2009, Schmuker et al., 2014, Esser et al., 2016, Moradi et al., 2018, Blum et al., 2017). Recently, the neuromorphic engineering community has started to dedicate significant effort in embedding synaptic plasticity in their hardware for emulating the adaptive capabilities of the brain (Azghadi et al., 2014).

At the system level, neurons in the adult brain communicate principally through sparse, all-or-none events in continuous time (Gerstner and Kistler, 2002). All other internal states such as neurotransmitter concentrations, synaptic states, and membrane potentials are local to the neuron. Such an architecture is highly scalable, thanks to sparse interprocess communication. However, harnessing neuromorphic hardware to solve real-world problems in a reliable fashion proved to be extremely challenging. This is because they require computational strategies that can operate robustly on local information and sparse global communication. Understanding the mechanisms of brain function and devising models and algorithms that operate under such conditions is the key endeavor of computational neuroscience modeling (Sompolinsky, 2014). Although technologies for imaging the brain and analyzing the resulting data are progressing rapidly, the understanding of its organizing principles is still largely incomplete. Our limited understanding of which brain mechanisms are necessary to achieve cognitive function weakens the technological prospects of the traditional bottom-up “brain-as-a-blueprint” approach to neuromorphic engineering. On the other hand, machine learning and deep learning provide relatively well-understood principles for solving problems of practical interest, with the caveat that most state-of-the-art machine learning algorithms rely on information that is not local to the computational building blocks of a neural substrate.

In this article, we introduce neuromorphic learning machines as a middle-ground solution between the bottom-up and top-down approaches by reconciling the architecture and dynamics of a neural substrate with the organizing principles of machine learning. This “middle-in” approach is consistent in spirit to Marr's line of inquiry, which strives to study a problem at the levels of theory, algorithm, and hardware (Marr, 1982). As such, our discussion will apply to the more modern and general sense of the term neuromorphic, i.e., that the machines compute with neuron-like units using local information. We will explore the benefits of viewing neuromorphic engineering through the lens of recent advances in artificial neural network and machine learning, i.e., to which extent will these algorithms guide us in neuromorphic hardware design, and what advantages would accrue from such hardware? Through this discussion, we aim to dispel some of the perceived differences and similarities between biologically inspired neural networks and artificial neural networks and provide engineers guidelines for increasing the technological impact of their neuromorphic hardware. In so doing, this review will outline the nature of possible bridges from neurobiology to machine learning and describe modern tools for investigating such bridges.

Embedded Learning to Solve the Challenges of Programming Neuromorphic Hardware

Despite the demonstrated scalability of the technology in analog (Moradi et al., 2018, Park et al., 2014, Schemmel et al., 2010) and digital (Merolla et al., 2014, Davies et al., 2018) technologies, achievements in the field remain modest in both breadth of application and scale compared with the state of the art. This is mainly because the concepts and methods for installing the dynamics necessary to express cognitive behaviors on these substrates are still in the early stages of development.

In the mixed signal domain, this problem is compounded by the technical difficulty of mapping the parameters of synapse and neuron models onto the underlying neuromorphic hardware (Neftci et al., 2011). In fact, hardware parameters adjusting the behavior of circuits are currents and voltages that do not have a trivial correspondence with the parameter types and values used in the computational models. Finally, the realities of circuit design, such as fabrication variability (device mismatch), operating noise, and limited dynamical range, add to the aforementioned difficulties. Early work solved the programming and device variability problem using iterative calibration of the neural building blocks (e.g., synapses, neurons, or populations of neurons) to reach desired dynamical behaviors. Calibration was demonstrated by fitting neural mean-field models expressed in terms of the underlying transistor dynamics (Neftci et al., 2011) and adapting connection probabilities such that the effect of fabrication mismatch is minimized (Neftci and Indiveri, 2010), iterative parameter search using neural measurement protocols (Bruederle et al., 2011), linear regression of encoders and decoders (Dethier et al., 2011) and spike-based maximum likelihood estimation (Russell et al., 2010). The calibrated building blocks can then be composed for synthesizing task-relevant computations (Neftci et al., 2013). These calibration procedures are costly, both in terms of external resources required to carry them out and device-specific engineering efforts. Owing to these difficulties, deterministic digital technologies are often preferred over mixed signal or analog ones. However, calibration procedures can be viewed as a form of learning, in the sense that the neural parameters are modified on the basis of measured error using a separate computer (Friedmann et al., 2017). A natural elaboration on this idea is to perform this learning in tandem with the learning of higher-level, task objectives. Machine learning methods for automated data analysis are particularly well suited to this task, thanks to their general-purpose, modular, and potentially fault-tolerant nature. As such, learning of the task can tighten the programmability gap between mixed signal and digital neuromorphic hardware.

Consequently, several studies employed machine learning and deep learning to synthesize spiking neural networks solving machine learning benchmark tasks in software (O’Connor et al., 2013, Cao et al., 2015, Hunsberger and Eliasmith, 2015, Diehl et al., 2015) and neuromorphic hardware (Schmuker et al., 2014, Moradi et al., 2018, Esser et al., 2016). This is achieved by mapping pre-trained deep neural networks onto spiking neural networks using a firing rate code. This approach can be improved by taking the precise spike timing into consideration during training (Mostafa, 2016), as well as hardware constraints (Severa et al., 2018, Esser et al., 2016). Following this idea, Esser et al. introduced energy-efficient deep neuromorphic networks, which create convolutional networks whose structure and parameters have been optimized under the constraints of the hardware through regularization and rounding (Esser et al., 2016). These approaches are described as “mapping techniques,” as they transfer fitted parameters from a highly controllable system (the computer or dedicated accelerator) to a less controllable one (the neuromorphic hardware). Although mapping techniques can leverage the highly optimized capabilities of existing machine learning frameworks (such as Caffe, Tensorflow, Theano, and Torch) and hardware (such as graphic processing units [GPUs] or dedicated accelerators), they cannot support the fast and energy-efficient learning in an online and incremental fashion as observed in animals.

For both parameter calibration and mapping techniques described earlier, an appealing solution is to tightly embed the learning capabilities on the neuromorphic hardware, meaning provisioning learning circuits where computations take place. Beyond improving energy-related figures, embedded learning can enable applications that are not practical with existing technologies, such as in learning “at-the-edge,” where access to remote computing resources is either not available or too slow or where data privacy is paramount. The remaining of this article will discuss embedded learning in neuromorphic hardware and propose avenues to address its key challenges.

Embedded Learning Rules for Resource-Constrained Learning

We argued that learning is an appealing approach for programming mixed-signal neuromorphic devices and for learning at the edge. Generally speaking, the embedding of a learning algorithm implies data locality (Box 1), whereby only a subset of variables is available to the learning processes. Along these ideas, we identify here research in learning machines as one that devises learning algorithms that take into account the dynamics and constraints that entail from the physical computing substrate. Research in learning machines aims to provide key insights on the neural mechanisms necessary for learning and, in some cases, guarantees on convergence through a rigorous mathematical description anchored in statistical machine learning. The discovery of such mechanisms is significant from a technological perspective because it would provide machine learning hardware that is extremely scalable and potentially implementable in a very-low-power fashion.

Box 1. Spatial and Temporal Locality in Neural Networks.

Locality is tightly dictated by the computational substrate and characterized by the set variables available to the processing elements, in one place. Many computations require more information than that available to neural processing elements. Such information can be non-local (it is available elsewhere) or global (it is shared among all processing elements).

To illustrate the concept of locality, we assume two neurons, A and B, and would like neuron A to implement some function on domain D defined as:

$$\begin{array}{l}D=D_{loc}\cup D_{nloc}\text{,}\\ \text{where }{D}_{loc}=\left\{w_{BA},S^A\left(t\right),u_A\left(t\right)\right\}\text{ and }{D}_{nloc}=\left\{S^B\left(t-T\right),u_B\right\}\text{.}\end{array}$$

Here, S^B(t−T) refers to the output of neuron B T seconds ago, u_A, u_B are the respective membrane potentials, and w_BA is the synaptic weight from B to A. Variables under D_loc are directly available to neuron A and are thus local to it.

On the other hand, variable S^B(t−T) is temporally non-local and u_B is spatially non-local to neuron A. Spatially global signals are often required for learning on practical tasks and even commonplace in the brain in the form of neuromodulation. Non-local information can be transmitted through special structures, for example, dedicated encoders and decoders for u_B and a form of working memory for S^B(t−T). An important challenge of neuromorphic computing is to map behaviorally relevant inference and learning on functions of D while minimizing the cost of communicating D_nloc. The suitability of a computation to a neural substrate can be quantified by the amount of information that must be communicated.

Such technology does not exist yet, and at least two challenges prevent its realization. First, the necessary operations for learning are rarely expressible in a local fashion. Solving this challenge is currently of limited interest to machine learning, as the field strives for mathematical optimality regardless of the computing substrate. Second, unlike inference, learning often requires higher precision parameters to average out noise and ambiguities in real-world data (Courbariaux et al., 2014), which presents challenges at all levels of implementation, but particularly in memory. Memory technologies to support embedded learning require reliability, density, and co-localization (CMOS compatibility). A technology that combines all three properties still does not exist at practical scales.

Biological brains are prime examples of learning machines that solved these challenges. They evolved with tight metabolic constraints and the need to adapt to new environments and changing bodies, sensors, and actuators, as a result of development, gradual degradation, and wear and tear (Sterling and Laughlin, 2015). Indeed, several studies convincingly argue that evolutionary pressure optimized nervous systems for both high metabolic efficiency and task accuracy. Sensory neurons adapt their responses to the regularities in their environment to increase the amount of transmitted information (Simoncelli and Olshausen, 2001), and further studies suggest that neurons that fire sparsely could optimize memory and energy (Olshausen and Field, 2004).

Can we take inspiration from biology to solve the challenges of embedded learning with neuromorphic hardware? Can machine learning techniques guide us in building neuromorphic learning machines? In the following paragraphs, we begin answering these questions around the relevant case of gradient descent and back-propagation in neural networks and neuromorphic hardware.

Gradient-Based Learning in Neuromorphic Architectures

Many machine learning algorithms rely on the gradients of a loss function. In artificial neural networks, the workhorse of learning is the gradient back-propagation (BP) algorithm (Box 2). The gradient BP rule relies on the immediate availability of back-propagated errors represented with high-precision memory. In digital computers, the access to this information funnels through the von Neumann bottleneck, which dictates the fundamental limits of the computing substrate.

Box 2. The Challenges of Gradient Back-Propagation in Neural Substrates.

In the light of recent machine learning and deep learning advances, we examine the relevant case of gradient-based learning and the BP algorithm. Suppose we would like to minimize the mean-squared cost function for one data sample. The cost in a single layer neural network is $L=(1/2){\sum }_i{e}_i^2,\text{with}{e}_i=\left(y_i-t_i\right)$, where e_i is the error of output neuron i, $y_i=\rho \left({\sum }_j{w}_{ij}{x}_j\right)$ is the activity of the output neuron i with activation function ρ, x is the data sample, and t_i is the label associated with the data sample. The task of learning is to minimize this cost over the entire dataset. This can be done efficiently using the gradient descent rule, which modifies the network parameters w in the direction opposite to the gradient:

$$w_{ij}\leftarrow w_{ij}-\eta \Delta w_{ij},\text{where }\Delta w_{ij}=\frac{\partial }{\partial w_{ij}}L={\rho }^{\prime }\left(\sum _j{w}_{ij}{x}_j\right)e_i{x}_j\text{,}$$ (Equation 1)

and where η is a small learning rate. In deep networks, i.e., networks containing one or more hidden layers, the weights of the hidden layer neurons are modified by back-propagating the errors from the prediction layer using the chain rule. Using superscripts l = 0,…,N to denote the layer (0 is input, N is output):

$$\frac{\partial }{\partial w_{ij}^l}L={\delta }_i^l{y}_j^{l-1},\text{ where }{\delta }_i^l={\rho }^{\prime }\left(\sum _j{w}_{ij}^l{y}_j^l\right)\sum _k{\delta }_k^{l+1}{w}_{ki}^{l+1}\text{,}$$ (Equation 2)

where the ${\delta }_i^N=e_i$, as in Equation 1 and $y_i^0=x_i$. This update rule is ubiquitous in deep learning (Rumelhart et al., 1987) and known as the gradient back-propagation algorithm. As depicted earlier, learning is typically carried out in forward passes (evaluation of the neural network activities) and backward passes (evaluation of δs). The computation of ${\delta }_i^l$ requires knowledge of the forward weights; thus, gradient BP relies on the immediate availability of a symmetric transpose of the network for computing the back-propagated errors. Often the access to this information funnels through a von Neumann bottleneck, which dictates the fundamental limits of the computing substrate. Distributing computations over multiple cores in GPUs is an effective solution to mitigate this problem, but even there the scalability of gradient BP is limited by its data and memory-intensive operations (Zhu et al., 2016, Seide et al., 2014), and more so in the case of fully connected networks (Seide et al., 2014). In addition, during training, large networks suffer from layer-wise locking, whereby computations of the derivatives of a deep layer may remain idle until the error can be computed at the top layer (Jaderberg et al., 2016). Such locking can be interpreted as a form of temporal non-locality.

The exact implementation of BP on a neural substrate is even more challenging (Baldi et al., 2016, Lee et al., 2016, Grossberg, 1987) because it requires (1) using synaptic weights that are identical to forward passes (symmetric weights requirements, also known as the weight transport problem); (2) carrying out the operations involved in BP, including multiplications with derivatives and activation functions; (3) propagating error signals with high, floating-point precision; (4) alternating between forward and backward passes; (5) changing the sign of synaptic weights; and (6) availability of targets (labels) (7) in the case of recurrent neural networks, an unfolded version of the network (as in BP-through-time). The essence of these challenges is that BP requires precise linear and non-linear transformations and information that is not local to the computational building blocks in a neural substrate, meaning that special communication channels must be provisioned (Baldi and Sadowski, 2016).

In the context of deep neural networks, the spatial non-locality of learning can be characterized using a concept of learning channel (Baldi and Sadowski, 2016), a special communication channel provisioned to enable the learning of deep layers. The BP rule implies a learning channel that is optimal in the space of possible learning algorithms, both in terms of expected improvement per step and the rate of learning (defined as “the number of bits transmitted to each weight through the backward channel divided by the number of operations required to compute/transmit this information per weight”). A subsequent study identified that the BP algorithm implies symmetries in the architecture, processing, states, and weights (Baldi et al., 2017), which can lead to non-localities that are not compatible with a biologically inspired architecture and thus prevent an efficient neuromorphic implementation.

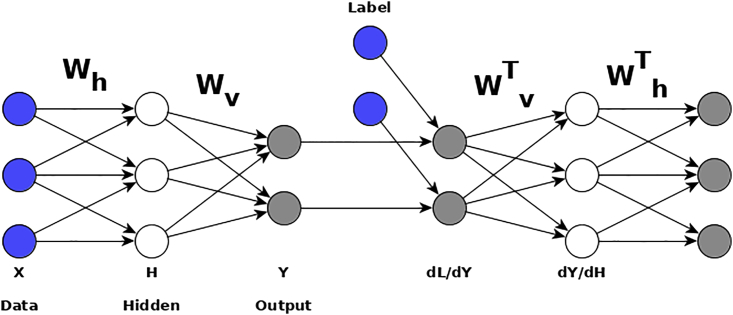
Interestingly, approximations to the BP learning channel that break these symmetries can still learn deep weights. One such family of algorithms are feedback alignment or random back-propagation (RBP) algorithms (Lillicrap et al., 2016, Baldi et al., 2016). These are approximations to the gradient BP rule that sidestep the non-locality problem by replacing weights in the learning channel with random ones, leading to remarkably little loss in classification performance on benchmark tasks (requirement [1] in Box 2). Although a general theoretical understanding of RBP is still a subject of intense research, extended simulations of linear networks show that, during learning, the network adjusts its feedforward weights such that they align with the (random) feedback weights, which are effective in communicating gradients (Lillicrap et al., 2016). Building on these findings, our recent results demonstrated event-driven random back-propagation (eRBP), an asynchronous spike-driven adaptation of random BP using local synaptic plasticity rules with the dynamics of spiking neurons (Neftci et al., 2017). The eRBP rule was tested on software simulations of digital neuromorphic hardware (Detorakis et al., 2017), with fixed-width representations for neural states and synaptic weights (Figure 1). Extended experimentations with eRBP show that the spiking nature of neuromorphic hardware and the lack of complex non-linear computations at the neuron do not prevent accurate learning on classification tasks (requirement [ii], [iii] in Box 2) and can operate continuously and asynchronously without alternation of forward or backward passes (requirement [iv] in Box 2). Our results showed that, up to moderate classification accuracies, digital neuromorphic hardware requires an equal or fewer number of SynOps compared with MACs to reach a given accuracy for both networks (Figure 1, right panel). Although a standard computer remains the architecture of choice if classification accuracy on a stationary dataset is the target regardless of energy efficiency, neuromorphic hardware is a strong contender if low-power learning on non-stationary data is the objective, since energy efficiency is improved at least by a factor equal to the achieved Joule/MAC to Joule/SynOp ratio and learning is on-going (Detorakis et al., 2017). Beyond BP and eRBP, there exist many plasticity rules highly relevant to neuromorphic implementations and related to gradient-based machine learning algorithms, such as contrastive divergence (Neftci et al., 2014) and independent component analysis (Isomura and Toyoizumi, 2016).

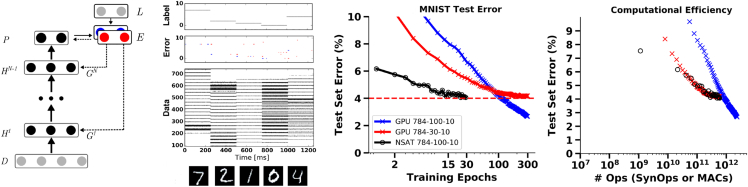
Figure 1.

Supervised Deep Learning in Spiking Neurons

The event-driven Random Back-Propagation (eRBP) is an event-based synaptic plasticity learning rule for approximate BP in spiking neural networks.

(Left) The network performing eRBP consists of feedforward layers (H¹,…,H^N) for prediction and feedback layers for supervised training with labels (targets) L. Full arrows indicate synaptic connections, thick full arrows indicate plastic synapses, and dashed arrows indicate synaptic plasticity modulation. In this example, digits 7,2,1,0,4 were presented in sequence to the network, after transformation into spike trains (layer D). Neurons in the network indicated by black circles were implemented as two-compartment spiking neurons. The first compartment follows the standard Integrate and Fire (I&F) dynamics, whereas the second integrates top-down errors and is used to multiplicatively modulate the learning. The error is the difference between labels (L) and predictions (P) and is implemented using a pair of neurons coding for positive error (blue) and negative error (red). Each hidden neuron receives inputs from a random combination of the pair of error neurons to implement random BP. Output neurons receive inputs from the pair of error neurons in a one-to-one fashion. (Middle) MNIST Classification error on the test set using a fully connected 784-100-10 network performed using limited precision states (8 bit fixed-point weights 16 bits state components) and on GPU (TensorFlow, floating-point 32 bits). (Right) Efficiency of learning expressed in terms of the number of operations necessary to reach a given accuracy is lower or equal in the spiking neural network (SynOps) compared with the artificial neural network (MACs). At this small MNIST task, the spiking neural network required about three times more neurons than the artificial neural network to achieve the same accuracy but the same number of respective operations. Figures adapted from Neftci et al. (2017) and Detorakis et al. (2017).

In all gradient-based learning rules, the continuous aspect of the learning is a particularly interesting side effect of a neuromorphic implementation, because it can support online learning in the sense that the inference model is updated sequentially, with each data sample. Furthermore, online stochastic gradient descent can process more data samples than batch gradient descent (LeCun and Bottou, 2004) while requiring less memory for implementation. Minibatch learning is the preferred choice in conventional hardware because it minimizes the impact of communication overhead by sequencing a large number of parallel operations. This overhead is caused by the architecture of the computer and the large amounts of data transferred across the platform. When computations are local (as in neuromorphic hardware), there is no such overhead and weight updates can be performed online without loss in speed. In fact, our empirical observations confirm that spiking networks often require fewer iterations of the dataset to reach the peak classification performance compared with the artificial neural network trained with batch gradient descent (Neftci et al., 2016, Neftci et al., 2017). This improved speed in learning is visible in the middle panel of (Figure 1) and can directly translate into power reductions on dedicated hardware.

Thus, machine learning inspiration for neuromorphic learning machines can lead to successful results, at a modest cost in accuracy. On the flip side, learning can become more efficient than a traditional implementation thanks to its inherently local and online operation. Although these conclusions may seem contradicting the discussed optimality of BP, our arguments took power into account as opposed to information-theoretic metrics only.

Data Efficient Learning

Despite the improved speed of learning, deep spiking neural networks operating in real time would require hundreds of hours to reach classification accuracies on MNIST comparable with that of artificial neural networks (Neftci et al., 2017). Furthermore, most deep learning approaches require massive amounts of data samples to learn. Assuming learning is performed with a stored dataset, the acceleration of the neural network emulations is a possible solution to this problem. Such accelerations can be achieved with time-accelerated hardware (Schemmel et al., 2010, Friedmann et al., 2017).

Another solution is to simplify the learning task by reducing the dimensionality of the data, the amount of data, and the number of iterations necessary to reach a target goal. Given the constraints on metabolic cost, it is plausible that brains evolved strategies that enable such reductions while keeping accuracy at an acceptable level. Indeed, senses in all organisms are highly tuned to their natural environment and arguably play an important role by strongly reducing the dimensionality of the sensory input (Olshausen and Field, 2004), which in turn greatly simplifies the learning task. Interestingly, neuromorphic vision, audition, and tactile sensors can play a similar role (Liu and Delbruck, 2010). Spurred by humans' ability to learn on prior knowledge, the search for data efficient algorithms has a long history in machine learning and cognitive sciences (Tenenbaum et al., 2011). To promote rapid acquisition of knowledge and generalization (Lake et al., 2017), some machine learning studies address the problem of transfer across tasks (Kansky et al., 2017, Yosinski et al., 2014) and meta-learning or learning-to-learn (Schmidhuber, 1987, Hochreiter et al., 2001, Andrychowicz et al., 2016). In colloquial terms, a computer can “teach” a learning machine how to learn in a class of environments. These techniques can be applied, for example, to improve or discover a learning algorithm (Andrychowicz et al., 2016) or optimize the parameters of synaptic plasticity dynamics (Bengio et al., 1990, Rounds et al., 2016). Furthermore, meta-learning is argued to be a principled approach to transfer learning, as the ability to generalize across a class of tasks implies transfer learning. Although these methods are not yet fully established, they provide exciting new avenues into neuromorphic learning machines designed along machine learning principles.

Synaptic Plasticity and Learning in Neuromorphic Hardware

Following the more high-level discussion, we detail here the concepts behind efficient synapse modeling and the state of the art of synapse and plasticity models employed in neuromorphic hardware.

Synapses are fundamental building blocks for computation and communication in biological neural networks. Biological neurons are characterized by a large fan-in, often many thousands of synapses per neuron. To efficiently implement the synaptic fan-in in hardware, it is common to leverage the linear summation property of post-synaptic currents by emulating many synapses with a single linear temporal filter (Bartolozzi and Indiveri, 2007). Provided that synaptic parameters (such as weights) can be stored for each connection, this approach requires only one filter per type of synapse (where the type can be characterized, for example, by different time constants), leading to a complexity that scales proportionally to the number of neurons.

Synaptic plasticity can be viewed as dynamics over synaptic parameters and face similar scalability challenges. To maintain scalability, plasticity dynamics often use a strategy similar to linear summation, i.e., that the eligibility of synaptic weight updates can be computed using linear temporal filters. Spike-timing-dependent plasticity (STDP) with exponential learning windows (Figure 2) is a popular model with such features, supported by empirical evidence (Bi and Poo, 1998, Sjöström et al., 2008) and compatible with Hebbian learning (Gerstner and Kistler, 2002). Thanks to its simplicity, scalability, computational efficiency and biological inspiration, nearly all neuromorphic learning hardware directly implement STDP (Pfeil et al., 2012, Galluppi et al., 2014, Davies et al., 2018, Detorakis et al., 2017, Arthur and Boahen, 2006, Venkataramani et al., 2014, Srinivasa and Cho, 2014, Dean et al., 2014). However, whether STDP or even point synapses can capture the salient features of neural computation is being challenged on multiple fronts. Experimental work argues that STDP alone cannot account for several observations in synaptic plasticity (Shouval et al., 2010). Theoretical work advocates that synapses must involve complex internal dynamics on multiple timescales to achieve extensive memory capacity (Lahiri and Ganguli, 2013). Furthermore, error-driven learning rules derived from first principles are not directly compatible with pairwise STDP (Pfister et al., 2006). These observations are not in contradiction with the seminal work of Bi and Poo (1998), as considerable variation in LTP and LTD is indeed observed.

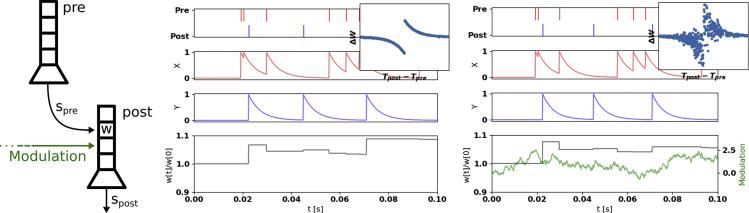
Figure 2.

Spike-Timing-Dependent Plasticity, Modulation, and Three-Factor Rule

The classical spike-timing dependent plasticity (STDP) rule modifies the synaptic strengths of connected pre- and post-synaptic neurons based on the spike history in the following way: if a post-synaptic neuron generates action potential within a time interval after the pre-synaptic neuron has fired multiple spikes, then the synaptic strength between these two neurons becomes stronger (causal updates, long-term potentiation [LTP]). On the other hand, if the post-synaptic neuron fires multiple spikes before the pre-synaptic neuron generates action potentials within that time interval, then the synaptic strength becomes weak (acausal updated, long-term depression [LTD]) (Bi and Poo, 1998, Sjöström et al., 2008). The learning window in this context refers to how weights change as a function of the spike time difference (insets in the panels). Generalizations of STDP often involve custom neural windows and state-dependent modulation of the updates.

The left plot shows an example of an online implementation of the classic STDP rule with nearest-neighbor interactions: $\Delta W\left(t\right)=s_{post}\left(t\right)X\left(t\right)+s_{pre}\left(t\right)Y\left(t\right)$, where X(t) and Y(t) are traces representing presynaptic and postsynaptic spike history, respectively. Nearest neighbor interactions refer to the fact that the weight update depends on the previous pre- or post-spike, respectively. The right plot is a modulated STDP rule corresponding to a type of three-factor rule: $\Delta W_M\left(t\right)=\Delta W\left(t\right)\cdot \text{Modulation}\left(t\right)$, where the three factors are pre-synaptic activity, post-synaptic activity, and modulation. For illustration purposes, here the modulation (green) is a random signal that multiplies the weight updates. In more practical examples, the modulation can represent reward (Florian, 2007) or classification error (Neftci et al., 2017).

In contrast to STDP, phenomenological synapse models provide a mechanistic model of the observed dynamics, for example, calcium dynamics (Graupner and Brunel, 2012, Shouval et al., 2002, Brader et al., 2007, Abarbanel et al., 2002), and internal consolidation states for long-term memory (Benna and Fusi, 2015). Phenomenological plasticity rules have provided inspiration to neuromorphic VLSI design of learning chips (Huayaney et al., 2016, Qiao et al., 2015, Chicca et al., 2013). The implementation of phenomenological synapses is appealing as it enables highly complex and continuous learning dynamics.

Unfortunately, the scalability of phenomenological synapse models remains challenging because every synapse requires one or more dynamical states. A more scalable approach using current technology can be achieved with so-called normative or top-down approaches. These approaches derive synaptic plasticity requirements from computational principles while being compatible with a neural substrate. They are potentially more scalable than phenomenological ones because only the computationally relevant features are retained. Three-factor rules are examples of normative approaches to synaptic plasticity (Urbanczik and Senn, 2014). The three factors involved are pre-synaptic activity, post-synaptic activity, and a third factor, which can be modulation or another variable relevant to the learning task. Three-factor rules have been shown to be compatible with a wide number of unsupervised, supervised, and reinforcement learning paradigms (Urbanczik and Senn, 2014), and implementations can have scaling properties comparable with that of STDP (Detorakis et al., 2017). Recent digital implementations of learning use three-factor rules, where the third factor is a modulation term that depends on an internal synaptic state (Davies et al., 2018) or postsynaptic neuron state (Detorakis et al., 2017). Our previously described learning rule, eRBP, is equivalent to a three-factor rule where the third factor is a linear, random function of classification error (Neftci et al., 2017). Within this normative approach, several promising extensions to the random back-propagation rule underlying eRBP are possible by exploiting the temporal dynamics of spiking neurons and synapses to learn complex spatiotemporal patterns (Zenke and Ganguli, 2017) and using local classifiers to prevent layer-wise locking and long-distance communication of errors (Mostafa et al., 2017).

Distilling Machine Learning and Neuroscience for Neuromorphic Learning Machines

We can now discuss how to synthesize neuromorphic learning machines by combining the fields of machine learning and neuroscience.

Two technological developments were instrumental to the recent successes of machine learning and deep learning: (1) the advent of GPUs for general-purpose computation (Cireşan et al., 2010) and (2) software solutions. The simplicity with which complex problems could be prescribed in machine learning frameworks allowed the utilization of dedicated vector/SIMD processors without having to write hardware-specific code (e.g., CUDA). This is enabled by a library of equivalent native implementations of the necessary basic operations and a computational graph of the mathematical operations that can be optimized and automatically differentiated.

This is a success scenario that would be extremely beneficial to reproduce with neuromorphic hardware. Based on our experience in spiking neural networks, neuromorphic engineering, and machine learning, this is possible, provided that accuracy on static datasets is not the only objective and hardware is designed with gradient-based learning in mind. In the following, we outline the basic requirements for such a neuromorphic machine learning software/hardware framework, namely, the matching neural and synaptic dynamics under a class of target objective functions. Then we describe our envisioned neuromorphic machine learning framework.

Matching Neural and Synaptic Dynamics

Several computational models of the brain argue that computational optimality hinges on plasticity dynamics and neural dynamics being matched (Lengyel et al., 2005, Pfister et al., 2006, Brea et al., 2013). Although such hypotheses help in guiding neuroscientific hypotheses and experiments, here we propose to use this approach to synthesize neuromorphic learning machines that make optimal use of neural or synaptic dynamics dictated by the hardware substrate. This approach is similar to how artificial neural networks are trained, where weight update rules are derived from a task-relevant objective function, the network architecture, and the neural activation function. The user-defined objective function, the neuron model, and the plasticity model are as follows.

Objective Function

The user defines an objective function $\mathcal{L}$(s, w) relevant to the task at hand (e.g., classification error, reconstruction error, and free energy), where w are trainable parameters and s are neural inputs and outputs (e.g., neural spikes, rates, and targets).

Neuron Model

We formulate a mathematical model of the neurons that provides a probabilistic description of the output s_i. We assume that the conditional probability of s_i given the input s can be expressed as:

$$P\left(s_i|\mathbf{s}\right)=\rho \left(u_i\left(t\right)\right)\text{ with }{u}_i\left(t\right)=\sum _j{w}_{ij}\left(\mathrm{ϵ}\ast s_j\left(t\right)\right)+\eta \ast s_i\left(t\right)\text{,}$$ (Equation 3)

where ρ_i is the stochastic intensity (the equivalent of the activation function in artificial neurons) and η and ϵ are kernels that reflect neural and synaptic dynamics, e.g., refractoriness, reset, and postsynaptic potentials (Gerstner and Kistler, 2002). The neuron model Equation 3 is kept intentionally general to encompass firing rate models and spiking models whose membrane potential is linear in the inputs. In a firing rate description, s represents input rates. In a spiking neuron description, s represents spike trains, and the neuron model is a type of Spike-Response Model (SRM) describing a class of integrate-and-fire (I&F) neuron models (Gerstner and Kistler, 2002), and ρ represents the probability of spiking. In spiking neurons, both kernels and stochastic intensity can be derived or estimated experimentally if the noiseless membrane potential (u_i(t)) can be measured at the times of the spike (Jolivet et al., 2006). This type of stochastic neuron model drives numerous investigations in theoretical neuroscience and forms the starting point for other types of adapting spiking neural networks capable of efficient communication (Zambrano and Bohte, 2016). Although we assumed a continuous-time description, Equation 3 is also consistent with a discrete-time description (Gerstner and Kistler, 2002).

Plasticity Model

Using gradient descent, the plasticity dynamics that minimize $\mathcal{L}$ are:

$$\Delta w_{ij}\propto \frac{\partial }{\partial w_{ij}}\mathcal{L}=\frac{\partial \mathcal{L}}{\partial s_i}{\rho }^{\prime }\left(u_i\right)\frac{\partial u_i}{\partial w_{ij}}\text{,}$$ (Equation 4)

which is a three-factor rule as discussed earlier.

These descriptions of objective function, neuron and plasticity model provide a clear framework for understanding biologically inspired neural networks, named as a sub-class of artificial neural networks. This sub-class is characterized by neurons that are potentially continuous-time, stochastic, and binary, with inputs filtered via kernels η and ϵ, and with strong constraints on data locality. We note that all these assumptions apply to devices following the foundational approach by Mead and colleagues (Mead, 1990) (e.g., Qiao et al., 2015, Benjamin et al., 2014), but other implementations may relax some or all of these assumptions (e.g., Loihi, True North chips are discrete-time and stochasticity is programmable).

The picture emerging from the earlier discussion is that spiking neural networks commonly implemented in neuromorphic hardware are strikingly similar to binary neural networks, a well-studied class of deep neural networks (Rastegari et al., 2016, Courbariaux et al., 2016). This fact is directly explored in some digital spiking neural network implementations (Yin et al., 2017). Furthermore, the statefulness of the neurons and the filtering of their inputs is consistent with recurrent neural networks, even when the network is of the feedforward type. Through this recurrence, neurons of the type Equation 3 have the ability to retain and operate on short temporal sequences.

The equivalence with artificial neural networks is interesting because several findings and “tricks of the trade” of deep learning may have a direct correspondence with biological neurons and synapses. Naturally, not every aspect has a neural equivalent because the resulting dynamics may be non-local or too involved. However, through this (in)compatibility, one can gain insight into the family of objective functions that a proposed neuron model or synapse model can optimize over the sensory data and thus define the range of solvable tasks for a given choice of neuromorphic hardware features. Consequently, we argue that neuromorphic hardware-algorithm co-design can greatly benefit from matching neural and synapse dynamics, possibly at the cost of biological plausibility.

We can now identify three different approaches in matching the objective, neuron and plasticity models: (1) neuron dynamics assumed, derive plasticity dynamics; (2) plasticity dynamics assumed, derive neural dynamics; (3) plasticity dynamics and neural dynamics assumed from neuroscience experiments and modeling. The last approach corresponds to the “analysis by synthesis” approach, which stems from the seminal work on neuromorphic engineering. In the goal of engineering the foundations for neuromorphic learning machines, we illustrate approaches (1) and (2) through the two following case studies.

Synaptic Plasticity Dynamics Matched to Neural Dynamics

Here we illustrate an error-triggered learning rule obtained from a modification of the superspike algorithm proposed by Zenke and Ganguli (2017). The neuron model follows a spiking version of Equation 3, where η = 0 (no refractoriness or reset) and ϵ is an exponential decay. This neuron model is similar to a current-based leaky I&F neuron but with the reset operation omitted to simplify the learning rule. Superspike employs a surrogate gradient for gradient descent of a van Rossum distance (VRD), i.e., a squared error function between output spike i and the target y(t) convolved with kernel α:

$$\mathcal{L}=VRD\left(\mathbf{y},\mathbf{s}\right)=\frac{1}{2}{{\int }_0^T\mathrm{d}t\left(\underset{error\left(t\right)}{\underbrace{\alpha \ast y\left(t\right)-\alpha \ast s\left(t\right)}}\right)}^2\text{,}$$

the plasticity model in Equation 4 becomes:

$$\Delta w_j\propto {\int }_0^T\mathrm{d}t\text{error}\left(t\right)\alpha \text{*}\left({\rho }^{\prime }\left(u\left(t\right)\right)\left(\mathrm{ϵ}\ast s_j\left(t\right)\right)\right)\text{.}$$ (Equation 5)

This rule is the basis of the superspike algorithm proposed by Zenke and Ganguli (2017) and can learn to recognize and generate arbitrary patterns of spikes. It consists of three factors: a modulatory component $\mathit{error}=\frac{\partial \mathcal{L}}{\partial s}$, a pre-synaptic component (ϵ∗s_j), and a post-synaptic component ${\rho }^{\prime }\left(u\right)$. Importantly, Equation 6 is not the classical STDP rule; rather, it is modulated by the error and is continuous in time. This is a direct consequence of the normative approach applied to the continuous-time neural and synaptic dynamics (encapsulated in ϵ). Continuous-time weight updates can be computationally expensive, especially in event-driven designs. A simple modification to this rule consists in triggering weight updates when the error is large. Mathematically, this corresponds to evaluating the integral at time points where the integrand is potentially large:

$$\Delta w_j\cong \sum _{t\in \mathbb{T}}\text{error}\left(t\right)\alpha \text{*}\left({\rho }^{\prime }\left(u\left(t\right)\right)\left(\mathrm{ϵ}\ast s_j\left(t\right)\right)\right)\text{.}$$ (Equation 6)

For illustration purposes, we define $\mathbb{T}=\left\{t_j,j\in \mathbb{N}\left|\right|error\left(t_j\right)|>C\right\}$ as error-triggered plasticity events, where C is a fixed threshold. (Even through weight updates are event driven, we note that the pre- and post-synaptic terms still involve continuous-time functions because of the nested temporal convolutions.). In Figure 3, we produce an example that learns to recognize an arbitrary spike train, using a neuron model Equation 3 with a logistic activation function, and a second order filter for ϵ, reflecting neural and synaptic dynamics. This example illustrates how synaptic plasticity rules can be derived, resulting in learning rules quite different from STDP, in that neither pre- nor post-event trigger weight updates but task-relevant error events. Related approaches for deriving plasticity rules were reported by Huh and Sejnowski (2017) and Anwani and Rajendran (2015).

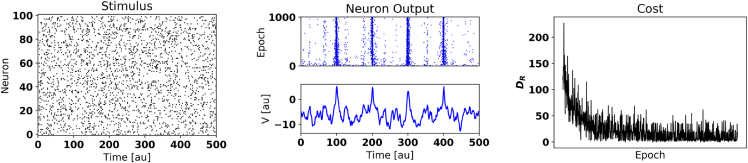
Figure 3.

Learning to Recognize Spike Trains with Local Synaptic Plasticity Rules

A spiking neuron trained with Equation 6 learns to fire at specific times (middle panel, vertical bars) of a Poisson input spike train stimulus (left panel) presented over 500 epochs. The middle panel shows the membrane potential of the neuron at the end of the learning (epoch 500). Weight updates were performed online, and the learning rate for each synapse was fixed. The right panel shows the van Rossum distance VRD during training.

Neural Dynamics Matched to Synaptic Plasticity Dynamics

The converse approach consists in matching the neuron model to a given plasticity model. To the best of our knowledge, this approach has not yet been applied in this context. We illustrate this novel approach with the example of metal oxide memristors biased with supra-threshold pulses (Serb et al., 2016). Memristors are a class of emerging nanodevices that can exhibit persistent changes in their resistance when their two terminals are suitably biased. Their low-power operation and potential scalability make them ideal candidates to overcome the memory-related challenges of neuromorphic hardware. The conductance dynamics can be captured by the following equation:

$$\Delta g_{ij}\propto s_i\left(t\right)s_j\left(t\right)-s_i\left(t\right)\sigma \left(\alpha g_{ij}+\beta \right)$$ (Equation 7)

where σ is the logistic function and α, β are parameters experimentally fitted to the memristor conductance update dynamics (Serb et al., 2016). The first term of this update rule is consistent with the outer-product incremental update (i.e., Hebbian), and the second term captures the non-linearity of the update. Owing to this non-linearity, it is not directly compatible with gradient descent on standard artificial neurons. However, when learning is modulated by the error and $\left(1-\rho \left(u_i\right)\right)$, the conductance gradient of the following neuron model is equal to Equation 7, making the memristor update rule and neuron model compatible with the exact gradient descent:

$$\begin{array}{l}\rho \left(u_i\right)=\sigma \left(u_i\right),\text{ with }{u}_i=b_i+\frac{1}{\alpha }\sum _j\left(\left(\alpha w_{ij}+\beta \right)s_j-S\left(\alpha w_{ij}+\beta \right)\right),\\ \Delta g_{ij}\propto \underset{modulation}{\underbrace{erro{r}_i\left(t\right)\left(1-\rho \left(u_i\right)\right)}}\rho \left(u_i\right)\left(s_j-\sigma \left(\alpha g_{ij}+\beta \right)\right)\text{,}\end{array}$$ (Equation 8)

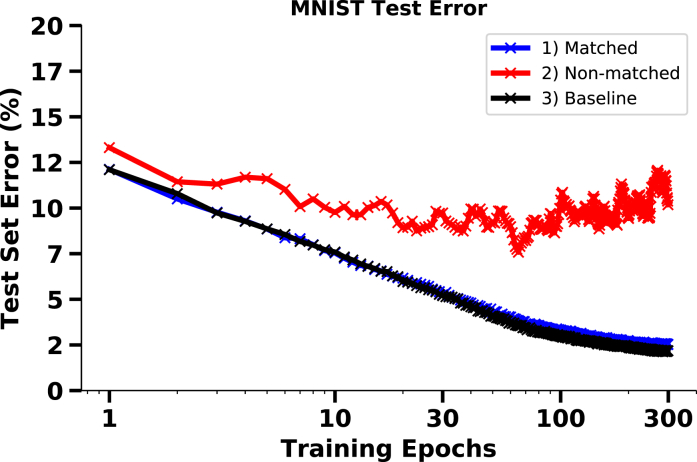
where b_i is a trainable bias term and S is the softplus function (i.e., the integral of the sigmoid function). The second term on the right-hand side, S(αw_ij + β), can be sampled periodically and equates to a weight-dependent bias. We note that the learning rule Equation 8 does not involve any temporal dynamics, so one can simply use a discrete-time, rate-based version of Equation 3. To illustrate this approach, we simulate the neuron and plasticity rule on an MNIST classification task, using three different neuron models for the hidden and output layers: (1) matched neuron model Equation 8 with memristor update rule Equation 7, (2) standard sigmoidal neuron with the memristor update rule, and (3) standard artificial neural network with exact gradient BP as baseline (Figure 4). The results show that the standard neuron that ignores the dependence of the update on the conductance performs poorly compared with the models with matched neuron-plasticity updates (1 and 3).

Figure 4.

Learning with Neuron Models Matched to Memristor Update Rules

MNIST classification task in a 784-100-10 network, using three different models: matched neuron model with memristor update rule (blue, Equation 8), sigmoidal neuron model with the memristor update rule (red, Equation 7), and standard artificial neural network with exact gradient BP as baseline (black). The sigmoidal neuron resulting from ignoring the non-linearity of the memristor performs poorly compared with the baseline.

Matching neural dynamics to synaptic dynamics is particularly interesting for working around nanodevice non-idealities for networks with a large number of synapses, since the neuron model is augmented to work around the synapse non-idealities.

A Neuromorphic Machine Learning Framework

Our discussion sets the stage for vertically integrated software foundations in neuromorphic learning algorithms capable of solving complex cognitive tasks. Here we lay out our vision for a neuromorphic machine learning framework and illustrate it using the foundations laid out earlier.

Machine learning frameworks often build a computational graph representing the mathematical operations of a program (Bergstra et al., 2010, Abadi et al., 2016). The workflow consists of first constructing the inference subgraph, or equivalently, designing a neural network and objective function with some knowledge of the hardware constraints (e.g., memory, speed, and host/device communication overhead), and then synthesizing the gradient subgraph (i.e., the learning channel). For this, one must be able to compute the gradients through the inference subgraph.

In the case of neuromorphic hardware, the hardware represents a significant portion of the computational graph. Thus, constructing the neural network is similar to building the inference subgraph, a fact that is implicitly exploited in mapping techniques. On the other hand, constructing the gradient subgraph in neuromorphic hardware is equivalent to building a learning channel and configuring the plasticity dynamics. The latter is achieved by following the above-mentioned guidelines to designing neuromorphic hardware that enable gradient-based learning. In addition, the structure of the synthesized learning channel must verify the constraints of the hardware. Interestingly, in gradient-based learning, the structure of this channel resembles the forward channel. In fact, in the case of BP, it is the symmetric transpose of the forward channel. Following this argument, and because we assume an informed user constructs the forward channel within hardware constraints, the learning channel will tend to be compatible with the hardware constraints as well. Although hardware compatibility is not guaranteed, approximate (surrogate) derivatives through feedback alignment (Lillicrap et al., 2016) or bootstrapped (Jaderberg et al., 2016) feedback can sidestep hardware constraints with reasonably small impact on performance. Our vision is that a community of users would contribute mathematical models of the forward and backward operations of the neuron (i.e., its gradient-matched dynamics) and different strategies for building learning channels.

The systematic construction of the learning channel must be aware of the locality of the variables. Defining the availability of each variable in a domain can be achieved through structured name hierarchies. Accessing variables across these domains would require dedicated communication channels, as well as dedicated encoders and decoders. Such channels are routinely used in existing frameworks for spiking neural networks such as the neural engineering framework (Eliasmith and Anderson, 2004) or STICK (Lagorce et al., 2015). They incur a significant cost in neurons and communication, and algorithmic advances should strive to reduce this communication as much as possible, while maintaining the learning performance.

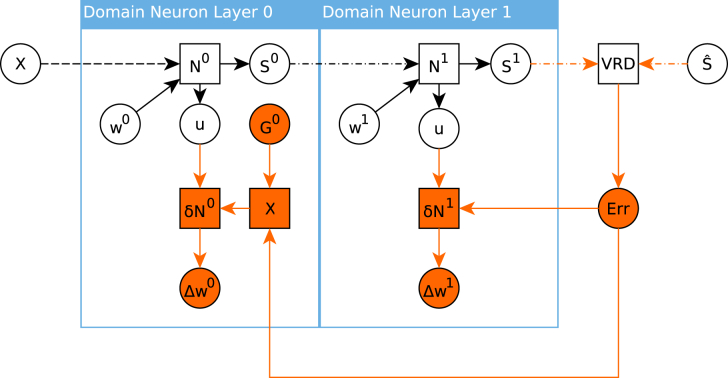
Figure 5 is an example of a computational graph that could be generated by our proposed framework corresponding to Figure 1. The figure illustrates a computational graph for a two-layer network optimizing VRD with direct feedback alignment.

Figure 5.

Example Computational Graph of a Two-Layer Network Implementing Direct Feedback Alignment

Square nodes represent operations and circular nodes represent variables. Here, N and δN are nodes referring to the neuron and its derivative. Nodes VRD and X correspond to van Rossum distance and multiplication, respectively. Dashed edges communicate spikes, whereas full edges represent real values.

Nodes N represent neurons, and δN are their respective derivatives. For example, N can represent the operation Equation 3, whereas its derivative, δN, can represent Equation 4. Dashed edges indicate spiking channels, whereas full edges indicate real-valued channels. When full edges cross a domain wall, e.g., the edges originating from the error node in Equation 4, a dedicated communication channel must be provisioned. On a platform supporting only spike-based communication, this information must be encoded in spikes. On the other hand, dashed edges crossing domains can be handled through efficient address-event communication protocols, such as in hierarchical AER (HiAER) (Park et al., 2017). In this example, the synthesized learning subgraph (red nodes and edges) is consistent with eRBP, via a random matrix G⁰. The symmetric case similar to back-propagation can be obtained by replacing G⁰ with W^1,⊤ and routing the errors via δN¹. This modification would involve different full edges crossing the domain walls.

Similar to modern high-level machine learning frameworks and hardware, our envisioned library will allow streamlining the construction of the learning channel in neuromorphic systems. Unlike traditional machine learning frameworks, this will lay out sensorimotor streams, online learning, and target-dedicated neuromorphic hardware. Thus, this library will contribute a much needed compiler for learning high-level function on neuromorphic hardware.

Concluding Remarks

As Carver Mead suggested decades ago, neuromorphic engineering and its applications are held back by our limited understanding of neural circuits' organizing principles, and less so by difficulties in implementation. Interestingly, the foundations of current deep neural networks were laid out during the same period. But at that time, computers could not scale to real problems such as visual recognition and natural language processing tasks. Today, many machine learning and neural networks can solve some of those problems (LeCun et al., 2015). These successes provide renewed interest in taking inspiration from machine learning to guide our understanding of the organizing principles in the brain and applying them to neuromorphic hardware. Researchers at the interface of these fields highlight the possible benefits in cross-fertilizing machine learning and neuroscience (Hassabis et al., 2017, Lake et al., 2017), in spite of a strong cultural gap between the two fields. This cultural gap is understandable: brain-inspired models, especially those based on spiking neuron models, severely restrict the breadth of computations during learning and inference. With the advent of powerful graphical processing units and dedicated machine learning accelerators, the brain-inspired approach to learning machines is often heavily criticized as being misguided. These criticisms are relevant to bottom-up designs, or metrics purely based on absolute accuracy at standardized benchmarks. However, in cases in which real-time adaptability, autonomy, or privacy is essential, learning must be performed closer to the sensors. In this situation, power becomes a key metric and neuromorphic hardware co-designed with learning algorithms can have significant advantages.

Although the traditionally bottom-up approach of neuromorphic engineering is well justified for analysis-by-synthesis research, widespread interest in this field will likely be driven by its technological and economic prospects. In this review, we argued that the technological success of neuromorphic learning machines is not compatible with a purely bottom-up approach using current technologies. With the close analogies with machine learning, we hope to encourage aspiring and experienced neuromorphic hardware engineers to carefully plan learning features by matching neural and synaptic dynamics under task relevant objective functions. Although several challenges remain open in learning with spiking neurons and a software platform for programming neuromorphic learning machine does not yet exist, we expect that matching neural and synaptic dynamics will go a long way in rendering hardware efforts compatible with ongoing algorithmic developments.