Abstract
A theoretical model is developed to investigate the role played by the particulate (two-phase) nature of blood on oxygen (O2) release in capillary-size vessels. Red cells flowing in single-file suspension through capillaries are modelled as evenly spaced, hemoglobin (Hb)-containing circular particles in a rectangular channel (two-dimensional case) or axisymmetric spheres in a circular tube (three-dimensional case). The model includes the free and Hb-facilitated transport of O2 and Hb-O2 kinetics inside the particles, diffusion of free O2 in the suspending phase, and a specified O2 tension at the capillary wall that drives the release of O2 from the particles as they traverse the capillary. The results are expressed in the form of a capillary mass transfer coefficient, an inverse resistance, that relates the spatial average flux of O2 out of the capillary to a driving force for O2 release. The results indicate that this coefficient depends significantly on particle spacing and clearance (channel size relative to particle size) but not significantly on the O2 tension at the capillary wall nor the eccentricity of the particles in the channel. It is also found that the capillary mass transfer coefficient can be several times smaller (more resistance) than that for a continuous Hb solution releasing O2. As a physiological application of the coefficients obtained, they are combined with a Krogh-type model for tissue, and the resulting analysis suggests that the fraction of total O2 transport resistance that resides inside the capillary is influenced significantly by the discrete nature of blood and can account for 30 to 70% of the total resistance to O2 transport from blood to tissue.
1. INTRODUCTION
The classical view of oxygen transport from blood to tissue, implicit in both experimental and theoretical studies, assumes that the mass transfer resistance for oxygen inside the capillary is secondary, if not negligible, to that outside the capillary in the tissue itself (cf. Popel, 1978; Salathé et al., 1980; Turek and Rakusan, 1981; Kayar et al., 1982; and Klitzman et al., 1982). Often in model studies if intracapillary resistance to oxygen transport is considered, the intra-capillary description is simplified by assuming that capillary blood is a continuous and homogeneous hemoglobin solution, thereby ignoring the particulate (two-phase) or discrete nature of blood (Fletcher, 1973, 1978). Since under normal conditions most of the oxygen carried by blood is bound to hemoglobin in the red cells, the continuum assumption disregards as well the particulate/discrete nature of the oxygen supply in capillaries.
Recently, Hellums (1977) used a simplified model of oxygen release from blood in capillaries and predicted that intracapillary oxygen transport can contribute 50% of the total resistance of oxygen transport to tissue. The prediction of a large intracapillary resistance rests directly on Hellums’ treatment of the oxygen supply as discrete, i.e., it is assumed that capillary blood consists of alternating red cell and plasma slugs of equal length and that oxygen release out of the capillary occurs only from the red cell slugs. Thus, only a fraction (one-half) of the capillary volume/surface area at any instant is functional in oxygen exchange.
The physiological significance of a nonnegligible resistance to intracapillary oxygen transport is important. It compels us to examine more closely the role of intracapillary physiological parameters in oxygen exchange, e.g., red cell (RBC) spacing, RBC velocity, and RBC clearance (RBC size relative to capillary size), to name a few. If intracapillary resistance to oxygen transport is significant, then any variable that influences the oxygen transport resistance in the capillary can affect ultimately the oxygen tension level and distribution in the tissue. Thus, a parameter such as red cell spacing, which is recognized traditionally as an important determinant of oxygen delivery, can obtain new significance for oxygen transport through any effect it has on intracapillary oxygen transport resistance.
Apart from the work of Hellums and co-workers, few studies have addressed the role of the particulate nature of blood on intracapillary oxygen transport and release. Federspiel and Sarelius (1984) investigated the effect of red cell spacing on the ability of capillary blood to supply a uniform flux of oxygen at the capillary wall; the question of the intracapillary oxygen transport resistance, however, was not addressed. Niimi and Sugihara (1984) examined the supply of oxygen to a Krogh-type model of tissue from a capillary in which the blood was described by lumped compartments for the red cells and the suspending plasma; the compartments were assumed to be homogeneous with mass transfer coefficients relating their interactions. The model predicted a significant difference between the average oxygen tensions in the red cell, plasma, and tissue compartments, with the size of the difference depending in part on capillary (tube) hematocrit. The oxygen tension in the tissue became especially dependent on capillary hematocrit for small values of that parameter. The study is limited, however, by the lumped-compartment approach for blood and by the difficulty in generalizing the results to other models of tissue.
The present theoretical study examines the effect of the particulate nature of capillary blood and hence oxygen supply on the release and transport of oxygen from blood in capillaries. The study is based on simplified geometrical models for red cells in suspension flowing through capillaries in single file. Though the geometry is simplified, the model demonstrates several key concepts about oxygen transport from particulate suspensions relevant to oxygen release in capillaries, the most notable being the effects of particle spacing and clearance in the channel. The results are presented primarily as suitably normalized mass transfer coefficients which relate the average flux of oxygen out of the capillary to a driving force for oxygen release. These coefficients are compared to mass transfer coefficients that describe the release of oxygen from continuum hemoglobin solutions, thus assessing the applicability of the continuum assumption for capillary blood. As an application of the model, the capillary mass transfer coefficients are applied to a simple Krogh-type model for the tissue in order to estimate the fraction of total mass transfer resistance for oxygen that is attributable to intracapillary transport.
2. THE MODEL
2.1. Model Geometry
The important feature of the model involves describing capillary blood as a two-phase fluid of red cells suspended in plasma. In this study both two-dimensional and axisymmetric three-dimensional models are investigated. The two-dimensional case idealizes red cells as circular particles in a rectangular channel that represents the capillary, while in the three-dimensional case spheres inside a circular tube are considered. The two-dimensional case is necessary to investigate the effect of particle-channel asymmetries that would be difficult to study in three dimensions. The model particles are slightly smaller than the channel dimensions, and they move through the channel in single-file flow separated by plasma gaps. Clearly, the in vivo geometry of red cells in a capillary is more complicated than what we are considering (cf. Bagge et al., 1980), but at this stage it is necessary to simplify the geometry in order to treat blood as a two-phase fluid. The implications of the simplified geometry are discussed in detail later.
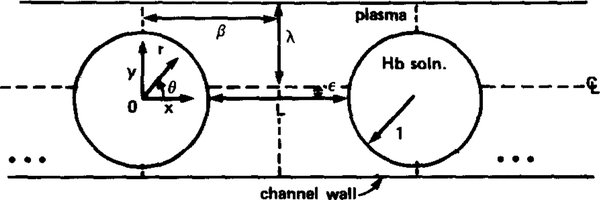
A schematic of the geometry is displayed in Fig. 1, in which the particles are understood to be circles in a rectangular channel for the two-dimensional case and axisymmetric spheres in a tube for the three-dimensional case. A frame of reference moving with the red cells is adopted for the subsequent analysis; hence, the coordinate systems (x, y) and (r, 0) are centered and fixed in the circular or spherical particles. Unless stated otherwise, all lengths are normalized by the particle radius, a. The discrete nature of capillary blood and oxygen supply are described in the model by several parameters, namely: L, the edge-to-edge separation between particles; λ, the clearance of the particles in the channel or tube (“clearance” refers to the size of the channel or tube relative to the particles and is defined by λ = d/a, where d is the channel half-width or tube radius); and ε, the eccentricity of the particles in the channel, i.e., whether the particles are centered (ε = 0) or off-centered (ε ≠ 0) with respect to the channel axis. Naturally, for the three-dimensional axisymmetric case the eccentricity of the spheres must be zero, i.e., ε = 0. Also shown in Fig. 1 is β, the axial distance from particle center (x = 0) to the midway (equidistant) plane between particles. Following physiological convention the separation between particles will usually be referred to in units of particle lengths, which for the simple particles considered here is equivalent to particle diameters.
FIG. 1.
Schematic of model geometry. Geometry is either two-dimensional or axisymmetric three-dimensional, where in the latter case particle eccentricity, ε, is zero.
2.2. Transport Equations
Red cell interior.
The red cell is modelled as a homogeneous hemoglobin solution inside an oxygen permeable membrane. The development of the equations describing oxygen transport inside the red cell closely follows other formulations (Moll, 1969; Kutchai, 1970; Sheth and Hellums, 1980; Clark et al., 1985). A hemoglobin molecule has four heme subunits, each capable of binding an oxygen molecule; thus four different oxyhemoglobin states are possible corresponding to hemoglobin with one to four oxygen molecules bound. A description at this level of detail is difficult, primarily because the reactions between oxygen and the four different oxyhemoglobin species are not characterized completely. Therefore, a simplification is made by assuming, as the above studies have, that the heme subunits of hemoglobin are distinct chemical species. Thus, the chemical composition of the red cell can be specified by the molar concentrations of free oxygen (oxygen dissolved in the cytosol), N1, oxygenated heme subunits, N2, and free heme subunits, N3. It can be further assumed that the total heme concentration, NT = N2 + N3, is uniform and constant in the red cell. Under these conditions, one can show that N2 and N3 are not independent since N3 is related simply to N2 by N3 = NT — N2. NT can be specified for a red cell, and hence N1 and N2 alone are sufficient to characterize the system (Snell, 1965).
The differential mass conservation laws for oxygen and oxyhemoglobin (i.e., oxygenated heme subunits) in the red cells, assuming constant density and diffusion coefficients, D1 and D2, for oxygen and oxyhemoglobin, respectively, are
| (1) |
| (2) |
where t is time, ∇2 is the Laplacian operator in either two or three dimensions, and T is the net rate that oxygen combines with a free heme subunit to form an oxygenated heme group. It is assumed that the red cells move through the capillary as solid bodies, and thus in a reference frame fixed to the particles, Equations (1) and (2) do not include terms describing the convective transport of oxygen inside the red cells. These terms may be important if red cells “tank-tread” (Gaehtgens, 1981) or deform continuously as they move through capillaries. Note that the latter equation, Eq. (2), describes the facilitated transport of oxygen in the red cell due to the diffusion of oxyhemoglobin molecules.
To obtain an expression for T it is necessary to model the kinetics of the reversible reaction between oxygen (O2) and heme groups (Hb),
While this is a difficult task, an important consideration is that the chosen kinetics must predict the experimentally determined equilibrium relation (Feq) between oxygen and oxyhemoglobin,
| (3) |
in the limit as T → 0 (Sheth and Hellums, 1980). It is assumed that T can be expressed as
| (4) |
where Ta is the association rate and Td the dissociation rate of the reaction. For the dissociation rate mass action kinetics are assumed to apply:
| (5) |
where K is the dissociation rate constant and can be estimated from experimental data. Then, Ta can be determined from the equilibrium constraint, Eq. (3), in the limit as T → 0. If for simplicity we choose the Hill approximation to the equilibrium relation,
| (6) |
where N50 and n are equilibrium parameters available from experimental data, then Ta is given in simplest form by
| (7) |
Thus, one obtains
| (8) |
from Eqs. (4), (5), and (7), and it can be verified that Eq. (8) does reduce to the Hill approximation, Eq. (6), in the limit as T → 0. There are other and perhaps better approximations to the oxygen—hemoglobin equilibrium relationship that could have been used in place of the Hill approximation, but these in general are more complicated and do not lead to a simple analytical form for T as in Eq. (8). In addition, for a given approximation to the equilibrium behavior the choice of rate expressions is not unique; the selection here represents the simplest reasonable choice. Model studies (Clark et al., 1985) have indicated that a large fraction of the red cell is at or very near chemical equilibrium; thus, the selection of T is less critical than the requirement that it predict faithfully the known equilibrium relation between oxygen and hemoglobin. The Hill equilibrium expression is known to be a weak approximation in the limit of either very low or very high hemoglobin saturation. Thus, results are only presented in the saturation range from 10 to 80%.
Plasma region.
The differential mass balance for free oxygen in the plasma region assuming constant density and diffusivity is given by
| (9) |
In the reference frame selected for the analysis, which moves with the red cells, the velocity field in the suspending plasma is complicated and circulating flows exist between red cells (cf. Gaehtgens et al., 1980). Thus, the potential exists for convective transport of oxygen and the appropriate term (, where V is the fluid velocity field vector) describing convective transport is included in Eq. (9). As a convention the superscript “(p)” denotes a quantity in the plasma region when necessary to avoid confusion with the same parameter for the red cell interior.
2.3. Boundary and Initial Conditions
Transport in the red cell and in the plasma regions are coupled through matching conditions at the red cell surface, r = 1. These conditions are continuity of oxygen flux and tension (partial pressure):
| (10) |
| (11) |
respectively, where α is the oxygen solubility coefficient that relates molar concentrations to oxygen tension, P, through the relations N1 = αP and . The assumption of a continuous oxygen tension across the membrane implies that a negligible transport resistance for oxygen exists there (Kreuzer and Yahr, 1960; Huxley and Kutchai, 1981). For oxyhemoglobin, a large molecule, it is assumed that the red cell membrane is an impenetrable barrier, and the oxyhemoglobin flux is zero there:
| (12) |
At the capillary wall the oxygen tension is set at PW:
| (13) |
This boundary condition is necessary so that intravascular oxygen transport can be studied without addressing complexities of the extravascular space. In general Pw can depend on position along the capillary wall and time. Since it is not known precisely what Pw is in vivo, we limit our consideration to constant and uniform Pw. The final results argue that this choice does not significantly limit the scope of the model.
It is further assumed that adjacent particles are evenly spaced and identical, and thus symmetry conditions can be imposed at x = 0 and x = β in the form
| (14) |
Clearly, adjacent red cells in a capillary can have different oxygen contents since they have entered the capillary at different times and have unloaded different amounts of oxygen, but the difference in oxygen tension will be minimized to some extent by hemoglobin buffering. Also, red cells in general are not necessarily evenly spaced inside the capillary. The symmetry assumption is necessary to avoid considering a long train of unevenly spaced particles with different oxygen contents. The final results, however, indicate that adjacent particles have a very small influence on oxygen diffusion from one another, except for the case of particles nearly touching, and thus the assumption of evenly spaced identical particles is not particularly limiting.
To complete the description initial conditions are imposed at time t = 0, when the particles enter the capillary:
| (15) |
where N1i, N2i, and are assumed to be uniform and in equilibrium (i.e., and N1i = Feq(N2i). Appropriate values for these initial quantities are difficult to assign because of precapillary losses of oxygen (Duling and Berne, 1970), and they can be significantly less than systemic values. The results, however, are presented in the form of a capillary mass transfer coefficient (discussed below), which does not depend on the initial conditions imposed. Thus, the initial values are chosen to correspond to red cells entering capillaries with hemoglobin saturations of 90%.
2.4. Simplification and Solution of Transport Equations
A scaling analysis of the transport equations leads to dimensionless forms for these equations and several useful simplifications, as discussed in more detail in Appendix A. Two primary simplifications can be made: (1) To a first approximation for the physiological conditions of interest here, convective transport of oxygen by the plasma velocity field in the reference frame moving with the particles is small relative to transport by molecular diffusion. Thus, the term, , is dropped from the plasma transport equation. This approximation is supported by more-detailed model calculations (Aroesty and Gross, 1970). (2) For the parameters relevant to this study, as listed and discussed below, the dimensionless coefficients associated with the time derivative terms in the free oxygen transport equations for both the red cell and plasma regions, Eqs. (1) and (9), are small in comparison to the remaining terms in their respective equations. Thus, these time derivative terms can be neglected safely (the quasisteady approximation), which was confirmed by comparing test calculations done with and without ∂/∂t in Eqs. (1) and (9) for several important cases. The quasisteady approximation is useful in the numerical solution of these equations (see Appendix B) and is best understood from the physical argument that hemoglobin has a large capacity for oxygen and acts as a buffer for local time variations in the free oxygen concentration, both in the red cell and in the plasma regions.
Applying the dimensional analysis outlined in Appendix A, the dimensionless transport equations are:
| (16) |
| (17) |
| (18) |
where C is the normalized free oxygen concentration, C = N1/N50 and ; S is oxyhemoglobin saturation, S = N2/NT; τ is dimensionless time; and where ρ = KNTa2/D1N50 and β = Ka2/D2 are dimensionless parameters that arise naturally from the scaling of the dimensional transport equations. To summarize, Eq. (16) describes the transport of free (dissolved) oxygen in the red cell; Eq. (17) describes the transport of bound oxygen in the red cell, i.e., facilitated transport; and Eq. (18) describes the transport of free oxygen in the plasma region, where the transport by convection is assumed to be small.
Solution of the transport equations is complicated by nonlinear kinetic terms, coupling among the equations, and the geometry of the problem. Thus, these equations are solved using numerical techniques that are discussed in more detail in Appendix B. The numerical solution to the transport equations, subject to the imposed boundary and initial conditions, provides the spatial profiles of free and bound oxygen concentration in and around a particle as a function of time as the particle traverses a capillary and unloads oxygen. These results are reported by calculating a capillary mass transfer coefficient that relates the average flux of oxygen out of the capillary to a driving force for oxygen release, as discussed below.
2.5. The Capillary Mass Transfer Coefficient, k
The capillary mass transfer coefficient, k, describing oxygen release is defined by
| (19) |
where F is the spatial average flux of oxygen out of the capillary and ΔPcap is a driving force for oxygen release from the capillary. The value of k can be considered as a conductance or inverse resistance for oxygen release from capillaries, and the limit k → ∞ corresponds to the common assumption of negligible capillary resistance to oxygen transport. Because of the assumed symmetries, instantaneous values of the flux at the capillary wall (which are obtained from the free oxygen concentration profile in the plasma using ) can be averaged from x = 0 to x = β to obtain F. In the two-dimensional case when eccentricity is not zero, the instantaneous flux is averaged over both the upper and lower channel wall. The appropriate driving force is a difference in oxygen tension between the particles and the capillary wall:
| (20) |
where P* is a characteristic intraparticle oxygen tension and Pw is the oxygen tension at the capillary wall, assumed constant and uniform here. P* is defined most conveniently by basing it on the mean saturation of a particle through the Hill approximation to the oxyhemoglobin equilibrium curve, i.e., Eq. (6) rewritten using oxygen tension in place of oxygen molar concentration:
| (21) |
where P50 is the oxygen tension saturating 50% of hemoglobin at equilibrium.
The capillary mass transfer coefficient, k, is calculated using the defining relations, Eqs. (19), (20), and (21), and solving the transport equations numerically to obtain the relation between F, , and Pw during oxygen unloading from a particle. The results presented in the next section are primarily in the form of a normalized mass transfer coefficient, k*, which is related to k by
| (22) |
This normalization arises from the dimensional analysis of the descriptive equations. In simple terms k* is a normalized conductance (inverse of resistance) for oxygen release. Hence, larger values of k* result in greater oxygen fluxes from the capillary for a given driving force in O2 tension.
2.6. Parameter Values
The values for the parameters used in this study are listed in Table 1 in their most common units. All parameters are chosen at or corrected to 37°. Parameters for the interior of the red cell are the same as those used and discussed in detail by Clark et al. (1985). In addition, parameters for the plasma region are needed: the diffusion coefficient comes from Kreuzer (1970) and the solubility coefficient from Spaan et al. (1980). Several geometrical parameters are also needed; but since they are difficult to assign precisely, reasonable ranges are considered. The clearance, λ, of red cells in a capillary has not been studied systematically, but inspection of photomicrographs from Gaehtgens et al. (1980) and Bagge et al. (1980) suggest that λ = 1.1 to λ = 1.5 is a reasonable range. This range is supported also by estimates from in vivo data given by Klitzman and Duling (1979). In dimensional terms these values correspond to minimum gaps between the particles and the channel wall of between 0.2 and 1 μm for the circular particles of radius 2 μm considered here. The separation, L, between particles is varied over a reasonable range from 0.1 to 3 particle lengths (Damon, 1984), which in dimensional terms represents a range for L between 0.4 and 12 μm.
Table 1.
MODEL PARAMETERS
| Geometrical parameters | ||
|---|---|---|
| a | Particle radius | 2 μm |
| d | Channel half width | 2.5 μm (2.1–3.0) |
| L | Particle spacing (edge-to-edge) | 0.4 μm - 12 μm |
| dt | Tissue characteristic dimension | 10 μm, 18 μm, 25 μm |
| Physical parameters | ||
| Red cell | ||
| NT | Total heme concentration (34 g% hemoglobin solution) | 2.03 × 10−5 mole cm−3 |
| P50 | Equilibrium parameter | 26 mm Hg |
| N50 | Equilibrium parameter | 4.12 × 10−8 mole cm −3 |
| n | Hill equation parameter | 2.7 |
| K | Kinetic constant | 44 sec−1 |
| D1 | Diffusion coefficient for oxygen | 9.5 × 10−6 cm2 sec−1 |
| D2 | Oxyhemoglobin diffusion coefficient | 1.44 × 10 7 cm2 sec −1 |
| α | Solubility coefficient for oxygen | 1.56 × 10−9 mole cm−3 mm Hg−1 |
| Plasma | ||
| Oxygen diffusion coefficient | 2.4 × 10−5 cm2 sec−1 | |
| α(p) | Oxygen solubility coefficient | 1.4 × 10 5 mole cm−3 mm Hg−1 |
| Tissue | ||
| Dt | Oxygen diffusion coefficient | 1.7 × 10−5 cm2 sec−1 - 2.6 × 10−5 cm2 sec−1 |
| αt | Oxygen solubility coefficient | 1.4 × 10−9 mole cm−3 mm Hg−1 |
3. RESULTS
3.1. Discrete Particles versus Continuous Hemoglobin Solutions
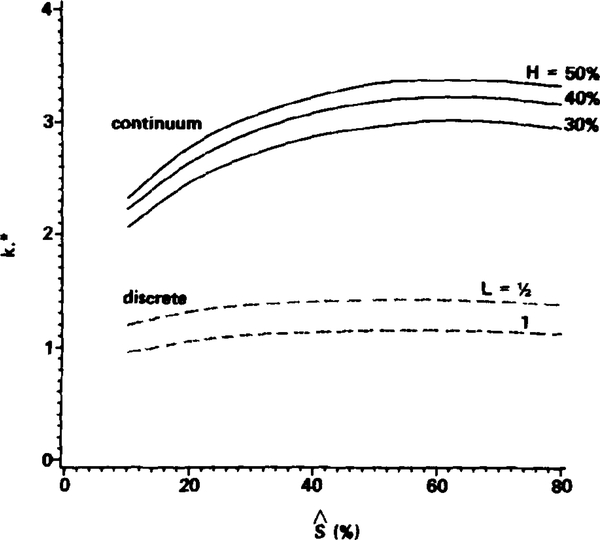
In this section typical results for the normalized capillary mass transfer coefficient, k*, for discrete particles are presented and compared with those for a continuous hemoglobin solution releasing oxygen (the continuum case). Recall that k* represents a conductance or inverse resistance to O2 release. The dashed curves in Fig. 2 represent the values of k* for two typical discrete cases of the two-dimensional circular particles. The particles are spaced L = 0.5 particle lengths apart in one case and L = 1.0 particle lengths apart in the other, with λ = 1.25, ε = 0, and Pw = 0 in both cases. The values of k* are displayed as functions of the mean saturation, , of the particles during oxygen release. Results are given in the range from to . Since the reference frame is fixed to a particle as it moves through the capillary, we follow the decrease in with time of a single particle rather than the decrease in with axial position in the capillary. Thus, the range of from 80 to 10% in Fig. 2 (following curves from right to left) corresponds to an interval of time over which we follow the particle while it is unloading oxygen in the channel and to relate that time interval to the axial position of the particle in the capillary requires specifying the particle velocity. However, we are interested primarily in characterizing the behavior of k* with ; thus, the time interval involved or the axial distance traversed in the capillary is immaterial and not displayed.
FIG. 2.
Comparison of normalized capillary mass transfer coefficients, k*, for discrete particles (dashed curves) and continuum hemoglobin solutions (solid curves) for the two-dimensional geometry. For the discrete case L signifies spacing in units of particle lengths (which is the diameter for the circular particles, 4 μm). For the continuum hemoglobin solutions, the hemoglobin content in the channel is equivalent to blood with a hematocrit of H. Parameters: Pw = 0, λ = 1.25, ε = 0.
It is clear from the dashed curves in Fig. 2 that k* is nearly independent of except for very small saturations. Below equal to 20%, k* begins to decrease due to the increasing resistance encountered for releasing the last remaining oxygen in the particle. In a large range of , however, k* is approximately constant.
It is interesting to compare the k* values for the discrete cases with those for some continuous hemoglobin solutions releasing oxygen, which are denoted by the solid curves in Fig. 2. These continuum hemoglobin solutions are equivalent to blood samples of hematocrits H = 30, 40, and 50% that are hemolyzed and dispersed uniformly in the channel. These hematocrit values are chosen only to represent a typical range used in previous model studies that have regarded capillary blood as a continuum hemoglobin solution. For the purposes of this illustrative comparison and for simplicity, oxygen release from nonflowing continuous hemoglobin solutions are considered. The applicable transport equations, therefore, are identical to those for inside the red cell in the discrete case, Eqs. (16) and (17), except for two differences: (1) Eqs. (16) and (17) are now applied to the entire channel, -λ ⩽ y ⩽ λ, subject to a specified oxygen tension Pw at the channel wall (obviously, transport in the plasma region and eccentricity, ε, do not enter into the continuum case); and (2) the continuum total hemoglobin concentration NT is now H times the NT value in a red cell, and several parameters should be adjusted according to the value of NT: namely the diffusion coefficient for oxygen (Kreuzer, 1970) and oxyhemoglobin (Spaan et al., 1980), and the oxygen solubility coefficient (Spaan et al., 1980), all of which depend to some degree on the hemoglobin concentration. The value of k is defined and normalized in the same manner for the continuum case as for the discrete case [refer to Eq. (22)] so that proper comparisons can be made between the k* values for the two cases.
Figure 2 shows clearly that k* for discrete particles is two to three times smaller than that for the continuum hemoglobin solutions, or in other words the discrete case leads to more mass transfer resistance to oxygen release. Thus, for the same driving force, ΔPcap, oxygen release from discrete particles is significantly slower than from continuum hemoglobin solutions. The explanation for the difference is investigated and discussed below.
3.2. Determinants of k* for Discrete Particles
In this section the dependence of k* on particle spacing, L, and clearance, λ, are presented for both the two-dimensional and axisymmetric three-dimensional cases; for the former case the effect of particle eccentricity in the channel, ε, is also presented, as is the effect of the oxygen tension at the capillary wall, Pw. The value of k* is not very sensitive to (see Fig. 2), and thus the subsequent comparisons are made primarily by displaying the average, , of the mass transfer coefficient. Unless stated otherwise, is the average value of k* in the range of from 80 to 20%.
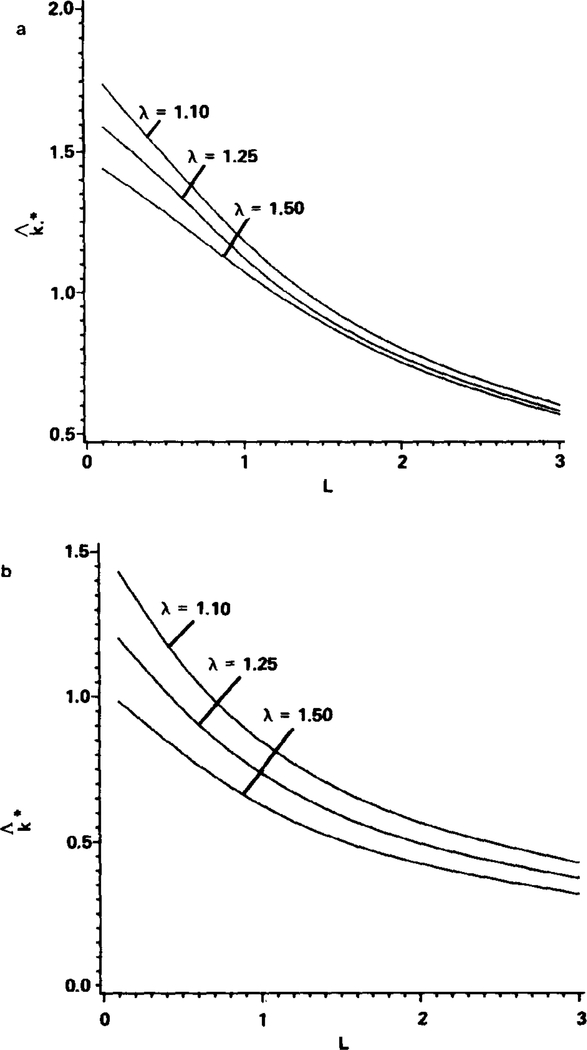
The dependence of on particle spacing and clearance is summarized in Figs. 3a and b for both the two- and axisymmetric three-dimensional cases, respectively. The values of are displayed as functions of L (following physiological convention the units for L are particle lengths, which are equivalent to the diameters of the particles here) for λ values of 1.10, 1.25, and 1.50. As expected, is greatest in the limit of nearly touching particles (L → 0) with small clearances in the channel (λ → l). The value of , however, is always significantly less than the values displayed in Fig. 2 for continuous hemoglobin solutions in the two-dimensional case. It is apparent from both Figs. 3a and b that the mass transfer coefficient decreases rapidly as the spacing between particles increases. This is a preliminary indication that the “zone-of-influence” inside the channel of oxygen released from a given particle does not extend substantially beyond the particle.
FIG. 3.
Effect of particle spacing, L, and particle clearance, λ, on the capillary mass transfer coefficient for the two-dimensional case (a) and the axisymmetric three-dimensional case (b). Shown is the average capillary mass transfer coefficient from = 80% to = 20%, , as discussed in the text. L is in units of particle lengths. Parameters: Pw = 0, ε = 0.
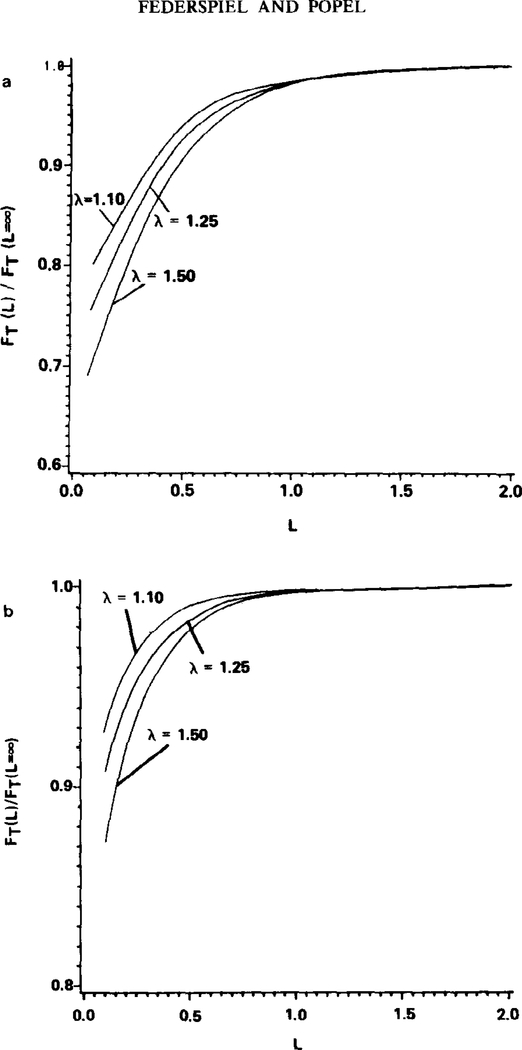
In order to investigate this “zone-of-influence” the results from Figs. 3a and b can be expressed in a different form. In Figs. 4a and b the total flow rate of oxygen, FT, out of the capillary from x = 0 to x = β when equals 50% is displayed as a function of particle spacing L. Equivalently, the value of FT can be considered to be directly proportional to the oxygen flow rate per red cell when equals 50%. This value of FT is normalized by the FT value at large spacings, FT (L = ∞). (In Figs. 4a and b, spacing is expressed in units of channel widths because fluid mechanical models suggest that the channel width is the relevant length characterizing particle interaction.) The normalized flow rate values are shown for λ = 1.10, 1.25, and 1.50. For particles that are nearly touching (L small), diffusional interaction reduces the total oxygen flow rate out of the capillary from x = 0 to x = β below that possible at large separations, by about 20 to 30% in the two-dimensional case (Fig. 4a) and 10 to 20% in the three-dimensional case (Fig. 4b). That is, for L small the total oxygen flow rate per red cell is reduced because of diffusional interaction between adjacent red cells. Note, however, that although the total oxygen flow rate per red cell is reduced by diffusional interaction when L is small, the oxygen flux (flow rate per unit area) at the capillary wall increases with decreasing L (Figs. 3a and b) because there are more red cells per unit length in the capillary.
FIG 4.
Extent of particle interaction for the two-dimensional case (a) and the axisymmetric three-dimensional case (b). FT is proportional to the total O2 flow rate per red cell when = 50%. For this figure only, spacing is in units of channel width. Parameters: Pw = 0, ε = 0, λ = 1.25.
More interesting is the behavior with increasing red cell spacing. At a spacing of about one channel width the total flow rate of oxygen out of the capillary between x = 0 and x = β reaches a maximum, and further increasing the spacing does not increase the flow rate of oxygen out of the capillary. Close inspection of concentration profiles revealed that the flux of oxygen from a particle through the capillary wall is limited to the near vicinity of the particle. As L is increased to one channel width, the flux of oxygen through the capillary wall around x = β becomes negligibly small compared with the flux across the capillary wall closer to the particle. Thus, a particle has a limited “zone of influence” with respect to oxygen flux. The particle cannot release oxygen through the capillary wall to any significant extent beyond its “zone of influence.” The results in Fig. 4 indicate that the “zone of influence” of a particle in approximate terms extends about one-half a channel width in front and behind the particle. Because of the limited “zone of influence” of a particle, the fraction of volume or surface area of a capillary that is functional in oxygen exchange at any instant is less than unity and depends on the particle spacing. This explains in part why the mass transfer coefficient for discrete particles is smaller than that for a continuum hemoglobin solution, which does not have a limited “zone of influence” and for which the entire capillary wall is functional at any instant in oxygen exchange.
The eccentricity of the particles in the channel has little effect on the capillary mass transfer coefficient as defined in this study. Typical results are listed in Table 2 for the two-dimensional geometry. An eccentricity of ε = 0.125 for λ = 1.25 corresponds to moving the centers of the particles from the channel centerline to a position halfway to the lower channel wall. Although the oxygen flux from the side of a particle closest to the channel wall increases, that from the other side decreases almost equally. Thus, the average flux F increases slightly, and k* is nearly unchanged by the eccentricity of the particles in the channel.
Table 2.
EFFECT OF ECCENTRICITY, ε, ON k*a
|
L (particle lengths) |
ε = 0 | ε = 0.125 |
|---|---|---|
| 0.1 | 1.63 | 1.66 |
| 0.5 | 1.42 | 1.44 |
| 1.0 | 1.15 | 1.17 |
| 2.0 | 0.79 | 0.80 |
Values of k* at = 50% for the two-dimensional geometry with P„ = 0 and λ = 1.25.
Table 3 indicates that the oxygen tension at the channel wall, Pw, also has a small influence on the capillary mass transfer coefficient. Values of k* when = 75, 50, and 25% are given in the two-dimensional geometry for Pw = 0, 10, and 20 mm Hg. It is fortunate that k* does not depend strongly on Pw since neither the in vivo range of Pw nor the distribution of Pw along the capillary wall is known precisely from experimental studies. Since k* is insensitive to the value of Pw, however, there is some confidence that the assumption of uniform Pw used in this study is not significantly detrimental, and the k* values computed here might be reasonable approximations for cases in which Pw is nonuniform along the capillary wall. Althouh k* is practically independent of Pw the value of the average flux out of the capillary, F, depends directly on Pw through the equations used in defining k, Eqs. (19) and (20).
Table 3.
EFFECT OF WALL OXYGEN TENSION, Pw, ON k*a
| S (%) | Pw = 0 mm Hg | 10 mm Hg | 20 mm Hg |
|---|---|---|---|
| 75 | 1.13 | 1.13 | 1.12 |
| 50 | 1.15 | 1.16 | 1.18 |
| 25 | 1.09 | 1.13 | *b |
L = 1 particle length, λ - 1,25, and ε = 0 in the two-dimensional geometry.
The particles never reach = 25% for that Pw.
3.3. Plasma Resistance to Intracapillary Oxygen Transport
The observation that k* depends significantly on the clearance of the particles in the channel suggests that the plasma region plays an important role in oxygen transport resistance inside the capillary. To investigate this further, the fraction of intracapillary mass transfer resistance due to the plasma region, Rp, is calculated. The value of Rp is defined by
| (23) |
where is the normalized capillary mass transfer coefficient for the hypothetical case of negligible transport resistance inside the particles, when the entire intracapillary resistance is due to the plasma region. The value of is computed analogously to k* except that it is assumed that the particles have no mass transfer resistance, and thus have a uniform oxygen tension, P*, which is a function of time as oxygen is being released. The plasma transport equation, Eq. (18), is then the sole governing transport equation and is solved subject to the boundary condition at the particle surface, r = 1, of a specified oxygen tension, P*, there. Because of the linear character of the transport equation in the plasma region, is independent of P* and Pw.
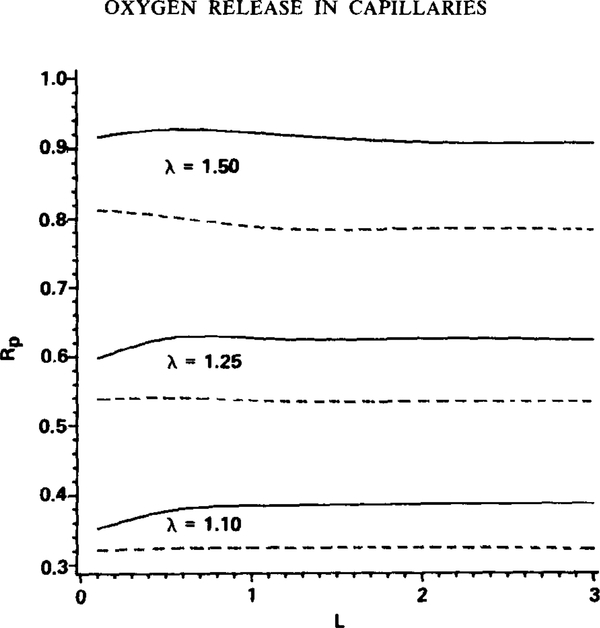
The plasma relative resistance to intracapillary oxygen transport, Rp, is displayed in Fig. 5 as a function of particle spacing, L, for values of λ equal to 1.10, 1.25, and 1.50 and for both the two-dimensional (solid curves) and three-dimensional (dashed curves) geometries. The value of Rp depends primarily on particle clearance rather than particle spacing. In addition, the plasma region appears to offer a disproportionately large fraction of the intracapillary mass transfer resistance: consider that with λ = 1.25, a plasma gap of 0.5 μm at the closest point between the particles and the channel wall, the plasma region accounts for about 60% of the intracapillary resistance; and with λ = 1.10, a 0.2-μm plasma gap at the closest point, the plasma accounts for about 35% of the intracapillary resistance. At first glance this may seem surprising since the diffusion coefficient for oxygen in plasma is over twice greater than that for oxygen in the red cell (Table 1). In the red cell, however, oxygen is also transported in the form of hemoglobin-bound oxygen (i.e., facilitated transport, represented by the transport equation for S), and it can be shown that the total effective diffusion coefficient for oxygen in a red cell can be greater than the diffusion coefficient for oxygen in the plasma region (cf. Federspiel, 1983). This result depends directly on the existence of facilitated transport of oxygen by hemoglobin in the red cell, which is eliminated when hemoglobin is either fully saturated or desaturated with oxygen (cf. Keller and Friedlander, 1966). Thus, in these limits, which occur outside the saturation range considered in this study, the plasma relative transport resistance, Rp, decreases, and the dominating transport resistance is in the red cell. The disproportionately large mass transfer resistance due to the plasma region accounts for part of the difference between the k* values for discrete particles and those for continuum hemoglobin solutions. This effect together with the limited “zone-of-influence” discussed above are the primary distinguishing factors between oxygen supply from discrete particles and that from a continuous hemoglobin solution.
FIG. 5.
Plasma mass transfer resistance, Rp, relative to the total intracapillary mass transfer resistance. L is in units of particle lengths. Results are given for the two-dimensional geometry (solid curves) and the axisymmetric three-dimensional geometry (dashed curves). Rp is the average value from = 80% to = 20%. Parameters: Pw = 0 and ε = 0.
3.4. Dimensional Oxygen Release Equation
The results presented above have been expressed in the form of a dimensionless mass transfer coefficient, which is an inverse resistance or a conductance for oxygen release from the model red cells in the capillary channel. It is also useful to have a simple dimensional expression with which oxygen release can be estimated from the results in this study. Thus, Eq. (22) is used (along with the necessary parameters in Table 1) to calculate the dimensional mass transfer coefficient, which can then be used in Eq. (19) to obtain a dimensional oxygen release equation. The oxygen release equation is
| (23.5) |
where F is the spatial average flux of oxygen out of the capillary in moles cm−2sec −l, and ΔPcap is the oxygen tension driving force between the red cells and the capillary wall (as defined under Section 2.5) in mm Hg. The factor, , is the dimensionless mass transfer coefficient, but it can more simply be regarded as a dimensionless factor correcting for the discreteness of the oxygen supply, i.e., depends on red cell spacing, L, and clearance, λ. The dependence of on L and λ can be obtained from Figs. 3a and b. If in approximate terms one thinks of F as being set by tissue oxygen metabolism and the capillarity of tissue, then Eq. (23.5) states that the magnitude of the transcapillary oxygen tension drop, ΔPcap, for a given F is determined by the discreteness of the oxygen supply as embodied in .
4. DISCUSSION
4.1. General Comments
The discrete nature of blood, i.e., that blood is a two-phase medium of red cells suspended in plasma, plays an important role in determining the transport resistance for oxygen release from blood in capillaries. For a given driving force for oxygen release from a capillary, the rate of release from discrete hemoglobin-containing particles can be on the order of two to three times slower than that from a continuum hemoglobin solution. Continuum hemoglobin solutions are used only for comparison to illustrate the results of the present model against those based on the more traditional treatment in model studies of capillary blood as a continuous hemoglobin solution. The continuum results in Fig. 1 should not necessarily be regarded as those representing a true hemolysate of capillary blood since in this case the situation is more complicated: e.g., hemoglobin concentration will be determined by capillary discharge hematocrit, which is unknown, and the chemical environment is likely to be altered by the hemolysis, which changes several parameters.
The capillary mass transfer coefficient, k*, can be considered as a conductance or inverse resistance to oxygen release from capillary blood. The conductance depends significantly on the spacing (separation) and clearance (capillary size relative to particle size) of the particles in the capillary. The strong dependence of k* on particle spacing reflects the limited “zone of influence” of a given particle. At a spacing of about one channel width, the flux of oxygen becomes negligibly small at the capillary wall midway between the particles. Thus, the particles cannot supply oxygen significantly beyond their “zone of influence,” and only a fraction of the capillary volume and surface area is functional at any instant in oxygen exchange. We have defined a capillary mass transfer coefficient based on a spatial average flux of oxygen out of the capillary from the particle center (x = 0) to the midparticle plane (x = β). It is important to remember, however, that the significant oxygen exchange occurs close to the particle, and if particle spacing, L, exceeds one channel width, then a region of the capillary wall around x = β receives only a negligibly small flux of oxygen.
The effect of clearance on the capillary mass transfer coefficient reflects the fact that the plasma region accounts for a significant fraction of the intracapillary resistance to oxygen transport, even if clearances are relatively small. In simple words, the plasma region reduces (“throttles”) the rate at which oxygen is released from particles as they travel through a capillary. This is entirely consistent with experimental studies of oxygen release from red cells in stopped-flow apparatus, where it is found that a small diffusion boundary layer of plasma around a cell can retard oxygen release (Huxley and Kutchai, 1981). Taken together, the effects of particle spacing and clearance, along with their respective underlying causes, result in a significant difference between the resistance to oxygen transport from discrete particles and that from a continuum hemoglobin solution in capillarysize channels.
A model with idealized two-dimensional and axisymmetric three-dimensional geometry for the particles and the channel is used in this study to simplify the analysis. Clearly, the in vivo situation is much more complicated, and the applicability of the model needs to be assessed. Primarily, the model addresses the discreteness of oxygen supply in capillaries and is a clear extension of previous models of intracapillary oxygen transport. It is not expected that the values of k* calculated in this study would describe precisely oxygen release from blood flowing through capillaries for the in vivo case. What is important is that the present model provides a simple framework in which to compare oxygen release from discrete particles to that from continuum hemoglobin solutions and in which to examine simply the prime determinants of the resistance to oxygen release from discrete particles.
The prime determinants of the oxygen transport resistance, l/k*, in the capillary are found to be particle spacing and particle clearance, the latter being more open to criticism since simple shapes are assumed for the red cells. Bagge et al. (1980) point out that a red cell may appear to be tightly fitted in a capillary, but closer examination from perpendicular viewing axes shows that the plasma gap separating the red cell from the capillary wall can be quite variable in size. Therefore, parts of the red cell are separated from the capillary wall by very small plasma gaps, and the oxygen that diffuses from these parts encounters a small transport resistance from the plasma. These parts of the red cell surface have limited area, however, and oxygen must also diffuse from parts of the red cell surface that are further from the capillary wall, hence encountering more plasma transport resistance. The model retains this effect qualitatively but in simpler form since the plasma gap between the particles used in this study and the channel wall is nonuniform. In fact, the importance of particle clearance and the appreciable intracapillary transport resistance of plasma predicted by the model are due precisely to the fact that not all oxygen molecules leaving a particle diffuse to the channel wall across the shortest plasma gaps, but some traverse longer paths and encounter more plasma transport resistance.
Another consideration in the use of simplified shapes for red cells is that the volume of the model red cells is smaller than that typical of mammalian red cells. This cannot be overcome by choosing a larger diameter for the particles. To do so would diminish the effect of the nonequilibrium boundary layer inside the red cell because the boundary layer is fixed in size and does not grow in proportion to the red cell size (cf. Clark et al., 1985). The volume of the model red cells becomes important to consider when one wants to know the time rate of oxygen saturation change during oxygen delivery; in this case, for a given flux of oxygen out of the red cell, the rate at which the O2 saturation of the cell changes depends on how much oxyhemoglobin (buffer) is in the cell (i.e., the cell volume). We have avoided these considerations by looking only at oxygen transport resistance (1/k*), which depends primarily on characteristic dimensions of the red cell and plasma regions. These characteristic dimensions are incorporated in the model geometry. It may be useful in future studies to address red cell shape more realistically than was done in this study, but to do so will require more experimental data about in vivo red cell shape. Thus, the present treatment of red cell shape and the related effects of red cell clearance on intracapillary oxygen transport should be considered as a first step toward addressing the more complicated in vivo situation.
In this analysis we have not dealt directly with capillary hematocrit as a parameter, but have instead used red cell spacing. Capillary hematocrit is related to red cell spacing, but it also depends on the shape of red cells in the capillary, how the red cells are folded in the capillary, and the capillary cross-sectional shape, none of which are known precisely from in vivo studies. Since idealized geometries are used in this study for the red cells and the capillary channel, it would be very difficult and perhaps misleading to discuss the results presented here in terms of capillary hematocrit rather than red cell spacing. Furthermore, it is red cell spacing that more closely and directly reflects the discreteness of the oxygen supply, and the results of this study suggest strongly that red cell spacing is an important oxygen transport variable in its own right.
A simplification of the model with respect to particle spacing is that only the case of evenly spaced particles is considered. In actuality, red cell spacing in capillaries in vivo is heterogeneous (Damon, 1984). Based on the results from this study, it is clear that adjacent red cells do not interact significantly with respect to oxygen release except when they are nearly touching. Thus, it seems reasonable to assume that the mass transfer coefficients computed in this study are reasonable estimates for the case of variably spaced red cells, but with the average mass transfer coefficient at any axial capillary location in the latter case dependent on the local red cell spacing. The applicability of this assumption, however, has not been tested and should be considered more closely.
The model adopts a reference frame moving with the particles, and in this reference frame convective transport of oxygen is not considered. Convective transport of oxygen in the plasma region due to the relative motion between red cells and plasma is assumed to be small based on scaling arguments and on past studies (Aroesty and Gross, 1970). Consequently, red cell velocity is not an important determinant of the capillary mass transfer coefficient and in fact enters the discussion only if one wants to convert the time coordinate to axial position in the capillary. Another possible mechanism for convective transport, however, exists in the red cells because fluid motions inside a red cell may be created by dynamic changes in red cell shape during capillary transit or by red cell “tank-treading” (Gaehtgens, 1981) in the capillary. In general, very little is known about red cell “tank-treading” in vivo; thus in this study it is assumed that the red cells move through the capillary as solid bodies, and the possibility of convective transport due to these fluid motions is not considered. Clark et al. (1981) estimated that these fluid motions inside the red cell would have little effect on free oxygen transport, but may play a role in the transport of bound oxygen in the red cell. More detailed studies indicate that the hemoglobin saturation inside the red cell during oxygen release even in the absence of convection is nearly uniform (Clark et al., 1985); thus, any fluid motions inside the cell may have only a small additional effect. Convective transport of oxygen inside the red cell, if important, would increase the value of the capillary mass transfer coefficient and hence reduce capillary mass transfer resistance. The complete answer, however, awaits further analysis.
The capillary mass transfer coefficient is considered only in the range of mean saturations between 80 and 10%, these numbers being physiologically relevant values for red cells in capillaries. Above or below this range, facilitated transport of oxygen by hemoglobin in the red cell becomes less important, and the capillary mass transport resistance increases (mass transfer coefficient decreases) as a result of increased transport resistance inside the cell. In addition, at low saturations transport resistance inside the red cell also increases due to the decrease in the kinetic rate of oxygen release from oxyhemoglobin. Thus, the mass transfer coefficients for oxygen release presented here can be used as upper-bound estimates for the conditions of very high or very low hemoglobin saturation not considered here.
A final comment about the analysis is that attention is only directed at how the discreteness of oxygen release in a capillary-size channel affects capillary mass transfer resistance and the mass transfer coefficient. It is clear from previous modelling studies (cf. Sheth and Hellums, 1983) that many of the other parameters used in this study and listed in Table 1 can also affect the value of the capillary mass transfer coefficient. As one example, the P50 of oxyhemoglobin would have a significant effect on oxygen release and resistance to oxygen transport. Thus we have attempted to use reasonable values for these parameters, but we have not attempted to explore the full physiologically relevant range of any parameter except those that characterize the discreteness of the oxygen supply.
4.2. Capillary versus Tissue Resistance to Oxygen Transport
The physiological importance of the capillary mass transfer coefficient and the discreteness of oxygen supply rests ultimately on the mass transfer resistance in the capillary relative to that in the tissue. That is, if the capillary provides 50% of the total mass transfer resistance for oxygen, as suggested by Hellums’ (1977) estimate, then those factors influencing the capillary mass transfer coefficient could affect the mean level and distribution of oxygen tension in the tissue. Conversely, if the capillary mass transfer resistance for oxygen is a small fraction of the total, then intracapillary factors would have a much smaller effect on tissue oxygenation directly except through altering oxygen delivery to the tissue.
The answer to the question of capillary versus tissue oxygen transport resistance requires combining capillary mass transfer coefficients of the kind computed here with a model for the tissue that addresses the known complexities and heterogeneities of tissue. As a first estimate, however, a simple model of tissue can be adopted in which to use the capillary mass transfer coefficients for the axisymmetric three-dimensional case. We assume that a circular capillary of radius, d, supplies oxygen to a surrounding annulus of respiring tissue, which receives oxygen only from that capillary. Then, if R represents a cylindrical radial coordinate emanating from the capillary axis, the tissue region corresponds to d ⩽ R ⩽ dt, where dt is the characteristic tissue dimension or intercapillary half-distance. The tissue transport equation for oxygen for a steady-state balance of consumption and diffusion in the radial direction only is
| (24) |
where αt, Dt, and M represent the tissue oxygen solubility, diffusion coefficient, and consumption, respectively, all assumed constant. The boundary condition at the capillary—tissue interface, R = d, involves the dimensional capillary mass transfer coefficient, k:
| (25) |
where P* is the characteristic red cell oxygen tension. Equation (25) states that the flux of oxygen out of the capillary into the tissue (−αtDt dPt/dR) is proportional to the difference between P* and Pt(R = d) with the capillary mass transfer coefficient being the proportionality factor. A no-flux condition, dPt/dR = 0, is imposed at the edge of the tissue region, R = dt. Thus, the tissue model is a Krogh cylinder but formulated with a boundary condition at the capillary that incorporates the capillary mass transfer coefficient.
The solution to the tissue transport equation is straightforward and the tissue oxygen tension profile given by
| (26) |
where γ = dt/d and ω = kd/2αtDt. The relative capillary resistance to oxygen transport, Rcap, is defined by
| (27) |
which represents the fraction of the entire oxygen tension drop that occurs in the capillary. From the solution to the tissue transport equation, Rcap can be given explicitly as
| (28) |
The value of Rcap is independent of M because of the simplified linear tissue model considered.
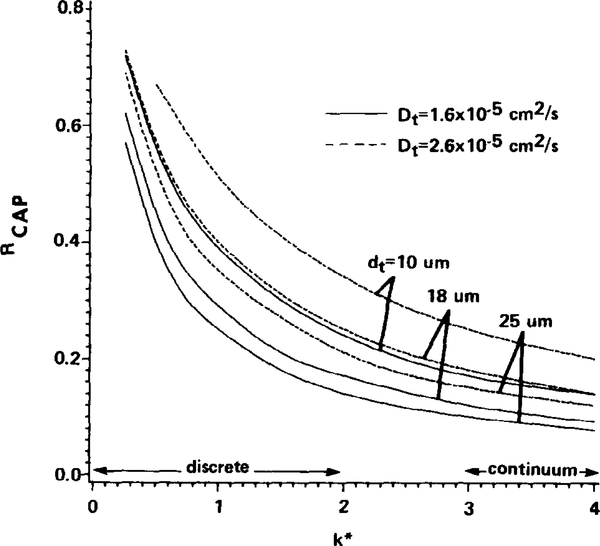
In Fig. 6, Rcap is given as a function of k*, the normalized capillary mass transfer coefficient. The curves correspond to values of dt of 10, 18, and 25 μm, which cover a representative range of characteristic tissue intercapillary half-distances in cardiac and skeletal muscle tissue. The solid curves in Fig. 6 are based on oxygen diffusivity in tissue of 1.6 × 10−5 cm2/sec, which is selected as a typical value used in previous model studies of oxygen transport in tissue (Popel, 1978; Fletcher, 1978; Salathé et al., 1980). Recent measurements in hamster soleus (an oxidative muscle) (Ellsworth and Pittman, 1984) indicate a much greater value of 2.6 × 10−5 cm2/sec for the oxygen diffusivity in tissue; thus Rcap is also displayed in Fig. 6 for this greater value of diffusivity (dashed curves). Values for the other tissue parameters used can be found in Table 1.
FIG. 6.
Capillary mass transfer resistance, Rcap, relative to total transport resistance from blood to tissue for the three-dimensional geometry (see text). Rcap is the fraction of the total oxygen tension drop occurring in the capillary. Tissue diffusivity, Dt, is 1.6 × 10−5 cm2 sec −1 (solid) or 2.6 × 10−5 cm2 sec −1 (dashed) and tissue dimension, dt, is 10, 18, or 25 μm.
As is evident from Fig. 6, Rcap depends strongly on k* in the range below k* = 2, which is interestingly the range of k* predicted for oxygen release from discrete spherical particles. In this range the relative capillary resistance can conceivably be as great as 30 to 70% depending on the selected values for dt, Dt, and k*. Above k* values of 3, which is the range of k* expected for continuum hemoglobin solutions, the relative capillary resistance is generally less than 20%. This may explain why models that have treated capillary blood as a continuum hemoglobin solution have discounted the importance of capillary mass transfer resistance.
The values of Rcap computed in this study are consistent with the estimate of Hellums (1977) and Baxley and Hellums (1984), which are based on a somewhat different model of intracapillary transport. They consider oxygen release from red cells modelled as cylindrical slugs separated by plasma gaps of length equal to the length of a red cell (the L = 1 case in this study); however, they assume that no oxygen leaves the capillary in the space between red cells. Consequently, they may overestimate the discreteness of oxygen supply (which lowers k*), but the overestimate may be compensated by the lack in their model of a plasma gap between the red cells and the capillary wall (which raises k*).
The tissue model neglects the possibility of facilitated diffusion by myoglobin in the tissue (cf. Wittenberg, 1970), which would decrease the resistance to oxygen transport in tissue. Thus, the presence of functioning myoglobin would increase the relative capillary resistance since the effective diffusivity for oxygen in tissue would be greater.
The relative capillary transport resistance depends on k* in a range where k* is strongly dependent on, among other things, the red cell spacing. Thus, red cell spacing could have a direct effect on tissue oxygen levels and the distribution of oxygen through its effect on the capillary mass transfer coefficient and hence the relative capillary resistance. This prediction stresses that red cell spacing, which is directly influenced by and related to capillary hematocrit, is an oxygen supply variable in its own right, quite apart from its role as a determinant of red cell flux and oxygen delivery. In other words, changes in red cell spacing that occur as a result of changes in capillary hematocrit can affect the level of oxygen tension in the tissue, not only by altering oxygen delivery, but also by altering the relative capillary mass transfer resistance to oxygen release and hence the fraction of oxygen tension drop occurring at the capillary level. This provides further support to the arguments put forth by Federspiel and Sarelius (1984) that suggest that in addition to the importance for oxygen transport of knowing the capillary red cell flux, it is also important knowing the individual determinants of capillary red cell flux, in particular, the red cell spacing.
ACKNOWLEDGMENTS
The authors express their gratitude to Ms. Alice Zilcha for her superb secretarial assistance. The assistance of The Biomechanics Institute in the final stages of manuscript preparation is also appreciated. The research was supported by grants from the National Institutes of Health, HL33172 and HL18292.
APPENDIX A
The molar concentrations of free oxygen and bound oxygen can be normalized as follows
where C is the dimensionless free oxygen concentration and S is the saturation of hemoglobin. Length scales are normalized using the particle radius, a, and thus the dimensionless operator ∇* is given by
Following Clark et al. (1985), dimensionless time, τ, is given by
which scales the oxygen unloading time for a red cell onto a dimensionless time interval of order one. The dimensionless velocity field, V*, is given by
where VRBC is red cell velocity.
Introducing the scaled variables into the transport equations results in
These equations describe, respectively, the transport of free oxygen in the red cell, bound oxygen in the red cell, and free oxygen in the plasma. The dimensionless groups that arise are
For the physiological parameters listed in Table 1, the first four dimensionless groups can be evaluated:
Thus, δ1 and δ2 are very small compared to the other terms in their respective equations, and they can be neglected with little error. This constitutes the quasisteady approximation.
The group, δ3, is a Peclet number (ratio of convective to diffusive transport). Using the values listed in Table 1 and a higher-end value for VRBC of 500 μm/sec (Damon, 1984), δ3 is about 0.4. This number is not compellingly small that it can be dropped without comment. It suggests that the effects of convection on the transport, though not entirely negligible, are small, especially for VRBC less than 500 μm/sec. Aroesty and Gross (1970) studied convective effects in capillaries more closely and concluded for small molecules like oxygen that convective transport is secondary to diffusive transport. Thus, in an effort to simplify the analysis, convection is not considered in the transport of free oxygen in the plasma.
APPENDIX B
The transport equations are solved numerically using a combination of techniques that are described briefly here. While the transport equations could have been solved using a finite difference technique with a rectangular grid in the channel, to do so would have required grid interpolation at the curved red cell surface, r = l. Our experience suggested such a technique would be inadequate since important gradients exist near the red cell surface that may be resolved ineffectively during grid interpolation there. Therefore, the following numerical techniques, albeit an unusual combination, reflect a desire on our part to employ techniques well-suited to the model formulated.
The transport equation for C(p) Eq. (18), is the linear Laplace equation, which can be solved analytically, but the differing geometries between the channel and the particles in both the two-dimensional and three-dimensional cases preclude a simple closed-form solution to the equation. Thus, the equation is solved numerically using the method of boundary collocation (Sangini and Acrivos, 1982), which is suited ideally to solving linear differential equations in complex geometries. This technique exploits the fact that an analytical solution to Laplace's equation can be obtained as an infinite series of appropriate eigenfunctions, each term in the series being multiplied by a constant that is determined from the boundary conditions. In our case because of complex geometry the constants are determined numerically rather than analytically as for standard geometries. The accuracy of the solution depends on where the infinite series is truncated for the numerical calculations.
The transport equations inside the red cell, Eqs. (16) and (17), are nonlinear and must also be solved numerically. These differential equations are discretized in the r and θ coordinates using orthogonal collocation and finite differences, respectively (cf. Finlayson, 1980, for a description of the numerical techniques discussed in this paragraph). Orthogonal collocation is chosen for the radial direction primarily because it is more efficient than finite differences at resolving the gradients in the boundary layer near the red cell surface. The discretization produces a set of algebraic nonlinear equations for C and first-order ordinary differential equations in time for S. The latter are integrated in the time direction using an Euler predictor—corrector scheme, while at each time step the algebraic equations for C are solved iteratively with a Newton—Raphson algorithm.
The coupling between the red cell and plasma transport equations, imposed by the matching boundary conditions, Eqs. (10) and (11), is introduced at each time step by solving the red cell and plasma transport equations together in an iterative fashion until the matching conditions are satisfied within a specified olerance.
The spatial and temporal resolution of the entire numerical scheme is increased (made more fine) until the instantaneous flux of oxygen out of the capillary converges within a specified tolerance of less than 1% difference between simulations of twofold difference in spatial and temporal resolution.
REFERENCES
- AROESTY J, AND GROSS JF (1970), Convection and diffusion in the microcirculation. Microvasc. Res. 2, 247–267. [DOI] [PubMed] [Google Scholar]
- BAGGE U, BRANEMARK P, KARLSSON R, AND SKALAK R (1980). Three dimensional observations of red blood cell deformation in capillaries. Blood Cells 6, 231–237. [PubMed] [Google Scholar]
- BAXLEY PT, AND HELLUMS JD (1983). A simple model for simulation of oxygen transport in the microcirculation. Ann. Biomed. Eng. 11, 401–416. [DOI] [PubMed] [Google Scholar]
- CLARK A JR., COKELET GR, AND FEDERSPIEL WJ (1981). Erythrocyte motion and oxygen transport. Bibl. Anat. 20, 385–388. [Google Scholar]
- CLARK A JR, FEDERSPIEL WJ, CLARK PAA, AND COKELET GR (1985). Oxygen delivery from red cells. Biophys. J. 47, 171–181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DAMON DH (1984). "Heterogeneity of Distribution of Blood and Erythrocytes in the Microcirculation of the Hamster." Ph.D. thesis, University of Virginia, Charlottesville, Va. [Google Scholar]
- DULING BR, AND BERNE RM (1970). Longitudinal gradients in periarteriolar oxygen tension. Circ. Res. 27, 669–678. [DOI] [PubMed] [Google Scholar]
- ELLSWORTH ML, AND PITTMAN RN (1984). Heterogeneity of oxygen diffusion through hamster striated muscles. Amer. J. Physiol. 246, H161–H167. [DOI] [PubMed] [Google Scholar]
- FEDERSPIEL WJ (1983). "Engineering Analysis of Two Blood Transport Problems. Ph.D. thesis, University of Rochester, Rochester, N.Y. [Google Scholar]
- FEDERSPIEL WJ, AND SARELIUS IH (1984). An examination of the contribution df red cell spacing to the uniformity of oxygen flux at the capillary wall. Microvasc. Res. 27, 273–285. [DOI] [PubMed] [Google Scholar]
- FINLAYSON BA (1980). "Nonlinear Analysis in Chemical Engineering. " McGraw—Hill, New York. [Google Scholar]
- FLETCHER JE (1973). A mathematical model of the unsteady transport of oxygen to tissues in the microcirculation In "Oxygen Transport to Tissue: Pharmacology, Mathematical Studies and Neonatology" (Bruley D and Bicher H, eds.), pp. 819–826. Plenum, New York. [DOI] [PubMed] [Google Scholar]
- FLETCHER JE (1978). Mathematical modeling of the microcirculation. Math. Biosci 38, 159–202. [Google Scholar]
- GAEHTGENS P (1981). In-vitro studies of blood rheology in microscopic tubes In "The Rheology of Blood, Blood Vessels, and Associated Tissues" (Gross DR and Hwang NHC, eds.), pp. 257–275. Sijthoff & Noordhoff, Alphen aan den Rijn, The Netherlands. [Google Scholar]
- GAEHTGENS P, DUHRSSEN C, AND ALBRECHT KH (1980). Motion, deformation, and interaction of blood cells and plasma during flow through narrow capillary tubes. Blood Cells 6, 799–812. [PubMed] [Google Scholar]
- HELLUMS JD (1977). The resistance to oxygen transport in the capillaries relative to that in the surrounding tissue. Microvasc. Res 13, 131–136. [DOI] [PubMed] [Google Scholar]
- HUXLEY VH, AND KUTCHAI H (1981). The effect of the red cell membrane and a diffusion boundary layer on the rate of oxygen uptake by human erythrocytes. J. Physiol 316, 75–83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- KAYAR SR, LECHNER AJ, AND BANCHERO N (1982). The distribution of diffusion distances in the gastrocnemius muscle of various mammals during maturation. Pfluegers Arch. 394, 124–129. [DOI] [PubMed] [Google Scholar]
- KELLER KH, AND FRIEDLANDER SK (1966). The steady-state transport of oxygen through hemoglobin solutions. J. Gen. Physiol 49, 663–679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- KLITZMAN B, DAMON DN, GORCZYNSKI RJ, AND DULING BR (1982). Augmented tissue oxygen supply during striated muscle contraction in the hamster. Circ. Res. 51, 711–721. [DOI] [PubMed] [Google Scholar]
- KLITZMAN B, AND DULING BR, (1979). Microvascular hematocrit and red cell flow in resting and contracting striated muscle. Amer. J. Physiol. 237(4), H481–H490. [DOI] [PubMed] [Google Scholar]
- KREUZER F (1970). Facilitated diffusion of oxygen and its possible significance; a review. Respir. Physiol 9, 1–30. [DOI] [PubMed] [Google Scholar]
- KREUZER F, AND YAHR WZ (1960). Influence of red cell membrane on diffusion of oxygen. J. Appl. Physiol. 15, 1117–1122. [DOI] [PubMed] [Google Scholar]
- KUTCHAI H (1970). Numerical study of oxygen uptake by layers of hemoglobin solution. Respir. Physiol. 10, 273–284. [DOI] [PubMed] [Google Scholar]
- MOLL W (1969). The influence of hemoglobin diffusion on oxygen uptake and release by red cells. Respir. Physiol 6, 1–15. [DOI] [PubMed] [Google Scholar]
- NIIMI H, AND SUGIHARA M (1984). Hemorheological approach to oxygen transport between blood and tissue. Biorheology 21, 445–461. [DOI] [PubMed] [Google Scholar]
- POPEL AS (1978). Analysis of capillary—tissue diffusion in multicapillary systems. Math. Biosci 39, 187–211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- SALATHE EP, WANG TC, AND GROSS JF (1980). Mathematical analysis of oxygen transport to tissue. Math. Biosci, 51, 89–115. [Google Scholar]
- SANGINI AS, AND AcR1vos A (1982). Slow flow past periodic arrays of cylinders with application to heat transfer. Int. J. Multiphase Flow 8, 193–206. [Google Scholar]
- SHETH BV, AND HELLUMS JD (1980). Transient oxygen transport in hemoglobin layers under conditions of the microcirculation. Ann. Biomed. Eng 8, 183–196. [DOI] [PubMed] [Google Scholar]
- SNELL FM (1965). Facilitated transport of oxygen through solutions of hemoglobin. L Theor. Biol 8, 469–479. [DOI] [PubMed] [Google Scholar]
- SPAAN JAE, KREUZER F, AND VAN WELY FK (1980). Diffusion coefficients of oxygen and hemoglobin as obtained simultaneously from photometric determination of the oxygenation of layers of hemoglobin solutions. Pfluegers Arch 384, 241–251. [DOI] [PubMed] [Google Scholar]
- TUREK Z, AND RAKUSAN K (1981). Lognormal distribution of intercapillary distance in normal and hypertrophic rat heart as estimated by the method of concentric circles: Its effect on tissue oxygenation. Pfluegers Arch. 391, 17–21. [DOI] [PubMed] [Google Scholar]
- WITTENBERG JB (1970). Myoglobin facilitated oxygen diffusion: Role of myoglobin in oxygen entry into muscle. Physiol. Rev 50(4). 559–636. [DOI] [PubMed] [Google Scholar]