Adaptive Response-Time-based Category Sequencing in Perceptual Learning

Abstract

Although much recent work in perceptual learning (PL) has focused on basic sensory discriminations, recent analyses suggest that PL in a variety of tasks depends on processes that discover and select information relevant to classifications being learned (Petrov, Dosher, & Lu, 2005; Kellman & Garrigan, 2009). In complex, real-world tasks, discovery involves finding structural invariants amidst task-irrelevant variation (Gibson, 1969), allowing learners to correctly classify new stimuli. The applicability of PL methods to such tasks offers important opportunities to improve learning. It also raises questions about how learning might be optimized in complex tasks and whether variables that influence other forms of learning also apply to PL. We investigated whether an adaptive, response-time based, category sequencing algorithm implementing laws of spacing derived from memory research would also enhance perceptual category learning and transfer to novel cases. Participants learned to classify images of 12 different butterfly genera under conditions of: 1) random presentation, 2) adaptive category sequencing, and 3) adaptive category sequencing with ‘mini-blocks’ (grouping 3 successive category exemplars). We found significant effects on efficiency of learning for adaptive category sequencing, reliably better than for random presentation and mini-blocking (Experiment 1). Effects persisted across a 1-week delay and were enhanced for novel items. Experiment 2 showed even greater effects of adaptive learning for perceptual categories containing lower variability. These results suggest that adaptive category sequencing increases the efficiency of PL and enhances generalization of PL to novel stimuli, key components of high-level PL and fundamental requirements of learning in many domains.

1. Introduction

Attaining expertise in many domains depends on changes in the way information is extracted – perceptual learning (Gibson, 1969; Kellman & Garrigan, 2009). In the last two decades, work in cognitive and neural sciences has witnessed a resurgence of interest in perceptual learning (PL). Most of this recent work has focused on simple sensory dimensions using a few specific stimulus values. In contrast, the focus of earlier PL research (Gibson, 1969) and the application of PL in virtually all real-world tasks involves discovery of invariance amidst variation.

These emphases relate to different scientific purposes. In the work of Eleanor Gibson, and in some recent work (e.g., Kellman, Massey, & Son, 2010; Kellman & Massey, 2013), the focus is on understanding how changes in information extraction advance performance in complex domains and real-world settings. The focus of many contemporary researchers on basic discriminations using a small set of simple stimuli relates to attempts to understand the neural bases of PL, especially receptive field changes in early cortical areas (e.g., Fahle & Poggio, 1993).

Much recent work suggests that learning effects in both so-called low-level and highlevel PL tasks often involve common principles and mechanisms, specifically discovery of what information makes the difference in classifications being learned (Petrov, Dosher, & Lu, 2005; Ahissar & Hochstein, 1999; Kellman & Garrigan, 2009). In work on basic sensory discriminations, for example, data have tended to favor models emphasizing selective reweighting of analyzers rather than receptive field changes (Petrov, Dosher, & Lu, 2005), and many PL results appear to be incompatible with explanation primarily in terms of changes in early receptive fields (Ahissar, 1999; Liu, 1999; Xiao, Zhang, Wang, Klein, Levi, & Yu, 2008; Wang, Zhang, Klein, Levi, & Yu, 2012; Crist et al, 2001; Ghose, Yang, & Maunsell, 2002; Garrigan & Kellman, 2008; for discussion, see Kellman & Garrigan, 2009).

The emphasis on discovery processes that lead to weighting of the most relevant analyzers strongly mirrors Gibson’s (1969) emphasis on selection of relevant structure; in fact, Gibson often used “differentiation learning” as a synonym for PL. Contemporary models based on selection of analyzers place the focus within the nervous system, whereas selection of information or discovery of invariants in the world places the focus outside the organism and onto the environment, but clearly these are two sides of the same coin (assuming that analyzers pick up relevant information from the environment). Findings that PL appears to occur only for constancy-based information, rather than any arbitrary sensory invariant, also implicate learning processes focused on extracting functionally relevant environmental properties (Garrigan & Kellman, 2008).

Understanding that PL processes involve discovery and selection of information not only helps to unify various PL tasks and results but has direct practical implications. Recent work suggests that domain-specific changes in information extraction attained through PL comprise a much larger component of expertise than is often understood (Kellman & Garrigan, 2009). This is true even in high-level, symbolic domains, such as mathematics, chess, and reading (de Groot, 1965; Chase & Simon, 1973; Goldstone, Landy, & Son, 2008; Kellman, Massey, & Son, 2010; Kellman & Massey, 2013; Thai, Mettler, & Kellman, 2011), where PL functions synergistically with other aspects of cognition. Learning technology based on PL, in the form of perceptual learning modules (PLMs), has been shown to accelerate crucial and otherwise elusive aspects of learning, including pattern recognition, transfer, and fluency, in domains as diverse as aviation training (Kellman & Kaiser, 1994), mathematics learning (Kellman, Massey, & Son, 2010; Massey, Kellman, Roth, & Burke, 2010), and medical learning (Drake, Krasne, Kellman, & Hillman, in press; Guerlain et al., 2004; Kellman, 2013).

The realization of the importance of PL in diverse learning tasks and the emergence of PL interventions raise the question of whether PL shares principles that have been found to improve or optimize other kinds of learning. When we learn new perceptual classifications, what principles govern successful learning? Are there ways of organizing the order of presentation of material such that learning is enhanced? Such questions form the basis for the following studies, which investigate effective training strategies for enhancing perceptual learning – especially when learning concerns sets of categories or natural kinds.

1.1. Spacing and Memory

One of the most robust and enduring findings in research on memory for factual items concerns the benefits of spaced practice relative to that of non-spaced practice. “Spaced” practice means repeated exposure of an item following delays or presentation of intervening items. In general, longer delays are more beneficial than shorter delays, up to some maximum after which the benefit to learning decreases (Glenberg, 1976; Benjamin & Tullis, 2010; Cepeda, Vul, Rohrer, Wixted, & Pashler, 2008). Maximum benefit may occur when representation of an item is just prior to – and no later than – the moment that its decaying memory trace becomes irretrievable; that is, items are best re-presented just before they are forgotten. Experimental evidence suggests that the value of a presentation of an item increases with the difficulty of successful retrieval (Benjamin, Bjork, & Schwartz, 1998; Pyc & Rawson, 2009). Pyc and Rawson (2009) labeled this idea the “retrieval effort hypothesis”: More difficult, but successful, retrievals are more beneficial.

Substantial data suggest that producing difficult but successful retrievals can be accomplished by expanding spacing during the course of learning. Expanding retrieval practice has been studied for nearly half a century (Pimsleur, 1967; Landauer & Bjork, 1978; Cull, Shaughnessy, & Zechmeister, 1996). Explanations of the value of expanded retrieval intervals usually invoke or assume an underlying notion of learning strength that increases with repeated presentations of an item. Learning strength can be thought of as a hypothetical construct related to probability of successful recall on a future test. When a new item is presented, learning strength may be low, but it typically increases with additional learning trials.

Although a preset schedule of expanding spacing intervals across trials will tend to correlate with increasing learning strength, the match may be far from perfect. Even if learning strength increases monotonically, preset intervals may expand too much or not enough. Moreover, learning of particular items by particular individuals may produce different courses of improving learning strength, and learning strength may actually be a non-monotonic function of trials, depending on item difficulty and relations among items being learned. Ideal spacing intervals, from the standpoint of the retrieval difficulty hypothesis, might involve, not predetermined intervals, but flexible spacing that matches current learning strength. Arranging learning to approximate such an ideal would benefit from an ongoing indicator of learning strength, one which might vary for different learners, items, and their interactions.

1.2. The ARTS System

Evidence indicates that response time (RT) is a useful indicator of retrieval difficulty, and thus of an item’s current learning strength (Pyc & Rawson 2009; Karpicke & Bauernschmidt, 2011).This relationship offers a useful way of updating spacing to track underlying learning strength: Adaptive methods can use an individual’s accuracy and RT performance data for learning items to dynamically schedule spacing intervals. Mettler, Massey, and Kellman (2011) showed that a system that determines spacing dynamically based on each learner’s accuracy and speed in interactive learning trials (the Adaptive Response-Time-based Sequencing or ARTS system) produced highly efficient learning and compared favorably with a classic adaptive learning system (Atkinson, 1972).

ARTS uses a priority score system, in which the priority for an item to reappear on each learning trial is computed as a function of accuracy, response time, and trials since the last presentation. The system also implements mastery criteria based on both accuracy and speed. As learning strength increases, as reflected in performance, delay intervals automatically expand in this system. Because all items compete for presentation on any trial, through their priority scores, the system concurrently implements adaptive spacing for all learning items. (See the Method section for further detail on the ARTS system).

ARTS was designed to test principles of learning and memorization of factual items (e.g., Mettler, Massey, & Kellman, 2011), but it can be applied to perceptual category learning as well, in cases where there are multiple categories to be learned. This situation occurs in many real world tasks, such as a dermatologist learning to identify different kinds of skin lesions, an air traffic controller learning to recognize different types of aircraft, or a chemist learning to recognize different types of molecular structures. In adaptive category sequencing, the ARTS system tracks learners’ accuracies and response times in order to assess the learning strength of categories. Each category is given a dynamically updated priority score, reflecting the relative importance of an exemplar of that category appearing on the next learning trial.

1.3. Relationship Between Perceptual Learning and Factual Learning

Although it is clear how adaptive spacing might be applied to PL, it is not clear whether the same principles of spacing and expanding the retrieval interval that improve item memory would enhance PL. There have not been many studies of PL in real-world learning domains, and there has been even less work exploring the conditions that optimize such learning. These two kinds of learning appear to involve different mechanisms, and they might require different arrangements to optimize learning.

Whereas item learning involves storing and retaining specific information, PL has been argued to contain two kinds of changes: discovery and fluency effects (Kellman, 2002). Discovery involves altering encoding processes to progressively locate the most relevant information for some task. Specific PL discovery effects, observed in both simple and complex PL tasks, include increasing selectivity and precision of information extraction as learning progresses; relevant features are encoded and irrelevant ones ignored (Gibson, 1969; Petrov, Dosher, & Lu, 2005). Other discovery effects involve the learner coming to notice higherorder relations that were initially not encoded at all, and/or coming to encode information in larger “chunks” (Chase & Simon, 1975; Gibson, 1969; Goldstone, 2000; Kellman & Garrigan, 2009). Fluency effects involve improved speed, greater parallel processing, and lower attentional load in picking up task-relevant information as learning progresses (Kellman & Garrigan, 2009; Schneider & Shiffrin, 1974).

All of these processes go well beyond storing and maintaining a specific memory trace. In learning a number of related perceptual classifications, commonalities or invariances that determine category membership must be discovered in PL, and conversely, in learning to differentiate different categories, distinguishing features must be discovered.

Despite differences in underlying mechanism, there are reasons to suspect that spacing may be beneficial in perceptual category learning as well as in factual learning. One reason is that interleaving exemplars of different categories may facilitate discovery of distinguishing features (Gibson, 1969), just as paired comparisons might (Mettler & Kellman, 2009; Kang & Pashler, 2012). On the other hand, discovering perceptual attributes shared by exemplars of a single category might better be served by encountering several exemplars close together in time; in other words, massed rather than spaced presentation. Perhaps a more compelling reason for an analogy between spacing benefits in fact learning and PL is the notion the best time to receive further practice is when learning strength has declined enough to make accurate performance relatively difficult. Although different specific mechanisms of learning may be at work in different domains, optimizing practice based on intervals that progressively increase as learning strength grows may be a commonality across types of learning.

There has been some earlier work on these questions. Kornell and Bjork (2008), compared interleaving and massing of learning items in perceptual category learning of artist’s painting styles. In the interleaved condition, one painting from each artist was presented in a sequence before any second painting from an artist was presented (each block of presentations contained 1 painting from each artist). In the massed condition, the 6 examples of each artist’s paintings were presented consecutively, followed by the entire set of another artist’s paintings, and so on, until all paintings from all artists were presented. They measured participants’ accuracy in classifying previously unseen paintings from each artist and found that interleaving led to greater success.

Kornell and Bjork’s results differ from that of some studies in memory and human performance that show advantages for blocked vs. randomized trials of practice (see Schmidt & Bjork, 1992, for a review). Similarly, some work in perceptual learning and unsupervised category learning shows benefits for massing, severe detriments for interleaving of stimuli (Zeithamova & Maddox, 2009; Kuai, Zhang, Klein, Levi, & Yu, 2005), or no advantage for either type of schedule (Carvalho & Goldstone, 2011). We wondered if schedules that combine spacing with modest amounts of massing could result in even greater learning than spacing or massing alone. This hypothesis was tested using a separate condition that combined blocking in the initial stages of learning with adaptive spacing in later stages (see below).

1.4. Purposes of Current Work: Adaptive Sequencing in PL

Can PL of natural categories be enhanced by adaptive spacing techniques that have been shown to improve learning for factual information?

To study this question, we used a learning task involving taxonomic classifications of images of butterfly (Lepidoptera) species. Natural stimuli such as these afford the type of feature discovery present in real-world perceptual learning, where, in contrast to most artificial stimuli, relevant stimulus features are richly perceptual, hierarchically organized, and distributed stochastically and non-independently across categories. We employed a web-based perceptual learning module (PLM) that included the ARTS system described above. The PLM presented butterfly images in pairs, one from a target category (target butterfly genus) and one from an alternate category. Participants were asked to choose the image that correctly matched the presented target category name. Feedback was given on each trial, and participants continued discriminating butterflies until they had learned the correct label-to-category mappings. Previous work suggests that paired comparisons across many trials are effective in eliciting PL (Mettler & Kellman, 2009; Walheim, Dunlosky, & Jacoby, 2011).

We continued the PLM until each learner met mastery criteria based on accuracy and speed of classification. We used mastery criteria because of their relevance to applications in real-world learning contexts, and from the standpoint of experimental control, they allowed us to assess learning after each learner had reached a similar endpoint. Mastery is also an important and natural feature of adaptive learning, in that use of objective mastery criteria can allow removal (“retirement”) of learned categories, allowing each learner to spend further learning effort where it is needed most. The benefits of using mastery criteria, however, come with a difficulty. Different learners require different numbers of trials to reach criterion. This leaves the experimenter with two dependent measures of learning – posttest performance and trials to criterion. To allow comparisons between conditions that included both of these measures, we combined them into a measure of learning rate or learning efficiency, defined as accuracy gains divided by learning trials invested.

Based on potential benefits of both spacing and massing in PL, and in view of earlier work indicating that complete massing is sub-optimal, we also included a condition with some initial massing of category exemplars (“mini-blocks”).

To ensure that learning involved discovery of perceptual structure, rather than memorization of instances, we assessed learning using an equal number of unfamiliar instances, never shown during the pretest or learning phases, and familiar instances, which could appear one or more times during learning.

Finally, we tested learning both in an immediate posttest and after a delay of one week. In studying spacing effects in perceptual learning, it is important to consider the possibility of transient performance effects that appear in immediate tests but might not survive in a delayed test, as has proven important in studies of other kinds of learning. Conditions that optimize performance on immediate tests may not be the ones that are best for durable learning (e.g., Schmidt & Bjork, 1994).

We tested three conditions: 1) a control condition that orders items in an unmodified random sequence, 2) an adaptive sequencing condition (ARTS) that changes the delay between presentations of a category as a function of learning strength, and 3) a condition that initially blocks 3 exemplars from a category sequentially (called “mini-blocks”), presented for two rounds before proceeding to standard adaptive sequencing. Because the adaptive sequencing conditions also included retirement, we anticipated that learning would be quicker there, and that performance at an immediate and 1 week delayed test would be most efficient for participants in those conditions (greatest learning per trial invested in training).

In a second experiment, we manipulated the degree of variability between categories to observe how adaptive sequencing interacts with category structure. Decreasing the variability, and thus making items within a category more similar to one another, is a way of approximating the effect that dynamic sequencing would have on a variety of types of categories. It is also more similar to a situation in which learning concerns individual items as opposed to categories of varying exemplars. Our prediction was that adaptive sequencing would operate as well when categories were of lower variability as when high, and we tested the efficacy of the adaptive scheduling algorithm in both cases without any modification to the parameters of our model.

2. Experiment 1

2.1. Method

2.1.1. Participants

54 undergraduate psychology students from the University of California, Los Angeles participated in an hour-long experiment for course credit. Participants returned one week after the first session for a delayed posttest. Four of 58 were disqualified: one because of a failure to complete a delayed posttest and three others, one from each condition, who failed to reach a learning criterion in the training session, as described below.

2.1.2. Displays and Materials

The materials for this study consisted of 108 images of Lepidoptera (butterfly) specimens arranged into 12 categories by genus (See Figure 1 for examples). Each category contained nine exemplars where one exemplar from each category was withheld during learning in order to be used as a test of transfer of learning to unseen items in the two posttest phases (see Figure 2).

Figure 1.

Examples of images used in the experiments. Three examples from each of two butterfly genera (trained categories) are shown. A) Examples of genus Aglais. B) Examples of genus Cethosia.

Figure 2.

Example distribution of one stimulus category across experiment phases. In pretest: Exemplar H1 is tested. In the learning phase, all category exemplars except H9 are presented. In each posttest, one previously seen exemplar, H1, and one novel exemplar not presented during the learning phase, H9, are tested.

A multidimensional scaling analysis was conducted to ensure categories occupied positions of roughly equivalent similarity distance from each other (implying equivalent learning difficulty), though there was some variability in difficulty across categories. The images used for both the immediate and delayed posttests were fixed for each subject. Images were presented in jpeg form in 16-bit color, where each image was 450×300 pixels. All pretest, training, and posttest sessions occurred within a web-based perceptual learning module (PLM). The PLM presented a text label of the category name in an upper middle position (as in the ‘sample’ position, of a ‘match-to-sample’ presentation). In pretest and posttest trials, four images were presented in the center of the screen in two rows and two columns (see Figure 3a). Only one image contained an exemplar from the target category – the distractors each contained an exemplar from one of three alternate categories. During training trials, two images were shown side by side in the middle of the screen just below the category label (a 2AFC presentation, see Figure 3b).

Figure 3.

Trial presentation formats in the assessment and learning phases of the experiments. A) Pretest and posttest: Each trial was a 4-alternative forced choice, where one of the 4 exemplars belonged to the target genus. B) Learning phase: Each trial was a 2-alternative forced choice, where one of the two exemplars belonged to the target genus.

2.1.3. Design

The experiment utilized a pretest/posttest design. A pretest measured baseline levels of perceptual category knowledge. Participants completed 12 trials where each category was presented as a target once, in random order. Each trial consisted of a match-to-label test; a four alternative forced choice between four images: exemplars from three incorrect categories and one exemplar from the correct target category. Pretest exemplars were randomly chosen at the start of the experiment and the same exemplars were displayed to all participants.

The training session consisted of a series of match-to-label trials, where each trial tested one target category. Trials consisted of a two alternative forced choice (2AFC) decision between two images: a randomly selected exemplar from the target category and a randomly selected exemplar from an alternate category. There were 3 between-subjects scheduling conditions that determined the order of presented categories: 1) purely random stimulus presentation 2) adaptive category sequencing with retirement, and 3) mini-blocks with adaptive category sequencing and retirement. The participant completed as many trials as necessary to reach a learning criterion.

An immediate posttest measured the degree of perceptual learning after a learning session. The immediate posttest was similar to the pretest but contained an additional trial for each category, for a total of 24 test trials. For each category, one trial was of a familiar exemplar (an image presented during training) and one trial was of a novel exemplar (not presented during training). The novel exemplar was used to measure transfer or generalization of category knowledge to unseen stimuli. The same posttest items were shown to all participants. A delayed posttest, given one week later, was identical to the immediate posttest and measured the amount of retention after a delay.

2.1.4. Adaptive Sequencing Algorithm

The sequencing algorithm calculated a priority score for each category, where, on any subsequent trial, priority scores were compared across categories to determine the likelihood of a category’s presentation on that trial. Details of the priority score calculation are given in Equation 1 (and below) and parameters are given in the appendix (Table A.1).

$$P_i=a\left(N_i-D\right)\left[b\left(1-{\alpha }_i\right)Log\left(R{T}_i/r\right)+{\alpha }_{i}W\right]$$ (1)

Priority P for category i was determined as a function of the number of trials since that category was last presented Ni, an enforced delay D (a constant, which was set to 2 in the experiments here), and the accuracy (ai) and response time (RTi) on the previous presentation of that category. Accuracy (ai) was a binary variable determined by the correctness of the user’s response: 0 if the question was answered correctly, 1 otherwise. This binary accuracy variable acted as a switch activating either the error part of the equation (for an incorrect answer) or the RT part of the equation (for a correct answer). The rationale was that RTs for incorrect answers were not considered informative for spacing. An incorrectly answered category was given a large priority increment (W) that typically ensured re-presentation after a delay of two trials. Correctly answered items were assigned a priority score that was a log function of RT (where the logarithm was used to weight small differences among RTs more heavily for shorter RTs than for longer ones). Parameters a, b, r, were weighting constants: a controlled the rapidity with which priority accumulated as a function of elapsed trials; b and r modulated the relation between RTs and spacing delays. Although priority score equations using response time and accuracy can take many forms, the parameters here were fixed and identical for both experiments, and were also the same as used in previously published research on item learning (Mettler, Massey & Kellman, 2011). Taken together, the elements of the priority score equation given here implement a number of principles of learning that have been derived in memory research, including rapid recurrence of missed items; but enforcing at least some delay in representing an item, to make sure the answer does not still reside in working memory; and stretching the retention or recurrence interval as learning strength, indicated by accuracy and RT, increases. Of course, these ideas are here extended to perceptual learning, so that categories, not items, are spaced, and presentation of a category typically involves a novel instance. Whether these principles, previously established in item learning contexts, make PL more efficient when embodied in the ARTS system is, of course, the primary experimental question.

Re-presented items were randomly chosen exemplars from the target category, where the odds of any exemplar being selected were 1/8. The adaptive sequencing conditions also included ‘category retirement,’ based on criteria that specified when a particular category was well learned enough to merit being dropped from the training set. Pilot testing determined the criterion levels that resulted in successful discrimination performance on a posttest and transfer tests of learning. The criterion level was 5 out of 6 correct with RT less than 3 seconds.

Adaptive sequencing with ‘mini-blocks’ (Adaptive/Mini-blocks condition) was identical to the Adaptive condition, but at the start of training participants received ‘miniblocks’ of 3 exemplars from the same category consecutively presented across sequential trials. Participants received two ‘mini-blocks’ per category before adaptively sequencing individual presentations of categories without blocking. We hypothesized that in this condition, a moderate degree of grouping of exemplars would aid in comparison processes known to enhance perceptual learning and category learning.

In the Random presentation condition, training sessions consisted of random selection of categories on each trial, with no constraints on the total number of times a category could be presented or the total number of presented stimuli from each category. This condition implemented a method for ending training after the accuracy for every category had reached the same retirement criteria as in the dynamic sequencing condition (5 out of 6 correct). This helped to ensure that the number of total presentations of individual categories would accurately reflect typical randomized learning schedules and remain distinct from the category retirement feature that was present in adaptively sequenced schedules.

2.1.5. Procedure

In the pretest, participants were presented with a category label at the top of the screen and four images in the center of the screen. Participants were instructed to indicate the image that belonged to the presented category label and to make their best guess if they did not know the answer. No feedback was given during this phase and the test took no more than 3–5 minutes.

The learning phase consisted of one session, no longer than 45 minutes, where participants were instructed to choose the image that best matched a presented genus label. Participants were shown one genus name at the top of the screen and images from two different butterfly genera side by side. Participants were asked to choose either the left or right image and respond using the keyboard. Responses were considered correct if the chosen image belonged to the correct genus. Participants were given 30 seconds to respond and were always provided with feedback. If a participant failed to respond within 30 seconds, the trial timed out and feedback was given, where a timeout was recorded as an incorrect response. Feedback consisted of highlighting the correct image and displaying ‘correct’ or ‘incorrect’ depending upon the accuracy of the participant’s response. In addition, the name of the target genus moved to a position underneath the correct image. Feedback displayed for a minimum of 3.5 seconds, although participants had up to 15 seconds to view the feedback before the screen was cleared. Participants could use the spacebar to progress to the next trial any time after the initial 3.5 seconds. Summary feedback was provided every 10 trials. Summary feedback consisted of a graph of average accuracies and response times for each previous 10 trial block.

Immediately after training, participants completed a posttest. After the posttest participants were asked to not study or review the information in the study. One week after the posttest, a delayed posttest was administered.

2.1.6. Dependent Measures and Analyses

Use of mastery criteria has many advantages both in real learning settings and in studies of learning, but it poses the problem of producing two kinds of data about the effectiveness of learning conditions. Learners’ posttest performance can indicate how much has been learned, but different conditions of learning may require differing amounts of time or learning trials to produce a certain amount of learning. Both indicators of learning effectiveness are important, and in real-world contexts, learning time, as well as amount learned, both matter. To capture the combined effects of time invested and posttest performance, we used a measure of learning efficiency, which consists of posttest performance (number of items correct) divided by the number of trials an individual participant completed during training. Specifically, this measure gives a learning rate that measures gains in accuracy per unit time (trials) invested (Equation 2):

$$\mathbf{E}={\mathbf{A}}_{\mathbf{p}}/\mathbf{T},$$ (2)

where: A_p = accuracy on posttest (number of items correct) and T = number of learning trials invested

Use of efficiency as our primary measure of learning not only combines learning results into a single, simple measure, but it is also useful here because learning to criterion typically results in participants having similar posttest accuracies. Comparing raw accuracy scores may be uninformative without regard to the duration of a participant’s training (see Underwood, 1964 for a discussion of the relative merits of ‘learning to criterion’ in experimental investigations of learning).

Whereas the efficiency measure captures learning gains per learning trials invested, we were also able extract a measure of learning after equal numbers of learning trials. To do this, we took the average number of learning trials required in the basic adaptive condition to reach the learning criteria, and we looked at accuracy and response times for conditions on the last two presentations of each stimulus category at that point in learning. This measure allows some indication of learning across conditions at a point where each condition had the same number of learning trials.¹

2.1.7. Predictions

In the Adaptive condition, it was expected that adaptive sequencing – where quick, correct answers to categories would delay their reappearance – would lead to more rapid learning and enhance discrimination even for difficult categories. It was thought that retirement of well learned categories would make learning more efficient to an even greater degree. We expected that the partial blocking in the Adaptive/Mini-blocks condition would perform better than the Random condition and that the Adaptive/Mini-blocks condition might even outperform the basic Adaptive condition. A similar effect of these conditions on transfer to novel stimuli was expected.

2.2. Results

Learning performance was measured using a pretest, a posttest administered immediately after training, and a delayed posttest administered one week after training. Pretest scores averaged 2.43 items out of 12, indicating that performance was no better than chance and that participants did not possess prior knowledge of butterfly genera. A between subjects ANOVA on proportion correct in the pretest confirmed no significant differences across the three conditions (F(2,51)=1.86, p=.17, η_p=0.07). Individual comparisons also showed no reliable differences (all ps > .20 for Random vs. Adaptive, Random vs. Adaptive/Mini-blocks, Adaptive vs. Adaptive/Mini-blocks, respectively). In addition, an examination of participant reaction times (RTs) on the pretest showed no reliable difference between conditions, neither in a between subjects ANOVA nor in individual comparisons (all ps > .19).

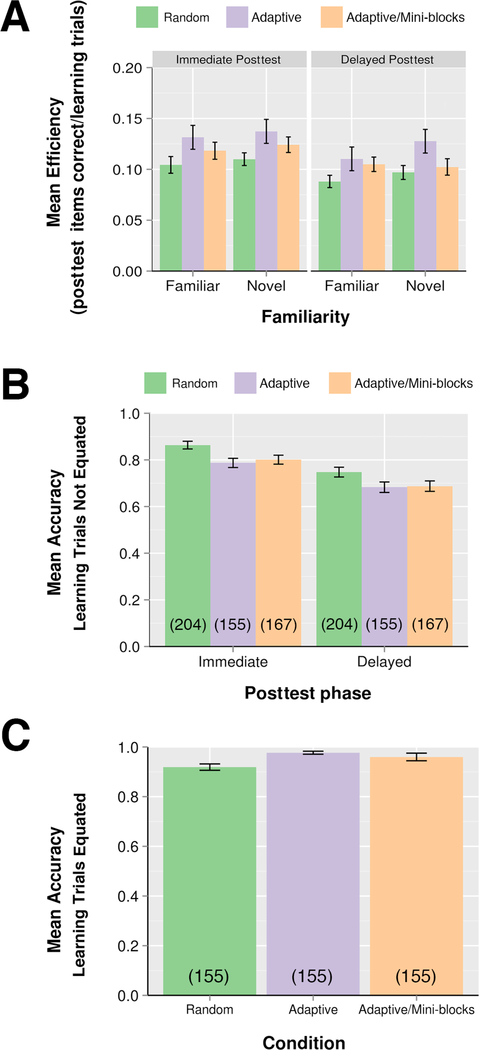
Learning efficiency was measured in the immediate and delayed posttests by dividing the number of correct posttest items by learning trials invested. Efficiency scores are shown in Figure 4A for the three scheduling conditions, and for both previously seen and novel instances in both immediate and delayed posttests. Efficiencies for the Adaptive condition were numerically higher than efficiencies in the Random and Adaptive/Mini-blocks condition for both immediate and delayed tests (Immediate posttest: M=0.13, vs. 0.11 and 0.12; Delayed posttest: M=0.12 vs. 0.09 and 0.10 respectively). We performed a 3 (condition – Adaptive, Random and Adaptive/Mini-blocks) by 2 (posttest phase – immediate vs. delayed) by 2 (previously seen vs. novel) mixed factor ANOVA with condition as a between-subjects factor and test phase and stimulus familiarity as within-subjects factors. The ANOVA revealed a marginally reliable main effect of scheduling condition (F(2,51)=2.45, p=.096, η_p=0.09). There was a reliable main effect of test phase (F(1,51)=51.52, p < .001, ηp=0.50), and no interaction of scheduling condition with test-phase (F(2,51)=0.16, p=.86, ηp=0.006).

Figure 4.

Learning results for Experiment 1. A) Mean efficiency scores by learning condition and posttest phase. Efficiency scores were the number of posttest items answered correctly divided by the number of trials invested in learning. Familiar stimuli were posttest items that had been shown during training, whereas novel stimuli were items that had not been presented previously. B) Mean accuracy results by learning condition and posttest phase. Accuracy is given as the percentage of 24 posttest questions answered correctly. These data indicate raw accuracy not corrected for number of learning trials; the number of learning trials in each condition is shown in parentheses. C) Mean accuracy by learning condition based on equal numbers of learning trials. Parentheses indicate trial number at which accuracy was measured, for the two most recent presentations of each category. In all graphs, error bars indicate ± one standard error of the mean.

There was a strong main effect of stimulus familiarity (F(1,51)=17, p < .001, η_p=0.25), due to the somewhat surprising result that performance in the posttests was superior for novel instances. There was also a marginally reliable interaction between condition and familiarity (F(2,51)=3, p=.059, η_p=0.105), apparently due to the greater superiority of transfer to novel instances in the Adaptive condition. There was no interaction between test phase and familiarity (F(1,51)=0.30, p=.59, η_p=0.006), nor was the three way interaction between condition, phase and familiarity reliable (F(2,51)=2.45, p=.097, η_p=0.08). Examining the interaction of condition and familiarity, there was a reliable efficiency advantage for the Adaptive vs. the Random condition for novel items at both immediate posttest (Adaptive: M=0.14; Random: M=0.11; t(34)=2.04, p < .05) and delayed test (Adaptive: M=0.12; Random: M=0.09; t(34)=2.27, p=.03) but the numerical advantage was marginal or unreliable for familiar items at immediate (Adaptive: M=0.13; Random: M=0.10; t(34)=1.69, p=.10) or delayed test (Adaptive: M=0.11; Random: M=0.09; t(34)=1.89, p=.067). Otherwise, there were no reliable differences between conditions with either novel or familiar stimuli at any test (all ps > .05). Because our hypothesis specifically concerned differences in conditions we conducted planned paired comparisons between each condition. Averaging across posttests, t-tests showed that the difference between Random and Adaptive conditions was significant (t(34)=2.08, p < .05, Cohen’s d=0.72). On the immediate posttest, these two conditions differed marginally (t(34)=2.02, p=.051, d=0.70) and on the delayed posttest, there was a reliable advantage for the Adaptive condition (t(34)=2.04, p < .05, d=0.71). Other comparisons between scheduling conditions were not significantly different (averaging over posttests, Random vs. Adaptive/Mini-blocks, p=.20, d=0.36; Adaptive vs. Adaptive/Mini-blocks: p=.33, d=0.43). Paired t-tests showed a reliable decrease between immediate vs. delayed posttests for all three conditions (all ps < .005).

Because efficiency scores represent the number of posttest items answered correctly per trial invested in training, differences between efficiency scores may appear small, but due to their proportional nature, are quite substantial in practical terms. For example, a difference between 0.12 and 0.10 would be a 20% difference in efficiency. In the present results, the efficiency advantage for the Adaptive condition compared to the Random condition amounted to 25% in the immediate posttest and 29% in the delayed posttest.

We also analyzed separately the two dependent measures that were components of the efficiency measure, number of learning trials and posttest accuracy for each participant. A between subjects ANOVA found significant differences between the number of training trials across the three schedules. Participants averaged 154.7, 167.4, and 204.3 trials in the Adaptive, Adaptive/Mini-blocks, and Random conditions, respectively - a reliable difference (F(2,51)=5.50, p=.007, η_p=0.18). Comparing means, the differences between the Adaptive and Random condition and between the Adaptive/Mini-blocks and Random condition were significant (t(34)=3.02, p=.005, Cohen’s d=1.01 and t(34)=2.42, p=.021, Cohen’s d=0.81 respectively). Trials did not differ reliably between the two adaptive conditions (t(34)=.85, p=.04, Cohen’s d=0.28).

Raw accuracy data (not corrected for number of trials invested) are shown in Figure 4B for each condition in both immediate and delayed posttests. A 3×2 ANOVA across scheduling conditions and both posttest phases found no effect of scheduling condition (F(2,51)=1.94, p=.153, η_p=0.07), an effect of test phase (F(1,51)=52.8, p < .001, η_p=0.508), and no interaction of phase and condition (F(2,51)=0.053, p=.95, η_p=0.002). Accuracies in the Random condition numerically exceeded those in the Adaptive and Adaptive/Mini-blocks conditions in both the immediate and delayed posttests (Immediate: M: .86 vs. .79 & .80, respectively; Delayed: M: .75 vs. .68 & .69, respectively). Individual comparisons showed a marginally significant difference between the Random and Adaptive conditions on the immediate posttest (t(34)=1.88, p=.069, d=0.63); however, the difference was not reliable at delayed posttest (t(34)=1.63, p=.11, d=0.55). No reliable differences were found in immediate posttest accuracy between the Random and Adaptive/Mini-blocks condition or between the two Adaptive conditions (ts(34)=1.57 and 0.30, ps=.13 and .76, respectively). Similarly, at delayed posttest, there was no reliable difference between the Random and Adaptive/Mini-blocks conditions, or between the two Adaptive conditions (ts(34)=1.34 and 0.10, ps=.19 and .92, respectively). All three conditions showed accuracy decreases between posttest and delayed posttest (all ps < .05).

We carried out an additional accuracy analysis by comparing the three learning conditions at a point when all three had the same number of learning trials. We determined the mean number of trials to reach criterion in the standard Adaptive condition and examined the performance of learners in the Random condition and the Adaptive/Mini-blocks condition after the same number of trials. The mean number of trials to reach learning criterion in the Adaptive condition was 155 trials (SD=48.2). In the Adaptive condition, we calculated the average accuracy across the last two presentations of each learning category at the time each learner reached learning criterion. In the Random and Adaptive/Mini-blocks conditions we calculated the average accuracy across the last two presentations of each learning category at the point when learners had received 155 learning trials. Mean proportions correct were .98, .96, and .92 for the Adaptive, Adaptive/Mini-blocks, and Random conditions respectively, after an average of 155 learning trials (see Figure 4C). An ANOVA showed a reliable main effect of learning condition (F(2,51)=6.1, p=.004). Individual comparisons indicated that the Adaptive condition had reliably higher accuracy than the Random condition (p=.004), and the Adaptive/Mini-blocks condition had marginally higher accuracy than the Random condition (p < .06). The two Adaptive conditions did not differ reliably (p > .9). (All p values were Bonferroni corrected.) There were no reliable differences in response times across conditions using a similar method of measuring RTs at an equivalent point in the three conditions (155 trials).

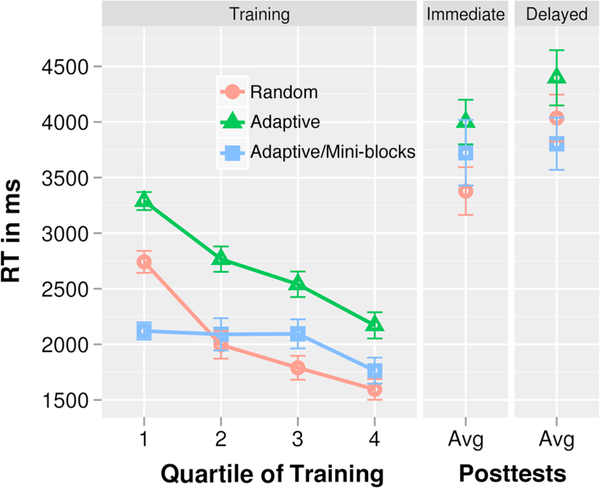
A final set of analyses examined mean response times (RTs) in both posttests. Only response times from correct trials were analyzed. Response times for Experiment 1 are shown in Figure 5, right two panels. A 3×2×2 ANOVA examined RTs across scheduling condition, posttest phase and across novel vs. familiar stimuli. There was no reliable main effect of scheduling condition (F(2,51)=1.78, p=.18, ηp=0.07), a significant main effect of phase (F(1,51)=6.54, p=.013, ηp=0.11), and no effect of familiarity (F(1,51)=2.98, p=.09, ηp=0.06). There were no reliable interactions (all ps > .20). RTs generally increased between immediate and delayed tests, but individual comparisons did not reveal reliable differences across posttests for any condition (all ps > .09).

Figure 5.

Mean response times by quartile of training phase and in the immediate and delayed posttests by scheduling condition in Experiment 1. Response times include accurate responses only. Error bars indicate ± one standard error of the mean.

3. Experiment 2

The purpose of Experiment 2 was to investigate the effect of within-category variability on adaptive spacing in PL. The spacing principles we tested here in PL were derived from memory research using fixed items that reappear at varying intervals. In applying these concepts to PL of categories, the category, not a fixed learning item, is the unit of spacing. When it is time for another learning trial, a new instance of the category, not a repeat of an item, is presented. Intuitively, it seems that the applicability of spacing principles derived from item learning research might be greater in PL for categories with lower variability, because new instances of a given category will tend to resemble earlier ones. Recurrence of a category containing low-variability instances more closely resembles re-presentation of an identical item.

This idea also applies to the ARTS adaptive learning system used here. Recall that ARTS uses response times from earlier trials to estimate learning strength. If a new exemplar of a category bears little resemblance to an earlier one, the estimate of learning strength derived for the earlier item may not predict learning strength of the current item. This problem should be more salient for high-variability categories and especially for categories that are disjunctive (i.e., an exemplar may be in the category by virtue of having either characteristic A or characteristic B). The integrity of the concept of learning strength seems likely to be greatest when it applies to an identical item recurring (as in item learning) and better for categories whose exemplars resemble each other than for those with highly variable exemplars.

3.1. Method

3.1.2. Procedure

Experiment 2 replicated the procedure of Experiment 1, but tested whether differences across learning conditions would be affected by the reduced variability of exemplars within each category. In Experiment 2 the exemplars in each category were made less variable in the following way: each category was composed of instances from one distinct species. In Experiment 1, each genus (category) was comprised of 3 distinct species, with 3 exemplars chosen from each of the 3 species. In Experiment 2, only one of the original 3 species was selected for each genus, and all 9 exemplars for the category were selected from that species, effectively reducing total category variability.

3.1.3. Participants

54 undergraduate psychology students participated in an hour-long experiment for course credit.

3.2. Results

As in Experiment 1, pretest accuracy across conditions did not differ from chance (M=.25, SD=0.11), and an ANOVA showed no reliable differences between conditions (F(2,51)=0.39, p=.68, η_p=0.02). Paired comparisons between conditions were also not significant (all ps > .40).

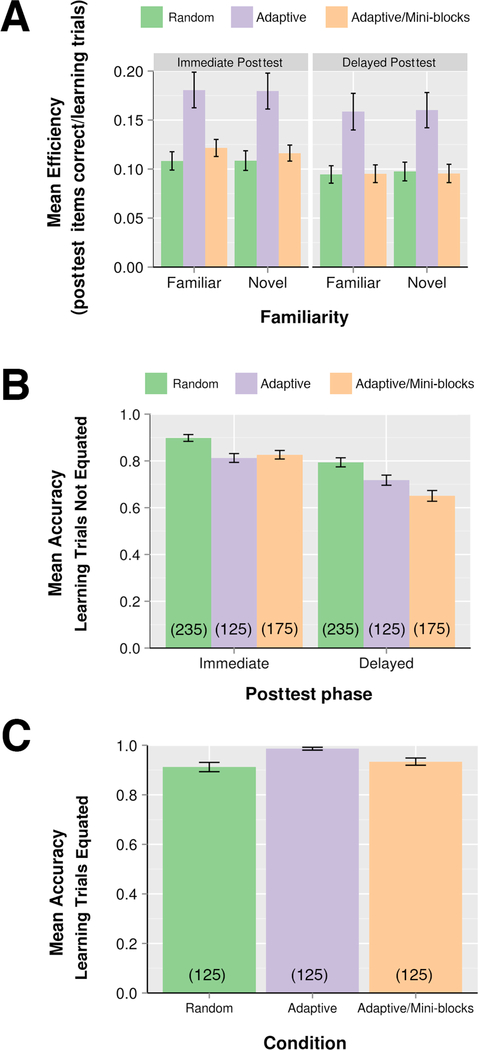
Efficiency scores are shown in Figure 6A for the three scheduling conditions in both immediate and delayed posttests and across novel and familiar items. Efficiency was generally higher in Experiment 2 than in Experiment 1, as learners required fewer trials to achieve criterion performance, especially in the Adaptive condition. Efficiencies for the Adaptive condition were higher than those in the Random and Adaptive/Mini-blocks condition for both immediate and delayed posttests (Immediate posttest: Ms= 0.18, vs. 0.10 and 0.11; Delayed posttest: Ms=0.16, vs. 0.096 and 0.095). A 3×2×2 mixed factor ANOVA with condition as a between-subjects factor, and test phase and stimulus familiarity as within-subjects factors, confirmed significant main effects of condition (F(2,51)=8.87, p < .001, η_p=0.26), test phase (F(1,51)=84.5, p < .001, η_p=0.62), and a marginal condition by test phase interaction (F(2,51)=2.6, p=.084, η_p=0.092). Paired comparisons revealed that the differences between Adaptive and both of the other two conditions (vs. Random and Adaptive/Mini-blocks) were reliable at immediate posttest (t(34)=3.49, p=.001, d=1.22 for Adaptive vs. Random, and t(34)=3.07, p=.004, d=1.09 for Adaptive vs. Adaptive/Mini-blocks) and at delayed posttest (t(34)=3.14, p=.004, d=1.1, and t(34)=3.17, p=.003, d=1.12), whereas the difference between Random and Adaptive/Mini-blocks conditions was not reliable (in either immediate or delayed posttest, both ps >.40). In percentage terms the Adaptive condition was 38% more efficient than Random in the immediate posttest and 39% more efficient than Random in the delayed posttest. Effect sizes for these comparisons exceeded 1.0 in both posttests. All conditions showed a reliable decrease in efficiency between immediate and delayed posttests (all ps < .002). There was no reliable main effect of familiarity (F(1,51)=0.01, p=.91, η_p<0.001), nor any reliable interaction between familiarity and phase (F(2,51)=1.06, p=.31, η_p=0.02), familiarity and condition (F(2,51)=0.49, p=.62, η_p=0.02), or between condition and phase (F(2,51)=0.07, p=.93, η_p=0.002). The lack of main effects or interactions involving familiarity indicate that, unlike Experiment 1, there was no advantage in the posttests for novel vs. previously exposed stimuli.

Figure 6.

Learning results for Experiment 2. A) Mean efficiency scores by learning condition and posttest phase. Efficiency scores were the number of posttest items answered correctly divided by the number of trials invested in learning. Familiar stimuli were posttest items that had been shown during training, whereas novel stimuli were items that had not been presented previously. B) Mean accuracy results by learning condition and posttest phase. Accuracy is given as the percentage of 24 posttest questions answered correctly. These data indicate raw accuracy not corrected for number of learning trials; the number of learning trials in each condition is shown in parentheses. C) Mean accuracy by learning condition based on equal numbers of learning trials. Parentheses indicate trial number at which accuracy was measured, for the two most recent presentations of each category. In all graphs, error bars indicate ± one standard error of the mean.

Trials to retirement differed between conditions; participants averaged 125.3, 174.8, and 234.9 trials in the Adaptive, Adaptive/Mini-blocks, and Random conditions, respectively. A one-way ANOVA with condition as the factor showed reliable difference (F(2,51)=10.04, p < .001, η_p=0.28). Paired comparisons indicated that all three conditions differed from one another. The Adaptive condition required fewer trials than the Random condition (t(34) = 3.82, p=.001, d=1.36); the Adaptive/Mini-blocks condition required fewer trials than Random (t(34)=2.17, p=.037), and the Adaptive condition required fewer trials than the Adaptive/Miniblocks condition (t(35)=−3.46, p=.002).

Raw accuracy data (not corrected for number of trials invested) are shown in Figure 6B for each condition in both immediate and delayed posttests. A 3×2 ANOVA, with scheduling condition as a between-subjects factor and post test phases as a within-subjects factor showed a marginally reliable main effect of condition (F(2,51)=2.71, p=.076, η_p=0.09), a reliable effect of test phase (F(1,51)=86.3, p < .001, η_p=0.63), and a reliable test phase by condition interaction (F(2,51)=3.62, p=.034, η_p=0.12). Accuracies in the Random condition numerically exceeded those in the Adaptive and Adaptive/Mini-blocks conditions in both the immediate and delayed posttests (Immediate: M: .90 vs. .81 & .82, respectively; Delayed: M: .79 vs. .72 & .65, respectively). Individual comparisons confirmed a reliable difference between the Random and Adaptive conditions on the immediate posttest (t(34)=2.19, p=.04, d=0.73), but consistent with the observed interaction, the difference was not reliable at delayed posttest (t(34)=1.47, p=.15, d=0.49). No reliable differences were found in immediate posttest accuracy between the Random and Adaptive/Mini-blocks condition or between the two Adaptive conditions (ts(34)=1.62 and 0.29, ps=0.11 and 0.77 respectively). At delayed posttest, there was no reliable difference between Adaptive and Adaptive/Mini-blocks (t(34)=1.09, p=.28, d=0.37), but there was a reliable difference between Random and Adaptive/Mini-blocks (t(34)=2.49, p=.01, d=0.84).

As in Experiment 1, we compared accuracies across conditions at a moment in training when each participant had accumulated about the same number of learning trials. Mean trials to criterion was 125 in the Adaptive condition (SD=49.9), and proportion correct for the last two presentations of each stimulus category for this condition at this point in training was .99 (see Figure 6C). In the Random and Adaptive/Mini-blocks conditions, performance measured from the 125th trial on the last two presentations of each category was .91 and .93 respectively. A one-way ANOVA comparing the learning conditions on this measure showed a reliable main effect of condition (F(51)=7.28, p=.002). Individual comparisons indicated that accuracy was reliably higher in the Adaptive condition than in the Random condition (p=.002) and also reliably higher in the Adaptive condition than in the Adaptive/Mini-blocks condition (p=.035). There was no reliable difference in accuracy after 125 trials between the Adaptive/Mini-blocks and Random conditions (p > .83) (all ps Bonferroni corrected).

Response times in the immediate posttest averaged 3.41, 3.48, and 2.64 sec per trial in the Adaptive, Adaptive/Mini-blocks, and Random conditions, respectively. In the delayed posttests, response times were more similar across conditions, with the Adaptive, Adaptive/Mini-blocks, and Random conditions averaging 3.73, 3.68, and 3.33 sec per trial respectively. These observations were confirmed by a 3×2×2 ANOVA across scheduling condition, posttest phase and familiarity which found a marginally significant main effect of condition (F(2,51)=2.83, p=.07, ηp=0.10), a main effect of phase (F(1,51)=11, p=.002, ηp=0.17), and a main effect of familiarity (F(1,51)=4.84, p=.032, ηp=0.86). There were no interactions between the factors (all ps > .20). Examining the effect of scheduling condition, there were significantly lower RTs for the Random condition than Adaptive (t(34)=2.37, p=.02, d=0.79) and Adaptive/Mini-blocks (t(34)=2.01, p=.05, d=0.69), but no difference between the two Adaptive conditions (t(34)=0.03, p=.98, d=0.01). Examining differences between immediate and delayed posttests, there were significant increases in RT for Random (p < .001), but not for Adaptive or Adaptive/Mini-blocks (both ps > .20). Individual comparisons showed that in the immediate posttest, response times in the Random condition were shorter than in either of the other conditions (Random vs. Adaptive, t(34)=2.74, p=.02, Bonferroni corrected; Random vs. Adaptive/Mini-blocks, t(34)=3.08, p < .012, Bonferroni corrected). Response times did not differ between the two Adaptive conditions (t(34)=0.113, p=.91). In the delayed posttest, there were no reliable response time differences between any two conditions (all ts(34) < 1.0, ps > .59, Bonferroni corrected).

3.3. Efficiency and Transfer across Experiments

We compared learning results across Experiments 1 and 2. First, a 3×2×2×2 ANOVA with between-subjects factors of scheduling condition and experiment, and within-subject factors of posttest phase and stimulus familiarity, showed a reliable main effect of condition (F(2,102)=10.79, p < .001, ηp=0.174), a large main effect of test phase (F(1,102)=132.6, p < .001, 0.56), no main effect of experiment (F(1,102)=2.30, p=.13, ηp=0.022) and a marginally significant interaction of scheduling condition and experiment (F(2,102)=2.89, p=.06, ηp=0.053). There was also a main effect of stimulus familiarity (F(1,102)=7.67, p=.007, ηp=0.07), and an interaction between stimulus familiarity and experiment (F(1,102)=8.65, p=.004, ηp=0.078). No other interactions were significant (all ps > .17). Individual comparisons showed that the source of the main effect of condition was greater efficiency in the Adaptive condition than in either of the other conditions (Adaptive vs. Random, t(70)=3.82, p < .001, d=.95; Adaptive vs. Adaptive/Mini-blocks, t(70)=3.10, p < .002, d=.77). The Adaptive/Mini-blocks and Random conditions did not differ reliably (t(70)=1.12, p=.27, d=0.26). The same pattern of results appeared when looking separately at results from the immediate posttest (Adaptive vs. Random, t(70)=3.89, p < .001, d=0.96; Adaptive vs. Adaptive/Mini-blocks, t(70)=2.95, p < .004, d=0.73; Adaptive/Mini-blocks vs. Random (t(70)=1.51, p=.14, d=0.36) or delayed posttest (Adaptive vs. Random, t(70)=3.64, p < .001, d=0.91; Adaptive vs. Adaptive/Mini-blocks, t(70)=3.18, p < .002, d=0.79; Adaptive/Miniblocks vs. Random (t(70)=.67, p=.51, d=0.16).

The condition by experiment interaction was due primarily to somewhat better efficiency shown by the Adaptive condition in Exp. 2 compared to Exp. 1 (t(34)=2.03, p=.05, d=0.69). Neither the Adaptive/Mini-blocks nor Random conditions differed reliably between Experiments 1 and 2 (ps=.64 and .83 respectively). The interaction of stimulus familiarity and experiment reflects the lack of any posttest advantage for novel stimuli in Experiment 2, unlike Experiment 1, which showed a clear difference.

4. General Discussion and Conclusion

4.1. General Discussion

In two experiments, we studied PL in a rich, natural domain that was unfamiliar to the participants. As in many real-world PL tasks, the goal of learning is to discover and encode features and relations that determine natural categories, allowing the learner to classify accurately previously unobserved instances. Specifically, we tested whether an adaptive sequencing algorithm implementing principles of spacing in an individualized manner could improve PL for natural categories. The algorithm varied intervals between presentations of new instances of each learning category based on each learner’s accuracy and RT in classifying instances of that category.

4.1.1. Effects of Adaptive Sequencing on Perceptual Learning

In both experiments, we found evidence of greater learning efficiency for adaptively sequenced learning over random presentation, in both immediate and delayed posttests. We included a test after a one-week delay, because immediate and delayed tests sometimes differ in interesting ways, and testing after a delay removes possible influences of relatively transient effects and is therefore considered a better measure of learning (Schmidt & Bjork, 1992). In Experiment 1, with higher variability categories (exemplars chosen from within any species in a genus), the efficiency advantage of adaptive sequencing was clearest for novel items in the posttests and for all items in the delayed posttest, which showed a 29% efficiency advantage over random presentation. Moreover, effect sizes for Adaptive vs. Random for both immediate and delayed posttests averaged around .7. Adaptive sequencing also reliably outperformed random presentation on a pure accuracy measure when learning conditions were compared after the same number of learning trials.

These learning effects were magnified in Experiment 2, in which lower variability categories (using only one species per genus) were used. In this experiment, the Adaptive condition showed highly reliable advantages over the Random condition in efficiency on both immediate and delayed posttests (on the order of 38–39%); for both familiar and novel items; and also when accuracy was compared directly across groups after the same number of learning trials.

The results have significance for understanding high-level PL in general and for applications of PL in real-world education and training domains. The spacing effect is one of the most important and robust principles of learning and memory (Dempster, 1988), and with memory for factual material, adaptive learning schemes have been shown to enhance efficiency by tailoring spacing to the individual learner’s course of acquisition of each item to be learned (Atkinson, 1972; Mettler, Massey, & Kellman, 2011; Pavlik & Anderson, 2008). The present work may be the first to apply adaptive spacing to PL. The present results indicate that adaptive sequencing can robustly improve learning. The effect sizes (ranging from around .7 in Exp. 1 to 1.2 in Exp. 2), as well as the percentage advantages in efficiency (25–29% in Exp. 1 to around 38–39% in Exp. 2) are of sufficient magnitude to be of substantial value in improving learning in complex learning domains in real-world settings.

4.1.2. Spacing in Perceptual Learning and Factual Learning

These results may also offer some insight into relations between PL and factual learning, where spacing has been more extensively investigated. In our studies, a fundamental principle in the adaptive condition was the stretching of the recurrence interval for categories based on speed of responding. The present findings that adaptive spacing improves PL for natural categories parallel similar effects of adaptive spacing for memory items. As such, it raises the question of what learning mechanisms may be shared across these domains. Storage of items in memory (fact or item learning) and discovering structure in displays that allows classification of new instances (PL) appear to involve substantially different mechanisms. In memory research, retesting an item when it is just about to be forgotten is usually considered in terms of memory trace decay (Pyc & Rawson, 2009), but in PL, learning progresses by more selective and fluent information extraction from presented displays. We believe that the common link is not that factual memory and PL involve the same mechanisms, but that a common principle of optimal learning applies to both. As learning to extract relevant information improves for one category, it becomes desirable to have a longer interval and/or more trials with intervening categories before returning for further practice on the initial category. PL involves discovery of invariance and allowable variation with categories (Gibson, 1969), but perhaps the most crucial component of PL is coming to encode distinguishing features between categories (Gibson, 1969). This process may be optimized by modulating the numbers of trials of intervening categories depending on the strength that category. If the learner is a poor classifier of instances of a category, many intervening trials of other categories may impede learning, but as learning improves, more intervening category experiences may be optimal. Although the underlying processes for item memory and PL are unlikely to be the same, learning in both domains can be enhanced by adjusting spacing to match changes in learning strength. And in both domains, because learning strength may not be predictable in advance and may vary by learners and categories, adaptive scheduling based on updated learning strength estimates, as was done here by the use of response times, may offer advantages over predetermined schedules.

4.1.3. Category Variability in PL

The advantage for lower variability categories can be easily interpreted in this context. The ARTS system uses response times, along with accuracy, from earlier trials to estimate learning strength. When a specific item recurs, as in factual learning contexts, an accurate and faster response can be straightforwardly interpreted as an improvement in learning. A primary goal of the present work was to investigate if the accuracy and speed can also be used to guide PL, where categories recur over spacing intervals but presented instances are novel. The results indicate that adaptive sequencing of categories is indeed beneficial, but the benefit is greater for categories with lower variability among instances. The instances of higher variability categories may involve a greater array of features and relations to be encoded; thus, a learner’s performance on an earlier instance of a category may be an imperfect predictor of learning strength for another item. High variability categories might even be disjunctive, in the sense that there is more than one characteristic that confers membership, or in the sense that irrelevant variation may differ from instance to instance. Where such differences exist, performance measured from one instance might provide little indication of the learning strength for another instance. Gibson’s classic work on PL emphasized discovery of invariance, but many natural categories may have a family resemblance structure (Rosch & Mervis, 1975; Wittgenstein, 1953). Perhaps even more crucially, the process of discovering distinguishing features of categories (Gibson, 1969) may also involve learning to ignore characteristics that are not diagnostic of category membership. These may also vary across instances of a single category.

We close this issue by noting that the situation may actually be more complicated. PL in category learning involves the discovery and selective encoding of diagnostic characteristics that govern category membership. Explanations of PL based on selection have been supported by considerable empirical and modeling work (e.g., Petrov, Dosher, & Lu, 2005). In PL contexts involving categorization of complex, multidimensional stimuli, one implication of selection is that, as learning progresses, members of the same category will likely come to resemble each other more. In this sense, the perceived “variability” of instances of a category likely changes through PL. It might be interesting in future research to develop measures of perceived similarity to look at stimulus variability as a dependent variable that changes in PL, in addition to its effects as an independent variable as in the present research.

4.1.4. Transfer in Perceptual Learning

A hallmark of perceptual learning in real-world domains is transfer of learning. Learners become able to accurately and fluently classify new exemplars of previously learned categories. To ascertain that true PL, rather than memorization of instances, was involved in the present studies, we used posttests with both familiar and novel instances. All of our results indicate that novel instances were classified at least as accurately as familiar instances. These outcomes indicate both that participants attained classification skills that generalized to previously unseen cases and also that our efforts to minimize instance repetitions during learning were successful.

The results of Exp. 1 actually suggested better performance for novel exemplars, and this tendency was strongest in the Adaptive condition at delayed posttest. While we cannot rule out some possible effect of interest here, this seems to us to be most likely an inconsequential finding. The set of novel exemplars used in the posttests was the same for all conditions, and this set may have simply been, on average, slightly less difficult than the familiar instances used in the posttest. No advantage for novel items appeared in Experiment 2, which used a different, fixed set of posttest items. If, paradoxically, there is some reason that PL in some conditions is actually stronger for novel instances, the current experiments were not designed to reveal this clearly. Use of a “jackknife” procedure, where each subject is presented different novel instances, would be preferable for a study focused on this issue. Our use of novel and familiar posttest items allowed clear comparisons across conditions, and provided clear evidence for transfer of learning, but it did not provide clear evidence for a novelty advantage.

4.1.5. Partial Blocking in PL.

Our data offer little or no support for initial blocking or massing of instances of a given category. At best, the Adaptive/Mini-blocks condition in the present experiments produced performance nearly equivalent to the Adaptive condition; it was often somewhat worse, and never better. The intuition behind blocking is that learning of commonalities within each category should be facilitated by seeing several instances in succession. This intuition appears to be incorrect, however. Earlier work (Kornell & Bjork, 2008) compared complete blocking to complete interleaving in studying examples of different artists’ painting styles and found a clear advantage of interleaving. In our Adaptive/Mini-blocks condition, we investigated whether some initial blocking, followed by interleaved, spaced practice might aid early learning of categories while still capturing the benefits of interleaving later. This approach never produced better performance than the regular Adaptive condition, in which there was consistent interleaving. It appears that stimulus presentation that facilitates the learning of contrasts that distinguish categories may be of greatest importance in arranging PL.

4.1.6. Learning to Criterion in PL

The studies reported used learning to criterion. Probably for reasons of experimental control, this is quite rare for studies of spacing in learning. It is, however, of primary importance in real learning settings. The most obvious methodological difficulty of studies using learning to criterion is that different participants and conditions will require different numbers of learning trials. The efficiency measure addressed this issue by combining both posttest accuracy and the number of learning trials invested; such a measure is likely to be useful in real-world learning settings where mastery in the shortest time is desirable. As reaching criterion in our Random condition generally required more trials than in the Adaptive condition, it is important to consider whether this feature alone provided the advantage of adaptive sequencing. To address this issue, we also examined accuracy after a similar number of learning trials in each group. As with the efficiency measure, this “apples to apples” comparison of accuracy also clearly showed advantages of adaptive sequencing.

A final note concerns our choice of comparison conditions. We chose to compare sequencing algorithms against random presentation - a notoriously effective schedule of practice that produces robust, albeit inefficient, learning in a variety of contexts. For example, random presentation automatically implements a type of spaced interleaving, and when unmodified, as in our experiment, can result in repeated presentation of critical stimulus material. Though random presentation has fared poorly in some experiments that have compared scheduling algorithms to random practice (as in Atkinson, 1972), it may be that in a learning domain with as few categories as in our experiment (12 categories), the benefits of random presentation may be quite large (compared to, for instance, learning a large number of independent factual items). The fact that our algorithms performed as well as they did is thus encouraging. Presumably, if we had compared adaptive sequencing to massed practice (blocking of all category exemplars) adaptive sequencing would have fared even better (c.f., Kornell & Bjork, 2008).

4.2. Conclusion

It is becoming increasingly clear that perceptual learning comprises a pivotal component in domains where humans attain high levels of expertise, including high-level cognitive domains that have traditionally been considered to have little to do with perception (for recent reviews, see Kellman & Garrigan, 2009; Kellman & Massey, 2013). More than one aspect of perceptual learning is important, including both discovery effects -- finding the information relevant to a classification -- and fluency effects --coming to handle the input quickly and/or with lower cognitive load (Gibson, 1969; Goldstone, 1998; Kellman & Garrigan, 2009; Shiffrin & Schneider, 1977). Perhaps most important in complex tasks is discovery of structural information amidst task-irrelevant variation (Gibson, 1969), with the hallmark of this kind of PL being that the learner can accurately and fluently classify previously unseen instances. Whether we consider a child who learns to see a new animal and correctly say “cat,” the skilled instructor who accurately derives language structure from a student’s poor handwriting, the “chick sexers” described by Gibson (1969) or the scientist intuitively grasping patterns in equations and graphs, the discovery of relevant structure and the ability to use it in new cases is important.

Both basic research and understanding of the widespread implications of perceptual learning raise questions about how to optimize it. Although a great deal of work has been done to understand principles of factual or procedural learning, relatively little work has asked these same questions about PL. No previous studies that we know of have investigated how adaptive spacing techniques might fare when learning consists, not of the memorization of words or facts, but in attuning perceptual systems to extract structure. Here we have shown that adaptive scheduling strategies that enhance declarative learning domains also apply robustly to learning perceptual classifications. Adaptive techniques lead to more efficient perceptual learning; these effects are strongest when categories have less internal variability rather than more; and the effects lead to transfer in classifying novel instances that is fully as accurate as performance on cases previously observed.

Abbreviations

PL

Perceptual Learning

Appendix

Table 1.

Parameters for the adaptive sequencing algorithm in Experiments 1 and 2.

Parameter	Value
a – Counter weight	0.1
b – Default weight	1.1
r – RT weight	1.7
W – Incorrect priority increment	20
D – Delay constant	2