Abstract
Learning in educational settings emphasizes declarative and procedural knowledge. Studies of expertise, however, point to other crucial components of learning, especially improvements produced by experience in the extraction of information: perceptual learning. We suggest that such improvements characterize both simple sensory and complex cognitive, even symbolic, tasks through common processes of discovery and selection. We apply these ideas in the form of perceptual learning modules (PLMs) to mathematics learning. We tested three PLMs, each emphasizing different aspects of complex task performance, in middle and high school mathematics. In the MultiRep PLM, practice in matching function information across multiple representations improved students’ abilities to generate correct graphs and equations from word problems. In the Algebraic Transformations PLM, practice in seeing equation structure across transformations (but not solving equations) led to dramatic improvements in the speed of equation solving. In the Linear Measurement PLM, interactive trials involving extraction of information about units and lengths produced successful transfer to novel measurement problems and fraction problem solving. Taken together, these results suggest 1) that PL techniques have the potential to address crucial, neglected dimensions of learning, including discovery and fluent processing of relations, 2) PL effects apply even to complex tasks that involve symbolic processing, and 3) appropriately designed perceptual learning technology can produce rapid and enduring advances in learning.
What aspects of scientific research on learning have relevance for education? In the educational literature, we find discussions of fact learning, conceptual understanding, procedure learning, constructing explanations, analogical reasoning, and problem solving strategies. Except for an occasional mention of pattern recognition, little hints at any role for perceptual learning. Likewise, studies of perceptual learning involving sensory discriminations among a small set of fixed stimuli appear to have little connection to real world learning tasks, least of all to high-level, explicit and symbolic domains such as mathematics. Despite this apparent irrelevance or neglect, perceptual learning – improvements in information extraction as a result of practice -- is one of the most important components of learning and expertise in almost any domain, including mathematics. It is also the component least addressed by conventional instruction; thus, problems of information selection and fluent extraction of structure pose major obstacles for many learners.
In this article, we describe the relevance and promise of applications of perceptual learning (PL) to high-level cognitive domains. We focus on mathematics learning but we hope the relevance to other areas of learning will be obvious. Applying PL to such domains is a startling and exciting endeavor. It is startling because some current conceptions of PL would preclude this kind of connection, and it is exciting because considerable evidence suggests that PL technology can address crucial and neglected dimensions of learning, offering the possibility of major advances in the effectiveness of learning in many domains.
We first summarize some characteristic improvements in human information extraction that derive from PL. Next we explain the connection between these changes in high and low level PL tasks, focusing on the notions of discovery and selection as unifying concepts. We then describe three examples of research on perceptual learning modules (PLMs) that apply these ideas to mathematics learning, each illustrating a separate strength of PL interventions. The current treatment is brief, and we refer the reader to other sources for more expansive discussion of some issues (Garrigan & Kellman, 2008; Kellman, 2002; Kellman, et al, 2008; Kellman & Garrigan, in press).
Characteristics of Expertise Generated by Perceptual Learning
In contrast to the literature on learning, scientific descriptions of expertise are dominated by PL effects. In describing their studies of master level performance in chess, Chase & Simon (1973) wrote: “It is no mistake of language for the chess master to say that he ‘sees’ the right move; and it is for good reason that students of complex problem solving are interested in perceptual processes.” (p. 387). Table 1 summarizes some of the well-known information processing changes that can derive from PL. Kellman (2002) suggested that these can be divided into discovery and fluency effects. Discovery pertains to finding the features or relations relevant to learning some classification, whereas fluency refers to extracting information more quickly and automatically with practice. Both discovery and fluency differences between experts and novices have since been found to be crucial to expertise in a variety of domains, such as science problem solving (Bransford, Brown & Cocking, 2001; Chi et al, 1981; Simon, 2001), radiology (Kundel & Nodine, 1975; Lesgold, et al., 1988), electronics (Egan and Schwartz, 1979), and mathematics (Robinson & Hayes, 1978).
Table 1.
Some characteristics of novice and expert information extraction. (See text.)
| NOVICE | EXPERT | |
|---|---|---|
| DISCOVERY Effects | ||
| SELECTIVITY: | Attention to irrelevant and relevant information | Selective pickup of relevant information/Filtering |
| UNITS: | Simple features | “Chunks”/Higher-order relations |
| FLUENCY Effects | ||
| SPEED: | Slow | Fast |
| ATTENTIONAL LOAD: | High | Low |
| SEARCH TYPE: | Serial processing | Some parallel processing |
Scope of Perceptual Learning
Eleanor Gibson, who pioneered the field of PL (for a review, see Gibson, 1969), defined it as “an increase in the ability to extract information from the environment, as a result of experience…” (1969, p. 3). She described a number of particular ways in which information extraction improves, including both the discovery and fluency effects noted above. Of particular interest to Gibson was “…discovery of invariant properties which are in correspondence with physical variables” (Gibson, 1969, p. 81). This view of PL applies directly to many real-world learning problems; although Gibson did not mention mathematics learning, her examples included chick sexing, wine tasting, map reading, X-ray interpretation, sonar interpretation, and landing an aircraft.
Much contemporary PL research differs from these earlier ideas, both in the types of learning problems studied and in theoretical context. It is common to consider PL as described by Fahle & Poggio (2002): “…parts of the learning process that are independent from conscious forms of learning and involve structural and/or functional changes in primary sensory cortices.” This emphasis derives from several related ideas. PL effects often show specificity to stimulus variables (such as orientation or motion direction) or observer variables (such as the eye or part of the visual field used in training). Specificity in learning (lack of transfer) has been assumed to indicate a low-level locus of learning effects, implying that mechanisms of PL are modifications, such as receptive field changes, in early sensory areas.
Confining PL to changes early in sensory systems would separate it from most real-world learning tasks involving higher order relations and extraction of invariant patterns from varying instances. If the supporting assumptions are correct, then the type of PL being studied recently has little to do with mathematics learning. Perhaps the discovery of invariance in complex tasks and modification of receptive fields in simple discriminations have little do with each other, and the best course would be to adopt different names for these different kinds of learning.
Such a division would be unfortunate, for two reasons. First, the assumptions supporting confinement of PL to early sensory cortices and simple sensory phenomena are not sustainable. Those that are logical assumptions, such as the idea that specificity of learning implies a low-level locus, are fallacies (Mollon & Danilova, 1996). Those that are empirical hypotheses appear to be false (for more extended discussions, see Garrigan & Kellman, 2008; Kellman & Garrigan, in press). For example, data about transfer from PL experiments have been inconsistent, and small task variations can lead to large differences in generality of learning (e.g., Liu, 1999; Sireteanu & Rettenback, 2000); single-cell recording data offer little support for receptive field modification as the explanation for PL, at least in vision (e.g., Ghose, Yang, & Maunsell, 2002). Furthermore, substantial evidence suggests that PL, even when oriented toward a low-level sensory discrimination, is guided by higher-level tasks (Ahissar & Hochstein, 2004), and attention (Seitz et al, 2005; Seitz & Watanabe, 2005), and may in fact be required to work through constancy-based representations (Garrigan & Kellman, 2008).
Perhaps the most important rationale for considering “high” and “low” level tasks together in PL is that they may share common principles and mechanisms. For Gibson, a key to PL was selection. Recent experimental results suggest that selection is a better explanation of many low-level PL phenomena than receptive field modification (Petrov, Dosher & Lu, 2005; Ahissar, et al 1998). Higher levels of processing receive inputs from below; learning processes discover which inputs are most relevant, and these inputs become more heavily weighted (Mollon & Danilova, 1996; Petrov et al, 2005). Processes of discovery and selective weighting offer concepts that apply to both laboratory studies of sensory discrimination and discovery of high-level invariance in ecologically important tasks.
Applications of PL to High-Level Learning Domains
Assuming the relevance of PL to complex tasks, one might still wonder about symbolic domains such as mathematics. Even Gibson’s examples -- wine tasting, recognizing aircraft or reading X-rays -- seem much less “cognitive.” Mathematics might be thought to involve only declarative knowledge and procedures. There are inherently symbolic aspects of mathematical representations that cannot be apprehended via information “in the stimulus.” This is true, but it is also true that mathematical representations pose important information extraction requirements and challenges. Characteristic difficulties in mathematics learning may directly involve issues of discovery and fluency aspects of PL. A number of studies indicate the role of PL in complex cognitive domains, such as mathematics (Goldstone, Landy & Son, 2008; Silva & Kellman, 1999), language or language-like domains (Reber & Allen, 1978; Reber, 1993; Saffran, Aslin & Newport, 1996; Gomez & Gerken, 1999), chess (Chase & Simon, 1973) and reading (Baron, 1978; Reicher, 1969; Wheeler, 1970). Some have asserted that in general, abstract concepts have crucial perceptual foundations (Barsalou, 1999; Kosslyn & Thompson, 2000; Landy & Goldstone, 2008). Moreover, in complex cognition it is important to realize that conceptual and procedural knowledge must work together with structure extraction. Both declarative and procedural knowledge depend on pattern recognition furnished by PL. Which facts and concepts apply to a given problem? Which procedures are relevant? How do we appropriately map parts of the given information into schemas or procedures? These are fundamentally information selection and pattern recognition problems.
Perceptual Learning Technology
The lack of PL techniques in instructional contexts owes not only to its neglect in learning research but also to the lack of suitable methods. The expert’s pattern extraction and fluency are thought to develop separately from formal instruction, as a result of experience. Yet recent efforts suggest that there are systematic ways to accelerate the growth of perceptual expertise, in areas as diverse as aviation training (Kellman & Kaiser, 1994), medical learning (Guerlain et al, 2004), language difficulties (Tallal, Merzenich, Miller, & Jenkins, 1998), and mathematics (Silva & Kellman, 1999; Kellman et al 2008).
In our work, we implement PL principles in perceptual learning modules (PLMs). Although a full description is beyond our scope here, we mention some elements of PL interventions. Although we lack complete models of PL in complex tasks, it appears that information extraction abilities advance when the learner makes classifications and (in most cases) receives feedback. Digital technology makes possible many short trials and appropriate variation in short periods of time, allowing the potential to accelerate PL relative to less frequent or systematic exposure to structures in a domain. Unlike conventional practice in solving problems, learners in PLMs typically discriminate patterns, compare structures, make classifications, or map structure across representations. In this short report, we summarize three applications of PLMs to mathematics learning, each highlighting a particular issue. The goal is to illustrate a range of applications of the approach.
Mapping Across Multiple Representations: The MultiRep PLM
Mathematical representations are aimed at making concepts and relations accurate and efficient, but they pose complex decoding challenges for learners. Each representational type (e.g., a graph, or an equation) has its own structural features and depicts information in particular ways. Perceptual extraction of structure from individual representations and mapping across representations present learning hurdles that are not well addressed by ordinary instruction. We developed the Multi-Rep PLM to help middle and high school students develop pattern recognition and structure mapping with representations of linear functions, in graphs, equations, and word problems. As in many PLMs, rather than having students solve problems for a numerical answer, we presented them with short, interactive classification tasks which facilitated fluent extraction of important features and patterns.
METHOD
Participants.
68 9th and 10th grade students, taking algebra or geometry at a diverse private school in Santa Monica, California participated in this study.
Design.
Students received a paper-and-pencil pretest and posttest containing two kinds of problems. Four problems required solving word problems involving linear functions. Eight translation problems involved presentation of a word problem, graph, or equation with the student being asked to translate the given target to a new representation -- specifically, to generate an appropriate graph or equation in response. There were four types of translation problem: equation to graph (EG), graph to equation (GE), word problem to equation (WE), and word problem to graph (WG). Students were not asked to generate word problems (i.e., equation or graph to word problem) because of the variability in possible correct responses.
Students in the PLM condition used a self-contained computer program that ran on a Windows platform with a point-and-click interface. The PLM consisted of short mapping trials, where students were presented with a target equation, graph, or word problem, and were asked to select among three possible choices for an equivalent representation depicting the same information. An example is shown in Figure 1. There were six types of mapping trials, comprising all possible pairs of word, equation, and graphical representations given as targets and choices. All equations were in the slope-intercept (y = mx + b) form. The program tracked responses and speed. Visual and auditory feedback followed each student response. Training consisted of two sessions of 60 trials each.
Figure 1.
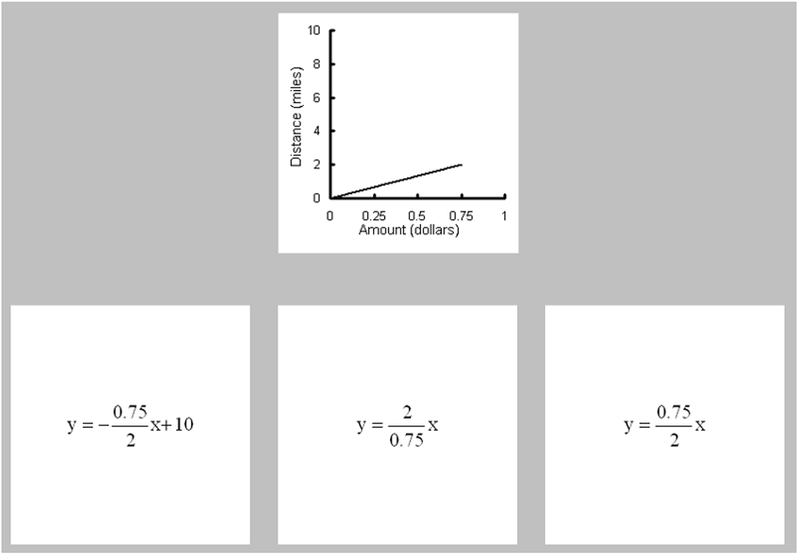
Example of a display in the MultiRep PLM. (See text.)
In a Control condition, students were asked to practice the same kinds of translation problems that appeared on the assessments. They were given packets with 32 problems including equal numbers of the four generation problem types, designed to closely resemble the translation problems on the assessments. Every time students completed a section of the practice packet, they were given an answer key to check their answers. Feedback stated the correct answer and offered no further explanations.
Procedure.
The students used two class periods on two consecutive days to complete the pretest, the instructional intervention, and the posttest. On the first day, students completed a brief background questionnaire, the pretest, and began their learning intervention (either practice packets or PLM). On the second day, students completed their learning interventions and took the posttest. Control and PLM conditions took comparable amounts of time.
RESULTS AND DISCUSSION
Primary results for translation problems for the PLM and Control conditions are shown in Figure 2. There were no significant differences in pretest accuracy between the Control and PLM conditions, t(67) = 1.11, p = .27. There was a robust interaction of test by condition, F(1,66) = 21.17, indicating that the PLM group improved from pretest to posttest more than the control group. Word problem solving (not shown) averaged about 85% in the pretest in both groups and did not vary between groups.
Figure 2.
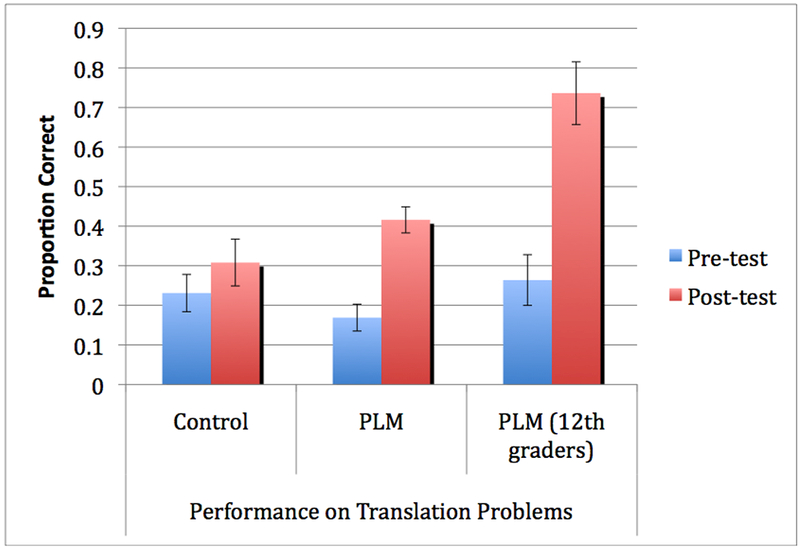
Results of MultiRep PLM study for translation problems by condition and test. Translation problems required students to generate a correct equation or graph given a word problem, graph, or equation. Control and PLM conditions from the experiment are shown in the left and middle sections. A comparison group of 12th graders run in a separate sample is shown in the rightmost column. Error bars indicate ± 1 standard error of the mean.
These results, from two short sessions of PLM use, indicate that practice in mapping problems across multiple representations led to strong improvements on a transfer task – generating the correct equation or graph from a word problem, graph, or equation. In contrast, for the Control group, the translation task in the posttest was not one of transfer; it was the same task practiced during training. The remarkable fact that the PLM group performed better on this transfer task than a control group that practiced the actual task suggests that the PLM produced improvements in structure extraction that are useful to other mathematical skills, such as representation generation.
We have carried out further studies in this paradigm; these raise a number of interesting issues and will be reported elsewhere (Son, Zucker, Chang & Kellman, in preparation). We include here, however, a 12th grade sample for comparison (Figure 1, rightmost data). Pretest scores indicate that even in grade 12, the initial ability to generate correct equations and graphs is poor. The large posttest gains for PLM users, however, indicate that older students may have greater readiness to benefit from the PLM.
From Knowledge to Fluency: Algebraic Transformations
One prediction of a PL approach is that it should be possible for a student to have relevant declarative and procedural knowledge in some domain and yet lack fluent information extraction skills. We tested this idea in work in algebra learning with students who had been instructed for half of a school year on the basic concepts and procedures for solving equations. The hypothesis was that despite reasonable student success in declarative and procedural learning, the “seeing” part of algebra is poorly addressed by ordinary methods and might be accelerated by a PL intervention focused on structures and transformations. For more complete details see Kellman et al (2008).
METHOD
Participants.
Participants were 30 8th and 9th grade students at an independent philanthropic school system in Santa Monica, California, tested after mid-year of a year-long Algebra I course.
Apparatus and Materials.
The PLM was tested on standard PCs using the Windows operating system in computer-equipped classrooms. All assessments and the PLM were presented on computer, with participants’ data being sent to a central server.
Design and Procedure.
The experiment was set up to assess the effects of PL techniques on learners’ speed and accuracy in recognizing algebraic transformations and the transfer of PL improvements in information extraction to algebra problem solving. A pretest was given on one day, followed by 2 days in which students worked on the PLM for 40 minutes per day. A post-test was administered the next day. For a subset of subjects, a delayed posttest was administered two weeks later. In the Algebraic Transformations PLM, participants on each trial selected from several choices the equation that could be obtained by a legal algebraic transformation of a target equation. An example is shown in Figure 3. Problems involved shifts of constants, variables or expressions. Accuracy and speed were measured, and feedback was given. Parallel versions of assessments were constructed such that corresponding problems on separate versions varied in the specific constants, variables, or expressions appearing in each equation. Each participant saw a different version in pretest, posttest and delayed posttest, with order counterbalanced across participants. Each version of the assessment contained recognition problems similar to those in the PLM and solve problems, used as a transfer test. Solve problems were basic Algebra I equations in a single variable, ranging from simple items (such as x − 5 = 2) to more complex “two step” problems (such as −6 = 3t / 5).
Figure 3.
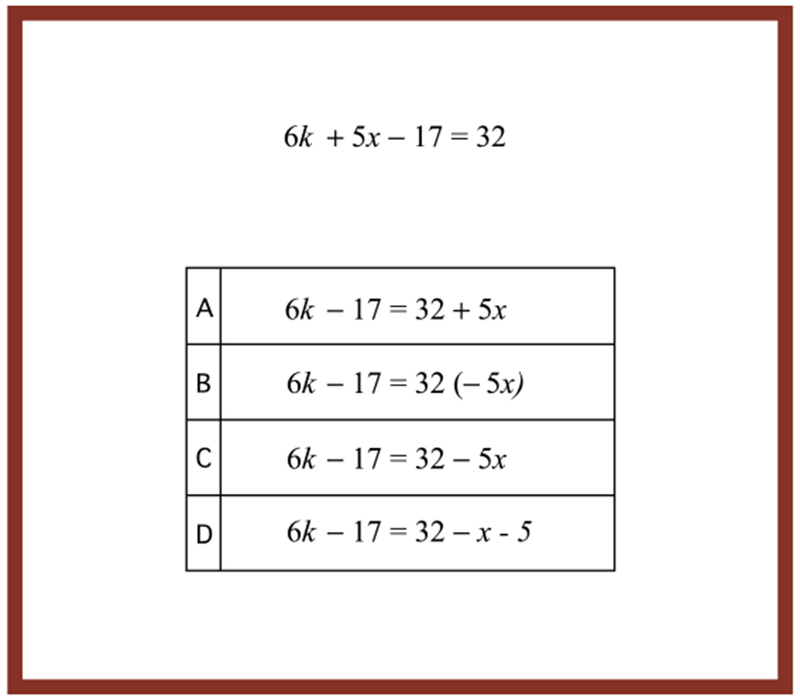
Example of a display in the Algebraic Transformations PLM. (See text.)
RESULTS AND DISCUSSION
Figure 4 shows the data from this study on the transfer task of equation solving, for students who completed the pretest, learning phase, posttest and delayed posttest. A key insight from this study comes from the pretest data. The accuracy of algebra problem solving was quite high for learners at the beginning of the study, averaging almost 80%. This level of competence indicates the success of instructional efforts in conveying concepts and procedures for solving equations. Yet students’ explicit knowledge contrasts with an obvious difficulty in fluent processing of structure: Students take about 28 sec per problem to solve simple algebra problems! This aspect of their problem solving was dramatically improved from PLM use. After two sessions, speed of solving had dropped to about 12 sec per problem. These gains were fully preserved after a two-week delay. Note that these learners never practiced solving equations in the learning phase; the PLM activity focused on recognizing structure and transformations. That this short intervention led to large and lasting gains in fluency suggests that PL methods can produce rapid advancement on dimensions of learning that are not well developed by conventional instruction.
Figure 4.
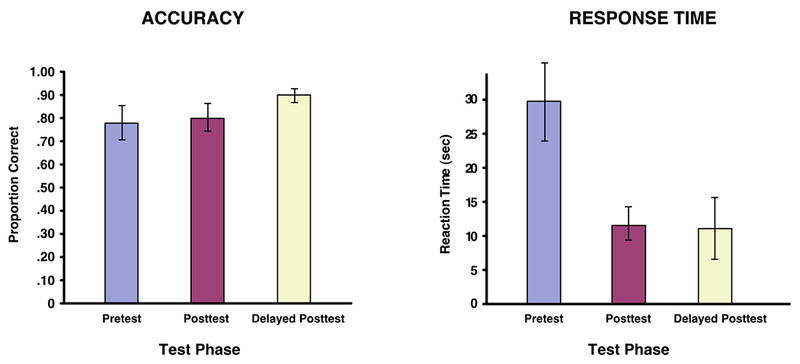
Results of Algebraic Transformations PLM study for the transfer task of solving algebraic equations. Data for pretest, posttest, and delayed posttest are shown for accuracy (left panel) and response time (right panel). Error bars indicate ± 1 standard error of the mean.
Fostering Structural Insight: Linear Measurement
U.S. students perform poorly on measurement problems on national and international standardized tests. Even basic skills, such as linear measurement with rulers, show significant deficits. For example, National Assessment of Educational Progress (NAEP) results indicate that many elementary and middle school students are unable to use a ruler that has been broken to measure a 2 ½ inch toothpick whose left end is aligned with 8 rather than 0 (NCES, 2008). Students’ incorrect responses suggest that they do not conceive of units of linear measurement as having extent. Further, they do not make a clear distinction between position and distance, and they have great difficulty using fractions to represent subdivisions of units.
In a current project, we are applying PL principles to concepts of measurement and fractions. One PLM addressed learning difficulties related to linear measurement. Explanations and demonstrations that students normally receive may be insufficient for them to extract relevant features and relations in measurement. As a result, they learn blind procedures that involve misunderstandings of measurement. We applied PL principles using interactive trials that emphasized students’ discrimination of position and distance and fostered their structural intuitions about units, including fractional units, in measurement problems.
Participants.
Participants were 63 6thgraders who participated in a PLM instructional intervention plus 78 7th graders and 8th graders who served as uninstructed control participants, all from an urban public middle school serving a predominantly low-income neighborhood.
Design.
The web-delivered PLM presented learners with a graphic display showing a ball on top of a ruler and a billiard cue poised to strike it. Learners were presented with four types of trials that varied the information given and what information was to be found (e.g., given the start and endpoint, find the distance traveled; or given the start point and distance traveled, find the endpoint). The user entered responses by keying them in using an onscreen interface or by dragging a marker on the ruler to the desired point. Once the learner had entered his or her response and pressed a button labeled “strike,” the billiard cue would carry out the event on the screen. Animated feedback was provided on each trial.
The learning items in the database varied in numerical values, whether rulers were fully or partially labeled, and whether they were partitioned in the most economical way to solve the problem or were over-partitioned (e.g., a ruler marked in units of 1/16 for a problem involving 1/8s). Items in the learning set were classified into 8 categories, including both fraction and integer problems.
Procedure.
6th grade students first completed a 44-point pencil and paper assessment with a variety of items related to linear measurement with integers and fractions, and adding and subtracting fractions. Equivalent versions were used in counterbalanced fashion for posttests and delayed posttests. Virtually all items were transfer items in that they did not directly resemble the trials presented to students during the PLM training. The control group of 7th and 8th graders, who did not participate in any study-related instruction, were administered the assessment just once, providing a baseline comparison for the 6th graders’ scores. After completing the pretest, 6th graders participated in a single introductory classroom lesson lasting 40 minutes that served to introduce the PLM and the main concepts involved. They then used the PLM software until they either met mastery criteria for all categories or until they had completed 6 sessions. Within 1 to 2 days of completing their last PLM session, students completed a posttest. Four months later, the 6th graders completed a delayed posttest, with no study-related activities occurring in the interim.
RESULTS AND DISCUSSION
As can be seen in Figure 5, prior to instruction, the 6th graders and the 7th and 8th grade control groups scored similarly. This result suggests that the substantial focus on these topics in normal curricula for these grades produces little improvement through the middle school years. PLM use produced significant improvement in the 6th grade intervention group, confirmed by a one-way ANOVA comparing the 6th, 7th, and 8th grade groups (F (2, 138) = 19.687, p < 0.001). The 6th graders achieved nearly identical scores on a delayed posttest administered four months later, indicating that their learning gains were fully maintained. Among the subscales, students’ performance improved in reading and constructing lengths with conventional and broken rulers, and they also made strong gains in fraction problem solving. As assessment problems were transfer items of varied kinds, it appears that the PLM guided students to see the relevant structures underlying units, measurement and fractions, replacing blind procedures used initially by many students.
Figure 5.
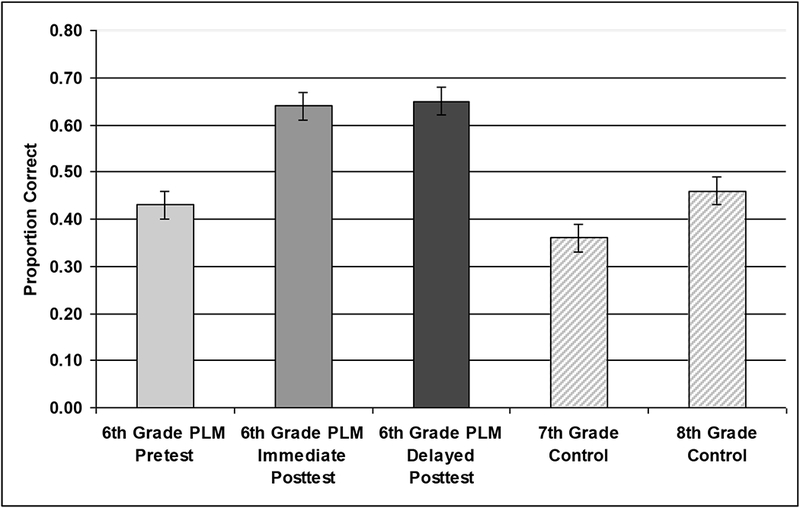
Results of Linear Measurement PLM. Pretest, posttest, and posttest accuracy after a 4-month delay on a battery of measurement and fraction problems are shown in the leftmost three columns. Seventh and 8th grade control groups are shown in the two columns to the right. Error bars indicate ± 1 standard error of the mean.
General Discussion
The study of PL interventions in education and training has barely begun, yet the promise is already clear. PL techniques have the potential to address crucial, neglected dimensions of learning. These include selectivity and fluency in extracting information, discovering important relations, and mapping structure across representations. Each PLM described here addressed an area of mathematics learning known to be problematic for many students. In each case, a relatively short intervention produced major and lasting learning gains, and in each case the learning transferred to key mathematical tasks that differed the training task.
Taken together, these results suggest that PL components play a strong role even in complex tasks that involve symbolic processing. They further indicate that appropriately designed PL technology can produce rapid advances in learning. Few learning interventions produce large learning improvements and transfer from short interventions as occurred in each experiment reported here. Further research will undoubtedly reveal even more about how to optimize discovery of structure and fluency in complex domains. Moreover, the synergy in complex tasks among perceptual, declarative and procedural learning poses important questions regarding both the detailed nature of the interactions and how in instruction they may be optimally combined.
Acknowledgments
The research reported here was supported in part by grants from the US Department of Education, Institute for Education Sciences, Cognition and Student Learning Program, through Grant R305H060070; the National Institute of Child Health and Human Development (NICHD)/ARRA Challenge Grant 5RC1HD063338; and from National Science Foundation Grant REC-0231826 to PK and CM. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the US Department of Education, NIH or the National Science Foundation. We gratefully acknowledge the efforts of Tim Burke, Zipora Roth, Joel Zucker, Amanda Saw, Hye Young Cheong, Warren Longmire, K.P. Thai, Norma Chang and Joseph Wise. We also wish to thank the students, teachers, and administrators at our partner schools for their roles in making this research possible.
Contributor Information
Philip J. Kellman, University of California, Los Angeles
Christine M. Massey, University of Pennsylvania
Ji Yun Son, University of California, Los Angeles.
References
- Ahissar M, & Hochstein S (2004). The reverse hierarchy theory of visual perceptual learning. Trends in Cognitive Sciences, 8(10), 457–464. [DOI] [PubMed] [Google Scholar]
- Ahissar M, Laiwand R, Kozminsky G, & Hochstein S (1998). Learning pop-out detection: Building representations for conflicting target-distractor relationships. Vision Research, 38(20), 3095–3107. [DOI] [PubMed] [Google Scholar]
- Baron J (1978). The word-superiority effect: perceptual learning from reading In Estes WK (Ed.), Handbook of learning and cognitive processes. Vol. 6 Hillsdale, NJ: Erlbaum. [Google Scholar]
- Barsalou LW (1999). Perceptual symbol systems. Behavioral and Brain Sciences, 22, 577–609. [DOI] [PubMed] [Google Scholar]
- Bransford JD, Brown AL, & Cocking RR (Eds). (1999). How people learn: Brain, mind, experience, and school. Washington, D.C.: National Academies Press. [Google Scholar]
- Chase WG & Simon HA (1973). Perception in chess. Cognitive Psychology,. 4(1), 55–81. [Google Scholar]
- Chi MTH, Feltovich PJ & Glaser R (1981). Categorization and representation of physics problems by experts and novices. Cognitive Science 5:121–152. [Google Scholar]
- Egan DE, & Schwartz BJ (1979). Chunking in recall of symbolic drawings. Memory & Cognition, 7(2), 149–158. [DOI] [PubMed] [Google Scholar]
- Fahle M, & Poggio T, (Eds.), (2002) Perceptual learning. MIT Press: Cambridge, MA. [Google Scholar]
- Garrigan P, & Kellman PJ (2008). Perceptual learning depends on perceptual constancy. Proc Natl Acad Sci U S A, 105(6), 2248–2253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghose GM, Yang T, & Maunsell JH (2002). Physiological correlates of perceptual learning in monkey v1 and v2. J Neurophysiol, 87(4), 1867–1888. [DOI] [PubMed] [Google Scholar]
- Gibson EJ (1969). Principles of perceptual learning and development. New York: Prentice-Hall. [Google Scholar]
- Goldstone RL, Landy D, & Son J (2008). A well-grounded education: The role of perception in science and mathematics. In Glenberg A, DeVega M, & Graesser A (Eds.) Proceedings of the Garachico Workshop on Symbols, Embodiment and Meaning, Universidad de La Laguna, Tenerife. [Google Scholar]
- Guerlain S, La Follette M, Mersch TC, Mitchell BA, Poole GR, Calland JF, Jianhong Lv, & Chekan EG (2004). Improving surgical pattern recognition through repetitive viewing of video clips. IEEE Transactions on Systems, Man, and Cybernetic - Part A: Systems and Humans. 34(6) 699–707. [Google Scholar]
- Kellman PJ (2002). Perceptual learning In Stevens’ Handbook of Experimental Psychology, Third Edition, Vol.3, H. Pashler H, and Gallistel CR, eds. New York: John Wiley & Sons, pp. 259–299. [Google Scholar]
- Kellman PJ & Garrigan PB (in press). Perceptual learning and human expertise. Physics of Life Reviews. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kellman PJ & Kaiser MK (1994). Perceptual learning modules in flight training. Proceedings of the 38th Annual Meeting of the Human Factors and Ergonomics Society, 1183–1187. [Google Scholar]
- Kellman PJ, Massey CM, Roth Z, Burke T, Zucker J, Saw A, Aguero K & Wise J (2008). Perceptual learning and the technology of expertise: Studies in fraction learning and algebra. Learning Technologies and Cognition: Special issue of Pragmatics & Cognition, 16:2 (2008), 356–405. [Google Scholar]
- Kosslyn SM, & Thompson WL (2000). Shared mechanisms in visual imagery and visual perception: Insights from cognitive neuroscience In Gazzaniga MS (Ed.), The new cognitive neurosciences (pp. 975–985). Cambridge, MA: MIT Press. [Google Scholar]
- Kundel H & Nodine CF (1975). Interpreting chest radiographs without visual search. Radiology, 116, 527–532. [DOI] [PubMed] [Google Scholar]
- Landy D & Goldstone R (2008). How abstract is symbolic thought? JEP: Learning, Memory and Cognition, 33(4), 720–733. [DOI] [PubMed] [Google Scholar]
- Lesgold A, Rubinson H, Feltovich P, Glaser R, & Klopfer D (1988). Expertise in a complex skill: Diagnosing x-ray pictures In Chi MTH, Glaser R, & Farr M (Eds.), The nature of expertise. Hilsdale, NJ: Lawrence Erlbaum Associates; 311–342. [Google Scholar]
- Liu Z (1999). Perceptual learning in motion discrimination that generalizes across motion directions. Proc Natl Acad Sci U S A, 96(24), 14085–14087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Massey CM, Kellman PJ, Roth Z & Burke T (in press). Perceptual learning and adaptive learning technology: Developing new approaches to mathematics learning in the classroom In Stein NL (Eds), Developmental and learning sciences go to school: Implications for education. [Google Scholar]
- Merzenich MM, Jenkins WM, Johnston P, Schreiner C, Miller SL, et al. (1996). Temporal processing deficits of language-learning impaired children ameliorated by training. Science, 271(5245), 77–81. [DOI] [PubMed] [Google Scholar]
- Mollon JD & Danilova M (1996). Three remarks on perceptual learning. Spat Vis, 10(1), 51–58. [DOI] [PubMed] [Google Scholar]
- National Center for Education Statistics. (2008). The Nation’s Report Card. Retrieved from http://nces.ed.gov/nationsreportcard/.
- Petrov AA, Dosher BA, & Lu ZL (2005). The dynamics of perceptual learning: An incremental reweighting model. Psychological Review, 112(4), 715–743. [DOI] [PubMed] [Google Scholar]
- Reber AS. & Allen R (1978). Analogic and abstraction strategies in synthetic grammar learning: A functionalist interpretation. Cognition, 6(3), 189–221. [Google Scholar]
- Reber AS (1993). Implicit learning and tacit knowledge. New York: Oxford University Press. [Google Scholar]
- Saffran JR, Aslin RN, & Newport EL (1996). Statistical learning by 8-month-old infants. Science, 274 (5294), 1926–8. [DOI] [PubMed] [Google Scholar]
- Reicher GM (1969). Perceptual recognition as a function of meaningfulness of stimulus material. Journal of Experimental Psychology, 81(2), 275–280. [DOI] [PubMed] [Google Scholar]
- Robinson CS, and Hayes JR (1978). Making inferences about relevance in understanding problems In Human Reasoning, Revlin R and Mayer RE, eds. Washington, DC: Winston. [Google Scholar]
- Seitz A, Lefebvre C, Watanabe T & Jolicoeur P (2005). Requirement for high-level processing in subliminal learning. Current Biology, 15(18), 753–755. [DOI] [PubMed] [Google Scholar]
- Seitz A & Watanabe T (2005). A unified model of task-irrelevant and task-relevant perceptual. learning. Trends in Cognitive Science, Vol 9(7) 329–334. [DOI] [PubMed] [Google Scholar]
- Silva AB & Kellman PJ (1999). Perceptual learning in mathematics: The algebra-geometry connection. In Hahn M & Stoness SC (Eds.). Proceedings of the Twenty-First Annual Conference of the Cognitive Science Society, Mahwah, NJ: Lawrence Erlbaum Associates, 683–688. [Google Scholar]
- Simon HA (2001). Observations on the sciences of science learning. Journal of Applied Developmental Psychology, 21, 115–121. [Google Scholar]
- Sireteanu R & Rettenback R (2000). Perceptual learning in visual search generalizes over tasks, locations, and eyes. Vision Research, 40, 2925–2949. [DOI] [PubMed] [Google Scholar]
- Son J, Zucker J, Chang N & Kellman PJ (in preparation). Perceptual learning across multiple representations of mathematical functions. [Google Scholar]
- Tallal P, Merzenich M, Miller S, & Jenkins W (1998). Language learning impairment: Integrating research and remediation. Scandinavian Journal of Psychology, 39(3), 197–199. [DOI] [PubMed] [Google Scholar]
- Wheeler DD (1970). Processes in the visual recognition of words. Dissertation Abstracts International, 31(2-B), 940. [Google Scholar]


