The challenging interpretation of instrumental variable estimates under monotonicity

Abstract

Background

Instrumental variable (IV) methods are often used to identify ‘local’ causal effects in a subgroup of the population of interest. Such ‘local’ effects may not be ideal for informing clinical or policy decision making. When the instrument is non-causal, additional difficulties arise for interpreting ‘local’ effects. Little attention has been paid to these difficulties, even though commonly proposed instruments in epidemiology are non-causal (e.g. proxies for physician’s preference; genetic variants in some Mendelian randomization studies).

Methods

For IV estimates obtained from both causal and non-causal instruments under monotonicity, we present results to help investigators pose four questions about the local effect estimates obtained in their studies. (1) To what subgroup of the population does the effect pertain? Can we (2) estimate the size of or (3) describe the characteristics of this subgroup relative to the study population? (4) Can the sensitivity of the effect estimate to deviations from monotonicity be quantified?

Results

We show that the common interpretations and approaches for answering these four questions are generally only appropriate in the case of causal instruments.

Conclusions

Appropriate interpretation of an IV estimate under monotonicity as a ‘local’ effect critically depends on whether the proposed instrument is causal or non-causal. The results and formal proofs presented here can help in the transparent reporting of IV results and in enhancing the use of IV estimates in informing decision-making efforts.

Key Messages

• Many instrumental variable (IV) effect estimates rely on a monotonicity condition.

• IV effect estimates under monotonicity typically pertain to an unidentifiable subgroup of the study population, not to the entire study population.

• The reporting and interpretation of IV estimates under monotonicity can be improved by presenting additional information on the size and characteristics of this subgroup, and on the sensitivity of estimates to deviations from the monotonicity condition.

• The feasibility of obtaining this information, and its practical utility when obtained, depend crucially on whether the proposed instrument is causal or non-causal.

Introduction

Instrumental variable (IV) methods are being increasingly used to estimate causal effects in observational studies.¹ For example, genetic variants are proposed as instruments in Mendelian randomization studies to estimate the effect of various behavioural and biological exposures, and proxies of physician’s preference are proposed as instruments to estimate the effect of pharmacological treatments.

A critical concern about IV analyses is that the proposed instruments—genetic variants, proxies for physician’s preference—may not be valid instruments. But, even if the proposed instruments were valid, many applications of IV estimation rely on the so-called monotonicity condition.^2,3 Informally, the monotonicity condition means that an instrument cannot increase the exposure or treatment level for some individuals and decrease it for others (formal definitions are provided below and in Textbox 1). In practice, reliance on monotonicity means that the IV effect estimate applies to a subgroup of the study population whose members are unknown. The effect in this unidentifiable subgroup is often referred to as a ‘local’ effect (as opposed to the ‘global’ effect in the full study population).^1,4

Box 1. Definition of the monotonicity condition in three settings.

Setting (a): causal instrument Z

• There are no individuals who would have been treated if their instrument Z were 0 and untreated if their instrument Z were 1 (i.e. no ‘defiers’ defined with respect to Z).

Setting (b): non-causal instrument Z with an unmeasured dichotomous causal instrument U_Z

• There are no individuals who would have been treated if their unmeasured causal instrument U_Z were 0 and untreated if their unmeasured causal instrument U_Z were 1 (i.e. no ‘defiers’ defined with respect to U_Z).

Setting (c): non-causal instrument Z with an unmeasured continuous causal instrument U_Z

• For all individuals in the study population, if individual i would have been treated had U_Z = u, then individual i would also have been treated for any value v such that v > u (i.e. no ‘defiers’ defined with respect to any pair of possible values of U_Z).

Clinical and public health decisions would ideally be guided by estimates of effects in the population or in subgroups defined by individual characteristics (e.g. age, sex). In contrast, the use of ‘local’ effects to guide decision making has some well-established limitations.^4–9 To see these limitations, consider the following thought experiment. Suppose you are told that a certain treatment slightly increases mortality risk in an unidentifiable subgroup of the population, and that members of the subgroup would have a greater mortality risk than the general population if they remained untreated. You will recognize that this information is not ideal to guide policy either for the entire population (perhaps others benefit from treatment) or for the unidentifiable subgroup (it is unknown who exactly is a member). And yet this type of ‘local’ effect is precisely that which is estimated in most IV analyses, even if it is not always made explicit in reporting.^1,10

Although ‘local’ effect estimates are not ideal to guide decision making, their relevance can be greatly increased when accompanied by more information. For example, treatment decisions could be better informed if, in the above thought experiment, you were told that the subgroup comprised 10% of the population, or that members of the subgroup were substantially more likely to be women. Fortunately, such information is obtainable when the proposed instrument causally affects the treatment of interest.^3,11–13 As such, it is generally recommended that investigators explicitly report: (1) the definition of membership in the subgroup; (2) the size of the subgroup; (3) characteristics of the subgroup members; and (4) the sensitivity of the effect estimate under deviations from monotonicity.^1,12,14,15 However, many proposed instruments—some genetic variants, proxies for physician’s preference—do not causally affect the treatment.⁷ This raises the question of whether these four pieces of information can be obtained in those settings.

Here we provide guidance for the reporting of IV analyses under monotonicity with both causal and non-causal instruments. (IV methods that do not require monotonicity^1,16–21 are briefly reviewed in the Supplementary data, available at IJE online.) We do so by helping investigators pose four questions about the local effect estimates obtained in their studies. (1) To what subgroup of the population does the effect pertain? Can we (2) estimate the size of or (3) describe the characteristics of this subgroup? (4) Can the sensitivity of the effect estimate to deviations from monotonicity be quantified? Below we discuss the answers to these questions in settings with both causal and non-causal dichotomous instruments. We start by reviewing the distinction between causal and non-causal instruments.

Causal and non-causal instruments

Suppose we are interested in estimating an effect of a dichotomous treatment or exposure A on a (dichotomous or continuous) outcome Y.Figure 1 (the canonical IV causal diagram) depicts a causal instrument Z which causes treatment, causes the outcome only through treatment, and shares no causes with the outcome.⁷Figure 2 depicts a non-causal instrument Z which is associated with treatment via a shared unmeasured cause that is itself a causal instrument. Figures 1 and 2 represent two of a number of possible ways the instrumental conditions may be satisfied.²²

Figure 1.

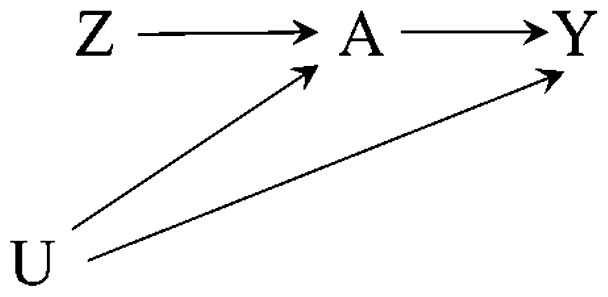
Causal diagram depicting an instrument Z, treatment A, outcome Y and unmeasured confounders U. Z is a causal instrument.

Figure 2.

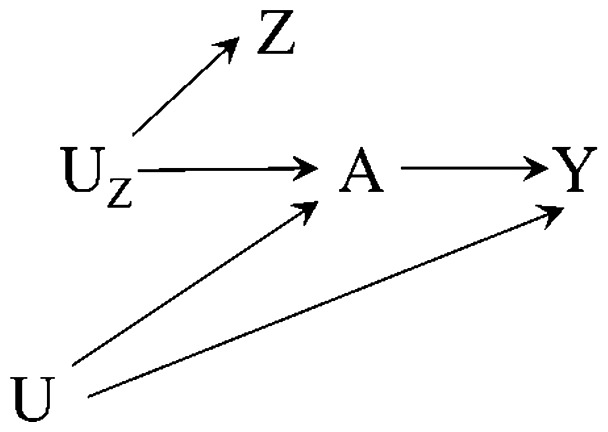
Causal diagram depicting an instrument Z, treatment A, outcome Y and unmeasured confounders U. Z is a non-causal instrument, in which Z and A share a cause U_Z that is itself a causal instrument.

For dichotomous instruments Z, the standard IV ratio:

$$\left(\text{E}\left[Y|Z=\text{1}\right]-\text{E}\left[Y|Z=0\right]\right)/\left(\text{E}\left[A|Z=\text{1}\right]-\text{E}\left[A|Z=0\right]\right)$$

or a similar method, is commonly used to identify a local causal effect under monotonicity. We will consider three settings:

1. a causal instrument Z, e.g. in a Mendelian randomization study, a genetic variant that causes the exposure of interest;

2. a non-causal instrument Z with an unmeasured dichotomous causal instrument U_Z, e.g. in a Mendelian randomization study, a genetic variant, identified from a genome-wide association data, which is associated with but does not cause the exposure;

3. a non-causal instrument Z with an unmeasured continuous causal instrument U_Z, e.g. in a pharmacoepidemiological study, prescription to the previous patient, which is used as a proxy for the unmeasured continuous physician’s preference which causally affects the treatment of interest.

We now explore the answers to questions (1)–(4) in settings (a), (b) and (c). Table 1 summarizes these answers; proofs are provided in the Supplementary data, available at IJE online. For illustration, we provide a numerical example with dichotomous proposed instrument, treatment and outcome that could have arisen under any of the three settings (Table 2). The estimated standard IV ratio is (0.025)/(0.1) = 0.25. That is, if the proposed instrument is valid and monotonicity holds, the risk of the outcome is 25 percentage points higher under treatment than under no treatment. The first question is: to which subset of the population does this causal risk difference apply?

Table 1.

Interpretation of the standard IV ratio under monotonicity in three settings

	Setting (a): measured causal dichotomous instrument	Setting (b): unmeasured causal dichotomous instrument	Setting (c): unmeasured causal continuous instrument
To what subgroup of the population does the effect pertain?	The ‘compliers’ defined with respect to the measured instrumenta	The ‘compliers’ defined with respect to the unmeasured instrumentb	The full study population, with individuals contributing unknown weightb
Can we estimate the size of the subgroup to which the effect pertains?	Yesa	No, unless we make further assumptionse	Superficially (everybody contributes but with unknown weights)
Can we describe (measured) characteristics of the subgroup to which the effect pertains?	Yesc	No, unless we make further assumptionse	N/A
Can we quantify the sensitivity of the effect estimate to deviations from monotonicity?	Yes, via sensitivity analysesa and partial identification strategiesd	Yes, can use sensitivity analyses (if bias parameters are specified for the causal instrument)e	N/A

N/A, not available.

^aSee Angrist, Imbens and Rubin 1996³ and Supplementary data (available at IJE online) for proof.

^bSee Hernán and Robins 2006⁷ and Supplementary data for proof.

^cSee Angrist and Pischke 2009¹¹ and Supplementary data for proof.

^dSee Richardson and Robins 2010¹,³ and Supplementary data for proof.

^eSee Supplementary data for proof.

Table 2.

Hypothetical data for a dichotomous covariate, proposed instrument, treatment and outcome. The proposed instrument can be causal (e.g. a causal genetic variant in a Mendelian randomization study), a non-causal proxy for a dichotomous causal instrument (e.g. a non-causal genetic variant in a Mendelian randomization study) or a non-causal proxy for a continuous causal instrument (e.g. a proxy for physician’s preference)

Number of subjects	Sexa	Proposed instrument	Treatment	Number of subjects who develop the outcome
5000	Male	0	Untreated	500
5000	Male	0	Treated	1000
4500	Male	1	Untreated	500
5500	Male	1	Treated	1000
5500	Female	0	Untreated	500
4500	Female	0	Treated	500
4000	Female	1	Untreated	500
6000	Female	1	Treated	1000

^aSex appears here as a descriptive covariate; it is not necessary for IV estimation.

Question 1: to what subgroup of the population does the effect pertain?

Setting (a): causal instrument Z

In randomized trials with dichotomous instrument and treatment, monotonicity means there are no individuals who would have been treated if they were randomized to no treatment and untreated if they were randomized to treatment (i.e. no ‘defiers’). More generally, monotonicity for setting (a) with a causal instrument Z means there are no individuals who would have been treated if their instrument Z were 0 and untreated if their instrument Z were 1. Under monotonicity, the standard IV ratio identifies the effect in the ‘compliers’, that is individuals who would be treated if their instrument Z were 1 and untreated if their instrument Z were 0.³ The effect in the ‘compliers’ is often referred to as the local average treatment effect or complier average causal effect. Thus, we would interpret our effect estimate as a causal risk difference of 25% among the ‘compliers’ only.

The terminology of ‘compliers’ and ‘defiers’ is widespread in IV analyses of observational studies, even if no true ‘compliers’ or ‘defiers’ exist in the absence of an intervention. In Mendelian randomization with a causal genetic variant measured, the ‘compliers’ are subjects who would have had the phenotype of interest (i.e. been ‘treated’ or exposed) had they had the genetic variant, but would not have had the phenotype had they not had the genetic variant (see formal mathematical expressions in Supplementary data, available at IJE online). For example, for Mendelian randomization studies of the effects of moderate versus low alcohol consumption using variation in the ALDH2 gene (for which the homozygote null variant is associated with adverse symptoms when drinking alcohol), a ‘complier’ is someone who would drink low amounts of alcohol if she had the homozygote null variant but would drink moderate amounts otherwise.^23,24 Informally, ‘compliers’ in Mendelian randomization studies are sometimes conceptualized as subjects for whom their lifestyle and environment are moderate so that their genotype determines their phenotype.

We cannot know whether a particular subject is a ‘complier’. For example, an exposed person with Z = 1 may be either a ‘complier’ or a so-called ‘always-taker’. Similarly, with rare exception,⁵ we cannot verify that there are no ‘defiers’ in our study population: the monotonicity condition is an assumption. In some settings, a deeper biological understanding of how the proposed instrument affects the exposure can help justify the assumption. For example, given the known association between variation in the ALDH2 gene and adverse symptoms when drinking alcohol, it seems plausible that there would be few if any individuals who would drink more alcohol if they did versus did not have the variant associated with the adverse symptoms.

Setting (b): non-causal instrument Z with an unmeasured dichotomous causal instrument U_Z

The standard IV ratio identifies the effect in the ‘compliers’ under monotonicity.⁷ However, monotonicity and compliance types in setting (b) are defined with respect to the unobserved causal instrument U_Z, not the observed surrogate Z. That is, the standard IV ratio identifies the effect in individuals who would be treated if their instrument U_Z were 1 and untreated if their instrument U_Z were 0, under the assumption that there are no individuals who would be treated if their instrument U_Z were 0 and untreated if their instrument U_Z were 1.

In the Mendelian randomization example with a proxy measure for the causal genetic variant, the ‘compliers’ are defined with respect to the unmeasured causal genetic variant and not the measured proxy. If, for example, a Mendelian randomization study using genome-wide association study (GWAS) data proposed a single nucleotide polymorphism (SNP) near the ALDH2 gene region as an instrument, the ‘compliers’ are defined with respect to the causal variation in the ALDH2 genotype and not necessarily the measured SNP. For Mendelian randomization studies that propose several genetic measures as candidate instruments from GWAS data, such designs could be conceptualized as pooling several estimates derived with unique instruments all mirroring setting (b). That is, under monotonicity, such designs are pooling estimates from several unidentifiable yet also potentially different subpopulations.²⁵

Setting (c): Non-causal instrument Z with an unmeasured continuous causal instrument U_Z

Monotonicity is defined as follows when the underlying causal instrument is continuous: if person i would have been treated had U_Z = u, then person i would also have been treated for any value v such that v > u. We will refer to the effect in subjects who would receive treatment when U_Z = u but would not receive treatment when U_Z = v for any value v < u as the u-specific marginal treatment parameter or MTP(u).²⁶ In the context of physician’s preference, if we conceptualize U_Z as the proportion of study subjects that a physician would treat, then MTP(0.4) would be the effect in persons who would have received treatment if they saw any physician who preferred treatment for 40% or more of the study subjects, but would not have received treatment had they seen any physician who preferred treatment at any level less than 40%. (Note: this definition presumes that all physicians with the same level of preference would make the same treatment decisions for all patients, which ignores additional complications of IV estimation under monotonicity when there are multiple versions of the proposed instrument.^4,5)

The standard IV ratio using a dichotomous proxy Z identifies a weighted average of the effects MTP(u) in the subgroups defined by all possible values u.⁷ Because every subject will belong to at least one of these subgroups, the standard IV ratio is estimating an effect that is derived from the full study population, but that is difficult to interpret because of the unknown weight given to each individual. Our effect estimate of 25% is a weighted average of local effects in subgroups, but we do not know the particular weight given to any specific subject.

Generally, all three settings lead to effects within subgroups (or weighted subgroups) that we cannot identify. This leads us to our next question.

Question 2: can we estimate the size of the subgroup to which the effect pertains?

Setting (a): causal instrument Z

If the instrument is valid and monotonicity holds, the proportion of ‘compliers’ is the denominator of the standard IV ratio.³ In our data example, we would estimate that the proportion of ‘compliers’ is 0.10; the causal risk difference in a subset comprising 10% of the study population is 25%.

Setting (b): non-causal instrument Z with an unmeasured dichotomous causal instrument U_Z

The observed data, the instrumental conditions and monotonicity alone do not allow identification of the proportion of ‘compliers’. As we show in the Supplementary data (available at IJE online), identifying this proportion requires quantifying the U_Z-Z association on the additive scale:

$$\text{Pr}\left[U_Z=\text{1}|Z=\text{1}\right]-\text{Pr}\left[U_Z=\text{1}|Z=0\right].$$

In some studies, we may be able to use external information to estimate this association. If, for example, we knew that the association between the unmeasured and measured genetic variants was 80% on the risk difference scale, then we would estimate that the proportion of ‘compliers’ in our example was 0.10/0.80 = 12.5%. (Note that perfect associations, such as what may occur in Mendelian randomization settings with a non-causal genetic variant in perfect linkage disequilibrium with the unmeasured causal variant, would imply that we estimate the same proportion of ‘compliers’ as we would if we had measured the causal instrument itself: 10%.) If we have no information about the magnitude of the U_Z-Z association, but are willing to assume that the correlation is positive, then the proportion of ‘compliers’ can be bounded: e.g. between 10% and 100% in our example.

Setting (c): non-causal instrument Z with an unmeasured continuous causal instrument U_Z

As explained above, the IV ratio identifies a weighted average of effects that would comprise effects from everybody in the study population if our assumptions held.⁷ Note that individual weights are not identifiable and thus interpretability or transportability of this effect is limited. Moreover, even if we did know the weights (e.g. because we had some information on the relationship between U_Z and Z), we do not know to whom each u-specific MTP(u) pertains.

Question 3: can we describe (measured) characteristics of the study population to whom the effect pertains?

Setting (a): causal instrument Z

Though we do not know who is a ‘complier’, under monotonicity we can calculate the prevalence of measured covariates in the ‘compliers’ relative to that in the study population by comparing the denominator of the IV ratio estimated within a level of a covariate with the denominator of the IV ratio estimated unconditionally.^11,12 In our numerical example, the estimated proportion of women among the ‘compliers’ is 75%, whereas the proportion of women in the full study population is 50%.

Setting (b): non-causal instrument Z with an unmeasured dichotomous causal instrument U_Z

The relative distribution of a measured covariate in the ‘compliers’ can be described if the covariate does not modify the relationship between the unmeasured instrument U_Z and the measured instrument Z on the additive scale. In a Mendelian randomization study with a non-causal genetic variant, this condition would hold if the association (e.g. due to linkage disequilibrium) between the measured and unmeasured variants does not vary across levels of the covariate. In our numerical example under this additional assumption, we would estimate the same proportion of women among the ‘compliers’ as we did in setting 1: 75%.

Setting (c): non-causal instrument Z with an unmeasured continuous causal instrument U_Z

Everybody in the study population contributes to the weighted effect estimate, but we do not know each individual’s relative weights and therefore cannot directly describe the characteristics of the weighted population.

Question 4: can we quantify the sensitivity of the effect estimate to deviations from monotonicity?

Setting (a): causal instrument Z

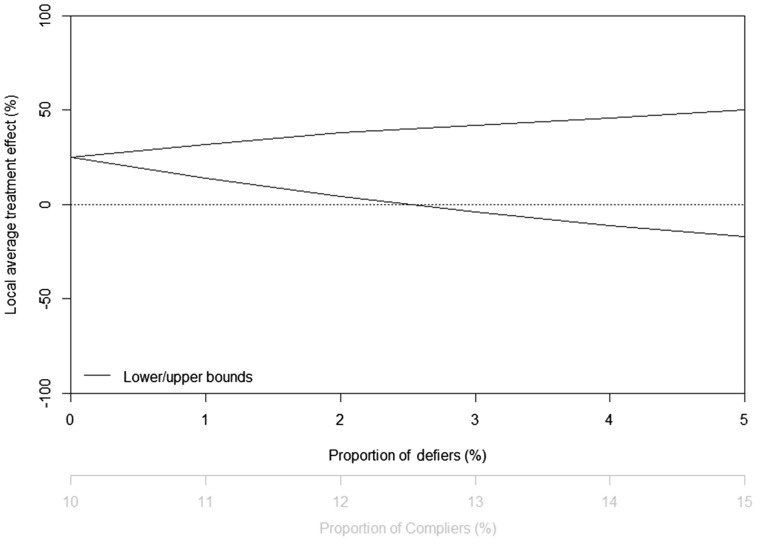
Angrist, Imbens and Rubin³ demonstrated that bias due to a monotonicity violation is a function of the relative proportion of ‘compliers’ and ‘defiers’ and the heterogeneity in the effects between the ‘compliers’ and ‘defiers’, and developed simple bias formulae using these bias parameters. More recent work by Richardson and Robins allows for bounding of the effect in the ‘compliers’ under specified violations of the monotonicity assumption that take into account the observed joint distribution of Z, A and Y.^13,27 For example, if we suspected that the proportion of ‘defiers’ in our data is 1%, then the effect in the ‘compliers’ is bounded between 14% and 32% (i.e. the direction of the effect is still identified, but the magnitude is less clear). In Figure 3, we provide bounds for the effect in the ‘compliers’ under a range of assumed proportions of ‘defiers’ between 0% and 5%.

Figure 3.

Bounds for the effect in the ‘compliers’ (the local average treatment effect) under some departures from monotonicity in setting (a). Note that for a specified proportion of ‘defiers’, the estimated proportion of ‘compliers’ also changes.

In practice, presenting analyses like those shown in Figure 3 can help underscore the robustness (or lack of robustness) of a particular study’s results. In our hypothetical data, our estimate of the direction of the effect in the ‘compliers’ is relatively robust to small monotonicity violations (e.g. a proportion of ‘defiers’ less than 2%). If these data were to come from a Mendelian randomization study in which the biological mechanisms of the genetic variant supported the plausibility of the monotonicity condition, this sensitivity analysis reassures us that theoretically possible but rare departures from monotonicity are unlikely to alter our conclusion that the effect in the ‘compliers’ is positive. (We note the data are theoretically consistent with more ‘defiers’ than 5%, but as a sensitivity analysis for monotonicity violations we restrict Figure 3 to this range.)

Setting (b): non-causal instrument Z with an unmeasured dichotomous causal instrument U_Z

As in setting (a), bias is a function of the relative proportion of and heterogeneity of the effects in ‘compliers’ and ‘defiers’, which are defined in setting (b) with respect to U_Z, not Z. This distinction may be important if we can use subject matter expertise or external data⁵ to inform the bias parameters in a sensitivity analysis. For example, when computing the potential bias in a Mendelian randomization study, the plausible distribution of compliance types ought to be informed by knowledge about the underlying causal genetic variant (U_Z) rather than the measured non-causal genetic variant (Z) used in the IV analysis.

Unlike in setting (a), we cannot apply bounds vis-à-vis Richardson and Robins¹³ because we do not observe the joint distribution of U_Z, A and Y. Thus in this setting, if we suspected that the proportion of ‘defiers’ in our data is 5%, we would need to further specify the effect in the ‘defiers’ to estimate the bias or a bias-corrected effect estimate in the ‘compliers’. If the correlation between the measured non-causal genetic variant and the underlying causal genetic variant was very strong (i.e. Pr[U_Z = 1|Z = 1]−Pr[U_Z = 1|Z = 0] very close to 1), we might consider applying bounds assuming our observed joint distribution of Z, A and Y closely approximates the joint distribution of U_Z, A and Y.

Setting (c): non-causal instrument Z with an unmeasured continuous causal instrument U_Z

Understanding bias due to a monotonicity violation in setting (c) is not straightforward. Consider first bias in approaches for identifying the MTP(u) for a specific level of U_Z = u if we had data on U_Z. When monotonicity does not hold, the partial derivative will be a function of the treatment effects in all subjects for whom treatment would be different had U_Z = u versus a value just below u (assuming this is smooth enough to even be differentiable). It is unclear if we should–or could–separate out the MTP(u) from these other subgroup treatment effects to derive a usable bias formula. In setting (c) where U_Z is not measured, trying to consider a bias formula for the weighted average of treatment effects would be even more convoluted.

Discussion

We have described improvements to the reporting of IV estimates under monotonicity by presenting four additional pieces of information. We have explained that the feasibility of obtaining this information, and its practical utility when obtained, depend crucially on whether the proposed instrument is causal or non-causal.

Because the distinction between causal and non-causal instruments is only rarely made in the IV methodology literature, let alone in reporting IV applications, consumers of IV analyses are not typically provided with enough information to interpret the effect estimates. Interestingly, although some have argued that causal diagrams provide little of value to IV methods because ‘the’ causal diagram is relatively simple,²⁸ the distinction between causal and non-causal instruments illustrates another example of how causal diagrams can be useful tools for responsible application and interpretation of IV analyses.²⁹ To demonstrate how accurate reporting would be carried out under different settings, we consider possible reports for a hypothetical Mendelian randomization study in Textbox 2.

Box 2. Interpretation of Mendelian randomization results under monotonicity

Suppose we conducted a Mendelian randomization study of the effect of alcohol use on risk of diabetes, and we are reasonably confident that the instrumental conditions hold. An IV analysis of our data (summarized in Table 2) yielded an effect estimate of 25 more diabetes cases per 100 individuals if they had consumed moderate amounts of alcohol versus if they had consumed low amounts of alcohol. Because we believe there is substantial heterogeneity in how alcohol may affect diabetes risk across individuals in our study, we conducted the IV analysis under the monotonicity assumption. To whom does our effect estimate apply?

The answer depends on whether our proposed instrument is causal. Let us discuss three possibilities:

• Our IV analysis was based on a well-established variation in the ALDH2 gene which it is reasonable to consider as a causal genetic variant. Then our effect estimate pertains to a subgroup of study participants whose alcohol use would have been moderate if they had the high-risk variant but low otherwise. Whereas we cannot be sure who belongs to this subgroup, its members comprise 10% of the original study population and are more likely to be female. Our estimates are relatively robust to violations of monotonicity (Figure 3).

• Our IV analysis was based on a genetic variant measured near the ALDH2 gene, likely in linkage disequilibrium with the causal variant but not itself causal. Then our effect estimate pertains to a subgroup of study participants whose alcohol use would have been moderate if they had the high-risk (unmeasured) ALDH2 variant but low otherwise. We cannot be sure who belongs to this subgroup, and are not able to describe them further at this stage. However, we plan to conduct a follow-up study that further measures the ALDH2 variant to better describe the size and characteristics of this subgroup, and the robustness of our estimates to violations of monotonicity.

• Our IV analysis was based on a newly discovered genetic variant from a recent GWAS on alcohol use, but we have no further information regarding the mechanisms by which the association between this variant and alcohol consumption arises. Then our effect estimate pertains to a subgroup of study participants whose size and characteristics we cannot define. Also, we do not know the robustness of our estimate to violations of monotonicity.

A common limitation of both causal and non-causal instruments is that IV estimation under monotonicity can only estimate ‘local’ effects in an unknown subset of the population. A typical argument in defence of ‘local’ effects is that the ability to describe the proportion of and distribution of measured characteristics in the subpopulation of ‘compliers’ dispels the concerns of identifying effects in unidentifiable subgroups. That is, whereas an effect estimate may only pertain to a subset (e.g. 10%) of the population, sometimes we can describe that 10% to such a degree that we can nearly (but not perfectly) target our decision-making efforts toward that subpopulation. Regardless of whether one agrees that this mitigating factor is enough to justify using such estimates to inform decision making, we have demonstrated that this rationale is often less appropriate for non-causal instruments. Whenever a non-causal instrument is proposed, it will usually be difficult, if not impossible, to describe the subpopulation to which the effect pertains with an informative level of detail. Although our focus has been on settings with dichotomous proposed instruments, interpretability of ‘local’ effects is generally even more complex for categorical (e.g. trichotomous) or continuous instruments, like those used in some Mendelian randomization studies.

An additional complication for IV estimation under monotonicity is that, in the absence of physical randomization, it is impossible to ensure that the proposed instrument is causal versus non-causal. For example, given the widespread use of genome-wide association studies to inform instrument proposals, most Mendelian randomization studies may be conceptualized as proposing non-causal instruments. However, even in those Mendelian randomization studies that propose a causal instrument, there is no guarantee that the instrument is indeed causal–a lack of guarantee underscored by recent findings demonstrating that previously classified ‘causal’ genetic variants for rare disorders are so prevalent that their classification as ‘causal’ is now being questioned.³⁰

Given the problems enumerated here and elsewhere,^5,8,9,18 some investigators may argue that this is a reason to completely avoid IV methods based on a monotonicity condition in Mendelian randomization or other observational studies. We suggest that the appropriateness of IV methods under monotonicity should be evaluated on a case-by-case basis. The results and formal proofs presented here can help in the transparent reporting of IV results, and in enhancing the appropriate and effective use of IV estimates in informing decision-making efforts.

Funding

This work was partly supported by the National Institutes of Health [R01 AI102634]. S.S. is supported by a DynaHEALTH grant (European Union H2020-PHC-2014; 633595).

Conflicts of interest: None declared.