Pleiotropy-robust Mendelian randomization

Abstract

Background

The potential of Mendelian randomization studies is rapidly expanding due to: (i) the growing power of genome-wide association study (GWAS) meta-analyses to detect genetic variants associated with several exposures; and (ii) the increasing availability of these genetic variants in large-scale surveys. However, without a proper biological understanding of the pleiotropic working of genetic variants, a fundamental assumption of Mendelian randomization (the exclusion restriction) can always be contested.

Methods

We build upon and synthesize recent advances in the literature on instrumental variables (IVs) estimation that test and relax the exclusion restriction. Our pleiotropy-robust Mendelian randomization (PRMR) method first estimates the degree of pleiotropy, and in turn corrects for it. If (i) a subsample exists for which the genetic variants do not affect the exposure; (ii) the selection into this subsample is not a joint consequence of the IV and the outcome; (iii) pleiotropic effects are homogeneous, PRMR obtains unbiased estimates of causal effects.

Results

Simulations show that existing MR methods produce biased estimators for realistic forms of pleiotropy. Under the aforementioned assumptions, PRMR produces unbiased estimators. We illustrate the practical use of PRMR by estimating the causal effect of: (i) tobacco exposure on body mass index (BMI); (ii) prostate cancer on self-reported health; and (iii) educational attainment on BMI in the UK Biobank data.

Conclusions

PRMR allows for instrumental variables that violate the exclusion restriction due to pleiotropy, and it corrects for pleiotropy in the estimation of the causal effect. If the degree of pleiotropy is unknown, PRMR can still be used as a sensitivity analysis.

Key Messages

• If genetic variants have pleiotropic effects, causal estimates of Mendelian randomization studies may be biased.

• Pleiotropy-robust Mendelian randomization (PRMR) produces unbiased causal estimates if: (i) a subsample can be identified for which the genetic variants do not affect the exposure; (ii) the selection into this subsample is not a joint consequence of the genetic variants and the outcome; and (iii) pleiotropic effects are homogeneous.

• If such a subsample does not exist, PRMR can still routinely be reported as a sensitivity analysis in any MR analysis.

• If pleiotropic effects are not homogeneous, PRMR can be used as an informal test to gauge the exclusion restriction.

Introduction

Establishing causal effects of treatments or exposures on behavioural and disease outcomes is of great public health importance.¹ The practice of ‘Mendelian randomization’ (MR) uses genetic variants as instrumental variables (IVs) for a certain modifiable exposure in order to estimate the causal effect of that exposure on a certain disease or other outcome.^2,3 This method has the potential to overcome the traditional biases due to confounding and reverse causality that plague observational studies.⁴ The past decade has seen increasing interest in MR,^4–7 and its potential is rapidly developing through the increasing number of genome-wide association studies (GWAS) that find robust associations between genetic variants and exposures of interest.^8,9

The assumptions of MR have been discussed extensively^2,10,11–13 and the advantages and disadvantages of MR are heavily debated.^14,15 Recently there has been much progress in dealing with the disadvantages of MR, yet the critical assumption remains the exclusion restriction: the proposed IV (genetic variant) should not directly affect the outcome.^14,15 Whereas this assumption can be contested in any IV approach, the assumption is even more critical in the context of MR, since the biological working of genes is usually poorly understood.^13,16

In particular, more and more studies show how the same genetic variant affects multiple outcomes through different biological pathways, a phenomenon known as biological (or horizontal) pleiotropy,¹⁷ and this violates the exclusion restriction. In contrast, mediated (or vertical) pleiotropy, in which a genetic variant is associated with a certain phenotype and this phenotype is causal for a second phenotype, is not problematic if one knows what is the primary phenotype.⁴ Therefore, we will only focus on biological pleiotropy, for brevity ‘‘pleiotropy’ from here.

In response to the possible problem of pleiotropy, a couple of MR approaches have been proposed. Davey Smith and Hemani suggest using multiple genetic variants consecutively as IVs, and argue that it is increasingly unlikely that 2, 3 or 4 different genetic variants produce the same estimate of the causal effect.⁴ Although an appealing argument, this approach still hinges critically on the assumption that at least some of the genetic variants do not violate the exclusion restriction. Moreover, this informal test cannot discriminate between violations of the exclusion restriction and heterogeneous causal effects different genetic variants will also produce different causal effects - if they affect different subgroups of the population, and these subgroups respond differently to the exposure.¹⁸ Kang et al. propose a method that produces valid estimates if at least 50% of the combined instrument strength across all variants originates from variants that satisfy the exclusion restriction.¹⁹ Whereas this is helpful, it is generally not possible to distinguish the valid IVs from the invalid IVs if the estimates based on different sets of IVs diverge.²⁰ Moreover this approach, like the weighted median estimator,²¹ still requires some of the genetic variants to satisfy the exclusion restriction.

Bowden et al. propose to apply the established method of Egger regression to the set of Mendelian randomization estimates (‘MR-Egger’).²⁰ The idea is that a violation of the exclusion restriction leads to a bias of the MR estimate that is inversely proportional to the first-stage coefficient of the IV on the exposure. Under the assumption that, across all genetic variants, the covariance between the effect of the IV on the outcome and the effect of the IV on the exposure is zero (‘InSIDE assumption’), IVs with a stronger effect on the exposure should give less-biased MR estimates. A regression of the MR estimates on the first stage coefficients including an intercept then provides a consistent estimate of the causal effect. As acknowledged by the authors, the InSIDE assumption cannot be tested and may not hold if the genetic variants used as IVs are correlated with confounders of the association between exposure and outcome. Moreover, in one-sample settings, MR-Egger may suffer heavily from weak instrument bias.^20,22

In this paper we build upon and combine two recent advances in the literature on IV estimation, which test and relax the exclusion restriction. We introduce the ‘plausibly exogenous’ method²³ in MR research to account for pleiotropy. Two studies have previously noticed the possibility of applying this method as a sensitivity analysis in the context of MR,^12,24 but no guidance is given on how to choose the essential input parameters. Our innovation is that we combine this method with another stream of research that designs auxiliary regressions to test for violations of the exclusion restriction.^25–30 The intuition is that in a subsample for which the first stage (that is, the effect of the IV on the exposure) is zero, the reduced form (that is, the effect of the IV on the outcome) should be zero too if the exclusion restriction is satisfied. Whereas this is traditionally used merely as a test of the exclusion restriction, there is no earlier notion that the reduced-form estimate obtained in this subsample is exactly the input required for the ‘plausibly exogenous’ method. We term the synthesis of these techniques ‘pleiotropy-robust Mendelian randomization’ (PRMR).

Simulation results show that if a subsample exists for which the first stage is zero, and the pleiotropic effects are homogeneous, it is possible to obtain unbiased estimates of causal effects using PRMR, even when all genetic instruments violate the exclusion restriction. We empirically illustrate our method by estimating the effect of: (i) tobacco exposure on body mass index (BMI); (ii) prostate cancer on subjective health evaluations; and (iii) educational attainment on BMI.

Methods

Mendelian randomization

In the general case, one is interested in the causal effect β of a certain exposure X on an outcome Y. The idea of MR is that there is a vector of genetic variants G (usually single nucleotide polymorphisms (SNPs), an allele score or polygenic score) that is known to be correlated with the exposure X, but is assumed to be uncorrelated with other (unobserved) determinants of the outcome Y. Consider the equations (we follow the notation of Bowden et al.²⁰ in matrix notation here):

$$Y=X\beta +G\alpha +{\epsilon }^Y$$ (1)

$$X=G\gamma +{\epsilon }^X$$ (2)

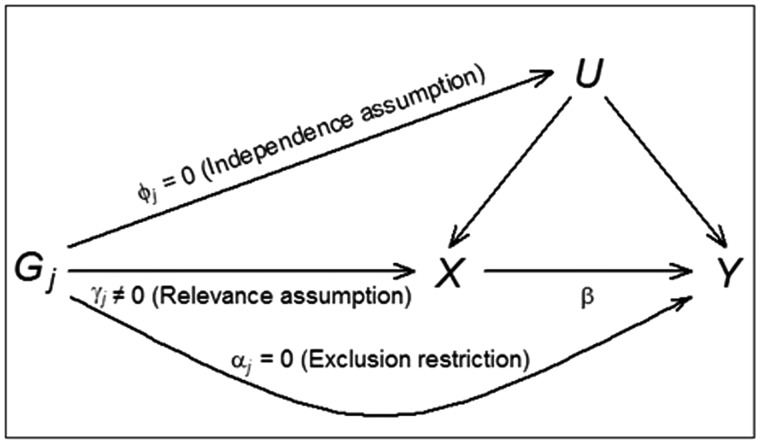
where Y is a (N × 1) vector of outcomes, X is a (N × 1) vector of exposures, G is a (N × r) matrix of r ≥ 1 genetic variants, the causal effect β is a scalar, the pleiotropic effect α and first-stage effect γ are (r × 1) vectors, ${\epsilon }^Y$and ${\epsilon }^X$ are (N × 1) composite error terms including unobserved confounders U and N denotes the sample size. The assumptions of MR are as follows (see Figure 1 for a graphical exposition).^12,13,16

Figure 1.

Illustrative diagram showing the standard MR model with its assumptions. The genetic effect of instrumental variable G_j on exposure X is γ_j; the genetic effect on unobserved confounder U is φ_j; the direct genetic effect on the outcome Y is α_j; and the causal effect of the exposure X on the outcome Y is β.

1. Relevance: the genetic variants G have an effect on the exposure X: γ ≠ 0.

2. Independence: the genetic variants G are uncorrelated with any confounders of the exposure-outcome relationship.

3. Exclusion restriction: the genetic variants G affect the outcome Y only through the exposure X: α = 0.

The use of genetic variants as IVs has at least two very attractive properties. First, publicly available GWAS results make it relatively straightforward to select genetic variants G for which γ ≠ 0, i.e. genetic variants that are robustly associated with the exposure of interest. Second, given that genetic variants are randomly distributed at conception, conditional on population stratification variables or, more stringent, parental genotype or family fixed effects, the independence assumption holds.³¹

The exclusion restriction is widely acknowledged as the most problematic assumption of MR.^14,15 In particular, the existence of pleiotropy would lead to a violation of the exclusion restriction, and α ≠ 0 in equation (1). In traditional MR it is assumed however that α is equal to 0, which leads to biased estimates of β, the causal effect of interest, if pleiotropy is present. Moreover, this bias gets amplified by the typically low explanatory power of the genetic variants for the exposure.³²

Pleiotropy-robust Mendelian randomization

In the ‘plausibly exogenous’ method,²³ the assumption that α = 0 is relaxed and replaced by a user-specified assumption on the plausible value, range or distribution of α. When the prior on α follows a Normal distribution with mean ${\mu }_{\alpha }$ and variance ${\Omega }_{\alpha }$, and the uncertainty about α reduces with the sample size (i.e. ‘local-to-zero’), then the estimate of the causal effect β in equation (1) is given by:

$$\widehat{\beta }\sim N(\beta +A{\mu }_{\alpha },V_{MR}+A{\Omega }_{\alpha }{A}^{\prime })$$ (3)

where N() indicates the Normal distribution, $A={(X^{\prime }G{(G^{\prime }G)}^{-1}{G}^{\prime }X)}^{-1}(X^{\prime }G)$, and β and V_MR are the traditional MR point estimate and variance-covariance matrix, respectively. Although the plausibly exogenous method can deal with any other prior distribution of α (see Conley et al.²³ for details), it gives no guidance on how to obtain a plausible value, range or distribution of α.

We can, however, estimate the value of α if there is a population subgroup for which the first stage is known to be zero. A recent stream of research emphasizes the identification of these subgroups to test the exclusion restriction.^25–30 An early example is Altonji et al. (2005),²⁵ who investigate the validity of the instrument ‘being Catholic’ to study the effect of attending a Catholic high school on a wide variety of outcomes. They identify a subsample of public eighth graders among whom practically nobody subsequently attends a Catholic high school. Hence among this subsample the first stage is zero, and any association between the IV (being Catholic) and the outcome reflects a direct effect, indicating a violation of the exclusion restriction. In the MR literature, the procedure bears similarities to the negative controls approach.³³ Davey Smith and colleagues^28–30 have used Asian women and never-drinkers, subsamples for which the first stage effect of genetic variants on alcohol consumption is (close to) zero, to validate their exclusion restriction.

This strategy is so far mainly used as a test of the exclusion restriction—only work-in-progress by Slichter³⁴ provides an alternative way of using subsamples with (close to) zero first stage effects to bound and estimate the causal effect of interest. Our innovation is using the result of this auxiliary regression as input for the ‘plausibly exogenous’ method. Hence, even if the exclusion restriction is found to be violated, the IV can still be used in the analysis.

Consider the reduced form equation that is obtained by substituting (2) into (1):

$$Y=G(\alpha +\beta \gamma )+({\epsilon }^Y+\beta {\epsilon }^X)$$ (4)

In a (sub)sample for which the first stage is zero (γ = 0), the reduced form coefficient of the genetic variant is an estimator for α. Practically, we suggest first estimating the reduced form (4) in a subsample for which γ = 0, to obtain estimates ${\mu }_{\alpha }=\widehat{\alpha }$ and ${\Omega }_{\alpha }$ equal to the squared standard error of $\widehat{\alpha }$. Thereafter, plug ${\mu }_{\alpha }$ and ${\Omega }_{\alpha }$ into the plausibly exogenous equation (3), to obtain estimates of the causal effect of interest $\beta$. The estimator is easy to obtain in standard software. For example, the user-written command ‘plausexog’ is readily available in STATA.³⁵

Assumptions PRMR

Apart from the requirement that a subsample exists for which the first stage is zero, PRMR has two key assumptions. First, PRMR assumes homogeneous pleiotropic effects, defined as an equal average pleiotropic effect of the genetic variants (or allele/polygenic score) in the two subsamples. Homogeneity is satisfied if the pleiotropic effects are the same for each individual, but also when the pleiotropic effects stem from a distribution with the same mean across the two subsamples. The second assumption is that the selection into the subgroup for which the first stage is zero is not driven by the genetic variants and the outcome. Violation of this second assumption would introduce collider bias.^16,36–38

The plausibly exogenous method has been originally developed for continuous outcomes, but it is also valid for binary outcomes under the monotonicity assumption (the instrument may have no effect on some people; all of those who are affected are affected in the same way), and in as far one is willing to estimate linear probability models for binary outcomes.³⁹

Simulation

We present a simulation study to illustrate the performance of regular MR through two-stage least squares (2SLS), the inverse variance weighting (IVW) method⁴⁰, MR-Egger regression and PRMR. Following Bowden et al. (2015),²⁰ we consider the following four scenarios with varying violations of the MR assumptions (see the Appendix for more details, available as Supplementary data at IJE online)):

1. no pleiotropy;

2. balanced pleiotropy, InSIDE satisfied (α parameters take positive and negative values, but are independent of the first stage parameters γ);

3. directional pleiotropy, InSIDE satisfied (α parameters take only positive values, but are independent of the first stage parameters γ);

4. directional pleiotropy, InSIDE not satisfied (α parameters take only positive values and are correlated with the first stage parameters γ).

As in Bowden et al. (2015), we assume that all of the SNPs violate the exclusion restriction in scenarios 2-4, and so we do not consider methods that require at least 50% of the SNPs to be valid. In all scenarios, we use: a sample size of 1000; 10 000 simulation runs; 25 genetic variants with minor allele frequency 0.30; and a causal effect β of 0.00 and 0.05. Statistical power is evaluated at a false-positive rate of 5%.

The simulation results in Table 1 show that, in a one sample setting, 2SLS and IVW produce very similar results, and that all methods give average estimates of β (almost) equal to the true value in the absence of pleiotropy and if pleiotropy is balanced. With directional pleiotropy (both when InSIDE is satisfied and when violated), the average estimates are biased away from the true value for 2SLS and IVW. MR-Egger performs slightly better, but still produces biased estimates. The results show that PRMR is able to produce unbiased estimates in all scenarios if the nature of pleiotropy is exactly known. Note however that the standard errors are artificially low because we assume in these simulations that there is no uncertainty regarding the pleiotropic effect.

Table 1.

Performance of two-stage-least-squares (2SLS), inverse-variance weighting (IVW), MR-Egger regression and PRMR in simulation study for one-sample Mendelian randomization with a null (β = 0.00) and a positive (β = 0.05) causal effect

		2SLS		IVW		MR-Egger		PRMR
Scenario	Mean F	Mean	Power	Mean	Power	Mean	Power	Mean	Power
β = 0.00
1: No pleiotropy, InSIDE satisfied	38.6	0.00 (0.01)	0.05	0.00 (0.01)	0.04	0.00 (0.03)	0.04	0.00 (0.01)	0.05
2: Balanced pleiotropy, InSIDE satisfied	38.6	0.00 (0.01)	0.14	0.00 (0.01)	0.06	0.01 (0.03)	0.06	0.00 (0.01)	0.05
3: Directional pleiotropy, InSIDE satisfied	38.6	0.04 (0.01)	0.92	0.04 (0.01)	0.85	0.01 (0.03)	0.06	0.00 (0.01)	0.06
4: Directional pleiotropy, InSIDE violated	39.3	0.13 (0.01)	1.00	0.13 (0.02)	1.00	0.04 (0.04)	0.18	0.00 (0.01)	0.06
β = 0.05
1: No pleiotropy, InSIDE satisfied	38.6	0.05 (0.01)	0.99	0.05 (0.01)	0.98	0.06 (0.03)	0.48	0.05 (0.01)	0.99
2: Balanced pleiotropy, InSIDE satisfied	38.6	0.05 (0.01)	0.97	0.05 (0.01)	0.91	0.06 (0.03)	0.36	0.05 (0.01)	0.99
3: Directional pleiotropy, InSIDE satisfied	38.6	0.09 (0.01)	1.00	0.09 (0.01)	1.00	0.06 (0.03)	0.52	0.05 (0.01)	0.99
4: Directional pleiotropy, InSIDE violated	39.3	0.18 (0.01)	1.00	0.18 (0.02)	1.00	0.09 (0.04)	0.60	0.05 (0.01)	1.00

Deviations from homogeneous pleiotropic effects, and non-zero first-stage coefficients in the subsample for which the first stage is expected to be zero, would produce biased estimates for α, and in turn the causal effect β. Note that both deviations produce a similar bias in the reduced form coefficient of equation (4), and since it is straightforward to test for a zero first stage coefficient, we only investigate the sensitivity of PRMR towards violations of homogeneous pleiotropy. Specifically, we re-run the above simulations of scenario 4 (InSIDE not satisfied), but now estimate the pleiotropic effect in a separately created sample of 250, 500 or 1000 individuals in which the pleiotropic effect deviates from the main sample by a factor ξ, i.e. α_{j,second-sample} = ξ × α_{j,main-sample}. We vary ξ from 0.5 to 1.5, which is equivalent to the pleiotropic effect in the second sample being 50% lower to 50% higher than the pleiotropic effect in the main sample.

If pleiotropy is homogeneous (ξ = 1), Table 2 shows that PRMR produces unbiased estimators, although the power is a little lower than in Table 1 because now we incorporate the uncertainty around the pleiotropy parameter. As expected, power to detect a causal effect becomes smaller for a reduced subsample in which the direct effect is estimated. If ξ < 1 (ξ > 1), PRMR overestimates (underestimates) the causal effect, but the 95% confidence interval (CI) still includes the true value. We conclude that PRMR is biased when pleiotropy is non-homogeneous, but that even 50% deviations from homogeneous pleiotropy produce a bias that is relatively modest compared with traditional methods like 2SLS, IVW and MR-Egger (compare Table 2 with Table 1, scenario 4).

Table 2.

Performance of PRMR in simulation study for one-sample Mendelian randomization with a null (β = 0.00) and a positive (β = 0.05) causal effect in a setting (scenario 4) of directional pleiotropy (InSIDE violated). ξ represent the multiplication factor for the direct effect in the second sample of size N₂

	PRMR (N2 = 250)		PRMR (N2 = 500)		PRMR (N2= 1,000)
Scenario	Mean	Power	Mean	Power	Mean	Power
β = 0.00
ξ = 0.50	0.02 (0.02)	0.08	0.02 (0.02)	0.10	0.02 (0.01)	0.26
ξ = 0.75	0.01 (0.02)	0.04	0.01 (0.02)	0.03	0.01 (0.02)	0.11
ξ = 1.00	0.00 (0.02)	0.03	0.00 (0.02)	0.02	0.00 (0.02)	0.06
ξ = 1.25	−0.01 (0.02)	0.06	−0.01 (0.02)	0.05	−0.01 (0.02)	0.09
ξ = 1.50	−0.02 (0.02)	0.10	−0.02 (0.02)	0.14	−0.02 (0.02)	0.19
β = 0.05
ξ = 0.50	0.06 (0.02)	0.72	0.06 (0.02)	0.95	0.06 (0.02)	0.98
ξ = 0.75	0.05 (0.02)	0.58	0.05 (0.02)	0.86	0.06 (0.02)	0.94
ξ = 1.00	0.04 (0.03)	0.43	0.04 (0.02)	0.70	0.05 (0.02)	0.85
ξ = 1.25	0.03 (0.03)	0.29	0.03 (0.02)	0.48	0.04 (0.02)	0.69
ξ = 1.50	0.03 (0.03)	0.18	0.03 (0.02)	0.27	0.03 (0.02)	0.49

Examples

To illustrate our approach, we exploit genetic data from the interim release of the UK Biobank⁴¹ to study: (i) the effect of tobacco exposure on BMI; (ii) the effect of prostate cancer on subjective health evaluations; and (iii) the effect of educational attainment on BMI. Following recommendations from the genotyping centre, we restrict the analyses in the UK Biobank to 112 338 (52, 53% female) conventionally unrelated individuals with ‘White British’ ancestry.⁴² We use the first 15 principal components (PCs) of the genetic relatedness matrix as provided by UK Biobank to further control for population stratification.^42,43 All individuals are born between 1934 and 1970. Imputed SNPs are converted to best-guess values, and for individuals with missing information on a specific SNP we impute the mean genotype from the sample. For all measures, we use reported values from the first interview round. A summary of the results of the exemplary analyses is presented in Table 3.

Table 3.

Summary of the regression results for the three exemplary analyses. The 95% confidence intervals are reported between parentheses

	Effect of tobacco exposure on BMI	Effect of prostate cancer on self-reported health	Effect of educational attainment on BMI
OLS	0.05 (0.04 – 0.06)	−0.17 (−0.22 – −0.12)	−0.11 (−0.11 – −0.10)
	P = 1.90 × 10−17	P = 9.17 × 10−11	P = 9.20 × 10−308
First stage effect	0.64 (0.49 – 0.80)	0.00 (0.00 – 0.00)	0.36 (0.33 – 0.39)
	P = 3.64 × 10−16	P = 2.45 × 10−3	P = 4.10 × 10−122
Pleiotropic effect	0.01 (−0.02 – 0.05)	−0.01 (−0.02 – 0.00)	λ ×
	P = 0.44	P = 1.81 × 10−3	First stage effect
2SLS	−0.24 (−0.40 – −0.08)	−1.26 (−5.26 – 2.75)	−0.39 (−0.47 – −0.31)
	P = 3.50 × 10−3	P = 0.54	P = 9.63 × 10−21
PRMR	−0.26 (−0.43 – −0.09)	4.51 (−0.89 – 9.91)	Depends on λ
	P = 2.70 × 10−3	P = 0.10	See Figure 2

The effect of tobacco exposure on BMI

The relationship between smoking and BMI has received considerable attention in the literature^44–48, and from these studies Wehby et al. (2012)⁴⁷ used MR to assess the causal effect of tobacco exposure on BMI. In existing GWAS, the SNPs that are robustly associated with smoking measures can mostly be traced back to nicotine dependence.⁴⁹ This provides a context to apply PRMR: after all, the development of nicotine dependence requires initiating smoking in the first place. Hence, the group of never smokers provides a subsample among whom the SNPs do not have an effect on tobacco exposure, and we can use this subsample to estimate the direct effect of the SNPs on the outcome measure BMI.

We use standardized values of rs12914385 as an instrument, the SNP with the strongest statistical association with the number of cigarettes smoked per day (CPD) from the only locus found to be associated with CPD in the GWAS from the Tobacco and Genetic Consortium.⁵⁰ CPD is measured as number of cigarettes currently smoked per day, and BMI is measured in kg/m². Ordinary least-squares (OLS) regression suggest a positive association between CPD and BMI (0.05, P = 1.90 × 10⁻¹⁷). The first stage regression of CPD on the SNP shows a strong positive association (P = 3.64 × 10⁻¹⁶, F = 66.47). Among never smokers, the SNP has a very modest positive association with BMI (0.01, P = 0.44). In contrast, among current smokers, there is a strong negative association with BMI (-0.16, P = 8.49 × 10⁻⁵). This provides evidence that the exclusion restriction is satisfied, and regular MR can be applied. The 2SLS results indicate a negative causal effect of tobacco exposure on BMI (−0.24, P = 3.50 × 10⁻³), suggesting an effect of tobacco exposure on BMI in the opposite direction of the OLS estimate. For comparison, PRMR provides an estimate of -0.26 (P = 2.70 × 10⁻³).

The exact point estimates in this example should be interpreted with caution, since the measured exposure CPD may not capture all dimensions through which the genetic variant affects tobacco exposure (e.g. serum cotinine levels).^51,52 Moreover, if among smokers the genetic variants affect both CPD and another smoking dimension (e.g. depth of inhaling), then the pleiotropic effect estimated in the group of never smokers would not provide an accurate estimate of the pleiotropic effect in the group of smokers.

The effect of prostate cancer on self-reported health

Earlier studies have reported on the effect of (prostate) cancer on health outcomes,^53–55 yet none of these studies used Mendelian randomization. Al Olama et al. (2014)⁵⁶ find 12 autosomal SNPs to be related to prostate cancer at genome-wide significance level among individuals from European descent. Since prostate cancer naturally is only a risk factor among males, the first stage (that is, the effect of genetic variants on prostate cancer) among females is zero. As a result, if the genetic variants are only associated with prostate cancer and not with any other male-specific determinant (e.g. impotence) of the outcome, the effect of these genetic variants on a certain outcome among females may be used as a reasonable estimate for α.

UK Biobank contains a self-report about whether a person was diagnosed by a doctor to have prostate cancer (1) or not (0). Subjective health is measured on a four-point scale ranging from excellent (4), via good (3) and fair (2) to poor (1). We build an allele score for prostate cancer using the results from the GWAS on prostate cancer,⁵⁶ since the allele score has more power than using the individual SNPs;^57–59 10 out of the 12 SNPs are available in the genetic data of UK Biobank. The allele score has been standardized to have mean 0 and standard deviation 1.

An OLS regression of subjective health on prostate cancer among males reveals that prostate cancer is negatively associated with subjective health (−0.17, P = 9.17 × 10⁻¹¹), and a regression of prostate cancer on the allele score shows that the allele score is positively associated with prostate cancer (P = 2.45 × 10⁻³, F = 9.21). A standard 2SLS regression with the allele score as instrument for prostate cancer produces a large negative effect of prostate cancer on subjective health (-1.26), but P = 0.54.

Using PRMR, we find that the allele score is negatively associated with subjective health among females (−0.009, P = 1.81 × 10⁻³), and this reduced form estimate is even larger in absolute terms than among males (−0.002, P = 0.53). This suggests that the exclusion restriction is violated and that the MR results are biased. When we plug in the reduced form estimate among females in the plausibly exogenous method, we find that the effect of prostate cancer on subjective health is estimated to be positive (4.51) among males, but this estimate is implausibly large and surrounded by a large 95% confidence interval (−0.89 to 9.91, P = 0.10). Hence, we cannot reject a zero effect of prostate cancer on self-reported health.

The effect of educational attainment on BMI

The education-health gradient is well documented and one of the most robust findings in social science.^60,61 Several studies reported before on the causal effect of educational attainment on BMI, with mixed findings, and apart from one study investigating the reverse effect of BMI on educational attainment,⁶² none of them used Mendelian randomization.^63–68

Educational attainment (EA) is constructed as years of education, as in the recent Educational Attainment GWAS (the UK Biobank data is used as out-of-sample replication sample in that study).⁶⁹ For educational attainment, we build an allele score from the 74 SNPs found to be associated with EA.⁶⁹ Of these 74 SNPs, 72 are available in UK Biobank.

An OLS regression of BMI on EA reveals that EA is negatively associated with BMI (−0.11, P = 9.20 × 10⁻³⁰⁸), and a regression of EA on the standardized allele score shows that the allele score is positively associated with EA (P = 4.10 × 10⁻¹²², F = 552.12). A 2SLS regression with the allele score as instrument for EA provides a negative estimate (-0.39) for the causal effect of EA on BMI, with P = 9.63 × 10⁻²¹. However, it is likely that the exclusion restriction is violated, since the allele score for EA is, conditional on population stratification controls, gender, and birth year, positively associated with birth eight (0.01, P = 0.04), a known confounder of the relationship between EA and BMI.⁷⁰

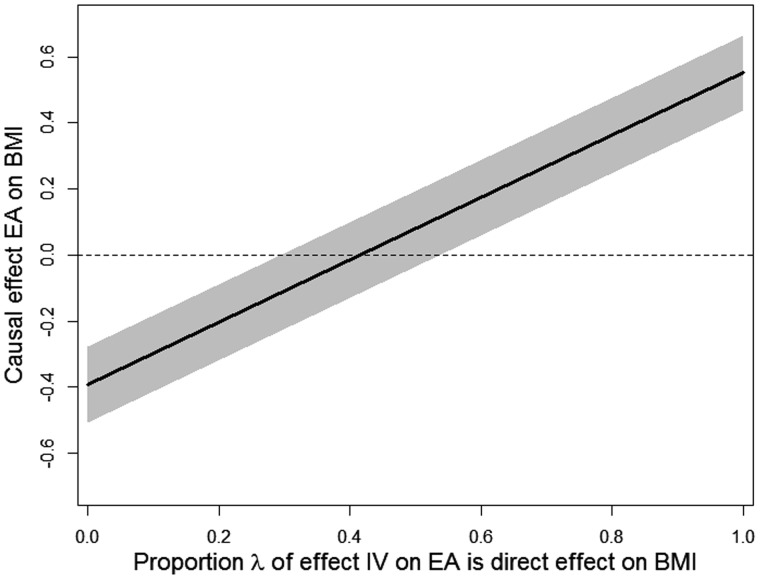
In contrast to the previous examples, here it is difficult to find a subsample for which the first stage is zero. Therefore we illustrate how PRMR can be used as a sensitivity analysis to determine how strong the violation of the exclusion restriction should be to render the causal effect β to be 0. Since one selects SNPs as IVs for their association with the exposure rather than the outcome, it seems plausible that, in absolute value, the standardized first stage effect of an IV on the exposure, γ, is larger than the standardized direct effect of that IV on the outcome, α. Therefore, we define the proportion 0 ≤ λ ≤ 1, and we set ${\mu }_{\alpha }$ equal to λ$\widehat{\gamma }$ and the variance ${\Omega }_{\alpha }$ equal to the squared standard error of $\widehat{\gamma }$. Subsequently, we apply equation (3) for different values of λ to find for which λ the corresponding β equals 0. When the first stage estimate has the opposite sign of the direct effect estimate, one needs to change the sign of $\widehat{\gamma }$ in this sensitivity analysis.

In our case, the first stage effect (allele score on EA) has plausibly the opposite sign of the direct effect (allele score on BMI) and hence we set ${\mu }_{\alpha }$ equal to -λ$\widehat{\gamma }$. The resulting estimates for β are plotted in Figure 2 as a function of λ. The estimate for λ = 0 corresponds to the MR point estimate, but the 95% confidence interval is a little wider because ${\Omega }_{\alpha }>0$. Moving along the x-axis, the causal effect of EA on BMI is estimated to be 0 when λ = 0.42, and the 95% confidence interval includes 0 already when λ = 0.29. Hence, a relatively mild violation of the exclusion restriction 29% of the first-stage effect implies that we cannot reject a zero effect of EA on BMI, producing at best weak evidence that EA causally reduces BMI.

Figure 2.

The causal effect of educational attainment (EA) on BMI, for varying values of λ (the percentage of the standardized effect of the IVs on EA which is considered to be the direct effect of the IVs on standardized BMI). The grey area represents the 95% confidence interval.

Conclusion

The fact that the pleiotropic effects of genes are poorly understood makes it difficult to use genetic variants as credible instrumental variables in Mendelian randomization. In this paper we argued that if: (i) one can identify a subsample for which genetic variants do not have an effect on the exposure; (ii) the selection into this subsample is not a consequence of both genetic variants and the outcome; and (iii) pleiotropic effects are homogeneous, PRMR provides a way to deal with violations of the exclusion restriction due to pleiotropy, and opens the door for several applications in epidemiology and social science research.

A simulation study showed that PRMR clearly outperforms existing methods if the exclusion restriction is violated. We illustrated our PRMR approach by estimating the causal effect of tobacco exposure on BMI, and the effect of prostate cancer on subjective health evaluations. In those two cases it is possible to identify subsamples where the effect of SNPs on the exposure are zero (never smokers and females, respectively), and this allows estimating, and if necessary correcting for, the pleiotropic effect.

We acknowledge that the two requirements for PRMR are not always satisfied. Yet, even if one is not willing to make the assumption of homogeneous pleiotropic effects, one can still use the subsample without an effect of the genetic variants on the exposure as a useful test of the exclusion restriction. Moreover, if one cannot identify a subsample without a first stage, as we illustrated for the estimation of the effect of education on BMI, PRMR still allows for an informative sensitivity analysis that could routinely be applied in all MR analyses.

Funding

This work was supported by the Netherlands Organization for Scientific Research [016-145-082 to H.v.K. and 016-165-004 to C.A.R.], and the National Institute on Aging [R01AG037398 to H.v.K.].