tRNA tracking for direct measurements of protein synthesis kinetics in live cells

Abstract

Our ability to directly relate results from test tube biochemical experiments to the kinetics in living cells is very limited. Here we present experimental and analytical tools to directly study the kinetics of fast biochemical reactions in live cells. Dye-labeled molecules are electroporated into bacterial cells and tracked using super-resolved single-molecule microscopy. Trajectories are analyzed by machine-learning algorithms to directly monitor transitions between bound and free states. In particular, we measure the dwell-time of tRNAs on ribosomes, and hence achieve direct measurements of translation rates inside living cells at codon resolution. We find elongation rates with tRNA^Phe in perfect agreement with previous indirect estimates, and that once fMet-tRNA^fMet has bound to the 30S ribosomal subunit, initiation of translation is surprisingly fast and does not limit the overall rate of protein synthesis. The experimental and analytical tools for direct kinetics measurements in live cells have applications far beyond bacterial protein synthesis.

Introduction

Since dawn of molecular biology, the reductionist’s approach has guided researchers to dissect the complexity of living systems into separately measurable units. In vitro reconstituted systems have been successfully exploited to deduce molecular mechanisms of the central biochemical pathways fundamental to all life forms. However, studying a molecular mechanism separately in isolated systems is not always sufficient. The cellular machineries work together in a finely tuned coalition, and the complexity of interactions is difficult to mimic in reconstituted systems due to macromolecular crowding, geometrical constraints, and our limited understanding of the detailed chemical composition at the single cell level. Studies of dynamic molecular processes directly inside the cell have also been challenging. While classical test-tube biochemistry has relied on tricks to synchronize the binding state of reacting molecules for kinetics measurements, this is difficult, if not impossible, to accomplish in a living cell where reactions are asynchronous and normally work under steady-state conditions. With the development of single-molecule approaches, the need to synchronize the molecules in the system of interest disappears, and in vivo reaction kinetics measurement should in principle be attainable.

Recent advances in the field of single-molecule fluorescence microscopy have opened up the possibility to probe molecular interactions directly inside cells. These studies commonly depend on fluorescent fusion proteins, because of their genetically encoded specificity and ease of use. Tracking of individual fluorescent fusion proteins has, for example, helped in determining the fractions of proteins that are in different binding states and how these different complexes are distributed in the cells ¹. However, to measure the rates of binding and dissociation reactions inside the cells by single-molecule tracking, it is necessary to detect the corresponding changes in the diffusion rate for individual molecules. Moreover, to reliably assign dwell times of different diffusional states, one would need sufficiently long and highly resolved trajectories, to observe the fluorophores through a whole reaction cycle. This has to some limited extent been possible with fluorescent protein labels ², but would be very difficult to generalize to reaction pathways involving several diffusional states or different timescales, due to the modest photon budget of the fluorescent proteins ³.

Recently Kapanidis and coworkers demonstrated how in vitro dye-labeled molecules could be introduced to live cells using conventional electroporation techniques ^4,5. This methodology opens up the possibility to use synthetic dyes for site-specific labeling of biomolecules to be studied in vivo. With their small size, the dyes make very gentle perturbations to the target molecules, and with their superior photophysical properties, their potential as tools for in vivo single-molecule tracking is encouraging.

Bacterial protein synthesis is a typical example of a complex biological process. Protein synthesis has been studied extensively over the years, and the combination of traditional biochemistry ^6–8, structural approaches ^9–11, and more recently single-molecule based in vitro techniques ^12,13, has led to a detailed picture of ribosome catalyzed protein synthesis ¹⁴. However, in order to connect this detailed picture with cell physiology, new techniques are needed to probe the dynamics of these processes inside the cell. In particular, the kinetics of the highly regulated steps of translation initiation has proven very difficult to disentangle using reconstituted systems. For example, the time for 50S subunit joining to the fMet-tRNA^fMet·30S·mRNA pre-initiation complex varies hundredfold in vitro dependent on concentrations of the individual initiation factors, where both low and high factor concentrations impede the process ^15,16. In the present study, we have developed experimental and analytical tools to directly measure biochemical reaction rates inside living cells. We apply this method on protein synthesis, and use electroporated dye-labeled tRNAs to extract quantitative kinetic data from protein synthesis with codon resolution inside live cells.

Results

Efficient electroporation of dye-labeled tRNA

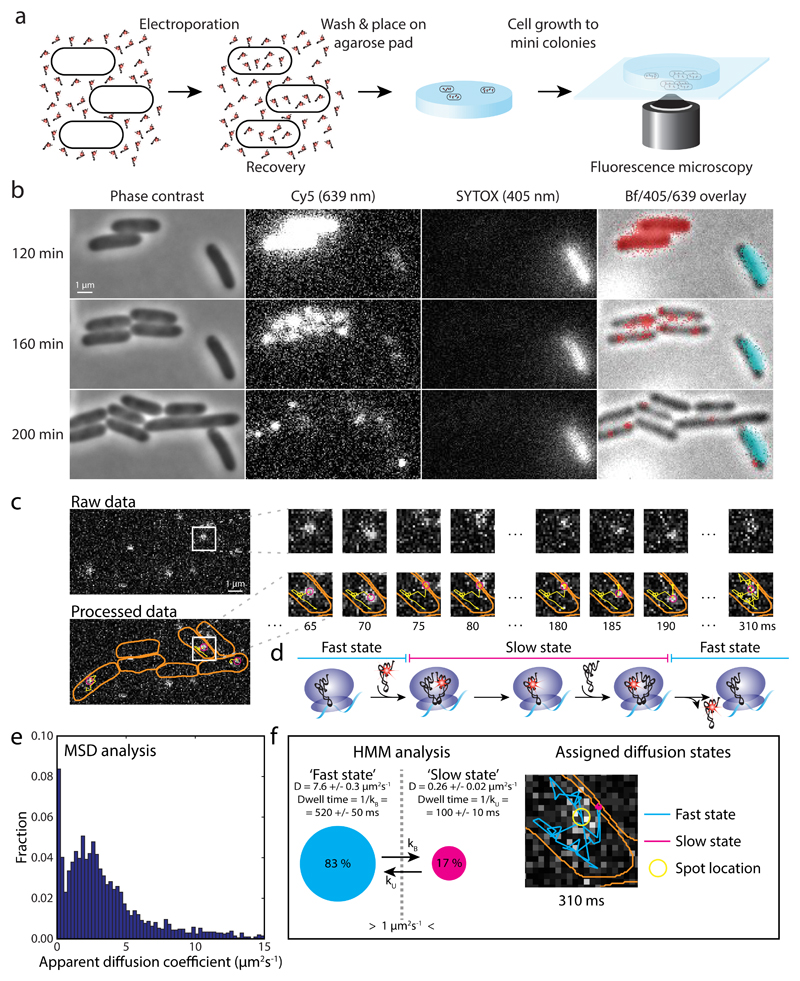
In vitro labeled and assayed Phe-[Cy5]tRNA^Phe (Supplementary Fig. 1) was introduced into DH5α E. coli cells by electroporation. After recovery, cells were plated on an agarose pad and imaged at 37°C (Fig. 1a). At 19 kV/cm electroporation field strength, and 100 nM Phe-[Cy5]tRNA^Phe, approximately 10% of the cells resume growth and division on the pad, and about 70% of those have internalized [Cy5]tRNA^Phe, with an average number of 80 fluorescent molecules per cell (Supplementary Notes). The fluorescent molecules are stable inside the cells, with no obvious decay on the hour timescale, and are distributed equally between daughters upon cell division (Fig. 1b). In all electroporation experiments presented below, the procedure includes growth from single cells to mini colonies (4 to 8 cells per colony) on the pads before fluorescence movie acquisition. To exclude single dead cells, the pads also contained SYTOX blue, selectively staining dead cells with damaged membrane (Fig. 1b).

Figure 1. Tracking of single [Cy5]tRNA^Phe in live E. coli cells.

a E. coli cells were electroporated with Phe-[Cy5]tRNA^Phe, recovered in RDM medium, washed, placed in dilute culture on an RDM-agarose pad, and allowed to grow to mini colonies prior to data acquisition. b Phase contrast, fluorescence, and bright field (Bf) imaging of cells after electroporation with Phe-[Cy5]tRNA^Phe. [Cy5]tRNA^Phe appear as bright pixels in Cy5 lane, and red pixels in overlay lane. SYTOX stained, i.e. dead cells (bright pixels in SYTOX lane, and cyan pixels in overlay lane), were omitted in the analysis. Live cells continued growing after laser exposure during data acquisition (Supplementary Fig. 2). c Time series of tRNA tracking at 5 ms per frame, showing cell outlines (orange), present location of the particle (magenta), and the particle trajectory over time (yellow). This example shows an apparent binding of approximately 100 ms. d Predicted diffusion of [Cy5]tRNA^Phe molecules being utilized on ribosomes. e Histogram of apparent diffusion coefficients for [Cy5]tRNA^Phe in live E. coli cells, estimated from MSD analysis of trajectories such as in panel c. f HMM estimated diffusion of [Cy5]tRNA^Phe in live E. coli cells, coarse-grained from a six-state model (Supplementary Table 1) into two states, ‘slow’ and ‘fast’, with a threshold of 1 µm²/s separating them. The right part shows the trajectory in panel c, now color coded with respect to diffusional state. 17,286 total time steps (n = 17,286) were included in the analyses in panel e and f.

Tracking of single fluorescent tRNAs inside live cells

To detect and track the movement of individual internalized [Cy5]tRNAs, we used stroboscopic laser illumination with 1.5 ms laser illumination per 5 ms camera exposure frame. Combining symmetry-based spot detection ¹⁷, maximum aposteriori estimates of position and localization uncertainty ¹⁸, and the u-track algorithm ¹⁹, we were able to follow the movement of single [Cy5]tRNA^Phe (Fig. 1c) up to more than hundred frames (See Supplementary Figs. 3a-3c for detection results). As can be seen in Supplementary Video 1 and Fig. 1c, the internalized Cy5-labeled tRNAs display diffusion patterns consistent with what would be expected for a tRNA being used repeatedly by the protein synthesis machinery, i.e. random fast diffusion interrupted by immobilization events, possibly reporting on binding of the tRNAs to an mRNA-tethered ribosome (Fig. 1d).

Further, the apparent diffusion coefficients of the tRNAs, estimated from mean-squared displacement (MSD) plots of trajectory segments, show a wide distribution of fast moving tRNAs, with the apparent binding events giving rise to a population (12%) with apparent diffusion < 0.5 µm²/s (Fig. 1e), potentially representing ribosome bound tRNA ^1,20. The diffusion pattern is robust between independent experiments (Supplementary Fig. 3d), and all data analyses in this study were therefore performed on cumulated data from independent experiments (two or more), with sample size n denoting the total combined number of trajectory time steps in the analysis.

To quantify binding events in terms of the accompanying changes in diffusion constant, we used a hidden Markov model (HMM) approach, which models the trajectories as random (Markovian) transitions between a set of discrete (hidden) states with different diffusion constants, accounts for pointwise localization errors and motion blur, and learns the underlying sequence of state transitions from data. The HMM algorithm performs maximum-likelihood inference of model parameters ¹⁸, and we used Akaike’s information criterion ²¹ (AIC) to determine the appropriate number of diffusive state to fit the data. For models of four states and more, we consistently found three major diffusive states at approximately 0.1 µm²/s, 3 µm²/s, and 6 µm²/s, with corresponding approximate occupancies at around, 15%, 50%, and 20% respectively (see Supplementary Fig. 3f and Table 1 for the six-state model, with lowest AIC). With increasing number of states, we find low occupancy (< 5%) states at 0.7 µm²/s and 5 µm²/s. In addition, for all model sizes we detect one or two states with significantly faster diffusion, > 20 µm²/s. Based on our analysis of simulated microscopy images (below), we believe these > 20 µm²/s states reflect tracking artifacts with no biological meaning. Considering that the intracellular concentration of EF-Tu roughly equals that of total tRNA ²², and that approximately 75% of tRNA^Phe is aminoacylated during exponential growth ^23,24, we tentatively assign the three major states as a [Cy5]tRNA^Phe·70S·mRNA complex, [Cy5]tRNA^Phe in ternary complex with EF-Tu and GTP, and free [Cy5]tRNA^Phe respectively. Tracking of a fluorescent fusion version of EF-Tu performed with similar experimental settings yielded a major (>75% occupancy) diffusional state at around 3 µm²/s (Supplementary Table 1), supporting the assignment of the 3 µm²/s tRNA diffusive state as the ternary complex.

All experimental datasets presented in this article were fitted to two- to seven- or eight-state models, with the best models (lowest AIC), shown in Supplementary Table 1. As the aim of the present study regards ribosome binding events however, we coarse-grain the best HMM fits into two states, ‘slow’ and ‘fast’, with a threshold of 1.0 µm²/s separating them (Fig. 1f and Supplementary Fig. 3f), in line with MSD-analysis of ribosome trajectories performed in ^1,20,25. The corresponding coarse-grained results for all experiments are shown in Supplementary Table 1, and our main focus in the following sections will be the slow state. An example of tracked molecules with HMM fitted diffusional states is shown in Supplementary Video 1.

Internalized fluorescent tRNAs take part in translation

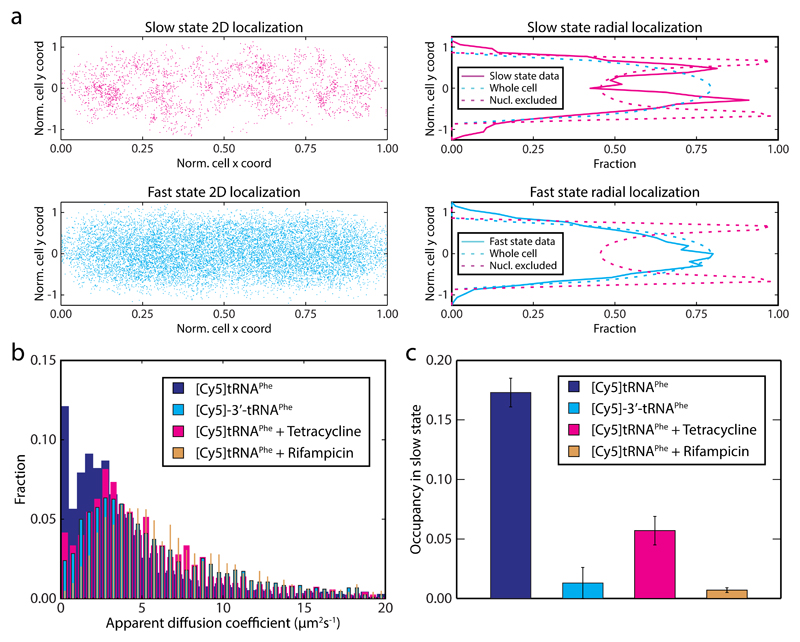
We next sought to evaluate whether the apparent [Cy5]tRNA^Phe binding events actually represent binding to ribosomes. We first note that [Cy5]tRNA^Phe molecules in the slow diffusional state are located more towards the cell periphery compared to [Cy5]tRNA^Phe in the fast state (Fig. 2a). Considering that ribosomes in growing cells are primarily excluded from the nucleoid in the centre of the cells^1,20, peripheral slow movement of [Cy5]tRNA^Phe fits well with the hypothesis that the slow state represents ribosome bound [Cy5]tRNA^Phe.

Figure 2. Internalized [Cy5]tRNA^Phe take active part in translation.

a Spatial distribution of [Cy5]tRNA^Phe in DH5α cells belonging to the slow or the fast diffusive state according to coarse-grained HMM analysis (n = 17,286). In the left panels, locations are plotted on normalized cell width and length coordinates. The right panels show the same data (excluding particles in cell poles and cell center, i.e. including particles within 0.2 < x < 0.4 or 0.6 < x < 0.8) projected on the short cell radial axis (solid lines). Dashed lines correspond to uniform distributions in the cytoplasm and nucleoid excluded regions respectively. b MSD-estimated apparent diffusion coefficients of 3’ inactivated tRNA, [Cy5]-3’-tRNA^Phe (n = 11,231) in live E. coli cells, as well as normal [Cy5]tRNA^Phe in mini colonies of E. coli cells treated with tetracycline (n = 10,415) or rifampicin (n = 12,042). Data for [Cy5]tRNA^Phe in non-treated cells (Fig. 2b) is shown for comparison. c HMM estimated occupancy of the dye-labeled tRNAs in the slow diffusional state (see Supplementary Table 1). The trajectories used were the same as in panel b. Error bars represent bootstrap estimates of standard errors.

In an attempt to specifically remove [Cy5]tRNA^Phe association to ribosomes, cells were subjected to the antibiotics rifampicin or tetracycline. Rifampicin inhibits RNA transcription, and hence, when all mRNAs have been degraded, no further translation can occur and there should be no functional binding of [Cy5]tRNA^Phe to ribosomes. Tetracycline on the other hand binds directly to the ribosome where it is believed to block binding of the aa-tRNA·EF-Tu·GTP ternary complex to the A site, resulting in ribosomes being trapped at start codons ²⁶. After antibiotic injection, both MSD analysis (Fig. 2b) and diffusion state analysis using the HMM approach (Fig. 2c and Supplementary Table 1) clearly show a decrease in binding events in presence of either of the drugs – the occupancy in the slow state decrease from 17% to 1% and 6% respectively.

By tracking 3’ deactivated [Cy5]-3’-tRNA^Phe we also found less binding events (1% occupancy in slow state), further supporting that the internalized normal [Cy5]tRNA^Phe takes part in protein synthesis on ribosomes (Figs. 2b and 2c).

In vivo kinetics of translation elongation

Under the assumption that the slow diffusive state of the [Cy5]tRNA^Phe represents productive tRNA usage on ribosomes, the apparent binding events allow a direct measure of mRNA translation kinetics in vivo. With rapid dissociation of deacylated tRNA from the E site ²⁷, one binding event would represent the total time of two consecutive elongation steps, i.e. two peptide bond formation steps, two translocation steps plus one aminoacyl-tRNA·EF-Tu·GTP ternary complex arrival time (Fig. 1d). We estimated the dwell times of the [Cy5]tRNA^Phe in the different diffusional states based on the transition matrix of the coarse-grained 2-state HMMs, and found the mean dwell time of [Cy5]tRNA^Phe on ribosomes to be 100 ± 10 ms (Supplementary Table 1).

The resulting [Cy5]tRNA^Phe dwell time on ribosomes fits very well with previous in vivo estimates of the average elongation rate, approximately 50 ms per amino acid incorporated at 37°C ²⁸; with in vitro biochemical measurements performed in reconstituted protein synthesis systems ²⁹; as well as the expected tRNA^Phe utilization frequency at this growth rate (Supplementary Notes).

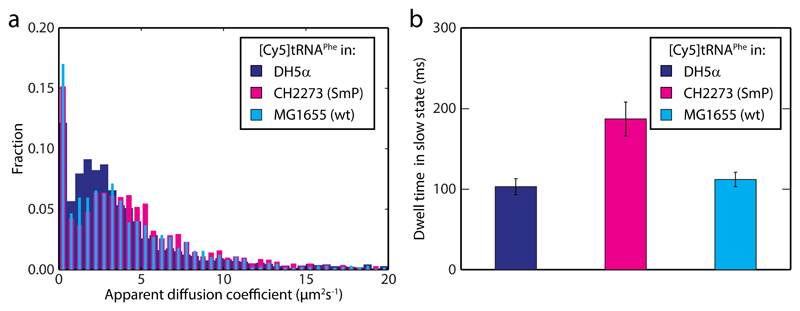
In order to further validate our in vivo kinetics assay we used an E. coli strain (CH2273) with a well characterized streptomycin pseudodependent phenotype, SmP, harboring two mutations in gene rpsL, encoding ribosomal protein S12. The resulting mutant ribosomes are hyper-accurate but slow ^30,31, and therefore need the error-inducing drug streptomycin to perform efficiently (See Supplementary Fig. 4 for growth curves). Phe-[Cy5]tRNA^Phe was thus electroporated into CH2273 cells, which were allowed to grow and divide in the absence of streptomycin. From both MSD (Fig. 3a) and HMM analysis (Supplementary Table 1) we find the diffusion of [Cy5]tRNA^Phe to be similar as in DH5α cells, with slow and fast state occupancies practically unchanged. Importantly however, the dwell time in the slow state, 190 ± 20 ms, is two-fold higher than in DH5α (Fig. 3b and Supplementary Table 1). This is in good agreement with previous measurements in vivo and in vitro, suggesting two- to three-fold slower translation rate ^30,31. Control experiments with the CH2273 genetic background strain (i.e. MG1655) give similar dwell times as in DH5α (Fig. 3b and Supplementary Table 1).

Figure 3. [Cy5]tRNA^Phe dwell time is longer on slow ribosomes.

a MSD-estimated apparent diffusion coefficients of [Cy5]tRNA^Phe in streptomycin pseudodependent CH2273 cells (SmP, n = 15,571), and the CH2273 genetic background strain, MG1655 (n = 10,239). Data for [Cy5]tRNA^Phe in DH5a cells (Fig. 1e) is shown for comparison. b HMM estimated dwell times for [Cy5]tRNA^Phe in the slow state (see Supplementary Table 1). The trajectories used were the same as in panel a. Error bars represent bootstrap estimates of standard errors.

Overall, the results with [Cy5]tRNA^Phe strongly suggest that by tracking single dye-labeled tRNAs we can measure translation kinetics with codon resolution in live cells.

Simulated microscopy validates the analysis pipeline

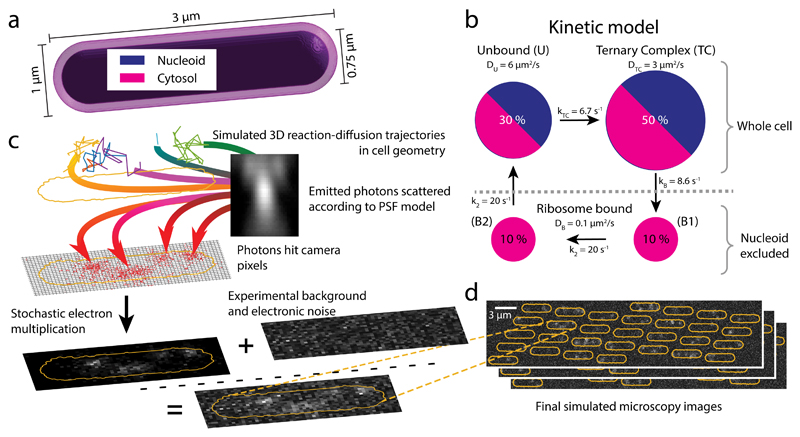
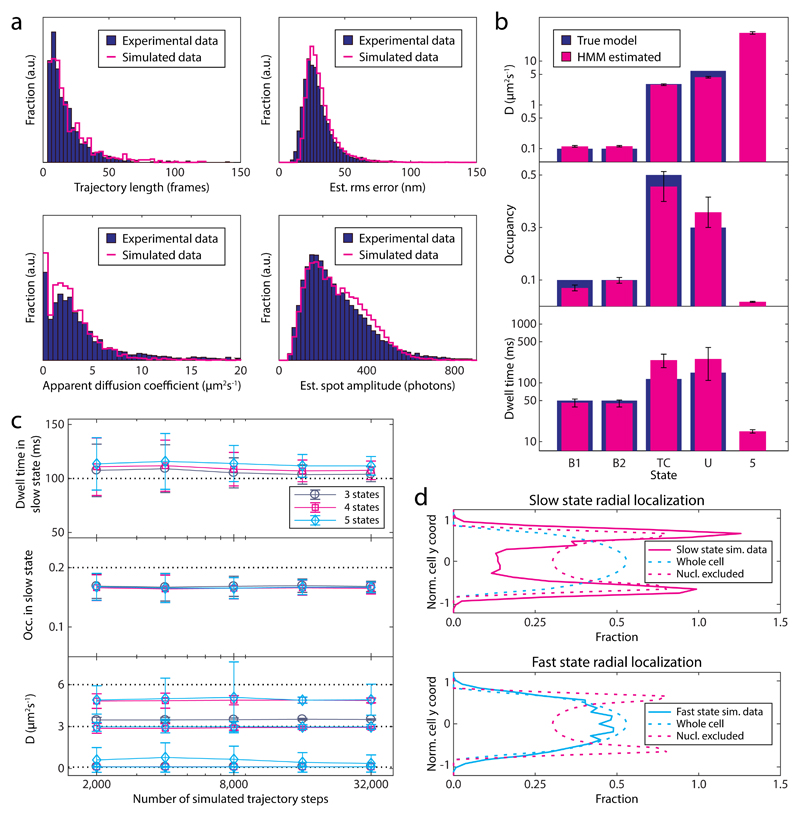
To investigate the precision and limitations of our single-particle tracking approach, we simulated microscopy of tRNA diffusion in cells and applied our analysis pipeline. Trajectories of single molecules, confined in a cell-shape geometry (Fig. 4a), were generated by sampling from a reaction-diffusion master equation ^32,33. For the tRNA-ribosome interactions, we used a kinetic model with four diffusive states (Fig. 4b): two bound (B1 and B2) states (tRNA in A and P site, D_B = 0.1 μm²/s), an unbound (U) state (D_U = 6 μm²/s), and a ternary complex (TC) state (D_TC = 3 μm²/s). Elongating ribosomes were modeled implicitly by excluding the bound states from the nucleoid region. The states inter-convert via a unidirectional reaction cycle (Fig. 4b), with reaction rates chosen so that the total mean dwell time of the bound states is 100 ms, and the total occupancy is 20%, 30%, and 50% for the bound, unbound, and ternary complex states, respectively, in accordance with our experimental results (Supplementary Fig. 3f). Next, the simulated trajectories together with experimental camera noise and point spread function were used as input for microscopy simulations (Figs. 4c and 4d).

Figure 4. Simulated single-molecule microscopy.

a Model geometry for reaction-diffusion simulations of translation cycles in E coli. The cytosol and nucleoid are modeled as concentric cylinders with spherical end caps. b tRNA kinetic reaction cycle. Ribosome bound states are excluded from the nucleoid, while the unbound and EF-Tu bound (Ternary Complex) states can access the whole cell. c Simulation stages for a single cell: 1-3 reaction-diffusion trajectories per cell are used as input for simulated images of moving dots, the optical and detection systems are simulated by an experimentally derived z-dependent point-spread function and EMCCD camera noise, using 1.5 ms illumination in 5 ms frames as in our experiments (see Online Methods). Finally, experimental background images are added to produce the synthetic movie. d Snapshots of a simulated field of view with 30 cells.

The simulated movies appear very similar to real ones (see Supplementary Video 1). Using the same analysis pipeline as for experimental data, we obtained statistics very similar to that of experimental movies (Fig. 5a and Supplementary Figs. 5b-c). Given this good agreement, we were confident to use the simulated movies to test the extent to which our analysis methods are able to reproduce the (known) underlying kinetic model, how much data is needed, and how robust the analysis is.

Figure 5. Analysis of simulated movies.

a Feature comparison of simulated (n = 16,389) to experimental [Cy5]tRNA^Phe data (same as in Fig. 1e). b Estimated HMM model parameters for the simulated data set. True values from the underlying kinetic model (Fig. 4b) are shown for comparison. c Convergence of HMM estimated diffusion constants and slow-state parameters. The graphs show mean and standard deviation from > 150 datasets, resampled with replacements from a large dataset of around 300,000 steps, analyzed with 3-, 4-, and 5-state HMMs. Dashed lines indicate true values (Fig. 4b). d Radial distribution of slow (< 1 μm²/s), and fast diffusive states, using the same data and HMM as in panel a and b. Dashed lines correspond to uniform distributions in the cytoplasm and nucleoid excluded regions, respectively. Error bars in the figure represent bootstrap estimates of standard errors.

First, we analyzed simulated data based on the default model (Fig. 4b), with the HMM analysis and AIC model selection, as described above. The HMM successfully identifies the four true diffusive states (Fig. 5b), plus a fifth low occupancy state with very high diffusion constant, which we attribute to artifacts introduced by the tracking algorithms. Regarding the bound state which is our primary interest, we see that the HMM nicely extracts the correct mean dwell times and diffusion coefficients, whereas occupancy is underestimated, probably because the nucleoid excluded region is out of focus to larger extent. Occupancies and diffusion coefficients for the faster states are reasonably well estimated, but the dwell times less so, possibly due to interference with the fast spurious state.

Second, we performed a convergence study without model selection to estimate the statistical uncertainty of the parameter estimates (Fig. 5c). Determining the bound state mean dwell time with a standard error of 10 ms requires 8,000-16,000 diffusive steps. We also see an upward bias of similar magnitude, probably due to the difficulty of detecting short events, and confirm the bias in occupancy as well.

Next, we tested the robustness of our analysis to various perturbations. First, we found that our analysis successfully detects bound dwell times down to 50 ms, but underestimates the mean dwell time by up to 25% when it exceeds the mean trajectory length (Supplementary Fig. 5d). Second, the estimated bound mean dwell time was little influenced by 50% changes in the intermediate diffusion constant D_TC (Supplementary Fig. 5e). However, while the analysis detects the removal of the state (Supplementary Table 1, Sim. model 4), it yields a spurious increase in bound dwell time by about 50%. Third, we confirmed that camera calibration errors (± 20% EMCCD gain error), which may affect the localization uncertainty estimates ¹⁸, do not change bound state dwell times significantly (Supplementary Fig. 5f).

In light of these tests, we conclude that our combined single-particle tracking and HMM analysis is capable of extracting correct states, localization (Fig. 5d) and mean dwell times for diffusion constants up to about 3 μm²/s and 200 ms.

In vivo kinetics of translation initiation

Whereas translation elongation is a fairly simple and well-studied process, the dynamics of translation initiation is still poorly understood. In particular, to date, no conclusive results regarding the timing of translation initiation in E. coli is available, and estimates range from hundreds of milliseconds to hundreds of seconds per initiation event ¹⁴. In vitro experiments using reconstituted systems suffer from the fact that the concentration of the individual components, such as the initiation factors, change the overall dynamics drastically, where e.g. the presence of initiation factor 3 slows down the 50S subunit joining step, but at the same time makes the process more accurate ^15,16. Hence, it is far from obvious under what conditions initiation of translation operates inside the cell. Furthermore, a long standing question has been whether initiation is limiting the overall translation rate. A commonly held view has been that during nutrient-rich growth, translation elongation is fast, due to high TC concentration, and initiation is rate-limiting ³⁴.

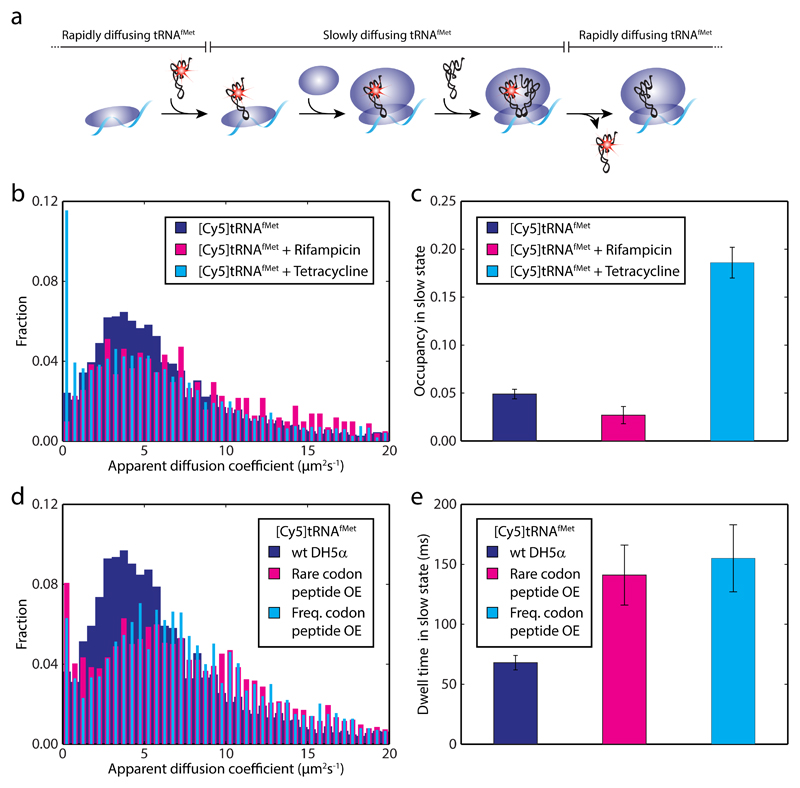
To probe specifically the kinetics of translation initiation, we labeled E. coli tRNA^fMet with Cy5 and confirmed its activity in vitro (Supplementary Figs. 6a-c). In analogy with the [Cy5]tRNA^Phe experiments, the intention was to measure the time [Cy5]tRNA^fMet spends bound to ribosomes, i.e. the time to dock the 50S subunit to the fMet-tRNA^fMet·30S·mRNA pre-initiation complex and to finish the first elongation cycle (Fig. 6a).

Figure 6. In vivo initiation kinetics using Cy5 labeled initator tRNA^fMet.

a Simplified scheme displaying the predicted diffusional behavior of [Cy5]tRNA^fMet molecules being utilized on ribosomes. The dwell time of a functional [Cy5]tRNA^fMet binding event to a ribosome includes joining of the large ribosomal subunit and one cycle of peptide elongation. b MSD-estimated apparent diffusion coefficients of [Cy5]tRNA^fMet in DH5a cells (n = 31,498) treated with rifampicin (n = 8,389) or tetracycline (n = 21,259) injected. c HMM estimated occupancy of [Cy5]tRNA^fMet in the slow diffusional state (see Supplementary Table 1). The trajectories used were the same as in panel b. d MSD-estimated apparent diffusion coefficients of [Cy5]tRNA^fMet in DH5α cells overexpressing a short peptide with a rare Arg codon (AGG read by tRNA^Arg4, n = 19,900) or frequent Arg codon (CGU read by tRNA^Arg2, n = 25,236) in second position. e HMM estimated dwell times for [Cy5]tRNA^fMet in the slow state with or without short peptides overexpressed (see Supplementary Table 1). The trajectories used were the same as in panel d. Error bars in panel c and e represent bootstrap estimates of standard errors.

We analyzed the diffusional behavior of fMet-[Cy5]tRNA^fMet in DH5α cells, and similar to [Cy5]tRNA^Phe, we observed rapid diffusion of the [Cy5]tRNA^fMet interrupted by short dwells in a slow diffusion state (Supplementary Video 2). In contrast to [Cy5]tRNA^Phe however, [Cy5]tRNA^fMet gives a very low fraction of molecules in the presumed ribosome bound state (Figs. 6b and 6c), with HMM-estimated occupancy of merely 5% (Supplementary Table 1). Given that start codons are approximately 10 times less frequent than Phe codons, this result might not seem so surprising, but this then also requires the tRNA^fMet dwell time on the ribosome to be considerably shorter than previous in vitro estimates of the time required to finish initiation. And in deed, HMM analysis results in a dwell time of 70 ms (± 10 ms) for [Cy5]tRNA^fMet in the slow state (Supplementary Table 1).

Provided that the first elongation cycle is as fast as an average cycle, i.e. around 50 ms, and that the probability of product formation once bound is close to one (in line with in vitro experiments ^15,35,36), the estimated ribosome bound dwell time of [Cy5]tRNA^fMet thus suggest that the subunit joining step is completed within 20 ms. This result would imply that, once fMet-tRNA^fMet has bound the small ribosomal subunit, initiation of translation is fast relative to an elongation cycle, and no build-up of pre-initiation or 70S ribosomes on start codons would be expected, contrary to what can be inferred from in vitro experiments ¹⁴.

To confirm that the slow diffusion state of [Cy5]tRNA^fMet represents ribosome binding events we investigated the effect of rifampicin and tetracycline also on [Cy5]tRNA^fMet diffusion. In presence of rifampicin, as with [Cy5]tRNA^Phe, the occupancy in the slow state decreases (3%, Fig. 6c). In the presence of tetracycline however, opposite to the effect on [Cy5]tRNA^Phe, a significant increase of [Cy5]tRNA^fMet in the slow state (19%, Fig. 6c) with longer dwells (140 ± 40 ms) is seen (Supplementary Table 1). These results are in line with recent ribosome-profiling data²⁶, showing start-codon specific stalling of ribosomes upon tetracycline treatment, suggesting authentic translation dependent ribosome binding events of [Cy5]tRNA^fMet in our assay.

Finally, to explore initiation of translation on a defined mRNA, with potentially perturbed initiation kinetics, we electroporated fMet-[Cy5]tRNA^fMet into DH5α cells overexpressing short peptides under T7 promoter including a rare or frequent Arg codon in second position, read by the low- and high-abundant tRNA^Arg4 and tRNA^Arg2 isoacceptors respectively. The hypothesis being that, in the rare Arg codon case, depletion of the charged pool of the low-abundance tRNA would slow down ribosomes on the second codon with [Cy5]tRNA^fMet still bound to the ribosomal P site. We noted that induction severely inhibited cell growth in both cases (also confirmed in bulk experiment, see Supplementary Fig. 6d), suggesting that the protein synthesis machinery was to a large extent occupied by translation of the short mRNAs.

The diffusion pattern of [Cy5]tRNA^fMet changes significantly upon peptide overexpression (Fig. 6d). We find that the occupancy in the slow state increases slightly to 7% and 6% in the case of rare and frequent Arg codon respectively (Supplementary Table 1), with a twofold increase in dwell time for both cases compared to the wild type strain (Fig. 6e). We see no increase in the slow-state occupancy or dwell-time in cells expressing T7 polymerase only (Supplementary Table 1). Overall these results show that we can modulate the binding frequency and dwell time of fMet-[Cy5]tRNA^fMet by changing the transcriptome of the cells, further supporting authentic ribosome binding of the labeled tRNA. The fact that the slow-state dwell-time increases to the same extent in both peptide-expressing strains however, might indicate that the exhausted charged pool of neither of the tRNA isoacceptors is sufficient to support this high consumption level, or possibly some other component of the translational machinery gets limiting.

Discussion

In the present study we have developed new experimental and analytical approaches to directly measure reaction rates inside living cells using electroporated fluorescent molecules. By using small organic dyes, we overcome the limitations of fluorescent proteins, and can target biological processes with minimal disturbances and follow individual molecules in reaction cycles for extensive periods of time. Similar to the work recently published by Kapanidis and co-workers ⁵, we make use of established protocols for in vitro dye-labeling of tRNAs (37 and 12 respectively). However, whereas Plochowietz et al ⁵ electroporated bulk tRNA, and never approached kinetics, we use specific tRNA species, and can hence with our new analytical tools extract codon specific tRNA dwell times on ribosomes.

By electroporation and tracking of Cy5-labeled tRNA molecules, we directly measure translation kinetics in exponentially growing E. coli cells. Trajectories are fitted using machine-learning algorithms, and we estimate the mean dwell time and occupancy of the tRNAs in different diffusional states. The absolute number of distinct diffusional states is difficult to estimate. AIC is known to sometimes overfit HMM-like models ³⁸, but the large number of states could also reflect experimental artifacts such as tracking errors, or complexity that goes beyond the model assumptions, e.g. in-sample variability from cell-to-cell variability, micro-heterogeneity in the cytoplasm ³⁹, or variability in bound-state properties when ribosomes bind to mRNAs of different sizes or occupancy (polysomes). We also find systematic differences in diffusive states in different bacterial strains (compare for example [Cy5]tRNA^Phe data in DH5α and MG1655) or in different growth conditions. This might reflect differences in cytoplasm composition because of altered growth rates or treatment with antibiotics (as has been observed previously ²⁰), or variability in tracking artefacts due to cell geometry variations. Judging from analyses of simulated microscopy data, we also see that faster diffusive species are significantly harder to track than slower ones with the current exposure timings (Fig 5b). Thus, it is possible that the HMM/AIC analysis finds extra states in addition to those reflecting the biochemical reaction cycle. To circumvent these difficulties, and since our main interest here is on ribosome binding events of tRNAs, we coarse-grained the AIC-optimal models with many states to two-state models, representing ribosome bound or unbound tRNA species. The choice of threshold, 1 µm²/s, was based on previous single-particle tracking data of ribosomal subunits ^1,20,25, but increasing or decreasing the threshold by 0.5 µm²/s only changes some of the numbers slightly (Supplementary Table 1), and does not affect the conclusions of this study. Similarly, our conclusions are insensitive to the exact number of states in detailed models.

We find the mean dwell time of tRNA^Phe in the slowly diffusing, ribosome bound state, about 100 ms, to be in good agreement with previous measurements of average elongation rates in vivo, i.e. 50 ms per codon ²⁸. As the bulk tRNA tracking in Plochowietz et al show ⁵, we also find binding events of tRNA^Phe to ribosomes mainly in the periphery of the cells, in accordance with nucleoid excluded translation ^1,20, and our tentatively assigned free tRNA diffusional state (6.5 µm²/s, Supplementary Table 1) agrees fairly well with their finding (8 µm²/s).

A direct comparison to in vitro results is complicated, since the 100 ms average dwell time includes the binding of an average ternary complex to the A site, and we know from previous analyses that there is a big variation in peptide bond formation rates dependent on aa-tRNA identity⁴⁰. However, assuming k_cat = 130 s^-1 for peptide bond formation for all aa-tRNAs ⁷, k_cat/K_m = 80 µM^-1s^-1 for the same process for an average ternary complex binding to the A site (in accordance with the Mg²⁺ titrations in ⁴¹ and the in vitro-in vivo calibration in ⁴²), and on average 2 µM available cognate ternary complex in the cell ^43,44, we can subtract peptide bond formation times and are left with 40 ms per EF-G catalyzed translocation step, which is in good agreement with results from in vitro experiments performed under in vivo like conditions^29,42.

Moving on to unknown territory, we find the mean dwell time of initiator fMet-tRNA^fMet on ribosomes to be surprisingly short, around 70 ms (with an uncertainty of about 20% judging from the analysis of simulated data), which is on the lower limit of what has been reported from reconstituted systems ^16,45. These results suggest that initiation of translation is fast once the 30S·fMet-tRNA^fMet pre-initiation complex has formed, and that these steps do not represent a bottle neck during translation as can be inferred from in vitro kinetics experiments^14,16,29,44.

In conclusion, we have developed new experimental and analytical tools for direct measurements of reaction kinetics in live cells, with fluorescently labeled tRNAs as a case study. We have quantitatively validated our analysis through extensive analyses of microscopy simulations which include a cell-like geometry and experimentally derived background fluorescence, camera noise, and optical point-spread function. We are optimistic that this combination of experimental methods, data analysis, and careful validation on simulated microscopy data, will open up new possibilities to calibrate the wealth of knowledge obtained from in vitro biochemistry to the conditions in living cells, and to further explore the dynamics of biochemical pathways in vivo, including but not limited to the protein synthesis machinery.

Online Methods

Experimental details

tRNA labeling and charging

For coupling of Cy5 to the 4-thiouridine at position 8 of E. coli tRNA^fMet (Chemical Block, Russia) 16 nmol of tRNA^fMet in 75 µl of labeling buffer (50mM Tris-HCl, pH 8.5) was added to 1 vial of dry disulfo-Cy5 mono-reactive maleimide dye (GE Healthcare), and incubated at 37 °C with occasional vortexing. After 3 h, the labeling mixture was transferred to a new vial of the same dye and incubated for 3 more hours. Then 0.1 volume of 3M NaOAc (pH 5.0) was added and unreacted dye was removed by phenol-chloroform extraction (phenol:chloroform 5:1 v/v, pH 4.5). The tRNA was then precipitated in EtOH, and finally dissolved in MilliQ water. Typical labeling yield was 10 ± 3%.

For coupling of Cy5 to the 3-(3-amino-3-carboxypropyl)uridine at position 47 of E. coli tRNA^Phe (tRNA Probes), 12 nmol of tRNA^Phe in 85 µl of labeling buffer (0.9 M NaCl, 50 mM Na-HEPES, pH 8.0) was mixed with 1 µl of 320 mM disulfo-Cy5 mono-reactive NHS ester dye (Lumiprobe) dissolved in anhydrous DMSO and incubated at 30 °C with occasional vortexing. After 6 h, with another 1 µl of dye added after 3 h, 0.1 volume of 3M NaOAc (pH 5.0) was added, and unreacted dye was removed as described for tRNA^fMet. Typical labeling yield was approximately 70%.

3’ terminus labeling of tRNA^Phe. First, for 3’ ribose oxidation, tRNA^Phe (59 µM final) was mixed with NaOAc (100 mM final, pH 5.0) and freshly dissolved KIO₄ (5 mM final) in 60 µl and incubated on ice for 35 min. To quench the reaction 7 µl of 100 mM ethylene glycol was added and allowed to react for additional 5 min on ice. The tRNA was twice precipitated in EtOH and redissolved in 25 µl of labeling buffer (100mM NaOAc pH 5.0 and 200 mM KCl). The sample was mixed with 0.3 µl of 75 mM disulfo-Cy5 mono-reactive hydrazide dye (Cyandyes) dissolved in anhydrous DMSO and incubated at room temperature with occasional vortexing. After 5 h, with another 0.3 µl dye added after 2.5 h, unreacted dye was removed as described for tRNA^fMet. Typical labeling yield was 24 ± 4%.

[Cy5]-3’-tRNA^Phe was purified from unlabeled tRNA using RP-HPLC. The tRNA was eluted at room temperature and a flow rate of 0.5 ml/min applying a linear gradient of 15-90% buffer B in A over 58 min (Buffer A: 20mM NH₄OAc, 10 mM MgCl₂, 400 mM NaCl, pH 5.0 in water; Buffer B: 20mM NH₄OAc, 10 mM MgCl₂, 400 mM NaCl, pH 5.0 in 80% (v/v) MeOH in water). Collected fractions were concentrated using 3 kDa spin column (Millipore). From absorbance of the final sample, the fluorophore-to-tRNA ratio for [Cy5]-3’-tRNA^Phe was determined as 0.95.

Aminoacylation of [Cy5]tRNA^Phe was performed by incubating of [Cy5]tRNA^Phe (12 nmol in 500 µl final) at 37 °C for 30 min in buffer (50 mM Tris-HCl, pH 7.5, 50 mM KCl, 10 mM MgCl₂) supplemented with ATP (1 mM), PEP (10 mM), β-mercaptoethanol (3 mM), PP_iase (10 µg/ml), PK (50 µg/ml), MK (2 µg/ml), Phe (200 µM), and PheRS (0.6 µM). The reaction was quenched by the addition of 0.1 volume of 3 M NaOAc (pH 5.0) and enzymes were removed by phenol-chloroform extraction (phenol:chloroform 5:1 v/v, pH 4.5). Phe-[Cy5]tRNA^Phe was purified from unlabeled and deacylated tRNAs using RP-HPLC (Fig. 1a) as described above for [Cy5]-3’-tRNA^Phe with resulting fluorophore-to-tRNA ratio equal to 1.

[Cy5]tRNA^fMet was purified after labeling using RP-HPLC (Supplementary Fig. 6) as described above, but with the linear gradient of 25-90% buffer B in A over 50 min, with resulting fluorophore-to-tRNA ratio equal to 0.9. Aminoacylation and formylation of [Cy5]tRNA^fMet (1200 pmol in 500 µl final) was performed in the same way as aminoacylation of [Cy5]tRNA^Phe, with the following changes: Met (200 µM), and MetRS (1 u/µl) instead of Phe and PheRS; and the addition of methionyl-tRNA formyltransferase (2 u/µl) and 10-formyltetrahydrofolate (1 mM). fMet-[Cy5]tRNA^fMet were finally purified from deacylated (and non-formylated) tRNAs using RP-HPLC as described above for [Cy5]-3’-tRNA^Phe (Supplementary Fig. 6).

Purified tRNAs samples were stored in frozen aliquots (-80°C) at 9-12 µM concentration in 5 mM KOAc, 10 mM KCl, and 0.2 mM MgOAc (pH 6.1) (buffer exchanged using Bio-Spin P-6 gel flitration columns). [Cy5]-3’-tRNA^Phe was stored at 3 µM concentration in MilliQ water.

Cell strains and media

ElectroMAX DH5α-E electrocompetent cells (Invitrogen), referred to as DH5α in the main text, were diluted 5 times with 10% glycerol water solution and stored in 20 µl aliquots at -80 °C.

The CH2273 strain (kind gift from Diarmaid Hughes), with SmP (streptomycin pseudodependent) phenotype is a reconstructed version of CH184 ⁴⁶, and carries two mutations (P91Q, R86S) in ribosomal protein S12 (rpsL), in an MG1655 background.

The EF-Tu-mEos2 fusion (in strain PL22A9) was created by lambda-red recombination in strain BW25993 of a PCR fragment containing mEos2-CmR downstream of tufA. Homology to the 3' region of tufA was included in the PCR primers, tufA-mEos2_Fw and tufA_3’_P1_CmR_Rev (sequences below). As template, an existing in-lab plasmid containing mEos2 linked to a CmR cassette was used.

For observation of translation initiation on a defined mRNA, a T7-polymerase driven expression system was established in the DH5α strain as follows. DH5α cells were transformed with pCS6 (Addgene plasmid #55752)⁴⁷ bearing the T7 polymerase gene, and pET3c-MRLFV bearing a short peptide sequence which has been shown to be non-toxic to the cell ⁴⁸, under T7 polymerase promoter. Two variants with rare (AGG) and frequent (CGU) arginine codon were prepared. pET3c-MR^aggLFV and pET3c-MR^cguLFV were made by PCR amplification of the whole pDMF6 backbone (pET3c derivative) using the reverse primer longPCR_RV containing an NdeI restriction site and the forward longPCR_ArgR_FW or longPCR_ArgF_FW primers respectively (see sequences below) containing both the peptide gene and an NdeI restriction site in an overhang. The linear PCR product was digested with NdeI and then self-ligated. In order to check to what extent expression of T7 polymerase affects cells, DH5α cells carrying only the pCS6 plasmid were used.

Cells (except unmodified DH5α) were prepared electrocompetent based on the procedure suggested in ⁴⁹. A low density LB overnight culture (OD₆₀₀ ≤ 0.5) was diluted 100-200 times in SOB medium (lacking Mg²⁺). Cells were grown at 37 °C until they reached OD₆₀₀ = 0.4, then cooled in ice-water bath for 30 min, harvested and washed 4 times with cold 10% glycerol water solution. The OD₆₀₀ was adjusted to 60 ± 10, cells were aliquoted (20 µl) and frozen in EtOH/dry ice bath for storage or used immediately without freezing.

In bulk, CH2273 strain was grown in the presence of streptomycin 100 µg/ml, cells with plasmids were grown in the presence of antibiotics corresponding to existing antibiotic resistance cassettes (spectinomycin 30 µg/ml for pCS6 and carbenicillin 100 µg/ml for pET3c-MRLFV). Antibiotics were omitted from the cell washing step and later on, including recovery after electroporation and microscopy experiments.

EZ Rich Defined Medium (RDM, from Teknova) with glucose (0.2%) as carbon source, was reconstituted, aliquoted and stored frozen at -20 °C. SOB medium, lacking Mg²⁺ (2.0% tryptone, 0.5% yeast extract, 10 mM NaCl, 2.5 mM KCl, pH 7.0), was prepared in house.

Primers for plasmid construction and lambda-red recombination

longPCR_RV: 5’-GATCGGTTAAATTATCAAACATATGTATATCTCC-3’

longPCR_ArgR_FW: 5’-TCATATCATATGAGGTTATTTGTTTAAGGATCCGGCTGCTAACAAAG-3’ (Arg codon is underlined)

longPCR_ArgF_FW: 5’-TCATATCATATGCGTTTATTTGTTTAAGGATCCGGCTGCTAACAAAG-3’ (Arg codon is underlined)

tufA-mEos2_Fw: 5’-CGTACCGTTGGCGCGGGCGTTGTTGCTAAAGTTCTGGGCATGAGTGCGATTAAGCCAGAC-3’ (Homology to 3' of tufA is underlined)

tufA_3’_P1_CmR_Rev: 5’-CGTTCTGACAGTACGAATAAGATATGCCGTCAACAAATGCGAAGCAGCTCCAGCCTACAC-3’ (Homology to downstream region of tufA is underlined)

In vitro dipeptide assay

Rapid kinetics dipeptide experiments using dye-labeled or unlabeled tRNAs were performed in polymix buffer in a quench-flow instrument according to ⁷. For [Cy5]tRNA^Phe experiments, 70S initiation complex carrying f[³H]Met-tRNA^fMet in P site and displaying UUU codon in A site, were reacted with the preformed Phe-[Cy5]tRNA^Phe·EF-Tu·GTP (or unlabeled Phe-tRNA^Phe) ternary complex. For [Cy5]tRNA^fMet experiments, 70S initiation complex carrying fMet-[Cy5]tRNA^fMet in P site (or unlabeled fMet-tRNA^fMet) and displaying UUU codon in A site, were reacted with the preformed [³H]Phe-tRNA^Phe·EF-Tu·GTP ternary complex. The extent of dipeptide formed was analyzed using RP-HPLC, and the data was fitted to a single-exponential equation using Origin (OriginLab). All components of the reconstituted protein synthesis system was a kind gift from Ehrenberg and Sanyal labs (Uppsala University, Sweden). The purification procedures of the components have been published in detail before (e.g. ⁷ and references therein).

Cell growth rates in bulk

Cells were grown overnight at 37 °C in RDM. 0.4 - 0.5 µl of overnight culture (the volume was adjusted to have equal final optical densities for different cell strains) were then inoculated in 200 µl fresh preheated RDM on a microplate and cells were grown at 37 °C in a microplate reader (Infinite M200 or Spark 10M, Tecan). Optical densities were measured every 5 min with a prior 1 min orbital shaking.

For the CH2273 strain, the overnight culture was grown in the presence of streptomycin (100 µg/ml) and diluted on the plate in the fresh RDM with or without streptomycin (100 µg/ml).

For overexpression of short peptides, modified DH5α cells and DH5α (with pCS6 only) were grown according to the general description above up to early exponential phase when expression of the peptide was induced by addition of arabinose (0.2%) and cAMP (1 mM). For non-induced cells, an equivalent volume of RDM was added.

A blank was subtracted from the growth curves and the exponential part of the curve was fitted with a rise exponential function in MagicPlot (MagicPlot Systems). For presentation in Supplementary Figs. 4 and 6, the data from one experiment (4-5 individual wells) were averaged. For doubling time estimation, the data from 2 independent experiments (4-5 individual wells each) were fitted separately and the results were averaged.

Electroporation and microscopy

20 µl of cells (OD₆₀₀ = 60 ± 10) were mixed with 2 pmol dye-labeled tRNA and incubated on ice for 1 min. The sample was transferred into an ice-cold 1 mm electroporation cuvette. Electroporation was performed using a MicroPulser instrument (Bio-Rad) by applying a 1.9 kV pulse (1.5 kV for MG1655 and CH2273 strains) which typically resulted in a decay time constant of 5.7 ± 0.1 ms. 500 µl of RDM (room temperature) was immediately added to the cuvette, and the cells were allowed to recover for 30 min shaking at 37 °C. The cells were then harvested by centrifugation (1150 rcf, 75 s) and washed 3 times with 37 °C RDM medium to remove non-internalized tRNA. Cells were re-suspended in RDM to OD₆₀₀ = 0.03, sparsely spread onto a 2% agarose pad (made with RDM) containing 3 µM of SYTOX Blue dead-cell stain. The sample was mounted on the microscope, where single cells were allowed to grow and divide to form mini-colonies of the size of 4-8 cells prior to imaging. The temperature of the sample was maintained at 37 ± 2 °C using a cage incubator encapsulating the microscope stage.

For rifampicin (200 µg/ml) and tetracycline (10 µg/ml) treatment, RDM containing antibiotic and SYTOX blue (3 µM) was injected to the sample with mini-colonies approximately 100 min after sample preparation. Imaging was performed 70-200 min later.

For overexpression of the short peptide, cells were allowed to form mini colonies and injection of RDM containing arabinose (0.2%), cAMP (1mM) and SYTOX blue (3 µM) was performed approximately 70 min after sample preparation. Imaging was performed 80-180 min later. In the control experiment with cells carrying only the pCS6 plasmid, induction was made by the injection of the same medium approximately 40 min after sample preparation and imaging was performed 70-140 min later.

For tracking of the EF-Tu-mEos2 fusion protein, an overnight culture of the PL22A9 strain in LB was diluted in RDM and grown until OD₆₀₀ ≈ 0.7. Cells were then spread onto a 2% agarose RDM pad, and grown for about an hour at 37°C before data acquisition.

Each microscopy experiment was performed in 2 – 5 replicas (each comprising 10-100 cell colonies with internalized [Cy5]tRNA. See Supplementary Table 1 for number of replicas) on different dates, generally using the same batches of electrocompetent cells and labeled tRNAs. The data was found consistent in between different repetitions and were combined for analysis.

Optical setup

An inverted microscope (Nikon Ti-E) with a CFI Apo TIRF 100x 1.49 NA (Nikon) objective was used. Fluorescence and bright-field images were recorded on an Andor iXon 897 Ultra EMCCD camera equipped with an additional 2.0x lens (Diagnostic Instruments DD20NLT). For phase contrast imaging, an Infinity 2-5M (Lumenera) camera was used. For [Cy5]tRNA tracking, a 639 nm laser (Coherent Genesis MX 639-1000 STM) with an output power density of 4.5 kW/cm² on the sample plane was used in stroboscopic illumination mode with 1.5 ms laser/5 ms camera exposures. For SYTOX Blue imaging, a 405 nm laser (Cobolt MLD) with an output power density of 17 W/cm² on the sample plane was used with continuous exposure of 21 ms.

For EF-Tu-mEos2 fusion protein tracking, cells were pre-bleached with 561 nm laser (Coherent Genesis MX 561-500 STM) (2 kW/cm², 5 s continuous exposure) in order to reduce fluorescent background. Then the photo-switchable mEos2 protein was activated with 405 nm laser (17 W/cm², 2 s continuous exposure) and tacking was performed with the same 561 laser in stroboscopic illumination mode with 4 ms laser/5 ms camera exposures.

The microscope was controlled using µManager, and automated acquisitions were performed using an in-house written µManager plugin.

Simulated single-molecule microscopy

Simulated reaction-diffusion kinetics The simulation geometry is illustrated in Fig. 4a, and the simulation parameters of the simulated models are given in Supplementary Table 2, where model 1 corresponds to the default model. The corresponding MesoRD model files are included in the supplementary software.

PSF measurement As a model of point-sources, fluorescent microspheres (FluoSpheres F8783) of size 0.02 μm were excited by 639 nm laser and imaged with the objective described above and a DMK 23U274 camera (The Imaging Source). The resulting image pixel size was 44 nm. A z-stack with 50 nm steps over a range of 10 μm was acquired with 300 ms exposure time.

PSF model construction (Supplementary Fig. 5a). A 100-by-100 pixel area with a single spot was manually selected, and a range of 61 image z-steps was extracted. The raw data was de-noised by removing an offset/background threshold of 1000 (roughly the 80% intensity quantile), and applying a mask, constructed as follows. First, pixels with intensity above the threshold was set to 1, and zero otherwise. Second, a morphological opening operation was applied (an erosion followed by a dilation) using a structuring element in the form of disk of radius 2 pixels, in order to remove small islands of spurious intensity, and finally normalize each image plane by the total intensity of the brightest plane. The reference position (x₀,y₀) of the PSF model was taken to be the radial symmetry center ⁵⁰ at the focal plane.

PSF simulation During SMeagol³³ simulations, a simulated photon emission event at (x_E,y_E,z_E) generates a photon on the camera chip at position (x_E+Δx,y_E+Δy). We define the 2-dimension distribution of (Δx,Δy) relative to the reference position (x₀,y₀)=(x_E,y_E) to be proportional to the normalized pixel intensity of the above PSF model, uniformly distributed in the PSF model pixels. Note that the normalized intensity, which we call p_F(z), is less than 1 for all image planes but one. We take this to mean that there is a finite probability 1-p_F(z) that the emitted photon is scattered outside the camera chip, which effectively models a z-dependent spot intensity. For efficient sampling, we factorize the PSF distribution as:

$$p\left(\Delta x,\Delta y|z\right)=p_F\left(\Delta x,\Delta y<\infty |z\right)p_x\left(\Delta x|z\right)p_y\left(\Delta y|\Delta x,z\right),$$

and create z-dependent lookup tables for p_F, p_X, and p_Y which are used during simulation. Matlab functions for constructing and sampling from the PSF model is attached in the supplementary software.

Simulated video microscopy The simulated movies are built in steps, starting from an experimental background, and then looping through each simulated cell position, where a few new fluorophore traces are added on top of the output from the previous iteration. A set of a few experimental background movies was used, were intensities varied slightly within experimental reproducibility. Since the simulation software does not generate phase contrast images, we simulated well separated cells and did not try to simulate the cell segmentation process. An example script of this simulation protocol, including runinput files and an experimental background movie, is given in the supplementary software.

Quantification and statistical analysis

Camera calibration

An image series using the experimental protocol was acquired, but with the EMCCD camera shutter closed. EMCCD offset, gain, and readout noise were estimated by fitting a statistical model suitable for low light intensity (one or zero photons per pixel) to the image series. These images mainly consist of electronic readout noise, plus occasional photons generated spontaneously on the EMCCD camera chip and electronmultiplied just like normal photoelectrons. Assuming that this dark current is low enough to generate at most one photon per frame and pixel leads to a pixel intensity distribution with a more tractable form than at higher intensity, and also circumvents the experimental difficulty of generating a stable and even illumination. In particular, dark images were modeled with a mixture model, where the value c_i,t of pixel i at time t is modeled as:

$$c_{i,t}=o_i+{\xi }_{i,t}+s_{i,t}\cdot m_{i,t}$$

Here, o_i is a constant offset, ξ_i,t are independent identically distributed (iid) Gaussian noise with zero mean and standard deviation σ, s_i,t are iid indicator variables that takes value 0 or 1 depending on whether a dark current electron was present or not, with p(s_i,t=1)=q, and m_i,t, models the electron multiplication noise of a single photoelectron by iid exponential variables with mean value 1/g, where g is the effective EMCCD gain. A very similar approach was used by ⁵¹, however, we explicitly include readout noise also for the dark current photons (s=1), but neglects spurious charges in the EM gain register. An expectation maximization algorithm was implemented to extract maximum-likelihood estimates of o_i, σ, q, and g from dark movies. The EM algorithm can be found as part of the uncertainSPT package¹⁸. At the light intensities (<0.01 photons per pixel) and data sets (50-200 frames), the EMCCD gain parameter is usually recovered within a few percent.

Single particle tracking

Cell segmentation For practical reasons, fluorescence movies of colonies with no or very few fluorescent tRNAs (≤ 2 fluorophores per cell colony) were not included in the analysis. Cell outlines were extracted from phase contrast images using the algorithm in ⁵², and incorrectly segmented or dead (SYTOX stained) cells where manually removed. Alignment between segmentated images and the fluorescence channel was done using landmarks in phase contrast and brightfield images. On a few occasions (≤ 2 cells per dataset), cells with what appeared to be fluorescent impurities or unspecifically bound fluorophores, completely immobilized for longer than 100 frames, were omitted from the analysis.

Spot detection, localization, and trajectory building Spots were detected using the the radial symmetry-based method of ¹⁷, as implemented by http://www.peterkovesi.com/matlabfns/Spatial/fastradial.m. Spot positions and position uncertainty were estimated using a symmetric Gaussian spot model and the maximum aposteriori fit ¹⁸, and trajectories were built using uTrack ¹⁹. We excluded spots >3 pixels outside live cells, spots with width (std) > 280 nm, spots with amplitute < 50 photons, and spots in cells with >2 spots. See Supplementary Notes for details.

Mean square displacement plots To extract mean-square-displacement (MSD)-based estimates of diffusion constants, trajectories were divided in segments of 7 positions, an MSD curve was computed using x- and y coordinates, and the apparent diffusion constant for that curve was estimated by a linear fit through the origin, i.e. MSD(t) = 2dDΔt∙t, using the first two points (t=1,2) of the MSD curve for each segment. Here, d = 2 is the dimension of the trajectories, Δt = 5 ms is the time step, and the apparent diffusion constant D is the fit parameter. This neglects a small offset due to motion blur and localization errors ⁵³, but constrains the estimate of D to be non-negative.

Hidden Markov modeling We used a diffusive HMM algorithm¹⁸ to analyze 2-dimensional trajectories (motion in the z, y plane). This HMM fits ensembles of trajectories for each experimental condition to a global model, handles missing positions, and makes explicit use of positions as well as localization uncertainties of each position¹⁸. The algorithm was restarted with 100 independent initial values to find global maximum likelihood estimates (MLE) parameters, initial state probability, transition probabilities, and diffusion constants, for each considered model size. In addition, we used custom scripts to systematically prune states and build smaller models, similar to the greedy search used by vbSPT³. We then used AIC²¹ to select the optimal model. Diffusion constant are estimated directly by the HMM maximum likelihood algorithm, as are posterior hidden state probabilities for each time step that we use to estimate overall occupancy. Mean dwell times were estimated from the diagonal of the maximum likelihood estimate of the HMM transition matrix, i.e., from the average probability of exiting a diffusive state. This mean dwell time estimate does not make use of dwell time histograms, and therefore works also when photobleaching and tracking difficulties produce trajectory lengths below the mean dwell time (Supplementary Fig. 5d), although an upward bias (probably due to the difficulty of detecting short events) is visible (Fig 5c).

To condense an HMM with many states to an effective two-state description, and guard against the tendency for AIC to overfit HMM-like models ³⁸, the hidden states were classified as "fast" or "slow" using a threshold value of 1 μm²/s (and 0.5 and 1.5 μm²/s as a robustness control). Coarse-grained occupancies and diffusion constants were calculated as weighted averages, while coarse-grained mean dwell times were estimated from a coarse-grained transition matrix (for details, see the function EMhmm.parameterEstimate in the uncertainSPT suite, https://github.com/bmelinden/uncertainSPT).

For spatial occupancy plots, positions were classified as belonging to a certain (coarse-grained) hidden state if the HMM posterior probability was > 95%, whereas more ambiguous positions were excluded.

EF-Tu-mEos2 tracking was performed similar to [Cy5]tRNA with the following changes. A scale factor of 1.9 for gaussian kernel radii and a threshold of 6.5 for spot extraction were used in the dot detection step. Spots with spot amplitude < 200 photons were discarded. For trajectory building, the search radius was constrained to 800 nm (non-adaptive), and gaps of up to two missing positions were allowed.