Malaria Ecology, Child Mortality & Fertility

Abstract

The broad determinants of fertility are thought to be reasonably well identified by demographers, though the detailed quantitative drivers of fertility levels and changes are less well understood. This paper uses a novel ecological index of malaria transmission to study the effect of child mortality on fertility. We find that temporal variation in the ecology of the disease is well-correlated to mortality, and pernicious malaria conditions lead to higher fertility rates. We then argue that most of this effect occurs through child mortality, and estimate the effect of child mortality changes on fertility. Our findings add to the literature on disease and fertility, and contribute to the suggestive evidence that child mortality reductions have a causal effect on fertility changes.

1. Introduction

The broad determinants of fertility are thought to be reasonably well identified by demographers, though the detailed quantitative drivers of fertility levels and changes are less well understood. The relationships between fertility and economic development, the status of women, access to family planning, pro-natalist or pro-planning policies, and mortality (both adult and child), have been elegantly theorized. Likewise, many researchers have empirically modeled these relationships in both cross-country and within-country analyses.

In quantitative terms, however, we continue to lack a good understanding of why some countries have experienced significant reductions of fertility rates, while many remain with very high fertility rates. Figure 1 maps the change in total fertility rates from 1965–2005, highlighting the variation across the developing world and even with regions. Much recent work has focused on the role of disease burden in driving fertility rates (Wilson, 2015; Lucas, 2013; Kalemli-Ozcan and Turan, 2011; Bleakley and Lange, 2009), with inconsistent results.

Figure 1:

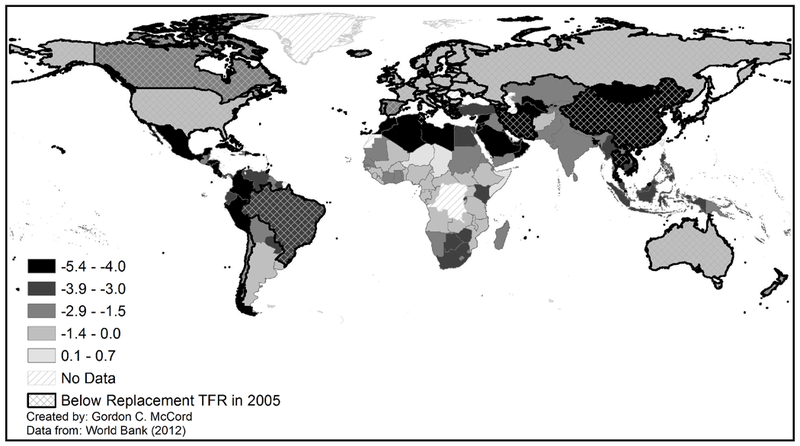
Change in Total Fertility Rates from 1965–2005

Most theories of the demographic transition put great stress on the causal link from high child mortality to high desired fertility. Simply put, when parents do not know whether their children will survive, they respond by having large families. In a high mortality context, cultural patterns age of marriage, social norms in child rearing, community support structures also favor high natality. The original model of the demographic transition, indeed, was driven almost solely by child mortality rates. Exogenous changes to child mortality (e.g., the advent of public health, safe drinking water, improved nutrition) were seen as the primary precursor to reduced fertility rates albeit with a lag of one or more generations. This lag reflected two things according to the standard analysis: first, the lag in perception of households that mortality rates had indeed come down persistently and reliably; and second, the lag in cultural norms surrounding marriage age, birth spacing, and family size all needed to promote the transition from high to low fertility. That said, recent experience suggests that the lag may be waning and that demographic transitions are happening with increased rapidity once “triggered” : whereas Western Europe’s transitions took over a century (1800–1930 for Britain), more recent large declines in fertility have happened in as little as twenty or fewer years, such as in Bangladesh, Mauritius, and Iran (Marandi et al., 2006). Most research attributes these declines to changes in access to family planning (Cleland et al., 1994; Aghajanian, 1991), though in some countries like Colombia family planning explains less than 10% of fertility decline (Miller, 2009). Other scholars emphasize female education (Lavy and Zablotsky, 2015) and child mortality (Raftery, Lewis, and Aghajanian, 1995), and still others suggest that with the advent of mass media, cultural changes such as those related to fertility behavior spread more rapidly than they once did (Cleland and Wilson, 1987; Bongaarts and Watkins, 1996). These shortening lags and the challenge of identifying the causal e ect of these factors leave open questions as to the relative importance of child mortality reduction in the context of 20th century fertility declines.

One issue that complicates this line of research is the question of causal directionality between child mortality and fertility choice. As explained in Ronsmans (1996), there is a direct biological effect of high fertility on child survival: short birth intervals can prevent mothers’ nutrient repletion in low-income settings, thus compromising the mother’s ability to provide nutrients to the fetus during pregnancy. Moreover, several scholars have shown that reduced family size affects human capital investment (Mogstad and Wiswall, 2016; Conley and Glauber, 2006; Joshi and Schultz, 2005). Likewise, the argument can be made that at least some of the powerful correlation represents increased child mortality due to higher fertility because of increased strain on household caloric resources and decreased parental care and supervision with the addition of more children.

With these concerns in mind, this paper uses a novel ecological index of malaria transmission exogenous to human intervention to study the effect of malaria on fertility. We find that temporal variation in malaria ecology is well-correlated to mortality, and pernicious malaria conditions lead to higher fertility rates. We then argue that most of this effect occurs through child mortality, and use an instrumental variable approach to estimate the effect of child mortality changes on fertility. Our results suggest that child mortality still plays a powerful role in fertility choice, an order of magnitude larger than the effect identified in some other studies using an IV approach (Schultz, 1997; Benefo and Schultz, 1996; Drèze and Murthi, 2001). We mention potential caveats to the identification strategy, but argue that the value of presenting a time-varying instrument to this literature is higher than the potential costs from concerns about the exclusion restriction. Our findings add to the literature on disease and fertility, and contribute to the suggestive evidence that child mortality reductions have a causal effect on fertility changes.

The paper proceeds by introducing an ecological index of malaria transmission strength in Section 2, followed by a discussion of relevant literature on child mortality and fertility in Section 3. Section 4 lays out the estimation strategy while Section 5 describes the data. Section 6 presents results and then Section 7 concludes.

2. Malaria Ecology and Mortality

To preview our empirical approach, we argue that the strength of malaria transmission as a function of ecological factors is exogenous to social dynamics, and use malaria ecology to study the disease’s effect on child mortality and fertility. Over our study period, malaria is the fourth leading cause of death (after neonatal disorders, diarrhea, and pneumonia) for children under five in low income countries (Black, Morris, and Bryce, 2003) and is responsible for at least one in every five child deaths in sub-Saharan Africa. Recent work associates up to 79% of the infant mortality reduction in malaria endemic zones of Kenya with the increased ownership of insecticide-treated bednets (Demombynes and Trommlerova, 2016). Malaria mortality, in turn, is highly sensitive to ecological conditions, allowing us to isolate exogenous variation in malaria and child mortality rates, with which we identify a causal effect on fertility.

Specifically, we employ an ecological index of malaria transmission used elsewhere in the literature (Kiszewski et al., 2004; Carstensen and Gundlach, 2006; McCord, 2016). The index is calculated monthly at a 0.5 degree spatial resolution (around 50 km at the equator), although in our analysis we aggregate it to the country level in 5-year averages to match the fertility data.¹ The index combines ecological factors—rainfall and temperature—with biological ones such as the human biting preference of each month’s dominant mosquito species that serves as the vector for the transmission of malaria [see McCord (2016) and the appendix for more details]. It is worth highlighting that the malaria ecology index does not include any information on human population nor on mosquito abundance; both variables affect actual malaria outcomes but are endogenous to fertility and public health efforts and are excluded from the index construction. The 1960–2010 average malaria ecology index is mapped in Figure 2 at the original 0.5 degree resolution, while Figure 3 maps the standard deviation of each country’s average MEI over the time period. The maps show that sub-Saharan Africa has the most pernicious malaria ecology over time, but that it also experiences the highest variability over time (this variability is what we exploit in our empirical work). While the underlying factors determining malaria transmission may be endogenous to human population movements over the course of thousands of years (through co-evolution with mosquito species), we assert that on the scale of recent decades the biophysical ecology of malaria transmission is exogenous. We employ a time-varying version of malaria ecology: this allows us to pursue a longitudinal strategy across countries over time, which in turn allows for a fixed-effects approach to factor out time-invariant country-specific determinants of fertility. The index varies month to month only with changes in temperature and changes in the dominant anopheles vector due to seasonality or varying precipitation. Each anopheles has a different preference for biting humans, referred to as a human biting index (HBI). Many parts of the world have both stable Anopheles vectors (breeding on brackish or other waters, with life cycles less sensitive to precipitation) and unstable vectors (which depend on a minimum level of precipitation for breeding). This means that there is year-to-year variation in the dominant vector of the grid cell as precipitation varies, and country-level fixed effects do not absorb the variation in the HBI portion of the malaria ecology index.

Figure 2:

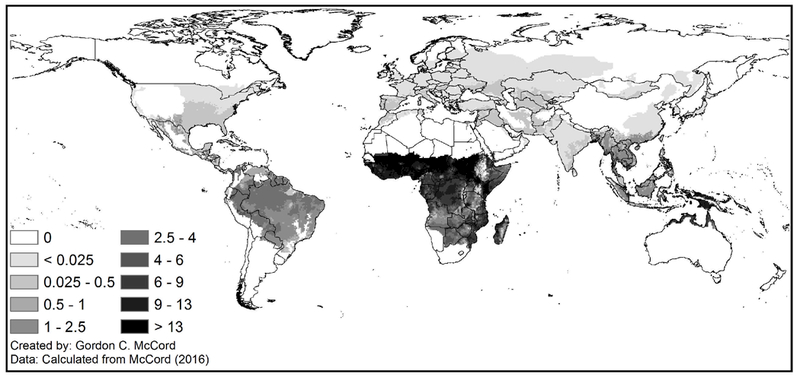
1960–2010 Average Malaria Ecology Index

Figure 3:

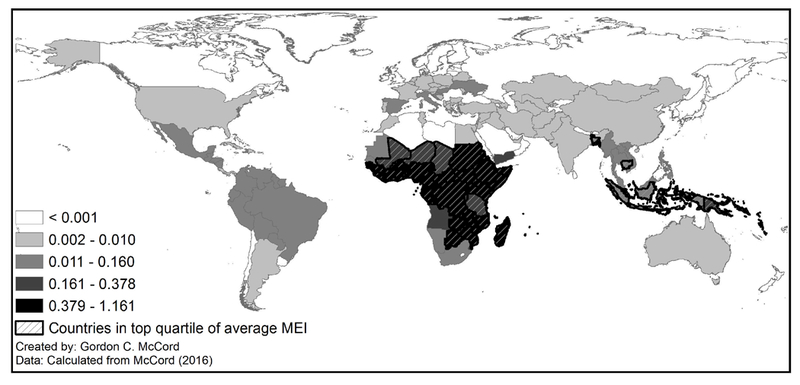
Standard Deviation of Country Average Malaria Ecology Index, 1960–2010

Temperature and precipitation are components of the index and likely affect fertility through other channels, for example through agricultural production (Jones and Olken, 2010) and thus the return to children’s labor on the eld. Another channel includes tropical weather-sensitive diseases besides malaria, such as sleeping sickness, dengue or yellow fever. However, the climatic variables enter the index in a specific nonlinear form emerging from the epidemiological dynamics of malaria, as illustrated in Figure 4. The figure shows the index at all levels of precipitation and temperature for an HBI of 0.5, as well as the value of several countries during an average month. Our identification comes from a very specific interaction of the anopheles vector (which does not cause other diseases besides malaria) and the weather. We nonetheless demonstrate that the effect of malaria on child mortality and on fertility is robust to controlling for temperature and precipitation as well as agricultural yield.

Figure 4:

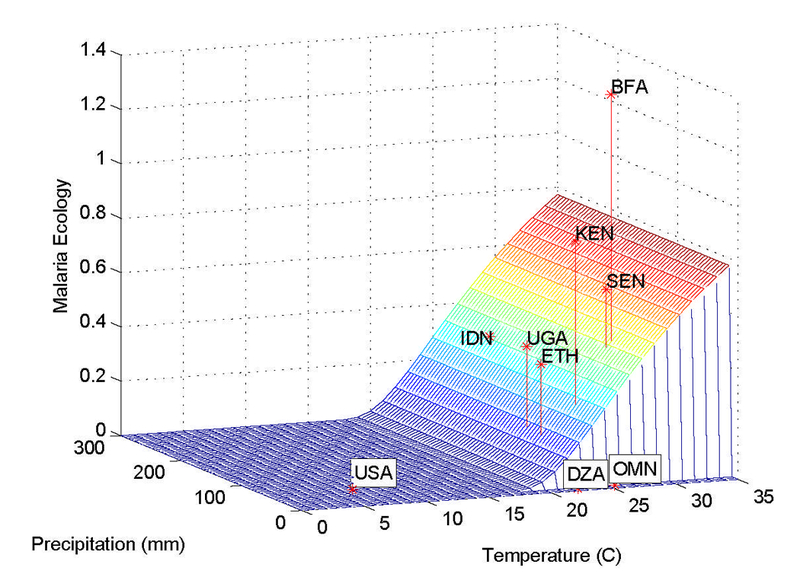
Malaria Ecology, Temperature and Precipitation for HBI = 0.5

3. Child Mortality and Fertility

Five possible relationships between fertility and mortality are supported in the literature. First, child mortality could affect fertility (the theory of demographic transition and choice theory) whether through child “hoarding” (as a precautionary insurance mechanism to guarantee surviving heirs) (Heer and Smith, 1968) or direct replacement (Cleland, 2001). Second, there could be a causal relationship from fertility to mortality. There is a direct biological effect of high fertility on child survival: short birth intervals can prevent mothers’ nutrient repletion in low-income settings, thus compromising the mother’s ability to provide nutrients to the fetus during pregnancy (Ronsmans, 1996; Maitra and Pal, 2008). Moreover, Caceres-Delpiano and Simonsen (2012) find evidence in the U.S. indicating that mothers with more children are more likely to suffer marital breakdown, receive welfare, and fall below the poverty line; in addition, fertility shocks increase the likelihood of mothers suffering from high blood pressure and obesity. In addition, the number of children affects risk of malaria-related death due to transmission across children, weakened immune systems due to caloric challenges, parental investment decisions (quality / quantity tradeoff ) and so on. Reduced family size has been found to affect human capital investment on the micro level (Conley and Glauber, 2006; Joshi and Schultz, 2005; LeGrand and Phillips, 1996)

Third, there could be an interdependent relationship between mortality and fertility, not only via the rst two mechanisms but also a shift along a quantity-quality tradeoff as countries transition out of a Malthusian dynamic and the returns to human capital investment increase (Galor and Weil, 2000; Chowdhury, 1988). Fourth, the relationship could be only temporary; the influential Becker-Barro economic theory of fertility postulates that falling child mortality lowers the average cost of raising surviving children since a greater proportion of the total investment in child rearing costs realizes a benefit (assuming little or no benefits from non-surviving children). Although fertility rates initially rise as child mortality declines, the theory predicts that the long-run depressive effect on fertility can only occur through changes in interest rates or parents’ wage rates (Becker and Barro, 1988). This comes from the fact that the Becker-Barro model assumes a target number of children that is independent of the child survival rate, so that a decline in child mortality leads to a compensating decrease in the birth rate. The long-term elasticity of 1 in the mortality-fertility relationship is a product of the choice in functional form (the short-term e ect of a mortality decline on fertility is ambiguous). Kalemli-Ozcan (2002) more explicitly focuses on the result of a change in child mortality by assuming that parents’ utility is convex in the number of surviving children and that parents take the uncertainty of child survival into account by having a precautionary demand for children. Thus when child mortality decreases, the resulting fertility reduction overcompensates for the change in child mortality, resulting in a shift along the quantity-quality tradeoff . Fifth, there may be no causal relationship between child mortality and fertility, and the two are spuriously correlated by being jointly determined in the process of economic development.

Empirical tests of these theories have tried to distinguish between child hoarding and child replacement with inconclusive results (Doepke, 2005; Chowdhury, 1988), while others have found that fertility rates impact mortality rates and not vice versa (Zakir and Wunnava, 1999). However, these specifications fail to acknowledge the causal directionality between child mortality and fertility choice, leading to mis-specified models. Other work tackles the estimation challenge using instruments for child mortality such as caloric availability (Schultz, 1997), presence of community health services and environment (Benefo and Schultz, 1996), and access to safe drinking water (Drèze and Murthi, 2001). None of these instruments are perfect, however, since one can imagine violations of the exclusion restriction in that they are correlated to economic development broadly. Moreover, all of the studies find either no statistical effects of instrumented child mortality on fertility in a panel, or a puzzlingly small elasticity. Converting the coefficients in these studies to percentages using sample means yields elasticities as low as 0.02–0.11, implying that “…four to fteen fewer child deaths are associated with a reduction of only one birth. We have no good explanation for the small size of this estimate of the fertility response to child mortality.” (Benefo and Schultz, 1996).

Quasi-experimental work using survey data has also led to varied conclusions on the effect of child mortality changes on fertility. Lucas (2013), for example, finds that malaria elimination in Sri Lanka increases likelihood of pregnancy. Wilson (2015) finds that expansion of health services to reduce mother-to-child transmission of HIV in Zambia decreases fertility rates. Bleakley and Lange (2009) find that hookworm eradication in the United States decreased fertility and increased investments in child education. Nobles, Frankenberg, and Thomas (2015) find that increased mortality due to the Indian Ocean tsunami in Indonesia led to higher fertility in women who had lost children as well as an earlier first birth among women in hardest hit communities. While these studies suggest that reduction of both morbidity and mortality reduces fertility, Wilson (2015) reviews other quasi-experimental work and notes that the effect of disease burden on fertility might be different depending on whether it is adults or children experiencing the burden, and whether the burden is mostly morbidity or mortality. Our work contributes to this literature by focusing on exogenous variation in a disease that causes significantly higher disease burden on children than adults.

4. Specifications

4.1. Malaria Ecology and Mortality

As a motivation for the adequacy of the malaria ecology instrument, we test its relationship to national level malaria mortality data from 1990–2005 as reported by the World Health Organization (Aregawi et al., 2008). The following specification tests the predictive power of the ecology-based malaria index on aggregate malaria mortality measures:

$$ln\left(malariamor{t}_{iy}\right)={\theta }_0+{\theta }_{1}ME{I}_{iy}+{\delta }_i+{\tau }_y+{\delta }_i\ast t+e_{iy}$$ (1)

We regress the annual malaria mortality (deaths per thousand people) for each country i on the malaria ecology index (MEI) for that year y, while controlling for country fixed effects (δ_i) and year fixed effects (τ_y), as well as country-specific time trends. Observations are weighted by population in order to account for the higher variance expected in smaller countries. Moreover, the serial correlation in our dependent variable may bias standard errors, which we adjust for by reporting Huber-White standard errors clustered by country in all regressions (Bertrand, Duflo, and Mullainathan, 2004).

4.2. Malaria Ecology and Fertility

We estimate the total effect of variation in malaria burden on fertility rates using the following reduced form equation:

$$ln\left(TotalFertilityRat{e}_{it}\right)={\beta }_0+{\beta }_{1}ME{I}_{it}+\Phi X_{it}+{\delta }_i+{\delta }_t+e_{it}$$ (2)

Note that the time subscript has been changed to t, since the temporal resolution of the fertility data is in 5-year averages. The advantage of using the MEI instead of malaria-related outcomes is that the latter are correlated to unobserved determinants of fertility (health system investments or income growth, for example). Using exogenous temporal variation in the MEI allows us to isolate the effects of malaria on fertility. Aggregating the MEI to 5-year averages reduces the variation, but does not diminish the degree to which the variable is exogenous.² The specification includes country dummies to control for time-invariant country characteristics that affect fertility, and regressions include global time dummies to flexibly control for secular trends. Controls include other fertility drivers such as average years of secondary school attainment among women, income per capita, temperature, precipitation, and cereal yields per hectare. There are many other variables affecting fertility decisions and outcomes, however they would only induce bias in our estimate of the malaria effect if they were correlated to each country’s temporal variation in the ecology of malaria transmission. As with other specifications, standard errors are clustered by country given serial correlation in the dependent variable.

4.3. Instrumenting for Child Mortality

The reduced form regression captures the total effect of malaria on total fertility rates, assuming that the malaria ecology is uncorrelated to other fertility drivers after partialling out country fixed effects and other controls. Given the importance of the role of child mortality changes in demographic dynamics, we use our malaria ecology index to contribute an empirical estimate of this relationship. Note that another strategy might have been to focus only on child deaths due to malaria as the endogenous variable, instrumented by malaria ecology. The two problems with this strategy stem from a lack of data. First, the cross-country panel data on malaria deaths is not available by age group, meaning that it includes deaths of children above the age of 5 and of adults. Secondly, cross-country malaria mortality data only begin in 1990, which would leave us with an insufficient timespan to study variation in fertility in the medium term (all-cause child mortality data, on the other hand, begin in 1960). Third, national reporting of malaria mortality is of notoriously poor data quality (Alonso and Tanner, 2013). Moreover, all-cause mortality is relevant given that pernicious malaria ecology can lead to child death not only due to severe malaria but also to opportunistic infections affecting immunosuppresed children parasitemic with malaria. Since malaria is a disease that mostly kills children [77% of global malaria deaths are in children under age 5 (World Health Organization, 2015)], we instrument for child mortality using malaria ecology using the following first and second stage specifications:

$$ln\left(ChildMortalit{y}_{it}\right)={\alpha }_0+{\alpha }_{1}ME{I}_{it}+\xi X_{it}+{\gamma }_i+{\gamma }_t+{\nu }_{it}$$ (3)

$$ln\left(TotalFertilityRat{e}_{it}\right)={\lambda }_0+{\lambda }_{1}ln\left(ChildMortalit{y}_{it}\right)+\text{Γ}{X}_{it}+{\delta }_i+{\delta }_t+e_{it}$$ (4)

Several caveats are in order with this specification. In order for malaria ecology to be a valid instrument, it is important that the instrument affect fertility only through child mortality. A review of the medical literature shows that malaria may have a direct effect on fertility through malaria-related severe anemia, reduced coital frequency, increased incidence of hypertensive diseases of pregnancy, and spontaneous abortion (Etard, Kodio, and Ronsmans, 2003; Maubert et al., 1999; Sartelet et al., 1996). Indeed, malaria elimination in Sri Lanka caused women to have their first live birth at a younger age, consistent with the fact that primagravidae are most at risk of spontaneous abortion due to malaria (Lucas, 2013). Since these effects of malaria prevent a live birth, and since the total fertility rate (TFR) counts only live births, then this effect should bias our estimate of the causal effect of child mortality on fertility toward zero.³

Maternal malaria during pregnancy is also associated with low birth weight and increased neonatal and infant mortality which is in line with our models. That said, there is some evidence that malaria may reduce lactation period (Bates et al., 2004), which might increase fertility through decreased child spacing. Malaria might also increase maternal mortality, however this does not a ect the calculation of total fertility rates; TFR is calculated as the average number of children a hypothetical woman would have if she were subject during her life to the fertility rates of a given period.

Malaria also causes morbidity in children, which might lead to a behavioral response in fertility. The Becker-Barro model of quantity-quality tradeoff suggests that changing incomes and the price of surviving children due to malaria would change fertility behavior and thus violate the exclusion restriction. Morbidity also affects cognition and therefore the returns to schooling. Bleakley (2010) finds that anti-malaria campaigns in four countries where malaria is largely not lethal led to children growing up to enjoy higher productivity and incomes, and also suggests e ects on schooling attainment. This changes the price of child quality in the Becker-Barro model, also potentionally violating the exclusion restriction of the instrument. Finally, adult mortality may have an independent effect on fertility (and child human capital investment) by changing the discount rate of mothers and fathers (Lorentzen, McMillan, and Wacziarg, 2008). However, we note that although malaria can kill adults, most malaria mortality occurs among children.

Although our instrumental variable strategy solves some of the issues in estimating the child mortality effect on fertility, we acknowledge the important caveats above and suggest the reader interpret the results with due caution.

5. Data

We compiled a national-level, cross-country dataset divided into 5-year intervals, beginning in 1960 and ending in 2010. This is determined largely by the fact that the U.N. Population Division, our main source for demographic data, uses five year averages for several of the key demographic variables considered in our analysis, such as total fertility rate (TFR) and child mortality. Whenever we use yearly time series data, we compute five year averages for 1961 through 1965, 1966 through 1970, and so forth. Means and standard deviations for the sample of country-years are presented in Table 1, and the countries in the sample are listed in Table 2.

Table 1:

Means and Standard Deviations of Variables in Sample

Variable	Mean	Standard Deviation	Min	Max
Year	1989	13.8	1965	2010
Total Fertility Rate	4.76	1.94	1.15	8.83
Under-5 Mortality Rate (per 1,000)	109.5	82.64	4.5	435.9
Malaria Ecology Index	2.92	3.99	0	16.74
Average Temperature (C)	20.4	7.2	−6.9	29.38
Average Yearly Precipitation (m)	1.18	0.81	0.015	3.98
GDP per capita, constant 2005$	2,053	2,359	120	14,650
Females’ Years of Secondary Schooling	1.6	1.4	0	6.9
Population (millions)	32.1	123	0.06	1,320
Cereal Yields per Hectare (kg/ha)	1,803	1,260	208	14,801

Table 2:

Sample of 133 Countries

Afghanistan	Czech Republic*	Lebanon	Senegal*^
Albania*	Djibouti	Lesotho*^	Sierra Leone*^
Algeria*	Dominican Republic	Liberia*^	Slovak Republic*
Angola	Ecuador*	Libya*	Solomon Islands
Argentina*	Egypt, Arab Rep*	Lithuania*	Somalia
Armenia*	El Salvador*	Macedonia, FYR	South Africa*
Azerbaijan	Equatorial Guinea	Madagascar	Sri Lanka*
Bangladesh*^	Eritrea	Malawi*^	St. Vincent and the Grenadines
Belarus	Estonia*	Malaysia*	Sudan*^
Belize*	Ethiopia	Mali*^	Suriname
Benin*^	Fiji*	Mauritania*^	Swaziland*
Bhutan	Gabon*	Mauritius*	Syrian Arab Republic*
Bolivia*	The Gambia*^	Mexico*	Tajikistan*^
Bosnia and Herzegovina	Georgia	Moldova	Tanzania*^
Botswana*	Ghana*^	Mongolia*^	Thailand*
Brazil	Guatemala^	Morocco*	Togo*^
Bulgaria*	Guinea	Mozambique*^	Trinidad and Tobago*
Burkina Faso	Guinea-Bissau	Myanmar*^	Tunisia*
Burundi*^	Guyana*	Namibia*	Turkey*
Cambodia*^	Haiti*^	Nepal*^	Turkmenistan
Cameroun*^	Honduras*	Nicaragua*^	Uganda*^
Cape Verde	Hungary*	Neiger*^	Ukraine*
Central African Republic*^	India*^	Nigeria	Uruguay*
Chad	Indonesia*	Oman	Uzbekistan
Chile*	Iran, Islamic Rep*	Pakistan*^	Vanuatu
China*	Iraq	Panama*	Venezuela, RB*
Colombia*	Jamaica*	Papua New Guinea*^	Vietnam*^
Cameros	Jordan*	Paraguay*	West Bank and Gaza
Congo. Dem Rep	Kazakhstan*	Peru*	Yemen, Rep*^
Congo. Rep*^	Kenya*^	Philippines*	Zambia*^
Costa Rica*	Korea, Dem. Rep.	Poland*	Zimbabwe
Cote d’lvoire*^	Kyrgyz Republic*^	Russian Federation*
Croatia	Lao PDR*^	Rwanda*^
Cuba	Lativa*	Sao Tome and Principe

^*Indicates country is in the 95-country sample

^{^}Indicates country is in the 39-country Low-Income sample

The variables used in the analysis are the following:

• TFR: Total fertility rate, or number of children per woman of reproductive age. Data from the U.N. Population Division reported as 5 year averages. Figure 1 maps TFR by country in 2005.

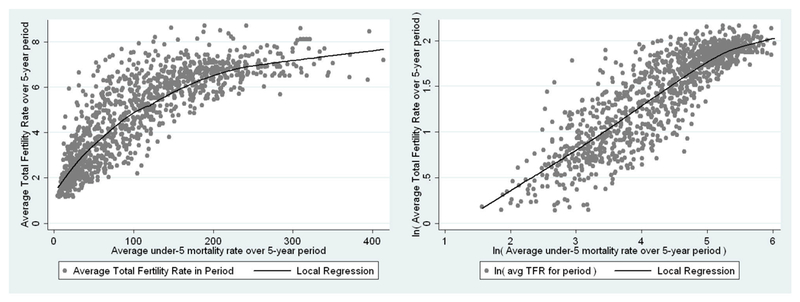
• Under-5 Mortality Rate: Data from the U.N. Population Division on the mortality rate in children under the age of 5, collected in averages over 5 year periods. Note that we use the natural logarithm of both total fertility and child mortality; the natural limits to a childbearing during a woman’s reproductive lifetime suggest a nonlinear relationship which calls for a log-log approach. Figure 5 shows the bivariate relationship between fertility and child mortality with and without logarithms; evidently the log-log form is more appropriate in the linear regression context.

• Malaria Mortality: National aggregates of malaria cases and mortality are from the World Health Organization (Aregawi et al., 2008). We use yearly data from 1990–2007 and divide by national population to generate rates per 1,000 population.

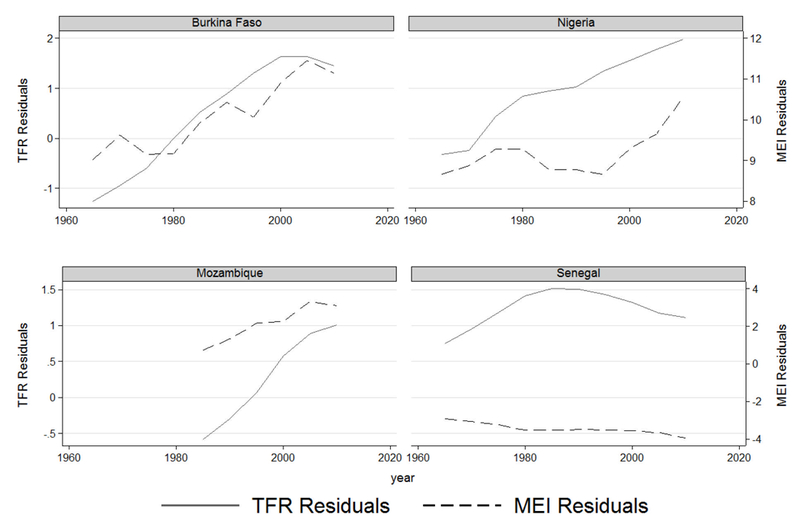
• Malaria Ecology Index: An ecologically-based spatial index of the stability of malaria transmission based on the interaction of climate with the dominant properties of anopheline vectors of malaria that determine vectorial capacity (Kiszewski et al., 2004; McCord, 2016). The index is constructed on a 0.5 degree spatial grid to derive the climatic characteristics of individual months, and then averaged over a 12-month period for every year, averaged across all grid cells in a country, and finally into 5-year averages to match the fertility data. For a complete description of the ME variable see the Appendix. Note that the index relies only on biophysical factors and not on human mortality or morbidity, and therefore provides variation that is exogenous to human intervention. Figure 6 shows the evolution of fertility and malaria ecology in four countries over the time span of our data, illustrating the positive association between trends in fertility rates and malaria risk after partialing out global trends.

• Temperature and Precipitation: The Malaria Ecology variable is constructed using temperature and precipitation data from the University of Delaware described in (Matsuura and Willmott, 2012). The data is available monthly at the 0.5 degree grid cell level from 1900–2010; we use data from 1960–2010.

• Log of GDP per capita in 2005 constant dollars. Yearly data are taken from the World Development Indicators database of the (World Bank, 2012). We calculate our own averages for each 5 year period.

• Average years of females’ secondary schooling: Data are from Barro and Lee (2013). We calculate our own averages for each five-year period. We chose secondary schooling to measure educational attainment since it was presumed that post-puberty adolescence and young adulthood were the critical time periods during which “fertility engines” would ignite (Wu and Martin, 2002).

• Population: Total population by country. Five year averages calculated from U.N. Population Division yearly data. For robustness, we re-run regressions using weighted least squares and weigh observations by country population in expectation that variance is likely higher in smaller countries. Results are unchanged.

• Cereal Yields per Hectare: Kilograms per hectare of harvested land of wheat, rice, maize, barley, oats, rye, millet, sorghum, buckwheat, and mixed grains (World Bank, 2012).

Figure 5:

Total Fertility Rates and Child Mortality Rates

Figure 6:

Fertility Rates and Malaria Ecology from 1960–2010

6. Results

6.1. Malaria Ecology and Mortality

The results in Table 3 show that positive deviations in the Malaria Ecology Index from a country’s mean and linear trend are associated with higher malaria mortality. Regression (i) includes country fixed effects to absorb time-invariant country characteristics correlated with malaria ecology and the average malaria deaths, and year fixed effects to flexibly absorb global trends. The coefficient on the malaria ecology index is 0.55, significant to the 99% confidence level. This suggest that a 1-point increase in the malaria ecology index is associated with a 55% higher level of mortality due to the disease. The within-country standard deviation of malaria ecology in the sample is 0.35, which means that a one standard deviation increase in malaria ecology leads to a 19% increase in malaria mortality on average. Given that trends in malaria ecology and malaria deaths might generate spurious correlation, regression (ii) adds country-specific linear trends to the specification and results in a coefficient on malaria ecology of 0.36, again significant to the 99% confidence level. These results indicate a robust association between the Malaria Ecology Index and malaria-related deaths.

Table 3:

Malaria Deaths and Malaria Ecology

Independent variables	Dependent Variable: ln( Malaria deaths per 1,000 people )
	(i)		(ii)
Malaria Ecology	0.55***		0.36***
	(0.18)		(0.09)
N		654
Countries		84
Years		1990–2007
Within R-squared	0.19		0.64
Country Fixed Effects	Y		Y
Year Fixed E ects	Y		Y
Country-Specific Linear Trend			Y

^***Standard errors in parentheses, indicates significant to 99% confidence

Regressions include a constant (not reported)

Regressions cluster standard errors by country, and weigh observations by population

6.2. Malaria Ecology and Fertility

Table 4 presents estimates of the effect of malaria ecology variation on fertility rates. Unlike the data for mortality from malaria, data on fertility at the national level are only available in 5-year intervals, so these regressions have a maximum of 10 observations per country given that the data are from 1965–2010. Regression (i) includes only country and year fixed effects, thus using all available data (133 countries). The coefficient on malaria ecology is 0.19 and is significant at the 99% confidence level, suggesting that a 1-point decrease in average malaria ecology over a 5-year period is associated with a 19% lower fertility rate (for reference, the within-country standard deviation of malaria ecology in our sample is 0.3). Column (ii) adds other drivers of fertility, such as female schooling and income per capita. There are many other variables affecting fertility decisions and outcomes, however they would only induce bias in our estimate if they were correlated to each country’s (exogenous) temporal variation in the ecology of malaria transmission. Both female education and income are negatively associated to fertility even after controlling for country and year fixed effects. The coefficient on malaria ecology remains consistent at 0.13, and significant to the 99% confidence level. Column (iii) adds average temperature, precipitation and cereal yields as controls, in case the malaria ecology index is picking up other weather-dependent processes besides malaria (such as other diseases or agricultural output). The coefficient on malaria ecology remains consistent and significant at 0.14. Given that the average MEI in sub-Saharan Africa is 6.8, then a halving of the malaria burden would correspond roughly to a 44% decrease in fertility rates (or, in the case of sub-Saharan Africa, a reduction from a total fertility rate of 6.8 in 1965 to 3.8). While fertility reduction would of course require a change in proximate variables such as contraception availability, a large fertility reduction resulting from reduced malaria is consistent with the high mortality resulting from the disease and high fertility rates resulting from child replacement and hoarding. Of course, human intervention cannot change the malaria ecology index per se, however public health interventions can reduce transmission by affecting other parts of malaria’s epidemiology.

Table 4:

Reduced Form Estimates of Malaria Ecology and Fertility

Independent Variables	Dependent Variable ln( TFR )
	(i)	(ii)	(xiii)
Malaria Ecology	0.19***	0.13***	0.14***
	(0.03)	(0.02)	(0.03)
Females’ Years of Sec. School		−0.08**	−0.08***
		(−0.02)	(0.02)
ln( GDP pc, constant US$ )		−0.09**	−0.08**
		(0.04)	(0.04)
Av. temperature over period (C)			−0.08**
			(0.04)
Av. precip. over period (mm)			0.03
			(0.05)
ln( Cereal Yield per Ha. )			−0.08
			(0.05)
N	1207	787	782
Countries	133	98	98
Within R-squared	0.74	0.81	0.81
Sample		All developing
Country Dummies	Y	Y	Y
Year Dummies	Y	Y	Y

Standard errors in parentheses, clustered by country

^***indicates significant to 99% confidence,

^**to 95%, and * to 90%.

Regressions exclude high-income countries.

All regressions include a constant (not reported)

6.3. Instrumenting for Child Mortality

In order to evaluate the effects of the child mortality rate on the total fertility rate we employ OLS, then OLS with country fixed effects, and then move to an instrumental variable framework (instrumenting for child mortality using malaria ecology). Table 5 presents the results. The OLS regression is presented in column (i), indicating that a 50% decrease in child mortality is associated with a 14% decrease in fertility. Column (ii) adds country fixed effects to absorb time-invariant omitted country characteristics that could confounding the relationship between child mortality and fertility, and the coefficient decreases to 0.24. These regressions are naive in that they ignore endogeneity problems, but they illustrate the positive association between fertility and child mortality. All regressions include global year dummies to flexibly control for secular trends and cluster standard errors by country.

Table 5.

Child Mortality and Fertility

Independent Variables	Dependent Variable
	ln( TFR )	ln( TFR )	ln (u5MR)		ln( TFR )	ln (u5MR)		ln( TFR )	ln (u5MR)		ln( TFR )	ln (u5MR)		ln( TFR )
	(i)	(ii)	(iii)		(iv)	(v)		(vi)	(vii)		(viii)	(ix)		(x)
			2SLS-FE			2SLS-FE			2SLS-FD			2SLS-FD
	OLS	Fixed Effects	1st Stage		2nd Stage	1st Stage		2nd Stage	1st Stage		2nd Stage	1st Stage		2nd Stage
Malaria Ecology			0.28***			0.29***			0.05***			0.09***
			(0.05)			(0.05)			(0.01)			(0.02)
ln( under-5 Mortality Rate )	0.28***	0.24***			0.66***			0.50***			0.48***			0.28**
	(0.04)	(0.04)			(0.08)			(0.11)			(0.14)			(0.12)
Females’ Years of Sec. School	−0.04**	−0.06***				−0.08**		−0.04*				−0.03**		−0.03***
	(0.02)	(0.02)				(0.03)		(0.02)				(0.01)		(0.01)
ln( GDP pc, const. US$ )	−0.02	−0.07**				−0.13*		0.02				−0.16***		0.05*
	(−0.02)	(0.03)				(0.07)		(0.04)				(0.03)		(0.03)
Av. temperature over period (C)	0.013***	−0.005				−0.18***		0.02				−0.06***		0.015*
	(0.003)	(0.02)				(0.06)		(0.03)				(0.01)		(0.008)
Av. precip. over period (mm)	−0.004	0.007				0.05		0.0001				−0.01		−0.03
	(0.03)	(0.05)				(0.08)		(0.06)				(0.03)		(0.02)
ln( Cereal Yield per Ha. )	−0.12***	−0.02				−0.30***		0.07				−0.06**		−0.01
	(0.03)	(0.05)				(0.08)		(0.07)				(0.03)		(0.03)
N	782	782		1207			782			1074			684
Countries	98	98		133			98			133			98
F-test on instrument			33.54			31.96			15.08			27.21
Cragg-Donald statistic			149.42			161.67			11.82			3.38
Within R-squared	0.85	0.83	0.82		0.69	0.87		0.79	0.08		0.77	0.22		0.80
Sample	All developing
Country Dummies	N	Y	Y		Y	Y		Y	Y		Y	Y		Y
Year Dummies	Y	Y	Y		Y	Y		Y	Y		Y	Y		Y

Standard errors in parentheses

^***indicates signicant to 99% condence

^**to 95%, and

^*to 90%.

All regressions include a constant (not reported), cluster standard errors by country, and exclude high-income countries.

We then move to instrumenting child mortality with the time-varying Malaria Ecology Index. Regression (iii) is the first stage of the basic regression without covariates, showing that a positive deviation from a country’s average malaria ecology increases child mortality. The magnitude suggests that the within-country standard deviation in Malaria Ecology of 0.3 would lead to an 8.4% increase in the child mortality. This is consistent with a disease that kills millions of children per year over the study period. The second stage is (iv), where the instrumented child mortality variable has a coefficient of 0.66 (an unreported regression limits the sample to the 98 countries with data for all controls, this coefficient becomes 0.57 with a standard deviation of 0.08). Regressions (v) and (vi) add the covariates. The first stage coefficient on malaria ecology is consistent, and the second stage coefficient on child mortality comes down to 0.50. The second stage finds female education to be significant and negatively associated to fertility, while GDP per capita is not. Temperature and precipitation are included to strengthen the case that malaria ecology is capturing the nonlinear relationship between climate and disease transmission, since the regression is partialing out the linear effects of temperature and precipitation. Including cereal yields assuages concerns that the malaria ecology instrument might be correlated with fertility changes through an agricultural channel, given that agricultural output can affect nutrition, health, returns to labor and fertility.

Finally, we estimate the preferred specifications using first differences (FD) instead of fixed effects. The first stage results in (vii) and (ix) still indicate a significant relationship between changes in malaria ecology and changes in child mortality, although the 0.05–0.09 coefficients are significantly smaller than fixed effects estimates. The second stage coefficients of 0.28–0.48 on child mortality are smaller than the second-stage results of the fixed effects estimates, but remain statistically significant and important in magnitude. The coefficient on the serial correlation of errors in FD is 0.46, which does not strongly warrant one model above the other. We present both, however, since the IV assumptions regarding correlation between the instrument and error terms differ slightly between FE and FD specifications (FE requires the instrument be uncorrelated to the demeaned unobserved variables, while FD has the less stringent requirement that the instrument be uncorrelated to the differenced values of those variables).

The second stage coefficients across the 2SLS models range from 0.28–0.66, which are larger than the corresponding 0.24–0.28 in the fixed-effects regressions without the instrumental variable. The larger 2SLS estimates suggest attenuation in the uninstrumented regression stemming from either measurement error or an omitted variable correlated positively with fertility and negatively with child mortality. Measurement error is certainly present; many of the countries in the sample have an underfunded apparatus for gathering vital statistics, and the use of sample data gathered every few years necessitates interpolation and smoothing that can generate attenuation of results. An important omitted variable that may be correlated positively to the total fertility rate and negatively to child mortality might be provision of prenatal care. Investments in maternal and child health would decrease the likelihood of miscarriage and mechanically increase the fertility rate in the short term, while also improve child health and decrease child mortality. This would attenuate the positive statistical association between child mortality and fertility, and help explain why using disease ecology as an exogenous instrument might lead to a larger estimate of the causal effect.

Another explanation for why the IV model identifies a larger causal effect is due to the estimate coming from the subpopulation of compliers where the instrument affects the child mortality treatment effect on fertility to a greater extent than in the entire population (Angrist, Imbens, and Rubin, 1996), as has been seen in other 2SLS applications (Lleras-Muney, 2005). In other words, those parents who have a child die due to malaria ecology differences at the margin may respond more elastically in terms of their subsequent fertility than those parents of children who die at other parts of the malaria ecology distribution. It is reasonable to expect countries with lower mortality and fertility levels to have a lower elasticity on fertility’s responsiveness to mortality. While countries with high infectious disease burdens (and therefore a stronger relationship between malaria ecology and the all-cause child mortality rate) have high child mortality rates, high fertility rates, and fertility dynamics driven by child hoarding and replacement, fertility in countries farther along the demographic transition likely have smaller responsiveness to variation in child mortality as other variables become the main drivers of fertility variation. This difference in the mortality-fertility elasticity across high-mortality and low-mortality countries would result in an IV estimate that is larger than OLS.

Figure 7 shows the main result graphically. We regress the endogenous variable (child mortality) on the instrument (malaria ecology) and on country and year fixed effects. Fertility and the instrumented child mortality are plotted against each other with a flexible polynomial and 95% confidence intervals after partialing out country and year fixed effects. The graph shows that for the domain where most of the data occur (shown in the histogram), the relationship between fertility and the exogenous child mortality variation is positive with tight local error bounds. The graph on the right repeats the exercise including all the covariates in Table 5 (female education, income, temperature, precipitation and cereal yields).

Figure 7:

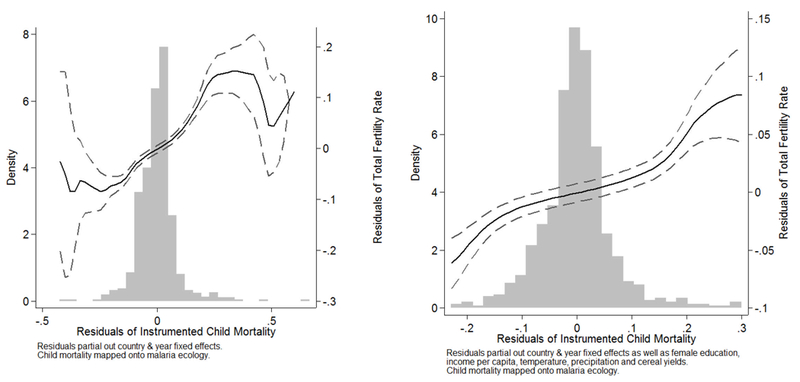
Fertility & Instrumented Child Mortality (1960–2005)

Across all specifications, the point estimates for malaria ecology on child mortality in the first stage and for child mortality in the second stage are consistent, and the estimated effect of child mortality on fertility is robust to inclusion of controls. The education variable is also significantly associated with fertility, however we do not interpret its coefficient as causal due to the potential endogeneity problems (it is likely jointly determined with fertility in the process of development). The controls nevertheless serve to give a range of plausible estimates on the child mortality variable given potential omitted variable bias.

The instrumental variables approach yields an estimated effect of child mortality of 0.28–0.66.This magnitude is socially consequential. For example, the Millennium Development Goal for child mortality a decrease by 66% from the 1990 rate would decrease TFR by 27%−52% (or a decrease of 1.7–3.3 births in sub-Saharan Africa from the 1990 level of 6.3). Child mortality still played a powerful role in fertility choice in the latter half of the 20th century, an order of magnitude larger than the effect identified in some other studies.

We test the endogeneity of the child mortality variable (the null of exogeneity can be rejected at a one percent alpha level) and the strength of the instrument. F-tests for the instrument in the rst stage are reported in Table 5; all are above the rule of thumb value of F=10 indicating that the instrument is strong (Staiger and Stock, 1997). To further dispel concerns of a weak instrument, we compute the Cragg-Donald statistic (Stock, Wright, and Motohiro, 2002), which tests underidentification by examining the smaller eigenvalue of the F-statistic matrix of the first stage regression. In all cases except (vii), the statistic exceeds the critical value of 16.38, suggesting that bias and significance test distortions due to a weak instrument are not a concern here.

6.3.1. Robustness Checks

Given our caveats on instrumenting child mortality with malaria ecology, we run the key specifications using a limited information maximum likelihood estimator with a modification parameter of α = 1 (Fuller, 1977), which is more robust than 2SLS with a weak instrument (Hahn, Hausman, and Kuersteiner, 2004; Hausman, Stock, and Yogo, 2005). Columns (i) and (ii) of Table 6 show that the coefficient on child mortality remains significant and of the same magnitude as the 2SLS estimates in Table 5, whether or not the controls are included. Given that this estimator is more robust than 2SLS in the presence of a weak instrument, the identical results affirm the strength of our instrument.

Table 6:

Robustness Checks

Independent Variables	Dependent Variable
	ln( TFR )	ln( TFR )	ln (u5MR)		ln( TFR )	ln (u5MR)		ln( TFR )	ln (u5MR)		ln( TFR )	ln (u5MR)		ln( TFR )
	(i)	(ii)	(iii)		(iv)	(v)		(vi)	(vii)		(viii)	(ix)		(x)
			2SLS-FE			2SLS-FE			2SLS-FE			2SLS-FE
	LIML	LIML	1st Stage		2nd Stage	1st Stage		2nd Stage	1st Stage		2nd Stage	1st Stage		2nd Stage
Malaria Ecology			0.31***			0.23**			0.25**			0.16**
			(0.06)			(0.10)			(0.10)			(0.07)
ln( under-5 Mortality Rate )	0.66***	0.50***			0.98***			0.31			0.49**			0.57**
	(0.88)	(0.10)			(0.13)			(0.21)			(0.20)			(0.24)
Females’ Years of Sec. School		−0.04***				−0.06*		−0.05**	−0.06*		−0.04	−0.12***		−0.06
		(0.02)				(0.03)		(0.02)	(0.03)		(0.02)	(0.04)		(0.04)
ln( GDP pc, const. US$ )		−0.02				0.04*		−0.07	0.06		0.004	−0.07		−0.01
		(0.04)				(0.06)		(0.04)	(0.07)		(0.05)	(0.07)		(0.05)
Av. temp. over period (C)		0.02				−0.15***		−0.02	−0.14*		0.03	−0.19**		0.005
		(0.03)				(0.08)		(0.05)	(0.08)		(0.05)	(0.09)		(0.05)
Av. precip. over period (mm)		0.0002				0.23		−0.03	0.25		−0.03	0.07		−0.06
		(0.05)				(0.16)		(−0.08)	(0.16)		(0.11)	(0.10)		(0.10)
ln( Cereal Yield per Ha. )		0.07				−0.08		0.19	−0.04		−0.07	−0.12		0.10
		(0.07)				(0.19)		0.15	(0.16)		(0.11)	(0.09)		(0.11)
China One-Child Policy									−0.09		−0.33***
									(0.07)		(0.03)
N	1207	782		1206			782			782		328
Countries	133	98		133			98			98		40
F-test on instrument	33.36	31.96	23.08			5.81			6.58			6.33
Cragg-Donald statistic	149.42	92.85	142.00			24.93			27.30			32.46
Within R-squared			0.92		0.83	0.92		0.91	0.93		0.77	0.85		0.64
Sample					All developing							Low-Income Only
Country Dummies	N	Y	Y		Y	Y		Y	Y		Y	Y		Y
Year Dummies	Y	Y	Y		Y	Y		Y	Y		Y	Y		Y
Population Weights	N	N	Y		Y	Y		Y	Y		Y	Y		N

Standard errors in parentheses

^***indicates signi_cant to 99% con_dence

^**to 95%, and

^*to 90%.

All regressions include a constant (not reported), cluster standard errors by country, and exclude high-income countries.

Columns (iii) and (iv) re-estimate the IV specification with population weights. The first stage coefficient of 0.31 is highly significant and slightly larger than the coefficient of 0.28 in the corresponding unweighted regression in column (iii) of Table 5. This suggests either that malaria has more of an effect on child mortality in larger developing countries, or that smaller countries have larger measurement error in their statistics which leads to attenuation. Similarly, the second stage coefficient of 0.98 is larger than the 0.66 analogue in column (iv) of Table 5. Columns (v) and (vi) add the controls to the regressions in (iii) and (iv); the first stage coefficient drops to 0.23, and the second stage coefficient drops to 0.31. While consistent with the child mortality coefficients in Table 5, here it is imprecisely measured.

Columns (vii) and (viii) add a dummy for China after 1980, since its fertility rate was to some extent artificially lowered by the one-child policy put in place in 1979 (we leave the population weights since this dummy would only be econometrically relevant in the population-weighted regressions, given China’s large size). The first stage estimate on malaria ecology remains significant and consistent at 0.25, and the second stage coefficient on child mortality is strongly significant at 0.49, consistent with the main specification in column (vi) of Table 5.

Finally, columns (ix) and (x) limit the sample to low-income countries. The results are qualitatively the same as using both middle- and low-income countries, with low-income countries having the same range of coefficients for child mortality in the second stage (0.57 compared with 0.50). Note that while the first stage regressions (v), (vi) and (ix) have Cragg-Donald statistics above the critical value, the F-statistics on the instrument indicate a weaker instrument than in the main specifications. Nevertheless, we note that the range of second-stage coefficients is consistent with those in Table 5.

6.3.2. Malarious Countries Only

The coefficient from IV is the local average treatment effect for the sub-population for which a change in the instrument affects the endogenous variable on the margin. In order to measure the average local treatment effect on countries where malaria ecology and child mortality are well-correlated, we repeat the analysis limiting the sample to countries with nonzero malaria incidence during the given time period. Results are in columns (i)-(iv) of Table 7, and are consistent with results in Table 5. The first-stage coefficients on malaria ecology of 0.33–0.37 are larger than the corresponding 0.28–0.29 range in the fixed effects models of Table 5. Larger coefficients for malarious countries makes sense given that including countries where malaria has been eliminated in the regression should attenuate the estimated relationship between malaria ecology and child mortality. The second-stage coefficients of 0.44–0.64 are consistent with the corresponding 0.50–0.66 range from the fixed effects estimates in Table 5. The overall results are therefore consistent with the malarious country subsample.

Table 7:

Malarious Countries Only

Independent Variables	Dependent Variable
	ln (u5MR)		ln( TFR )	ln (u5MR)		ln( TFR )	ln (malaria MR)		ln( TFR )	ln (malaria MR)		ln( TFR )
	(i)		(ii)	(iii)		(iv)	(v)		(vi)	(vii)		(viii)
	2SLS			2SLS			2SLS			2SLS
	1st Stage		2nd Stage	1st Stage		2nd Stage	1st Stage		2nd Stage	1st Stage		2nd Stage
Malaria Ecology	0.37***			0.33***			0.94**			0.68***
	(0.05)			(0.05)			(0.44)			(0.25)
ln( under-5 Mortality Rate )			0.64***			0.44***
			(0.07)			(0.09)
ln( Malaria Mortality Rate )									0.09*			0.09***
									(0.05)			(0.03)
Females’ Years of Secondary School				−0.09***		−0.06***
				(0.03)		(0.02)
ln( GDP per capita, constant PPP US$ )				−0.20**		−0.01
				(0.08)		(0.04)
Av. temperature over period (C)				−0.16***		−0.002
				(0.06)		(0.03)
Av. precipitation over period (mm)				0.02		−0.01
				(0.09)		(0.07)
ln( Cereal Yield per Ha. )				−0.19**		−0.01
				(0.08)		(0.06)
N		1082			750			106				524
Countries		117			90			60				74
F-test on instrument	58.25			36.59			4.66			7.64
Cragg-Donald statistic	194.07			101.59			9.49			28.50
Within R-squared	0.72		0.68	0.87		0.82	0.27		0.69	0.16		0.57
Sample	Malarious Only			Malarious Only			Malarious Only (1990–2007 5yr)			Malarious Only (1990–2007 all years)
Country Dummies	Y		Y	Y		Y	Y		Y	Y		Y
Year Dummies	Y		Y	Y		Y	Y		Y	Y		Y

Standard errors in parentheses

^***indicates signi_cant to 99% con_dence

^**95%

^*90%.

Constant not reported, std. errors clustered by country, and high-income countries excluded.

Columns (v)-(viii) limit the sample to malarious countries that have malaria mortality data starting in 1990 and use malaria ecology to instrument for malaria deaths. Columns (v)-(vi) use the five-year timespans to match the rest of our analysis, while columns (vii)-(viii) use every year from 1990–2007.⁴ The results are qualitatively the same: malaria ecology is associated with deaths from malaria in the first stage, and while first-stage coefficient is statistically significant in both (v) and (vii), the F-statistic of the instrument suggests that it is not strong. The second stage coefficients on malaria deaths are identical in both (vi) and (viii). The coefficient of 0.09 is smaller than the corresponding coefficients on under-5 mortality, but this is not surprising for two reasons. First, the malaria deaths data include deaths of adults and children over the age of 5, which may affect fertility differently or not at all. Secondly, the malaria mortality data is of notoriously poor quality (Alonso and Tanner, 2013), leading to measurement error, weakening the instrument in the first stage, and attenuating coefficients towards zero. Despite these data problems, these regressions are consistent with our overall findings as they suggest that interannual variation in malaria ecology does affect malaria deaths, and these deaths have an effect on fertility behavior.

A second concern is that our child mortality effect might only be valid for children dying from malaria. However, there is nothing in the demography literature that identifies a differentiated fertility response to a child death depending on the cause of death (though one might imagine different fertility responses between health-related deaths and confliict-related deaths, for example). Nonetheless, whether there is a differentiated fertility response depending on cause of child death is beyond the scope of this paper, but in the absence of such evidence we maintain that our estimated child mortality coefficient is a contribution to the quantitative study of fertility dynamics.

6.3.3. Model Limitations

Two limitations of the study should be pointed out. The first, which is mentioned above, is that variation in malaria ecology might affect adult mortality and morbidity, and that these in turn may affect fertility rates, thus violating the exclusion restriction. Adult mortality from malaria is far less than child mortality [around 77% of global malaria deaths are in children under the age of 5 (World Health Organization, 2015)], and adult mortality would change parental discount rates and might lead them to reduce fertility. This would bias our estimate towards zero, but any other effects would be confounding our estimate. Malaria’s effects on adult morbidity might raise or lower fertility (on the one hand, morbidity might lower fertility due to miscarriages, but on the other hand desired fertility might rise as the value of child labor on the farm rises when parents cannot work).

Another important concern is that the variables being studied (fertility, child mortality, and malaria ecology) might have underlying time trends at the country level generating spurious correlations even after country and year fixed effects. Adding country-specific trends to country and year fixed effects yields a second stage coefficient on child mortality of 0.78. While positive and not inconsistent with the higher part of the 0.28–0.66 range of our 2SLS results, the coefficient is not statistically significant because country-specific time trends absorb too much variation. This is unsurprising given the slow-moving nature of the TFR variable (it is a national measure smoothed into 5-year averages) and that the panel has only 10 time periods. Our results add to suggestive macro-level evidence of the role of child mortality, but more research using refined micro data will be needed to accurately pinpoint the causal effect of child mortality on fertility.

7. Conclusions

We have employed malaria ecology as a novel instrument to study the effect of child mortality on fertility, adding to recent studies on how disease can drive fertility rates (Wilson, 2015; Lucas, 2013; Bleakley and Lange, 2009). Our results show that the malaria ecology index generates exogenous temporal variation in fertility, which we argue operates largely by affecting child mortality. With appropriate caveats, we instrument child mortality using the malaria ecology index to contribute to the empirical demography literature. The results suggest that child survival is a quantitatively important driver of fertility. The demographic transition has proceeded in the widest range of social settings: rural and urban, male-dominated and gender equal, impoverished and middle-class (Cleland, 2001). Since the child mortality transition has also proceeded in a wide range of settings, it is plausible that it has been an important driver of fertility decline.

Child mortality is not the only important driver of a demographic transition. Family planning through contraception, sexual behavior and abortion is a proximate determinant affected by socioeconomic variables such as income, education, and health (Bongaarts, Frank, and Lesthaeghe, 1984). A transition requires that the change in desired fertility be allowed to translate into a change of actual fertility through the proximate variables (especially contraception use). Though we have focused on better quantifying the role of reducing child mortality, the importance of other variables affecting fertility should not be understated.

Our results herald the possibility of a rapid fertility transition in high-mortality countries, particularly those with a large malaria burden. Child survival in low income settings can be dramatically improved in a short period (United Nations Millennium Project, 2005). Similarly, other determinants of fertility such as female schooling, agricultural yields and family planning policy, may change in just a few years. Sub-Saharan Africa’s TFR in 1990 was 6.3, and in 2013 it was 5.1 (World Bank, 2012). If child mortality decreases by two-thirds compared to 1990, our results predict a decrease in TFR of around 2–3 babies, around half of the reduction necessary to reach replacement fertility of 2.1. If in addition female education and access to family planning are improved, the prospect for a voluntary, rapid, policy-supported transition to lower fertility in Africa looks reasonable.

More research is needed to fully explain the causes of rapid fertility transitions in the last few decades. Our models do not attempt to solve the endogeneity issues with the control variables, nor focus on modeling the lag structure. Moreover, the coarse spatial and temporal resolution of our data prevent us from fully accounting for country-specific trends in child mortality and in fertility, threatening the causal interpretation. Nevertheless, this paper adds to the evidence of a quantitatively important effect of child mortality on fertility behavior. To our knowledge, no paper has employed a time-varying exogenous instrument to tackle the endogeneity problem between fertility and child mortality. Whereas previous estimates of the elasticity of fertility to child mortality using IV have failed to find statistical significance or have found perplexing small magnitudes, our result suggests that child mortality accounts for almost half of the fertility reduction during the demographic transition.

Appendix: Time-Varying Malaria Ecology Index

We develop a time-varying version of the Malaria Ecology Index proposed in Kiszewski et al. (2004). Malaria Ecology is an ecologically-based spatial index of the stability of malaria transmission based on the interaction of climate with the dominant properties of anopheline vectors of malaria that determine vectorial capacity. Malaria is a disease of climate because a key part of the life cycle of the parasites (sporogony) depends on a high ambient temperature and because vectors require sufficient rainfall to provide breeding sites. Additionally, the intensity of malaria transmission depends on the specific mosquito species that are present and their relative attraction to humans versus animals. The Malaria Ecology Index measures the effects of ambient temperature (using a monthly average from 1901–1990) on the force of transmission of malaria, as expressed through the length of the incubation period of the parasite in the mosquito’s gut, and therefore the proportion of the vector population able to survive long enough to become infectious. The index is constructed on a 0.5 degree spatial grid to derive the climatic characteristics of individual months, and then averaged over a 12-month period. The first step is to identify the distribution of anopheline species across the world using observation records and satellite-based vegetation maps to identify likely habitats where observations have not been recorded.

A dominant species is identified for each spatial zone, and for each month (in cases where there is a seasonal pattern to the dominant species). An ecological screen was created for the presence or absence of a vector during particular months. For those vectors that breed mainly in temporary water, a minimum precipitation threshold of 10mm per month, lagged one month, is used to judge when the vector would be present in the site during a given month. Vectors that mainly exploit permanent or semi-permanent bodies of water were considered to be independent of seasonal uctuations in rainfall unless empiric evidence indicated otherwise. In temperate or altitudinous regions, temperature thresholds are used to determine whether parasites can develop in mosquito vectors in a particular month, assuming that malaria parasites cannot develop when the mean monthly temperature remains below 15°C. Note that the mosquito presence screen is ecology-based and not affected by human activity; indeed, it is worth keeping in mind that public health interventions against malaria serve to break the transmission cycle, but do not eliminate the presence of the vector itself (even until today, Anopheles mosquitoes capable of transmitting malaria can be found throughout the US and Europe, places where malaria has been largely eradicated).

The basic formula for Malaria Ecology combines climatic factors, the presence of different mosquito vector types and the human biting preference of the different mosquito vectors. The index expresses the factors that most powerfully and perennially influence the intensity of malaria transmission. It uses, therefore, a subset of the vectorial capacity equation without terms for mosquito abundance, vector competence, or recovery rate for infected people. To calculate the duration of the extrinsic incubation period “E,” the index was calculated for each month, and biting activity was designated based on the average monthly temperature and Moshkovsky’s degree-day-based formulae:

$${\mathit{MalariaEcology}}_{i,\mathit{year}}={\left({\displaystyle \sum \frac{a_{i,m}^2\ast p_{i,m}^E}{-ln(p_{i,m})}}\right)}_{year}$$

Where: m = month (1–12)

i = identity of dominant vector

a = proportion biting people (0–1)

p = daily survival rate (0–1)

E = length of extrinsic incubation period (in days) =$\frac{111}{(temperature-16)}$

Because it is built upon climatological and vector characteristics on a cell-by-cell basis, Malaria Ecology is exogenous to public health interventions and economic conditions. The Malaria Ecology index correlates strongly to malaria incidence, especially in the absence of public health interventions. Even a cursory comparison of the map of the geographic extent of malaria risk and Malaria Ecology show clear similarities: the high latitudes of the northern hemisphere are both where malaria was eliminated first, and also the malaria ecology index is lowest without being zero.

We re-calculate the index month-by-month using the same methodology using monthly data for temperature and precipitation. The index is aggregated to the country level without weighting by population to prevent potential endogeneity if humans can migrate internally to adapt to malaria prevalence.