Bayesian data analysis in the phonetic sciences: A tutorial introduction

Abstract

This tutorial analyzes voice onset time (VOT) data from Dongbei (Northeastern) Mandarin Chinese and North American English to demonstrate how Bayesian linear mixed models can be fit using the programming language Stan via the R package brms. Through this case study, we demonstrate some of the advantages of the Bayesian framework: researchers can (i) flexibly define the underlying process that they believe to have generated the data; (ii) obtain direct information regarding the uncertainty about the parameter that relates the data to the theoretical question being studied; and (iii) incorporate prior knowledge into the analysis. Getting started with Bayesian modeling can be challenging, especially when one is trying to model one’s own (often unique) data. It is difficult to see how one can apply general principles described in textbooks to one’s own specific research problem. We address this barrier to using Bayesian methods by providing three detailed examples, with source code to allow easy reproducibility. The examples presented are intended to give the reader a flavor of the process of model-fitting; suggestions for further study are also provided. All data and code are available from: https://osf.io/g4zpv.

1. Introduction

In phonetics and other related areas of the language sciences, the vast majority of studies are designed to elicit several data points from each participant for each level of the linguistic variable of interest. This design poses difficulties for classic ANOVA models, which can accommodate only one random effect at a time, so that either the sets of data-points for each participant or the sets of data-points for each item must be replaced with the mean values (Clark, 1973). Over the last two decades, phoneticians have addressed these difficulties by turning to other methods, and linear mixed models—sometimes referred to as multilevel or hierarchical linear models—have become a standard tool, perhaps the standard tool for analyzing repeated measures data. The lme4 package (Pinheiro and Bates, 2000; Baayen et al., 2008; Bates et al., 2015b) in R has greatly simplified model specification and data analysis for repeated measures designs. Even more recently, a Bayesian alternative to frequentist linear mixed models has become available, largely due to the emergence of a new programming language, Stan (version 1.17.3) (Stan Development Team, 2017b). In this article, we provide a tutorial introduction to fitting Bayesian linear mixed models. In order to make it easy for the newcomer to Bayesian data analysis to fit models, we use the popular and powerful R package brms, version 2.1.9 (Bürkner, 2016), which uses lme4 syntax that researchers in linguistics and psychology are familiar with.

Fitting Bayesian models takes more time and effort than their frequentist analogues. Why bother to learn this relatively complex approach? We feel that there are several important advantages to fitting Bayesian models. Perhaps the most important one is that it gives us a degree of flexibility in defining models that is difficult to match with frequentist tools (Lee, 2011; Nicenboim and Vasishth, 2016). We discuss an example below. A second advantage of Bayesian modeling is that we can focus our attention on quantifying our uncertainty about the magnitude of an effect. Instead of drawing a conclusion like “gender affects voice onset time”, using the Bayesian framework we can identify a credible interval of plausible values representing the effect. In other words, we can present a probability distribution of plausible values, instead of focusing on whether a particular confidence interval does or does not contain the value 0. Such quantitative summaries of an effect tell us much more about the research question than binary statements like “effect present” or “effect absent.” A third advantage of Bayesian data analysis is that we can incorporate prior knowledge or beliefs in the model in an explicit way with the use of so-called informative priors. Such a use of priors is not widespread, but could be a powerful tool for building on what we already know about a research question. Finally, frequentist tools like lme4 can run into convergence problems when an attempt is made to fit a “maximal” random-effects structure (Barr et al., 2013).¹ Bayesian linear mixed models will always converge once so-called regularizing priors are used; we explain this point below. In this tutorial, we will provide an informal introduction to Bayesian data analysis, and then present three examples involving retrospective measurements of productions in a large cross-linguistic phonetic corpus. These examples are intended to provide a practical first entry to Bayesian data analysis. We do not aim to cover all aspects of Bayesian modeling here, but suggestions for further reading are provided at the end. In our examples, we will focus on (generalized) linear mixed models (Pinheiro and Bates, 2000; Baayen et al., 2008; Bates et al., 2015b), because they are a standard tool today in experimental research in linguistics and the psychological sciences. We assume in this paper that the reader knows how to fit linear mixed models using the R package lme4 (Bates et al., 2015b). Accessible introductions to linear mixed models are in Gelman and Hill (2007) and McElreath (2016).

All data and code are available from https://osf.io/g4zpv. The additional code examples provided there cover some further issues not discussed in this paper.

2. An informal introduction to Bayesian data analysis

Consider a simple case where we carry out an experiment in which we measure voice onset time in milliseconds in recordings of word-initial stops such as Mandarin /t^h/ and /k^h/ produced by male and female participants. Participants in each gender category are asked to produce multiple stop-initial words, resulting in repeated measurements of VOT from each participant. The first few lines and last few lines of an example data-frame is shown in Listing 1.

For i = 1, …, I participants and j = 1, …, J items, we often want to fit a so-called varying intercepts and varying slopes linear mixed model of the type specified in (1) – the equation for a frequentist linear mixed model for the effect of gender on VOT. A notational convention we use here: a varying intercept always has index 0, and a varying slope has index 1 (or higher, in the case the case of multiple regression). Thus, a varying intercept for item j is written w_0,j and a varying slope is written w_1,j (or w_2,j, for a second predictor, and so on). Fixed intercepts and slopes also have the same numerical subscript convention of 0 for intercepts, and 1 (or a higher index) for the slope (with increasing numbers in the case of multiple predictors).

Using these notational conventions, a frequentist linear mixed model for the effect of gender on VOT could be specified as follows:

Subject item gender VOT
F01 kh^.l&r 0.5 105
F01 kh^.l&r 0.5 120
F01 khA9 0.5 104
F01 khE.ts&p 0.5 127
F01 khek 0.5 141
F01 khev 0.5 106
…
M20 thub −0.5 66
M20 thuT −0.5 67
M20 twhI.stIxd −0.5 69
M20 twhi.z&rz −0.5 93
M20 thIn −0.5 85

Listing 1: Example data-set from English.

$$VO{T}_{ij}={\beta }_0+u_{0,i}+{\omega }_{0,j}+({\beta }_1+{\omega }_{1,j})\times \text{\hspace{0.17em}gende}{r}_{ij}+{\in }_{ij}$$ (1)

Assuming that the categorical variable is sum-coded (e.g., +0.5 for female, −0.5 for male), the intercept β₀ represents the grand mean, and the slope β₁ the difference in means between the two levels of gender. These are the so-called fixed effects. The terms u_0,i and w_0,j are, respectively, the by-participant and by-item adjustments to the intercept coefficient β₀, and w_1,j is the by-item adjustment to the slope term for gender, β₁. The varying intercepts for subjects, u_0,i, are assumed to be distributed as Normal(0, σ_u0); similarly, the varying intercepts for items w_0,j have the distribution Normal(0, σ_w0), and the varying slopes for item by gender, w_1,j have the distribution Normal(0, σ_w1). The residual error, ϵ, is assumed to have the distribution Normal(0, σ_e). Finally, the varying intercepts and slopes for item, w_0,i, w_1,j are assumed to have correlation ρ_w. In lme4 syntax, the above model corresponds to the following (datE stops refers to the data frame):

lmer(VOT ~ 1 + gender + (1 | subject) + (1 + gender | item), dat = datE_stops)

Because lme4 assumes an intercept term, the 1 + can be omitted, as in:

lmer(VOT ~ gender + (1 | subject) + (gender | item), dat = datE_stops)

The above model requires the estimation of the parameters listed in 2. (Note that in Bayesian linear mixed models, u_0i, w_0j, w_1j are also parameters; but these are not of primary interest in studies such as this example which address questions only about group effects rather than about patterns of differences across individuals or across items.)

$${\beta }_0,{\beta }_1,{\sigma }_{u0},{\sigma }_{\omega 0}{\sigma }_{\omega 1},{\rho }_{\omega },\sigma {}_e$$ (2)

Again, the intercept β₀ represents the grand mean VOT. Note that it does not make sense to fit varying slopes for gender by participants in this model because gender is a between-participants factor (i.e., we can’t investigate the effect of gender on the participants). Gender is, however, a within-items factor, so varying slopes for gender can be fit by items (i.e., we can investigate the effect of gender on the items).

In the frequentist framework, we would just need to run the lmer function as shown above. However, in the Bayesian linear mixed model, some more work is needed before we can run the corresponding function in the package brms. While it is possible to fit the previous function with brms without the specifications described below, this would make use of default priors, which may not be adequate for every data-set.

The very first step is to define prior distributions for each of the parameters in the model (this step is explained below). Once the priors are defined, the model is fit, as we will show below. The end product of a Bayesian analysis is a so-called joint posterior distribution of all the parameters. These posterior distributions show the probability distributions of plausible values of the parameters, given the data and the model. These posteriors are then used for statistical inference.

2.1. Defining priors

We start by choosing the following prior distributions for the parameters in the model. The notation “~” should be read as “is distributed as.” Normal₊(0, 100) is a short-hand for a truncated (or half) normal distribution with mean 0 and standard deviation 100, which includes only positive values. The choice of a truncated normal distribution instead of a normal distribution is necessary for the priors on standard deviations, because standard deviation cannot be less than 0.

1. β0 ~ Normal(0, 200)
2. β1 ~ Normal(0, 50)
3. σe ~Normal+(0, 100)
4. σu0 ~ Normal+(0, 100)
5. σw0, σw1 ~ Normal+(0, 100)
6. ρw ~ LKJ(2)

When defining priors, it is a good idea to visualize them so that the researcher can decide whether these are reasonable. The priors chosen here are visualized in Figure 1.

Figure 1:

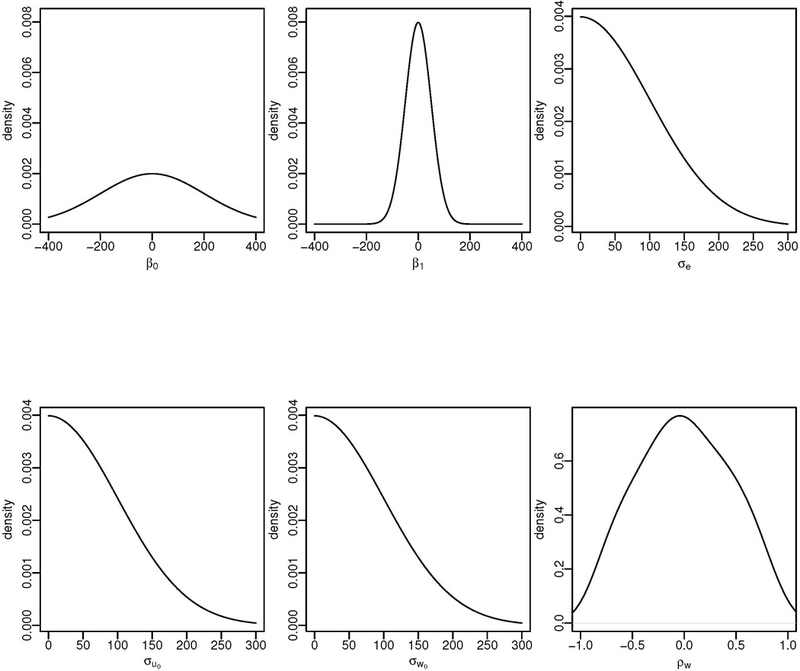
Prior distributions for the parameters of the varying intercepts and varying slopes linear mixed model. The prior for the grand mean parameter β₀ is a normal distribution with mean 0 and standard deviation 200 (Normal(0, 200)); the prior for the parameter representing the effect of gender, β₁, is Normal(0, 50); the priors for all the standard deviations are N ormal₊(0, 100); and the prior for the correlation between the random effects is a so-called LKJ(ν = 2) prior, which is explained in the main text.

Priors express beliefs about the plausible values of the parameters; these beliefs can be based on expert or domain knowledge, or could be based on already-available data. For example, the theoretically interesting parameter for us is the effect of gender, β₁. This is assumed here to have a prior distribution Normal(0, 50), which implies that the parameter is believed to lie between −100 and +100 ms with probability 95%. This range arises because 95% of the probability in a Normal distribution with mean and standard deviation σ is contained within the approximate range μ ± 2 × σ. This prior for β₁ assumes quite a wide range of possible values; it could easily be much more constrained. For example, if we know from previous research that gender effects on VOT are unlikely to be larger than 40 ms, the prior Normal(0, 20) could be quite reasonable. As we will show below, a so-called sensitivity analysis (which is standard practice in medicine, economics, and other fields) can be useful to check whether the posterior distribution of the parameter is affected by the prior specification.

The prior on the standard deviations, Normal₊(0, 100), is a truncated normal distribution and expresses that a value below 0 is impossible, and that larger values (larger than 200) are unlikely. Why did we assume that values larger than 200 are unlikely? This decision should ideally come from knowledge about and experience with VOT data. However, nothing hinges on this particular choice of prior; we could have chosen a prior that is even more spread out (has an even larger standard deviation) without any substantial change in the outcome.

An important point to notice in the prior specification for the intercept β₀ is that we allow negative values in the prior distribution. Since we focus in this paper on the Mandarin aspirated stops and the English voiceless stops (i.e., categories that are defined by having positive VOT), we could in principle constrain the prior to allow only positive values. However, because there is sufficient data in the present examples, these decisions about the prior will not have a major impact on the posterior distribution. If we had a small amount of data to work with, the prior would be highly influential in determining the outcome.

The correlation parameter ρ_w uses the LKJ-correlation prior which is based on a method for generating random correlation matrices developed by Lewandowski et al. (2009). This takes a numerical parameter that determines the shape of the distribution. A standard choice is to choose the LKJ(2) prior, because it assumes that extreme values (±1) are highly unlikely. This prior, which is currently only available in Stan (Stan Development Team, 2017b) (and hence in brms), can be used for essentially arbitrarily large correlation matrices of random effects.

The priors we have chosen here allow a broad range of values for the parame-ters, and are called regularizing, weakly informative priors (Gelman et al., 2017). “Regularizing” here means that extreme values are disallowed or downweighted; for example, a prior on a correlation parameter would be regularizing if it disallows or downweights extreme values such as −1 or +1, which are quite unlikely in data. Weakly informative priors give some minimal amount of information and have the objective of yielding stable inferences (see also Chung et al., 2013; Gelman et al., 2008). For most applications of Bayesian modeling, it is standard to use regularizing, weakly informative priors, but informative priors based on expert opinion or prior knowledge can and should be considered as well; we illustrate this with an example below.

library(brms)
priors <-c(set_prior(“normal(0, 200)”, class = “Intercept”),
set_prior(“normal(0, 50)”, class = “b”, coef = “gender”),
set_prior(“normal(0, 100)”, class = “sd”),
set_prior(“normal(0, 100)”, class = “sigma”),
set_prior(“lkj(2)”, class = “cor”))

Listing 2: Example of prior specification in brms.

2.2. Specifying priors in brms

The prior specification in Listing 2 defines different priors for each class of parameter. Class Intercept is the intercept parameter (i.e., β₀), class b are all the slopes in a model (in this case it indicates the β₁ parameter), i.e., the slope for gender; the parameter for gender can be marked by writing the name of the predictor variable in the data-frame (here, female is coded as +1/2 and male as −1/2). The parameters of class sd are the standard deviation parameters for the random effects (in this case, σ_u0, σ_w0, and σ_w1) and the class sigma is the standard deviation of the residual error ϵ (i.e., σ_e). The parameters of class sd and sigma are automatically constrained by brms to not have values lower than 0. That is, normal(0, 100) in this class within brms refers to the normal distribution with standard deviation 100 and truncated at 0: Normal₊(0, 100). Finally, the parameter of class cor is the correlation parameter, and can be used to define LKJ priors for correlations in an essentially arbitrarily complex random effects structure. It is this LKJ prior that ensures that the correlation parameter(s) can generally be estimated, even when data are relatively sparse. Note, however, that when data are too sparse to estimate such parameters, the uncertainty of the estimate will be high—one would learn nothing new (beyond what is specified through the prior distribution) about that parameter from the data.

2.3. Specifying the linear mixed model in brms

After we have defined the priors as shown above, we define the linear mixed model using lme4 syntax, as shown in Listing 3. The brms code has some differences from lme4. At this beginning stage, it is not important to understand every detail.

1. The term family = gaussian() makes explicit the underlying likelihood function that is implicit in lme4. Other linking functions are possible, exactly as in the glmer function in lme4.

2. The term prior takes as argument the list of priors we defined in Listing 1. Although this specification of priors is optional, the researcher should always explicitly specify each prior. Otherwise, brms will define a prior by default, which may or may not be appropriate for the research area. We return to this point below.

3. The term iter refers to the number of iterations that the sampler makes to sample from the posterior distribution of each parameter (by default 2000).

4. The term warmup refers to the number of iterations from the start of sampling that are eventually discarded (by default half of iter).

5. The term chains refers to the number of independent runs for sampling (by default four).

6. The term control refers to some optional control parameters for the sampler, such as adapt delta, max treedepth, and so forth.

The values used in Listing 3 for iterations, warmup, chains, and the control structure often suffice for phonetic and psycholinguistic/psychology data-sets. Most of these values are the default values for those terms,² and in case they lead to warnings, Stan and brms will print out detailed suggestions on how to proceed; the researcher should follow the instructions in the warning messages, and consult the guide to Stan’s warnings (mc-stan.org/misc/warnings.html).

After the Bayesian linear mixed model has been fit by running the code shown in Listing 3, the next question is: how to draw inferences from the model output, and how to summarize the results? In the next sections, we work through some examples illustrating the steps. In our first example below, in order to illustrate the advantages of using Stan and brms, we also compare the performance of the Bayesian model with the frequentist estimates.

m1M <-brm(formula = VOT ~ gender + (1 | subject) + (gender | item),
data = datM_stops, family = gaussian(), prior = priors,
iter = 2000, chains = 4, control = list(adapt_delta = 0.99))

Listing 3: Example of model specification in brms.

3. Research questions

In our case study, we use published voice onset time (VOT) data measured in milliseconds for word-initial stops elicited from 10 adult female and 10 adult male speakers that use differences in VOT in some way to contrast at least two series of stops. We use data from 20 speakers of Dongbei (Northeastern) Mandarin Chinese (Li, 2013) and 20 speakers of North American English (Kong et al., 2012). The target stop productions were elicited in the same way across the two languages, using a picture-prompted word-repetition task that was developed to elicit word productions from young children (Edwards and Beckman, 2008). Because the VOT measurements were made using the same criteria by the same group of researchers and their research assistants, they are amenable to evaluating the following questions:

1. Does VOT in the long-lag stops (aspirated stops in Mandarin and voiceless stops in English) differ by gender in each language?

   Li (2013), Peng et al. (2014), and Ma et al. (2017) show that in three different varieties of Mandarin, women tend to produce aspirated stops with longer VOT values relative to men. In motivating her study, Li reviews many previous studies showing that in both North American English and British English, women tend to produce voiceless stops with longer VOT values relative to men. These studies include Morris et al. (2008), Robb et al. (2005), Ryalls et al. (1997), and Swartz (1992).

2. Is VOT in the long-lag stops predicted by speaker’s typical vowel duration (as a proxy for speech rate)?

   A number of studies reviewed in Simpson (2012) suggest that cross-linguistically, women tend to speak more slowly and clearly. For example, Byrd (1994) measured longer utterance durations in female speakers of North American English and found that they tend to use less vowel reduction. Similarly, Hillenbrand et al. (1995) and many others have shown that female speakers produce longer stressed vowels than men. Building on this work as well as on work such as Kessinger and Blumstein (1997) and Pind (1995) showing that VOT is correlated with speaking rate, Li (2013) suggests that it is important to test for effects of inter-speaker rate differences when examining apparent gender effects on VOT values.

3. Are there cross-linguistic differences between English and Mandarin for questions 1 and 2?

We investigate each of these questions next.

3.1. Question 1: The effect of gender on VOT in long-lag stops

In order to address question 1, we begin by plotting voice onset time values for each participant in each language, grouping the participants by gender: see Figure 2. As the figure shows, the female speakers on average have longer VOT values than male speakers in the stops in the long-lag category (i.e., the voiceless stops of English and the aspirated stops of Mandarin). In contrast, in the other stop type, the effect of gender is either in the opposite direction (in the unaspirated stops of Mandarin), or non-existent (in the voiced stops of English). Li (2013) interpreted the interaction between gender and stop type for Mandarin as evidence that the effect of gender is an indirect result of a gender effect on speech clarity, with male speakers tending to reduce the contrast between unaspirated and aspirated stops and female speakers tending to enhance it. Evaluating the evidence for this interpretation of the Mandarin interaction is complicated by the fact that the distributions of the VOT values for the speakers with aspirated stops cover a wider range and are more skewed relative to the distributions for the unaspirated stops (and the same is true for the voiceless stops relative to the voiced stops for the seven English speakers who produced short-lag VOT values for all tokens of /d/ and /g/). This pattern suggests that a log transform is in order (Gelman and Hill, 2007, pp. 59–65). However, the fact that thirteen of the English speakers produced at least some tokens of voiced stops with voicing lead precludes a simple application of the transform to address the question of the gender effect in both languages using the same model. In keeping with the purpose of this tutorial introduction, therefore, we will defer the problem of how the gender effect depends upon the stop type for a future paper, and here include just the VOT values for the stop types with long-lag VOT, namely, the aspirated stops of Mandarin and the voiceless stops of English.

Figure 2:

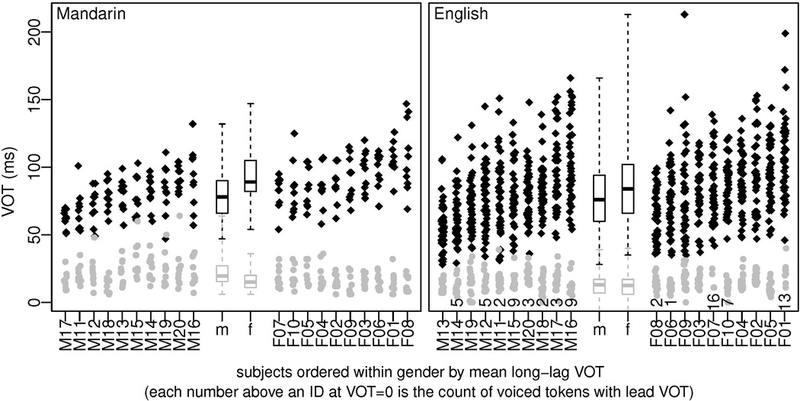
Stripcharts showing the distribution of VOT values for each of the participants, grouped by language (with Mandarin speakers in the left panel and English speakers in the right panel) and by gender within each language. The black diamonds represent aspirated/voiceless stops (which are analyzed in this paper), and the grey shaded dots are for unaspirated/voiced stops (the analysis of which is beyond the scope of the current paper, as noted in the main text). In the panel on the right, the numbers {13, 1, 16, 2, 7, 2, 5, 5, 9, 9, 3, 2, 3} above the subject IDs for five of the females and eight of the males are counts of voiced tokens with lead VOT. Boxplots in the center of each panel show the median, inter-quartile range, and range for each gender and stop type. (The whiskers for the minimum VOT for English voiced stops are well below the bottom of the plot, due to the 77 tokens with voicing lead.)

We fit the Bayesian linear mixed model shown in Listing 3 for Mandarin and for English repeated here in Listing 4 for convenience. Along the way, we also fit the corresponding lme4 models.

m1E <-brm(formula = VOT ~ gender + (1 | subject) + (gender | item),
data = datE_stops, family = gaussian(), prior = priors,
iter = 2000, chains = 4, control = list(adapt_delta = 0.99))

Listing 4: Model specification in brms to address Question 1.

3.1.1. Summarizing the results of a Bayesian analysis

Recall that the outcome of a Bayesian analysis is the joint posterior distribution of the parameters of the model. Summarizing a Bayesian analysis involves computing summary statistics of the marginal distributions of the parameters of interest.

We can summarize the relevant posterior distributions graphically using the function stanplot. This function calls the package bayesplot (Gabry and Mahr, 2017). In Listing 5, we plot the posterior distributions of the model m1E using histograms.

stanplot(m1E, type=“hist”)

Listing 5: Code for plotting posterior distributions of the model m using histograms.

The plots produced by bayesplot are based on the popular package ggplot2 (Wickham, 2009) and thus plots made with bayesplot can be modified with ggplot2 syntax. In Figures 3 and 4, for example, we modified the plots by overlaying circles to represent the posterior means, and solid horizontal lines to show 95% Bayesian credible intervals, as well as overlaying triangles and dashed lines to represent the frequentist lme4 means and 95% credible intervals, for Mandarin and English respectively. Note that by default lme4 only outputs point value estimates for the standard deviation and correlation parameters; the Bayesian model will always deliver a posterior distribution.

Figure 3:

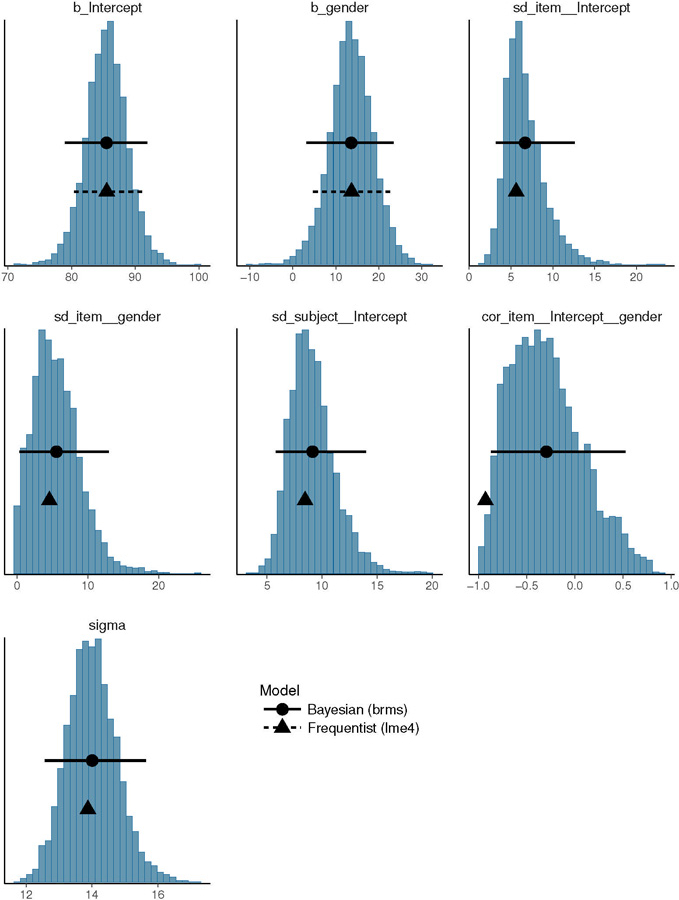
Posterior distributions of the parameters for the Mandarin linear mixed effects model investigating the effect of gender on VOT. The circles and the solid lines represent the mean of the posterior and the 95% Bayesian credible intervals respectively; the triangles and the dashed lines represent the frequentist (lme4) estimates and the 95% frequentist confidence intervals respectively.

Figure 4:

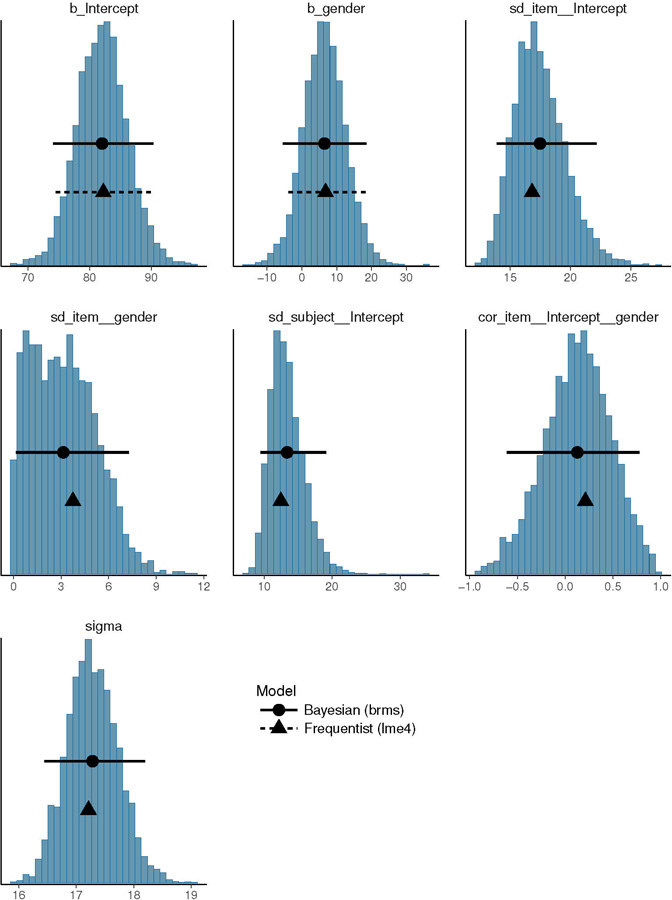
Posterior distributions of the English data investigating the effect of gender on VOT. The circles and the solid lines represent the mean of the posterior and the 95% Bayesian credible intervals respectively; the triangles and the horizontal dashed lines represent the frequentist (lme4) estimates and the 95% frequentist confidence intervals respectively.

To repeat and clarify, the figures show the posterior distributions overlaid with 95% credible intervals: these are the range over which we can be 95% certain that the true values of the parameter lie, given these particular data and the model. The posteriors for the Mandarin data show that female speakers have an increased VOT (over the grand mean), with an estimated mean 14 ms, and a 95% credible interval 3, 23 ms. While the estimate and confidence interval from the lme4 model look superficially similar, credible intervals have a different meaning than frequentist confidence intervals; the latter refer to intervals that would contain the true unknown point mean value if the experiment were hypothetically repeated multiple times. Thus, a single confidence interval technically does not tell us about the uncertainty about our estimate of the parameter (although researchers often treat frequentist confidence intervals as Bayesian credible intervals). For more on confidence intervals versus credible intervals, see Morey et al. (2015).

Comparing the parameter estimates of lme4 vs. Stan, we see the effect of regularizing priors most dramatically in the correlation parameter. The lme4 estimate for the correlation is on the boundary (−1), indicating a failure to estimate the parameter (Bates et al., 2015a). In lme4, a correlation estimate near +1 or −1 suggests that there is insufficient data to estimate this parameter, and a simpler model without the correlation parameter should be fit (Bates et al., 2015a).

Consider now the Bayesian estimate for the correlation. Like all posterior distributions in a Bayesian analysis, this is a compromise (analogous to a weighted mean) between the prior and the data: when data are sparse, the prior will dominate in determining the posterior, but when there are sufficient data-points, the data will largely determine the posterior and lead to estimates similar to lme4’s. Notice, for example, that the correlation’s posterior distribution is widely spread out between −1 and 1; the estimate is near zero but it has very high uncertainty. This wide distribution of the correlation is due to the regularizing effect of the LKJ(2) specification. Note that with brms, we have succeeded in estimating the posterior distribution of the parameter in the sense that we will not have a convergence failure. But we haven’t learnt much about plausible values of the correlation parameter. If we had much more data from Mandarin, we could in principle get very accurate estimates of the correlation (which may or may not be 0). But as things stand, all that the inclusion of the correlation parameter in the model achieves is that it incorporates this source of uncertainty in the model. Also note that, in this particular data-set for Mandarin, the correlation parameter is not going to affect our posterior distribution of the effect of gender (β₁); without the correlation parameter, the posterior distribution has the same mean and credible interval (13, 95% credible interval 3, 24 ms). Such a no-correlation model can be fit in brms using the double-vertical-bar syntax of lme4:

VOT ~ gender + (1 | subject) + (1 + gender || item)

This is equivalent to the following:

VOT ~ gender + (1 | subject) + (0 + gender | item) + (1 | item)

The posteriors from the English data show that the effect of gender has an estimated mean 6 ms, 95% credible interval −5, 18 ms. We discuss the interpretation of this and the Mandarin result in section 3.1.3.

3.1.2. Interpreting the results of a Bayesian analysis

Having fit the models for Mandarin and English, we now discuss different ways of drawing inferences from the posterior distributions. Our favored approach is to display the posterior distribution of the parameter of interest, because we believe that the researcher’s focus should be on the estimate of the parameter and our uncertainty of that estimate. However, other approaches exist; we discuss hypothesis testing using Bayes factors, and predictive evaluation using an approximation of leave-one-out cross validation.

3.1.3. Interpreting the posterior distribution

How to interpret these posterior distributions of the gender effect? If we had carried out a frequentist analysis using a package such as lme4, we would have found a “significant” effect of gender on VOTs in Mandarin but “no significant effect” of gender in English. We can see this by just examining the frequentist confidence intervals for the effect of gender in Figures 3 and 4: if the error bar in the frequentist estimate for the gender effect spans zero on the x-axis, the effect would not be significant at Type I error probability of 0.05.

Should the conclusion be that Mandarin shows effects of gender but English does not? As statisticians have repeatedly pointed out (Wasserstein and Lazar, 2016), these kinds of binary decisions (based on p-values or any other statistic such as confidence intervals) are common but highly misleading. On the one hand, when power is low, if an effect comes out significant it is guaranteed to be an overestimate (Vasishth et al., 2018). On the other hand, when power is low and an effect is found to be non-significant, this often misleads researchers into the invalid belief that they have shown that the null hypothesis is true. An example from psycholinguistics is Phillips et al. (2011), where the absence of interference effects are presented as evidence of absence. We suggest that the focus should instead be on obtaining the estimates and our uncertainty of these estimates. Furthermore, in order to interpret the effect of gender in these languages, the totality of the evidence available in the literature for these languages should be quantitatively investigated, using, for example, a meta-analysis (J¨ager et al., 2017; Nicenboim et al., 2018). Evidence synthesis has been taken to a new level through the MetaLab project at Stanford (http://metalab.stanford.edu). Phonetics can also benefit greatly by quantifying what we have learnt from previous studies, instead of classifying the literature on a phenomenon into two bins, significant and non-significant results.

From the Mandarin and English data (taken out of the context of previous work on this topic), we would conclude that there is some evidence for the effect of gender on VOT in the two languages.

Notice that we are not rejecting any null hypothesis here, and we are computing no p-value. The most useful information we can obtain from a Bayesian model is the posterior distribution of the parameter of interest (here, β₁). However, if necessary, one can use this posterior to carry out hypothesis testing using Bayes factors (Lee and Wagenmakers, 2014).

3.1.4. Using Bayes factor for hypothesis testing

Simplifying somewhat, the Bayes factor is the ratio of the likelihoods of the two models under comparison; for more details, see Lunn et al. (2012). For example, if we want to carry out a Bayes factor analysis of the effect of gender on VOT in Mandarin, and if our null hypothesis is that the effect of gender is the point value 0, we would compare the following two models m1M and m0M:

## m1M: more complex model
VOT ~ 1 + gender + (1 | subject) + (1 + gender | item)
## m0M: simpler model
VOT ~ 1 + (1 | subject) + (1 + gender | item)

We will follow the convention of indicating with a subscript the order in which the models are being compared. For example, the Bayes factor, BF₁₀, indicates the extent to which the data supports m1M over m0M; BF₀₁ would indicate the support for m0M over m1M. A convention followed in Bayesian statistics (Jeffreys, 1939) is that a Bayes factor value of 10–30 would constitute strong evidence in favor of the more complex model, and smaller values, say 3–10, constitute weaker evidence. Values close to one indicate no meaningful evidence for one model or the other. Values below 0.10 would favor the simpler model and therefore the null hypothesis.

Example code for computing the Bayes factor is shown in Listing 6. The full model m1M has the same syntax as shown earlier, except that one term must be added: save all pars = TRUE; this specification is needed to save the samples for all parameters as the samples are needed for the Bayes factor calculation. After fitting the full model m1M, one fits the reduced model, and then one can compare the two models using the function bayes factor in brms. Note the order of the models m1M and m0M in the function; this order matters in interpreting the Bayes factor because it is a ratio of likelihoods of two alternative models. A ratio like 3 computed using the function bayes factor(m1M, m0M) states that data is three times more likely to have occurred under m1M than m0M. If the function call had been bayes_factor(m0M, m1M), the output would be 1/3.

When computing Bayes factors, it is generally a good idea to check the sensitivity of the Bayes factor to the prior for the parameter we are interested in testing. This is because the Bayes factor can change depending on the choice of the prior, even in cases where the posterior is not (or barely) affected by the change in prior. For example, in the Mandarin case, we computed Bayes factors under three different priors for β₁, the effect of gender. Table 1 shows that when the prior on β₁ is very constrained (Normal(0, 20)), the evidence is in favor of an effect of gender. With increasingly diffuse priors, the evidence for the effect of gender becomes progressively weaker. Table 1 also shows the mean and 95% credible interval for the gender parameter; this remains largely unchanged despite the different priors used (with more diffuse priors, the estimate of the mean changes slightly).

Table 1:

The influence of the prior on Bayes factor; an example from the Mandarin data. The models being compared are linear mixed effects models with and without the gender factor.

Prior on β1	BF10	Posterior of β1
		Estimate	Lower	Upper
Normal(0, 20)	6.45	12.83	3.11	22.15
Normal(0, 50)	3.14	13.47	3.4	23.53
Normal(0, 70)	2.44	13.59	3.53	23.62

# We use the same priors as before:
priors_N50 <-c(set_prior(“normal(0, 200)”, class = “Intercept”), set_prior(“normal(0,50)”, class = “b”, coef=“gender”), set_prior(“normal(0, 100)”, class = “sd”), set_prior(“normal(0, 100)”, class = “sigma”), set_prior(“lkj(2)”, class = “cor”))
## full model:
m1M <-brm(formula = VOT ~ 1 + gender + (1 | subject) + (gender | item), data = datM_stops,
family = gaussian(),
prior = priors_N50,
save_all_pars = TRUE,
iter = 10000, warmup = 2000,
chains = 4,
control = list(adapt_delta = 0.99))
## null model and priors:
priors_N50_null <-c(set_prior(“normal(0, 200)”, class = “Intercept”), set_prior(“normal(0, 100)”, class = “sd”), set_prior(“normal(0, 100)”, class = “sigma”), set_prior(“lkj(2)”, class = “cor”))
m0M <-brm(formula = VOT ~ 1 + (1 | subject) + (gender | item), data = datM_stops,
family = gaussian(),
prior = priors_N50_null,
save_all_pars = TRUE,
iter = 10000, warmup = 2000,
chains = 4,
control = list(adapt_delta = 0.99))
BF10 <-bayes_factor(m1M, m0M)

Listing 6: Example code showing how Bayes factor can be computed in brms.

Thus, the Bayes factor is being affected by the prior. The point to take away here is that Bayes factors can be a useful tool, but one should think carefully about the prior, and one should report Bayes factors under several different priors, including informative ones. In the present case, for example, the more diffuse priors might be quite unrealistic. Researchers in psycholinguistics and phonetics are not used to thinking about what constitutes a reasonable prior; but this is not unusual in areas like medicine, where expert opinion often needs to be incorporated into the data analysis (O’Hagan et al., 2006).

One further point to keep in mind when computing Bayes factor using brms is the following. It is advisable to set the number of iterations to 10000, with a warm-up of 2000; this can be important because sometimes the Bayes factor calculation in brms, which uses the bridgesampling package (Gronau et al., 2017), needs more than the usual number of samples (2000 iterations, with 1000 warm-up iterations) to accurately compute the Bayes factor. It is generally a good idea to repeatedly run the bayes_factor function on the fitted models to ensure that the value doesn’t change much; if the value returned by the bayes_factor function varies a lot, then the number of iterations should be increased further.

3.1.5. Assessing model convergence

In Bayesian modeling, it is important to check whether the model has converged. One metric for convergence is the so-called ^{ˆ Ȓ} statistic (Rhat in the model output); this is the ratio of the between to within chain variance. When each of the chains is sampling from the posterior, the end-result is that the amount of between-chain variability is approximately the same as the within-chain variability, so that the ratio of these variances is approximately 1. Thus, an Rhat of approximately 1 for each parameter is one indication that the model has converged. In addition, one should check the effective sample size (n_eff). This is an estimate of the number of independent draws from the posterior distribution. Since the samples are not independent, n_eff will generally be smaller than the total number of samples. How large n_eff should be depends on the summary statistics that we want to use. But as a rule of thumb, n_eff should be larger than 10% of the total number of samples. Thus, in our case, the number of samples is 4000 (1000 from each of the four chains, having discarded the first 1000 as warm-up), so n_eff should ideally be larger than 400.

summary(m1E)
Family: gaussian
Links: mu = identity; sigma = identity
Formula: VOT ~ gender + (1 | subject) + (gender | item)
Data: datE_stops (Number of observations: 836)
…
Population-Level Effects:
Estimate Est Error l-95% CI Eff Sample Rhat
Intercept 82.00 4.12 74.08 90.30 391 1.00
gender 6.49 6.07 −5.42 18.50 562 1.01

Listing 7: An extract from the summary output from a fitted brms model.

The fitted models above provide information about convergence diagnostics. As shown in Listing 7, the summary function in brms provides information regarding the Rhat and n eff diagnostics.

Apart from Rhat values and the number of effective samples, another indication of successful convergence is that, when the chains are plotted, they overlap. This is a visual check that confirms that the chains are mixing well. Figure 5 shows an example trace plot for the Mandarin model’s fixed effects parameters (the intercept and slope). This plot is generated using a built-in function call:

stanplot(m1M, pars = c(“^b”))

Figure 5:

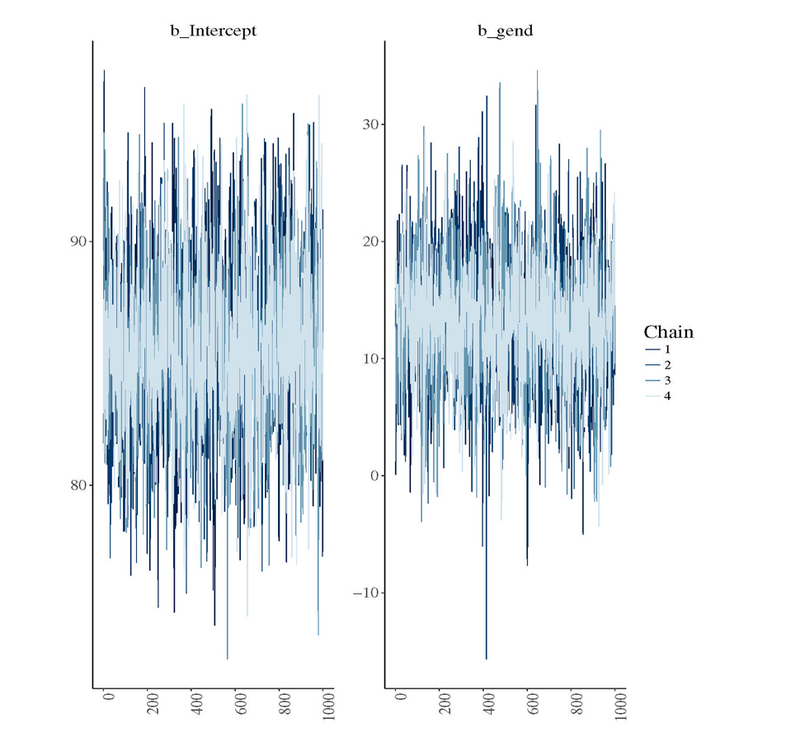
Trace plots for the fixed effects parameters in the Mandarin data.

If the chains had not converged, one would see the trajectories of the chains going in different directions.

A more detailed investigation of convergence can also be achieved using the shinystan package (Stan Development Team, 2017a). This package provides a self-contained graphical user interface for interactively exploring the posterior of a Bayesian model, including help and glossaries. For example, we can explore the model m1M in the following way:

library(shinystan)
shiny_m1M <-launch_shinystan(m1M)

While convergence problems may seem daunting at first, suggestions regarding how to fix them appear on brms output when warnings are printed. Moreover, in many cases the convergence problems appear due to an incorrect model specification (e.g., having varying slopes for gender by participants in the previous model: …+ (gender | subject)), or in the selection of priors (e.g., using a uniform prior when there is not enough data), and thus they can be easily fixed. In some specialized models (not discussed here), convergence problems are due to the geometry of the posterior distribution and this may require reparameterization by modifying the Stan code generated by brms (using make stancode()); see the Reparameterization section of the Optimizing Stan Code chapter in the Stan documentation (Stan Development Team, 2017b). Discussion of this topic is beyond the scope of this introductory tutorial.

3.1.6. Assessing model fit, sensitivity analysis, and model comparison

One commonly used method for assessing how well the model matches up with the observed data is to use so-called posterior predictive checks. Essentially, we generate many instances of new data after computing the posterior distributions of the parameters and compare them to observed data.

Posterior predictive samples can easily be generated from model fit using brms. An example is shown in Figure 6. This figure was generated by typing the following command, which compares the data with 100 predicted samples:

pp_check(m1M, nsamples = 100)

Figure 6:

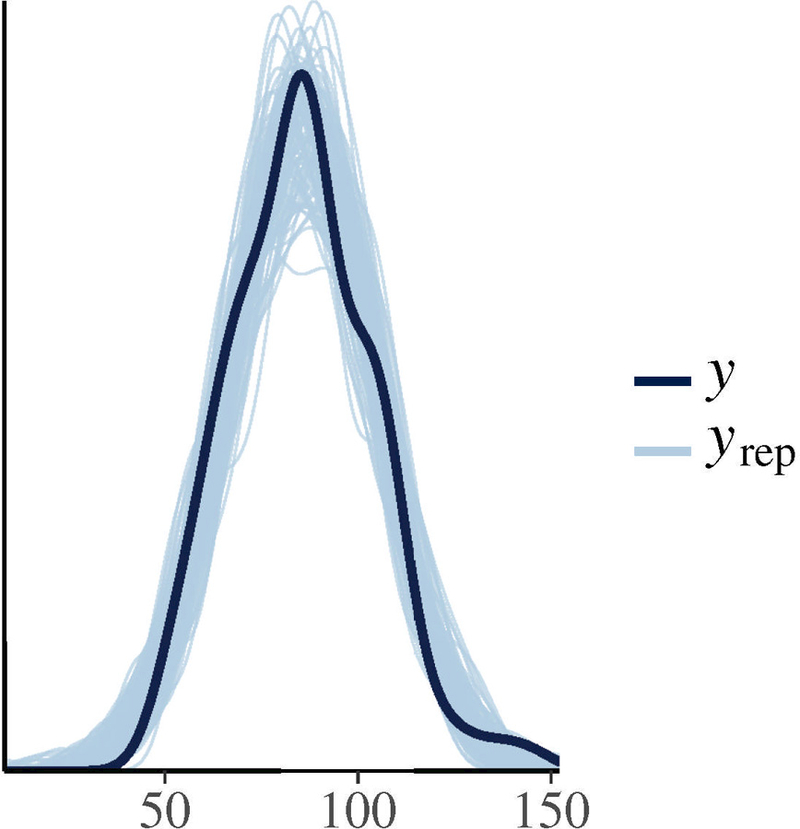
Posterior predictive checks for the Mandarin data. The lines marked y_rep refer to the posterior predictive values generated by the model, and the black solid line are the observed data.

Here, the observed data are plotted alongside the predicted data generated by the model. If the predicted and observed data have similar distributions, we can conclude that the model has a reasonable fit.

There is an obvious drawback to this approach: one is evaluating the model against the very data that was used to estimate the parameters. It should not be surprising that the model predicts data that were used to fit the parameters! However, when model assumptions are grossly violated, even this easy test will fail. For example, if there are some (say, 5%) 0 ms VOTs in a data-set (e.g., due to speech errors or some other reason), or if there is a mixture of distributions generating the data (as in the case of the English voiced stops produced by the 13 speakers who had prevoicing in some of their tokens), and the model assumes a Gaussian likelihood, the posterior predictive distributions and the distribution of the data will not line up. For a real-life example of such a situation, see Vasishth et al. (2017). In Figure 7, we use the Mandarin data to simulate such a situation by randomly replacing 5% of the data with 0 ms values. The mismatch between the data and the posterior predictive values is clear visually.

Figure 7:

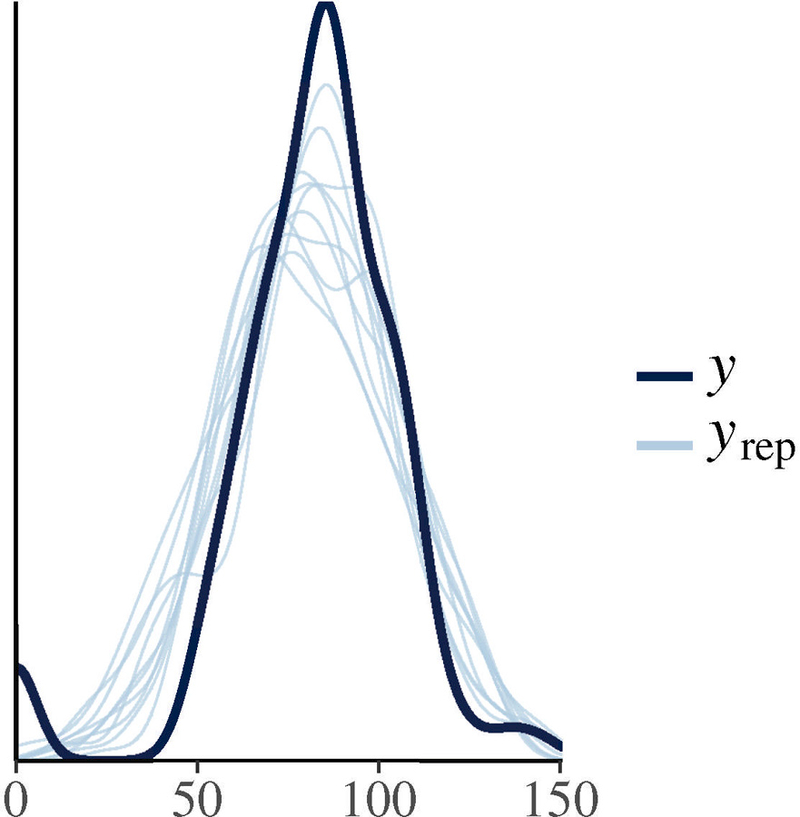
An artificial example of how a mismatch between the model assumptions and the data can lead to poor posterior predictive fits. Here, 5% of the Mandarin VOT values were randomly replaced with 0 ms values and the same model as the one for research question 1 was fit. Now the posterior predictive check shows that the lack of fit between the data and the predicted values.

A better approach for evaluating the predictive performance of a model may be to test the model’s predictions against new data, or against held out subsets of data (Vehtari and Ojanen, 2012; Gelman et al., 2014; Piironen and Vehtari, 2015). This procedure is called k-fold cross validation. Another variant is called leave-one-out (LOO) cross-validation; in LOO, we leave one data point out and fit the model, and then predict the held-out data-point (Vehtari et al., 2015a). The distance between the predicted and observed data can then be used to quantify the relative predictive error when comparing competing models. The brms package provides tools for doing these kinds of model evaluations. In brms one can do an approximation of LOO cross-validation using the built-in function loo (Vehtari et al., 2015b). In the above example for LOO, the function call is simple: loo(m1M, m0M). The output of this command in the present case would be a quantity called the LOO Information Criterion (LOOIC) for each model; this quantifies the estimated predictive error, and displayed alongside this predictive error is its standard error. The function loo also computes the difference in estimated predictive error between the two models, along with a standard error of the difference. These two quantities can then be used to compare the two models: we compute the difference in LOOIC values of the two models (ΔLOOIC), and then use the standard error to determine whether the difference in LOOIC includes 0 as a value by computing ΔLOOIC ± 2 × SE.

Listing 8 shows the output of the model comparison using LOO. Here, the difference in predictive error, the final line in the output, is ΔLOOIC ± 2 × SE = −0.86 ± 2.12 = −5.1, 3.38. The Bayes factor based hypothesis test showed some weak evidence in favor of m1M, LOO shows virtually no difference between the models. This is because the experimental manipulation produced a very small change in the predictive performance of m1M in comparison with m0M. This absence of a difference in predictive performance does not mean that small effects are not important for evaluating a phonetic theory. In general, even with moderate sample size, it can be difficult to compare nested hierarchical models (such as linear mixed models) based on predictive performance (Wang and Gelman, 2014).

This method of model selection is useful, however, when one is interested in comparing the predictive performance of very different competing models. For fully worked examples of this approach (with reproducible code and data) in the context of cognitive modeling in psycholinguistics, see Nicenboim and Vasishth (2018) and Vasishth et al. (2017).

Thus, our analysis demonstrates how a complete data analysis can be carried out in the Bayesian framework. To recapitulate the steps:

loo(m1M, m0M)

## LOOIC SE
## m1M 1653.38 22.32
## m0M 1654.74 22.57
## m1M -m0M −1.37 2.18

Listing 8: Model comparison using PSIS-LOO. A smaller value of LOOIC indicates a model with better predictions.

1. Explore the data using graphical tools; visualize the relationships between variables of interest.

2. Define model(s) and priors.

3. Fit model(s) to data.

4. Check for convergence (Rhat, n eff, trace plots).

5. Carry out inference by

   1. summarizing and displaying posterior distributions, or
   2. computing Bayes factors with several different priors for the parameter being tested, or
   3. evaluating predictive performance of competing models using k-fold cross-validation or approximations of leave-one-out cross-validation.

A Bayesian analysis is clearly more involved than a frequentist one and requires some thought and judgment when defining priors. The models can take a long time to compile, but the reward is substantial: one can turn the focus to quantitative estimates of effect sizes. This is much more informative than the significant/not-significant distinction, as discussed earlier. When quantitative models exist, these empirical estimates can be compared against model predictions. In cases where quantitative models don’t yet exist, empirical estimates provide the basis for developing such models.

In the remainder of the paper, we address the other two questions we posed, and in doing so, demonstrate the flexibility of the Bayesian framework.

3.2. Question 2: The effect of typical vowel duration on VOT

Recall from section 3 that the second research question was whether the VOT in the long-lag stops is predicted by the speaker’s typical vowel duration (as a proxy for speech rate). In order to investigate the effect of vowel duration on VOT, we can use the vowel duration for each participant as a predictor to a model in the same way we used gender before; the only difference is that the vowel duration is a continuous measure, whereas gender was a categorical variable that we coded using sum contrasts.

One question that arises here is: How do we estimate the vowel duration for each speaker? One possibility is to take the mean vowel durations from the same long-lag stop trials that provide the VOT values and use those as a predictor; another is to take the mean vowel durations from the unaspirated (Mandarin) and voiced (English) trials. We take the second alternative in this paper in order to avoid using information from the long-lag trials twice in the same model.

Figure 8 shows, for the two languages, the relationship between the mean VOTs and mean vowel duration, along with the standard errors of each mean (the error bars). This uncertainty expressed by the standard deviation arises because we measure each participant’s vowel duration and VOT values multiple times, and these measurements will naturally have some error about the (unknown) true value for that participant.

Figure 8:

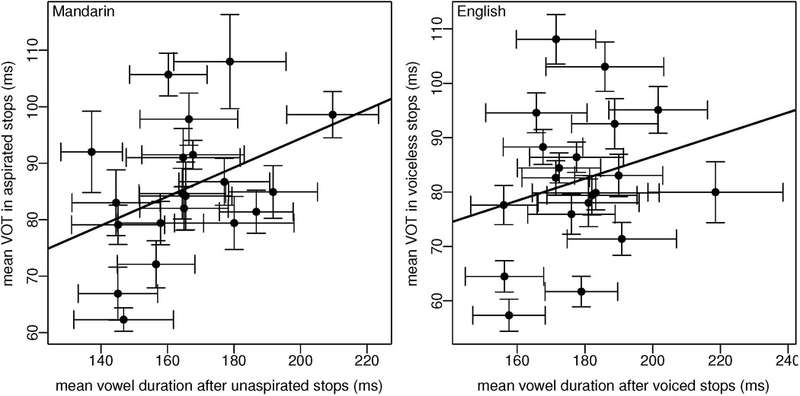
Mean VOT values are shown against mean vowel duration in the two languages; the error bars represent standard errors of each measure. There seems to be a positive relationship between the means; we see this from the linear regression line fitted to the means. But this linear fit does not take the uncertainty of these estimated means into account.

Looking at Figure 8, it seems that there is a linear relationship between mean vowel duration and mean VOT in both languages. A linear model fit to the data yields the following estimates for Mandarin: mean 0.26, 95% confidence interval −0.02, 0.53. For English, the estimates are: 0.2, 95% confidence interval −0.18, 0.59.

However, what these linear models do not take into account is the uncertainty of each of the estimated mean values. It is well-known that aggregating data in this way can lead to correlations arising from ignoring the relevant variance components.³

In our models, we will take the measurement errors of the mean VOT and mean vowel duration estimates into account. Thus, if the VOT and vowel duration estimated for one participant i is VOT_i and vdur_i, we can also record the standard errors of these estimates, and take that uncertainty into account in our model. Such a measurement error model is straightforward to implement in brms, and is shown in Listing 9. Here, we define priors for the intercept and slope fixed effect, and for the standard deviation of the residuals. The predictor includes not only vowel duration but also the corresponding standard error; this is written me(c_meanvdur, sevdur), where c_meanvdur is the centered mean vowel duration, and sevdur is the standard error of the mean vowel duration. For defining the prior for this predictor, we use the concatenation of the string me(c_meanvdur, sevdur), with the brackets and commas stripped out: mec_meanvdursevdur. This is just how brms deals with this parameter name. We chose a Normal(0, 5) prior for the predictor. As an exercise, the reader may wish to change this prior to Normal(0, 10) to see whether the posterior changes substantially (it should not). The dependent variable, meanVOT, also has a standard error associated with it, and this is expressed in brms by writing meanVOT | se(seVOT). An important detail in brms syntax when fitting a measurement error model on the dependent variable is that residual error is estimated by adding the term (1 | subject).

3.3. Interpreting the results

## data frame used: head(meansM)
## # A tibble: 6 × 5
## subject meanVOT seVOT c_meanvdur sevdur
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 F01 106. 3.79 –5.31 11.6
## 2 F02 86.7 4.16 11.5 13.7
## 3 F03 97.8 4.62 0.879 14.7
## 4 F04 84.9 4.68 26.2 13.4
## 5 F05 84.6 4.49 –1.11 13.0
## 6 F06 98.6 4.10 44.1 13.8
priors_normal5 <-c(set_prior(“normal(0, 200)”, class = “Intercept”), set_prior(“normal(0,5)”, class = “b”,
coef = “mec_meanvdursevdur”),
set_prior(“normal(0, 20)”, class = “sdme”),
set_prior(“normal(0, 20)”, class = “sd”))
m2M_error <-brm(formula = meanVOT | se(seVOT) ~ me(c_meanvdur, sevdur) + (1 | subject),
data = meansM, family = gaussian(), prior = priors_normal5, iter = 2000, chains = 4,
control = list(adapt_delta = 0.999,
max_treedepth=15))

Listing 9: Measurement error model, investigating the effect of vowel duration on VOT in Mandarin.

The estimates from the two measurement error models (for Mandarin and English) are shown in Figure 9 and Tables 2 and 3. The tabular summaries are an alternative way to summarize the posterior distributions of interest. The 95% credible intervals give us a way to quantify our uncertainty about the estimates of interest. What is the difference in the estimates from the standard frequentist linear model estimates and the measurement error model estimates? The linear model gave an estimate of 0.26 for Mandarin, with 95% confidence interval [−0.02, 0.53]. The corresponding measurement error model yields an estimated posterior mean of 0.65, with a wider 95% credible interval [−0.3, 2.78]. Similarly, the frequentist estimates for English are 0.2, [−0.18, 0.59], while the measurement error model estimates are 1.51, [−5.23, 7.26]. The greater width of the Bayesian credible intervals arises due to the uncertainty added by the measurement error terms on the independent and dependent variables; differently put, without measurement error included, the frequentist confidence intervals reflect overconfidence about the estimates.

Figure 9:

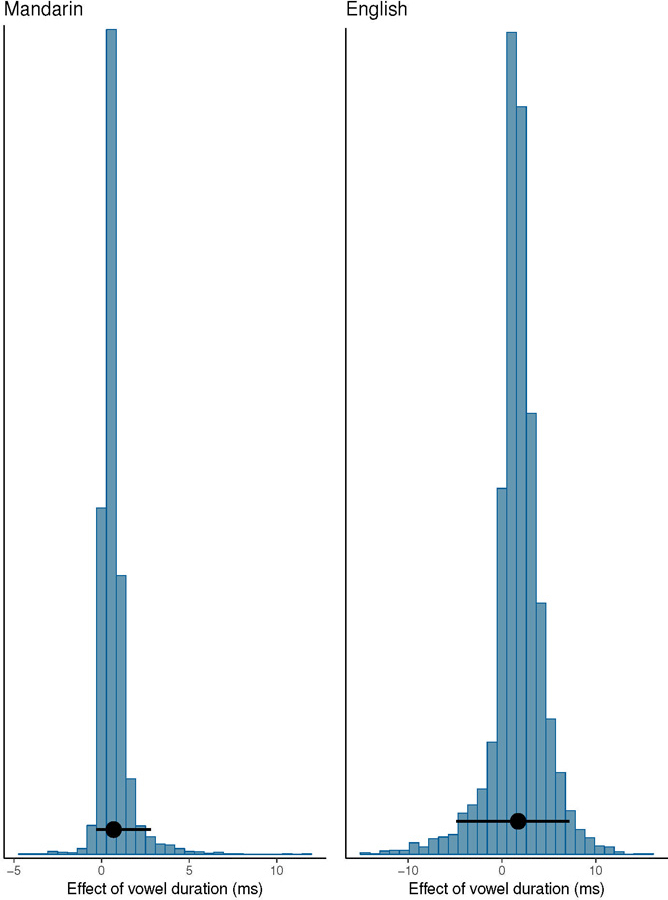
Posterior distributions of the effect of vowel duration in Mandarin and English. Also shown are 95% credible intervals.

Table 2:

Estimates from the measurement error model for Mandarin.

	Estimate	Lower	Upper
Intercept, ${\widehat{\beta }}_0$	85.73	78.61	94.05
Mean vowel duration, ${\widehat{\beta }}_1$	0.65	−0.3	2.78

Table 3:

Estimates from the measurement error model for English.

	Estimate	Lower	Upper
Intercept, ${\widehat{\beta }}_0$	86.78	59.67	118.01
Mean vowel duration, ${\widehat{\beta }}_1$	1.51	‒5.23	7.26

These results could mean that mean vowel duration is not a good measure of speech rate (which might yet have an effect on VOT; cf. Kessinger and Blumstein, 1997 and Pind, 1995). Another possibility is that the effect is very small, and that we do not have enough data to draw any conclusions. As always, an important question to ask is, how do the present data relate to existing work on this topic? A quantitative evaluation of the current data in the context of existing estimates is a very important but underappreciated tool. If we had a systematic way to summarize our prior knowledge on this question, we could have incorporated this knowledge by using informative priors in the analysis.

3.4. Question 3: Cross-linguistic differences between Mandarin and English for questions 1 and 2

We turn next to the question: are there cross-linguistic difference between Mandarin and English in the gender effect on VOT, and in the effect of vowel duration on VOT? We can address this question by fitting two separate hierarchical models: (a) the main effects and interaction of language and gender, (b) the main effects and interaction of mean vowel duration and language. For simplicity, we ignore measurement error on the mean vowel duration, but this can be easily added to the model if necessary.

As Tables 4 and 5 show, we see some evidence for gender (mean 11 ms, 95% credible interval 3, 18); and some weak evidence for vowel duration affecting VOT (mean 4 ms, 95% credible interval 0, 8). All other effects have wide uncertainty and have means not far from 0.

Table 4:

The main effects of gender and language, and their interaction.

	Estimate	Lower	Upper
Intercept, ${\widehat{\beta }}_0$	83.79	77.34	90.54
Gender, ${\widehat{\beta }}_1$	10.61	2.76	18.44
Language, ${\widehat{\beta }}_2$	3.70	‒10.43	17.17
Gender:Language, ${\widehat{\beta }}_3$	6.35	‒8.97	21.98

Table 5:

The main effects of centered and scaled vowel duration and language, and their interaction.

	Estimate	Lower	Upper
Intercept, ${\widehat{\beta }}_0$	83.75	76.74	90.26
Mean vowel duration, ${\widehat{\beta }}_1$	3.98	‒0.15	7.94
Language, ${\widehat{\beta }}_2$	3.34	‒10.22	16.54
Mean vowel duration:Language, ${\widehat{\beta }}_3$	1.69	‒6.29	9.79

4. Concluding remarks

We have attempted to provide a practical entry point into Bayesian modeling using the package brms, which serves as a convenient and easy-to-use front-end to the probabilistic programming language Stan. Other ways to use Stan are through the front-end rstanarm (Gabry and Goodrich, 2016), and the R package rstan (Guo et al., 2016). The package rstanarm has fewer customizations possible compared to brms, but has precompiled code for commonly used models, which leads to faster data analysis. Other versions also exist for python (pystan), Matlab, Mathematica, Julia, Stata; see mc-stan.org for more detail on these alternatives.

In order to develop a better understanding of this approach to analyzing data, it is important to acquire experience and further exposure to fitting and interpreting models. Several useful books have recently appeared that are intended for a general audience. Two important recent ones are Kruschke (2014) and McElreath (2016); these provide a complete introduction to different aspects of Bayesian modeling.

Bayesian methods also find application in cognitive modeling; two useful introductory books are Lee and Wagenmakers (2014) and Farrell and Lewandowsky (2018).

Highlights.

• A hands-on introduction to using the brms package for Bayesian data analysis.

• Examples discussing how to decide on priors, and how to carry out sensitivity analyses.

• Examples showing how to evaluate model fit using posterior predictive checks.

• Examples showing different approaches to inference: reporting posterior distributions, Bayes factor, cross-validation.

• Example using measurement error models demonstrating the flexibility of Bayesian modeling.