Abstract
Objective: Develop the methodological foundation for interactive use of Markov process decision models by patients and physicians at the bedside.
Design: Monte Carlo simulation studies of a decision model comparing two treatments for benign prostatic hypertrophy: watchful waiting (WW) and transurethral prostatectomy (TUR).
Measurements: The 95% confidence interval (CI) for the mean of the Markov model; the correlation of a linear approximation with the full Markov model; the predictive performance of the approximation; the information index of specific utilities in the model.
Results: The 95% CI for the gain in utility with initial TUR was -1.4 to 19.0 quality-adjusted life-months. A multivariate linear model had an excellent fit to the predictions of the Markov model (R2 = 0.966). In an independent data set, the linear model also had a high correlation with the full Markov model (R2 = 0.967); its predictions were unbiased (p = 0.597, paired t-test); and, in 96.4% of simulated cases, its treatment recommendation was the same.
Conclusion: Using the linear model, it was possible to efficiently compute which health state had the largest contribution to the variance of the decision model. This is the most informative utility value to elicit next. The most informative utility at any point in a sequence changed depending on utilities previously entered into the model. A linear model can be used to approximate the predictions of a Markov process decision model.
In the early 1980s the goal of medical decision analysis was to help individual patients make difficult medical decisions. Most medical decision analyses are performed with computers, and computers may be a reasonable tool for conducting decision analytic “dialogues” with the patient. In these dialogues, a measure of the uncertainty of the decision model's recommendation is important in terms of validity and acceptability. Many decision models, such as Markov or semi-Markov process models, are extremely complex, and methods for confidence interval determination can be computationally expensive, making interactive use of these models impossible. We sought a simple method of summarizing the uncertainty inherent in a Markov process model that could be used on a real-time scale. We introduce a Monte Carlo method for confidence interval calculation for Markov models. Using a previously published Markov model, we show that the results of this Monte Carlo simulation can be summarized accurately using a simple linear model. This model can then be used interactively, with a drastic decrease in computation time, to provide decision support for individual patients. We discuss the advantages of this method over other computational methods for interactive decision support.
Background
Decision modeling is often used to evaluate the risks and benefits of medical treatments or screening programs for groups of patients or the nation as a whole. In this role, decision analysis is now widely accepted,1 though there are still a few skeptics.2 When first applied by Pauker and others in the mid 1970s,3 however, the purpose of performing decision analyses was quite different. Rather than focusing on policy issues, decision analysis was initially thought to be an important tool for helping physicians and patients with critical medical decisions.4 Computers have long been thought to be an important part of the process of bringing decision analysis to the bedside.5 It was also hypothesized, in some of the first publications of decision models, that application of this approach could be completely automated.6 However, in contrast to diagnostic expert systems, there are currently no decision-analytically based systems for generating treatment recommendations in wide clinical use.
Often, decision models involve tradeoffs between quality and quantity of life. In this situation, some of the most important inputs to the model are the patient's preferences regarding survival duration and quality of life. This conclusion has been demonstrated for a wide variety of decision models.7,8,9,10 Therefore, therapeutic decision support systems require the elicitation of patients' preferences for life in poor health. The technology for using computers to elicit preferences is rapidly evolving.11,12,13,14,15 Soon it may be possible to use automated computer interviewing techniques to make preference elicitation a form of human computer dialog12 after the model proposed by Slack.16 This approach may solve the problem of incorporating patient preferences into decision support software.
Markov Process Models
Decision modeling methods have also evolved since the mid-1980s from the use of decision tree representations to Markov model representations,1 creating potential problems for would-be developers of decision support systems. The computations required for Markov model predictions are so complex that it was simply not practical to perform these analyses at the bedside when the methods were first described. Several hours or even several days might be needed to perform the computations on a desktop computer.
Markov models are simple representations of time-dependent cyclic processes. The primary advantage of a Markov process is the ability to describe, in a mathematically convenient form, the time-dependent transitions between health states. The amount of time spent in each health state in the Markov process model is combined with the quality weight for being in that state. The sum over all health states and periods of time in the model is the expected number of quality-adjusted life years (QALYs) of the treatment option. The treatment option with the highest number of expected QALYs is the preferred option.
When the medical processes being modeled are complex and occur over long time periods, or when the cycle length of the Markov process is small, the computing power needed to calculate Markov chains increases dramatically. In order to use these models for decision support, we sought a computationally trivial method of summarizing the results of these complex models.
Uncertainty in Decision Models
In order to evaluate the usefulness of the process of interactive decision analysis, it is vital that the program have some benchmark of the uncertainty of its conclusions. Previous work in expert systems has used various ad hoc17 and probabilistic methods18 to estimate uncertainty in recommendations. However, none of these is directly applicable to Markov representations.
The traditional approach that decision analysts use to assess the uncertainty in a treatment recommendation is sensitivity analysis. In sensitivity analysis, the effect of uncertainty in one or more of the input variables (either model probabilities or utilities) on the output of the model (usually the difference in expected utility) is examined. Most decision analysts perform one-way or at most two-way sensitivity analyses (varying one or two variables at a time). Performing systematic sensitivity analyses in more than two dimensions is impractical because of the computational complexity. Moreover, visualizing simultaneous variability in more than two dimensions is difficult.
One approach to gauging the effect of uncertainty of a decision model (and in particular a Markov process) is to use first-order Monte Carlo simulation. This approach is even more computationally expensive than other methods for computing the expected value of Markov processes. In this approach, a single hypothetical patient is run through the model as follows. The patient starts in one of the initial health states in the model (e.g., surgery). Each subsequent transition in the Markov model is simulated by random draws from a uniform distribution, U(0, 1). The transition is made if the value of the draw exceeds the point probability estimate for the transition. A patient entering the process is “followed” through the simulation until he or she reaches an “absorbing” state, such as death. Running this simulation many times results in a probability distribution of the relevant outcome (e.g., QALYs) for the individual. The number of times that the individual outcome for one arm of the model exceeds that of the other outcome is a measure of the uncertainty in the model.19
Several authors have tried to refine this approach by combining Monte Carlo simulation with either logistic regression20 or Classification and Regression Trees21 to determine the truly important combinations of variables and utilities. However, these methods do not assign any degree of certainty to predictions about which treatment is best for an individual.
Confidence Intervals for Decision Models
An alternative approach is to compute a confidence interval for the expected value of the model's prediction. Confidence intervals are a useful statistical device, allowing users to judge how confident they can be that one option is better on average than another. In decision analysis, this is the certainty that the expected number of QALYs afforded by one treatment option will exceed that in another. The degree to which the confidence interval for the difference in expected quality of life overlaps zero is the chance that, given the uncertainty in the variables underlying the analyses, the predictions of the analysis are wrong. If computer programs are to be used to provide support for critical decisions, it is essential that such programs be able to estimate their confidence in the recommendation. Traditional one-way sensitivity analyses do not provide enough information about the overall confidence in the decision to be useful in this task.
There are many methods for confidence interval calculations for decision models,22 including the delta method23 and probabilistic simulation methods. Regarding the latter, Critchfield and Willard24 and Doubilet et al.25 have published probabilistic Monte Carlo methods for confidence intervals for decision trees. In the Monte Carlo methods, it is assumed that the input probabilities for the decision model are not fixed probabilities but rather are distributions of values whose central tendencies are the point estimates used in the original model. Once the distributions for these probability estimates are specified, the decision model can be run many times (Monte Carlo simulation), first choosing values for each probability from its respective distribution, then calculating the difference in expected value between the two options in question. When this process is repeated many times, sampling from the appropriate distributions for each probability estimate in the model, the result is a probabilistic analysis that answers how sensitive the model's expected value is to uncertainty in its probabilities. Uncertainty in utility estimates can also be modeled probabilistically.25 The advantage of simulation methods over the delta method is that fewer assumptions are made about the multivariate distributions of the underlying model parameters.
Later in this paper we describe an approach for extending the Monte Carlo confidence interval method to Markov process models (see Methods). Therefore, in theory, we could compute the confidence level of a recommendation in an individual using this approach. However, because of the computational complexity of Monte Carlo simulation methods for Markov models, this method would not, in the foreseeable future, be appropriate for use in computer programs to assist patients with medical decision because it requires many minutes (even hours) of computation, even on fast desktop computers.
Expected utility calculation for any decision model is linear in health state utilities. This can be seen by the following formula:
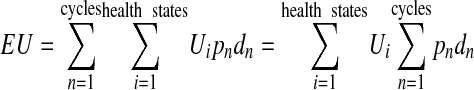 |
where Ui represents utility values, pn represents the cycle-dependent probability of being in that health state as determined by the Markov model, and dn represents the discount rate.
Since the utility values are fixed, they contribute linearly to expected utility, as shown by the right-hand side of the equation. We hypothesized that expected utility might as well be approximately linear over small perturbations in model probabilities.
Thus, a simple multivariate linear model could be used to summarize the results of a Monte Carlo simulation of a Markov process. This approach would provide a significant simplification (and large decrease in computation time) that might allow these methods to be used in real time.
Below, we outline our approach to Monte Carlo simulations of Markov processes and their summary by linear models. We describe how we applied these methods to a decision originally modeled with a Markov process and known to be sensitive to patient preferences. We then show that the output of the Monte Carlo simulation can be summarized with a multivariate linear model and demonstrate how this model could be used in a real-time application for medical decision making.
Methods
Distributions of Input Probabilities for Markov Process Models
We define two general types of transition probabilities in decision models. The first we call “immediate transition probabilities,” and the second we call “Markov transition probabilities.” Immediate transitions probabilities are the simple probabilities that describe a single transition that occurs for all patients at a certain stage in a Markov process model. For example, in the model we examined, a classic choice between surgery and medical treatment for a disease (see below), patients who undergo surgery have a certain chance of significant relief of symptoms. If the symptoms are not relieved by surgery, the patients either remain moderately symptomatic or occasionally become severely symptomatic. These “transitions” are immediate in the sense that the health state transitions definitely occur in the month after surgery. These transitions stand in contrast to the second type of probability, which we call Markov transition probabilities. In this case, a postsurgically “cured” patient has a small monthly chance of recurrence of symptoms but a much larger chance of remaining asymptomatic. These transition probabilities are more akin to rates and are thus modeled differently.
Distributions for immediate transition probabilities (to be used in Monte Carlo simulations) can be modeled simply with binomial or other distributions. For example, if the point estimate of cure after surgery was taken from a single trial (say, 80 of 100 patients reported cure), then the distribution of the immediate transition probability for cure can be modeled as binomial (100, 0.8)/100—that is, a binomial distribution of 100 trials with success probability, 0.8, divided by 100. If multiple events can occur after surgery (e.g., cure, worsened symptoms, death), the multinomial distributions can be approximated with successive binomial distributions, as suggested by Doubilet et al.25
Distributions for Markov transition probabilities are somewhat more
complex. If the point estimate for a transition probability is taken from a
trial report that calculated the Kaplan-Meier point estimate (with confidence
intervals reported), the distribution for this rate can be approximated with a
normal distribution. More often, however, censoring times are not reported,
and the trial reports only the number of events (d) happening per person-time
of follow-up (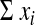 ). The point estimate of the
transition probability,
). The point estimate of the
transition probability, 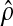 , is
, is
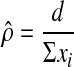 ,,
and the distribution of this point estimate can be approximated for general
censoring patterns by treating
,,
and the distribution of this point estimate can be approximated for general
censoring patterns by treating
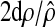 as a chi-squared
variable on 2d degrees of
freedom.26 The
resulting confidence intervals are similar to those obtained from likelihood
ratio methods. For example, if 9 transitions occur over 359 person-days of
follow-up, then the distribution for
as a chi-squared
variable on 2d degrees of
freedom.26 The
resulting confidence intervals are similar to those obtained from likelihood
ratio methods. For example, if 9 transitions occur over 359 person-days of
follow-up, then the distribution for
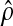 (the daily transition probability)
can be approximated by chi-squared (18 d.f.)/(2*359). If transition
probabilities are known from multiple studies, these probabilities can be
combined meta-analytically and approximated with normal distributions.
(the daily transition probability)
can be approximated by chi-squared (18 d.f.)/(2*359). If transition
probabilities are known from multiple studies, these probabilities can be
combined meta-analytically and approximated with normal distributions.
Distributions for Utility Values
The distributions chosen for input utility values can be modeled in many different ways. If utility data are available from multiple subjects, those distributions can be used directly. Otherwise, beta distributions25 or even uniform distributions can be used. Alternatively, if the simulation process is to be used interactively for a single user, the user may specify a fixed value for the utility estimate for life in poor or perfect health.
Example
We used the methods noted above to perform a Monte Carlo sensitivity analysis for a previously published Markov process decision analysis of transurethral resection (TUR) surgery versus expectant therapy (watchful waiting, or WW) for men with symptomatic benign prostatic hyperplasia (BPH),27 a decision thought to be sensitive to patient preferences. We first reconstructed the Markov model based upon the published report. We reviewed the primary trial reports from which the probability assumptions were taken. We then ran a Monte Carlo analysis of the decision model, which simulated uncertainty in both transition probabilities and utilities. We fit the output data (the distribution of the difference in expected utility between TUR surgery and WW) to a linear model using standard least squares regression. The process is reviewed below.
Decision Model
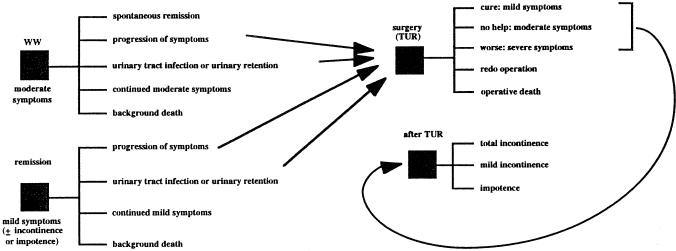
Using Tables 2 through 5 of their original article, we reconstructed the Markov process decision model published by Barry et al.27 A schematic of the model is shown in Figure 1. Watchful waiting is thought to represent a reasonable “treatment” option for men who are moderately bothered by symptoms of BPH for two reasons: spontaneous remission can occur with expectant follow-up (WW), and surgery is associated with an immediate risk of death and complications, such as postoperative mild and total urinary incontinence and impotence. The “down side” of WW is that symptoms of moderate BPH can progress to severe symptoms, necessitating surgery at some later time when surgical risks might be higher. In addition, there are moderate risks of urinary retention and urinary tract infection given WW, risks that are substantially reduced (80% in Barry's model) by surgery. Barry et al. presented the results of multiple one-way sensitivity analyses.
Figure 1.
Schematic of Markov process decision model for TUR versus WW for men with BPH.
The Markov chain simulation of the Barry et al. decision model was programmed in Excel 5.0 (Microsoft Corporation, Redmond, WA) on a Power Macintosh personal computer. As in the model of Barry et al., the cycle length was 1 month and the Markov process simulation was run for 360 months. Point estimates for transition probabilities used were the same as those in Barry's model. We fitted operative mortality to a logistic function using reported data from Barry et al. with age as the dependent variable using the 12-week figures. We used baseline death rates from 1988 vital statistics life tables.
The distribution parameters for point probabilities and utilities used in the model are shown in Appendix 1. In each case, the model from Barry et al. used probability estimates from single trials. Meta-analytic estimates for input probabilities were therefore not used. For Markov transition probabilities we calculated the person-time follow-up used as the denominator for the chi-squared distributions from the number of persons making the transition in the original report and the point estimate of the probability used in Barry's model. Wide ranges for utility distributions and discount rates were modeled with uniform distributions as a first pass to ensure that the output results of the simulation would be useful in linear fitting.
Monte Carlo Simulations
Monte Carlo simulations were performed within the Excel spreadsheet for the model using Crystal Ball software version 3.0 (Decisioneering, Boulder, CO). This software allows specification of many different types of distributions for input values to a spreadsheet. After the input values are chosen, the spreadsheet is calculated (difference in expected utility between TUR and WW), and the output value is displayed graphically and stored in another portion of the spreadsheet. In our analyses, we assumed independence between parameters in the model. However, Crystal Ball allows partial correlations between input value distributions.
Each spreadsheet calculation takes about 20 seconds on a Macintosh 8500 computer with a 120-MHz 604 PowerPC microprocessor; 500 Monte Carlo simulations for this model require about 2.8 hours of calculation time.
Linear Fitting
We ran the Monte Carlo simulation 1000 times, drawing randomly from the specified distributions. We then performed a linear regression, with the difference in expected utility as the dependent variable and the input values for probabilities and utilities as the independent variables. Results of this fitting were evaluated in terms of Pearson's correlation coefficient. To determine the accuracy of the predictive model, we compared the distribution of output values from the linear approximation with those of the full Markov model in an independently generated validation data set (n = 500 trials). Linear regression and other statistical tests were performed using the JMP statistical package (Cary, NC).
Results
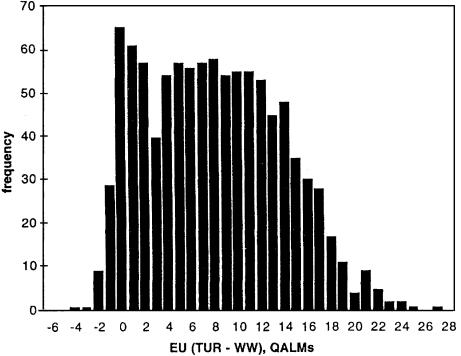
Figure 2 shows the results of 1000 Monte Carlo simulations of the Markov model for TUR versus WW for a 70-year-old man with moderate symptoms of BPH. The results indicate that, given the uncertainties in the probability distributions determined by the actual data and the very wide ranges for uncertainty in utility values, TUR is generally preferred to WW. The mean gain in expected utility of TUR over WW was 7.50 quality-adjusted life months (QALMs), and the 95% confidence interval was - 1.40 to 19.00. Note that the utility value distributions chosen for this Monte Carlo run were very wide and extended into ranges that are probably not clinically relevant. This was done to maximize the generalizability of the linear fit to the output values.
Figure 2.
Histogram of results of Monte Carlo run of Markov process model. The difference in expected utility for TUR versus WW is shown in quality-adjusted life months (QALMs). Areas to the right of 0 indicate that TUR is preferred. The mean difference for this run was 7.49 QALMs (TUR preferred), and the 95% CI was -1.40 to 19.00 QALMs. This simulation requires about 2.8 hours of computation on a Macintosh computer 8500 with a 120-MHz 604 PowerPC processor.
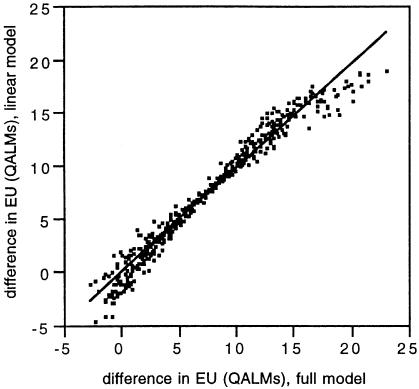
Appendix 2 shows the results of a standard least squares analysis with the probability and utility values as independent variables and the difference in expected utility as the dependent variable. The Pearson's R2 was 0.966, indicating a good fit to the results of the Monte Carlo simulation using the Markov process model. The linear approximation was an accurate and unbiased predictor of estimates from the full Markov model. In an independent data set (n = 500), the correlation (R2) between the predictions of the full model and the linear approximation was 0.967. The average difference between predictions of the full model and the approximation was 0.026 QALMs. This difference was not statistically significant (p = 0.597, paired t-test). In 95.4% of simulations, the treatment recommendation (e.g., the sign of the difference in expected utility for the two treatment options) was the same for the full model and the linear approximation. In the 4.6% of simulations where there was a difference, the “loss” in utility from acting on recommendations drawn from the approximation rather than the full Markov model ranged from 0.42 to 2.4 QALMs (mean difference, 1.4 QALMs) (Fig. 3).
Figure 3.
Plot of the difference in expected utility between the two treatment options estimated by the full Markov model (X-axis) and the linear approximation (Y-axis) in an independently generated validation data set. Expected utility is measured in terms of quality adjusted life months (QALMs).
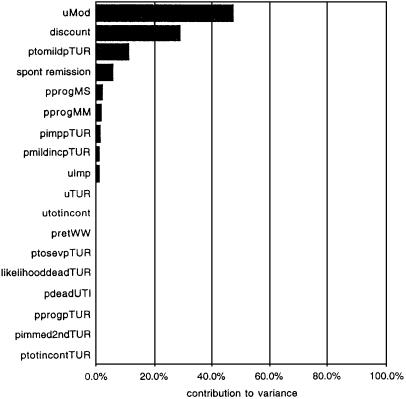
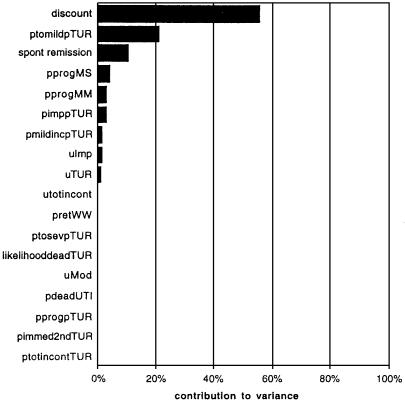
The linear approximation was then used to perform a Monte Carlo simulation with the same probability inputs but with “population” ranges (a priori ranges) of utility values used in one-way sensitivity analyses in the original report of Barry et al.27 Running 1000 Monte Carlo simulations using the linear model took less than 1 minute. The 95% confidence interval for the utility gain associated with TUR, -3.19 to 4.62, was considerably smaller than the original run because the utility ranges selected were narrower. Figure 4 shows the relative contribution of uncertainty in each probability and utility estimate to the overall variance observed in the linear model (and by extension the Markov process model). The largest contributor is uncertainty in the utility value for life with moderate symptoms of BPH. This parameter thus has the highest information index (e.g., knowledge of this parameter reduces the variability of prediction the most).28 The calculation of the information index is similar to the value of perfect information for a parameter in a decision model,29 except in this context it includes both uncertainty in model parameters and the distribution of utility values.
Figure 4.
Contribution of each parameter in the linear model to the total variance of the linear simulation. As expected from previous results,8 the greatest reduction in variance can be achieved by learning about the patients' preferences for life with moderate symptoms of BPH (“uMod”).
The linear model can now be used for interactive decision support in the following way. Knowledge of the utility of moderate symptoms of BPH will reduce the overall variance the most. Assume that the computer program describes this state and elicits a utility of 0.9 for the state. (For purposes of this analysis, we will assume that we know the utility precisely at this point. However, we could easily include measurement error in utility values within this framework.) The computer now quickly reruns the simulation study (using the linear model approximation), and the 95% confidence interval for the difference in EU is -1.52 to 4.31 QALMs. The results of the simulation favor the TUR treatment option, but the 95% confidence interval for the difference in expected utility still includes zero. Figure 5 shows that the discount rate now contributes the most to the observed variance. Suppose now that this rate is measured and is for purposes of this example 3%. The simulation is run once more, and now the 95% confidence interval for the difference in expected utility is 1.19 to 5.01. Now the analyst or a computer program (see discussion below) could be confident in recommending TUR over WW without further measurement of the patient's preferences. Note that the program has moved from the wide “population” confidence interval for prediction to a more narrow individual one. This approach integrates both uncertainty in preferences for health states (some as yet unmeasured in the individual) and uncertainty in the parameters of the decision model itself (i.e., the transition probabilities). For some models and some sets of preferences, the 95% confidence intervals for the difference in expected utility may never exclude zero. At this point, the analyst might make three conclusions: the decision is a toss-up for this individual; the patient should consider other aspects of the decision not directly incorporated in the model; or the model's parameters need to be determined with more precision (i.e., larger studies are needed).
Figure 5.
Recalculation of the contribution of residual uncertainty in model parameters and utilities to the overall variance of the simulation. The results now show that the discount rate has the greatest contribution to the variance and, as a result, the highest information index.
An additional refinement can be made to simplify even further the computation of approximate confidence intervals for Markov processes. Calculation of this value is trivial once the linear summary is computed. If the distribution of the linear model's output were nearly normal, the confidence intervals could be described simply by calculating the variance of the process. If the various random variables, Yi, of the decision model are independent and the decision model can be summarized accurately by the linear model:
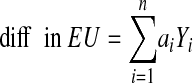 |
then the variance of difference in expected utility can be summarized as
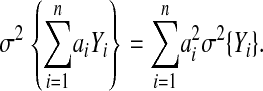 |
The 95% confidence interval then is described by {mean ± 1.96σ}. The exact variance for the linear model, calculated using the formula above, was 4.15. Using the exact variance and the normal approximation, the approximate 95% confidence interval was -3.08 to 4.92. This is compared with -3.19 to 4.62 for the Monte Carlo simulation.
Discussion
It has been a long-standing goal of researchers to develop software that generates treatment recommendations for individual patients. Early work in this area included summarization of decision models in tables6 and the use of rule-based expert systems, sometimes linked to mathematical models.30,31,32 In this early work, researchers recognized the importance of representing the residual uncertainty in computations by the system.17 In the MYCIN program, Shortliffe and others used a metric called “certainty factors” to weigh evidence for and against use of a particular drug therapy in treating sepsis and to direct the acquisition of new evidence. However, one of the primary drives for reformulation of expert-system methods toward a more normative approach (for example, belief network methods) was the ability to use probability distributions to explicitly represent uncertainty in an expert system.18
While belief networks are an appropriate model for single-point-in-time decision making for a patient's diagnosis, the Markov model, with its ability to deal with changes in outcomes over time, has become the standard for representing therapeutic decisions. One important problem that has prevented development of decision support systems based on Markov models is the difficulty in automating—to some degree at least—the application of the decision model to generate clinical insights. In early experiments with expert systems, the authors of these systems realized that physicians had to understand the basis of a program's recommendations before they would act upon them.6 Shortliffe and other realized that one could create explanations for rule-based expert systems by use of a “rule interpreter” that explained the program's reasoning methods.33 Langlotz et al. proposed a similar “heuristic” approach to explain the findings of decision tree models.34
However, the primary method by which decision analytic methods generate new insights into the structure of problems is sensitivity analysis. Although this method generates a qualitative understanding of the behavior of the model, there are limits to its use for purposes of explanation. Multiple sensitivity analyses are computationally expensive and may confuse the inexperienced users. Probabilistic sensitivity analyses, using Monte Carlo methods, overcome this problem by summarizing the entire nature of uncertainty in a decision model with a single output histogram. Confidence intervals also provide a relatively straightforward way of assessing uncertainty in a model's recommendations.
The results of our study show that, while complex calculations are required to perform probabilistic analyses of Markov process decision models, these results can be summarized in a highly accurate, dynamically accessible form using simple multivariate linear models. The development of rapid methods for approximation of sensitivity analyses, in our opinion, has been an important and—until now—missing technology that has prevented application of Markov decision models at the bedside.
The alternative to rapid approximation is exhaustive precomputation of sensitivity analyses. This requires storage of this precompiled information in an accessible way. Sanders et al.35 have described the use of a World Wide Web (WWW) site repository of such precompiled information. While this approach is interesting, it obviously has its limits. If the patient differs from the “base-case” of the model in more than two factors, it will be difficult to find the correct precompiled sensitivity analysis result. All possible combinations of differences cannot be precomputed, and tools for indexing all this information to make it accessible to users are likely to be very complex.
A second useful feature that is only feasible with rapid approximation methods is calculation of the information index as described by Critchfield and Willard.24 The information index describes the nature of the a posteriori distribution of the output value (the difference in EU) with the additional knowledge of a certain input variable (e.g., the utility of life with moderate symptoms of BPH) and the a priori distribution of the output value. The information index has many possible uses in the design of user interfaces for patient decision support systems. One model for the “look and feel” of a patient/computer decision support program is that proposed by Slack.16 In this model, the computer holds a “discussion” with a patient and acts as the patient's agent with the goal of increasing the patient's autonomy in the medical decision-making process. Improved computational abilities, in particular the capability for real-time computation of the information index, may make it possible to use this model for interface design. Calculation of the information index of each utility value or other parameters in the model allows the computer to “dialogue” with the patient on a topic-by-topic basis, moving from topics of greatest important to those of least importance. Because utility values for the model can be elicited one at a time (after careful explanation of the health state), this process would be much closer to a true dialogue. Further, depending upon an individual's preferences, the computer may be able to measure utilities for only some of the health states in the model (yet it would make no a priori assumptions about which states those would be). If greater precision is needed in the utility for any given health state, the computer could simply repeat the preference elicitation for that state and improve the precision of its estimate of the patient's true utility value. The patient's physician can contribute to this “discussion” by customizing the probability distributions in the model based on his or her understanding of the patient's disease process. Using this approach, the program can become a vehicle for encouraging informed discussions about preferences and outcomes consistent with the goals of Slack's model.
If the process of performing a decision analysis for an individual can be completely or almost completely automated by using methods similar to that described above, the costs of individualizing decisions may be quite low. Nease et al.36 have argued that, for many decisions, it might be cost-effective to individualize treatments based on preferences. We are currently working on the development of tools to implement this approach over the World Wide Web by combining use of automated interviews to elicit preferences13 with rapid tools for calculation of the recommendations from decision models. If this approach is successful, the costs individualizing treatment recommendations in a domain would be very low.
If the costs are low and the technology is widely available (through a medium such as the World Wide Web), individualization of therapy is not an issue so much of cost-effectiveness as it is one of ethical imperative. Physicians simply cannot ignore the implications of differences in values between patients—and differences between physicians and patients37—if there are readily available means to incorporate patient preferences into treatment decisions.
Conclusions
Interactive use of Markov models to generate medical insights requires large amounts of computational power. While there is no way to avoid complex calculations in generating decision models, using linear models appears to be a useful tool for summarizing the output of decision models. These tools are especially useful for dynamic calculation of multivariate sensitivity analyses. While the accuracy of linear approximations may vary for different Markov process models, investigators can rapidly determine this as part of initial studies; more complex empirical models might be used if necessary, including interaction terms, nonlinear models, or spline functions. When combined with computer methods for preference elicitation, these tools (or other numerical summarization methods for decision models) may help bring decision analysis to the patient's bedside.
Acknowledgments
We thank the anonymous reviewers of this manuscript for their insightful comments. We also thank Samuel Chiu and Jeffrey Cornwell for their help with work on modeling of variance of Markov processes that eventually led to this paper.
Appendix I
Table 1.
| Transition* | Type of Probability† | Point Estimate | Range | Patients Making Transition | Total Number of Patients or Follow-up Time‡ | Reference Number |
|---|---|---|---|---|---|---|
| ptotincontTUR | Bin | 0.005 | — | 5 | 932 | 38 |
| pmildincTUR | Bin | 0.037 | — | 6 | 164 | 38 |
| pimpTUR | Bin | 0.049 | — | 8 | 163 | 38 |
| ptosevTUR | Bin | 0.058 | — | 5 | 86 | 38 |
| ptomildTUR | Bin | 0.791 | — | 68 | 86 | 38 |
| pimmed2ndTUR | Bin | 0.015 | — | 26 | 1750 | 39 |
| pspontremiss | Chi Sq | 0.024 | — | 31 | 1292 | 40 |
| pprogpTUR | Chi Sq | 0.0018 | — | 77 | 42778 | 41 |
| pretWW | Chi Sq | 0.00033 | — | 2 | 6060 | 42 |
| pprogMM | Chi Sq | 0.004 | — | 10 | 2496 | 43 |
| pprogMS | Chi Sq | 0.0049 | — | 24 | 4898 | 40 |
| pdeadUTI | Bin | 0.027 | — | 1 | 35 | 44 |
| likelihooddeadTUR | Nor | 1.0 | SD =.1 | — | — | EO |
| discount rate | Uni | — | (.03,.15) | — | — | EO |
| uMod | Uni | — | (.5,.97) | — | — | 27 |
| uImp | Uni | — | (.5,.95) | — | — | 27 |
| uTUR | Uni | — | (.5,.95) | — | — | 27 |
| utotincont | Uni | — | (.4,.9) | — | — | 27 |
The transitions occurring in the Markov process model. ptotintontTUR = probability of total incontinence after TUR; pmildincTUR = probability of mild incontinence after TUR; pimpTUR = probability of impotence after TUR; ptosevTUR = probability of severe symptoms after TUR; ptomildTUR = probability of mild symptoms after TUR; pimmed2ndTUR = probability of having an immediate second TUR surgery; pspontremiss = probability of spontaneous remission given watchful waiting (WW); pprogpTUR = probability of progression of symptoms after TUR; pretWW = probability of urinary retention (and urinary tract infection in Barry's model) given WW; pprogMM = probability of progression of symptoms from mild to moderate severe (followed by TUR in the model); pprogMS = probability of progression of symptoms from moderate to severe (also followed by TUR in the model); pdeadUTI = probability of death from hospitalization with urinary tract infection; likelihooddeadTUR = relative risk of death after TUR surgery compared with point estimate (estimated from a logistic equation); uMod = utility of moderate symptoms of BPH; uImp = utility of postoperative impotence; uTUR = utility of month of surgery itself; utotincont = utility of life with total urinary incontinence; EO = expert opinion.
Type of probability distribution used to model distribution of Markov process probability. Bin = binomial; Chi Sq = chi squared; Nor = normal; Uni = uniform.
For binomial probabilities, the total number of patients available to make the transition. For Markov transition probabilities, the number of patient-months in the original reports over which time the transitions occurred.
Transition Probabilities and Utility Values Used in Markov Process Model of Transurethral Surgery (TUR) vs. Watchful Waiting. The first column lists the transition in the model (for example, the probability of total incontinence after TUR). The second column lists the type of probability distribution used to model the distribution of the point estimate. In the case of “immediate transitions,” binomial or normal distributions were used according to the type of data available (reference listed in seventh column). The third column lists the point estimate used in Barry's model. The fourth column lists the range chosen for uniform distributions for the discount rate and utilities. The fifth and sixth columns list the number of patients in the original report making the transition. For example, 5 of 932 patients undergoing TUR reported total incontinence after the surgery. The distribution for this point estimate is therefore binomial (.005, 932 trials)/932. In the case of “Markov transition probabilities,” the sixth column lists the person-months of follow-up.
Appendix II
Table 2.
| Term | Estimate | Std Error | t Ratio | Prob > |t| |
|---|---|---|---|---|
| Intercept | 29.597527 | 0.894322 | 33.09 | <.0001 |
| mildinc | -0.071275 | 0.01468 | -4.86 | <.0001 |
| imp | -0.085916 | 0.012722 | -6.75 | <.0001 |
| tosev | -0.029642 | 0.016263 | -1.82 | 0.0687 |
| tomild | 0.1779516 | 0.008936 | 19.91 | <.0001 |
| spont | -0.084709 | 0.006269 | -13.51 | <.0001 |
| retWW | -0.075034 | 0.024232 | -3.1 | 0.002 |
| progMM | 0.0789936 | 0.011098 | 7.12 | <.0001 |
| progMS | -0.058997 | 0.007105 | -8.3 | <.0001 |
| likedeadTUR | -0.491865 | 0.34509 | -1.43 | 0.1544 |
| discount | -31.80544 | 0.968205 | -32.85 | <.0001 |
| uMOD | -40.52618 | 0.253739 | -159.7 | 0 |
| uimp | 3.6425216 | 0.272316 | 13.38 | <.0001 |
| uTUR | 1.0558866 | 0.270074 | 3.91 | <.0001 |
| utotincont | 0.549728 | 0.240574 | 2.29 | 0.0225 |
Summary of Linear Model Fit for Monte Carlo Simulation of TUR vs. WW Markov Model. The output value (the difference in expected utility between TUR and WW) is calculated as the sum of the product of the input values (which vary with each run of the Monte Carlo simulation) and the parameter estimates. The Pearson's R2 was 0.966.
Supported by a grant (LM 05626-02) from the National Library of Medicine and the Ambulatory Care Fellowship, Department of Veterans Affairs.
References
- 1.Pauker SG, Kassirer JP. Decision analysis. N Engl J Med. 1987;316: 250-8. [DOI] [PubMed] [Google Scholar]
- 2.Asch DA, Hershey JC. Why some health policies don't make sense at the bedside. Ann Intern Med. 1995;122: 846-50. [DOI] [PubMed] [Google Scholar]
- 3.Pauker SG, Kassirer JP. Therapeutic decision making: a cost-benefit analysis. N Engl J Med. 1975;293: 229-34. [DOI] [PubMed] [Google Scholar]
- 4.Pauker SG, Kassirer JP. The threshold approach to clinical decision making. N Engl J Med. 1980;302: 1109-17. [DOI] [PubMed] [Google Scholar]
- 5.Pauker SG, Kassirer JP. Clinical decision analysis by personal computer. Arch Intern Med. 1981;141: 1831-7. [DOI] [PubMed] [Google Scholar]
- 6.Gorry G, Kassirer J, Essign A, Schwartz W. Decision analysis as the basis for computer-aided management of renal failure. Am J Med. 1973;55: 473-84. [DOI] [PubMed] [Google Scholar]
- 7.O'Meara J, McNutt R, Evans A, Moore S, Downs S. A decision analysis of streptokinase plus heparin as compared with heparin alone for deep-vein thrombosis. N Engl J Med. 1994;330: 1864-9. [DOI] [PubMed] [Google Scholar]
- 8.McNeil BJ, Pauker SG, Sox HC, Tversky A. On the elicitation of preferences for alternative therapies. N Engl J Med. 1982;306: 1259-62. [DOI] [PubMed] [Google Scholar]
- 9.Barry MJ, Mulley AJ, Fowler FJ, Wennberg JW. Watchful waiting versus immediate transurethral resection for symptomatic prostatism: the importance of patients' preferences. JAMA. 1988;259: 3010-17. [PubMed] [Google Scholar]
- 10.Gage BF, Cardinalli AB, Albers GW, Owens DK. Cost-effectiveness of warfarin and aspirin for prophylaxis of stroke in patients with nonvalvular atrial fibrillation. JAMA. 1995;274: 1839-45. [PubMed] [Google Scholar]
- 11.Lenert L, Hornberger J. Measurement of quality of life in clinical trials. In: Cimino J (ed). Proc Annu Symp Comput Appl Med Care. Philadelphia: Hanley & Belfus, 1996.
- 12.Lenert LA, Michelson D, Flowers C, Bergen MR. IMPACT: an object-oriented graphical environment for construction of multimedia patient interviewing software. In: Gardner RM (ed). Proc Ann Symp Comput Appl Med Care. Philadelphia: Hanley & Belfus, 1995; 319-24. [PMC free article] [PubMed]
- 13.Lenert LA, Soetikno R. Automated computer interviews to elicit utilities: potential applications in the treatment of deep venous thrombosis. J Am Med Inform Assoc. In Press. [DOI] [PMC free article] [PubMed]
- 14.Sumner W, Nease R, Littenberg R. U-titer: a utility assessment tool. In: Clayton PD (ed). Proc Annu Symp Comput Appl Med Care. New York: McGraw-Hill, 1991; 701-5. [PMC free article] [PubMed]
- 15.Nease R et al. Variation in patient utilities for outcomes of the management of chronic stable angina: implications for clinical practice guidelines. JAMA. 1995;273: 1185-90. [PubMed] [Google Scholar]
- 16.Slack WV, Slack CW. Patient-computer dialogue. N Engl J Med. 1972;286: 1304-9. [DOI] [PubMed] [Google Scholar]
- 17.Shortliffe EH, Buchanan BG. A model of inexact reasoning in medicine. In: Buchanan BG, Shortliffe EH (eds). Rule Based Expert Systems. Reading, MA: Addison-Wesley, 1984; 233-71.
- 18.Heckerman DE, Horvitz EJ, Nathwani BN. Toward normative expert systems: Part I. The Pathfinder project. Methods Inf Med. 1992;31: 90-105. [PubMed] [Google Scholar]
- 19.Sonnenberg FA, Beck JR. Markov models in medical decision making: a practical guide. Med Decis Making. 1993;13: 322-38. [DOI] [PubMed] [Google Scholar]
- 20.Merz JF, Small MJ, Fischbeck PS. Measuring decision sensitivity: a combined Monte Carlo-logistic regression approach. Med Decis Making. 1992;12: 189-96. [DOI] [PubMed] [Google Scholar]
- 21.Hornberger JC, Habraken H, Bloch DA. Minimum data needed on patient preferences for accurate, efficient medical decision making. Med Care. 1995;33: 297-310. [DOI] [PubMed] [Google Scholar]
- 22.Manning WG, Fryback DG, Weinstein MC. In: Gold MR, Siegel JE, Russell LB, Weinstein MC (eds). Cost-Effectiveness in Health and Medicine. New York: Oxford University Press, 1996.
- 23.O'Brien GJ, Drummond MF, Labelle RJ, Willan A. In search of power and significance: issues in the design and analysis of stochastic cost-effectiveness studies in health care. Med Care. 1994;32: 150-63. [DOI] [PubMed] [Google Scholar]
- 24.Critchfield GC, Willard KE. Probabilistic analysis of decision trees using Monte Carlo simulation. Med Decis Making. 1986;6: 85-92. [DOI] [PubMed] [Google Scholar]
- 25.Doubilet P, Begg CB, Weinstein MC, Braun P, McNeil BJ. Probabilistic sensitivity analysis using Monte Carlo simulation: a practical approach. Med Decis Making. 1985;5: 157-77. [DOI] [PubMed] [Google Scholar]
- 26.Cox D, Oakes D. Analysis of survival data: Monographs on Statistics and Applied Probability. London: Chapman and Hall, 1984.
- 27.Barry MJ, Mulley AG, Fowler FJ, Wennberg JW. Watchful waiting versus immediate transurethral resection for symptomatic prostatism. JAMA. 1988;259: 3010-17. [PubMed] [Google Scholar]
- 28.Critchfield GC, Willard KE, Connelly DP. Probabilistic sensitivity analysis methods for general decision models. Comput Biomed Res. 1986;19: 254-65. [DOI] [PubMed] [Google Scholar]
- 29.Howard R. Information Value Theory. IEEE Transactions on Systems Science and Cybernetics 1966;SSC-2(1): 779-83.
- 30.Yu VL, Buchanan BG, Shortliffe EH, et al. Evaluating the performance of a computer-based consultant. Comput Methods Programs Biomed. 1979;9: 95-102. [DOI] [PubMed] [Google Scholar]
- 31.Shortliffe EH, Davis R, Axline SG, Buchanan BG, Green CC, Cohen SN. Computer-based consultations in clinical therapeutics: explanation and rule acquisition capabilities of the MYCIN system. Comput Biomed Res. 1975;8: 303-20. [DOI] [PubMed] [Google Scholar]
- 32.Gorry GA, Silverman H, Pauker SG. Capturing clinical expertise: a computer program that considers clinical responses to digitalis. Am J Med. 1978;64: 452-60. [DOI] [PubMed] [Google Scholar]
- 33.Scott A, Clancey W, Davis R, Shortliffe E. Methods for generating explanations. In: Buchanan B, Shortliffe E (eds). Rule-based Expert Systems. Reading, MA: Addison-Wesley, 1984.
- 34.Langlotz CP, Shortliffe EH, Fagan LM. A methodology for generating computer-based explanations of decision-theoretic advice. Med Decis Making. 1988;8: 290-303. [DOI] [PubMed] [Google Scholar]
- 35.Sanders GD, Dembitzer AD, Heidenreich PA, McDonald KM, Owens DK. Presentation and explanation of medical decision models using the World Wide Web. J Am Med Inform Assoc. 1997. In press. [PMC free article] [PubMed]
- 36.Nease RF Jr., Owens DK. A method for estimating the cost-effectiveness of incorporating patient preferences into practice guidelines. Med Decis Making. 1994;14: 382-92. [DOI] [PubMed] [Google Scholar]
- 37.Lenert L, Markowitz D, Blaschke T. Primum non nocere? Valuing of the risk of drug tosicity in therapeutic decision making. Clin Pharmacol Ther. 1993;53: 285-91. [DOI] [PubMed] [Google Scholar]
- 38.Fowler FJ Jr., Wennberg JE, Timothy RP, Barry MJ, Mulley AG Jr., Hanley D. Symptom status and quality of life following prostatectomy. JAMA. 1988;259: 3018-22. [PubMed] [Google Scholar]
- 39.Melchior J, Valk WL, Foret JD, Mebust WK. Transurethral prostatectomy: computerized analysis of 2,223 consecutive cases. J Urol. 1974;112: 634-42. [DOI] [PubMed] [Google Scholar]
- 40.Ball AJ, Feneley RC, Abrams PH. The natural history of untreated “prostatism.” Br J Urol. 1981;53: 613-6. [DOI] [PubMed] [Google Scholar]
- 41.Holtgrewe H, Valk W. Late results of transurethral prostatectomy. J Urol. 1964;91: 51-55. [DOI] [PubMed] [Google Scholar]
- 42.Birkhoff JD, Wiederhorn AR, Hamilton ML, Zinsser HH. Natural history of benign prostatic hypertrophy and acute urinary retention. Urology. 1976;7: 48-52. [DOI] [PubMed] [Google Scholar]
- 43.Craigen AA, Hickling JB, Saunders CR, Carpenter RG. Natural history of prostatic obstruction: a prospective survey. J R Coll Gen Pract. 1969;18: 226-32. [PMC free article] [PubMed] [Google Scholar]
- 44.Gleckman R. Community acquired urosepsis. In: Gleckman R, Gantz N (eds). Infections in the Elderly. Boston: Little Brown & Co, 1983.