Life Expectancy Predictions for Older Diabetic Patients as Estimated by Physicians and a Prognostic Model

Abstract

Background: Multiple medical organizations recommend using life expectancy (LE) to individualize diabetes care goals. We compare the performance of patient LE predictions made by physicians to LE predictions from a simulation model (the Chicago model) in a cohort of older diabetic patients. Design: Retrospective cohort study of a convenience sample (n = 447) of diabetes patients over 65 years and their physicians. Measurements: Physicians provided LE estimates for individual patients during a baseline survey (2000–2003). The prognostic model included a comprehensive geriatric type 2 diabetes simulation model (the Chicago model) and combinations of the physician estimate and the Chicago model (“And,” “Or,” and “Average” models). Observed survival was determined based on the National Death Index through 31 December 2010. The predictive accuracy of LE predictions was assessed using c-statistic for 5-year mortality; Harrell’s c-statistic, and Integrated Brier score for overall survival. Results: The patient cohort had a mean (SD) age of 73.4 (5.9) years. The majority were female (62.6%) and black (79.4%). At 5 years, 108 (24.2%) patients had died. The c-statistic for 5-year mortality was similar for physicians (0.69) and the Chicago model (0.68), while the average of estimates by physicians and Chicago model yielded the highest c-statistic of any method tested (0.73). The estimates of overall survival yielded a similar pattern of results. Limitations: Generalizability of patient cohort and lack of updated model parameters. Conclusions: Compared with individual methods, the average of LE estimates by physicians and the Chicago model had the best predictive performance. Prognostic models, such as the Chicago model, may complement and support physicians’ intuitions as they consider treatment decisions and goals for older patients with chronic conditions like diabetes.

The growing population of older people with diabetes presents a significant public health problem around the world.¹ In the United States, the number of people over 65 diagnosed with diabetes is expected to rise from 8.1 million patients in 2000 to 16.8 million by 2050.² Diabetes treatment goals have historically aimed to achieve near-normal levels of glucose (hemoglobin A1c [HbA_1C] <7%), blood pressure (<130/80 mmHg), and cholesterol to reduce the risk of complications. However, these goals are inconsistently achieved in practice³ and often require intensive treatment.⁴ Clinical trials that inform diabetes recommendations^5–7 usually exclude older and sicker patients.⁸ Thus, it is unclear what glycemic target goal clinicians should aim for in the older patient, as this population is highly heterogeneous in terms of complications, comorbidities, and functional status,⁹ and these factors influence a patient’s health goals and the potential outcomes of intensive treatment. Patient-centered care for older patients with diabetes therefore requires individualized glycemic targets.

Recognizing the need to individualize diabetes care, multiple medical organizations have recommended using life expectancy (LE) as an approach to selecting optimal glycemic targets for elderly patients. In 2003, an American Geriatrics Society/California Healthcare Foundation panel issued one of the earliest guidelines recommending the use of LE to guide individualization of diabetes care in older patients.¹⁰ They recommended that patients with limited LE (5 years or less) to live should strive for moderate glucose control (HbA_1C <8%), while patients with greater LE should pursue more intensive goals, as observable benefits require 9 years of ongoing intensive glucose control.⁵ In 2012, the European Association for the Study of Diabetes and the American Diabetes Association both recommended an individualized approach to selecting glucose control targets based on variables such as decreasing LE, increasing cognitive and functional impairment, and frailty.^11,12

While multiple guidelines now advise using LE in making medical decisions, carrying out this recommendation in practice is both ethically controversial and technically challenging. Physicians and patients can provide LE estimates, but prior studies on LE estimation have often found that both physicians and patients are generally overly optimistic.^13–19 In an effort to systematically generate LE predictions, we created a simulation model for older patients with type 2 diabetes, the “Chicago model,” that produces estimates of patient LE and the risk of complications. While a number of mortality prediction models are available,²⁰ the present study aimed to externally validate the prognostic accuracy of the Chicago model compared with the status quo of prognostication: the physician’s judgment. We compare the accuracy of predictions of patients’ LE (5-year mortality and overall survival) estimated by the Chicago model, the patient’s physician, and several combinations of these estimates in a cohort of older patients with diabetes.

Methods

Patient Cohort

Patients with diabetes age 65 and older were enrolled in a study of treatment preferences and goals between December 2000 and January 2003 as previously described.²¹ Eligible patients were identified before visiting a University of Chicago internal medicine, geriatrics, or endocrinology clinic. Of 1,067 potential participants telephoned, 694 answered and 607 agreed to participate. Fifty-two patients were no-shows, leaving 555 who were surveyed (80% of approached patients). Of these, 108 were excluded from this analysis if their medical and/or death record was unverifiable (8 patients), LE predictions were missing (94 patients), or they fulfilled multiple exclusion criteria (6 patients). Four hundred forty-seven patients constituted the final patient cohort. Patients’ clinical values, if available, were extracted from the medical records and used for risk factors and biomarkers in the Chicago model. Average values from the National Health and Nutrition Examination Survey²² based on patient age, sex, and race were used to replace missing data. This study was approved by the University of Chicago Institutional Review Board.

The Chicago Model

The Chicago Type 2 Geriatric Diabetes Simulation Model (“Chicago model”) is a Markov Chain Monte Carlo simulation model created using Microsoft Excel–based @Risk 4.5 (Palisade Corporation, Newfield, NY). The model’s general structure has been previously described.²³ This model integrates the United Kingdom Prospective Diabetes Study (UKPDS) Outcomes Model,²⁴ a series of integrated diabetes complication models based on the UKPDS cohort, and a 4-year mortality index developed from the Health and Retirement Study.²⁵ The Chicago model accounts for demographics, functional status, comorbid illness, risk factors, and duration of diabetes. The initial LE for each patient was obtained by running the Chicago model for 1,000 repetitions, and odds of death were multiplied by 2.75 to account for higher background mortality rates in patients with diabetes.²⁶ The estimated LE was transformed into a binary indicator of limited LE (≤5 years) if applicable for the analysis.

It is important to note that data on three functional status measures that are integrated into the 4-year mortality index were not collected in the patient survey. Two questions (“Because of a health or memory problem, do you have any difficulty with managing your money—such as paying your bills and keeping track of expenses?” and “Because of a health or memory problem, do you have any difficulty with pulling or pushing large objects like a living room chair?”) were approximated with other survey questions (Mini-Mental Status Examination²⁷ score <17 or diagnosis of dementia and “How much does your health now limit you in doing moderate activities, such as moving a table, pushing a vacuum cleaner, bowling, or playing golf?”). One question (“Because of a health or memory problem, do you have any difficulty with walking several blocks?”) was omitted because no analogous question existed.

Physician Estimates

For each patient enrolled, a one-page survey was distributed to the patient’s physician after the visit. The surveyed physician had to be responsible for the patient’s diabetes care and willing to complete the survey for each patient enrolled in the study. Seventy-seven of 79 eligible physicians agreed to complete the survey. After patient exclusions, 63 physicians (10 geriatricians, 38 internists, and 15 endocrinologists) provided estimates. Physicians filled in a blank in response to the question, “How many years do you estimate that this patient will live?” Similar to the Chicago model’s estimate, this value was either made into a binary indicator for limited LE (≤5 years) or kept as a continuous value.

Combinations of Physician Estimates and Chicago Model: The “And,” “Or,” and “Average” Models

We considered three additional methods of generating binary classifications of “limited LE” (≤5 years) to approximate how a physician might interact with a prognostic model in practice to decide whether or not a patient’s LE should be considered limited. In these models, estimates by the model and physician are combined according to several different decision rules. These models are referred to as the “And” model (both the physician and model predict limited LE), the “Or” model (either the physician or model predict limited LE), and the “Average” model (limited LE is determined by the mean of the physician and model’s estimates). In the “And” model, a patient is considered to have limited LE if and only if both the physician and the Chicago model generate LE predictions that are less than or equal to 5 years. In the “Or” model, a patient is considered to have limited LE if either the physician or the Chicago model generate an LE prediction that is less than or equal to 5 years. Finally, in the “Average model,” the mean of LE estimates from the physician and the Chicago model is generated. If the mean of these estimates is less than or equal to 5 years, the patient is considered to have limited LE. The “Average model” also provides a third point estimate of the patient’s LE, in addition to the binary classification of limited LE. These categorization schemes are based on how we believe physicians interact with the model or other prognostic information in a real-life clinical setting.

Observed Survival

Observed survival was determined by querying the National Death Index (NDI) from 1 January 2001 to 31 December 2010. Patients’ first and last names, birth date, last known state of residency, and last date of contact were submitted to the NDI. All information submitted matched NDI records for 172 subjects (“perfect matches”). Twenty-eight submissions returned as “partial matches” due to missing or incorrect information were judged to be matches after comparison to electronic medical records. One additional date of death was identified through electronic medical records.

Statistical Analysis

When assessing the prognostic accuracy of physician and model estimates, we used several different measures depending on the type of predictive estimate; for 5-year mortality (a binary indicator for death at or before 5 years from the date of survey), we calculated sensitivity, specificity, positive predictive value (PPV), negative predictive value (NPV), receiver-operating characteristic (ROC) curve, and c-statistic. The c-statistic is equivalent to the area under the receiver-operating characteristic curve (AUC), incorporating both sensitivity and specificity (a c-statistic of 0.5 indicates predictive value no better than random chance and c-statistic of 1.0 indicates perfect prediction). To evaluate the accuracy of LE estimates overall (survival time), we first censored those who lived at the end of observation period. The observed survival time was compared with predicted estimates from physician and four models using time-dependent ROC curve,²⁸ Harrell’s c-statistic,²⁹ and integrated Brier score (IBS).^30,31 Harrell’s c-statistic is an adapted c-statistic that accounts for length of survival. The integrated Brier score is an overall measure for the inaccuracy of a prediction model whose value ranges from 0 to 1 (smaller values indicate better performance and a value of 0.25 indicates a lack of discriminatory power). The measure is a weighted average of the squared distance between the observed survival status and the predicted survival probability of a model. Among different evaluation metrics, c-statistic, the most commonly used, was considered as the primary method in this article. All analyses were conducted using R version 3.0.1.

Results

Baseline Characteristics and Properties of LE Estimates

The mean (SD) follow-up period was 8.9 (0.6) years (range = 7.9–10.1 years) for the 447 patients in the study cohort (Table 1). One hundred eight (24.2%) subjects died at or before 5 years from the date of survey, while 201 (45%) subjects died by the end of the follow-up period. Properties of LE estimates differed by source (Figure 1). Physicians predicted the highest average LE of 9.3 (4.8) years, the widest range (0.5–30 years), while the Chicago model had the shortest mean LE prediction (7.3 (3.7) years, range = 1.1–18.6 years). The mean LE estimate of the combination of the physician and model’s estimates was 8.3 (3.5) years (range = 1.0–21.3 years). Physicians tend to predict LE in integer values and their estimates cluster in 5-year increments (e.g., 5, 10, 15 years, etc.), while the model outputs more evenly distributed across the range (see Figure 2 for predicted and observed survival curves).

Table 1.

Patient Characteristics (N = 447)

Sociodemographic characteristics
Female, n (%)	280 (62.6)
Race, n (%)a
Black	355 (79.4)
White	66 (14.8)
Asian	2 (0.5)
Hispanic	13 (2.9)
Other	11 (2.5)
Age (years), mean (SD)	73.4 (5.9)
Age, n (%)a
65–69	137 (30.7)
70–74	125 (28.0)
75–79	115 (25.7)
80–94	70 (15.7)
Education, n (%)a
Less than high school	131 (29.3)
High school graduate	115 (25.7)
High school and higher	198 (44.3)
No answer	3 (0.7)
Self-reported income, n (%)a
<$10,000	102 (22.9)
$10,001–$25,000	118 (26.5)
$25,001–$50,000	102 (22.9)
>$50,000	53 (11.9)
Did not know/refused	71 (15.9)
Marital status, n (%)a
Married or living as if married	194 (43.4)
Divorced/separated/widowed	236 (52.8)
Single (never married)	17 (3.8)
Clinical characteristics
Type 2 diabetes, n (%)	446 (99.8)
Duration of diabetes mellitus (years), mean (SD)	13.2 (10.4)
Duration of diabetes mellitus (years), n (%)a
0–5	132 (29.5)
6–10	96 (21.5)
11–15	80 (17.9)
15–20	47 (10.5)
>20	92 (20.6)
Body mass index, mean (SD)	30.0 (6.5)
Hemoglobin A1c (%), mean (SD)	7.65 (1.63)
Hemoglobin A1c <7%, n (%), N = 439	157 (35.7)
Systolic blood pressure (mmHg), mean (SD)	143.6 (22.6)
Systolic BP <130 mmHg, n (%), N = 434	101 (23.3)
LDL cholesterol (mg/dL), mean (SD)	106.1 (39.5)
LDL cholesterol <100 mg/dL, n (%), N = 336	169 (50.3)
Total number of diabetes medicines, mean (SD)	0.9 (0.8)
Total number of hypertension medicines, mean (SD)	1.6 (0.9)
Total number of lipid-lowering medicines, mean (SD)	0.4 (0.5)
Complications, n (%)	197 (44.1)
Nephropathy	80 (17.9)
Neuropathy	93 (20.8)
Retinopathy	57 (12.8)
Peripheral vascular disease	83 (18.6)
Charlson Comorbidity Index score, mean (SD)	3.07 (1.81)
Mortality outcomes
Deceased by the end of 5 years, n (%)	108 (24.2)
Deceased by the end of the study period, n (%)	201 (45.0)

^a.Percentages may not add up to 100 due to rounding.

Figure 1.

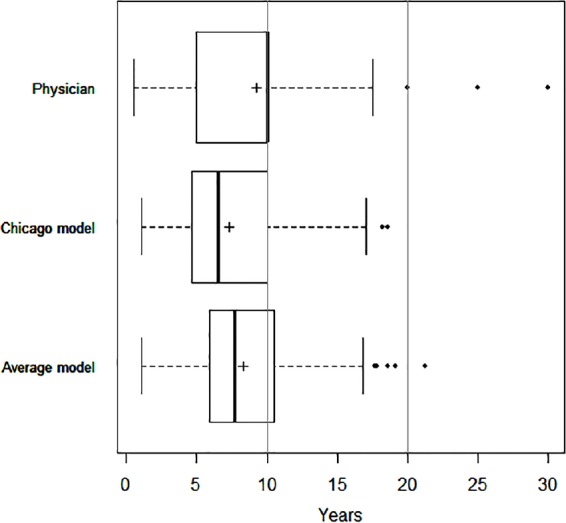
Boxplot display of life expectancy (LE) predictions by patients, physicians, and prognostic models. Boxplot displays the median (bold vertical line), interquartile range (IQR; solid line box), 1.5 IQR adjacent values (whiskers), outliers (points), and the mean value (+) for LE predictions by physicians (“How many years do you estimate that this patient will live?”), the Chicago model, and the Average model (mean of physician’s LE prediction and LE output of Chicago model).

Figure 2.

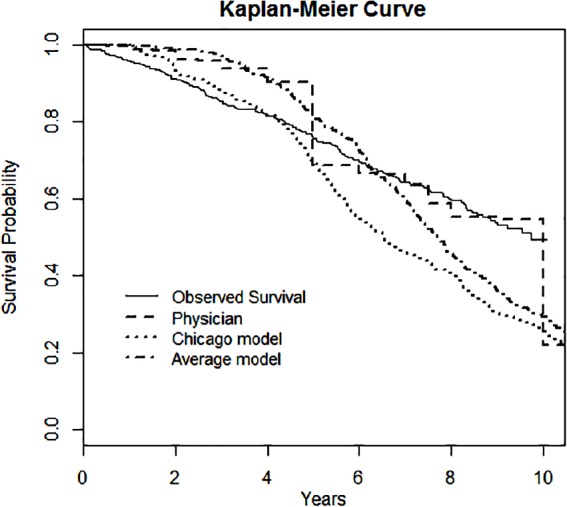
Survival outcomes of observed patient death versus predicted survival by physician, the Chicago model, and the average model.

The physicians and the Chicago model were not divergent in their overall estimates of 5-year mortality, with the physician guessing correctly 70% of the time to the Chicago model’s 68% (Table 2). For approximately two thirds (66%) of study subjects, the prediction of 5-year mortality generated by the physician and the model were the same (n = 62 for 5-year mortality and n = 232 for LE >5 years), and differed in about a third (34%) of subjects (n = 75 for only the model predicting 5-year mortality and n = 78 for only the physician predicting 5-year mortality). Among 75 study subjects for whom the model predicted 5-year mortality and the physician did not, 31% were deceased at 5 years and 69% were alive. Among 78 study subjects for whom the physician predicted 5-year mortality and the model did not, 37% were deceased at 5 years and 63% were alive.

Table 2.

Comparison of Life Expectancy (LE) Predictions by Physician, Chicago Model, and Observed Patient Death (N = 447)

	Observed Death
	Alive at 5 Years, n (%)	Dead at 5 Years, n (%)
Physician’s prediction
Alive at 5 years	256 (57)	51 (11)
Dead at 5 years	83 (19)	57 (13)
Chicago model’s prediction
Alive at 5 years	253 (57)	57 (13)
Dead at 5 years	86 (19)	51 (11)

Predictive Performance for 5-Year Mortality

Properties of predictions by the Chicago model, physicians, and combinations of the Chicago model and physician estimates (“And,” “Or,” “Average” models) of 5-year mortality (death by 5 years from date of survey) were calculated (Table 3). The physician and Chicago model estimates performed similarly, with the performance of the “Average” model exceeding the Chicago model and physician estimates, as well as the “And” and “Or” models for 5-year mortality according to the c-statistic, though these estimates had wide confidence intervals and differences were not statistically significant. As expected by the way these models are defined, the “Or” model had the highest sensitivity (0.74) and NPV (0.88) but the lowest specificity (0.60), while the “And” model had the lowest sensitivity (0.26) and NPV (0.79) but the highest specificity (0.90). The “And” model had the lowest (worst) c-statistic for 5-year mortality (0.58), followed by the “Or” model (0.67) and the Chicago model (0.68). The c-statistic generated for the physician estimate (0.69) was slightly higher. The “Average” model outperformed all of the other models, generating the highest c-statistic (0.73) for 5-year mortality.

Table 3.

Performance Metrics of Life Expectancy (LE) Predictions for 5-Year Mortality and Overall Survival Time by Physicians, the Chicago Model, the Average of the Physician and the Chicago Model, the “And” Model, and the “Or” Model

	5-Year Mortality					Overall Survival
	Sensitivity	Specificity	PPVa	NPVb	c-Statistic ± SE (95% CI)c	Harrell’s c-Statistic ± SE (95% CI)d	IBSe
Physicianf	0.53	0.76	0.41	0.83	0.69 ± 0.027 (0.67–0.74)	0.65 ± 0.027 (0.64–0.74)	0.148
Chicago modelg	0.47	0.75	0.37	0.82	0.68 ± 0.028 (0.63–0.78)	0.66 ± 0.028 (0.63–0.74)	0.147
Average modelh	0.35	0.87	0.46	0.81	0.73 ± 0.026 (0.68–0.78)	0.69 ± 0.026 (0.68–0.78)	0.140
And modeli	0.26	0.90	0.45	0.79	0.58 ± 0.023 (0.53–0.63)	NAj	NAj
Or modelk	0.74	0.60	0.37	0.88	0.67 ± 0.024 (0.62–0.72)	NAj	NAj

Note: PPV = positive predictive value; NPV = negative predictive value; SE = standard error; CI = confidence interval; IBS = integrated Brier score.

^a.Positive predictive value: true positives/(true positives + false positives).

^b.Negative predictive value: true negatives/(true negatives + false negatives).

^c.Area under the receiver operating characteristic (ROC) curve (AUC or c-statistic). The c-statistic is equivalent to the area under the receiver-operating characteristic curve, incorporating both sensitivity and specificity (a c-statistic of 0.5 indicates predictive value no better than random chance and c-statistic of 1.0 indicates perfect prediction).

^d.Harrell’s c-statistic.²⁹

^e.Integrated Brier score, a predictive accuracy score function that takes one values between 0 and 1, with lower values indicating better predictive performance.^30,31

^f.Physician’s answer on a patient-specific questionnaire to the question, “How many years do you estimate that this patient will live?” The physician’s answer to this question was converted to a binary indicator of predicted five-year mortality when the answer to this question was 5 years or less.

^g.Chicago model generates a point estimate of the patient’s LE which is turned into a binary indicator of 5-year mortality when it was equal to 5 years or less.

^h.Average model takes the mean of the point estimates generated by the physician and the Chicago model and uses this as its predictor. The average model is also converted into a binary indicator of predicted 5-year mortality when the average is equal to 5 years or less.

^i.“And” model predicts 5-year mortality when both the physician and the Chicago model predict 5-year mortality.

^j.NA = not applicable. Performance metrics for overall survival time cannot be computed for these models because they generate a binary classification of limited LE rather than a point estimate of LE.

^k.“Or” model predicts 5-year mortality when either the physician or the Chicago model predict 5-year mortality.

Predictive Performance for Overall Survival

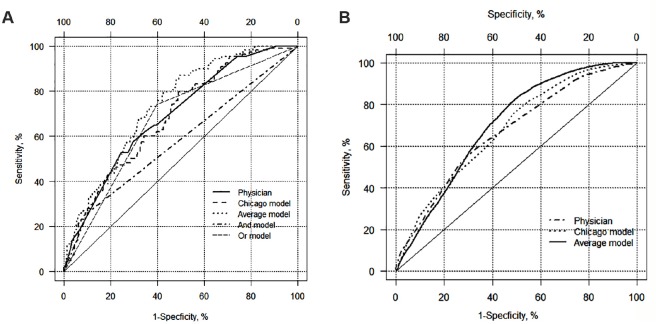
Metrics to compare performance of physicians, the Chicago model, and the average of the Chicago model estimate and physician estimate for predicting overall survival time (Harrell’s c-statistic and IBS) were also calculated (Table 3). See Figure 3A and B for time-dependent ROC curves for overall survival. The Harrell’s c-statistic was similar for the physician (0.65), the Chicago model (0.66), and the average of the Chicago model and physician (0.69). Similarly, physician estimates had the highest (worst) IBS (0.148); the mean of the physician and model estimate had the lowest (best) (0.140).

Figure 3.

(A) ROC curve for 5-year mortality. The diagonal solid line indicates a test with no discriminatory power (area under the curve equal to 0.5). (B) ROC curve for overall survival time. The diagonal solid line indicates a test with no discriminatory power (area under the curve equal to 0.5).

Discussion

The inaccuracies of physicians and patients in predicting LE are well-established, and prognostic models are a promising approach, with numerous models and calculators having been developed (http://eprognosis.ucsf.edu/).²⁰ An important limitation of these models is that they are always developed using data from past observations, and therefore are the results of the historical timing of diagnosis, natural history of disease, and effects of past treatments, all of which evolve over time. Given the limitations of both physicians and these models, it is critical to examine how their predictions may actually be used in real clinical situations. Our study provides insight into how a simulation model of LE in older patients with diabetes performs in a specific patient population and how this model’s predictions compare to, interact with, and supplement the judgment of physicians.

Predictions of LE made by physicians are admittedly subjective, and we did not systematically examine whether a physician’s experience or expertise was correlated with prognostic accuracy in this study. However, physicians have access to other information that may be critical for predicting LE, such as a patient’s resilience or social support, that are harder to operationalize as model inputs. When we compared their estimates to the Chicago model, which is a relatively complex microsimulation model that accounts for multiple clinical domains as well as comorbidity and functional impairment, we did not find substantial differences in predictive performance for 5-year mortality or survival duration. Both methods of LE prediction had relatively low sensitivity, somewhat higher specificity, and had similar c-statistics for predicting 5-year mortality. While the different combination models we evaluated varied in their predictive performance, they had modest predictive power at best, and point toward deficiencies in what we know about prognosis. However, the improved performance of the “Or” model with respect to sensitivity and the average model with respect to the c-statistic suggest that physician and model estimates may be best used in concert rather than independently.

At present, we suspect that physicians do not frequently differentiate diabetes goals and treatments based on prognosis. We have previously found, in our own practice, that glycemic control levels are nearly identical for older patients with different health status based on physician observations and that the sickest patients are on the most intensive regimens.³² The tendency of physicians to not alter their actions in response to relevant information, or status quo bias,³³ may lead to overtreatment of patients unlikely to benefit from intensive therapy or at high risk for adverse events,^34–36 as well as undertreatment of patients likely to benefit from intensive therapy. If physicians were consistently provided with prognostic information at the point of care, they might be able to overcome status quo bias and make clinical decisions more tailored and in tune with the health status and trajectory of individual patients. Within the context of this study, in the two thirds of patients for whom the physician and Chicago model predictions were concordant, the model could have helped confirm the physician’s intuition and treatment plan. However, for the one third of patients for whom predictions were discordant, the physician faces a dilemma of how to use the new information provided by the model—ignore it, adopt it, or somehow incorporate it. In this study, both types of discordance resulted in about a one third chance of 5-year mortality. If a physician’s prognostication can be used in tandem with external prediction, it may lead to increased accuracy of LE prediction and increase willingness to consider prognostic models.

This study utilizes a unique data set of LE estimates from physicians made on an individual-patient basis to externally validate the predictive performance of a simulation model compared to the physician’s “off-the-cuff” estimate. Limitations of this study include that subjects received care at a single academic medical institution (University of Chicago Medicine) and that the prognostic abilities of physicians may not be representative of physicians elsewhere. Patients are also largely drawn from a specific demographic and socioeconomic group (mostly African Americans residing in Chicago’s South Side) distinct from the populations used to create the model; the same exercise in another population might look different. Last, the Chicago model does not yet incorporate updated estimates of diabetes complications and mortality,³⁷ which may better reflect current diabetes care practices.

Despite the proliferation of new recommendations to incorporate LE into medical decisions, including whether to prescribe medications,³⁸ undergo cancer screenings,³⁹ and refer patients to hospice care,¹³ the controversies and challenges of estimating prognosis in clinical practice have been infrequently studied. Predicting the LE of patients with acute conditions and short survival horizons remains difficult, and LE prediction may be even more difficult in older patients with chronic conditions like diabetes, in which long survival horizons are possible.⁴⁰ Advances in health information technology and the increased presence of computers in primary care settings have led to experimentation with real-time decision support tools integrated into electronic medical records.⁴¹ In the near future, LE estimates from prognostic models could be similarly integrated and referenced during clinical encounters. The modest performance of the Chicago model provides evidence for the need to develop and validate a more contemporary model of diabetes complications that reflects the diversity of the United States. Even with the limitations of current data sources, our results suggest that prognostic models have the potential to complement and support physicians as they work with patients to make complex decisions about chronic disease management at advanced ages.