Frequency-dependent antidromic activation in thalamocortical relay neurons: effects of synaptic inputs

Abstract

Objective.

Deep brain stimulation (DBS) generates action potentials (APs) in presynaptic axons and fibers of passage. The APs may be antidromically propagated to invade the cell body and / or orthodromically transmitted to downstream structures, thereby affecting widespread targets distant from the electrode. Activation of presynaptic terminals also causes trans-synaptic effects, which in turn alter the excitability of the post-synaptic neurons. Our aim was to determine how synaptic inputs affect the antidromic invasion of the cell body.

Approach.

We used a biophysically-based multi-compartment model to simulate antidromic APs in thalamocortical relay (TC) neurons. We applied distributed synaptic inputs to the model and quantified how excitatory and inhibitory inputs contributed to the fidelity of antidromic activation over a range of antidromic frequencies.

Main results.

Antidromic activation exhibited strong frequency dependence, which arose from the hyperpolarizing afterpotentials in the cell body and its respective recovery cycle. Low-frequency axonal spikes faithfully invaded the soma, whereas frequent failures of antidromic activation occurred at high frequencies. The frequency-dependent pattern of the antidromic activation masked burst-driver inputs to TC neurons from the cerebellum in a frequency-dependent manner. Antidromic activation also depended on the excitability of the cell body. Excitatory synaptic inputs improved the fidelity of antidromic activation by increasing the excitability, and inhibitory inputs suppressed antidromic activation by reducing soma excitability. Stimulus-induced depolarization of neuronal segments also facilitated antidromic propagation and activation.

Significance.

The results reveal that synaptic inputs, stimulus frequency, and electrode position regulate antidromic activation of the cell body during extracellular stimulation. These findings provide a biophysical basis for interpreting the widespread inhibition/activation of target nuclei during DBS.

1. Introduction

Deep brain stimulation (DBS) is an effective, reversible and adjustable surgical treatment for movement disorders, including essential tremor (ET), dystonia, and advanced Parkinson’s disease [1, 2]. DBS applies high-frequency (typically 130 – 185 Hz) voltage or current pulses via an electrode implanted into a specific target in the basal ganglia or thalamus. Despite the clinical success and effectiveness of DBS, the precise mechanisms of action remain unclear [2, 3]. Functional imaging studies [4-7] indicate that the effects of DBS span multiple anatomical structures, resulting in widespread inhibition/activation of regions across the brain. Electrophysiological recordings [8-10] show that DBS antidromically activates presynaptic terminals or axons passing near the targets. The resulting spikes in afferent axons excite the synaptic inputs impinging on local cells, which in turn alter the firing in those cells. Importantly, the antidromic action potentials (APs) may propagate to invade the cell body and dendrites. They may also reach axon collaterals and then spread re-orthodromically to affect downstream structures distant from the electrode. This suggests that antidromic activation is a potential mechanism underlying the widespread effects of DBS [11]. However, the pattern of antidromic activation in the cell body is still not fully understood. We used computational modeling to quantify the effects of synaptic inputs on antidromic invasion of the cell body across a range of extracellular stimulation frequencies.

The therapeutic effects of DBS are highly dependent on the stimulation frequency, and high frequencies (> 90 Hz) are usually required for improvement of motor symptoms [12, 13]. Electrophysiological recordings [14, 15] indicate that the generation of antidromic spikes is sensitive to DBS frequency, and cells fail to follow high frequency antidromic activity. Previous studies considered the effects of axonal branching [16], neuronal geometry [16, 17], and sodium conductance of the axonal initial segment (AIS) [17] on the antidromic propagation of APs. Further, the trans-synaptic effects generated by DBS may inhibit or excite local neuronal elements, dependent on whether GABAergic or glutamatergic terminals predominate [9, 10, 18, 19], thereby influencing the fidelity of antidromic invasion. Earlier evidence [20-22] indicate that the contributions of synaptic inputs to both changes in transmembrane potential and transmembrane resistance influence the firing of the cell body in response to DBS.

The objective of this study was to determine how excitatory and inhibitory synaptic inputs affect antidromic activation over a range of stimulation frequencies. We used a computational model to simulate antidromic APs in thalamocortical (TC) relay neurons. Our results revealed that synaptic inputs, antidromic frequency, and stimulus-induced polarization all contributed to the pattern of antidromic activation. While these results are consistent with the idea that high-frequency DBS causes widespread effects by antidromic activation of regions distant from the electrode, they suggest that the rate and pattern of activity in antidromically activated neurons may be profoundly different than that of the applied stimulation.

2. Methods

2.1. Computational model

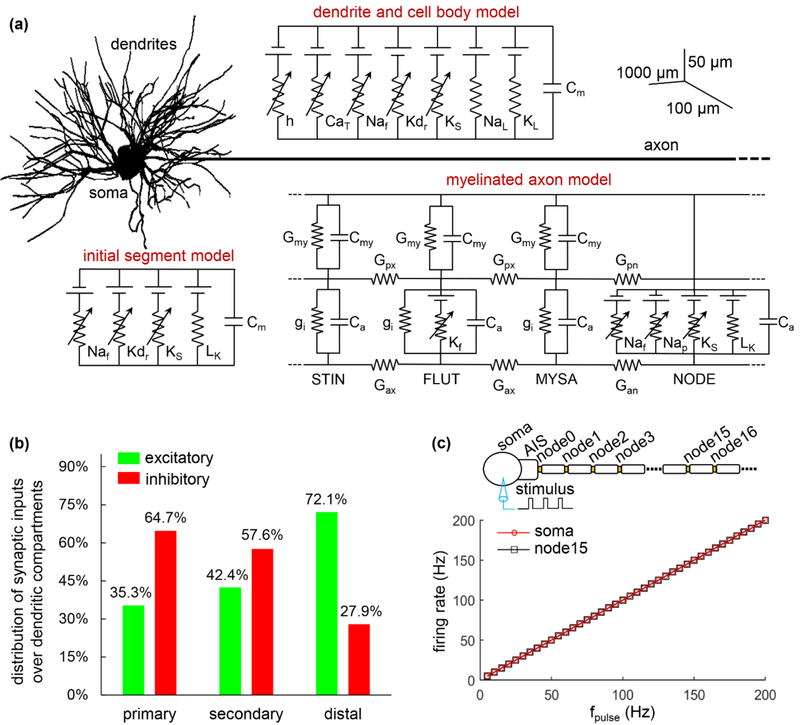
We used a morphologically realistic biophysically based computer model (figure 1(a)) to quantify the interactions between synaptic inputs and antidromic activity in TC relay neurons. This model was previously validated by McIntyre et al. [20] to replicate a wide range of electrophysiological properties of TC cell recorded in vitro. The model included a 3-compartment cell body (diameter: 26.654 ± 5.967 μm), a 251-compartment dendritic tree, a 3-compartment axon initial segment (AIS) (diameter: 2.283 ± 0.765 μm), and a myelinated axon (diameter: 2 μm). The three-dimensional (3D) morphology of the dendritic tree was reconstructed from a filled TC cell from the ventrobasal nucleus of a young rat [23]. Each compartment in the dendrites and the soma was represented by same membrane model. The axon was modeled with a concentric double-cable structure including 30 nodes of Ranvier [20, 24].

Figure 1.

Computational model of TC relay neuron. (a) Schematic of the model, which includes a multi-compartmental soma, an AIS, a myelinated axon and a 3D dendritic tree. The compartments in the soma and dendrites included hyperpolarization-activated cation (h), T-type Ca²⁺ (Ca_T), fast Na⁺ (Na_f), delayed rectifier K⁺ (Kd_r), slow K⁺ (K_s), Na⁺ (Na_L) and K⁺ (K_L) linear leakage currents, and membrane capacitance (C_m). The AIS included fast Na⁺, delayed rectifier K⁺, slow K⁺, and linear leakage (L_K) currents, and membrane capacitance. The myelinated axon was modeled with node of Ranvier, myelin attachment segment (MYSA), paranode main segment (FLUT), and internode segment (STIN). Each node included fast Na⁺, persistent Na⁺ (Na_p), slow K⁺, and linear leakage currents, and membrane capacitance (C_a). Two concentric layers were used to model MYSA, FLUT, and STIN, which included a linear conductance (G_my, g_i) and membrane capacitance (C_my, C_a). The FLUT also included a fast K⁺ (K_f) current in the axolemma. There were axoplasmic (G_ax, G_px) and periaxonal conductances (G_an, G_pn) connecting two compartments in the myelinated axon. The biophysics and morphology of the model followed McIntyre et al. [20]. (b) Ratio of excitatory (green) and inhibitory (red) inputs over each group of the dendrites. (c) Somatic and axonal firing rate as a function of pulse frequency f_pulse. Suprathreshold stimulus was injected into the soma, and membrane responses were recorded in the soma and axon (i.e., node15). Pulse amplitude was 30 nA, and pulse duration was 0.1 ms.

2.2. Synaptic inputs

We simulated synaptic inputs by randomly assigning either excitatory or inhibitory synaptic conductance to each compartment in the dendrites and cell body. Following Sato et al. [25], we divided the dendrites into three groups: a dendrite that originates from the cell body is defined as a primary dendrite until it branches, the branched sections from a primary dendrite are defined as secondary dendrites until they branch again, and any sections distal to the second branches are regarded as distal dendrites. The distribution of either type of synapse within each group of the dendrites was based on electron microscopic reconstructions of glutamatergic (excitatory) and GABAergic (inhibitory) terminals on TC neurons in the cat ventral lateral nucleus [25] and is summarized in figure 1(b). Note that there were only inhibitory synaptic inputs to somatic compartments.

An alpha function was used to model the time course of synaptic conductances. The postsynaptic current generated by a presynaptic event was computed as $I_{syn}\left(t\right)=g_{syn}\frac{t}{{\tau }_{syn}}{e}^{\left[1-t/{\tau }_{syn}\right]}\left(V_m-E_{syn}\right)$, which was a function of synaptic conductance g_syn, synaptic reversal potential E_syn, and synaptic time constant τ_syn. For excitatory synaptic inputs, the parameters of the alpha function were set according to the AMPA conductance [20]: τ_syn = 0.775 ms and E_syn = 0 mV, and for inhibitory synaptic inputs the parameters were set following the GABAa conductance [20]: τ_syn = 1.401 ms and E_syn = −85 mV. As only a small number of representative synapses were included in the model, the values of excitatory peak conductance g_exc and inhibitory peak conductance g_inh were not based on specific experimental data. Therefore, we performed a sensitivity analysis to examine the effects of stimulus-induced synaptic action on antidromic activation of the cell body across a range of synaptic conductances.

Each synapse was activated by two factors in our simulations. One was the trans-synaptic effect generated by extracellular stimulation [20, 21]. To simulate this effect, we assumed that applied stimulus pulses always activated spikes in presynaptic terminals projecting to the simulated TC neuron. In this case, all the synapses were activated simultaneously at the onset of each stimulus pulse. The second factor was the intrinsic synaptic input. We limited each compartment to a single intrinsic input, which was simulated as either a 20 Hz Poisson train [26] or a 5.8 Hz burst train [27]. Varying the frequency of the intrinsic Poisson input produced little effect on antidromic activation of the TC relay neuron, since the effects of these asynchronous inputs were much weaker than the synchronous stimulus-induced trans-synaptic inputs. The burst train was used to simulate the excitatory inputs from the cerebellum to the thalamus, and its rate was consistent with the predominant interburst frequency of ventral intermediate thalamus neurons in humans with essential tremor [28].

2.3. Simulations

The TC model was implemented in NEURON (v7.5) [29] with a time step of 0.025 ms. The resting potential of each segment was − 70 mV. We applied monophasic pulses to stimulate the TC model neuron and evoke antidromic activity. Pulse width was 0.1 ms, and pulse frequency was varied from 5 Hz to 200 Hz at a step size of 5 Hz. The output of the TC model was recorded for 3 s with each stimulation frequency, and − 20 mV was used as a threshold to detect spikes in the cell body and node of Ranvier.

There are differences in the antidromic responses in distant nuclei and in local neurons subject to polarization by extracellular stimulation. To represent the former, we applied suprathreshold (0.8 nA) pulse trains intracellularly to the middle node of Ranvier to activate axonal spikes with a frequency from 5 Hz to 200 Hz. There was no membrane polarization mediated by extracellular stimulation in this case, and we quantified the effects of synaptic inputs on somatic invasion by axonal spikes at different frequencies. Subsequently, we examined the fidelity of antidromic activation of the cell body in local neurons with extracellular stimulation, which was performed using either cathodic or anodic current. We placed the TC model within an infinite homogenous, isotropic medium with a conductivity of σ = 0.303 S/m [30]. Current pulses were delivered by a point source electrode placed at a position of (x₀, y₀, z₀). For the neural segment at location (x, y, z), the extracellular potential was calculated as $V\left(x,y,z\right)=\frac{I_{stim}}{4\pi \sigma \sqrt{{\left(x_0-x_0\right)}^2+{\left(y-y_0\right)}^2+{\left(z-z_0\right)}^2}}$ [30, 31], where I_stim is the amplitude of extracellular current pulse. Since the threshold current I_th for activation of the model varied with the electrode position and stimulus polarity, we used I_stim = 1.2I_th as a suprathreshold amplitude to stimulate the TC neuron. We calculated V(x, y, z) for each individual segment and applied it to the corresponding segment with the extracellular mechanism in NEURON.

We also simulated the interactions of antidromic activation and burst activity in the TC model during extracellular stimulation. A larger excitatory conductance (g_exc = 0.2 nS) was used to generate rhythmic burst activity in the absence of DBS. Since the majority of cerebellar terminals synapse on proximal and secondary dendrites in thalamic neurons [25, 32], the distribution of excitatory inputs within each dendritic group was: primary: 35.3% burst and no Poisson; secondary: 33.3% burst and 9.1% Poisson; distal: 27.3% burst and 44.8% Poisson. The distribution of inhibitory synapses was indicated in figure 1(b), and their inputs were a 20 Hz Poisson train. Applying extracellular stimulation to TC neurons will activate cerebellar axon terminals, and the resulting spikes may collide with orthodromic spikes as they antidromically propagate to the soma. To simulate the spike collision, we assumed the length and diameter of the cerebellar axons was L = 80 mm and D = 5.7 μm, respectively [33, 34]. The conduction velocity in afferent fibers was estimated by v = 6D [35], where v was in m/s and D was in μm. An orthodromic spike was annihilated by an antidromic spike initiated in cerebellar axon terminals if their interval was less than d/v [36]. Coefficient of variation (CV) was used to quantify the regularity of somatic and axonal firing patterns, and was calculated as the standard deviation of the interspike intervals (ISIs) over a period of 3 s divided by the mean of the ISIs.

2.4. Model validation

To validate the model, we compared its behavior with published patterns of firing under somatic intracellular stimulation. We applied intracellular suprathrehsold pulse trains (30 nA) with different frequencies to stimulate the cell body. We examined the transmembrane potentials in the soma and in the middle node of the axon, and transmembrane potential exceeding − 20 mV was used to detect APs. The APs generated in the cell body followed the stimuli in a 1:1 ratio, and 100% of them were transmitted down the axon (figure 1(c)), as reported by McIntyre et al. [20].

3. Results

3.1. Fidelity of antidromic invasion is reduced at high frequencies

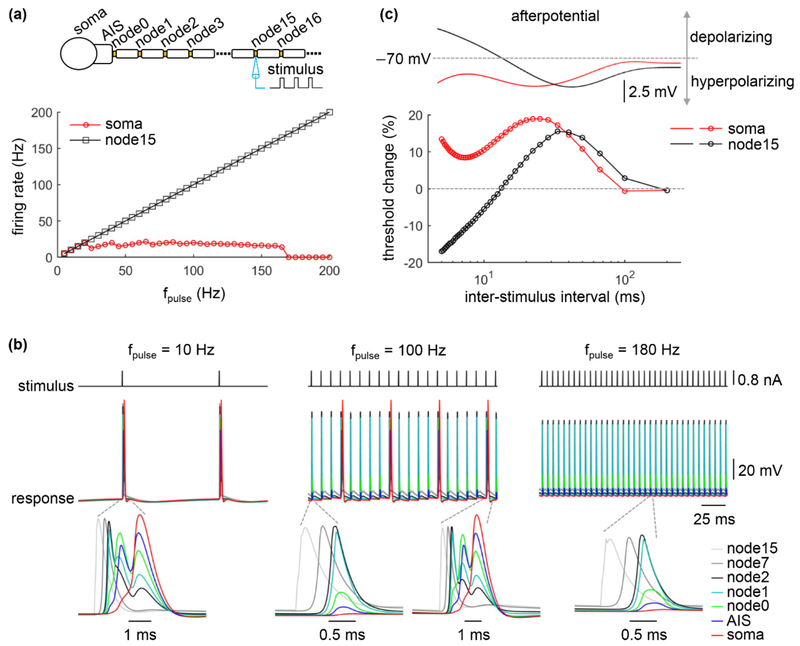
We first quantified the effects of stimulation frequency on invasion of the cell body by antidromic axonal spikes in the absence of synaptic inputs. A suprathreshold pulse train with a frequency between 5 Hz and 200 Hz was applied intracellularly to node15. The activation and propagation of spikes in the axon was highly reliable, and the rate of antidromic spikes was identical to the stimulus frequency (figure 2(a)). There was little attenuation in spike amplitude during propagation from node15 to node2 (figure 2(b)), but from node1, the amplitude of antidromic spike began to decrease. At low frequencies (< 25 Hz), each antidromic spike reliably activated the AIS and soma, while at moderate frequencies (25 Hz ≤ f_pulse < 170 Hz) there were frequent failures of antidromic activation in the AIS and soma. With high frequencies (≥ 170 Hz), axonal spikes were unable to invade the soma, and antidromic excitation was blocked. Thus, the cell body was unable to follow high frequency antidromic activity, resulting in a decoupling between somatic firing and axonal firing, as observed previously in models of extracellular simulation [20, 21].

Figure 2.

Effects of antidromic frequency on somatic invasion by axonal spikes. (a) Somatic and axonal firing rate as a function of pulse frequency f_pulse. Stimulus train suprathreshold for activation of axonal spikes at each stimulation frequency was injected in the node15. Firing rate was calculated in the soma and in node15. Pulse amplitude was 0.8 nA, and pulse width was 0.1 ms. (b) Voltage responses recorded at the individual compartments during axonal intracellular stimulation. Pulse frequency was f_pulse = 10 Hz, 100 Hz, and 180 Hz. (c) Top panel: afterpotentials of the cell body and node15 on the same time scale as the recovery cycle. Bottom panel: threshold change of the cell body and node15 as a function of interstimulus interval. A suprathreshold conditioning stimulus (pulse width: 0.1 ms) was followed by a test stimulus (pulse width: 0.1 ms). The threshold of the test pulse for activating APs was determined. The amplitude of the conditioning pulse was 30 nA for the soma and 0.8 nA for node15. Inter-stimulus interval was determined by 1/f_pulse, and f_pulse was increased from 5 Hz to 200 Hz at a step size of 5 Hz.

We applied a two-pulse conditioning–test paradigm to quantify the recovery cycle of the soma and axon in the TC neuron model. The afterpotentials in the node included both depolarizing and hyperpolarizing components, which increased excitability and decreased excitability, respectively, for the test pulse across short and long interpulse intervals. However, the stimulus pulse amplitude was always suprathreshold for activation of the node of Ranvier, and the axon responded faithfully across stimulus frequencies. The afterpotentials in the soma were exclusively hyperpolarizing and thus decreased excitability for the test pulse across all interpulse intervals (figure 2(c)). At low pulse frequencies, the interpulse interval was long enough that there was little change in the excitability of the soma, and each antidromic spike reliably activated the soma. At moderate stimulus frequencies, the cell body responded to the first axonal spike, but subsequent antidromic spikes fell within the hyperpolarizing afterpotentials and somatic APs were unable to follow the antidromic spikes. However, temporal summation of subthreshold responses led to AP firing in the soma at a frequency lower than the antidromic frequency. When the antidromic frequency further increased, the cell body exhibited no summation of antidromic spikes and no APs occurred in the soma.

Note that each AP in the soma was able to re-activate the AIS, but the AP amplitude was attenuated dramatically as it was transmitted down the axon (figure 2(b)). The delay between the original antidromic AP and the soma-initiated orthodromic AP was not long enough to permit re-activation of the first node (based on the recovery cycle), and there were no recurrent spikes in the axon.

3.2. Synaptic inputs modulate antidromic invasion of the soma

Antidromic activation may occur in both distant nuclei and local neurons during DBS-like extracellular stimulation. In regions distant from the electrode, there is no stimulus-induced polarization or stimulation evoked trans-synaptic inputs, and we examined the effects of synaptic inputs on antidromic activation with no trans-synaptic inputs during axonal intracellular stimulation.

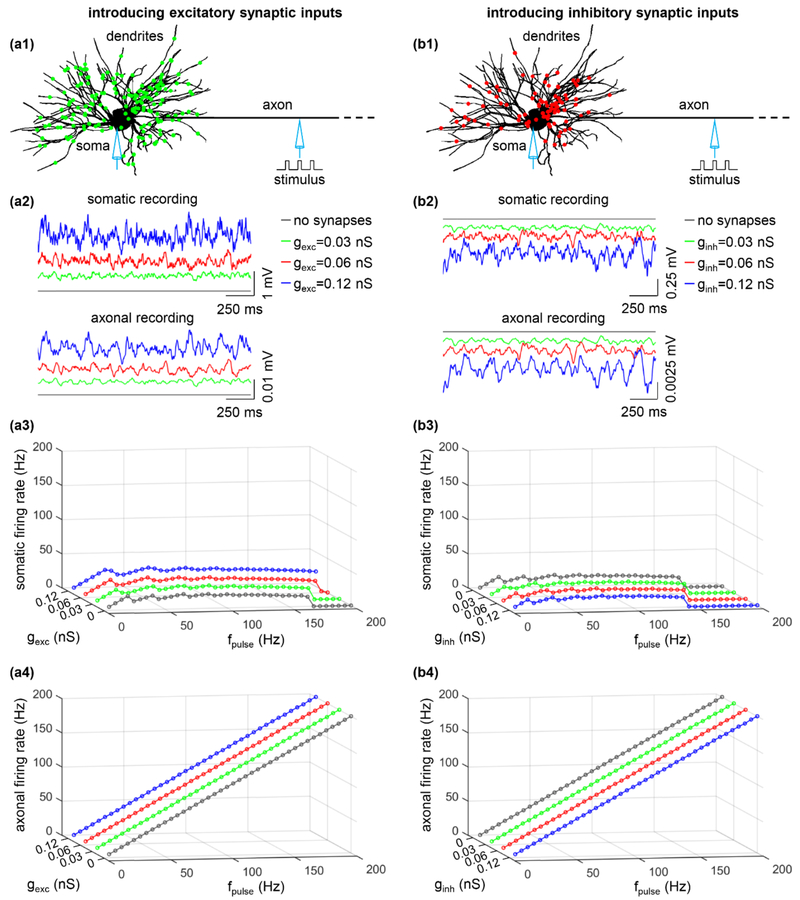
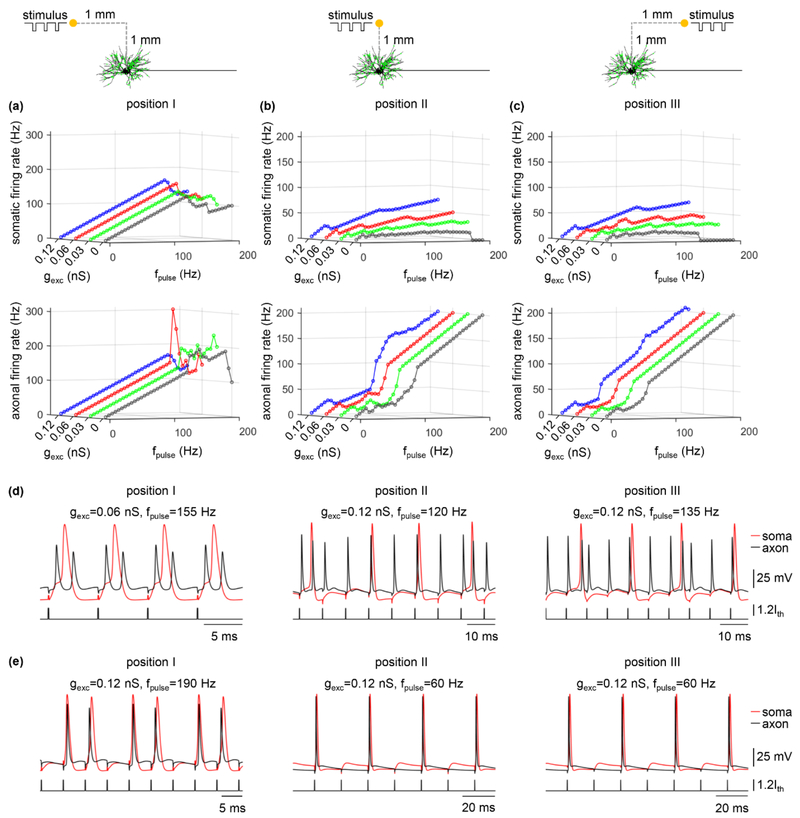
We assigned excitatory inputs to primary, secondary, and distal dendrites with proportions based on the distribution of synapses observed experimentally (figure 3(a1)). The excitatory synaptic conductance g_exc was set to 0.03 nS, 0.06 nS, or 0.12 nS, which were subthreshold for activating the cell body. Increasing g_exc increased somatic excitability (figure 3(a2), top) and made the soma more likely to respond to antidromic spikes (figure 3(a3)). With g_exc = 0.12 nS, the soma generated APs in response to 100% of antidromic spikes at f_pulse = 30 Hz, whereas it only followed 50% of 30 Hz antidromic spikes with g_exc = 0 nS. The effects of excitatory synaptic inputs were especially pronounced at high antidromic frequencies, where, in the absence of excitatory inputs, no antidromic activation occurred at f_pulse ≥ 170 Hz. Increasing g_exc had limited effects on the excitability of the axon (figure 3(a2), bottom), which did not alter its firing rate (figure 3(a4)).

Figure 3.

Effects of (a) excitatory and (b) inhibitory synaptic inputs on antidromic activation. (a1) The distribution of excitatory (green) inputs was shown schematically over the TC model neuron. (a2) Somatic (top) and axonal (bottom) transmembrane voltage produced by a 20 Hz Poisson activation of all synapses in the absence of axonal stimulus. g_exc = 0 nS (without synapses), 0.03 nS, 0.06 nS, and 0.12 nS. (a3) Somatic firing rate as a function of g_exc and f_pulse. (a4) Axonal firing rate as a function of g_exc and f_pulse. (b1) Distribution of inhibitory (red) inputs over the TC relay model. (b2) Somatic and axonal membrane voltage produced by a 20 Hz Poisson activation of all synapses in the absence of axonal stimulus. g_inh = 0 nS (without synapses), 0.03 nS, 0.06 nS, and 0.12 nS. (b3) Somatic firing rate as a function of g_inh and f_pulse. (b4) Axonal firing rate as a function of g_inh and f_pulse. Each synaptic input was a 20 Hz Poisson train, and there was no stimulus-evoked trans-synaptic input. Suprathreshold pulse train (width: 0.1 ms, amplitude: 0.8 nA) was applied intracellularly to node15.

We also determined the effects of inhibitory synaptic inputs, modeled by assigning them to the dendrites and soma with proportions based on the distribution of synapses observed experimentally (figure 3(b1)). The synaptic conductance g_inh was set to 0.03 nS, 0.06 nS, or 0.12 nS. Increasing g_inh of individual inputs hyperpolarized the soma (figure 3(b2), top) and suppressed its response to antidromic spikes (figure 3(b3)). This effect was most pronounced at high antidromic frequencies, and the f_pulse at which no somatic invasion occurred dropped from 170 Hz with no inhibitory synaptic inputs to 145 Hz at g_inh = 0.12 nS. Introducing inhibitory synapses produced limited effects on axonal excitability (figure 3(b2), bottom) and did not alter axonal firing (figure 3(b4)).

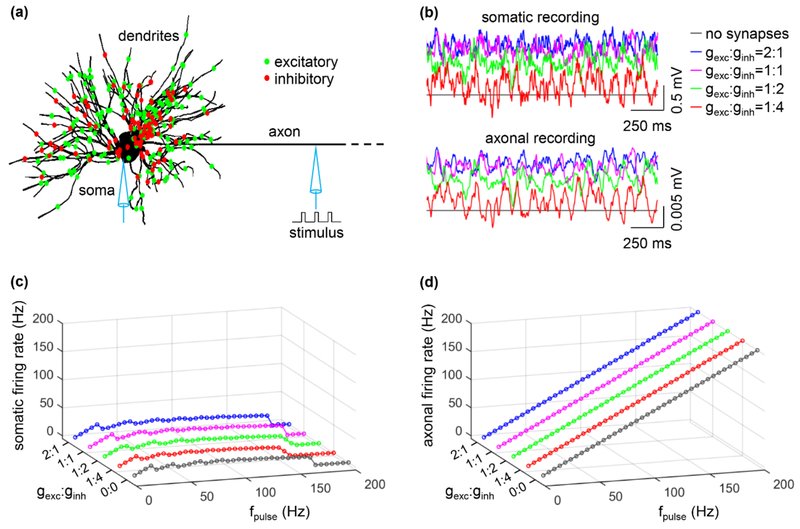
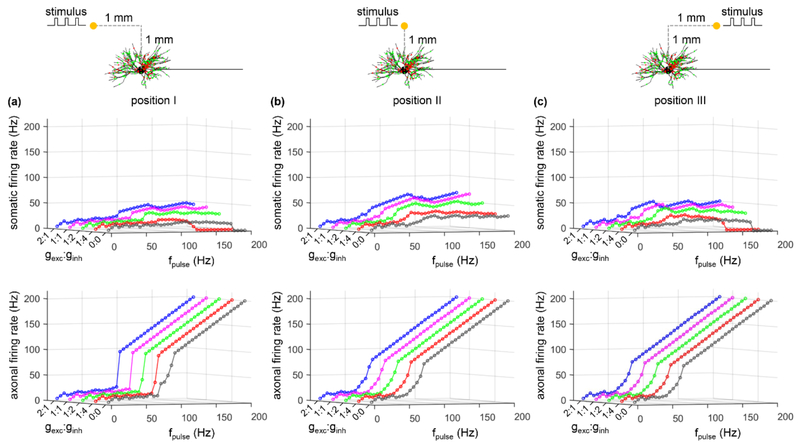
Subsequently, we examined antidromic activation of the soma with a distribution of both excitatory and inhibitory synaptic conductances on the dendrites and cell body and varying ratios of excitatory to inhibitory synaptic conductance, g_exc: g_inh (figure 4(a)). Increasing g_exc: g_inh resulted in depolarization of the soma (figure 4(b), top) and increased the fidelity of antidromic invasion of the soma by axonal spikes (figure 4(c)). Conversely, decreasing g_exc:g_inh resulted in hyperpolarization of the soma and decreased the fidelity of antidromic invasion (figure 4(c)). We tested several ratios of excitatory to inhibitory conductance, which produced only small changes in axonal excitability (figure 4(b), bottom) and did not alter the axon responses to intracellular stimuli (figure 4(d)). Excitatory inputs had a more pronounced effect on antidromic activation of the soma than inhibitory inputs, even though the latter were distributed more closely to the soma.

Figure 4.

Effects of ratio of excitatory to inhibitory conductance, g_exc: g_inh, on antidromic activation. (a) Distribution of excitatory (green) and inhibitory (red) inputs over the TC relay model. (b) Somatic (top) and axonal (bottom) transmembrane voltages produced by a 20 Hz Poisson activation of all synapses in the absence of axonal stimulus. g_exc was set to 0.06 nS and g_inh was varied according to the value of g_exc: g_inh. (c) Somatic firing rate as a function of g_exc: g_inh and f_pulse. (d) Axonal firing rate as a function of g_exc: g_inh and f_pulse. In (c) and (d), g_exc: g_inh = 0:0 means there are no synaptic inputs. Each synaptic input was a 20 Hz Poisson train, and there was no stimulus-evoked trans-synaptic input. Suprathreshold pulse train (width: 0.1 ms, amplitude: 0.8 nA) was injected in node15.

The above results were simulated by representing intrinsic synaptic inputs as subthreshold. When using suprathreshold synaptic conductances for the Poisson inputs, the fidelity of somatic invasion over a range of the stimulus frequencies was further increased compared to that with subthreshold excitatory conductances, and the block of antidromic excitation at high frequencies disappeared. Further, there may be slight differences in the timing of synaptic inputs and the timing of when antidromic spikes arrive at the soma. Therefore, we repeated simulations incorporating “jitter” in the timing of stimulus-evoked trans-synaptic inputs (1 ms ± 0.5 ms, mean ± s.d.), and these differences produced virtually no impact on the effects of synaptic inputs on the frequency dependence of antidromic activation (data not shown).

3.3. Antidromic activation of the cell body during extracellular stimulation

In addition to activating presynaptic axon terminals and generating direct activation of (the axon of) the postsynaptic neuron, extracellular stimulation also causes spatially distributed polarization of the postsynaptic cell [20, 30], which can alter excitability and may influence patterns of antidromic activation. We therefore quantified antidromic activation of the cell body with extracellular stimulation.

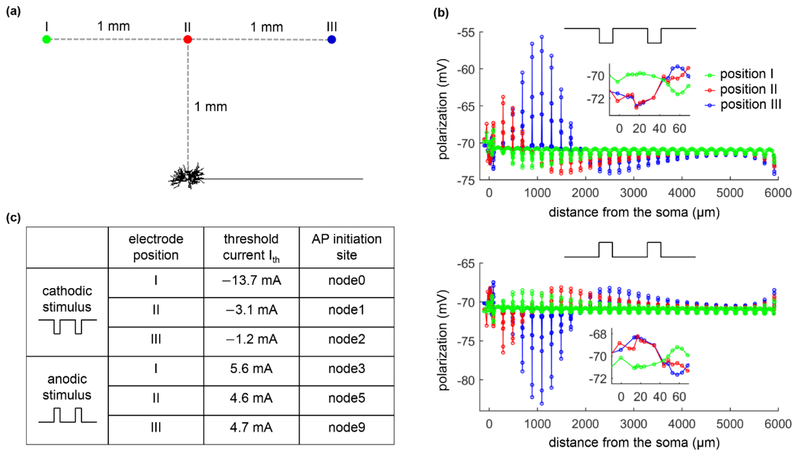
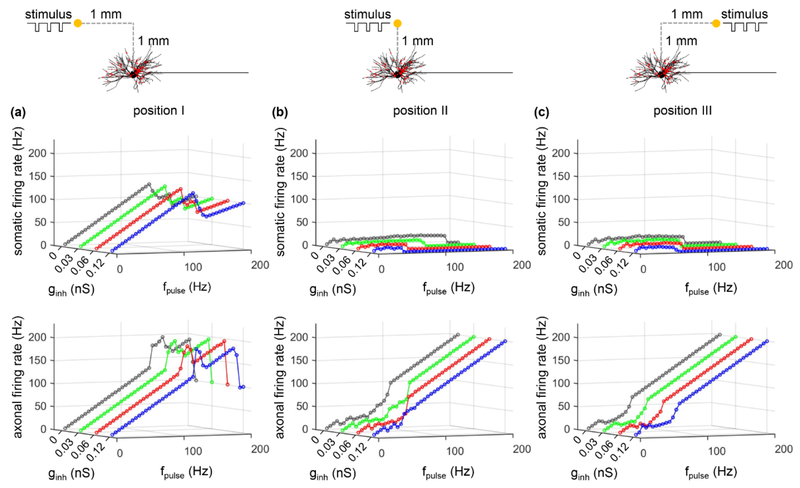
Pulse trains of different frequencies were applied extracellularly using a point source electrode to activate the TC relay neuron, and antidromic activation was quantified at three positions of the extracellular electrode (figure 5(a)). As described previously [20, 30], extracellular stimulation resulted in complex patterns of transmembrane polarization in the distributed TC model neuron, dependent on the location and orientation of the neural segments and the polarity of electrical current (figure 5(b)). With cathodic stimulation, the cell body was hyperpolarized when the point source electrode was placed over the cell body (position II) or over the axon (position III), while the axon near the AIS exhibited differential polarization across the three electrode positions (figure 5(b), top). When the electrode was placed over the dendritic arbor (position I), the cell body and the node of Ranvier (i.e., node0) closest to the AIS were depolarized by cathodic pulses, while the AIS and other axon segments were hyperpolarized. The polarization was reversed during anodic stimulation (figure 5(b), bottom). These complex patterns of polarization resulted in different threshold currents and spike initiation sites across the electrode positions (figure 5(c)). But for all cases we examined, APs were always initiated in the axon.

Figure 5.

Action potential initiation in the TC relay model during extracellular stimulation. (a) A point source electrode was placed at position I: (x_s − 1000, y_s + 1000, z_s), position II: (x_s, y_s + 1000, z_s), or position III: (x_s + 1000, y_s + 1000, z_s). (x_s, y_s, z_s) is the coordinate of the central point of the cell body (unit: μm). (b) Membrane polarization as a function of the distance from the cell body at 0.1 ms after the onset of a subthreshold (1 mA, 0.1 ms) extracellular pulse. (c) Threshold current I_th and spike initiation site at each electrode position with cathodic and anodic stimulation.

We quantified activation of the soma and axon in response to cathodic stimulation over a range of stimulus frequencies for each of the three electrode positions and different synaptic parameters (i.e., g_exc, g_inh, and g_exc: g_inh), and the results are summarized in figures 6-8. For all three positions of the electrode, the firing rate of the soma showed similar trends as g_exc, g_inh, or g_exc: g_inh was varied, and the somatic activity was decoupled from axonal activity. At low pulse frequencies, the soma responded to 100% of the stimuli, but the fidelity of somatic activity decreased as f_pulse increased. Increasing g_exc or g_exc: g_inh increased the fidelity of antidromic invasion of the soma, while increasing g_inh or decreasing g_exc: g_inh reduced the fidelity of antidromic invasion. Compared to position II or III, varying g_exc, g_inh, or g_exc: g_inh resulted in small changes in somatic firing rate with the electrode placed at position I. This was because the large threshold (I_th = −13.7 mA) of cathodic current at position I resulted in strong transmembrane polarization in the TC model, which dominated the responses in the cell body. Further, orthodromic recurrent discharge occurred in the node of Ranvier under some conditions at each electrode position (figure 6(d)), resulting in an axonal firing rate higher than f_pulse. With the electrode at position II or III, some applied pulses fell within the hyperpolarizing afterpotentials of the node (i.e., period of decreased excitability) at low frequencies, resulting in failures of activation of the axon (figure 6(e)) and an antidromic firing rate less than f_pulse. This phenomenon occurred at high frequencies when the electrode was placed at position I. We also applied anodic stimulation to examine the antidromic activation of the cell body over a range of stimulus frequencies for all electrode positions by varying g_exc: g_inh. The results were similar to those with cathodic stimulation (figure 9). Thus, the predictions by intracellular axonal stimulation were largely reproduced during extracellular stimulation. In separate simulations, the intrinsic synaptic inputs were represented as subthreshold. With suprathreshold synaptic conductances, the strong action of synchronous trans-synaptic inputs activated by extracellular stimulation drove the cell body to follow the stimulus. In this case, the somatic firing was dominated by the stimulus-induced trans-synaptic inputs, not by antidromic activation.

Figure 6.

Effects of excitatory inputs on antidromic activation with electrode placed at (a) position I, (b) position II, and (c) position III during cathodic stimulation. Somatic (top) and axonal (bottom) firing rate as a function of g_exc and f_pulse. g_exc = 0 nS (no excitatory inputs), 0.03 nS, 0.06 nS, and 0.12 nS. (d) Voltage responses recorded in the soma and node15 at three positions. There were recurrent orthodromic spikes in the axon. (e) Voltage responses recorded in the soma and node15 at three positions. The axon failed to respond to 100% of the stimulus. Each synaptic input was a 20 Hz Poisson train. Pulse amplitude was 1.2I_th, and pulse width was 0.1 ms.

Figure 8.

Effects of ratio of excitatory to inhibitory conductance on antidromic activation with electrode placed at (a) position I, (b) position II, and (c) position III during cathodic stimulation. The firing rate of the cell body (top) and axon (bottom) as a function of g_exc: g_inh and f_pulse. With g_exc: g_inh = 0:0, there was no synaptic inputs. With g_exc: g_inh = 2:1, 1:1, 1:2, and 1:4, g_exc was set to 0.06 nS and g_inh was varied according to the value of g_exc: g_inh. Each synaptic input was a 20 Hz Poisson train. Pulse amplitude was 1.2I_th, and pulse width was 0.1 ms.

Figure 9.

Effects of ratio of excitatory to inhibitory conductance on antidromic activation with electrode placed at (a) position I, (b) position II, and (c) position III during anodic stimulation. The firing rate of the cell body (top) and axon (bottom) as a function of g_exc: g_inh and f_pulse. With g_exc: g_inh = 0:0, there was no synaptic inputs. With g_exc: g_inh = 2:1, 1:1, 1:2, and 1:4, g_exc was set to 0.06 nS and g_inh was varied according to the value of g_exc: g_inh. Each synaptic input was a 20 Hz Poisson train. Pulse amplitude was 1.2I_th, and pulse width was 0.1 ms.

Transmembrane polarization produced by extracellular stimulation was also an important factor regulating antidromic activation of the soma. During cathodic stimulation, the fidelity of antidromic invasion with electrode at position I was much higher than position II or III (figures 6-8). When the electrode was placed at position I, the cell body was depolarized by each cathodic pulse, which increased its excitability. With the electrode at position II or III, the cell body was hyperpolarized by cathodic stimuli and the excitability was decreased, which reduced the fidelity of antidromic activation. Similarly, the anodic pulses applied with the electrode at position II or III depolarized the cell body and increased its excitability, which resulted in the higher fidelity of antidromic invasion than position I (figure 9).

3.4. Antidromic activation masks burst-driver inputs to TC neurons

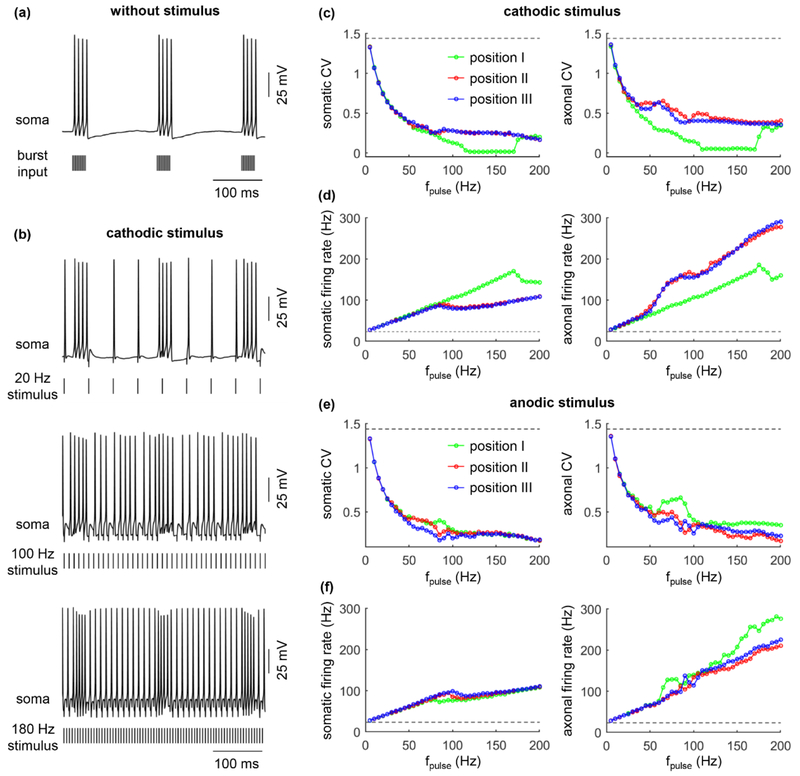
TC neurons exhibit rhythmic bursts of activity, which has been implicated in the genesis of essential tremor in humans [27, 28, 37]. The driver of this pathological activity is thought to be the burst oscillations in cerebellar afferents [27, 28], which are mainly located near the soma of TC neurons [25, 32]. We examined the interactions of antidromic activation and burst activity in the TC model neuron during extracellular stimulation.

Without extracellular stimulation, the cell body exhibited 5.8 Hz burst spiking with a 23.2 Hz mean firing rate (figure 10(a)), which was analogous to recordings in human thalamic neurons with essential tremor [28, 38]. With extracellular stimulation, antidromic activation masked the burst activity in the soma (figure 10(b)) and reduced the CV of the spike train in both the soma and axon (figures 10(c) and (e), left). Increasing the stimulation frequency resulted in more antidromic activation of the cell body (figures 10(d) and (f), left) and more collision block of bursting impulses in the cerebellar input axons, thus facilitating the masking of burst-driver inputs from the cerebellum. At high stimulation frequencies, antidromic activation still occurred in the cell body due to the high excitatory synaptic conductance (g_exc = 0.2 nS), and the burst-driver inputs were not completely blocked by collision in the afferent axons. These factors collectively resulted in the “visible” burst activity in the TC model at high stimulation frequencies (figure 10(b), bottom). The fidelity of somatic firing was dependent on the electrode position. When the electrode was placed at position I, the membrane depolarization generated by cathodic stimulation facilitated antidromic activation, which produced more masking of somatic bursting compared to position II and III, especially at high stimulation frequencies. Similarly, anodic stimulation with the electrode at position II or III produced more masking of somatic bursting compared to position I, which was pronounced at moderate stimulation frequencies. Since the synaptic conductance of excitatory inputs was larger than in previous simulations, the stimulus-induced trans-synaptic effects overpowered the effects of stimulus-induced polarization on antidromic activation. As a result, there was little difference in the CV of the output between the three electrode positions at high stimulation frequencies. Further, the cell body was unable to follow high stimulation frequencies due to the failures of antidromic activation (figures 10(d) and (e)). The APs in the axon included those generated by extracellular stimulation and orthodromic activity originating in the soma, which resulted in a higher firing rate than stimulation frequency (figures 10(d) and (e), right).

Figure 10.

Interactions between antidromic activation and burst activity in model thalamic neuron. (a) Burst spiking in the cell body with no extracellular stimulation. Distribution of burst and Poisson inputs were indicated in Methods. g_exc = 0.2 nS and g_inh = 0.06 nS. (b) Voltage responses in the soma with 20 Hz, 100 Hz, and 180 Hz cathodic stimulation at electrode position II. (c) CV of the somatic (left) and axonal (right) firing as a function of f_pulse during cathodic stimulation. (d) Somatic (left) and axonal (right) firing rate as a function of f_pulse during cathodic stimulation. (e) CV of the somatic and axonal (right) firing as a function of f_pulse during anodic stimulation. (f) Somatic (left) and axonal (right) firing rate as a function of f_pulse during anodic stimulation. The dotted line in (c)-(f) indicated the CV or firing rate without extracellular stimulation. Three positions of the electrode were indicated in figure 5(a). Pulse amplitude was 1.2I_th, and pulse width was 0.1 ms.

4. Discussion

We used a biophysically-based computational model of the TC relay neuron to analyze the pattern of antidromic activation in the cell body. We quantified the effects of stimulation frequency and synaptic inputs on somatic invasion by antidromic spikes. Four main conclusions are supported by our simulations: 1) The recovery cycle of the cell body accounts for the failure of antidromic activation by high-frequency axonal spikes; 2) Excitatory synaptic inputs increase the fidelity of antidromic invasion of the soma, and dominate the effects of inhibitory inputs, which suppress antidromic activation; 3) Local depolarization of the cell body by extracellular stimulation facilitates antidromic invasion; 4) Antidromic activation of the cell body masks the burst-driver inputs to TC relay neurons.

4.1. Frequency-dependent antidromic activation

The direct, first-order effect of DBS is activation of local neuronal elements. Recordings made in projection nuclei showed that DBS in the cerebellar-receiving area of thalamus increased the firing in downstream cells of motor cortex via glutamatergic efferents [39]. The axonal firing in our simulations matched well with these experimental recordings. Importantly, DBS-like extracellular stimulation preferentially activates the fibers of passage, presynaptic terminals, and axons close to the electrode [8-11, 16, 21, 22, 40]. This arises from the fact that thresholds for activation of these elements are lower than for direct excitation of local cells [16, 21, 41]. Both experimental [42, 43] and computational [20, 21, 30] studies indicated that APs were initiated in the axon of local cells during extracellular stimulation. The antidromic APs may then invade the soma or reach a branch point and spread re-orthodromically to activate or inhibit targets far from the site of electrode. With the computational model, we showed that each axonal spike reliably invaded the soma at low antidromic frequencies. At moderate frequencies, there was frequent failure of somatic invasion, and all somatic activation may cease as antidromic frequency further increased. This indicates that antidromic activation of the soma is strongly dependent on antidromic frequency and results in differential patterns of activity in the soma and axon [20].

Computational models predict that neuronal responses exhibit strong frequency dependence during DBS-like stimulation, including selective activation of local cells and fibers of passage [21], selective antidromic conduction of spikes in branched axons [16], alterations in the regularity of firing patterns [44, 45], and suppression of low-frequency oscillatory activity [46]. Further, electrophysiological recordings in motor cortex cells indicated that the reliability of antidromic spikes depended on the frequency of subcortical [14] or subthalamic nucleus (STN) [15] DBS. At low frequencies, the antidromic spike reliably followed each stimulus pulse. But there were significantly more failures of antidromic spike as the stimulation frequency was increased. Even within a same cell, stimulus-generated responses recorded in different segments were dependent on the stimulation frequency. At low frequencies, the cell body and the axon typically responded faithfully to 100% of the stimuli [20, 21]. High-frequency stimulation inhibited cell bodies in the stimulated nucleus [9, 10, 41] while increasing the output firing [39]. McIntyre et al. [20] showed that the apparently contradictory responses generated at high frequencies arose from the dissociation of firing activity in the cell body and efferent axon. Our simulations are consistent with these previous studies, and we extend these prior observations to show that the dissociated responses arise from the hyperpolarizing afterpotentials of the cell body and the subsequent failure of antidromic activation.

The recovery cycle of the soma was a primary factor in determining frequency-dependent antidromic activation. The recovery cycle was identified in human motor and sensory axons [47-49], and includes periods of decreased (supernormal) and increased (subnormal) threshold [47]. Mammalian neurons generate both depolarizing and hyperpolarizing afterpotentials, and experimental [47-49] and computational [24] studies suggest that these afterpotentials determined the threshold for generation of subsequent impulses. Further, the time course of the afterpotentials is different in the cell body and axon [21, 50]. Our simulations indicated that only hyperpolarizing afterpotentials occurred in the cell body in TC relay neurons and these afterpotentials decreased the excitability of the soma, thereby contributing to the failure of antidromic activation at high frequencies. This finding provides a biophysical basis for the frequency-dependent responses during different frequencies of extracellular stimulation. Note that the (exclusively) hyperpolarizing afterpotentials are not a generalized phenomenon in other brain regions. For example, the afterpotentials of the cell body in mammalian motoneurons include both depolarizing and hyperpolarizing afterpotentials [21, 51]. There was slow K⁺ current in the soma of TC neurons, and its activation was the principal mechanism for their hyperpolarizing afterpotentials [24].

4.2. Synaptic effects on antidromic activation

Extracellular stimulation generates both antidromic and orthodromic responses, i.e., direct first-order effects. Spikes in presynaptic terminals activate relevant synapses to cause indirect second-order effects, i.e., stimulus-generated trans-synaptic effects. The trans-synaptic effects produced by DBS generated limited impact on the threshold of TC relay neurons [20], but significantly inhibited somatic spikes in globus pallidus internus (GPi) neurons [22]. Importantly, excitatory inputs altered the output of motoneurons in a frequency-dependent manner [21]. Extending these prior results, our simulations systematically quantified the effects of trans-synaptic inputs on antidromic activation over a range of antidromic frequencies and synaptic conductances. Activating inhibitory synapses suppressed antidromic activation by reducing the excitability of local cells, while activating excitatory inputs increased excitability and promoted antidromic activation. These findings explain the frequency-dependent relationship between synaptic inputs and antidromic activation.

In TC relay neurons, there are an abundance of distal dendrites, which primarily received excitatory inputs from the cortex via cortico-thalamic pathway [26], while inhibitory synapses are mainly distributed on peri-somatic dendrites [25]. Even though excitatory inputs are mainly distributed further from the soma, they are more dense than inhibitory inputs [25] and played a stronger role in determining antidromic activation than inhibitory inputs. Earlier recordings made in thalamic neurons exhibited both excitation and inhibition within the stimulated nucleus [52], which may stem in part from the prevalence or strength of excitatory relative to inhibitory inputs within the thalamus [53]. Similar responses were recorded in STN neurons during STN DBS [18] and globus pallidus externus (GPe) neurons during GPe DBS [9]. In contrast, GABAergic afferent terminals predominate on GPi neurons [54], and their responses are primarily inhibitory during GPi DBS [9]. Our predictions are comparable to these recordings, and suggest that the net effects of DBS-induced trans-synaptic inputs are dependent on the distributions of inhibitory and excitatory presynaptic terminals.

4.3. Limitations of modeling approach

The predictions of our simulations provide insights into antidromic activation of the cell body of TC relay neurons, which are difficult to achieve with experimental approaches. However, there are limitations of our modeling approach. First, we only considered a TC relay neuron model in our simulations. Recordings showed that antidromic activation may also occur in motor cortex [14, 15, 19, 55], GPe [56], GPi [10], and STN [57] neurons. The morphologies, ion channels, and synaptic distributions of these neurons are substantially different from TC relay neurons, and thus the patterns of antidromic activation may be different, as well. The model did not include extracellular K⁺ accumulation, which can affect axonal excitability and antidromic propagation during extracellular stimulation [16]. Further, extracellular stimulation was represented very simply as a point source electrode in a homogenous, isotropic medium, while the tissue surrounding the DBS electrode is inhomogeneous and anisotropic, which can affect stimulus-induced polarization and thus antidromic activation [58].

As well, we did not model all synapses on TC relay neurons due to the limited availability of experimental data. There were a total of 254 synaptic inputs on the cell body and dendrites of the model TC neuron, and this represented only a small fraction of the total synapses on TC relay neurons. Similarly, there was uncertainty about the synaptic conductances. In addition, we did not explicitly define the afferent axons and presynaptic terminals. These limitations of the model of synaptic inputs could play important roles in determining the trans-synaptic effects of extracellular stimulation on antidromic activation. However, our simulations showed that the antidromic activation of the cell body exhibited a similar pattern across antidromic frequencies over a range of synaptic conductances, and thus the specific value of subthreshold synaptic conductance was a secondary concern. Moreover, synaptic fatigue/depletion or synaptic plasticity were also not considered in the synaptic input model. The lack of activity-dependent changes in synaptic efficacy made our simulations unable to predict the long-term effects of extracellular stimulation on antidromic activation.

4.4. Implications for understanding the effects of DBS

A clear and complete understanding of the mechanisms of action of DBS is still lacking [2, 3]. Functional magnetic resonance imaging and positron emission tomography demonstrated that DBS produced alterations in neural activity over widespread regions of the brain [4-7]. One mechanism contributing to the distributed effects of DBS is antidromic activation [11, 16]. Increasing evidence confirms that DBS excites presynaptic terminals and axons of passage, as these elements have lower thresholds for activation. For example, STN DBS antidromically activates the neurons in the motor cortex [15, 19, 55], GPi [10], GPe [56], and thalamus [7], and GPi DBS results in antidromic activation of thalamic neurons [8]. The APS generated in local axons may antidromically invade the soma, thereby altering activity of those projecting neurons. Moreover, there is extensive branching of axons projecting to the target nuclei of DBS, and their collaterals extend to multiple brain regions [16]. As a result, antidromic APs may also propagate orthodromically down the axon collaterals, and influence neuronal activity in remote downstream structures. Using computational models to identify the factors determining antidromic activation could contribute to understanding how DBS activates widespread regions of the brain.

Antidromic activation can occur in both local and distal nuclei of the brain and contribute to the mechanisms of DBS. Antidromic activation of neurons located in distant nuclei could desynchronize and modify the abnormal firing in the primary motor cortex [15]. Antidromic activation of local cell bodies can contribute to the dissociation of somatic and axonal activity in thalamic neurons [20], rectify pathological firing [45], and lead to creation of an “Informational lesion” of the stimulated nucleus [45], thereby preventing the propagation of abnormal signals within the basal ganglia-thalamus-cortical loops. Further, antidromic activation of local cells could alter generation of and, subsequently responses to, recurrent activation or inhibition by axon collaterals, a situation the is clearly a component of the thalamic circuit.

The effects of DBS in alleviating the symptoms of movement disorders are highly dependent on stimulation frequency. With higher frequencies (≥ 90 Hz), tremor is effectively suppressed by DBS of the thalamus [12, 13], while low-frequency (< 60 Hz) thalamic stimulation results in the aggravation of tremor [59] or bradykinesia [60], and can even evoke tremor in healthy persons [61]. A necessary step toward a mechanistic understanding of the frequency-dependent effectiveness of DBS is to determine how different frequencies of extracellular stimulation alter neuronal activity in target nuclei. Functional imaging [62] suggested that there was a strong correlation between DBS frequency and motor cortex activity during STN DBS, and electrophysiological recordings [15] revealed that STN DBS antidromically activated the motor cortex in a frequency-dependent manner via the hyperdirect pathway from STN. Our results demonstrating strong frequency-dependent antidromic activation provide a basis to interpret the frequency-dependent effects of DBS on symptoms.

Although thalamic DBS is an effective therapy for treating ET, the neural mechanisms underlying its action are still not well understood. Recordings made in the cerebello-thalamocortical pathway implicated the bursting activity in the thalamus in the genesis of ET in human patients [28, 37]. Clinical and computational studies [27, 45, 63] showed that thalamic DBS alleviated tremor in ET by masking pathological bursting in cerebellar–thalamic neurons via regularization of neuronal output. It was also suggested that the most effective location of DBS electrode for suppressing tremor was close to the cerebellar fibers that terminate in the thalamus [27, 63, 64]. Our results predicted that antidromically activating the cell body contributed to DBS masking the burst-driver inputs from the cerebellum to TC neurons, thereby preventing the propagation of pathological activity in the cerebello-thalamocortical pathway [45].

5. Conclusions

We developed a quantitative understanding of the factors contributing to antidromic activation of the cell body during DBS-like extracellular stimulation. Antidromic frequency, synaptic inputs, and membrane polarization produced by extracellular stimulation all contributed to determining the fidelity of somatic invasion by antidromic spikes. The frequency dependence of the antidromic activation was attributed to the hyperpolarizing afterpotentials in the recovery cycle of the cell body. The excitatory/inhibitory synaptic inputs and stimulus-induced polarizations regulated antidromic activation by altering somatic excitability. These predictions should be considered when understanding the complicated, widespread effects of DBS on local, upstream, and downstream circuits, which have significant implications for the functional imaging studies of DBS action.

Figure 7.

Effects of inhibitory inputs on antidromic activation with electrode placed at (a) position I, (b) position II, and (c) position III during cathodic stimulation. The firing rate of the cell body (top) and axon (bottom) as a function of g_inh and f_pulse. g_inh = 0 nS (no inhibitory inputs), 0.03 nS, 0.06 nS, and 0.12 nS. Each synaptic input was a 20 Hz Poisson train. Pulse amplitude was 1.2I_th, and pulse width was 0.1 ms.