Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2018 Sep 5;8:13283. doi: 10.1038/s41598-018-31296-7

Discovery of topological nodal-line fermionic phase in a magnetic material GdSbTe

M Mofazzel Hosen 1, Gyanendra Dhakal 1, Klauss Dimitri 1, Pablo Maldonado 2, Alex Aperis 2, Firoza Kabir 1, Christopher Sims 1, Peter Riseborough 3, Peter M Oppeneer 2, Dariusz Kaczorowski 4, Tomasz Durakiewicz 5,6, Madhab Neupane 1,✉
PMCID: PMC6125290  PMID: 30185891

Abstract

Topological Dirac semimetals with accidental band touching between conduction and valence bands protected by time reversal and inversion symmetry are at the frontier of modern condensed matter research. A majority of discovered topological semimetals are nonmagnetic and conserve time reversal symmetry. Here we report the experimental discovery of an antiferromagnetic topological nodal-line semimetallic state in GdSbTe using angle-resolved photoemission spectroscopy. Our systematic study reveals the detailed electronic structure of the paramagnetic state of antiferromagnetic GdSbTe. We observe the presence of multiple Fermi surface pockets including a diamond-shape, and small circular pockets around the zone center and high symmetry X points of the Brillouin zone (BZ), respectively. Furthermore, we observe the presence of a Dirac-like state at the X point of the BZ and the effect of magnetism along the nodal-line direction. Interestingly, our experimental data show a robust  Dirac-like state both below and above the magnetic transition temperature (TN  = 13 K). Having a relatively high transition temperature, GdSbTe provides an archetypical platform to study the interaction between magnetism and topological states of matter.

Introduction

The discovery of three-dimensional (3D) topological insulators turned out to be an enthralling achievement of the last decade1,2. A 3D ℤ2 topological insulator (TI) is described as a crystalline solid that acts as a traditional insulator in the bulk but has surface Dirac electron states which are conducting, gapless, or even spin polarized1–5. The discovery of such materials with spin-momentum locking dates back to 20071–5 when the bismuth-based 3D TI Bi2Se3 was reported. This initiated a domino effect of subsequent discoveries, where one new exotic state led to another, broadening our knowledge of quantum matter and increasing the number of researchers focused on this novel field. Consideration of electronic states protected by time-reversal, crystalline, and particle-hole symmetries have led to the prediction of many novel 3D materials, which can support Weyl, Dirac, and Majorana fermions, and new types of insulators such as topological crystalline insulators and topological Kondo insulators, topological superconductors, as well as 2D quantum spin Hall insulators with large band gaps capable of surviving room-temperature thermal excitations3,6–11. Recent attention has focused on exploring non-trivial topological behavior in metals and semimetals without bulk band gaps, which can support symmetry protected gapless points in the Brillouin zone12–24.

Topological materials offer transformational opportunities by providing platforms for entirely new classes of fundamental science studies of quantum matter as well as developing new paradigms for the design of devices for wide-ranging applications in next generation electronics, communications, and energy technologies1,2. It is envisaged that novel quantum materials will render another breakthrough in technology development. Up to date, available topological materials are mostly nonmagnetic, with very few magnetic topological semimetals25–28. Therefore, there is an especially urgent need to find new magnetic topological materials so that the unique potential for fundamental science studies and applications can be explored. This new realm may provide us with new exotic states which could be helpful in revolutionizing technology.

In this report, we present a systematic study of an antiferromagnetic compound GdSbTe in order to discover the topology and magnetism of this material using angle-resolved photoemission spectroscopy (ARPES), thermodynamic measurements, and first-principles calculations. Remarkably, GdSbTe is isostructural with the nodal-line semimetal ZrSiS29,30 and related compounds, which have been shown to exhibited a diamond-shaped Dirac line node as well as four-fold degenerate nodes at the high-symmetric points of the Brillouin zone (BZ)29–41. GdSbTe has a relatively high magnetic transition temperature TN = 13 K, and hence its ordered state can be accessed by ARPES and other experimental techniques.

Our systematic electronic structure studies reveal the presence of multiple Fermi surface pockets such as a diamond-, and circular-shaped pockets around the Γ, and X points, respectively, in the first BZ of GdSbTe. Our data show that this system is not only structurally but also electronically similar to ZrSiS and related nonsymmorphic Dirac materials. Importantly, we observe a Dirac like state at the X point in both the paramagnetic and antiferromagnetic states. Furthermore, we reveal the effect of magnetism along the nodal-line direction of the BZ. Our findings provide a platform for discovering new exotic quantum phases emerging due to the interplay of magnetism with the topological phases.

Results

Crystal structure and sample characterization

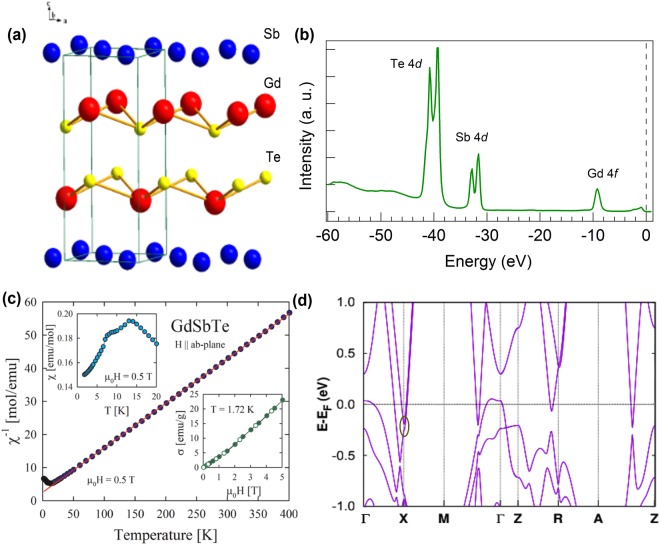
We start our discussion by presenting the crystal structure of GdSbTe. Similar to other ZrSiS-type materials, it has a nonsymmorphic tetragonal unit cell with space group P4/nmm. As shown in Fig. 1a, the Gd-Te bilayers are sandwiched between the layers of Sb atoms forming a square net. The single crystals used in the present study were first examined via spectroscopic core-level measurements. The observed sharp peaks (Fig. 1b) due to the Te 4d (~40 eV), Sb 4d (~33 eV) and Gd 4 f (~8.5 eV) electronic states prove the excellent quality of the specimen. Figure 1c displays the magnetic properties of GdSbTe. Above 15 K, the magnetic susceptibility, χ(T), obeys a Curie-Weiss law with the effective magnetic moment μef = 7.71 μB and the paramagnetic Curie temperature θ = −19 K. The experimental value of μef is close to that expected for a trivalent Gd ion (7.94 μB). The large negative value of θ signals strong antiferromagnetic exchange interactions. As shown in the upper inset of Fig. 1c, the compound orders antiferromagnetically at TN = 13 K, and undergoes another magnetic phase transition near 8 K. At the lowest temperature attained in the present work, i.e. T = 1.72 K, the compound bears an antiferromagnetic state, as supported by the character of the magnetization isotherm displayed in the lower inset of Fig. 1c. The magnetic field variation of the magnetization, σ(H), exhibits some tiny inflection near 1.5 T, which can be attributed to a metamagnetic-like phase transition. In stronger fields, σ(H) of GdSbTe shows a feebly upward behavior, which indicates that an expected field-induced ferromagnetic arrangement of the gadolinium magnetic moments can be achieved in this compound in magnetic fields much stronger than the maximum field of 5 T available in the present study. The ab-initio calculated bulk band structure of GdSbTe is displayed in Fig. 1d. Importantly, at around 0.2 eV below the Fermi energy, a Dirac-like feature with a small gap is observed at the X point of the BZ.

Figure 1.

Figure 1

Open in a new tab

Crystal structure and sample characterization of GdSbTe. (a) Tetragonal crystal structure. Layers of Sb atoms form a square net. Sheets of Gd atoms are separated by two Te layers. (b) Core-level spectrum. Here, we clearly observe sharp peaks due to Te 4d (~40 eV), Sb 4d (~33 eV) and Gd 4 f (~8.5 eV) states. The black dashed line represents the Fermi level. (c) Temperature dependence of the reciprocal magnetic susceptibility measured in a magnetic field of 0.5 T applied within the crystallographic a-b plane. Solid line represents the fit of Curie-Weiss law to the experimental data. Upper inset: low-temperature magnetic susceptibility data. Lower inset: magnetic field variation of the magnetization taken at 1.72 K with increasing (full circles) and decreasing (open circles) magnetic field strength. (d) Ab-initio calculated bulk band structure along the high-symmetry directions. Red circle indicates the approximate position of the Dirac point.

Fermi surface and observation of nodal-line state

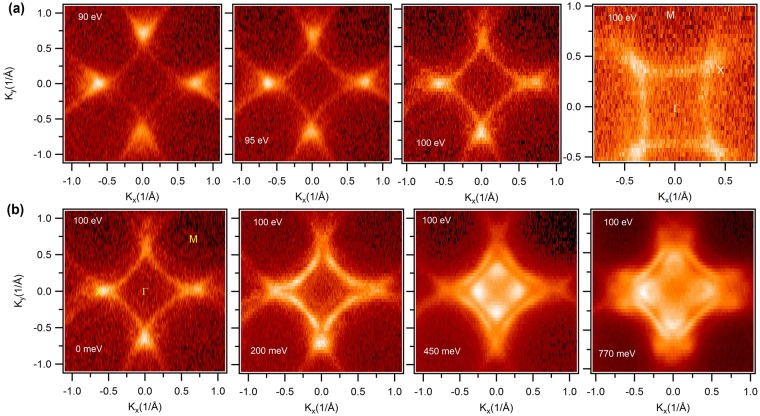
Figure 2a shows Fermi surface maps of GdSbTe in its paramagnetic states at various incident photon energies. High symmetry points and energies are noted in the plots. The overall Fermi surface is similar to previously reported data on ZrSiS-type materials (see also supplementary information)30,39. The topological nodal-line states along the M-Γ-M directions form a diamond shaped Fermi pocket around the center of the BZ. Furthermore, we observe small circular shaped Fermi pockets around the X points of the BZ, respectively (see Supplementary Fig. 3). The rightmost panel of Fig. 2a shows the Fermi surface in a different orientation. Figure 2b shows the constant energy contour plots at various binding energies. Moving towards the higher binding energy we observe that the diamond shape gradually evolves into two diamonds. At a higher binding energy a small circular pocket-like feature evolves along the Γ-X direction. The small pocket is clearly visible in the constant energy contour plot with a binding energy of 770 meV which is in the vicinity of the Dirac point along this direction.

Figure 2.

Figure 2

Open in a new tab

Fermi surface and constant energy contour plots. (a) Experimentally measured Fermi surface maps at various photon energies and at different high symmetry directions. The rightmost panel represents the Fermi level in a different orientation with high symmetry points. Photon energies are noted in the plots. (b) Constant energy contour plots at various binding energies. Energies are noted in the plots. High symmetry points are indicated in the leftmost plot. All the measurements were performed at the ALS beamline 4.0.3 at a temperature of 21 K.

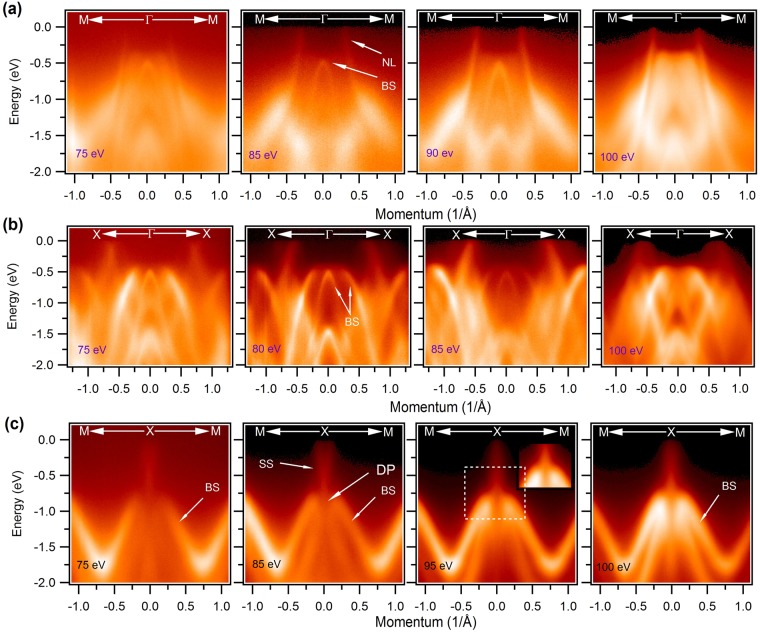
To reveal the nature of the states along the various high symmetry directions, we present photon energy dependent ARPES measured dispersion maps in Fig. 3. The photon energy dependent measurements help to identify the origin of the bands i.e. surface or bulk originated. In contrast to bulk bands, the surface bands do not disperse with incident photon energy. Figure 3a shows the measured dispersion maps along the M-Γ-M direction at various photon energies, where Dirac line node phase has been observed. The photon energies are noted in the plots. The linearly dispersive state which forms the nodal-line (NL) in our measured ARPES spectra do not disperse with the photon energy hence suggesting the surface origin which is consistent with the previously reported result of ZrSiS-type materials29,30,39. Furthermore, another bulk band is observed to bend over at around 500 meV below the chemical potential. Figure 3b represents the dispersion maps along the X-Γ-X direction (see Supplementary Fig. 9 and Note 5 for low temperature dispersion maps). A Dirac-like dispersion is observed at around 770 meV below the Fermi level. Near the Γ point two bulk bands are observed where the top of one band is almost flat. Such features are not observed in other reported ZrSiX-type materials, therefore, further theoretical investigation is required. To fully understand the nature of the state at the X point, we present dispersion maps along the M-X-M high symmetry direction in Fig. 3c. Photon energies are noted in the plots. The Dirac like state is observed at the X point of the BZ and does not disperse with photon energy (see also Supplementary Fig. 4 and Note 2). The Dirac point is located at around 770 meV below the Fermi level. Our ab-initio slab calculations confirm the existence of this Dirac point near the observed energy, and indicate that this is surface-derived (see Supplementary Fig. 5(b)). In the vicinity of the Dirac point two other bulk bands are observed. This feature is not normal since a surface state usually does not coexist within the projected bulk bands. Therefore, one can expect bulk-surface band hybridization in the vicinity of the Dirac point. Furthermore, we have collected all our data approximately around the normal emission with varying temperature (see Figs. 3c and 4, and Supplementary Figs. 4 and 5) and photon energies where the bands do not show any sort of broadening effect. The inset of Fig. 3(c) shows the zoomed dispersions near the Dirac point where bulk states overlap with the surface state.

Figure 3.

Figure 3

Open in a new tab

Dispersion map along the high symmetry directions. (a) ARPES measured dispersion maps along the M-Γ-M direction at various photon energies. Nodal-line is observed to be in the vicinity of the chemical potential. (b) Dispersion maps along the high symmetry X-Γ-X direction. (c) Band dispersion along the M-X-M direction. Dirac-like state is observed. Measured photon energies are noted in the plots. Inset shows the zoomed view near the Dirac point marked with dashed white rectangular box. All the measurements were performed at the ALS beamline 4.0.3 at a temperature of 21 K. We note that, NL = nodal line, BS = bulk state, SS = surface state, DP = Dirac point.

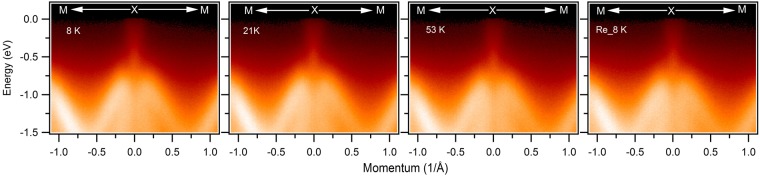
Figure 4.

Figure 4

Open in a new tab

Temperature dependent measurement of dispersion maps along the M-X-M direction. Measured temperature are noted on the plots. Re_8 K indicates the dispersion map after thermal recycle (8 K → 21 K → 53 K → 8 K). All the measurements were performed at the ALS beamline 4.0.3 using a photon energy of 90 eV.

Observation of antiferromagnetic Dirac state

The Dirac semimetal (DSM) conserves the time reversal symmetry and spatial inversion symmetry and requires the protection by some crystalline symmetry12,13. The Dirac semimetal breaks into a Weyl semimetal if either of the aforementioned symmetries is broken. Interestingly, the Dirac semimetal may exist even if both time reversal symmetry and inversion symmetry are broken23,24. This kind of situation is proposed to exist in some antiferromagnetic semi-metallic materials. When a material undergoes a magnetic phase transition from paramagnetic to ferromagnetic or antiferromagnetic, the time reversal symmetry is broken. If time reversal symmetry (T) and spatial inversion symmetry (P) are broken, the Dirac semimetal no longer exists, however, their product may remain conserved24. For the DSM to survive, the desired AFM material should exhibit ordered moments such that P and T are individually broken but PT is conserved and in addition the crystalline symmetry (in the case of the 111 compounds the non-symmorphic symmetry) protecting the DSM state in the non-magnetic state is not violated. In addition, the AFM state would need to be robust against SOC and correlation effects so that the aforementioned conditions can still be met24,28. Since the antiferromagnetic (AFM) transition temperature is 13 K in the GdSbTe system, it can provide a platform to study the effect of magnetism and topology. We present dispersion maps along the M-X-M direction both below and above the magnetic transition temperature of this material in Fig. 4. Temperature values are indicated in the plots. Interestingly, we observe robust Dirac like state in both paramagnetic and antiferromagnetic phases (see also Supplementary Fig. 5 and Note 3). Our thermally recycled dispersion maps (8 K → 21 K → 53 K → 8 K) indicates the robust nature of the Dirac state in GdSbTe. Although the time reversal symmetry (T) is broken in the magnetic phase of GdSbTe, a potential product of the rotation-inversion operator with the time-reversal operator may be responsible for topological state protection in the AFM state. Furthermore, owing to the robust Dirac state at the X point of the BZ, one can expect to see the effect of magnetism at the other points of the BZ. To show that, we have performed spectral weight transfer analysis and symmetrization of the energy distribution curves along the nodal-line direction (see Supplementary Note 4 and Figs 7 and 8). Clear observation of a large deviance of intensities between the energy range from −0.15 to 0 eV and a kink in the symmetrized data confirm the effect of magnetism in the nodal-line direction.

Discussion

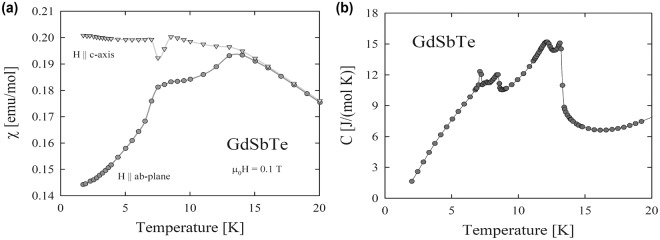
In order to shed some light on the magnetic structure of GdSbTe and the corresponding topological states below TN, low-temperature measurements of the thermodynamic properties were performed (see Fig. 5). It should be noted that the strongly uniaxial crystal structure of this compound favors an Ising type of spin arrangement that is indeed observed for numerous isostructural antiferromagnets. Usually, the magnetic structures of such phases consists of ferromagnetically coupled (001) planes which are arranged along the c-axis in an antiferromagnetic +−, ++ −−, or +− −+ manner. For these types of magnetic ordering a spatial rotation-inversion operator might combine with time-reversal operator to provide the necessary preservation of symmetry that enables the protection of the topological states23.

Figure 5.

Figure 5

Open in a new tab

Low-temperature thermodynamic properties of single-crystalline GdSbTe. (a) Temperature dependence of the magnetic susceptibility measured in a magnetic field of 0.1 T applied along the crystallographic c axis (triangles) and the tetragonal a–b plane (circles). (b) Temperature dependence of the specific heat.

However, the magnetism in GdSbTe is complex and not yet resolved. Our magnetic data (see Fig. 5a) indicate that in the ordered state the Gd magnetic moments are confined within the tetragonal a–b plane. The magnetic susceptibility measured along and perpendicular to the c axis exhibits in the ordered state quite unusual temperature dependencies, which hints the occurrence of several spin reorientation transitions. This finding is supported by the heat capacity data (see Fig. 5b). Determination of the spatial inversion operator, or perhaps a complex yet expected for this structure roto-inversion operator will be possible once the multiple magnetic structures in GdSbTe are determined.

In conclusion, we have performed an experimental study of GdSbTe using ARPES and thermodynamic measurements. The results were supplemented by first-principles calculations. Our studies revealed the topological nodal state and confirmed that the overall electronic structure in GdSbTe is similar to those observed for ZrSiS-type materials. Most importantly, we discover a Dirac-like state both below and above the magnetic transition temperature of 13 K. With a relatively high Néel temperature, GdSbTe is a good platform for studying the interplay between magnetism and topology.

Methods

Crystal growth and characterization

Single crystals of GdSbTe were grown by chemical vapor transport method using iodine as a transporting agent42,43. The chemical composition of the crystals was checked by energy-dispersive X-ray analysis using a FEI scanning electron microscope equipped with an EDAX Genesis XM4 spectrometer. Single crystal X-ray diffraction (XRD) experiment was performed on a Kuma-Diffraction KM4 four-circle diffractometer equipped with a CCD camera using Mo Kα radiation. The results indicated the tetragonal space group P4/nmm (No. 129) with the lattice parameters a = 4.3104(5) Å and c = 9.1233(15) Å. The XRD scans revealed that the platelet-shaped crystals have their large surface perpendicular to the crystallographic c-axis. Magnetic measurements were performed in the temperature range from 1.72 K to 400 K and in external fields up to 5 T using a Quantum Design MPMS SQUID magnetometer. The heat capacity was measured in the temperature range 2–20 K employing a Quantum Design PPMS platform.

Spectroscopic characterization

Synchrotron based ARPES measurements were performed at Advanced Light Source (ALS) beamlines 4.0.3 and 10.0.1.1 equipped with a Scienta R8000 and R4000 hemispherical electron analyzer setup, respectively. Similarly, helium lamp based ARPES measurements were performed at the Laboratory for Advanced Spectroscopic Characterization of Quantum Materials (LASCQM) with R3000 hemispherical analyzer at University of Central Florida. The angular resolution was set to be better than 0.2°. And the energy resolution was set to be better than 20 meV. The samples were cleaved in-situ under the vacuum condition better than 3 × 10−11 torr and at a temperature around 21 K.

Electronic structure calculations

The electronic structure calculations were carried out using the Vienna ab-initio Simulation Package (VASP)44,45, and the generalized gradient approximation (GGA) used as the DFT exchange-correlation functional46. Projector augmented-wave pseudopotentials47 were used with an energy cutoff of 500 eV for the plane-wave basis, which was sufficient to converge the total energy for a given k-point sampling. To simulate the surface effects, we used 1 × 5 × 1 supercell for the (001) surface, with a vacuum thickness larger than 19 Å.

Electronic supplementary material

Supplementary Information (3.7MB, pdf)

Acknowledgements

M.N. is supported by the Air Force Office of Scientific Research under Award No. FA9550-17-1-0415 and the startup fund from UCF. P.M., A.A., and P.M.O. acknowledge support from the Swedish Research Council (VR), the Röntgen- Ångström Cluster, and the Swedish National Infrastructure for Computing (SNIC). T.D. is supported by NSF IR/D program. We thank Jonathan Denlinger and Sung-Kwan Mo for beamline assistance at the LBNL.

Author Contributions

M.N. conceived the study; D.K. synthesized the samples and performed the transport characterization; M.M.H. and M.N. performed the measurements and analysis with the help of G.D., K. D., F.K., C.S., T.D., P.R. and M.N.; M.M.H. and M.N. performed the figure planning; A.A., P.M. and P.M.O. performed the ab-initio calculations; M.M.H. and M.N. wrote the manuscript with input from all authors. M.N. was responsible for the overall research direction, planning and integration among different research units.

Data Availability

The data that support the findings of this study are available from the corresponding author upon request.

Competing Interests

The authors declare no competing interests.

Footnotes

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Electronic supplementary material

Supplementary information accompanies this paper at 10.1038/s41598-018-31296-7.

References

  • 1.Hasan MZ, Kane CL. Colloquium: topological insulators. Rev. Mod. Phys. 2010;82:3045–3067. doi: 10.1103/RevModPhys.82.3045. [DOI] [Google Scholar]
  • 2.Qi X-L, Zhang S-C. Topological insulators and superconductors. Rev. Mod. Phys. 2011;83:1057–1110. doi: 10.1103/RevModPhys.83.1057. [DOI] [Google Scholar]
  • 3.Hasan, M. Z., Xu, S.-Y. & Neupane, M. Topological Insulators: Fundamentals and Perspectives (eds Ortmann, F., Roche, S. & Valenzuela, S. O.) (John Wiley & Sons, New York, 2015).
  • 4.Neupane M, et al. Observation of quantum-tunnelling-modulated spin texturein ultrathin topological insulator Bi2Se3 films. Nat. Commun. 2014;5:3841. doi: 10.1038/ncomms4841. [DOI] [PubMed] [Google Scholar]
  • 5.Hosen MM, et al. Distinct multiple fermionic states in a single topological metal. Nat. Commun. 2018;9:3002. doi: 10.1038/s41467-018-05233-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Fu L. Topological crystalline insulators. Phys. Rev. Lett. 2011;106:106802. doi: 10.1103/PhysRevLett.106.106802. [DOI] [PubMed] [Google Scholar]
  • 7.Xu Q, et al. Two-dimensional oxide topological insulator with iron-pnictide superconductor LiFeAs structure. Phys. Rev. B. 2015;92:205310. doi: 10.1103/PhysRevB.92.205310. [DOI] [Google Scholar]
  • 8.Neupane M, et al. Surface electronic structure of the topological Kondo-insulator candidate correlated electron system SmB6. Nat. Commun. 2013;4:2991. doi: 10.1038/ncomms3991. [DOI] [PubMed] [Google Scholar]
  • 9.Neupane M, et al. Observation of the spin-polarized surface state in a noncentrosymmetric superconductor BiPd. Nat. Commun. 2016;7:13315. doi: 10.1038/ncomms13315. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 10.Neupane M, et al. Electronic structure and relaxation dynamics in a superconducting topological material. Sci. Rep. 2016;6:22557. doi: 10.1038/srep22557. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Neupane M, et al. Non-Kondo-like Electronic Structure in the Correlated Rare-Earth Hexaboride YbB6. Phys. Rev. Lett. 2015;114:016403. doi: 10.1103/PhysRevLett.114.016403. [DOI] [PubMed] [Google Scholar]
  • 12.Wang Z, Weng H, Wu Q, Dai X, Fang Z. Three-dimensional Dirac semimetal and quantum transport in Cd3As2. Phys. Rev. B. 2013;88:125427. doi: 10.1103/PhysRevB.88.125427. [DOI] [Google Scholar]
  • 13.Neupane M, et al. Observation of a three-dimensional topological Dirac semimetal phase in high-mobility Cd3As2. Nat. Commun. 2014;5:3786. doi: 10.1038/ncomms4786. [DOI] [PubMed] [Google Scholar]
  • 14.Yang B-J, Nagaosa N. Classification of stable three-dimensional Dirac semimetals with nontrivial topology. Nat. Commun. 2014;5:4898. doi: 10.1038/ncomms5898. [DOI] [PubMed] [Google Scholar]
  • 15.Neupane M, et al. Observation of Dirac-Like Semi-Metallic Phase in NdSb. J. Phys.: Condens. Mat. 2016;28:23LT02. doi: 10.1088/0953-8984/28/23/23LT02. [DOI] [PubMed] [Google Scholar]
  • 16.Dimitri K, et al. Dirac state in a centrosymmetric superconductor αPdBi2. Phys. Rev. B. 2018;97:144514. doi: 10.1103/PhysRevB.97.144514. [DOI] [Google Scholar]
  • 17.Huang S-M, et al. A Weyl Fermion semimetal with surface Fermi arcs in the transition metal monopnictide TaAs class. Nat. Commun. 2015;6:7373. doi: 10.1038/ncomms8373. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Weng H, Fang C, Fang Z, Bernevig BA, Dai X. Weyl Semimetal Phase in Noncentrosymmetric Transition-Metal Monophosphides. Phys. Rev. X. 2015;5:011029. [Google Scholar]
  • 19.Xu S-Y, et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science. 2015;349:613. doi: 10.1126/science.aaa9297. [DOI] [PubMed] [Google Scholar]
  • 20.Lv BQ, et al. Experimental Discovery of Weyl Semimetal TaAs. Phys. Rev. X. 2015;5:031013. [Google Scholar]
  • 21.Belopolski I, et al. Criteria for Directly Detecting Topological Fermi Arcs in Weyl Semimetals. Phys. Rev. Lett. 2016;116:066802. doi: 10.1103/PhysRevLett.116.066802. [DOI] [PubMed] [Google Scholar]
  • 22.Hasan MZ, Xu S-Y, Bian G. Topological insulators, topological superconductors and Weyl fermion semimetals: discoveries, perspectives and outlooks. Phys. Scr. 2015;T164:014001. doi: 10.1088/0031-8949/2015/T164/014001. [DOI] [Google Scholar]
  • 23.Mong RSK, Essin AM, Moore JE. Antiferromagnetic topological insulators. Phys. Rev. B. 2010;81:245209. doi: 10.1103/PhysRevB.81.245209. [DOI] [Google Scholar]
  • 24.Tang P, Zhou Q, Xu G, Zhang S-C. Dirac fermions in an antiferromagnetic semimetal. Nat. Phys. 2016;12:1100–1104. doi: 10.1038/nphys3839. [DOI] [Google Scholar]
  • 25.Borisenko, S. et al. Time-reversal symmetry breaking type-II Weyl state inYbMnBi2. arXiv:1507.04847 (2015).
  • 26.Hirschberger M, et al. The chiral anomaly and thermopower of Weyl fermions in the half-Heusler GdPtBi. Nat. Mater. 2016;15:11611165. doi: 10.1038/nmat4684. [DOI] [PubMed] [Google Scholar]
  • 27.Wang Z, et al. Time-Reversal-Breaking Weyl Fermions in Magnetic Heusler Alloys. Phys. Rev. Lett. 2016;117:236401. doi: 10.1103/PhysRevLett.117.236401. [DOI] [PubMed] [Google Scholar]
  • 28.Schoop LM, et al. Tunable Weyl and Dirac states in the nonsymmorphic compound CeSbTe. Sci. Adv. 2018;4:eaar2317. doi: 10.1126/sciadv.aar2317. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Schoop LM, et al. Dirac cone protected by non-symmorphic symmetry and three-dimensional Dirac line node in ZrSiS. Nat. Commun. 2016;7:11696. doi: 10.1038/ncomms11696. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Neupane M, et al. Observation of Topological Nodal Fermion Semimetal Phase in ZrSiS. Phys. Rev. B. 2016;93:201104(R). doi: 10.1103/PhysRevB.93.201104. [DOI] [Google Scholar]
  • 31.Burkov AA, Hook MD, Balents L. Topological nodal semimetals. Phys. Rev. B. 2011;84:235126. doi: 10.1103/PhysRevB.84.235126. [DOI] [Google Scholar]
  • 32.Phillips M, Aji V. Tunable line node semimetals. Phys. Rev. B. 2014;90:115111. doi: 10.1103/PhysRevB.90.115111. [DOI] [Google Scholar]
  • 33.Weng H, et al. Topological node-line semimetal in three-dimensional graphene networks. Phys. Rev. B. 2015;92:045108. doi: 10.1103/PhysRevB.92.045108. [DOI] [Google Scholar]
  • 34.Kim Y, Wieder BJ, Kane CL, Rappe AM. Dirac Line Nodes in Inversion-Symmetric Crystals. Phys. Rev. Lett. 2015;115:036806. doi: 10.1103/PhysRevLett.115.036806. [DOI] [PubMed] [Google Scholar]
  • 35.Xie LS, et al. A new form of Ca3P2 with a ring of Dirac nodes. Appl. Phys. Lett. Mat. 2015;3:083602. [Google Scholar]
  • 36.Hu J, et al. Evidence of topological nodal-line fermions in ZrSiSe and ZrSiTe. Phys. Rev. Lett. 2016;117:016602. doi: 10.1103/PhysRevLett.117.016602. [DOI] [PubMed] [Google Scholar]
  • 37.Takane D, et al. Dirac-node arc in the topological line-node semimetal HfSiS. Phys. Rev. B. 2016;94:121108(R). doi: 10.1103/PhysRevB.94.121108. [DOI] [Google Scholar]
  • 38.Hu J, et al. Quantum oscillation studies of topological semimetal candidate ZrGeM (M=S, Se, Te) Phys. Rev. B. 2017;95:205134. doi: 10.1103/PhysRevB.95.205134. [DOI] [Google Scholar]
  • 39.Hosen MM, et al. Tunability of the topological nodal-line semimetal phase in ZrSiX-type materials. Phys. Rev. B. 2017;95:161101(R). doi: 10.1103/PhysRevB.95.161101. [DOI] [Google Scholar]
  • 40.Hosen MM, et al. Observation of gapless Dirac surface states in ZrGeTe. Phys. Rev. B. 2018;97:121103(R). doi: 10.1103/PhysRevB.97.121103. [DOI] [Google Scholar]
  • 41.Chen C, et al. Dirac Line-nodes and Effect of Spin-orbit Coupling in Non-symmorphic Critical Semimetal MSiS (M=Hf, Zr) Phys. Rev. B. 2017;95:125126. doi: 10.1103/PhysRevB.95.125126. [DOI] [Google Scholar]
  • 42.Wang C, Hughbanks T. Main Group Element Size and Substitution Effects on the Structural Dimensionality of Zirconium Tellurides of the ZrSiS Type. Inorg. Chem. 1995;34:5524–5529. doi: 10.1021/ic00126a024. [DOI] [Google Scholar]
  • 43.Singha R, Pariari A, Satpati B. and Mandal., Titanic magnetoresistance and signature of non-degenerate Dirac nodes in ZrSiS. Proc. Natl. Acad. Sci. USA. 2017;114:2468–2473. doi: 10.1073/pnas.1618004114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 44.Kresse G, Furthmuller J. Efficient iterative schemes for ab initio total energy calculations using a plane-wave basis set. Phys. Rev. B. 1996;54:11169. doi: 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
  • 45.Kresse G, Hafner J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B. 1993;48:13115. doi: 10.1103/PhysRevB.48.13115. [DOI] [PubMed] [Google Scholar]
  • 46.Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B. 1999;59:1758. doi: 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
  • 47.Perdew JP, Burke K, Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996;77:3865. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information (3.7MB, pdf)

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon request.

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES