The temperature dependence of the helical twist of DNA

Abstract

DNA is the carrier of all cellular genetic information and increasingly used in nanotechnology. Quantitative understanding and optimization of its functions requires precise experimental characterization and accurate modeling of DNA properties. A defining feature of DNA is its helicity. DNA unwinds with increasing temperature, even for temperatures well below the melting temperature. However, accurate quantitation of DNA unwinding under external forces and a microscopic understanding of the corresponding structural changes are currently lacking. Here we combine single-molecule magnetic tweezers measurements with atomistic molecular dynamics and coarse-grained simulations to obtain a comprehensive view of the temperature dependence of DNA twist. Experimentally, we find that DNA twist changes by ΔTw(T) = (−11.0 ± 1.2)°/(°C·kbp), independent of applied force, in the range of forces where torque-induced melting is negligible. Our atomistic simulations predict ΔTw(T) = (−11.1 ± 0.3)°/(°C·kbp), in quantitative agreement with experiments, and suggest that the untwisting of DNA with temperature is predominantly due to changes in DNA structure for defined backbone substates, while the effects of changes in substate populations are minor. Coarse-grained simulations using the oxDNA framework yield a value of ΔTw(T) = (−6.4 ± 0.2)°/(°C·kbp) in semi-quantitative agreement with experiments.

INTRODUCTION

DNA is the storage medium for genetic information in all cellular life and increasingly used as a construction material for artificially designed nanostructures. Many of the structural and mechanical properties and conformational transitions of DNA have been mapped out in a series of landmark single-molecule measurements (1–4). At the same time, significant effort has been directed at modeling DNA at various scales, from atomistic models (5–10) to more coarse-grained representations (11–20). Precise knowledge and predictive models of the structural and mechanical properties of DNA and their dependencies on solution conditions are a prerequisite for a quantitative understanding—and ultimately optimization—of its biological and technological functions.

A central property of DNA is its helicity. Famously discovered by Watson and Crick (21) with experimental input from Franklin and Wilkins (22), the helicity of DNA has been measured using a range of methods, including X-ray diffraction (23), Förster resonance energy transfer (24) and AFM/STM imaging (25) or enzyme digestion (26) and is in the range of ∼10.5 bp/turn. Measurements using circular plasmids and electrophoretic mobility have demonstrated that the overall helical twist of DNA depends on temperature, with twist decreasing with increasing temperature. Initial estimates (27) reported a change in the helical twist of ΔTw(T) = −4 to −5°/(°C·kbp); subsequent work, using the correct value for the unwinding angle per ethidium molecule (28,29) obtained −10 to −11°/(°C·kbp). Later, measurements based on electrophoretic mobility were extended up to thermophilic temperatures close to the DNA melting transition (30) and found a linear temperature dependence up to 80°C with a coefficient of −10.5°/(°C·kbp) (31). Strick et al. observed unwinding of the helix at the level of individual molecules from (fairly limited) measurements on lambda-phage DNA in magnetic tweezers (MT) (32). They found the helix to unwind by −13.4°/(°C·kbp), an effect ∼30% larger than seen in previous bulk studies.

On the simulation side, Everaers and coworkers performed a molecular dynamics (MD) study of DNA over a broad range of temperatures (33) and found an average decrease of ∼0.5° in the basepair step parameter twist in going from 0 to 77°C, which corresponds to a change in helicity of approximately −6.5°/(°C·kbp). Another MD and coarse-grained simulation study predicted roughly −4°/(°C·kbp) (34). These estimates are about half of the experimentally determined value. However, a direct comparison with experiment is complicated by the fact that the local basepair step twist is generally not identical to the overall helical twist (15,19,33,35,36). Importantly, the experimental measurements capture the relative global rotation of the two DNA ends and, therefore, a proper definition of the coordinate determined in simulations is important for a direct comparison.

Here, we use high-resolution single-molecule MT measurements to quantify the temperature dependence of the helical twist of DNA. We critically compare the experimental results to both atomistic MD and coarse-grained simulations using the oxDNA framework to provide a stringent test on current simulation protocols and to give microscopic mechanistic insight into the origin of the temperature dependence of DNA twist.

Experimentally, we determine the temperature dependence of the helical twist of DNA ΔTw(T) using a novel, custom built implementation of a temperature-controlled MT. Our setup is similar to previous implementations of temperature-controlled MT (37,38) and was optimized for simplicity of operation and implementation as well as for the ability to use the temperature control module as an optional add-on to an existing MT setup. Using this instrument, we obtained DNA rotation-extension curves (i.e. measurements of DNA tether extension vs. linking number) as a function of temperature, which allow us to determine the change in helical twist as a function of temperature in the range of 24–42°C. Our measurements are in good agreement with prior bulk studies and, in addition, show that the temperature dependent helical change is not force-dependent, in the force range where torque-induced melting is negligible and the overall twist-extension response of DNA is symmetric (i.e. for stretching forces < 1 pN).

From a microscopic point of view, one would expect no change of the ensemble-averaged twist with temperature if the associated free energy profile is harmonic and temperature-independent. However, the underlying free energy profile is a result of a large number of interatomic interactions involving not only DNA but also the surrounding water molecules and ions. In MD simulations, these interactions are captured by atomistic force fields, which are under constant development, with major updates released recently (39,40). To analyze the response of twist to temperature at atomic resolution, we performed a series of ∼μs, atomic resolution, explicit solvent MD simulations of a mixed 33 bp DNA sequence at temperatures ranging from 7°C to 47°C using the OL15 Amber force field (39). In addition, we ran control simulations using the earlier released bsc0 force field (41). We use a scheme involving coordinate frames at each end of the DNA molecule to determine the change in twist, mimicking the experimental setup. To investigate the microscopic origin of the twist temperature dependence, we use local conformational descriptors inferred from MD data for assessing various structural contributions to the overall twist change.

We complement the atomistic MD simulations with coarse-grained simulations using the oxDNA framework (42,43). Unlike atomistic models of DNA, coarse-grained models explicitly simulate only a reduced number of effective degrees of freedom, which are chosen such as to represent selected physically relevant processes in the system. While no longer allowing for the explicit representation of the full microstructure, coarse-grained models reduce the computational cost and allow access to time and length scales that currently cannot be treated in all-atom simulations. In particular, oxDNA represents DNA on the level of individual nucleotides treated as rigid bodies with three interaction sites each, coupled by physically motivated attractive and repulsive potentials. The model has been developed with a focus on the thermodynamics of double-strand denaturation and shows good agreement with the experimentally observed behavior of DNA under mechanical stress in a variety of systems (42,44–46). A combination of the atomistic and coarse-grained perspectives has proven beneficial to provide a comprehensive picture of the molecule at multiple scales, e.g. to study DNA under superhelical twist in closed circular systems (46). Our oxDNA simulations of a 600 bp DNA construct allow us to compare the atomistic and coarse-grained perspectives and, in particular, to test to what extent the observed temperature dependence of DNA twist can be captured by oxDNA.

MATERIALS AND METHODS

Magnetic tweezers measurements

Experiments on DNA were performed in a home-built magnetic tweezers setup described previously (47). For temperature-controlled measurements we supplied the setup with two heating circuits: one for objective heating and one for heating of the flow cell baseplate. We attach a single heating foil (KHLV-0502/10-P, Omega) around the objective (60×, Plan Fluorite with correction collar, NA 0.9 or 100×, Plan Fluorite, NA 0.75, Olympus) and two separate heating foils to the bottom of the baseplate (Supplementary Figure S1). We chose the material of the baseplate to be aluminum because of its good heat conductivity. The two circuits are connected in series and operate with the same power supply (HWS-50A-24/A, TDK-Lambda). Each circuit is controlled by a PID controller (CN7823, Omega) and via solid-state relays (SSRDC100VDC12, Omega). Pt100 temperature sensors (SA1-RTD, Omega), placed as indicated in Supplementary Figure S1, serve as temperature sensors in both circuits in the feedback loop (Supplementary Figure S5). We used the vendor (Omega) provided software for control and read-out. For the connection of the controller to the computer a RS485 to USB converter (USB-RS485-WE-1800-BT, FTDI Chip) was used (Supplementary Figure S5). Measurements used 7.9 and 20.6 kbp DNA constructs described previously (48,49). Specific and torsionally constrained coupling of the DNA to magnetic beads (streptavidin-coated 1.0 μm diameter MyOne; Life Technologies) and the flow cell surface was achieved through ligation with ∼600 bp PCR-generated DNA fragments, comprising multiple biotin- and digoxigenin-modified dUTP moieties (Jena Bioscience), respectively. The DNA construct was first coupled to the streptavidin-coated beads by incubating 5 ng of the DNA construct with 2 μl of MyOne beads in a final volume of 20 μl of phosphate buffered saline (PBS; Sigma-Aldrich) for 10 min. The DNA-bead solution was subsequently diluted into 100 μl PBS and introduced into the flow cell. The preparation of the flow cell and the selection of tethers are carried out as described (47). Rotation-extension measurements to determine the helical twist of DNA were performed in 1× PBS using conventional magnetic tweezers with two cubic magnets (5 × 5 × 5 mm³; W-05-N50-G, Supermagnete), oriented in a vertical configuration (50).

Molecular dynamics simulations

We used a DNA oligomer (33 bp, sequence GAGAT-GCTAA-CCCTG-ATCGC-TGATT-CCTTG-GAC), that was previously used to study DNA allostery (51,52). In the simulations we used the SCP/E water model and added 150 mM KCl salt parameterized according to Dang (53). The equilibration protocol was identical to that in reference (52). Independent trajectories of 1 μs each at 1 atm and at 280, 290, 300, 310 and 320 K (7, 17, 27, 37 and 47°C) were calculated using the Amber suite of programs and the OL15 (39) and bsc0 (41) force fields. The mass repartition scheme implemented in the pmemd module of Amber enabled us to use a time step of 4 fs (54). Mass repartition was only used for the solute with bond constraints on all bonds involving hydrogen atoms using the SHAKE algorithm (55). Mass repartition was not used for the solvent since the analytic bond constraint algorithm, SETTLE (56), used for the solvent is compatible with a 4 fs time step even with the original mass distribution. The scheme has been found to give thermodynamic and kinetic results compatible with simulations without mass repartition for several test systems (54). Conformational analysis programs 3DNA (57) and Curves+ (58), as well as in-house scripts, were used for the analysis.

Coarse-grained simulations using oxDNA

We simulated a 600 bp DNA double-strand using the oxDNA2 version of the model (43) which includes a Debye–Hückel representation of screened electrostatics, and set the monovalent ionic strength to 150 mM to match experimental conditions. OxDNA simulations were run at T = 300, 310, 320 and 340 K (27, 37, 47 and 67°C). Double-strands are set up in a homogeneously underwound state with a fixed overall twist angle. After pre-equilibration, production simulations are run for at least 2.5 μs of simulated time for each system. As in previous applications of oxDNA to similar systems (45) the overall twist of the system is kept constant by fixing the strand ends in stiff harmonic traps and preventing the double-strand from passing over its own ends. Being an implicit-solvent model, oxDNA requires addition of a noise term to Newton‘s equations of motion to ensure the appropriate representation of diffusive behavior of particles. As in previous work (45,46), this was implemented using an Andersen-like thermostat (59).

Model for the effect of local basepair melting on overall DNA twist

In the oxDNA runs, we observed delocalized and short-lived broken basepairs (see below and Supplementary Figure S14). We can estimate the effect of these short-lived defects by performing an average over the twist angles along a double-strand that has N_D denatured basepairs, out of N total basepairs. Since the single denatured basepairs are separated along the double-strand, they typically cause disruption of two consecutive twist angles (the one with their precursor and their successor). The average twist angle <α> can be estimated as follows (where α_D and α₀ are the twist angle of denatured and intact basepairs, respectively):

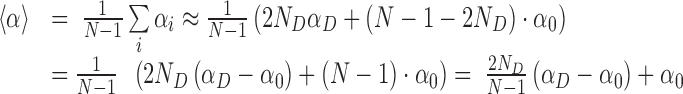(1)

We can estimate the change of <α> with temperature, assuming that α_D and α₀ remain constant and that the dominant effect is a change in N_D:

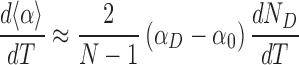(2)

The change in the number of denatured basepairs with temperature can be determined directly from simulations (Supplementary Figure S14C), giving a numerical value of 0.05 bp·°C⁻¹ in the average model. Using α_D = 0° and α₀ = 34.8°, as determined from the free-energy landscape of local twists measured from simulations (Supplementary Figure S14D), we find: d<α>/dT ≈ −5°/(°C·kbp).

RESULTS AND DISCUSSION

Temperature controlled magnetic tweezers measurements

In magnetic tweezers (MT) DNA molecules are tethered between ∼μm-sized magnetic particles and a flow cell surface (50,60,61) (Figure 1A). Magnets mounted above the flow cell enable the application of calibrated stretching forces (50,62,63) and can be used to control the twist of the DNA tether (49,60,64–66).

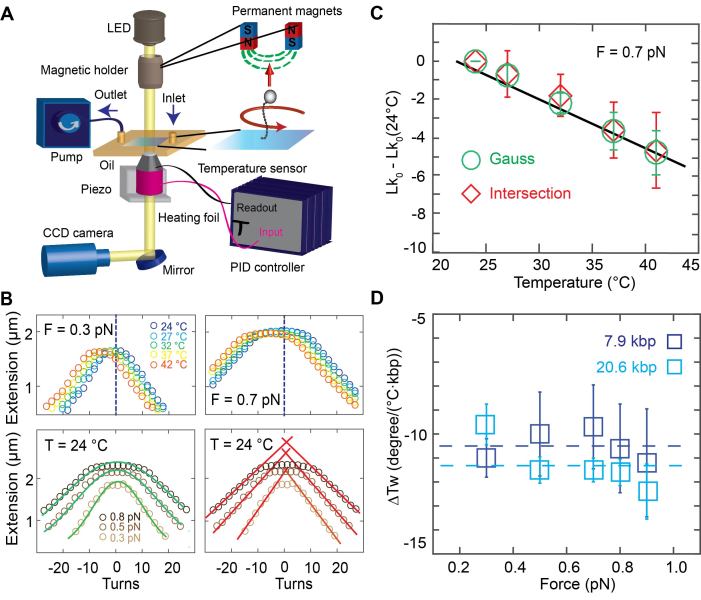
Figure 1.

Temperature controlled DNA rotation-extension measurements. (A) Schematic of the temperature controlled magnetic tweezers setup. In MT, DNA is tethered between the surface and magnetic beads in a flow cell. An inverted microscope is used to image the flow cell surface onto a CMOS camera. Monochromatic light illuminates the flow cell from top. Permanent magnets are placed on a translational and rotational motor on top of the flow cell to apply stretching forces and torsional control, respectively. A pump is used for buffer exchange. A heating foil around the objective is used to locally heat the flow cell and controlled using a PID controller. (B) Top: Rotation-extension measurements for 7.9 kbp DNA at 0.3 pN (top left) and 0.7 pN (top right) and different temperatures. The center of the extension vs. turns curve shifts to negative turns with increasing temperature. Bottom: Illustration of the approaches to determining the centers of the rotation curves. Gaussian fits (green lines) to the extension vs. applied turns data at F = 0.3, 0.5 and 0.8 pN. The center of the Gaussian function of each curve is used to determine the center of the curves along the turn axis (bottom left). Linear fits (red) to the plectonemic regime of the rotation-extension curves at positive and negative applied turns. Here the intersection of the linear fits is used to determine the center (bottom right). (C) Changes in the DNA linking number with temperature are determined from the shift of the centers of the rotation curves. Data shown here are for 7.9 kbp DNA at 0.7 pN; symbols and error bars are the mean and standard deviation from seven molecules. ΔTw(T) is determined from the fitted slope. (D) Temperature dependence of the helical twist ΔTw(T) as a function of applied force. Data are for 7.9 kbp DNA (dark blue) and 20.6 kbp DNA (light blue), repectively. Symbols and error bars are the mean and standard error of the mean from at least seven individual molecules for each measured force and DNA length. The change in helical twist does not depend on force, within error, as both data sets are consistent with a force-independent ΔTw(T) (dashed lines; reduced χ² = 0.04 for the 7.9 kbp DNA with ΔTw(T) = (−10.5 ± 0.6)°/(°C·kbp); reduced χ² = 0.24 for the 20.6 kbp DNA with ΔTw(T) = (−11.5 ± 1.0)°/(°C·kbp).

To control the temperature of the flow cell environment, we mounted resistive heating foils and thermocouple temperature sensors to both the metal baseplate of the flow cell holder and around the objective (Supplementary Figure S1). We tested three options for temperature control: only objective heating, only baseplate heating, and the combination, objective and baseplate heating in parallel. In all cases the current through the heating foils was controlled with a PID controller that enabled independent control of the objective and baseplate heating circuits. Using a custom-made flow cell with temperature sensors inserted at the approximate position of the field of view of the microscope and at the flow cell periphery, we found that objective heating is sufficient to reliably heat the system locally (Supplementary Figures S1 and S2), but leaves the temperature at the edges of the flow cell (far away from the objective) almost unaffected. Conversely, we found that if only the baseplate was heated, the temperature at the position of the objective was almost unaffected (Supplementary Figure S1). For applications where it is sufficient to temperature control the local environment in the observation volume of the MT measurement, we found that objective heating alone is sufficient. In particular, using objective heating only, the feedback sensor located at the objective, a temperature sensor inserted into the immersion oil between objective and flow cell surface, and a sensor in the observation volume within the flow cell all gave consistent temperatures (<0.5°C deviation; Supplementary Figure S2). Use of objective heating only has the advantage of requiring only one simple heating circuit that can readily be added to existing MT setups. Using this approach, we control the temperature in the local flow cell environment from room temperature to 42°C (which is the maximum recommended temperature for the objective used by the vendor's specifications), achieving constant temperatures over long periods of time (> hours). The heating circuit is fast and reaches the adjusted temperature in ∼1 min. However, in order to have constant temperatures from the beginning of the measurement, it is recommended to let the system equilibrate for 15–20 min. We observed that the expansion of the brass objective upon heating leads to a systematic change in the vertical position of plastic beads unspecifically attached to the flow cell surface that was monitored using the standard MT position tracking procedures. The observed expansion was consistent, within experimental error, with the thermal expansion coefficient of brass (Supplementary Figure S3). We note that even though we used a separate temperature sensor on the objective for feedback in all measurements reported here, in principle the tracked position of fixed reference beads could be used for temperature feedback, if it is desirable to simplify the temperature control circuitry even further.

Experimental determination of the temperature-dependence of DNA twist

Using our custom-made temperature controlled (Supplementary Figure S4) MT set up, we recorded rotation-extension curves for 7.9 kbp (Figure 1B) and 20.6 kbp DNA (Supplementary Figure S5) constructs attached to the flow cell surface via multiple digoxigenin–antidigoxigenin labels and to 1.0 μm-diameter magnetic MyOne beads via multiple biotin-streptavidin linkages. We recorded traces in the force range from 0.3 to 0.9 pN and the temperature range from 24 to 42°C. The rotation-extension curves shift systematically along the turn-axis to a negative number of turns with increasing temperature (Figure 1B).

To systematically quantify the shifts in the rotation-extension curves, we used two different approaches to determining the centers of the rotation curves (Figure 1B, bottom), which corresponds to Lk₀, i.e. the point where the DNA molecule is torsionally relaxed. One approach is to fit a Gaussian to the extension vs. applied turns data and to use its center position as Lk₀ (Figure 1B, bottom left). A second approach is to perform line fits to the regions where the tether length decreases linearly with the applied number of turns, i.e. the plectonemic regions of the rotation-extension curves, and to then determine the intersection points of the fitted lines as Lk₀ (Figure 1B, bottom right). While both methods gave identical results (Figure 1C), within experimental error, we found the approach of fitting a Gaussian to be more robust, since it does not require setting a fitting range, and we used the Gaussian fits in the subsequent analyses.

The change in Lk₀ determined from rotation-extension curves with temperature is linear (Figure 1C). Averaging over all forces, we find a change in DNA helical twist of ΔTw(T) = (−10.5 ± 0.6)°/(°C·kbp) for the 7.9 kbp DNA construct and ΔTw(T) = (−11.5 ± 1.0)°/(°C·kbp) for the 20.6 kbp construct, where we have reported the mean and standard error of the mean determined from nine and seven individual molecules, respectively. In the range studied (0.3–0.9 pN), we do not see any statistically significant force dependence of ΔTw(T), for neither of the two DNA constructs. In particular, if we only include the three lowest forces (0.3, 0.5, 0.7 pN) in the analysis, we find ΔTw(T) = −10.2 ± 0.7 and −10.9 ± 1.1°/°C·kbp for the 7.9 and 20.6 kbp DNA data, respectively, which is within experimental error of the values obtained from the entire force range.

We note that it is straightforward to apply larger forces in the MT; however, at forces ≥1 pN the rotation-extension behavior becomes pronouncedly asymmetric, due to torque-induced melting of DNA upon underwinding (32,67), which precludes the determination of the curves’ centers as outlined in Figure 1B. Here, we limit our measurements to the force range where the rotation-extension response remains approximately symmetric, under the conditions of our measurement (pH 7.4, ∼150 mM monovalent salt; Supplementary Figures S6 and S7). At lower ionic strength, more extreme pH conditions, or even higher temperatures than used in this study rotation-extension curves become asymmetric (37,68,69) even at forces of ≤0.9 pN. In fact, we observe some slight asymmetry in the curves at 0.9 pN for the 20.6 kbp DNA construct, likely due to its lower GC content compared to the 7.9 kbp DNA (45% versus 55%, respectively), however, the effect is small enough to not preclude our analysis to determine the center of the extension-rotation curves (Supplementary Figure S6).

Our results for the overall value of ΔTw(T) for the two DNA constructs investigated are in agreement, within experimental error, with one another and with previous bulk measurements. Nonetheless, we find that the change in the helical twist for our 20.6 kbp DNA construct is ∼10% larger compared to the 7.9 kbp construct. This small difference might be due to the difference in GC content of the constructs—the 7.9 kbp DNA consists of 55% GC, while the 20.6 kbp DNA has 45% GC—or due to other sources of experimental variability.

Molecular dynamics simulations of temperature-dependent changes of DNA twist

Our ability to accurately measure the overall change in DNA helical twist with temperature provides a sensitive test for current MD force fields for nucleic acids. Conversely, atomistic MD simulations have the potential to provide microscopic mechanistic insights into the change in twist of DNA with temperature. We performed atomic-resolution MD simulations of a 33 bp mixed DNA sequence with explicit inclusion of water molecules and ions at five different temperatures ranging from 7 to 47°C (Materials and Methods). No restraints (in particular, no pulling force) were applied on the DNA molecule. The newly released OL15 force field (39) was used to model DNA interatomic interactions. Simulations were run for 1 μs at each temperature and snapshots were recorded every 10 ps.

To compare the MD results to experimental data, we extracted the DNA end-to-end twist in a way that closely mimics the experimental measurements. Two coordinate frames were assigned to the ends of the DNA molecule (Figure 2A) that were defined as follows: First, for the three penultimate basepairs at each end (basepairs 2–4 for R₁ and 30–32 for R₂, Figure 2A, within the contours marked in red) the standard base-fixed coordinate frames (70) were computed and subsequently averaged using the quaternion averaging introduced in reference (71). Second, each mean frame was projected onto the mean helical axis, computed as the average of the helical axes assigned to the three pairs by the 3DNA conformational analysis program (57). Third, the end-to-end twist between the two frames R₁ and R₂ was computed, using a definition exactly analogous to the local basepair step twist employed in 3DNA. In this ‘mean plane’ definition the twist is the rotation in the plane normal to the mean of the Z-axis of R₁ and R₂. The mean plane definition has the property that twist differences are invariant with respect to the initial constant rotation offset of the frames about their Z-axis (see Supplementary Information). This definition corresponds to the experimental setup where the initial rotational setting of the beads is also not known.

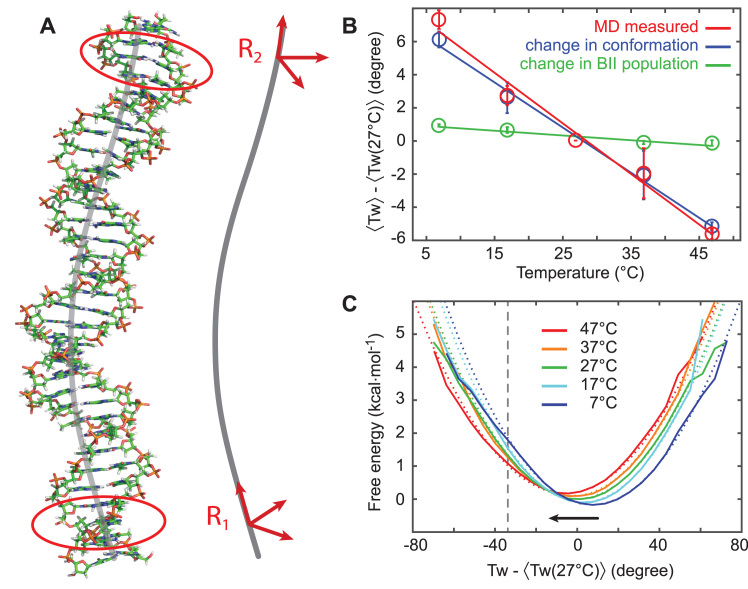
Figure 2.

Determination of DNA twist from atomistic MD simulations. Results from atomic-resolution unrestrained molecular dynamics (MD) simulations of a 33 bp DNA oligomer at different temperatures. (A) Snapshot of the DNA structure from a MD simulation and definition of the right-handed orthonormal frames that were attached to the oligomer ends, mimicking the experimental setup. Base-fixed frames in three pairs close to the ends (marked by red contours) were averaged and then projected onto the helical axis (gray), yielding the end frames R₁ and R₂. (B) End-to-end twist between R₁ and R₂ as a function of temperature (red circles). Symbols are the average over the entire trajectory, error bars are estimated by repeating the analysis for the first and the second halves of the trajectories and calculating mean difference between these values and the value for the entire trajectory. The resulting twist temperature slope (red line) for the OL15 Amber force field is (−11.1 ± 0.3)°/(°C·kbp). We decompose the change in twist as a superposition of the change in populations of the BI/BII backbone substates and the conformational change of the individual substates. It is seen that the change in BI/BII substate populations, with substate conformations taken constant (green) contributes only very weakly, whereas the conformational change of the individual substates (blue) almost account for the total observed change. (C) Twist free energy landscapes computed from the Boltzmann inversion (solid lines) and harmonic fits with the same mean and variance (dotted lines). The potentials are overall harmonic, with a slight anharmonicity for undertwisting at low temperatures (to the left of the indicated grey, vertical line). All twist values are plotted relative to the mean twist at 27°C.

The end-to-end twist was analyzed for each of the snapshots of the MD trajectory at all simulated temperatures (Figure 2B, data in red). We find the twist to decrease almost linearly in the range of 7–47°C. The least-squares fitted linear dependence gives ΔTw(T) = (−11.1 ± 0.3)°/(°C·kbp), in excellent quantitative agreement with experimental values. The underlying end-to-end twist free energy landscapes computed by the Boltzmann inversion of the probability distributions (Figure 2C) are nearly harmonic, with slight anharmonicities only for undertwisting at low temperatures (roughly starting from a 37° undertwist at 7 and 17°C, marked by a vertical line in Figure 2C).

Employing identical simulation protocols and twist definitions, we also performed simulations with the earlier bsc0 Amber force field (41). Once again, the twist decreases almost linearly with temperature and the underlying free energy profiles are nearly harmonic. However, the slope is (−7.5 ± 1.7)°/(°C·kbp), which deviates significantly from the experimental value and from the MD simulations with the OL15 force field. The simulated oligomer using bsc0 suffers from numerous basepair breaks and transient non-canonical states of the glycosidic angle χ near the oligomer ends. Filtering out these contaminated snapshots changes the twist temperature dependence slope only weakly, indicating the slope to be an intrinsic property of the bsc0 parameter set and not an end effect. Thus, the OL15 force field captures the temperature dependence of twist better than the earlier bsc0 force field.

We performed control calculations to test whether the definition of twist angle had an influence on the results. Three alternative definitions of twist were analyzed. One approach is to define the end frames R₁ and R₂ as above but to compute the end-to-end twist using the axis-angle rotation parameters, used e.g. in the conformational analysis program Curves+ (58). In this ‘axis-angle’ approach, the relative rotation from R₁ to R₂ is parameterized by a vector whose length is equal to the rotation angle and whose direction is that of the rotation axis. The twist is defined as the third component of the vector in any of the two frames R₁ or R₂. Two additional approaches to computing the twist are based on summing individual contributions along the helix. These approaches computed the total twist either as the sum of local twists or as the sum of helical twists along the oligomer (between basepairs 3 and 31). The local basepair step twist is a parameter of the rotation connecting two successive basepairs, irrespective of the helical axis. The helical twist, in contrast, describes the rotation with respect to the helical axis. While the two are often similar in DNA, they are different in e.g. the A-RNA helix where the bases are inclined with respect to the helical axis (70).

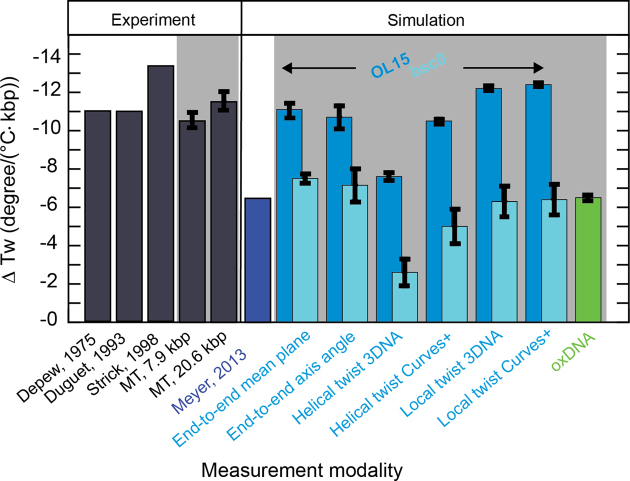
The results are summarized in Figure 4 (and Supplementary Table S1). Since the axis-angle twist is not invariant with respect to the rotation offset, the computed values for ΔTw(T) vary with the initial rotational setting and a range of values is reported (Supplementary Table S1). For each force field, we find that the range of values for ΔTw(T) from the axis-angle definition overlaps with the value determined using the mean-plane definition. Summing the local or helical twists yield similar, though not identical, slopes compared to the end-to-end twist definitions. The only exception is the sum of the helical twists using the 3DNA definition that give consistently smaller slopes, for both force fields. Independent of the definition of twist, the bsc0 force field consistently finds slopes that are too small, by about a factor of two, compared to both the OL15 force field and the experimental data. The temperature dependence of the DNA twist of −6.5°/(°C·kbp) deduced by Everaers et al. (33) is very close to the values that we find using the same bsc0 force field.

Figure 4.

Values for the change of DNA twist with temperature ΔTw(T) from measurements and simulations. Dark gray bars indicate values obtained from experiments. Indicated with the light grey background are values that were obtained as part of this work. Blue colors refer to data from all-atom MD simulations. Lighter blue colors represent data generated in this work with the OL15 and bsc0 force fields, respectively. Green represents the value gained by coarse-grained oxDNA simulations within this work.

In summary, the mean-plane end-to-end twist has the advantages (i) that it closely mimics the experimental situation and (ii) that it does not depend on the rotation offset. We note that the end-to-end twist does not depend on the local twists only, but also on local bending coordinates roll and tilt (see below), which are in general not zero.

Microscopic model for the change in twist from MD simulations

To obtain insight into the microscopic mechanism for the observed temperature dependence of DNA twist, we first explore the possibility of local melting, i.e. breaking of the Watson–Crick basepairs. We consider a pair to be broken if at least one hydrogen bond is broken, defined by a donor-acceptor heavy atom-distance >4 Å. The populations of the broken pairs are illustrated in Figure 5. We note that the amount of melting observed in the MD simulations is in agreement with the values found in oxDNA simulations (see below). However, the molten basepairs in the MD simulations do not have a significant effect on the overall change in twist with temperature (Supplementary Figure S8). This indicates that local melting is not the main mechanism for the temperature dependence of DNA twist in MD simulations. This may be due to the rather small perturbation of the local basepair step geometry upon melting (Supplementary Figure S9). In particular, the mean values of the local twist of steps containing a broken pair are similar to unbroken basepairs; only the variance of twist values significantly increases upon basepair breaking in the MD simulations (Supplementary Figure S9). The mean value of the local twist for broken basepairs is still 33.5° for OL15 and 31.5° for bsc0, with standard deviations increasing from ca. 6° at 7°C to 9° at 47°C for both force fields. Broken pairs are typically slightly open towards the major groove and induce only moderate structural changes to the basepair steps in which they are involved (Supplementary Figure S9).

Figure 5.

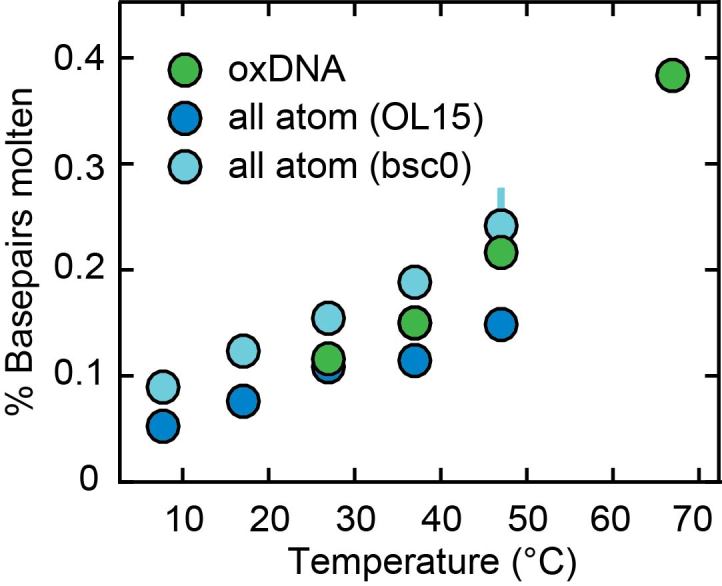
Fraction of broken basepairs as a function of temperature. In the all-atom molecular dynamics calculations with the OL15 (dark blue circles) and bsc0 (light blue circles) force fields, the two basepairs at each end of the oligomer were excluded from the analysis and broken pairs are defined as pairs where at least one hydrogen bond donor-acceptor distance exceeds 4 Å. In oxDNA (green circles) broken pairs are defined as basepairs where the interaction energy is less than 15% of the value for a fully formed pair. Errors (from splitting the trajectory in half) are smaller than symbols for most points.

Another potential mechanism for the temperature dependence of DNA twist might be related to the flips of the backbone angles γ from their canonical g+ to t conformation. These flips are rare and reversible in MD using modern force fields (39–41), but are associated with very low local twist and may therefore play a role. However, excluding the snapshots with at least one γ flipped does not change the twist temperature slope in any significant way (Supplementary Figure S8).

Thus, other conformational changes must be operative in MD. The end-to-end twist depends on the end frames, which, in turn, are functions of the orientation of the individual bases. To simplify the analysis, we first replace the end frames associated with the base groups (bases within red contours in Figure 2A) by a single basepair frame (computed by 3DNA) in the middle of the group, i.e. basepair 3 for R₁ and basepair 31 for R₂. Thus, we omit both base frame averaging in the group and the helical axis projection. This approach is motivated by the fact that the base pairing remains stable and the basepair normals nearly coincide with the helical axis (in contrast to the A-RNA helix where the basepairs would be inclined with respect to the helical axis). The validity of the approximation is not a priori clear, since the effect is subtle and a proper treatment of other DNA features does require the projection of basepair frames onto the helix axis (15). However, the computed slope, (−10.7 ± 0.2)°/(°C·kbp), is very close to the original one, which justifies the simplified approach.

In this approximation, the end frames can be easily expressed in terms of the local rotational coordinates. Assuming an oligomer of N basepair steps between R₁ and R₂, we have

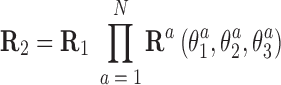(3)

where columns of the matrices R₁, R₂ are coordinates of the unit vectors of the frames R₁, R₂ in the lab frame and 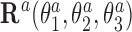is the matrix of relative rotation connecting the two successive basepair frames in step a, parameterized by the local rotational coordinates of step a (local tilt, local roll and local twist, respectively). We use the parameterization of the relative rotation defined in 3DNA. Assuming that the orientation of the oligomer in space plays no role, we can choose the frame R₁ to coincide with the lab frame and therefore 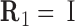, the identity matrix. Thus, the end-to-end twist ω can be expressed as a function of the local coordinates,

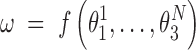(4)

The local coordinates span just a small domain of the conformational space - the maximum standard deviations of the local roll, tilt and twist are 5.5°, 7.6° and 8.4°, respectively. Thus, the function f can plausibly be linearized in that domain and, in this approximation the ensemble average of ω at temperature T is given by

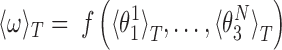(5)

The local coordinates may depend on temperature through various mechanisms. One obvious possibility is related to the DNA backbone substates BI (defined by the torsion angles ϵ and ζ as ϵ-ζ < 0), and BII (ϵ-ζ > 0). We observe no other significant backbone substates in our simulations. A lot of research effort has been devoted to decipher the dependence of DNA structure on BI/BII substates (see for instance (72,73)). In particular, it has been discovered that the conformation of a given step depends not only on the BI/BII backbone states within that step but also on the states of neighboring backbone fragments. The influence of the 3′ flanking backbone states, first observed for the CG steps in MD of a Dickerson-Drew dodecamer (74) was later generalized to all pyrimidine-purine (YR) steps (8). A recent comprehensive MD study of DNA oligomers containing all tetranucleotide sequences (10) identified the influence of the 5′ neighboring backbone fragments as well. Thus, the conformation of a given step depends on six backbone fragments, two inside the step, two at its 3′ side and two at its 5′ side. Since each fragment can be in one of two substates (BI or BII), we have 64 substates to consider for every step. As temperature changes, the populations of these 64 substates also change, implying a change of the step conformation. The differences in conformation between the substates can be quite significant—local twist may differ by several degrees (10). The resulting change, however, is far from obvious as, for instance, the inner and the 5′ outer BII states increase, whereas the 3′ outer BII states decrease local twist (10).

In addition to changes in the backbone substate populations with temperature, the step conformation for a fixed substate can also be temperature dependent. To investigate these two effects separately, we write the ensemble average of the coordinate 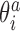at temperature T as

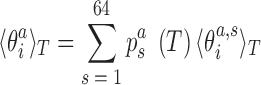(6)

where 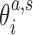are coordinates associated with step a and substate s, and 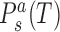are the substate populations as functions of temperature. Introducing the differences

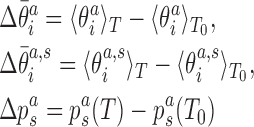(7)

with respect to values at a reference temperature T₀ (we choose T₀ = 27°C), Equation (6) can be rewritten as

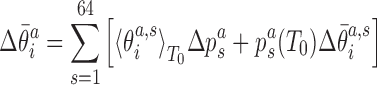(8)

where we have neglected the second order terms in the differences. Thus, the change of the local coordinates is decomposed into two contributions: the change due to the temperature dependence of the substate populations assuming constant substate conformations (the first term in the sum in Equation 8) and the change of the substate conformations assuming constant populations (the second term in the sum in Equation 8). Replacing the ensemble averages by averages over the simulated MD trajectories, we substitute the values from Equations (7) and (8) into Equation (5) to predict the temperature change of the end-to-end twist from the changes of local coordinates.

If both terms in Equation (8) are included, the predicted ΔTw(T) is (−10.8 ± 0.2)°/(°C·kbp), very close to the slope obtained by directly monitoring the end-to-end twist (−11.1 ± 0.3°/(°C·kbp), red data in Figure 2B). Keeping just the first term in Equation (8) implies a model in which the temperature change of the end-to-end twist is exclusively due to change in populations of the BI/BII backbone substates. However, the results show that this model predicts almost no change of the twist with temperature at all (Figure 2B, green), its slope being just (−1.0 ± 0.1)°/(°C·kbp). In contrast, keeping just the second term in Equation (8) implies a model in which the change of end-to-end twist takes place exclusively due to temperature changes in conformation of the individual backbone substates. This second model gives ΔTw(T) = (−9.7 ± 0.1)°/(°C·kbp), suggesting that it is the conformational change of the individual BI/BII backbone substates that is largely responsible for the observed temperature dependence of DNA twist, while the changes in substate populations with temperature play only a minor role.

Sequence- and length dependence of twist changes with temperature

The quantitative agreement between the experimentally measured twist temperature change and the result from atomistic MD simulations is encouraging. Nonetheless, our simulation used a 33 bp DNA segment, significantly shorter than what was used experimentally. In addition, while the simulated 33 bp DNA sequence has a mixed sequence composition and is expected to reasonably approximate sequence-averaged behavior, the role of sequence dependence on the observed effects could be explored in more detail. A more comprehensive exploration of the length- and sequence space is currently beyond the reach of atomistic MD. The sequence examined is already long for all-atom MD standards: for instance, recent extensive simulation studies used sequences 18 bp (8) or 22 bp (10) long. We note that the number of solvent molecules involved in the simulation increases roughly with the third power of the sequence length. Thus, a substantial elongation of the studied sequence (to be simulated at several different temperatures) would be prohibitively expensive, let alone involving multiple such sequences. To get at least a partial insight into the sequence dependence, we examined various subsequences of the given sequence. The results are shown in Supplementary Figure S10. Subsequences of 11 bp (roughly one helical turn) span a range of ΔTw(T) between −9 and −13.5°/(°C·kbp), in reasonable agreement with the experimental values. Twist changes determined from any of the subsequences of at least 21 bp (two helical turns) already agree with experiment, within experimental error (Supplementary Figure S10), suggesting that the results from our MD simulations converge relatively rapidly to sequence averaged values.

Coarse-grained simulations of DNA with oxDNA

To complement the atomistic MD simulations, we performed coarse-grained simulations using oxDNA. An advantage of coarse-graining is that much longer DNA molecules can be simulated than is currently possible using atomistic representations. We note that there are other coarse-graining schemes, such as the 3SPN.2 model (18), but their systematic exploration is beyond the scope of this study. We performed simulations for several 600 bp DNA systems, ∼20-fold larger than the MD simulations and approaching the DNA lengths used in MT. Simulations were run at various levels of twist and subject to a constant pulling force of 0.7 pN at 27, 37, 47 and 67°C using the oxDNA average parameterization, which uses one set of parameters for all basepairs (Figure 3). Control calculations using the sequence-dependent parameterization of oxDNA on 600 bp systems with random sequences of a GC content of 45 and 55 percent gave essentially identical results, within error (Supplementary Figure S11).

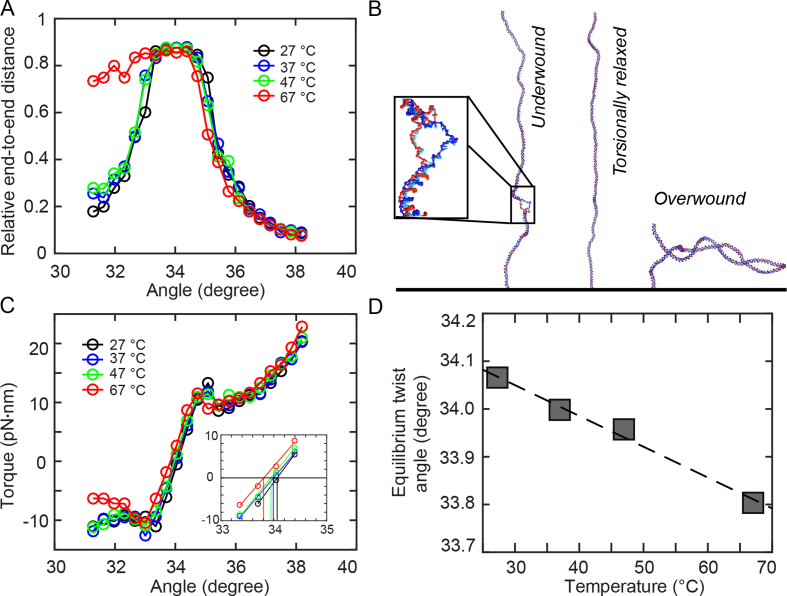
Figure 3.

Coarse-grained oxDNA simulations. Results from coarse-grained oxDNA simulations of a 600 bp double-stranded DNA system in the average-base parametrization at 150 mM monovalent salt. A stretching force F = 0.71 pN was used in all simulations. (A) Extension vs. imposed mean twist angle for 27, 37, 47 and 67°C. Note that for 67°C, denaturation bubble formation occurs in the undertwisted system (angles ≤ 33°), leading to asymmetric curves. (B) Molecular conformations observed in oxDNA simulations at T = 67°C for an angle of 31.6°, showing a denaturation bubble (left), 34.0°, showing an extended double-strand (center) and 37.2°, showing a plectoneme (right). For the 31.6° snapshot, a closeup of the 23-bp denaturation bubble is shown in the inset. (C) Torque response at different temperatures, showing a linear regime close to the equilibrium angle, followed by an overshoot and a post-buckling torque which increases more slowly upon further twisting. The inset shows a zoom of the data with the interpolation in the linear torque-regime and determination of the equilibrium angle corresponding to zero torque. (D) Equilibrium twist angles for the different temperatures determined by linear interpolation of the torque response shown in C to zero torque. The black line indicates a linear fit of temperature dependence, yielding ΔTw(T) = −6.5°/(°C·kbp).

oxDNA reproduces the rotation-extension response of double-stranded DNA under twist and tension (Figure 3A and Supplementary Figure S12). A direct comparison to the experimental curves for F = 0.7 pN and 37°C shows good agreement of extensional behavior (Supplementary Figure S12). For 67°C, we observe an asymmetric extension curve, indicating thermally aided melting upon underwinding, similar to previous experimental results (37). Representative structures from oxDNA simulations in the linear, plectonemic and partially denatured states are shown in Figure 3B.

The torque response of the simulated system as a function of the average twist angle per basepair step shows a linear torque response for small deviations from equilibrium twist (Figure 3C). Upon further over- or underwinding, the system exhibits a torque overshoot at the point where the DNA buckles to form plectonemes, similar to experimental observations (75–77) and a post-buckling state for which the torque increases more slowly upon further twisting (Figure 3C). Unlike for larger molecules usually used in experiments, the post-buckling torque is not strictly constant in the simulations due to a finite size effect: for high twist, the plectoneme takes up almost the entire simulated 600 bp double-strand. In this situation, further twist can only be absorbed by tighter winding of the end loop, leading to a small but nonzero torque response in the plectonemic regime. Control simulations with shorter (300 bp) and longer (1200 bp) simulated DNA chains show that finite size effects in the post-buckling regime decrease with increasing DNA lengths, as expected (Supplementary Figure S13).

We observe an overall shift of the torque response to induced twist to smaller angles upon heating, indicating a decrease of the average twist angle per basepair with increasing temperature. As described in previous work (45), extension curves of the 600 bp simulated system exhibit larger finite size effects compared to the experimental system, making it difficult to determine the zero-twist state by directly fitting to the extension curve as done for experimental data. Hence, we determined the mean twist angle of the torsionally relaxed state directly from the torque response by interpolating the linear part of the torque response curve to determine the angle corresponding to zero torque (Figure 3C, inset). Control calculations with longer and shorter DNA chains suggest that the linear torque response regime is independent of the simulated DNA length and not affected by finite size effects (Supplementary Figure S13). The mean twist angle for zero torque decreases as a function of temperature (Figure 3D). A linear fit of the temperature dependence yields a change of (−6.4 ± 0.2)°/(°C·kbp), which is smaller than the experimentally determined value, but still relatively close to the experimental results, in particular for the 7.9 kbp DNA measurements. Various approximations are inherent in the coarse-graining approach of oxDNA, concerning both the molecule structure and the representation of physical interactions experienced by the molecule. Given these simplifications, the value obtained with oxDNA is in fair agreement with the experimental findings and at the level of deviations observed for the different atomistic force fields (bsc0 and OL15, Figure 4).

Delocalized melting of basepairs in oxDNA simulations

Given the encouraging, semi-quantitative agreement between the temperature dependence of DNA twist predicted by oxDNA with the experimentally determined value, we again analyzed the simulated conformations to gain a mechanistic understanding of the observed trend. As in previous applications of the oxDNA framework (45), we defined basepairs to be formed when their hydrogen-bonding interaction energy dropped below −4.13·10⁻²¹ J (equal to k_BT at T = 300 K), corresponding to ∼15% of the value for a fully formed bond. We observe intermittent, short-lived opening of basepairs in the double-strand due to thermal fluctuations, which do not, however, lead to stable formation of denaturation bubbles (Supplementary Figure S14). Depending on temperature we find on average between 0.6 basepair breaks at 27°C up to 2.2 at 67°C for the torsionally relaxed 600 bp system (Figure 5). In order to determine if the decrease of the mean twist angle with temperature observed in simulations is due to the local basepair melting, we developed a simple model to calculate the effect of denaturing single basepairs on the average twist angle (‘Model for the effect of local basepair melting on overall DNA twist’ in Materials and Methods) and apply it to systems which are almost torsionally relaxed at the different simulated temperatures. Using the simulation data, our model predicts a twist angle decrease from delocalized basepair denaturation alone of −5°/(°C·kbp). This value is close to the total twist change with temperature observed in the oxDNA simulations; these findings suggest that in the oxDNA simulations, the overall unwinding of the DNA helix with increasing temperature can almost be entirely attributed to delocalized and short-lived basepair melting.

CONCLUSIONS

We have presented a new, operationally straightforward implementation of temperature-controlled MT and used the instrument to determine the change in DNA twist with temperature ΔTw(T). We find ΔTw(T) to be independent of force, in the force range that avoids torque-induced melting, and to be independent of GC content, within experimental error. Averaging over all MT data, we obtain a value of ΔTw(T) = (−11.0 ± 1.2)°/(°C·kbp). Atomistic MD simulations find ΔTw(T) values in excellent quantitative agreement with experiments (Figure 4). To determine accurate values for ΔTw(T) from MD simulations, care must be taken to properly define the end-to-end twist, as opposed to simply summing the individual basepair step twist values, which tends to yield smaller values for ΔTw(T). In addition, we found that the OL15 force field yields significantly more accurate results compared to the older bsc0 parameter set (Figure 4). The excellent agreement between MD simulations and experiments found in this work suggests that current nucleic acids force fields and simulations protocols are sufficiently advanced to predict even subtle features of DNA structure.

Coarse-grained simulations using the oxDNA framework yield values of ΔTw(T) that are smaller, but still reasonably close to experimental results. This level of agreement is encouraging, in principle, given the considerable approximations inherent in the coarse-grained framework and the fact that oxDNA was primarily parameterized to capture the thermodynamics of double-strand formation.

Both the atomistic and coarse-grained simulations enable us to suggest microscopic mechanisms of twist temperature dependence. Extensive analysis of our all-atom MD data suggests that the resulting twist change is predominantly due to temperature dependence of structures associated with individual BI/BII backbone conformational substates. In contrast, temperature-dependent changes in the populations of the substates play a minor role in the MD simulations.

While both all-atom MD and oxDNA simulations predict a similar fraction of molten basepairs (Figure 5), the two simulation methods differ markedly in how much molten basepairs affect the temperature-dependent change in twist. Analysis of the all-atom MD simulations shows that local basepair melting does not significantly contribute to the temperature-dependence of DNA twist, since molten pairs—defined by a loss of at least one of the hydrogen bonds—have twist values that are close to (within 5%) the values for intact basepairs (Supplementary Figure S9). In contrast, broken basepairs in the oxDNA framework—defined by a loss of interaction energy between bases—have close to zero twist (corresponding to the secondary minimum in Supplementary Figure S14). The large decrease in twist upon basepair melting in the oxDNA simulations accounts for most of the overall predicted change in twist in the model (see ‘Model for the effect of local basepair melting on overall DNA twist’ in Materials and Methods). As the magnitude of ΔTw(T) predicted by oxDNA is still smaller than what is observed experimentally and in atomistic simulations using the OL15 force field and since the microscopic interaction potentials are significantly simplified in oxDNA, the oxDNA results for the microscopic origin of twist temperature dependence may be less realistic. At least in part, the reasonable agreement achieved by oxDNA may be due to a fortuitous cancellation of error, where the twist change upon basepair breaking is overestimated, while the change in intact basepairs is underestimated. We note that it can be hard to interpret the microstructures in oxDNA and/or to map the microstructures in oxDNA to atomistic structures, due to the top-down coarse graining approach inherent in oxDNA, which is optimized to preserve thermodynamics and not microstructures (78). It will be interesting to see to what extent other coarse-graining schemes are able to provide a more accurate description, while remaining computationally tractable.

In summary, experimental values for ΔTw(T) provide a stringent test on DNA simulation protocols that will be useful in testing other coarse-graining schemes and atomistic force-fields in the future. While being a relatively subtle effect, even small changes in DNA twist can play important roles, for example for the pitch and curvature of higher-order DNA origami structures (79–81). In addition, the delocalized and temporary basepair breaks revealed by the simulations might well serve as important nucleation points for proteins binding to DNA or for conformational transitions of the DNA helix.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

German Research Foundation (DFG) through Sonderforschungbereich [SFB 863 to J.L. and M.Z.]; Grant Agency of the Czech Republic [17-14683S to T.D. and F.L.]. Funding for open access charge: Deutsche Forschungsgemeinschaft.

Conflict of interest statement. None declared.