Skip to main content
PMC home page
Proceedings of the Royal Society B: Biological Sciences logoLink to Proceedings of the Royal Society B: Biological Sciences
. 2018 Aug 29;285(1885):20181273. doi: 10.1098/rspb.2018.1273

Species diversity rises exponentially with the number of available resources in a multi-trait competition model

Andres Laan 1,✉, Gonzalo G de Polavieja 1,✉
PMCID: PMC6125918  PMID: 30158308

Abstract

Theoretical studies of ecosystem models have generally concluded that large numbers of species will not stably coexist if the species are all competing for the same limited set of resources. Here, we describe a simple multi-trait model of competition where the presence of N resources will lead to the stable coexistence of up to 2N species. Our model also predicts that the long-term dynamics of the population will lie on a neutral attractor hyperplane. When the population shifts within the hyperplane, its dynamics will behave neutrally, while shifts which occur perpendicular to the hyperplane will be subject to restoring forces. This provides a potential explanation of why complex ecosystems might exhibit both niche-like and neutral responses to perturbations. Like the neutral theory of biodiversity, our model generates good fits to species abundance distributions in several datasets but does so without needing to evoke inter-generational stochastic effects, continuous species creation or immigration dynamics. Additionally, our model is able to explain species abundance correlations between independent but similar ecosystems separated by more than 1400 km inside the Amazonian forests.

Keywords: coexistence, neutral theory, multi-trait competition

1. Introduction

Understanding species coexistence has been a long-standing problem in ecological research. Early models of species competition struggled to explain how large numbers of species could stably coexist. MacArthur and Levins showed that, in pure resource competition models, the number of coexisting species will generally not exceed the number of limiting resources in the environment [1]. Likewise, in 1970 Robert May considered more complex competition models, where species could also have direct effects on each other's dynamics, and found that stable coexistence would not occur unless species become increasingly decoupled from one another as species diversity increased [2] (decoupled species populations change over time as if they were non-interacting). The theoretical difficulties in explaining coexistence stand in stark contrast to what we observe in nature. Even in apparently featureless environments like the surface water of the ocean, hundreds of plankton species are known to stably coexist [3]. The same conclusion emerges from studies of more complex systems like tropical forests, where more than 200 different species of trees can be found in a single hectare-sized plot [4].

Over the past decade, models have started to emerge which are able to explain coexistence in complex ecosystems if species interactions are constrained to have a certain structure. For example, Posfai et al. recently described a chemostat model in which constraint structure imposed by cellular trade-offs facilitated coexistence of a large number of species even in homogeneous and resource-poor environments [5]. A very different model of competition for growth space in trees also leads to stable coexistence of species [6,7]. Here, coexistence originates from the model's zero-sum intransitive competition dynamics and it requires higher order interactions to be robustly stable. Despite recent progress, the problem of large-scale species coexistence has not yet been solved in general. Both the chemostat model and the zero-sum growth space competition model rely on rather specific assumptions about underlying competition dynamics. These dynamics are unlikely to be equally applicable to all known diverse ecosystems and some empirical work indicates that they might not capture some of the specific systems they were designed to model [8]. When the assumptions of the models are violated, species diversity may rapidly collapse (see [5], electronic supplementary material and [7]). Therefore, research is still needed on whether other types of competition models might also lead to stable coexistence of diverse communities.

Here, we study a multi-trait game theory competition model based on a new combinatorial version of the hawk-dove game [9]. We find that when limited by N resources, our model will lead to a stable coexistence of up to 2N species. The coexisting species will persist indefinitely in a hybrid state where they are simultaneously capable of exhibiting both niche and neutral dynamics, depending on how the population is perturbed. Like the many other models which contain neutral dynamics, our model generates good fits to species abundance distributions in several empirical datasets, though our model does not require modelling dispersal, immigration or ongoing speciation in order to achieve this result. We also explore the implications of our model for species removal experiments and we prove that the invasibility criterion often used to experimentally study coexistence [10] is a sufficient rather than a necessary feature of stable coexistence models. Finally, we show that our model correctly predicts the approximate magnitude of species abundance correlations between similar but dynamically independent ecosystems.

2. Methods

(a). Formulation of the model

Our model took inspiration from the hawk-dove game studied in evolutionary game theory [9,11]. The hawk-dove game is characterized by two strategies: the hawk strategy and the dove strategy. Hawks and doves mix in the population randomly and compete against one another. When two hawks meet, both suffer a fitness loss of (V − C)/2 (where V is the value of the resource they are competing for and C is cost of mutual competition, also C > V > 0). On the other hand, when a hawk meets a dove the dove surrenders and the hawk increases its fitness by V while a dove gets nothing. When two doves meet they split the resource and each gets V/2 increase in fitness. The game is at equilibrium if the frequency of hawks in the population is equal to pH = V/C (see the electronic supplementary material, appendix S1.1 for an extended discussion of a hawk-dove game and its underlying assumptions).

In our extension, each species participates in N hawk-dove micro games simultaneously. Each micro game can be thought as being a competition for a different kind of essential resource. Micro game 1 might correspond to competition for light, micro game 2 for competition for nitrogen and so on. Each micro game has its corresponding parameters. For micro game i, we denote these with values Vi and Ci. Alternatively, the micro games might be thought of as representing competition over niche aspects in a multi-dimensional niche space [12].

Each species must choose a micro strategy (either play hawk or play dove) for each of the N micro games. For the case of four micro games, for example, a macro strategy for an individual specifies how to play in the four games. An example macro strategy may be H1 D2 D3 H4, which specifies to play hawk in game 1, dove in game 2, dove in game 3 and hawk in game 4. Furthermore, we postulate that if two individuals have exactly the same macro strategy then they belong to the same species. The total pay-off of a macro strategy is determined by the sum of pay-offs gathered in all of the N micro games.

For N micro games there is a total of 2N different macro strategies. The state of the population is then characterized by 2N probability values πj, where πj is the probability of encountering macro strategy j. The population is at equilibrium when every strategy has the same expected fitness. As all N micro games are independent from one another in terms of pay-offs, then the population must be in equilibrium with respect to each of the N games. Therefore, the probability of encountering the hawk strategy in game k (pHk) must be equal to pHk = Vk/Ck (see the electronic supplementary material, appendix S1.2 for an extended derivation). We can write that condition in terms of the probabilities of the composite strategies as 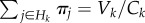Inline graphic, where j ∈ Hk stands for all the macro strategies j which involve playing hawk in the micro game k. We get one such equation for each of the N games and another equation which requires that all the probabilities sum to 1. Therefore, we end up with N + 1 equations for 2N variables and the final solution is under-determined. In effect, the mathematical structure of the solution is constrained to lie somewhere inside a 2N − N − 1 dimensional hyperplane. Within that hyperplane, all solutions are equally good and therefore there is plenty of room for neutral drift between the strategies.

(b). A description of empirical datasets

In order to test our new model, we numerically computed the species abundance distributions that the model predicts in equilibrium (see the electronic supplementary material, appendix S1.3) and we compared the simulation results against empirical species abundance distributions. In particular, we use data from the Barro Colorado tree community [13] and measurements of Mediterranean plankton species richness [14]. The Barro Colorado dataset relies on a comprehensive census of 50 hectare-sized sites of tropical forest in Panama. A comprehensive census identified all trees with a diameter larger than 10 cm at breast height (1.3 m). The resulting dataset of species abundances is publicly available and was downloaded from [13]. The plankton dataset was obtained by doing a count of all the species visible after fixation with an inverted Utermohl microscope. The total volume of water examined was 5 l. The water samples originated near the coast of Spain with exact sampling locations described in [14]. The data of species counts was provided in table 2 of [14].

(c). Modelling species abundance correlations

In our model, the equilibrium abundance of a species is a function of two factors: the hawk-dove game parameters Vk and the initial species distribution (see the electronic supplementary material, appendix S1.5). If we consider independent ecosystems (no mutual species exchange via immigration), then we may assume that the initial species abundance distributions there are statistically independent from one another. On the other hand, if the two ecosystems are broadly physically similar [13,15–18], then the hawk-dove game parameters may be similar even for isolated systems (examples would include American and European taiga, Ecuadorian and Peruvian rainforest or isolated Mediterranean hyper-saline vents).

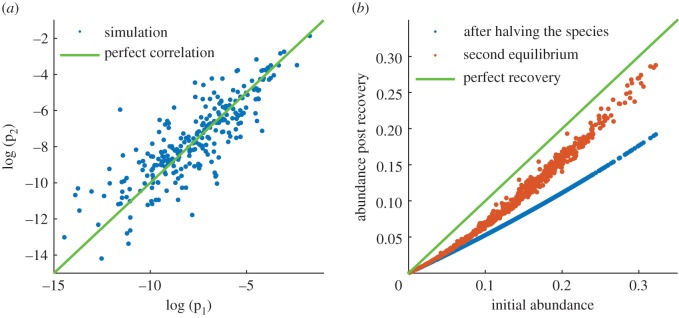
We wished to quantify the degree to which similar but independent ecosystems could produce correlated species abundance distributions. For this purpose, we used a paired runs protocol. Each paired run was composed of two simulations. For each simulation, we independently sampled the initial species distribution from the uniform random distribution, while both simulations within a run shared the same Vk values (after each run the Vk were re-sampled uniformly at random in the range from 1 to 1.9 for the subsequent run). After that, we numerically integrated the system to find the equilibrium solution for both simulations within a run. Then, we calculated the correlation between the logarithms of the species probabilities across the two simulations (see example in figure 2a). We repeated this procedure 100 times to derive and estimated value of the species abundance correlations.

Figure 2.

Figure 2.

Open in a new tab

Repeated simulations and perturbations. (a) A scatter plot of the log probabilities of species abundances across two independent runs of the model. (b) Simulation of how the population reacts to perturbations after reaching an equilibrium. The blue points plot the prevalence of a species after its numbers were halved against its initial prevalence. The red points show population recovery after a new equilibrium has been reached. Green line shows hypothetical perfect recovery.

3. Results

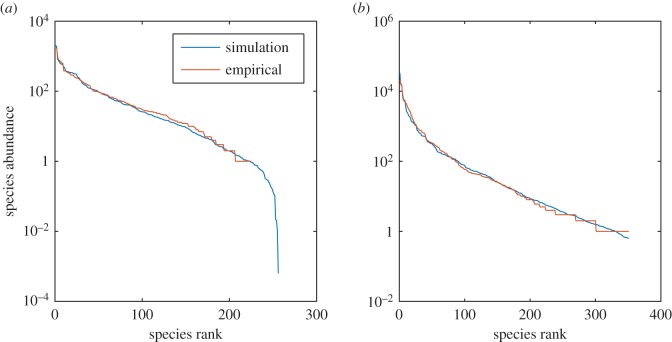
We tested whether our model reproduces the species abundance distribution in the Barro Colorado tree community (BCI)—a standard large-scale dataset for community ecology [13]. As the community contains around 200 species, we chose a value of N = 8 (the minimal value capable of producing 200 species in our model) and we sampled each Vi independently and uniformly at random in the range from 1 to 1.9. The starting probability distributions of all 2N species were chosen from a uniform random distribution and normalized to sum to one. We simulated the replicator equation (see the electronic supplementary material, appendix S1.3 for details on the simulation protocol) in various random starts and observed the equilibrium state distributions of strategy probabilities frequently converging to the lognormal distribution, which is very different from our starting state—the uniform probability distribution. The same also held true if we initialized the population from a Gaussian distribution. We found an excellent match between the simulation and empirical data (figure 1a). We obtained a similar result for a Mediterranean phytoplankton dataset [14,19] (figure 1b). A quantitative comparison of our model, an analytic solution to neutral theory [20,21], the lognormal and the gamma (the Gambin model) distributions [22] indicated similar performance for the four models with neutral theory performing best on the BCI dataset while the hawk-dove game performed best for the plankton dataset (see the electronic supplementary material, appendix S1.4 for details).

Figure 1.

Figure 1.

Open in a new tab

Species abundance distributions (SADs). SADs for two datasets—the Panamanian trees dataset [13] (a) and the North-West Mediterranean phytoplankton [14] (b). Red, empirical distributions; blue, model results at equilibrium. Simulation parameters for BCI dataset as given in the main text. For the phytoplankton, we used N = 9 (needed because we have more species) and V was sampled uniformly at random between 1 and 1.99 to generate greater variance. Furthermore, a cut-off at 350 species was used when presenting the histogram to better facilitate comparison with data.

A mathematical analysis of our model shows how the lognormal distribution emerges to capture the species abundance distribution. As we show in the electronic supplementary material, appendix S1.5, the equilibrium probability distribution for each macro strategy in each simulation is proportional to the products of the equilibrium probabilities of its component micro strategies. For example, the probability of observing the macro strategy j = H1H2D3H4D5 is proportional to πj ∝ pH1pH2pD3pH4pD5. As all micro strategies are equally represented in the list of all macro strategies, we can view the full collection of macro probabilities as arising from a set of random products over the component micro strategy probabilities. Just like random sums tend to the normal distribution according to the central limit theorem, random products tend to the lognormal distribution, and this explains why the lognormal distribution emerges in our model [23] (the electronic supplementary material, appendix S1.6).

Some species abundance distributions have been described as having a limited degree of multi-modality [24]. In this respect, we note that under certain distributions of Vi values, multi-modal species distributions emerge in our model (the electronic supplementary material, appendix S1.7).

As shown in Methods, our model implies that the equilibrium solution for the population abundances will lie somewhere along a neutral hyperplane. The existence of a whole plane of equilibrium solutions means that, depending on the initial conditions, we may end up with very different equilibrium abundance values for each species across independent runs of the model. At the same time, our formula for the final abundance distribution (see the electronic supplementary material, appendix S1.5) also indicates that the parameters of the hawk-dove games influence the expected abundances of the strategies. This opens up the possibility of finding correlated species abundance distributions across independent ecosystems that have similar values for the hawk-dove game pay-offs.

We used the procedure of paired runs described in the Methods to quantify the expected average correlation between the species abundance distributions across two independent (non-interacting) ecosystems. In 100 simulations, we consistently found a strong average correlation between the log species probabilities of independent ecosystem pairs with a mean correlation value of 0.75 and a standard deviation of 0.08 (N = 100, 95% confidence intervals 0.734 and 0.765 for the mean). The simulations led us to conclude that uncoupled ecosystems could indeed show correlated abundance distributions under our model. This value is close to the correlation value of 0.83 ± 0.03 reported for the abundances of the 254 tree species which occur in both Ecuadorian and Peruvian forests [15] (the two sites are located 1400 km apart), since approximately 20% of our paired runs produce a correlation value of 0.83 or greater.

Ecosystems are often subject to unpredictable stimuli which could negatively impact population stability and diversity. Hence, we examined how our neutral equilibrium solutions will react to perturbations. We reasoned that unlike the fully neutral model, our model should show partial recovery from perturbations. To see why, let us assume that we reduce the total number of one strategy type, which we exemplify using the H1D2D3 type. Then, we have created a deficiency in the population of H1, D2 and D3 component strategies. In the one-dimensional hawk-dove game, if the frequency of hawks exceeds the equilibrium frequency of hawks, then the average fitness of doves exceeds the average fitness of hawks. The opposite is true if the frequency of hawks is below the equilibrium hawk frequency [9]. Owing to the assumption of additive fitness, the same conclusions hold in the component games of the multi-dimensional hawk-dove game. Hence, by depleting the population of the H1, D2 and D3 strategies, those micro strategies now have greater fitness than the D1, H2 and H3 strategies (we call this a fitness excess).

After the perturbation, the H1D2D3 is the only macro strategy which experiences a fitness excess across all three of its component micro strategies. Many other species in the population might transiently experience increased fitness (for example the species H1D2H3 probably experiences a fitness excess due to its first two components), but H1D2D3 is the only species which experiences increased fitness along all its three components and therefore has the largest fitness advantage. Therefore, H1D2D3 will experience the greatest growth rate out of all present species and this temporary fitness boost will promote partial recovery of the H1D2D3 from perturbations.

We simulated a perturbation scenario to examine the degree to which populations will recover from perturbations (figure 2b). Following the experimental study from [25], we removed half of the members of one species from a community at equilibrium and subsequently observed its recovery. We plot the results of 600 simulations. In each simulation, we first let the population converge to an equilibrium, then we removed half the members of one species, and we let the population recover. We found there is always recovery with respect to the perturbation (red points are above the blue points, although the recovery is not perfect (red points versus green line). Finally, we observe in our simulations that the more prevalent a species is initially, the better its levels recover. This result qualitatively mirrors what is observed in plant community dynamics [25].

Negative density dependence during a perturbation is not the only criterion which is used to experimentally distinguish coexistence from co-occurrence (co-occurrence can be driven by other processes besides coexistence, like migration from surrounding areas). Another stronger test which is sometimes used is the invasibility test [10], in which a species A is removed from a community, the community is allowed to converge to a new equilibrium, and species A is thereafter reintroduced to a community at a low level. If the species A subsequently increases in prevalence it passes the invasibility test.

In simulations of our model, we find that species who are able to coexist do not pass the invasibility test. In 600 experimental simulations, we reintroduced species A into a community of seven other individuals whose dynamics had previously converged to equilibrium. In all 600 simulations, species A declined in prevalence after it was reintroduced to the community, even though it was introduced to the community at a level which was far below its typical prevalence (mean prevalence without interference 0.13 ± 0.07,  N = 600, prevalence enforced at reintroduction 0.01). Therefore, our model illustrates that the invasibility test may be sufficient but is not a necessary criterion by which one can experimentally distinguish coexistence from co-occurrence (i.e. passing the invasibility test guarantees coexistence but failing the test does not rule out the possibility of coexistence).

The reason why the species in our model behave in different ways during perturbation and an invasibility experiment lies in the fact that during an invasibility experiment, the community is allowed to converge to a new equilibrium after A is removed. Thus, before A is reintroduced, the population will contain just the right mix of the different hawk strategies and the reintroduction of A will create an excess of the strategies which the species A embodies. Therefore, A typically will experience increased competition compared to other species and it will decline in numbers after it is reintroduced.

Some recently proposed coexistence models lack robustness against certain deviations in species fitness parameters [5], so we studied whether our model is robust in this respect. In particular, we considered what happens when the additive assumption of pay-offs is violated to some small degree. When our model pay-off matrix is perturbed by a random matrix, we find that biodiversity slowly collapses over time (electronic supplementary material, figure S1). However, this collapse can be easily halted when we add a small self-inhibition term to the model (see the electronic supplementary material, figure S1 and appendix S1.8). Biologically, the self-inhibition term may represent a mechanism such as species-specific pathogen transmission or it could capture the emergence of a species-specific predator. We conclude that our coexistence model is robust to small imperfections which will inevitably occur in real biological systems.

4. Discussion

We have proposed a model of species interactions which reveals a new mechanism of coexistence that explains how exponentially more than N species can persist on N resources. Our coexistence mechanism also holds the potential to explain how models which are niche based at the level of assumptions can lead to outcomes which are consistent with predictions from the neutral theory of biodiversity [26]. In the following discussion, we will highlight the key similarities and differences between our approach and the unified neutral theory (UNT) and then discuss more general implications of our model in the context of coexistence research.

The UNT [4] is both based on the neutrality assumption and produces neutrally stable outcomes. The neutrality assumption is often referred to as the assumption of ecological equivalence and it states that under certain conditions all species have equal fitness. Its introduction was motivated by the success of a similar assumption in neutral theories of molecular evolution, which assumed that all mutations were fitness neutral [27]. Likewise, speciation events are assumed to be fitness neutral in the UNT as well [4,28].

Our theory explains mechanistically how neutral speciation could arise in nature. To see why, consider a two-resource ecosystem composed of the coexisting H1D2, the D1D2 and the H1H2 species. If such a community is in equilibrium, then the strategies H1 and D1 produce an equal pay-off in competition for the first resource and the strategies H2 and D2 must also produce an equal pay-off in competition for the second resource. Therefore, the D1H2 species would have the same fitness as all the other extant strategies and thus such a speciation event would be neutral with respect to the existing population.

Our theory also parallels the neutral theory because both models produce neutrally stable population dynamics. In the UNT, all possible configurations of species are neutrally stable. Neutral stability means that in the absence of stochastic effects, any extant configuration would persist indefinitely while no configuration is self-restoring (perturbations are allowed to accumulate instead of being resisted). Owing to stochastic birth–death and speciation processes, the community dynamics undergoes drift and the system passes through many equally stable population configurations [29]. Our model also leads to a plurality of possible equilibrium configurations, all of which are constrained to lie on a hyperplane which is neutrally stable.

In addition to the above similarities, our model contains a number of features which make it different from the neutral theory of biodiversity and perhaps more closely suited to modelling realistic ecosystems. First, species in our model are not ecologically equivalent. As we showed in the main text, species which are more prevalent in one simulation of our model are likely to be more prevalent in another independent simulation as well and this matches what we find in experiments on well-separated plots in Amazonian forests [15]. The UNT model, by contrast has not been able to explain such long-distance correlations although it has been highly successful in explaining correlations on a smaller scale [13]. Remarkably, this qualitative finding of similarity between independent systems [16,17] holds true whether we are considering the American and Eurasian taigas [18,30], deep hypersaline anoxic basins of the Eastern Mediterranean [31] or Amazonian forests [15].

Another attractive feature of our model as compared with the UNT concerns reactions to perturbations. Species removal experiments and perturbation experiments indicate that many ecosystems react to perturbations in a way which tends to suppress the effects of perturbations [25,26,32–35]. The UNT model again lacks this feature while our model resists most random perturbations (figure 2b). Other models have been proposed which are composed of groups of niches within which species show neutral dynamics [36,37]. Such models are also expected to exhibit partial recovery from perturbations. However, in these models the restoring force is expected to be uniformly distributed across all the species within the perturbed niche, while our model shows that it is the perturbed species which experiences the strongest restorative force (see figure 2b, and the associated argument in the Results section).

The last two characteristics (resistance to perturbations and a correlation between species traits and species abundance) would be traditionally regarded as characteristics of niche models [10,25]. Thus our model simultaneously shows both niche-like and neutral patterns and could be said to help unify the niche and neutral perspectives on ecosystem dynamics.

In contrast with other attempts to combine niche and neutral theories, we do not need to model factors like ongoing speciation events, stochastic inter-generational dynamics, immigration from a surrounding community or dispersal limitations [38–42]. Even in a fully mixed population with deterministic dynamics and no source of new species, we obtain an approximately lognormal species abundance distribution at equilibrium.

Even though our model shares many similarities with the neutral theory, the lognormal distribution is generated in our model via a different mechanism. The lognormal emerges in our model through repeated application of many multiplicative terms (see the electronic supplementary material, appendix S1.6). This theoretical rationale might help to alleviate some of the criticisms of the lognormal distribution as an ad hoc construct and an improper null model in the context of population ecology [43,44]. Owing to the attracting nature of the hyperplane, the equilibrium is also reached very fast, which may be an advantage over other models where kinetic equilibriums can be slow to emerge and are transient in nature [45].

The central object which enabled us to achieve neutral outcomes through niche mechanisms was the hyperplane attractor structure of our model. We anticipate that even if the details of our model prove to be inaccurate in some respects, this underlying mathematical structure may nevertheless be present in many other models which display neutral and niche dynamics simultaneously. This is likely to be the case because the only way that neutral drift and restorative dynamics can simultaneously coexist is if dynamics are neutral along some directions but restoring on others—the very property which defines an attractor manifold.

In fact, one model with both niche and neutral dynamics is the chemostat model of Posfai et al. [5] and here too an attractive hyperplane emerges as a result of competitive dynamics. Although not pure hyperplane models, the emergent neutrality model [46] and the competitive life-history trade-off model of coexistence [47] also lead to multiple regions of trait space where dynamics are approximately neutral within a niche. Hyperplane models have previously proved useful in analysing other complex networks such as neural dynamics [48]. We hope that our model will stimulate further research into attractor hyperplanes in theoretical ecology.

Although our model was structured around the hawk-dove game, this is not a necessary condition for the hyperplane to emerge. The model could be extended to other types of games as the components from which the multi-trait strategies are built. As long as the component games have evolutionarily stable mixed strategies as their equilibriums, our mathematical arguments about the existence of the hyperplane hold.

Our model also offers a new potential solution to the paradox of the plankton. The paradox of the plankton refers to an observation made by Hutchinson that oceanic waters contain fewer than 10 distinct growth resources (light, nitrogen, carbon, iron, phosphorous, silicon and a few potential others) yet it supports more than a hundred stably coexisting species [3]. Hutchinson remarked that this empirical finding contradicted the competitive exclusion principle, which stated that the number of coexisting species in equilibrium should not exceed the number of resources [32]. The contradiction became known as the paradox of the plankton and it has spawned many decades of research and dozens of proposals explaining how the paradox might be overcome [49].

Our model proposes that the number of coexisting species grows exponentially with the number of available resources and the presence of seven to 10 different types of resources is enough to support the coexistence of between 100 and 1000 species: a range which appears to be a good match with what is experimentally observed in plankton communities [3,14]. Thus, our model offers a new potential explanation for the paradox of the plankton and its predictions could be tested further in future empirical work.

One other noteworthy feature of our model is its property that species in our model will fail the invasibility test [10] even though coexistence in the model is clearly stable. In this regard, our model parallels other complex multi-species coexistence models which are also known to fail that test [50]. We hope that a more extended examination of such complex coexistence models will stimulate experimentalists to develop improved tests of coexistence more suitable for complex ecological communities.

Finally, it should be noted that like many other ecological models, our model makes certain simplifications whose effects need to be more comprehensively examined in future models. Our species currently lack inter-individual variability [51] and we have not yet provided a way to incorporate evolutionary processes into the model [52]. Also, the assumptions of approximately additive pay-offs may not completely hold for some species orders where trait trade-offs impose constraints on the pay-off matrix [53]. As we showed in the electronic supplementary simulations, our model displays some robustness to violations of the additive pay-off assumption but the precise limits of robustness and the effects of pay-off correlations need to be mapped more extensively in follow-up research. In the future, it will also be interesting to incorporate considerations of stochasticity and dispersal limitations into our baseline model to facilitate further comparisons between existing models in the literature [29].

Supplementary Material

Supplementary
rspb20181273supp1.pdf (705.1KB, pdf)

Acknowledgements

A.L. acknowledges an FCT PhD fellowship. We are grateful to Simon Levin and Ned Wingreen for discussions and the reviewers as well as the editor for comments on how to improve the manuscript.

Data accessibility

Matlab code and data to reproduce the figures is available for download from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.b06f3s2 [54].

Authors' contributions

A.L. devised the project, analysed and modelled data and wrote the paper, G.G.d.P. supervised the project, helped in analysis and modelling and wrote the paper.

Competing interests

We declare we have no competing interests.

Funding

Our research is funded by Champalimaud Foundation (Lisbon).

References

  • 1.MacArthur R, Levins R. 1964. Competition, habitat selection, and character displacement in a patchy environment. Proc. Natl Acad. Sci. USA 51, 1207–1210. ( 10.1073/pnas.51.6.1207) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.May RM. 1972. Will a large complex system be stable? Nature 238, 413–414. ( 10.1038/238413a0) [DOI] [PubMed] [Google Scholar]
  • 3.Hutchinson GE. 1961. The paradox of the plankton. Am. Nat. 95, 137–145. ( 10.1086/282171) [DOI] [Google Scholar]
  • 4.Hubbell SP. 2001. The unified neutral theory of biodiversity and biogeography. Monographs in population biology. Princeton, NJ: Princeton University Press. [Google Scholar]
  • 5.Posfai A, Taillefumier T, Wingreen NS. 2017. Metabolic trade-offs promote diversity in a model ecosystem. Phys. Rev. Lett. 118, 028103 ( 10.1103/PhysRevLett.118.028103) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Allesina S, Levine JM. 2011. A competitive network theory of species diversity. Proc. Natl Acad. Sci. USA 108, 5638–5642. ( 10.1073/pnas.1014428108) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Grilli J, Barabás G, Michalska-Smith MJ, Allesina S. 2017. Higher-order interactions stabilize dynamics in competitive network models. Nature 548, 210–213. ( 10.1038/nature23273) [DOI] [PubMed] [Google Scholar]
  • 8.Godoy O, Stouffer DB, Kraft NJ, Levine JM. 2017. Intransitivity is infrequent and fails to promote annual plant coexistence without pairwise niche differences. Ecology 98, 1193–1200. ( 10.1002/ecy.1782) [DOI] [PubMed] [Google Scholar]
  • 9.Kokko H. 2013. Dyadic contests: modelling flights between two individuals. In Animal contests (eds Hardy IC, Briffa M), pp. 5–32. Cambridge, UK: Cambridge University Press. [Google Scholar]
  • 10.Siepielski AM, McPeek MA. 2010. On the evidence for species coexistence: a critique of the coexistence program. Ecology 91, 3153–3164. ( 10.1890/10-0154.1) [DOI] [PubMed] [Google Scholar]
  • 11.Smith JM, Price GR. 1973. The logic of animal conflict. Nature 246, 15–18. ( 10.1038/246015a0) [DOI] [Google Scholar]
  • 12.Colwell RK, Rangel TF. 2009. Hutchinson's duality: the once and future niche. Proc. Natl Acad. Sci. USA 106, 19 651–19 658. ( 10.1073/pnas.0901650106) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Condit R. et al. 2002. Beta-diversity in tropical forest trees. Science 295, 666–669. ( 10.1126/science.1066854) [DOI] [PubMed] [Google Scholar]
  • 14.Margalef R. Through the looking glass: how marine phytoplankton appears through the microscope when graded by size and taxonomically sorted. Barcelona, Spain: Scientia Marina. [Google Scholar]
  • 15.Pitman NC, Terborgh JW, Silman MR, Nú nez V, Neill DA, Cerón CE, Palacios WA, Aulestia M. 2001. Dominance and distribution of tree species in upper Amazonian terra firme forests. Ecology 82, 2101–2117. ( 10.1890/0012-9658(2001)082%5B2101:DADOTS%5D2.0.CO;2) [DOI] [Google Scholar]
  • 16.Segar ST, Pereira RA, Compton SG, Cook JM. 2013. Convergent structure of multitrophic communities over three continents. Ecol. Lett. 16, 1436–1445. ( 10.1111/ele.12183) [DOI] [PubMed] [Google Scholar]
  • 17.MacDonald G. 2002. Biogeography: introduction to space, time and life. Hoboken, NJ: John Wiley and Sons. [Google Scholar]
  • 18.Swanson DK. 2003. A comparison of taiga flora in north-eastern Russia and Alaska/Yukon. J. Biogeogr. 30, 1109–1121. ( 10.1046/j.1365-2699.2003.00901.x) [DOI] [Google Scholar]
  • 19.Pueyo S. 2006. Diversity: between neutrality and structure. Oikos 112, 392–405. ( 10.1111/j.0030-1299.2006.14188.x) [DOI] [Google Scholar]
  • 20.Volkov I, Banavar JR, Hubbell SP, Maritan A. 2003. Neutral theory and relative species abundance in ecology. Nature 424, 1035–1037. ( 10.1038/nature01883) [DOI] [PubMed] [Google Scholar]
  • 21.McGill BJ, Maurer BA, Weiser MD. 2006. Empirical evaluation of neutral theory. Ecology 87, 1411–1423. ( 10.1890/0012-9658(2006)87%5B1411:EEONT%5D2.0.CO;2) [DOI] [PubMed] [Google Scholar]
  • 22.Ugland KI, Lambshead PJD, McGill B, Gray JS, O'Dea N, Ladle RJ, Whittaker RJ. 2007. Modelling dimensionality in species abundance distributions: description and evaluation of the Gambin model. Evol. Ecol. Res. 9, 313–324. [Google Scholar]
  • 23.Dennis B, Patil GP. 1987. Applications in ecology. In Lognormal distributions (eds Crow EL, Shimizu K), pp. 303–330. New York, NY: Marcel Dekker Inc. [Google Scholar]
  • 24.Vergnon R, Van Nes EH, Scheffer M. 2012. Emergent neutrality leads to multimodal species abundance distributions. Nat. Commun. 3, 663 ( 10.1038/ncomms1663) [DOI] [PubMed] [Google Scholar]
  • 25.Levine JM, HilleRisLambers J. 2009. The importance of niches for the maintenance of species diversity. Nature 461, 254–257. ( 10.1038/nature08251) [DOI] [PubMed] [Google Scholar]
  • 26.Matthews TJ, Whittaker RJ. 2014. Neutral theory and the species abundance distribution: recent developments and prospects for unifying niche and neutral perspectives. Ecol. Evol. 4, 2263–2277. ( 10.1002/ece3.1092) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Kimura M. 1983. The neutral theory of molecular evolution. Cambridge, UK: Cambridge University Press. [Google Scholar]
  • 28.De Aguiar MAM, Baranger M, Baptestini E, Kaufman L, Bar-Yam Y. 2009. Global patterns of speciation and diversity. Nature 460, 384–387. ( 10.1038/nature08168) [DOI] [PubMed] [Google Scholar]
  • 29.Rosindell J, Hubbell SP, Etienne RS. 2011. The unified neutral theory of biodiversity and biogeography at age ten. Trends Ecol. Evol. 26, 340–348. ( 10.1016/j.tree.2011.03.024) [DOI] [PubMed] [Google Scholar]
  • 30.Korchagin A, Karpov V. 1974. Fluctuations in coniferous taiga communities. In Vegetation dynamics (ed. Knapp R.), pp. 225–231. Berlin, Germany: Springer. [Google Scholar]
  • 31.Stock A, Edgcomb V, Orsi W, Filker S, Breiner HW, Yakimov MM, Stoeck T. 2013. Evidence for isolated evolution of deep-sea ciliate communities through geological separation and environmental selection. BMC Microbiol. 13, 150 ( 10.1186/1471-2180-13-150) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.MacArthur RH. 1968. The theory of the niche. In Population biology and evolution (ed. Lewontin RC.), pp. 159–176. Syracuse, NY: Syracuse University Press. [Google Scholar]
  • 33.Dıaz S, Symstad AJ, Chapin FS III, Wardle DA, Huenneke LF. 2003. Functional diversity revealed by removal experiments. Trends Ecol. Evol. (Amst.) 18, 140–146. ( 10.1016/S0169-5347(03)00007-7) [DOI] [Google Scholar]
  • 34.Hulme PE, Bremner ET. 2006. Assessing the impact of Impatiens glandulifera on riparian habitats: partitioning diversity components following species removal. J. Appl. Ecol. 43, 43–50. ( 10.1111/j.1365-2664.2005.01102.x) [DOI] [Google Scholar]
  • 35.Chave J. 2004. Neutral theory and community ecology. Ecol. Lett. 7, 241–253. ( 10.1111/j.1461-0248.2003.00566.x) [DOI] [Google Scholar]
  • 36.Leibold MA, McPeek MA. 2006. Coexistence of the niche and neutral perspectives in community ecology. Ecology 87, 1399–1410. ( 10.1890/0012-9658(2006)87%5B1399:COTNAN%5D2.0.CO;2) [DOI] [PubMed] [Google Scholar]
  • 37.Chisholm RA, Pacala SW. 2010. Niche and neutral models predict asymptotically equivalent species abundance distributions in high-diversity ecological communities. Proc. Natl Acad. Sci. USA 107, 15 821–15 825. ( 10.1073/pnas.1009387107) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 38.Chave J, Muller-Landau HC, Levin SA. 2002. Comparing classical community models: theoretical consequences for patterns of diversity. Am. Nat. 159, 1–23. ( 10.1086/324112) [DOI] [PubMed] [Google Scholar]
  • 39.Gravel D, Canham CD, Beaudet M, Messier C. 2006. Reconciling niche and neutrality: the continuum hypothesis. Ecol. Lett. 9, 399–409. ( 10.1111/j.1461-0248.2006.00884.x) [DOI] [PubMed] [Google Scholar]
  • 40.Haegeman B, Loreau M. 2011. A mathematical synthesis of niche and neutral theories in community ecology. J. Theor. Biol. 269, 150–165. ( 10.1016/j.jtbi.2010.10.006) [DOI] [PubMed] [Google Scholar]
  • 41.Fisher CK, Mehta P. 2014. The transition between the niche and neutral regimes in ecology. Proc. Natl Acad. Sci. USA 111, 13 111–13 116. ( 10.1073/pnas.1405637111) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 42.Allouche O, Kadmon R. 2009. A general framework for neutral models of community dynamics. Ecol. Lett. 12, 1287–1297. ( 10.1111/j.1461-0248.2009.01379.x) [DOI] [PubMed] [Google Scholar]
  • 43.Williamson M, Gaston KJ. 2005. The lognormal distribution is not an appropriate null hypothesis for the species–abundance distribution. J. Anim. Ecol. 74, 409–422. ( 10.1111/j.1365-2656.2005.00936.x) [DOI] [Google Scholar]
  • 44.McGill BJ. 2003. A test of the unified neutral theory of biodiversity. Nature 422, 881–885. ( 10.1038/nature01583) [DOI] [PubMed] [Google Scholar]
  • 45.Holt RD. 2006. Emergent neutrality. Trends Ecol. Evol. (Amst.) 21, 531–533. ( 10.1016/j.tree.2006.08.003) [DOI] [PubMed] [Google Scholar]
  • 46.Scheffer M, van Nes EH. 2006. Self-organized similarity, the evolutionary emergence of groups of similar species. Proc. Natl Acad. Sci. USA 103, 6230–6235. ( 10.1073/pnas.0508024103) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 47.Bonsall MB, Jansen VA, Hassell MP. 2004. Life history trade-offs assemble ecological guilds. Science 306, 111–114. ( 10.1126/science.1100680) [DOI] [PubMed] [Google Scholar]
  • 48.Seung HS. 1996. How the brain keeps the eyes still. Proc. Natl Acad. Sci. USA 93, 13 339–13 344. ( 10.1073/pnas.93.23.13339) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 49.Roy S, Chattopadhyay J. 2007. Towards a resolution of ‘the paradox of the plankton’: a brief overview of the proposed mechanisms. Ecol. Complexity 4, 26–33. ( 10.1016/j.ecocom.2007.02.016) [DOI] [Google Scholar]
  • 50.Levine JM, Bascompte J, Adler PB, Allesina S. 2017. Beyond pairwise mechanisms of species coexistence in complex communities. Nature 546, 56–64. ( 10.1038/nature22898) [DOI] [PubMed] [Google Scholar]
  • 51.Dingemanse NJ, Both C, Drent PJ, Tinbergen JM. 2004. Fitness consequences of avian personalities in a fluctuating environment. Proc. R. Soc. Lond. B 271, 847–852. ( 10.1098/rspb.2004.2680) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 52.Shoresh N, Hegreness M, Kishony R. 2008. Evolution exacerbates the paradox of the plankton. Proc. Natl Acad. Sci. USA 105, 12 365–12 369. ( 10.1073/pnas.0803032105) [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 53.Fynn R, Morris C, Kirkman K. 2005. Plant strategies and trait trade-offs influence trends in competitive ability along gradients of soil fertility and disturbance. J. Ecol. 93, 384–394. ( 10.1111/j.0022-0477.2005.00993.x) [DOI] [Google Scholar]
  • 54.Laan A, de Polavieja GG. 2018. Data from: Species diversity rises exponentially with the number of available resources in a multi-trait competition model Dryad Digital Repository. ( 10.5061/dryad.b06f3s2) [DOI] [PMC free article] [PubMed]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Data Citations

  1. Laan A, de Polavieja GG. 2018. Data from: Species diversity rises exponentially with the number of available resources in a multi-trait competition model Dryad Digital Repository. ( 10.5061/dryad.b06f3s2) [DOI] [PMC free article] [PubMed]

Supplementary Materials

Supplementary
rspb20181273supp1.pdf (705.1KB, pdf)

Data Availability Statement

Matlab code and data to reproduce the figures is available for download from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.b06f3s2 [54].

Articles from Proceedings of the Royal Society B: Biological Sciences are provided here courtesy of The Royal Society

RESOURCES