The instrumental resolution of a moire extensometer in light of its recent automatisation

Abstract

This paper assesses the instrumental resolution of a mechanical extensometer in light of its recent automatisation. The instrument takes advantage of the moire phenomenon of optical interference to measure angular rotation in two perpendicular planes and displacement in three dimensions. Our assessment systematically defines an analytical solution for the complete interpretation of a generic moire pattern and a set of mathematical approximations for the moire patterns used to measure rotation and displacement. The ultimate sensitivity of the automated instrument is determined on the basis of a generic least square differences fitting procedure while the instrumental resolution is defined on the basis of realistic, rather than optimal, scenarios: the resolution of the rotation measurements are in the order of 8.7*10^-5 rad while the resolution of the displacement measurements are better than 5 μm. This assessment represents the first step towards a global numerical repository for processed data recorded by the automated extensometers.

1. Introduction

Fracture monitoring represents an important theme in basic and applied geological research [1,2,3]. Such discontinuities influence the mechanical properties of the rock mass and, therefore, the impetus for studying fracture behaviour is often stimulated by the need to protect lives and infrastructure [4,5,6]. This type of monitoring is commonly hindered by the fact that fractures often move incrementally while their behaviour is often characterised by rotation and slip [7,8,9]. In the 1960s, to overcome these problems, a mechanical extensometer was designed to measure fracture behaviour on the basis of the moire phenomenon of optical interference [10,11]. Moire patterns are generated when two identical sets of superposed periodic gratings move with respect to one another [12,13]. It has long been understood that such patterns are particularly adept at registering minute perturbations because they magnify any relative movement [14,15]. The instrument, known as a TM-71, is able to simultaneously record rotation in two perpendicular planes and displacement in three dimensions [16,17]. Nearly half a century later, due to its robust design, it is still used extensively in geological research [18,19,20]. These instruments, for example, record fault behaviour at more than one hundred sites across the monitoring network EU-TecNet [21,22,23].

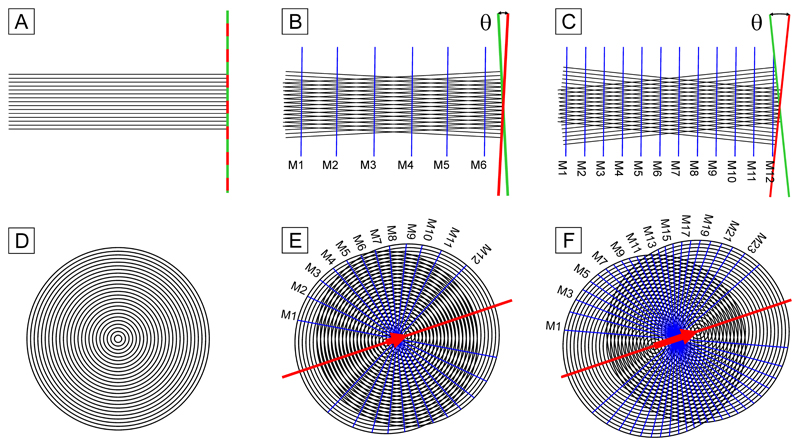
The instrument is held securely across a fracture using two connecting arms drilled into the opposing sidewalls while the moire patterns are generated on two pairs of plane parallel glass plates [24]. In effect, one glass plate in each pair is mechanically attached to one of the fracture sidewalls via its connecting arm while the other is attached to the opposing fracture sidewall via its connecting arm. Each of the plates is etched with one set of circular gratings and two sets of linear gratings orientated perpendicular to one another [17]. Figure 1(A-C) presents schematic representations of the parallel moire patterns generated by two sets of superposed linear gratings. The number of moire interference fringes increases as the angle of mutual rotation becomes greater. These patterns are only sensitive to rotation while remaining unaffected by the magnitude and direction of displacement. Figure 1(D-F) presents schematic representations of the hyperbolic moire patterns generated by two sets of superposed circular gratings. The number of moire interference fringes increases as the centre to centre distance becomes greater. These patterns are sensitive to the magnitude and direction of displacement while remaining unaffected by rotation.

Figure 1.

(A-C) Schematic representations of the parallel moire patterns, represented by the blue lines, generated by the two sets of superposed linear gratings etched into the glass plates of the mechanical extensometer. (D-F) Schematic representations of the hyperbolic moire patterns, represented by the blue lines, generated by the two sets of superposed circular gratings etched into the glass plates of the mechanical extensometer. The red arrows indicate the displacement vector.

It was originally intended that information about fracture behaviour would accumulate on the basis of low frequency manual readings [24,25]. The extensometer has already been installed across some fractures for more than forty years [26]. These instruments, especially those in the fault monitoring network EU-TecNet, are generally located underground as such settings suppress daily and seasonal climatic fluctuations [27,28]. Recent advances are overcoming the data collection challenges associated with the engineering of energy efficient, wired, robust instruments in locations where there is seldom a guaranteed energy supply or means of telecommunications [17,24]. The majority of studies, until now, have drawn conclusions from a limited number of instruments spread across relatively small geographical areas [29,30,31]. There is a clear need to move towards a more global approach in which data analysis incorporates as many automated instruments as possible. Our ultimate aim, therefore, is to facilitate a numerical global repository for processed data recorded by the automated extensometers.

The singular advantage of this extensometer is that it remains one of the only instruments to measure deformation by simultaneously assessing rotation and displacement as completely independent variables over periods ranging from minutes to decades [17,24]. Furthermore, critically, it does not require a priori assumptions regarding the principal deformation directions. In this paper the instrumental resolution of the extensometer is assessed in light of its recent automatisation. The assessment has been made in a number of steps which define, first, an analytical solution for the complete interpretation of a generic moire pattern and, second, a set of mathematical approximations for the moire patterns used to measure rotation and displacement. It is then possible to determine the ultimate sensitivity of the automated instrument on the basis of a generic least square differences fitting procedure. The instrumental resolution is defined on the basis of realistic, rather than optimal, scenarios. Finally, our theoretical modelling of the moire patterns is compared to the actual interference fringes generated by the automated extensometer.

2. Analytical solution of a generic moire pattern

The first step towards a thorough assessment of the instrumental resolution demands an analytical solution for the complete interpretation of a generic moire pattern. It is assumed that the gratings are periodic and identical. The behaviour of a geological fracture can be described fully on the basis of its relative angular rotation and the absolute direction and magnitude of its relative displacement r.

To begin with it is necessary to address the mathematical description of a pair of two dimensional periodic gratings, T⁽¹⁾(r) and T⁽²⁾(r), denoting the transparency of each pattern, T^(k) ∈ [0, 1]. Each T^(k)(r) can be expanded as a Fourier series in order to express it in terms of a discrete infinite sum:

$$T^{(k)}(\mathit{\text{r}})={\displaystyle \sum _{n=-\infty }^{\infty }{T}_n^{(k)}{e}^{in{\xi }^{(k)}(\mathit{\text{r}})}}$$ (1)

Where T_n^(k) is denoted as the argument function and ξ^(k)∈[−π,π] is the phase of the periodic transmission function of each pattern. In the following we assume that the transmission function of a grating is rectangular with the transmissivity of unity for ξ∈[−π/2,π/2] and zero outside this interval. Due to the fact that both gratings are identical, T⁽¹⁾(r) = T⁽²⁾(r), and the transmission of a grating pair is given by the product of the transmissions of individual gratings. Therefore, the transmission, T(r), of the grating pair can be expressed as:

$$T(\mathit{\text{r}})=T^{(1)}(\mathit{\text{r}})\ast T^{(2)}(\mathit{\text{r}}\prime )={\displaystyle \sum _{n=-\infty }^{\infty }{\displaystyle \sum _{m=-\infty }^{\infty }{T}_n{T}_m{e}^{i[n\xi (\mathit{\text{r}})+m\xi (\mathit{\text{r}}\prime )]}}}$$ (2)

The explicit expression for the effective light transmission, Φ(r), of the moire pattern can be obtained by averaging the transparency randomly over all phases. This effect stems from the limited spatial resolution of the receiving sensor, irrespective of whether these are the photoreceptor cells in a human eye or the pixels in a digital imaging sensor, as they collect averaged photon amplitude.

$$\Phi (\mathit{\text{r}})={\displaystyle \sum _{n=-\infty }^{\infty }{\displaystyle \sum _{m=-\infty }^{\infty }{T}_n{T}_m\langle e^{i[n\xi (\mathit{\text{r}})+m\xi (\mathit{\text{r}}\prime )]}\rangle =\frac{1}{4}+2}{\displaystyle \sum _{n=1}^{\infty }|T_n{|}^2\text{cos}[n\left(\xi (\mathit{\text{r}})-\xi (\mathit{\text{r}}\prime )\right)]}}$$ (3)

In the calculation of the phase average in Equation 3 we used the fact that the pitch of the grating, i.e. the ratio between the transparent and opaque segments, is 1:1, from which it follows T₀=1/2. Further, T_-n=(T_n)*, since T(r) is a real function of r. The final accuracy of this analytical solution depends on the number of terms included in the description of the Fourier expansion of the gratings. If T_n and ξ are known it is concluded that Equation 3 is valid for any moire pattern and contains no loss of fidelity within the random phase approximation.

3. Mathematical approximations

The second step towards a thorough assessment of the instrumental resolution demands a set of mathematical approximations for the linear and circular gratings etched into the glass plates of the moire extensometer. Table 1 summarises the coefficients T_n and the arguments ξ needed for the analytical solution presented in Equation 3 in order to generate the moire patterns discussed in this paper. It should be noted that T_n are the same in each of the studied cases and Λ is the periodicity of the grating in lines per mm. In the table we denoted $\mathit{\text{k}}=\frac{2\pi }{\Lambda }(-\text{sin}\phi ,\text{cos}\phi )$ the wave vector perpendicular to a linear grating while φ ∈ [−π,π] is the angle of the direction of a line of a linear grating with the positive x axis. Due to the isotropy of a circular grating its phase function contains only the length $k=\left|\mathit{\text{k}}\right|=\frac{2\pi }{\Lambda }$ of the wave vector.

Table 1.

The coefficients T_n and the phase ξ needed for the analytical solution presented in Equation 3.

Grating	Tn (n = 1, 2,…, ∞)	ξ(r)
Linear grating (parallel)	$T_n=\frac{\text{sin}\left(\frac{\pi n}{2}\right)}{\pi n}$	k.r
Circular grating (concentric)		kr

3.1. Linear gratings

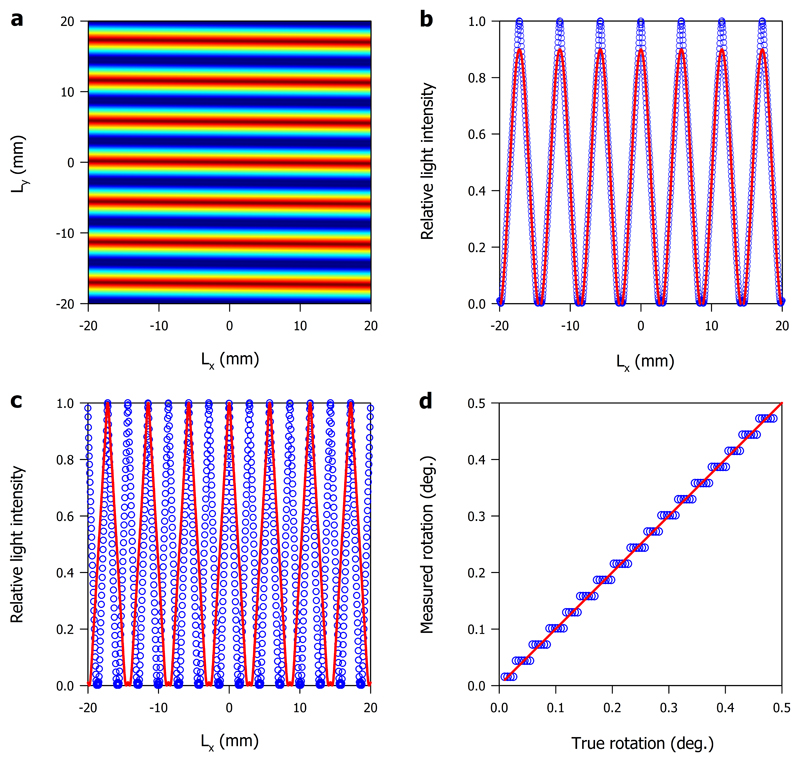
The extensometer measures rotation across a fracture using the moire patterns produced by two sets of superposed linear gratings. As shown in Figure 1 (A-C), these gratings generate a family of parallel interference fringes in which the total number of fringes reflects the rotation angle between the two superposed sets of gratings. Figure 2A shows a theoretical moire pattern generated by two such sets rotated relative to one another by one degree, calculated from Equation 3. This plot covers an area of 4 cm x 4 cm and has used a grating periodicity of 0.1 mm. Figure 2B compares two light intensity profiles in which the sum of Equation 3 has been extended from the first term, n = 1, to n = 11. These terms, in practise, represent two measures of numerical accuracy and concomitant computational cost: n = 1 represents the simplest possible graphical representation while n = 11 offers a more detailed representation at the cost of ten additional numerical iterations. The two intensity profiles demonstrate that only a minor improvement results from extending the sum beyond the first term. Therefore, selecting n = 1 is sufficient to reproduce the fundamental features of the parallel moire patterns: the number and location of the oscillations and the intensity of the transmitted light. Figure 2C emphasises the remarkable rotational sensitivity of the two sets of superposed linear gratings using two light intensity profiles in which the open circles and solid red line correspond to a relative rotational change of one degree.

Figure 2.

(A) A theoretical moire pattern generated by two sets of superposed linear gratings rotated relative to one another by 1°. (B) Two light intensity profiles extracted using n = 1, represented by a solid red line, and adding from n = 1 to n = 11, represented by open circles. (C) Two light intensity profiles in which the open circles and solid red line correspond to a one degree increase in the angle of mutual rotation. (D) Measured rotation plotted against true rotation comparing a procedure in which the rotation is obtained by fringe counting, represented by open circles, against a generic full profile fitting procedure, represented by a solid red line.

It is important to describe how this quantitative information is extracted from the aforementioned parallel moire patterns. Once the number of fringes on both pairs of glass plates is known, it is possible to use a simple trigonometric transformation to quantify the amount of rotation in both the horizontal and vertical planes [16]. The precision of the rotation measurements is a function of the linear grating density which has always remained constant at one hundred lines per mm. However, despite this consistency, two slightly conflicting figures are reported in the literature: 1.6*10^-4 rad [21,30] and 3.2*10^-4 rad [22,32]. Figure 2D compares the fringe counting procedure against a generic profile fitting procedure using theoretically measured rotation plotted against true rotation. This figure shows that it is possible to significantly improve instrumental sensitivity by fitting an entire image instead of manually counting individual fringes: although the finite camera acquisition resolution renders small steps in the profile fitting procedure these are undoubtedly far smaller than those rendered by the manual counting of individual moire fringes. This improvement may be of crucial importance when trying to detect very small perturbations in the rotational behaviour of a geological fracture. In Section 4 it is demonstrated that the ultimate instrumental resolution for measuring rotations is in the order of 8.7*10^-5 rad.

3.2. Circular gratings

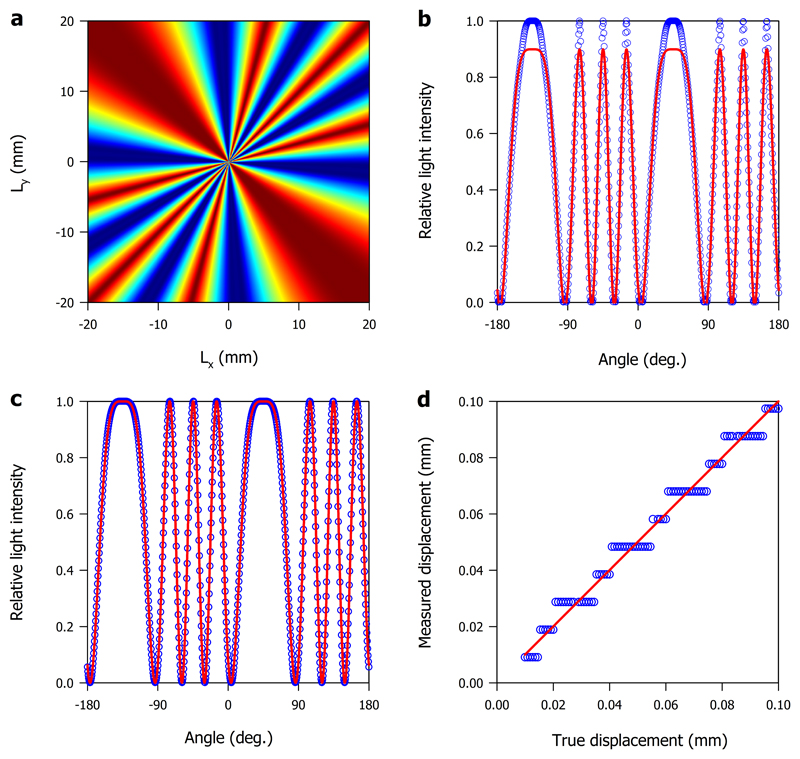
The extensometer measures displacement across a fracture using the moire patterns produced by two sets of superposed circular gratings. As shown in Figure 1 (D-F), these gratings generate a family of hyperbolic interference fringes in which the total number of fringes reflects the centre to centre distance between the individual plates while the symmetry of the fringes indicates the direction of the displacement [6]. Figure 3A shows a theoretical moire pattern generated by two such sets displaced relative to one another by 200 μm along a principal axis orientated NW-SE, calculated from Equation 3. This plot covers the same area and has used the same grating periodicity as in Figure 2A. Figure 3B compares two light intensity profiles for the selected cases of n = 1 and n = 11. These profiles, as with those extracted from the linear gratings, demonstrate that selecting the first term, n = 1, is sufficient to reproduce the fundamental features of the parallel moire patterns: the number and location of the oscillations and the intensity of the transmitted light. However, in contrast those generated by the linear gratings, the moire patterns generated by the circular gratings present a radial dependence near the centre of the hyperbolic fringes. It is, therefore, important to assess the distance at which profiles can be extracted as this ensures that sets of profiles can be averaged at specific radial distances without compromising the extracted data. Figure 3C illustrates this radial dependence using two light intensity profiles extracted from two sets of superposed circular gratings in which the open circles were taken at a distance of R = 1 cm and the solid red line was taken at a distance of R = 2 cm. The fact that these profiles produce the same results has two implications: first, the information contained in the profile can be averaged with a concomitant benefit on the signal to noise ratio and, second, any increase in the diameter of the concentric gratings would not improve the instrumental performance.

Figure 3.

(A) A theoretical moire pattern generated by two sets of superposed circular gratings displaced relative to one another by 200 μm along a principal axis orientated NW-SE. (B) Two light intensity profiles extracted using n = 1, represented by a solid red line, and adding from n = 1 to n = 11, represented by open circles. (C) Two light intensity profiles in which the open circles were extracted at a distance of R = 1 cm and the solid red line was extracted at a distance of R = 2 cm. (D) Measured displacement plotted against true displacement comparing a procedure in which the displacement is obtained by fringe counting, represented by open circles, against a generic full profile fitting procedure, represented by a solid red line.

It is again important to describe how this quantitative information is extracted from the aforementioned hyperbolic moire patterns. Once again the number of fringes on both pairs of glass plates allows the use of a simple transformation to quantify the amount of displacement in three dimensions [16]. These represent fundamental geological variables: the x-coordinate represents dilation or constriction across the fracture; the y-coordinate represents sinistral or dextral displacement; and the z-coordinate represents normal or reverse displacement. The resolution of the displacement measurements is a function of the circular grating density, which can range from twenty to eighty lines per mm. This disparity partly explains the broad spectrum of claims concerning instrumental resolution that abound in the literature, which range from 50 μm [22,25] down to 7 μm [17,33]. Figure 3D, in the same manner as Figure 2D, compares the fringe counting procedure against a generic profile fitting procedure using theoretically measured displacement plotted against true displacement. Once again this shows that it is possible to significantly improve instrumental sensitivity by fitting an entire image instead of manually counting individual fringes. In the following section it is demonstrated that the ultimate instrumental resolution for measuring displacements is less than 5 μm.

4. Defining instrumental sensitivity and resolution

In Section 2 we defined an analytical solution for the complete interpretation of a generic moire pattern and in Section 3 we defined a set of mathematical approximations for the moire patterns used to measure rotation and displacement. It is now possible to determine the ultimate instrumental sensitivity limits and the resolution of the rotational and displacement measurements of this extensometer in light of recent automatisation. At this point we should emphasise that absolutely none of the mechanical elements of the extensometer, including its glass plates, have been modified as a result of automatisation. By envisaging a least squares fitting procedure for quantitative data extraction, the ultimate instrumental resolution may be constrained by experimental limitations such as: the size of the moire gratings; the camera bit colour depth resolution; the camera lateral resolution; and the assigned computational, data storage, and communications bandwidth capacity. These parameters can be tuned so that the fitting capacity nears submicron sensitivity. However, any such aspirations have to be balanced against the cost of achieving them and, therefore, the ultimate limits of instrumental sensitivity are based on acceptable, rather than optimal, performance.

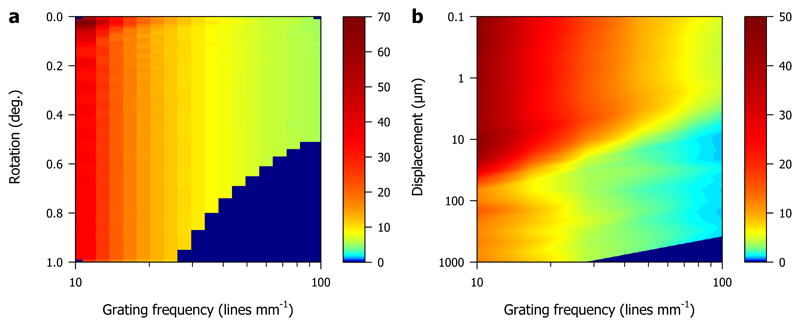
The parameters incorporated here correspond to: grating frequencies that range from ten lines per mm to one hundred lines per mm; typical displacement magnitudes that range from 0.1 μm to 1000 μm; fixed 720-step profile extraction for both the linear and circular gratings, which is feasible with the vast majority of affordable two-megapixel cameras with 8 bit colour depth photographing areas of 5 x 5 cm; imposing a minimum difference of one hundred digital steps change on the profile extracted from the imaged moire pattern. The latter ensures that the initial profile and the modified profile are sufficiently different to be detected. In practise, irrespective of whether data are being extracted from parallel or hyperbolic moire patterns, each oscillation must keep a minimum amount of data points in order for it to be detected and analysed accurately. It is, therefore, necessary to declare how many data points constitute one oscillation so that two consecutive fringes are properly resolved. A trial and error approach using actual datasets has indicated that this value ranges from five to ten data points per oscillation. It is proposed that a circumspect resolution limit of ten data points per oscillation should be accepted. Anything below this limit poses a risk to subsequent automated data analysis and, therefore, the plots in Figure 4, detailed in the following paragraphs, both contain a triangular area denoted as the camera resolution limit. This represents the region in which it is not possible to reliably detect oscillations.

Figure 4.

(A) The rotation resolution of the automated instrument in degrees as a function of the various parameters described in Section 4. (B) The displacement resolution of the automated instrument in μm as a function of the various parameters described in Section 4. The black areas to the bottom right of each plot indicate regions excluded due to the limited resolution of the image acquisition.

The resolution of the rotation measurements is defined on the basis of numerical simulations made with realistic camera settings. Figure 4A shows this resolution, i.e. the smallest detectable change, for a range of grating densities on the horizontal axis and, significantly, the slight dependence of the resolution on the already accumulated rotation on the vertical axis. Inspection of this plot reveals that the maximum angular resolution of the instrument is in the order of 8.7*10^-5 rad. This figure is reasonably consistent with those given previously for the moire extensometer. Until now, the density of the linear gratings etched into the glass plates has always remained constant at one hundred lines per mm, but this plot may enable future monitoring projects to select a more suitable linear grating density according to the anticipated amount of rotation: it can be seen that the instrumental rotation resolution improves with higher grating densities but higher grating densities reduce the potential measuring range. This limitation reflects the fact that greater numbers of fringes cannot be resolved by conventional digital imaging sensors.

The resolution of the displacement measurements is again defined on the basis of numerical simulations made with realistic camera settings. Figure 4B shows this resolution for a range of grating densities on the horizontal axis and, significantly, the dependence of the resolution on the already accumulated displacement on the vertical axis. Inspection of this plot reveals that, for practical grating densities, the displacement resolution of the instrument is less than 5 μm. This figure is again reasonably consistent with those given previously for the moire extensometer. The density of the circular gratings etched into the glass plates may range from twenty to eighty lines per mm. In part the density is selected to reflect the behaviour of the monitored fracture and in part it also reflects the technological advances needed to etch more closely spaced gratings. This plot may again enable future fracture monitoring projects to select a more suitable circular grating density according to the anticipated amount of displacement. It can be seen that the instrumental displacement resolution improves with higher grating densities. Increasing the grating density beyond one hundred lines per mm does not offer a significant benefit as the greater number of fringes cannot be resolved by conventional digital imagining sensors. On the basis of the foregoing we recommend an initial offset of 100 μm.

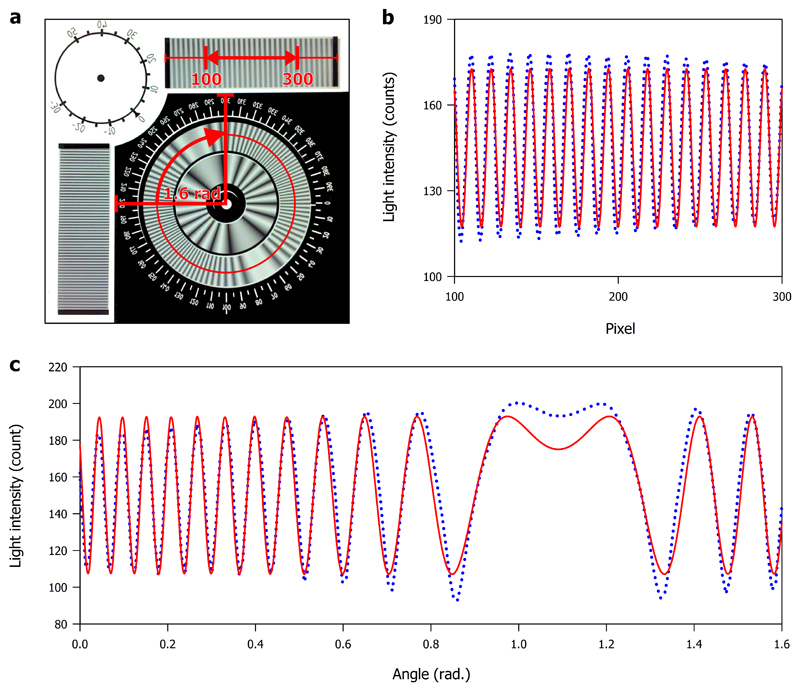
It is, finally, important to compare our theoretical modelling of the moire patterns with the actual interference fringes. Figure 5A presents a real example of an image captured by the automated extensometer. The rotations are obtained from two sets of superposed linear gratings, with an actual width of 3.1 cm, which have each been etched with a density of one hundred lines per mm. The parallel fringes resemble the theoretically generated fringes presented in Figure 2A. The displacements are obtained from two sets of superposed circular gratings, with an actual width of 3.5 cm, which have each been etched with a density of eighty lines per mm. The hyperbolic fringes resemble the theoretically generated fringes presented in Figure 3A. Figure 5B demonstrates that a generic least squares fitting procedure renders a curve which satisfactorily overprints the experimental data points, represented by a solid red line, obtained from the superimposed linear gratings shown in Figure 5A. In this example, the observed angular rotation is in the order of 7.8*10^-3 rad. Figure 5C demonstrates that a generic least squares fitting procedure again renders a curve which satisfactorily overprints the experimental data points, represented by a solid red line, obtained from the superimposed circular gratings shown in Figure 5A. In this example, the observed displacement is 221 μm while the direction of the displacement is 62.48°.

Figure 5.

(A) A real example of an image captured from the automated extensometer. This shows the parallel moire patterns generated by two sets of superposed linear gratings, etched at one hundred lines per mm, and the hyperbolic moire pattern generated by two sets of superposed circular gratings, etched at eighty lines per mm. (B) The extracted light intensity profile extracted from the linear gratings, between 100 and 300 pixels, and the corresponding least squares fitting of the data using Equation 3. Only half the total profile is presented in order to highlight the correspondence between the experimental and modelled results. (C) The extracted light intensity profile extracted from the circular gratings, between 200 and 300 grad (= 1.6 rad), and the corresponding least squares fitting of the data using Equation 3. It should be noted that only the outer corona is used for the fitting procedure. Only a quarter of the total profile is presented in order to highlight the correspondence between the experimental and modelled results.

The spiral grids may develop asymmetric hyperbolic fringe patterns once the instrument has been installed in the field. Such asymmetry usually reflects an imperfect contact between the glass plates and this may be caused by, for example, perturbations in the planarity of the glass plates, particulates trapped between the glass plates, improper clamping of the glass plates, or rotation of the instrument during monitoring. Asymmetry in the hyperbolic fringe pattern makes it more difficult to define the principal axis and this is significant because the principal axis represents the direction of the displacement. Marti et al. (2013) presented an algorithm for processing symmetrical hyperbolic fringe patterns on the basis of a double fold strategy. This algorithm is also perfectly adept at processing asymmetrical hyperbolic fringe patterns. The algorithm uses a trial and error approach to consider all possible angles and then the angle which matches most closely is known to define either the principal axis or the axis perpendicular to it. Then the algorithm counts the density of critical points, i.e. maxima or minima per unit angle, and defines the principal axis at that with the lowest density of critical points. When the hyperbolic fringe pattern is asymmetric, the double fold strategy cannot produce a perfect match, but the trial and error approach ensures that a closer match cannot be made.

5. Conclusions

Fracture monitoring represents an important theme in basic and applied geological research but there are only a limited number of instruments which are able to record movements in more than one dimension. In this paper we have assessed the instrumental resolution of a moire extensometer in light of its recent automatisation. The instrument uses moire patterns to measure rotations in two perpendicular planes and displacements in three dimensions. This assessment determined an analytical solution for the complete interpretation of a generic moire pattern. The solution is valid for any moire pattern and contains no loss of fidelity within the random phase approximation. It then determined a set of mathematical approximations for the moire patterns needed to measure rotation and displacement. In turn it was found that the instrumental sensitivity improves significantly as a result of using a generic profile fitting procedure. The resolution of the rotation and displacement measurements were then calculated on the basis of realistic, rather than optimal, scenarios. It was demonstrated that the automated extensometer attains realistic rotation resolutions in the order of 8.7*10^-5 rad and realistic displacement resolutions of less than 5 μm. The novelty of the manuscript lies in the fact it enables users of the automated extensometer to compare their experimentally derived images with the presented mathematical model in order to calculate the amount of rotation and displacement. To model the data, we use our mathematical description of the moire patterns, while a standard least squares procedure renders the best fit. This study represents the first step towards a numerical global repository for processed data recorded by the automated extensometers.