Measuring Magnetically-Tuned Ferroelectric Polarization in Liquid Crystals

Abstract

Materials showing coupling phenomena between magnetism and (ferro)electricity, i.e., magnetoelectric effects, have attracted a great deal of attention due to their potential applications for future device technologies such as sensors and storage. However, conventional approaches, which usually utilize materials containing magnetic metal ions (or radicals), have a major problem: only a few materials have been found to show the coupling phenomena at room temperature. Recently, we proposed a new approach to achieve room-temperature magnetoelectrics. In contrast to conventional approaches, our alternative proposal focuses on a completely different material, a "liquid crystal", free from magnetic metal ions. In such liquid crystals, a magnetic field can be utilized to control the orientational state of constituent molecules and the corresponding electric polarization through magnetic anisotropy of the molecules; it is an unprecedented mechanism of the magnetoelectric effect. In this context, this paper provides a protocol to measure ferroelectric properties induced by a magnetic field, that is, the direct magnetoelectric effect, in a liquid crystal. With the method detailed here, we successfully detected magnetically-tuned electric polarization in the chiral smectic C phase of a liquid crystal at room temperature. Taken together with the flexibility of constituent molecules, which directly affects the magnetoelectric responses, the introduced method will serve to allow liquid crystal cells to acquire more functions as room-temperature magnetoelectrics and associated optical materials.

Download video file ^{(50.5MB, mp4)}

Introduction

Research on the magnetoelectric (ME) effect, the induction of electric polarization (magnetization) by a magnetic (electric) field, has been focused towards the novel types of applications such as sensors and storage technologies. With recent studies on ME multiferroics1,2,3,4, the target systems in the field of ME study are extended to various types of solid-state materials, including inorganic, organic, and metal-organic frameworks, by utilizing spin-lattice couplings dexterously5,6,7,8,9. However, room-temperature operation, which must be accomplished for practical utilization of ME materials with their ME couplings, is still a challenging issue, and a very limited number of single-phase materials have been reported as room-temperature magnetoelectrics to date10.

Liquid crystals, which possess an orientational order, sometimes with a partial positional one, have also been examined with respect to ME materials in recent years11,12,13,14,15. One of the advantages of liquid crystals as ME materials is their operation temperature, as liquid-crystal phases are typically stabilized around room temperature. An example of ME liquid crystals reported so far is a composite between magnetic nano-platelets with perpendicular magnetic anisotropy and liquid crystals showing the nematic phase, known as the simplest liquid-crystal phase possessing only one-dimensional orientational order15. It shows the converse ME effect, the induction of magnetization by an electric field, through the electric-field manipulation of the coupled platelet and molecular orientations.

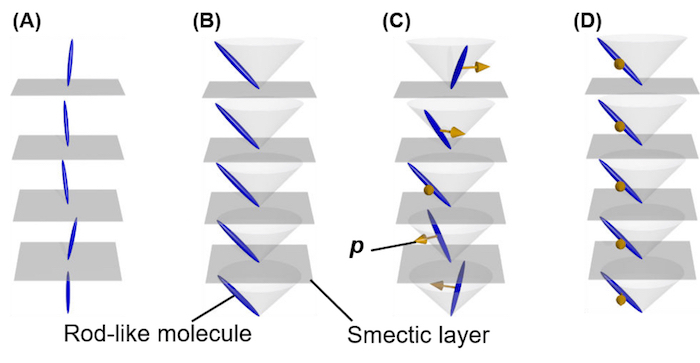
More recently, another unique strategy to establish the ME effect in liquid crystals was proposed16. The focus of this strategy is to create a chiral smectic C (SmC*) phase with one-dimensional positional order, resulting in a diffused layer structure called the smectic layer. One characteristic of the SmC* phase is that a molecular orientation vector n is coupled with a local electric dipole moment p. This correlation is provided by the combination of tilted orientation of the rod-like constituent molecules with respect to the smectic layer normal n₀ and the chirality-induced mirror (and inversion) symmetry breaking in the molecules. From the viewpoint of symmetries, the former changes the symmetry from D_∞h (the so-called SmA phase, Figure 1A) into C_2h (the so-called SmC phase, Figure 1B), and the latter breaks the mirror symmetry of C_2h so that the symmetry is reduced into C₂ (the SmC* phase, see each layer in Figure 1C). In each SmC* layer, the presence of finite polarization is allowed along the C₂ axis, which is normal to both n₀ and n. The strong coupling between n and p is essential for ferroelectricity in liquid crystals. In the SmC* phase, n aligns in the helicoidal manner through layer by layer (Figure 1C), and thus there is no macroscopic polarization. Ferroelectricity in such liquid crystals is achieved by using strong surface effects, which stabilize the homogeneously oriented state of n known as a surface-stabilized ferroelectric liquid-crystal (SSFLC) state (Figure 1D). It should be noted that ferroelectric polarization reversal always accompanies a switching of the bi-stable orientation states through the coupling between n and p17. As the inverse effect, a change in molecular orientation of the SmC* phase is expected to give rise to a change in electric polarization. Through magnetic anisotropy caused by spins on magnetic elements and/or aromatic rings in liquid-crystal molecules and the flexibility of n in a liquid-crystal state due to weaker molecular interactions than in a solid crystal state, n is also tunable by a magnetic field. Thus, the SmC* phase can be transformed into a magnetic-field-induced homogeneously oriented state similar to an SSFLC state. Therefore, the direct ME effect, the induction of electric polarization by a magnetic field, is achieved as the development of macroscopic electric polarization is induced by a homogeneous alignment of n coupled with p, in all the layers.

We introduce procedures to prepare liquid-crystal cells for the investigation of ME couplings and methodologies to detect the ME effect. A method for the preparation of liquid-crystal cells was reported in detail previously18. Here, we modified this method for dielectric and ME measurements. With the method detailed here, we detected magnetically-tuned electric polarization, that is, the direct ME effect, in a liquid crystal showing the SmC* phase at room temperature.

Protocol

1. Preparation of Liquid-Crystal Cells and the Determination of the Cell Gap

1. Preparation of liquid-crystal cells

   1. Cut glass substrates coated with indium/tin-oxide (ITO) on one side into the desired size (typical size: 10 x 10 x 1.1 mm, Figure 2A). To cut the substrates, scratch a line on their face with a glass cutter and break off excess glass manually.
   2. Wash the cut glass substrates using a detergent in an ultrasonic bath at 35 kHz for 30 min. Rinse them with deionized water in the ultrasonic bath for 10 min. Replace deionized water and rinse the substrates 5 times to remove contaminants (Figure 2B). Blow off remaining water with an air-duster-gun with care not to touch the widest faces of the substrates.
   3. Drip polyimide solutions (alignment layer planer in Table of Materials) onto the ITO-coated side of the washed substrates, and spin-coat the solutions at 5000 rpm for 30 s (Figure 2C). Bake the substrates at 200 °C for 1 h to remove the solvent and cure the polyimide thin films.
   4. Put the substrates on an XZ stage so that the ITO- and polyimide-coated side of the substrates faces upwards. Place the substrates under a roller covered with a velvet cloth and fix the substrates by air suctioning (Figure 2D). Apply a uniform and soft pressure on the substrates with the roller by adjusting the height of the stage. Note: Here, the XZ stage was made by a machine shop at Osaka University.
   5. Rotate the roller and move the stage back and forth under the roller 5 times along the horizontal direction to rub the substrates by the velvet cloth. Dip the rubbed substrates into isopropyl alcohol in a 10 – 50 mL glass container for 1 min to remove contaminants, and dry them at 80 °C for a few minutes.
   6. Glue the two substrates together with 12 μm thickness flat resin films as spacers. Note that adhesive points are placed only at the edge of the substrates and the inner sides of the glued substrates are coated with the ITO and polyimide. Make sure that the opposite substrates have been rubbed antiparallel and are slightly shifted (about 2 mm) to provide enough spaces for electrical terminals on both of the substrates (Figure 2E).
   7. Glue the conducting wires on the above-mentioned spaces for terminals by using silver conducting paste (Figure 2F). Bake the substrates with conductive wires at 150 °C for 1 h to remove the solvent in the silver conductive paste.
2. Determination of cell gap 19

   1. Irradiate the blank cells prepared in 1.1.7 with white light propagating normal to their widest face. Measure the transmission spectra using an optical spectrometer, and observe pseudo-sinusoidal oscillation (Figure 3), which appears due to the Fabry-Pérot effect20.
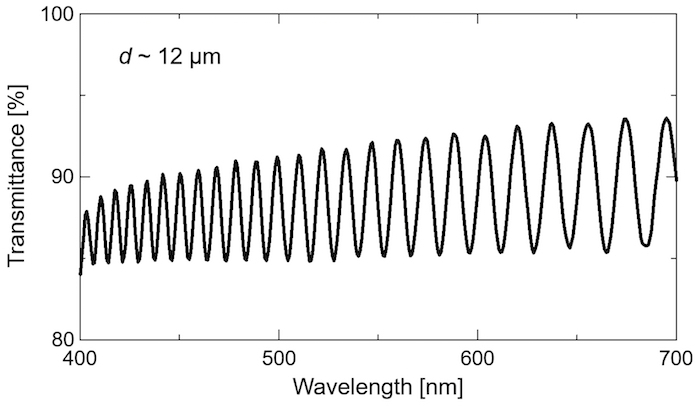
   2. Estimate the cell gap d by using the relationship d = λ₁λ₂/2(λ₂-λ₁), where the wavelengths λ₁ and λ₂ denote a pair of adjacent peak-wavelengths in the transmission spectra.

2. Preparation of the Liquid-crystal Mixture and Introduction into the Cells

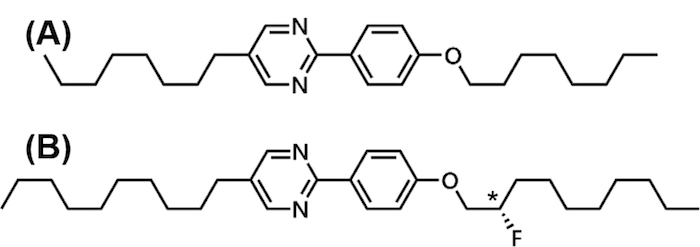
1. Mix two compounds, 5-octyl-2-(4-octyloxyphenyl) pyrimidine (compound 1: Figure 4A) and (S)-5-decyl-2-[4(2-fluorodecyloxy) phenyl] pyrimidine (compound 2: Figure 4B) with a mass ratio of 3:1 in a glass vial. Prepare 100 mg of the solution in total (75 mg of compound 1 and 25 mg of compound 2).

2. Put the prepared blank cell from step 1.1.7 on a hot stage, keeping the temperature at 80 °C, a temperature at which the mixture from 2.1 is in the isotropic liquid phase (Figure 5). Introduce the mixture from step 2.1 into the cell by using a spatula and capillary action. Keep the cell temperature at 80 °C for 30 min, then cool down to room temperature at a rate of about 5 °C/min.

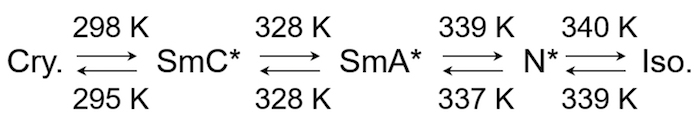
3. Sample Characterization

1. Place a cell filled with the mixture from step 2.2 on a hot stage between two crossed polarizers and irradiate it with light. Observe textures of the mixture with changing temperature from room temperature to 80 °C at a rate of 5 °C/min by using a microscope (and a short-pass filter with tuning range of ~600 nm to enhance the visibility, as necessary), and identify liquid-crystal phases from polarization micrographs21 (Figure 6).

2. Determine the phase transition sequence and transition temperatures from the observed textures (Figure 5). For the SmC* phase, estimate the helicoidal pitch as double the stripe width.

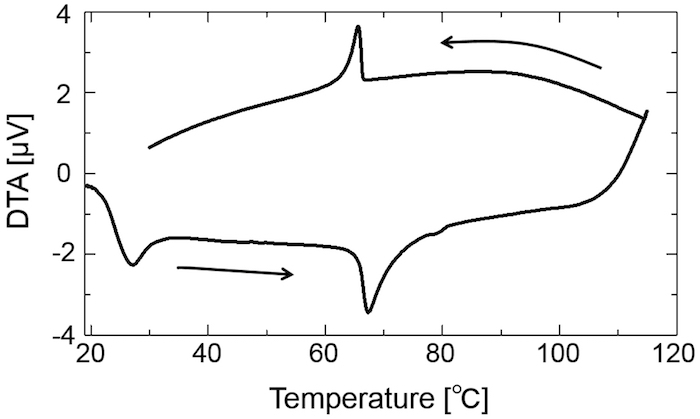
3. Confirm the first-order phase transition temperatures of the mixture prepared in 2.1 by differential thermal analysis (DTA; see Table of Materials and manufacturer’s instructions), which provides a peak (or dip) anomaly at a first-order phase transition (Figure 7).

4. Dielectric and Magnetoelectric Measurements

1. Prepare a commercial superconducting magnet (see Table of Materials) equipped with temperature controllers (2 - 400 K) and magnetic field (up to 9 T).

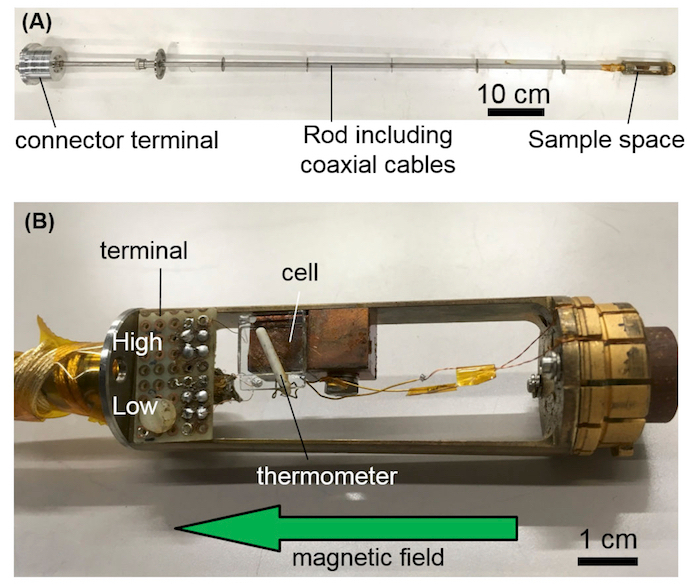
2. Prepare a homemade insert for the superconducting magnet, which consists of three major parts: sample space, a rod including four coaxial cables, and a connector terminal (Figure 8A).

3. Glue the cell prepared in 2.2 on the sample space of the insert (Figure 8B). Connect the two conductive wires of the cell to the terminals (high and low) of the sample space by soldering. Make sure of the cell orientation so as to apply a magnetic field in the direction parallel to the substrates of the cell. Place a thermometer on the widest plane of the cell in order to measure the sample temperature accurately and introduce the insert into the superconducting magnet.

4. Connect the connecter terminals to an LCR meter (see Table of Materials) with coaxial cables. Measure the dielectric constant as a function of temperature and magnetic field by means of quasi-four terminal methods with the LCR meter (see manufacturer’s instructions and our previous work16).

5. Connect the connecter terminals to an electrometer (see Table of Materials) with coaxial cables. Measure the magnetic-field and temperature dependence of displacement current with the electrometer while sweeping a magnetic field and temperature at a constant rate (1.0 T/min for sweeping magnetic field and 5 K/min for sweeping temperature; see manufacturer’s instructions and our previous work16). Obtain electric polarization by integrating the displacement current as a function of time.

Representative Results

The protocol is deemed a success only if the ME effect in liquid-crystal samples is observed. Here we measured the direct ME effect in a liquid-crystal sample prepared by the aforementioned procedures. For the measurements, an in-plane magnetic field was applied with the angle tilted by about 45° from the rubbing direction (normal to smectic layers), because the largest magnetic-field-induced polarization was detected in this configuration16.

Figure 9A shows the temperature profiles of electric polarization. In the SmA* phase, no electric polarization develops either with or without a magnetic field, meaning that the SmA* phase is not magnetoelectric. This result is well explained by the isotropy in the plane perpendicular to the principal axis, which is normal to the smectic layers, of the SmA* phase with point group D_∞ (consider mirror symmetry breaking from D_∞h of the SmA phase). In the SmC* phase, on the other hand, finite polarization develops by applying magnetic fields. This result demonstrates an ME coupling in the SmC* phase of the liquid crystal and suggests the modification in the molecular orientation state from the simple helicoidal state in which the sum of p in the respective layers cancels out.

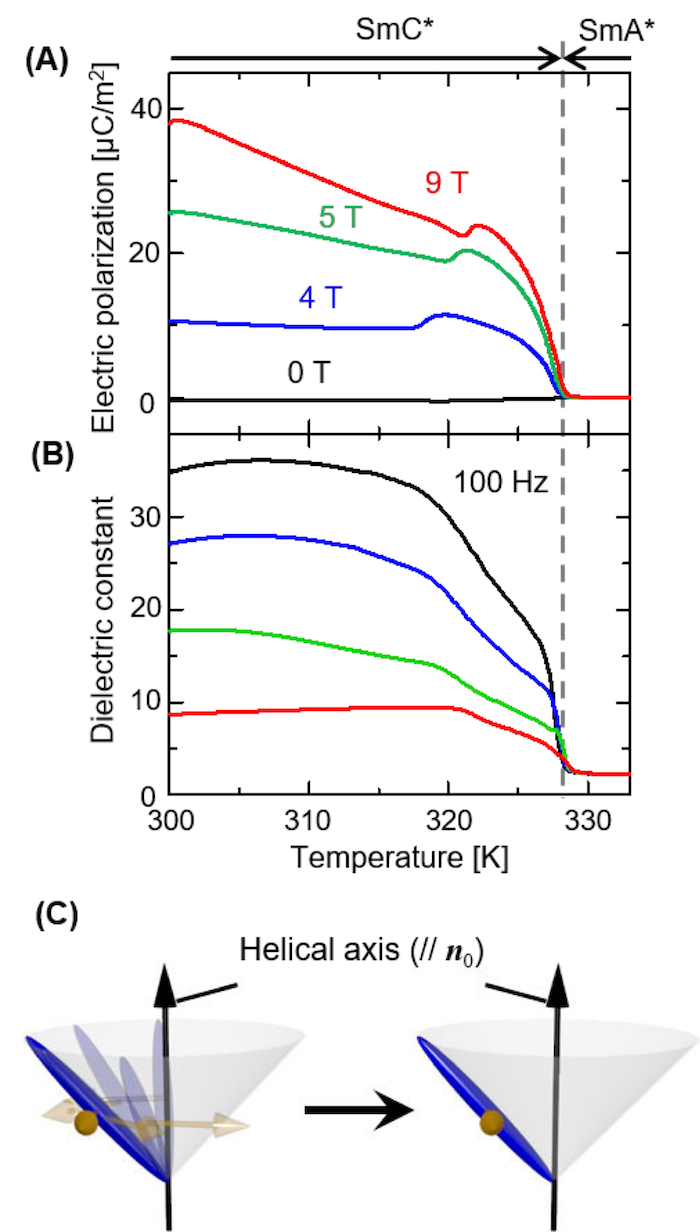
In contrast to the development of electric polarization, the characteristic enhancement of dielectric constant in the SmC* phase is suppressed by a magnetic field (Figure 9B). The enhancement in SmC* is ascribed to the so-called Goldstone mode, which is known as a characteristic mode in the SmC* phase22,23. This mode corresponds to the phase fluctuations in the azimuthal orientation of the tilted direction (left panel of Figure 9C). This mode is suppressed by applying a magnetic field (right panel of Figure 9C) due to magnetic anisotropy of constituent molecules, which prefers a parallel arrangement of n with a magnetic field, as reported previously24,25,26,27. The suppression of the Goldstone mode indicates that a phase transition takes place from the SmC* phase to a field-induced phase that is similar to an SSFLC state (Figure 1D). Thus, the application of a magnetic field induces a homogeneously oriented state of n, which was named the magnetic-field-induced ferroelectric liquid-crystal (MIFLC) state16.

To obtain a straightforward result showing ME activity of the target, we examined magnetic-field dependence of electric polarization at fixed temperature. As a result, it was found that magnetically induced electric polarization is present in the SmC* phase while absent in the SmA* phase (Figure 10A). This provides a direct evidence of the ME activity of the mixture studied here in the SmC* phase, that is, magnetically-tuned ferroelectric polarization in a liquid crystal. The suppression of dielectric constant by a magnetic field is apparent (Figure 10B), giving further evidence of the realization of the MIFLC state in the magnetic field (Figure 10C).

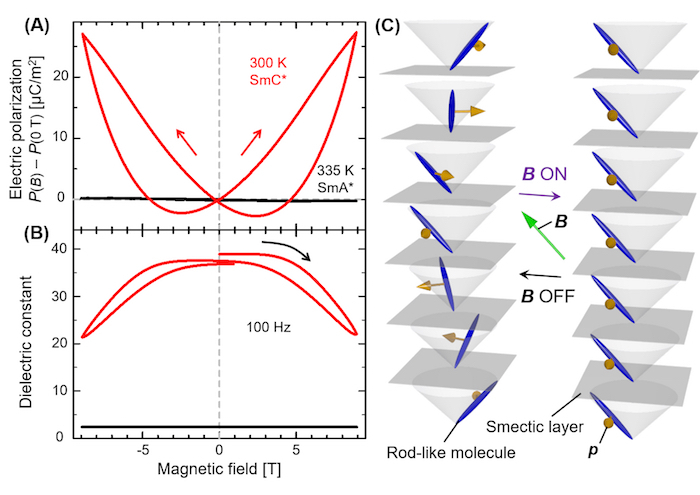
Figure 1: Schematics of molecular orientation states in several smectic liquid-crystal phases.(A) The SmA, (B) SmC, and (C) SmC* phases, and (D) an SSFLC state. Blue rods, gray planes, and ocher arrows represent average orientation of rod-like molecules, smectic layers, and electric dipole moments, respectively. Here constituent molecules are achiral for (A) and (B) and chiral for (C) and (D). Please click here to view a larger version of this figure.

Figure 2: Preparation of liquid-crystal cells for measurements of ME effect.(A) Cutting and (B) cleaning of ITO-coated glass substrates in an ultrasonic bath. (C) Spin-coating of polyimide on the ITO-coated side of the substrates. (D) Rubbing of the substrates by a velvet cloth to make liquid-crystal molecules align along a single direction. (E) Gluing of the substrates by an epoxy resin with spacers, and (F) that of the substrates and conductive wires by silver paste. Please click here to view a larger version of this figure.

Figure 3: Transmission spectrum of a blank cell. The cell gap (d) can be estimated from the wavelengths at local maxima in the spectrum (see text). Please click here to view a larger version of this figure.

Figure 4: Molecular structures of the compounds used in this study. (A) 5-octyl-2-(4-octyloxyphenyl) pyrimidine and (B) (S)-5-decyl-2-[4(2-fluorodecyloxy) phenyl] pyrimidine. Please click here to view a larger version of this figure.

Figure 5: The phase transition sequence of the mixture from step 2.1. Here, Cry., N*, and Iso., denote crystalline, chiral nematic, and isotropic liquid phases, respectively. Numerical values represent the phase transition temperatures. Please click here to view a larger version of this figure.

Figure 6: Polarization micrographs of textures of the mixture. Micrographs of (A) SmC*, (B) SmA*, (C) N*, and (D) Iso. phases. The images of (A) and (B) were taken in the same sample area with light passing through a short-pass filter and have been modified from Ueda et al. 201716. The filter was utilized to enhance the visibility of the periodic structure in the SmC* phase. A and P denote the directions of two crossed polarizers sandwiching the sample. The images in (C) and (D) were obtained without the filter. Please click here to view a larger version of this figure.

Figure 7: Differential thermal analysis (DTA) on the mixture. Asterisks indicate peak (or dip) anomalies observed in DTA, which correspond to first-order phase transition temperatures. Please click here to view a larger version of this figure.

Figure 8: Photographs of the setup for ME measurements. (A) A photo of the homemade insert for a superconducting magnet and (B) an enlarged view of the insert in the sample space. Please click here to view a larger version of this figure.

Figure 9: Temperature profiles of dielectric properties and magnetic field suppression of the Goldstone mode. (A) Electric polarization and (B) dielectric constant taken at 100 Hz in selected magnetic fields. (C) A schematic illustration of the suppression of the Goldstone mode. This figure has been modified from Ueda et al. 201716. Please click here to view a larger version of this figure.

Figure 10: Direct magnetoelectric effect and magnetodielectric effect.(A) Magnetic field profiles of electric polarization and (B) dielectric constant taken at 100 Hz in the SmC* (red, at 300 K) and SmA* (black, at 335 K) phases. (C) Schematic illustration of the operation mechanism of the ME effect observed in this study. A helicoidal molecular orientation state (left panel) is reversibly transformed into a homogeneously molecular oriented state termed an MIFLC state (right panel, see text) by applying a magnetic field B through magnetic anisotropy, where molecular orientation prefers to be parallel to the magnetic field direction. This figure has been modified from Ueda et al. 201716. Please click here to view a larger version of this figure.

Discussion

The experimental results showed that the methods described here successfully demonstrated the ME coupling in the liquid crystal. The observed ME and magneto-dielectric effects can be associated with the orientational transition of molecular orientation in a fixed smectic layer structure. However, the layer normal direction n₀ in the layer structure can be also changed by applying a magnetic field through magnetic anisotropy. This is because the molecules prefer to have a parallel arrangement of n and a magnetic field through their magnetic anisotropy. The parallel arrangement of n₀ and a magnetic field is also more stable than the helicoidal state in the SmC* phase, as the MIFLC state.

To observe the ME and magneto-dielectric effects successfully, proper steps to obtain the SmC* phase are critical. Prior to the respective measurements, the sample is heated up to the isotropic liquid phase and then is cooled down to the SmA* phase at zero magnetic field in order to align the layer normal n₀ along the rubbing direction. Otherwise, a field cooling procedure from the isotropic liquid phase with high fluidity in constituent molecules to the SmA* phase develops a parallel arrangement of n₀ with a magnetic field through magnetic anisotropy of the molecules. Then, a magnetic field is applied in the SmA* or SmC* phase, where a smectic layer structure has well developed, so that we may examine the dielectric property in the smectic phases with a fixed layer structure.

In addition, an appropriate cell-surface effect that is strong enough to fix the smectic layer structure but weak enough to give flexibilities in molecular orientation is also crucial. To achieve an optimum balance between the two states, one has to find the best conditions of a cell-gap length, rubbing strength, and amount of chiral dopant. If the surface effect is too weak, the smectic phase which induces ferroelectricity does not develop. Meanwhile if it is too strong, a robust SSFLC state is stabilized and cannot be tuned by a magnetic field.

In this paper, only the result of a direct ME effect is presented. However, liquid-crystal cells prepared by the protocol can be also utilized to examine a converse ME effect, i.e., electric-field control of magnetism. Furthermore, the ME effect established in liquid crystals so far, including that demonstrated here, accompanies the change in molecular orientation that dominates the optical properties of liquid crystals. Therefore, the magnetic (electric) change in electric polarization (magnetization) is expected to simultaneously provide a magneto- (electro-) optical effect28. The liquid-crystal cells prepared by the present method have transparent electrodes so that such optical properties can be explored together in the same sample.

Liquid-crystal phases typically appear around room temperature, and thus liquid crystals provide a good platform for establishing room-temperature ME activities. Besides, the strategy confirmed here can be applied to any liquid crystals as long as they show SmC* phases. Thus, more sophisticated ME functionalities are expected to be developed by allowing proper choice of target materials.

Disclosures

The authors have nothing to disclose.