Mono-exponential, diffusion kurtosis and stretched exponential diffusion MR imaging response to chemoradiation in newly diagnosed glioblastoma

Abstract

Purpose

To quantify changes and prognostic value of diffusion MRI measurements obtained using mono-exponential, diffusion kurtosis imaging (DKI) and stretched exponential (SE) models prior and after chemoradiation in newly diagnosed glioblastoma (GBM).

Methods

Diffusion-weighted images (DWIs) were acquired in twenty-three patients following surgery, prior chemoradiation and within 7 days following completion of treatment, using b-values ranging from 0 to 5000s/mm². Mono-exponential diffusion (apparent diffusion coefficient: ADC), isotropic (non-directional) DKI model with apparent diffusivity (Dapp) and kurtosis (Kapp) estimates as well as SE model with distributed-diffusion coefficient (DDC) and mean intra-voxel heterogeneity (α) were computed for all patients prior and after chemoradiation. Median values were calculated for normal appearing white matter (NAWM) and contrast-enhancing tumor (CET). The magnitudes of diffusion change prior and after chemoradiation were used to predict overall survival (OS).

Results

Diffusivity in NAWM was consistent for all diffusion measures during chemoradiation, while diffusivity measurements (ADC, Dapp and DDC) within CET changed significantly. A strong positive correlation existed between ADC, Dapp, and DDC measurements prior to chemoradiation; however, this association was weak following chemoradiation, suggesting a more complex microstructural environment after cytotoxic therapy. When combined with baseline tumor volume and MGMT status, age and ADC changes added significant prognostic values, whereas more complex diffusion models did not show significant value in predicting OS.

Conclusions

Despite increased tissue complexity following chemoradiation, advanced diffusion models have longer acquisition times, provide largely comparable measures of diffusivity, and do not appear to provide additional prognostic value compared to mono-exponential ADC maps.

INTRODUCTION

Patients with glioblastoma (GBM) have dismal overall survival, ranging from 5 months for surgical resection alone [1] to between 12 and 18 months with maximal safe resection followed by radiation therapy combined with temozolomide and adjuvant temozolomide [2]. Despite this aggressive treatment, GBM manifest resistance and recurrence is almost always observed. After first line treatment failure, there is no standard of care for recurrent GBM with demonstrable survival benefits [3].

Magnetic resonance imaging (MRI) is a critical tool for both initial diagnosis and clinical management of GBM. Although standard measures of therapeutic efficacy rely on changes in contrast enhancing and/or non-enhancing T2w-FLAIR tumor burden, as outlined in the Response Assessment in Neuro-Oncology (RANO) criteria [4], additional relevant functional information of tumor cellularity may be estimated by diffusion-weighted imaging (DWI), reflecting microscopic diffusion of water molecules. The apparent diffusion coefficient (ADC), dependent on the magnitude of observed water diffusivity or mobility within a tissue, has been shown to be negatively correlated with tumor cellularity [5, 6, 7, 8]. Although an oversimplification, a decrease in ADC is generally thought to represent increased tumor cellularity and areas of proliferative, active tumor [9], while an increased ADC is generally reflective of hypo-cellular tissue characterized by cell destruction, edema, and/or necrosis. ADC has been shown to be useful for the assessment of tumor response in chemoradiation treatment regimens [10, 11, 12].

The classical, simple DWI experiment assumes that diffusion is unrestricted, such that the expected displacement follows a Gaussian distribution, allowing for the application of a mono-exponential model [13, 14]. However, in the brain and other seemingly complex tissues, several obstacles can prevent free water diffusion including cell membranes, the myelin sheath, extracellular matrix proteins, extracellular macromolecules, local molecular charge, and different degrees of membrane permeability [15]. Thus, more sophisticated models were developed to better characterize this complex environment, including diffusion kurtosis imaging (DKI), which models both the apparent diffusivity (Dapp) as well as kurtosis (Kapp) or deviation from Gaussian diffusion [16]. Another model that has shown potential value is the stretched exponential (SE) diffusion model [17, 18], which characterizes a distributed diffusion coefficient (DDC) and diffusion “heterogeneity index” (α, alpha). Although more complex diffusion models may be more accurate in terms of tissue characterization [19, 20], they often require longer acquisition times for additional data as well as greater levels of diffusion-encoding (i.e. b-values) [21], which can be challenging for older MR systems with lower performance gradients and may lead to long echo times and thus lower signal to noise. Thus, questions remain as to the potential added value of these models given these added technical challenges.

The purpose of the current study was to quantify the changes and potential prognostic value of diffusion MRI measurements obtained using mono-exponential, DKI and SE diffusion models before and after chemoradiation in newly diagnosed GBM. Patient age, baseline tumor volume and O₆-methylguanine-DNA methyltransferase (MGMT) status were included in multivariable hazard ratio model to predict overall survival.

METHODS

Patient Characteristics

Twenty-three patients with histology confirmed newly diagnosed GBM were prospectively enrolled in this NIH-sponsored study between December 19, 2012 and June 8, 2015. All patients met the following inclusion criteria: (1) pathology-confirmed GBM, (2) treatment with standard external beam radiotherapy (typically in 2 Gy fractions given once daily for 5 days over a 6-week period, totaling 60 Gy) and concomitant temozolomide (75 mg/m²/day, 7 days per week during radiotherapy, followed by a 4-week break, then 6–12 cycles of adjuvant therapy at 150 mg/m²/day to 200 mg/m²/day), (3) baseline (postsurgical, pre-chemoradiation) and post-treatment MR images acquired using advanced diffusion MRI, (4) contrast enhancing tumor volume ≥1cm³ for both time points. The MGMT methylation analysis has been performed with previously described protocol [22] standardized as standard of care in our institution. This study was performed in accordance with the Health Insurance Portability and Accountability Act (HIPAA), and all patients signed consent forms approved by the institutional review board (IRB).

Anatomical and Diffusion MRI Acquisition

All MRI scans were acquired using a 3T scanner (Trio MAGNETOM; Siemens Healthcare, Erlangen, Germany) and all anatomic MRI scans were in adherence to the standardized brain tumor imaging protocol (BTIP) [23]. A T2-weighted fluid-attenuated inversion-recovery (FLAIR) sequence was acquired in the axial plane with the following scan parameters: TR/TE=10810/85ms, flip angle 160°, 50 contiguous slices with a 3mm slice thickness and no interslice gap, a resolution of 0.75×0.75mm with an acquisition matrix of 320×320. A three-dimensional T1-weighted image was obtained using a magnetization-prepared rapid gradient echo (MPRAGE) sequence with the following parameters: TR/TE=2100/2.06ms, 192 contiguous slices with 1mm³ isotropic voxel size, and an acquisition matrix of 256×256. The same 3D-T1w sequence was also acquired after the intravenous injection of a gadolinium contrast agent (gadopentetate dimeglumine, Magnevist; Bayer HealthCare, Wayne, New Jersey) at a concentration of 0.1mmol/kg.

Diffusion-weighted imaging (DWI) was performed prior to the injection of contrast using a single-shot echo-planar imaging sequence in the axial plane. The parameters for the diffusion-weighted scan were: TR/TE=13400/103ms, a flip angle of 90°, 52 contiguous slices, a slice thickness of 3mm and no inter-slice gap, an in-plane resolution of 2mm×2mm with acquisition matrix of 128×128. Ten different b values were acquired: 0, 50, 100, 250, 500, 750, 1000, 2500, 3500 and 5000 s/mm². Non-zero DWIs were collected along the x, y, and z orientations and averaged together (isotropic measurements, non-tensor). The total acquisition time for the DWI scan was 6 minutes.

Post-Processing of Diffusion-Weighted MRI

Mono-exponential diffusion model proposed by Le Bihan et al., [14] assumes non-restricted, Gaussian diffusion providing a measurement of the apparent diffusion coefficient (ADC), as described in the equation:

$$\frac{S_{(b)}}{S_0}=ex{p}^{(-b\cdot \mathit{ADC})}$$ (eq. 1)

where S₀ is the non-diffusion-weighted signal, S_(b) the signal intensity in the presence of a diffusion-encoding gradient, and b is the level of the diffusion weighting. ADC was calculated from a mono-exponential fit that used 3 b values (0, 500 and 1000 s/mm²), which are diffusion weighting strengths typically acquired in clinical practice.

To quantify the diffusion kurtosis in biological tissues, we used all available 10 b-values and previously described method which includes both Gaussian and non-Gaussian diffusion components [16, 21]:

$$\frac{S_{(b)}}{S_0}=ex{p}^{(-b\cdot \mathrm{D}\mathit{app}+\frac{1}{6}{b}^2\cdot \mathrm{D}ap{p}^2\cdot \mathrm{K}\mathit{app})}$$ (eq. 2)

where Dapp is the kurtosis-corrected apparent diffusion coefficient, and Kapp is the apparent kurtosis. Note that a Kapp value of 0 reflects pure Gaussian diffusion (mono-exponential signal decay), while higher Kapp values reflect increasingly hindered and/or restricted diffusion.

The stretched exponential model assumes the diffusion MR signal decay is a continuous distribution of sources with multiple compartments and different rates of decay [17, 18]:

$$\frac{S_{(b)}}{S_0}=ex{p}^{{(-(b\cdot \text{DDC})}^{\mathrm{\alpha }})}$$ (eq. 3)

where distributed diffusion coefficient (DDC, μm²/ms) represents the mean intra-voxel diffusivity and the intra-voxel diffusion heterogeneity (α) represents a single Gaussian compartment when α = 1 and as α → 0, multiple separable proton pools with different diffusivity are present.

Parametric maps of all diffusion models were computed using least squares regressions, with in-house MATLAB scripts (Version 2017a, MathWorks).

Image Registration

All images were registered to the post-contrast T1w image using a 12-degree of freedom-transformation with a mutual-information cost function and a tri-linear interpolation (FLIRT, http://www.fmrib.ox.ac.uk/fsl/; FSL Version 5.3).

Regions of Interest

Two regions of interests (ROI) were segmented using a semi-automatic procedure and the Analysis of Functional NeuroImages (AFNI) software (NIMH Scientific and Statistical Computing Core; Bethesda, MD, USA). These regions of interest comprised normal appearing white matter (NAWM) and contrast-enhancing tumor (CET) from T1+C images. The NAWM ROI selection was based on manual selection of contralateral white matter, while the segmentation of CET was performed using a semi-automatic method, similar to previously described methods [24]. Briefly, a large ROI was drawn over both contrast-enhancing regions on the T1+C (including necrosis). Then, an intensity threshold was manually chosen to extract the CET (without necrosis) from the T1+C images. All volumes are reported in cubic centimeters (cc).

Statistical Analysis

Mean, standard deviation with coefficient of variation or median with interquartile percentile were reported for each fit and ROI. The normality of each distribution was evaluated using Shapiro-Wilk test. For normal distribution, Student’s t test was applied, while non-parametric Wilcoxon-Mann-Whitney test of medians was used when the measurement variable did not meet the normality requirements. A one-way ANOVA and pairwise tests using the Wilcoxon-Mann-Whitney method was used to estimate changes in diffusion measures before and after chemoradiation and differences between diffusion models. Linear regression between diffusivity measures from each diffusion model was performed both before and after chemoradiation to determine whether the correlation characteristics changed following cytotoxic therapy. A Cox multivariable proportional hazards model was used to determine whether any of the clinical characteristics (age at the time of diagnosis, MGMT status or baseline tumor volume) in combination with diffusivity metrics could predict patient survival. As all diffusional fits are performed from the same patient sample, we assessed the predictive value of each fit separately to avoid any errors of co-linearity. Kaplan-Meier curve analyses were used in conjunction with Log-Rank test, to demonstrate OS differences according to diffusion model selected from Cox model. A p<0.05 was considered to indicate a statistically significant result. All the statistics were performed using JMP Pro13 (SAS^®).

RESULTS

The median patient age was 57 years (range, 33–72 years) with a median OS of 666 days (interquartile range, 344–1209 days). All patients demonstrated contrast enhancement on their respective T1w-Gd images. The pre-chemoradiation mean CET volume was 16.7±11.3cc. The mean CET volume was not significantly lower after chemoradiation compared to baseline, pre-chemoradiation scan (14.1±13.3cc, p=0.231, Mann-Whitney).

Fig. 1 displays one responsive GBM patient (OS of 25.7 months) with anatomic T1w-post contrast enhancement, ADC, Dapp, Kapp, α and DDC maps derived from mono-exponential, DKI and SE fits at pre- and post-chemoradiation. This patient shows active tumor regions with contrast enhancement (presented within rectangles) at both time points and consequent changes of diffusivity metrics between pre- and post-chemoradiation. Note that the highest changes were observed using standard measures of ADC (0.202μm²/ms).

Figure 1. Glioblastoma in the left occipital lobe in a 57-year-old woman with 25.7 months of survival.

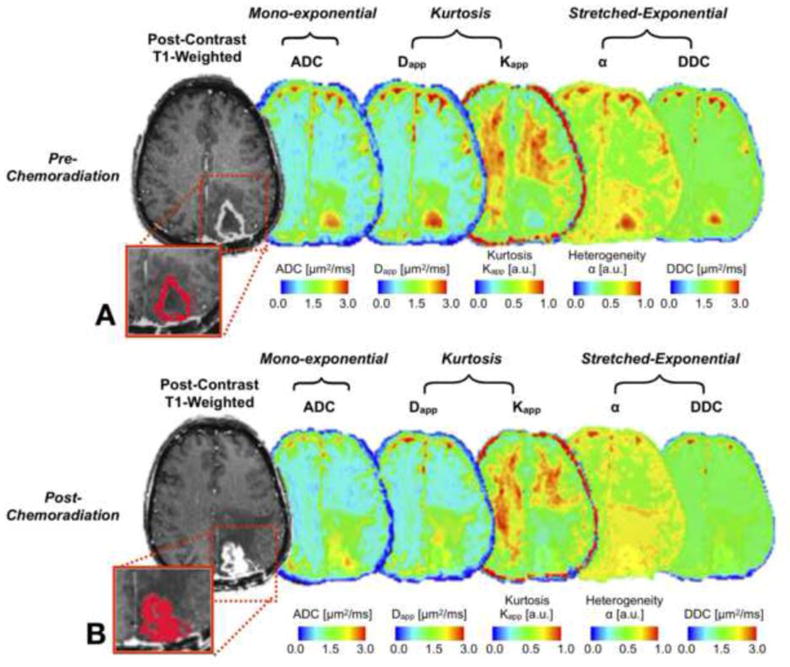
Tumor volumes are overlaid on post-contrast T1w images (in red, within rectangle) for one representative slice. Pre- and post-chemoradiation, post-contrast T1w images show contrast enhancing tumor with central necrosis and perilesional hypo-intense signal intensity, suggesting edema. ADC, Dapp, α and DDC maps exhibit lower values in CET regions compared to central necrosis, while Kapp demonstrates moderate intensity in CET regions. Note that ADC and Dapp maps show high positive changes after chemoradiation. Change in values between pre- and post-chemoradiation time-points: ADC=0.202μm²/ms, Dapp=0.143μm²/ms, Kapp= -0.043, α=0.076 and DDC= − 0.007μm²/ms.

Reproducibility of ADC, Dapp, Kapp, α and DDC values in NAWM

ADC in NAWM was 0.828±0.036μm²/ms at pre-chemoradiation, with no statistical difference compared to the post-chemoradiation time point (0.831±0.049μm²/ms, p=0.865, Fig. 2A). Similarly, Dapp displayed comparable measures at pre- (0.878±0.044μm²/ms) and post-chemoradiation (0.876±0.060μm²/ms, p=0.701, Fig. 2B). No difference in diffusion kurtosis (Kapp) was observed in NAWM between pre- (0.807±0.046) and post-chemoradiation (0.803±0.044, p=0.740, Fig. 2C). The diffusion heterogeity (α) did not change within NAWM between pre- (0.596±0.005) and post-chemoradiation (0.594 ±0.005, p=0.239, Mann-Whitney, Fig. 2E). Additionally, the DDC from the SE model was also similar between the pre- (1.344±0.005μm²/ms) and post-chemoradiation (1.343±0.005μm²/ms, p=0.514, Fig. 2D) time points.

Figure 2. Comparison of different diffusivity measurements (median) within contrast-enhancing tumor (CET) and NAWM regions before and after chemoradiation.

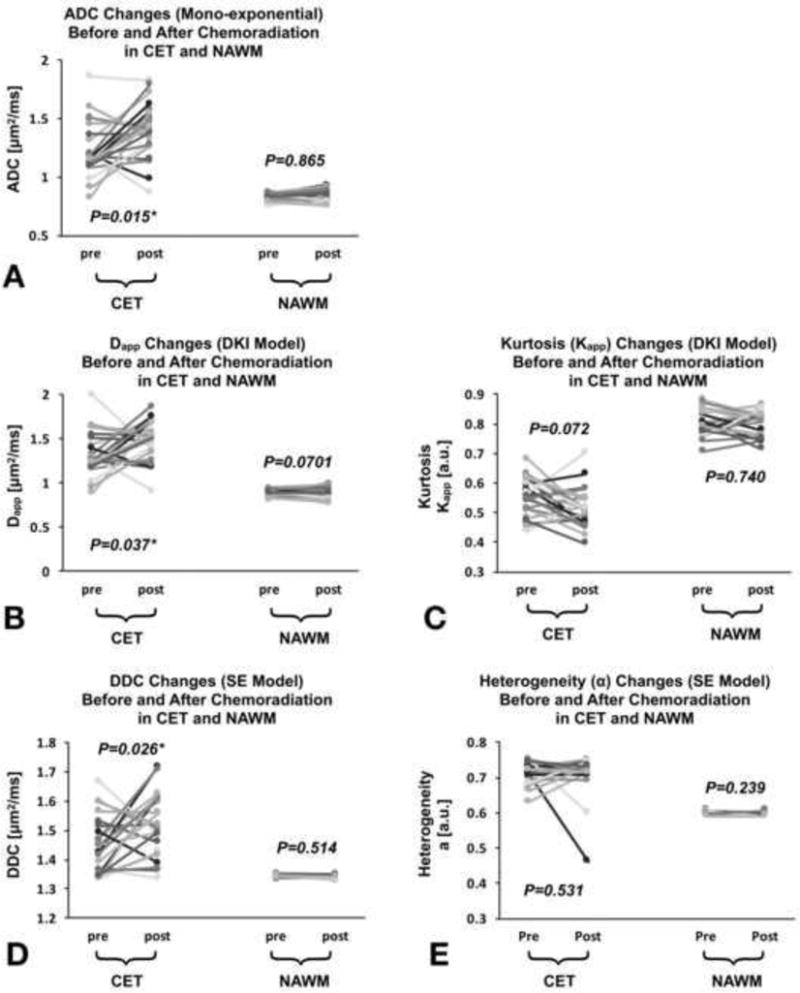
Graphs of ADC (A), Dapp (B), Kapp (C), DDC (D) and α values (E). No differences were found in NAWM from all diffusivity measurement and that across time. ADC, Dapp and DDC were significantly lower within CET before chemoradiation compared with post-chemoradiation, while there were no statistical differences for Kapp and α values. The CET values of ADC, Dapp, α and DDC were significantly higher to NAWM (p<0.0001) at pre- and post-chemoradiation while Kapp maps showing significantly lower values in CET (p<0.0001). The gray scale was used to visualize figures easier.

Despite no significant differences between pre- and post-chemoradiation time points, measures of Dapp using DKI displayed a higher coefficient of variation across patients (5.051 and 6.941% for pre- and post-chemoradiation, respectively) in NAWM tissues compared to ADC (4.463 and 6.008%), Kapp (5.745 and 5.513%), (0.905 and 0.949%) and DDC (0.384 and 0.395%). When comparing NAWM and CET regions, as expected, we observed significantly higher values within CET regions with respect to ADC, Dapp, α and DDC maps for both pre- and post-chemoradiation time points (p<0.0001), while Kapp maps showed significantly lower values in CET regions compared to NAWM (p<0.0001).

Chemoradiation response assessed by ADC, Dapp, Kapp, α, and DDC maps

Tumors showed considerable changes in diffusion metrics following chemoradiation. The mean ADC at pre-chemoradiation was 1.233±0.230μm²/ms, while at post-chemoradiation it was significantly higher (1.406±0.234μm²/ms, p=0.015) (Fig. 2A). Similarly, Dapp at pre-chemoradiation (1.329±0.249μm²/ms) was lower than measures following chemoradiation (1.479±0.221μm²/ms, p=0.037) (Fig. 2B). However, measures of Kapp did not show significant changes within CET regions after chemoradiation (pre: 0.551±0.063; post: 0.515±0.068, p=0.072, Fig. 2C). Comparable to mono-exponential measures of ADC and Dapp, measures of DCC showed a significant increase following chemoradiation (pre: 1.444±0.098μm²/ms; post: 1.511±0.109μm²/ms, p=0.025, Mann-Whitney, Fig. 2D) and intra-voxel homogeneity (α) did not change appreciably when comparing pre- (0.715±0.029) and post-chemoradiation measurements (0.710 ±0.062, p=0.531, Mann-Whitney, Fig. 2E). All quantitative values and are summarized in Supplementary Table A.

Next, the association between measures of diffusivity was explored both before and after chemoradiation. Prior to chemoradiation, a significant correlation was observed between ADC and Dapp in CET regions (R²=0.973, p<0.0001, Fig. 3A). Similarly, pre-treatment measures of ADC and DDC were also highly correlated (R²=0.82, p<0.0001, Fig. 3C). However, despite these significant correlations, absolute measures of diffusivity were not identical as illustrated by the slope of the regression line deviated from both pre- and post-chemoradiation (ADC versus Dapp; 1.078±0.006 and ADC versus DDC; 1.146±0.030, p<0.0001).

Figure 3. Graphs of linear correlation between ADC, Dapp and ADC, DDC within contrast-enhancing tumor (CET) regions before (A and C) and after (B and D) chemoradiation.

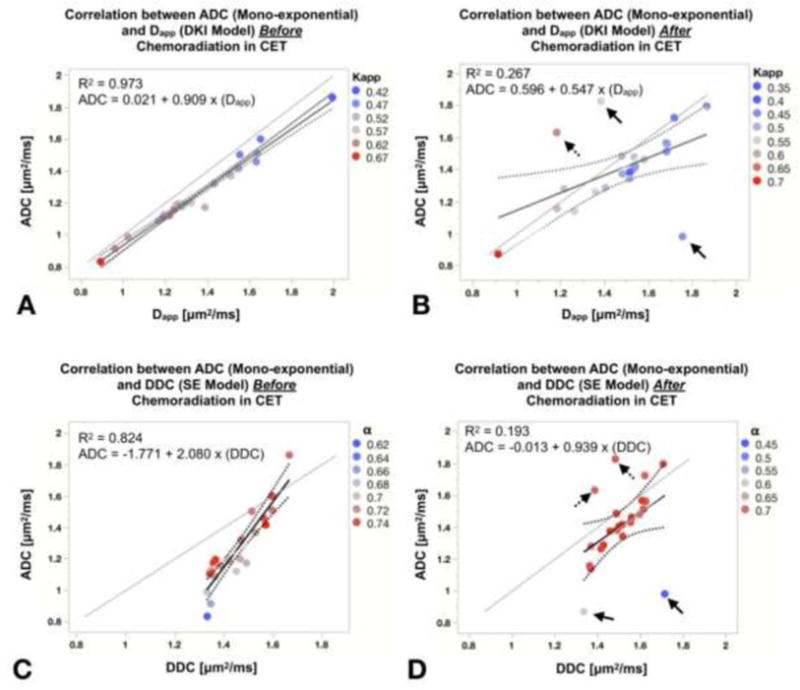
ADC demonstrates a high correlation with other diffusivity measurements at the pre-chemoradiation time point, while increased discordance was observed between ADC and other measures of diffusivity following completion of chemoradiation. Regression parameters are reported for each fit and each marker is color-coded according to the second metric from the same fit (e.g. Kapp values for A). Solid and dashed arrows represent patients with low or high diffusion values than median value of second metric from the same fit. Gray lines indicating the one-to-one relation between each diffusion metrics.

A significant, but weak correlation was observed between ADC and Dapp (r²=0.26, p<0.05 compared to a slope of zero, Fig. 3B). Outliers from a 95% confidence interval appeared to demonstrate high (dashed arrow) or low (solid arrow) Kapp compared with the group median. The correlation between ADC and DDC was also moderate, but still significant, at the post-chemoradiation time point (r²=0.19, p<0.05, Fig. 3D) with obvious outliers that exhibit a wide range of diffusion heterogeneity (α). Similar to pre-treatment scans, absolute measures of diffusivity were correlated but were not identical, as the slope of the regression line was not equal to unity (ADC versus Dapp; 0.793±0.487 and ADC versus DDC; 1.221±0.130, p<0.0001).

Multivariable Cox proportional hazards models suggested tumor volume, MGMT status and diffusion kurtosis or stretched exponential diffusion model parameters were not predictive of OS, while age and slope changes in standard, mono-exponential ADC were significantly predictive (age: HR=0.303, p=0.007 and ADC: HR=1.177, p=0.002) (Table 1). Using the median change in ADC to stratify risk, patients with lower change in ADC had a median survival of 427 days (interquartile range, 344–854 days), while patients with a large increase in ADC had a median OS of 726 days (interquartile range, 536–1350 days). The difference of survival was significant between two groups of patients, with a hazard-ratio of 2.931 (p=0.027, Log-Rank, Fig. 4).

Table 1.

Quantitative measures of all diffusional metrics at pre- and post-chemoradiation.

	Overall Survival
Variables	Hazard ratio	95% CI		p-value
Age	0.303	0.057	0.86	0.007*
CET Volume	0.703	0.415	1.059	0.1
MGMT status	0.02	0	1.658	0.093
ADC slope (μm2/s)	1.177	1.016	1.482	0.002*
Age	0.922	0.766	1.111	0.354
CET Volume	0.963	0.752	1.287	0.751
MGMT status	0.814	0.427	1.123	0.813
Dapp slope (μm2/s)	0.991	0.925	1.033	0.706
Kapp slope (a.u)	0.952	0.744	1.109	0.563
Age	0.924	0.729	1.102	0.371
CET Volume	0.923	0.735	1.151	0.449
MGMT status	0.573	0.03	6.082	0.646
DDC slope (μm2/s)	1.006	0.986	1.029	0.519
α slope (a.u)	1.079	0.81	1.46	0.582

Mean, standard deviation (Std-Dev) and coefficient of variation (CV) were reported for each fit and ROI. The results of normality test (Shapiro-Wilk test) as well as corresponding Student’s or Wilcoxon-Mann-Whitney tests were reported for each fit and ROI

Figure 4. Overall survival by log-rank test based on the median change in ADC between pre- and post-chemoradiation time points.

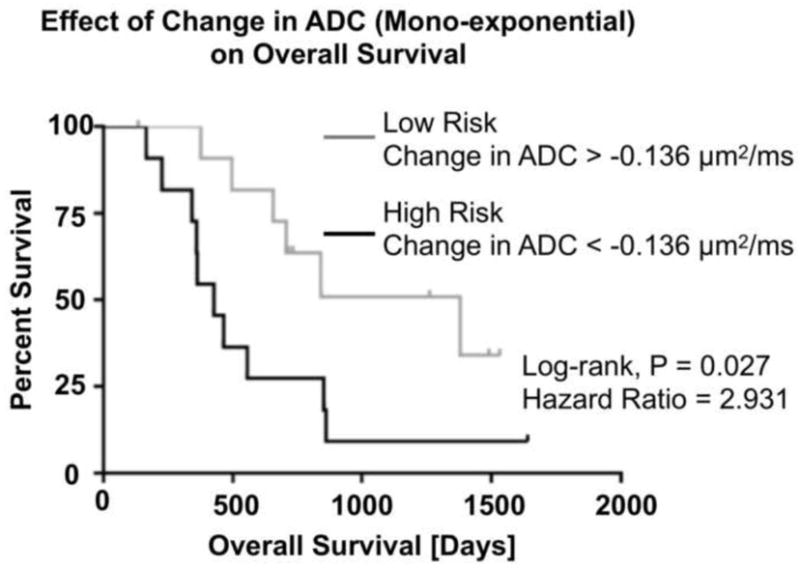
Results suggest patients with large, positive changes in ADC have higher OS compared to stable or decreasing ADC changes (HR = 2.931, p = 0.027, Log-Rank).

DISCUSSION

DWI has been shown to be extremely useful in the clinical evaluation of brain tumors. For example, DWI has shown some value in differentiating post-treatment progressive enhancement (i.e. pseudoprogression) from true tumor progression [25]. Histogram-based analyses have been shown to be predictive biomarkers for tumor genetic subtypes (e.g. isocitrate dehydrogenases 1 (IDH 1)) [26] as well as OS in recurrent GBM patients treated with anti-VEGF monotherapy at first or second relapse [27, 28, 29]. However, the biophysical basis of DWI in brain tumors is not completely understood [30], and clinically implemented DWI sequences and models represent a simplified assessment of the complex microstructure present in tumor. Recent improvements in MR gradient technology allow significant increases in diffusion sensitivity without prohibitive signal-to-noise degradation. More complex diffusional models have been introduced on the basis of higher b values (>3500s/mm²) to characterize apparent diffusivity (Dapp), diffusion kurtosis (Kapp), distributed diffusion coefficient (DDC), as well as intra-voxel diffusion heterogeneity (α) [17, 18]. These sophisticated models are being increasingly used to understand differences in biological tissues in various brain pathologies [31, 32], including promising characterization and grading of glioma [33, 34, 35].

Results within NAWM in the current study were reproducible over time. At the pre-chemoradiation time point, the observed differences of cerebral diffusivity between NAWM and CET were in agreement with previously reported works [34, 36]. However, we found higher values of α within the tumor, suggesting less diffusion heterogeneity, as compared with the study of Kwee et al., [36]. These differences may be explained by the fact that we only included regions of pure contrast enhancement, whereas Kwee et al. considered whole tumor region in their analyses. Another important point that could result in differences is the relative number of b-values in the current study (10 b-values up to 5000s/mm²) compared to the study by Kwee et al. (4 b-values: 0, 1000, 2000, and 4000s/mm²). Finally, Kwee et al. reported results from untreated patients that may represent a more heterogeneous (e.g. lower α values) tumor compare to post-surgical and/or post-chemoradiation diffusional behavior.

Results from the current study suggest simple mono-exponential measures of ADC using 3 b-values are highly correlated with more advanced measures of diffusivity, particularly after surgery and prior to chemoradiation. This is supported by high diffusion heterogeneity measures (α>0.7), which consequently suggests DDC ≈ ADC. Interestingly, we observed increasing discordance between diffusion measurements across the various models when evaluating the tumor after completion of chemoradiation, which may suggest a more complex microenvironment perhaps consisting of cells in various stages of lysis and destruction. However, only a few patients showed obviously lower α values or high Kapp after chemoradiation.

Results from multivariable Cox regression suggest that increases in standard clinical measures of ADC is a significant predictor of patient outcome, while more sophisticated diffusion measures do not appear to provide prognostic value. These results are consistent with previous studies showing that significant increases in ADC within CET regions between pre- and post-chemoradiation time points were associated with a better OS [37]; however, to the best of our knowledge, no clinical studies have explicitly evaluated changes in non-Gaussian parameters (kurtosis and stretched exponential fits) before and after standard chemoradiation or other upfront treatments (e.g. anti-angiogenic drugs), nor have studies reported changes in these parameters in relation to clinical outcome in GBM. Due to the relatively limited number of patients in the current exploratory study, it is conceivable that this population was not representative of the larger patient population, patient age, MGMT status, post-surgical or residual tumor volume did not appear prognostic. This may have also been due to the fact that post-surgical, pre-chemoradiation scans were obtained between 15–30 days after surgery due to the need to obtain advanced imaging. Thus, contrast enhancing portions of the tumor could reflect a combination of post-surgical enhancement and residual disease. A larger study may be warranted to better isolate potential differences between diffusion models during or after treatment response; however, generally speaking, the current study suggests the higher post-processing complexity and increased scan time to perform these advanced diffusion MR measurements did not appear justified as we did not observe obvious added clinical value. Finally, based on our results and clinical setting, mono-exponential diffusional modeling is superior to other models.

Supplementary Material

11060_2018_2910_MOESM1_ESM

Supplementary Figure A. Glioblastoma in the left occipital lobe in a 65-year-old man with 13.1 months of survival. Pre- and post-chemoradiation, post-contrast T1w images, ADC, Dapp, Kapp, α and DDC maps are shown. Small changes were observed in all diffusion measurements. Change in values between pre- and post-chemoradiation time-points: ADC=0.002μm²/ms, Dapp=−0.015μm²/ms, Kapp=−0.028, α=0.014 and DDC=−0.035μm²/ms.

Table 2.

Cox multivariable proportional hazards models: prediction of overall survival with each fit and clinical variables.

Fit/ROI	Estimate	Pre-Chemoradiation	Post-Chemoradiation	Shapiro-Wilk (p-value)	Student’s t-test (p-value)	Wilcoxon (p-value)
ADC-NAWM μm2/ms)	Mean	0.828	0.831	0.5486	0.8650
	Std-Dev	0.036	0.049
	CV	4.463	6.008
Dapp-NAWM μm2/ms)	Mean	0.878	0.876	0.2654	0.7013
	Std-Dev	0.044	0.06
	CV	5.051	6.941
Kapp-NAWM (a.u)	Mean	0.807	0.803	0.0818	0.7405
	Std-Dev	0.046	0.044
	CV	5.745	5.513
α-NAWM (a.u)	Mean	0.596	0.594	<.0005		0.2399
	Std-Dev	0.005	0.005
	CV	0.905	0.949
DDC-NAWM (μm2/ms)	Mean	1.344	1.343	0.7293	0.5140
	Std-Dev	0.005	0.005
	CV	0.384	0.395
ADC-CET (μm2/ms)	Mean	1.233	1.406	0.5493	0.0153
	Std-Dev	0.23	0.234
	CV	18.679	16.679
Dapp-CET (μm2/ms)	Mean	1.329	1.479	0.6502	0.037
	Std-Dev	0.249	0.221
	CV	18.747	14.962
Kapp-CET (au)	Mean	0.551	0.515	0.7187	0.0726
	Std-Dev	0.063	0.068
	CV	11.487	13.223
α-CET (a.u)	Mean	0.715	0.71	<.0001		0.5312
	Std-Dev	0.029	0.062
	CV	4.182	8.797
DDC-CET (μm2/ms)	Mean	1.444	1.511	0.0202		0.0258
	Std-Dev	0.098	0.109
	CV	6.793	7.272

Hazard ration, 95% confidence interval and p-values are reported for each fit in combination of age (at the time of diagnosis) and baseline CET volume as potential clinical variables influencing the outcome. Note that slope values are expressed in μm²/s in order to reduce impact of dimensions in the Cox model

Acronyms

MRI

Magnetic Resonance Imaging

DWI

Diffusion Weighted Imaging

ADC

Apparent Diffusion Coefficient

Dapp

Diffusion corrected Apparent Diffusion Coefficient

Kapp

Apparent Kurtosis Coefficient

DDC

Distributed Diffusion Coefficient

α(alpha)

Intra-Voxel Diffusion Heterogeneity

NAWM

Normal Appearing White Matter

CET

Contrast-Enhancing Tumor

GBM

Glioblastoma