Mechanical Mapping of Spinal Cord Growth and Repair in Living Zebrafish Larvae by Brillouin Imaging

Abstract

The mechanical properties of biological tissues are increasingly recognized as important factors in developmental and pathological processes. Most existing mechanical measurement techniques either necessitate destruction of the tissue for access or provide insufficient spatial resolution. Here, we show for the first time to our knowledge a systematic application of confocal Brillouin microscopy to quantitatively map the mechanical properties of spinal cord tissues during biologically relevant processes in a contact-free and nondestructive manner. Living zebrafish larvae were mechanically imaged in all anatomical planes during development and after spinal cord injury. These experiments revealed that Brillouin microscopy is capable of detecting the mechanical properties of distinct anatomical structures without interfering with the animal’s natural development. The Brillouin shift within the spinal cord remained comparable during development and transiently decreased during the repair processes after spinal cord transection. By taking into account the refractive index distribution, we explicitly determined the apparent longitudinal modulus and viscosity of different larval zebrafish tissues. Importantly, mechanical properties differed between tissues in situ and in excised slices. The presented work constitutes the first step toward an in vivo assessment of spinal cord tissue mechanics during regeneration, provides a methodical basis to identify key determinants of mechanical tissue properties, and allows us to test their relative importance in combination with biochemical and genetic factors during developmental and regenerative processes.

Introduction

In response to a mechanical stimulus, many cell types, including neurons and glia, change their properties and behavior (1, 2, 3, 4, 5). This includes morphological changes (6, 7, 8) as well as alterations of migration (9), proliferation (10), and differentiation (7). The cellular susceptibility to mechanical signals is termed mechanosensitivity and has been the subject of recent studies documenting the involvement of mechanical signals in developmental and pathological processes. Axonal growth during optic tract development in Xenopus laevis, for instance, is guided by temporally changing stiffness gradients in adjacent brain tissue (11). Microglial cells and astrocytes in rat brains display an activated phenotype and increase expression of inflammatory genes and proteins, which is indicative of reactive gliosis, when exposed to a mechanical stimulus that deviates from their physiological mechanical environment (12). Oligodendrocyte precursor cells increase their expression of myelin basic protein and display an elaborated myelin membrane on stiffer substrates as compared to more compliant substrates, indicating a preferred mechanical environment for differentiation (7). Among others, these examples demonstrate an intricate interplay between the mechanosensitivity of distinct neural cell types and the mechanical properties of their respective microenvironments. In vivo, these microenvironments are formed by the surrounding nervous tissue, whose mechanical properties are thought to be determined by the combined material properties of neighboring cells, extracellular matrix, and the degree of cross-linking (13). As these determinants of tissue mechanics change during development and after pathological events, concomitant changes of mechanical tissue properties and their direct involvement in a wide range of central nervous system conditions and diseases are likely (14, 15, 16, 17).

Severe injury to the mammalian spinal cord prompts a biochemical signaling cascade that eventually leads to the formation of a glial-fibrotic scar. The scar tissue has not only been shown to prevent axonal regrowth across the lesion site because of its biochemical composition (18, 19) but has also been proposed to act as a mechanical obstacle (19, 20). Unlike mammalian systems, in which the loss of motor and sensory function associated with traumatic spinal cord injury is permanent, zebrafish are able to restore motor function and repair spinal cord tissue even after complete spinal cord transection (21). In adult zebrafish, functional recovery correlates with an orchestrated cellular response that includes proliferation (22, 23, 24, 25), migration (23, 25, 26), differentiation (22, 25, 27), and morphological changes (22, 23). Radial glial cells, for example, proliferate and give rise to new motor neurons that mature and integrate into the spinal circuitry (22). Descending axonal projections severed by the injury initiate regrowth and eventually traverse the injury site (25, 28). These regenerative events take place in a time interval of approximately 6–8 weeks post-injury (22, 25). Larval zebrafish have been shown to share the regenerative capacity with their adult counterparts, as they too respond to spinal cord transection by proliferation, neurogenesis, axonal regrowth, and functional recovery (29, 30, 31, 32) yet with a much shorter recovery time (29, 31, 33).

In light of the aforementioned examples of neural mechanosensitivity and stiffness changes of nervous tissue during development and disease, we submit that the mechanical characterization of zebrafish spinal cord tissue poses an intriguing addition to biochemical analysis and might help to elucidate the role of mechanical signaling during spinal cord development and successful spinal cord repair.

To quantify the mechanical properties of biological samples, a variety of standard measurement techniques have been developed (34, 35). Micromanipulation of nanoparticles and cells (36), ferrofluid microdroplets (37), optical tweezers (38), traps (39) and stretchers (40), micropipette aspiration (41), and cell-shape analysis (42) allow the local measurement of mechanical properties of single cells or tissues at a molecular to cellular scale. Parallel plate measurements and tissue shape analysis (43) provide mechanical data for bulk tissues. However, only a fraction of the techniques suitable for in vivo measurements of mechanical tissue properties allows the spatial mapping of the intrinsic mechanical properties of whole native tissues (44). These include, e.g., atomic force microscopy (AFM)-based indentation (45, 46, 47), sonoelastography, and magnetic resonance elastography (48). Although the former necessitates direct physical contact between indenter and sample and can therefore only measure the surface of a dissected, possibly sectioned tissue, the latter lack spatial resolution in the range relevant for cellular mechanosensitivity and required for samples with small dimensions such as zebrafish larvae.

Brillouin spectroscopy allows measurements of mechanical properties and is widely used in the material sciences. The technique is based on the inelastic Brillouin scattering process between incident photons and mass density fluctuations (acoustic phonons) due to inherent, traveling sound waves in the sample (see Materials and Methods) (49, 50). It gives access to the phonon’s properties that are related to the viscoelasticity of the sample, e.g., the longitudinal storage and loss moduli. With the emergence of virtually imaged phased array (VIPA)-based spectrometers in the last decade, this technique has become applicable for the point-wise measurement within living biological samples to build up a three-dimensional image with diffraction-limited resolution (51). Brillouin microscopy has so far been applied to the human cornea (52, 53, 54), murine carotid arteries (55), ruminant retina (56), rabbit bone tissue (57), and zebrafish embryos (58, 59, 60). Here, we exploit the optical transparency and high regenerative capacity of zebrafish larvae to systematically explore the in vivo mechanical properties of larval tissue during development and repair using a custom-built Brillouin microscopy setup.

The obtained Brillouin images reveal the different mechanical properties of varying anatomical structures within living zebrafish larvae. We find that the Brillouin shift of the spinal cord remained comparable during development. After spinal cord injury, we detect a significant but transient drop of the Brillouin shift at the lesion site. Thus, our experiments demonstrate for the first time to our knowledge that zebrafish spinal cord tissue, mechanically mapped inside living and intact animals, presents distinct mechanical signals to mechanosensitive cells during development and regeneration. We also show explicitly that the influence of refractive index changes within the perispinal area of zebrafish larvae can be neglected when calculating the longitudinal moduli from the measured Brillouin signal and that there are significant differences between tissues in situ and after dissection. This work constitutes the methodical basis to identify key determinants of mechanical central nervous system tissue properties and to test the relative importance of mechanics in combination with biochemical and genetic factors during biologically important processes in vivo.

Materials and Methods

Brillouin scattering

Brillouin scattering is an inelastic scattering process between the incident light and periodic mass density fluctuations due to traveling sound waves with sound velocity V within the sample. This results in an upward and downward frequency shift ν_B (i.e., Brillouin shift) of the incident light, which is given by (50, 61):

$${\nu }_{\text{B}}=\frac{2\text{cos}\left(\mathit{\Theta }/2\right)}{\lambda }\times n\times V=\zeta \times \sqrt{M^{\prime }}\text{with}\zeta =\frac{2\text{cos}\left(\mathit{\Theta }/2\right)}{\lambda }\times \frac{n}{\sqrt{\rho }},$$ (1)

where Θ is the scattering angle and λ the wavelength. The material properties of the sample are described by the longitudinal modulus M′, the refractive index n, and the mass density ρ, of which the refractive index and the mass density are directly coupled for most biological samples (62, 63, 64, 65, 66). Hence, the Brillouin shift depends only on mechanical properties (i.e., the longitudinal modulus and the mass density) and is itself a mechanical property.

The theoretical linewidth Δ (full width at half maximum) of the Brillouin peak is given by (67, 68)

$$\text{Δ}={\zeta }^2\times \frac{M^{″}}{{\nu }_{\text{B}}}=2\pi {\zeta }^2\times \eta ,$$ (2)

where M″ is the loss modulus and η the viscosity. However, the measured linewidth Δ_B is given by a convolution of the theoretical linewidth and the intrinsic linewidth of the spectrometer, leading to a biased calculation for the viscosity η_B.

Brillouin microscope

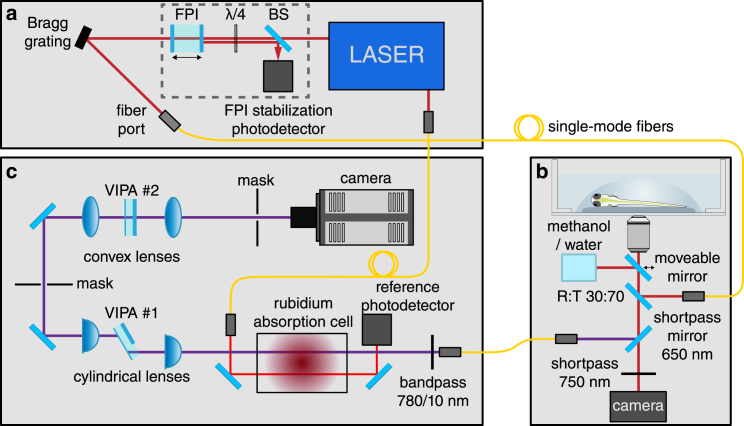
Our Brillouin microscope (Fig. 1) is based on a two-stage VIPA interferometer design from Scarcelli et al. (51, 69, 70, 71). As the illumination source, we use a frequency-modulated diode laser (DLC TA PRO 780; Toptica, Gräfelfing, Germany) emitting at 780.24 nm, the central frequency of which is stabilized to the D₂ transition of rubidium ⁸⁵Rb. For this purpose, a probe beam from the laser is transmitted through an Rb molecular absorption cell. The intensity behind the cell is measured by a reference photodetector and used as an input signal for the lock-in frequency stabilization. The laser spectrum is cleaned using a Bragg grating (Ondax NoiseBlock; Ondax, Monrovia, CA) to increase the laser mode to amplified spontaneous emission (ASE) ratio by 10 dB to over 65 dB. Although this ASE ratio already allows in vivo measurements in zebrafish larvae (shown in Figs. 2, 3, 4, and 5), some Brillouin spectra from positions with strong reflections inside the specimen cannot be evaluated (see Supporting Materials and Methods, Note S1). This can be mitigated by a further suppression of the ASE. We therefore implemented a Fabry-Pérot interferometer (FPI) in the illumination path with the cavity length stabilized to the central laser frequency. For this purpose, the light reflected at the FPI is guided to a photodetector. The acquired intensity signal is then used as input signal for an adjusted Pound-Drever-Hall control scheme (72). The FPI leads to a reduction of the laser mode to ASE ratio by 20 to ∼85 dB. This improvement yields clean spectra for measurements that were previously affected by strong reflections. The improved setup was used for the measurements shown in the last two figures and all Brillouin measurements shown in the Supporting Materials and Methods.

Figure 1.

Scheme of the custom-built confocal Brillouin microscope. The setup consists of (a) a diode laser to illuminate the specimen, (b) a confocal microscope, and (c) the Brillouin spectrometer. The light inelastically scattered in the specimen is collected in the backscattering direction and coupled into a two-stage VIPA spectrometer including a molecular absorption cell filled with rubidium. The spectrogram is acquired with an scientific complementary metal-oxide-semiconductor camera and evaluated using a self-written MATLAB program. BS, polarizing beam splitter.

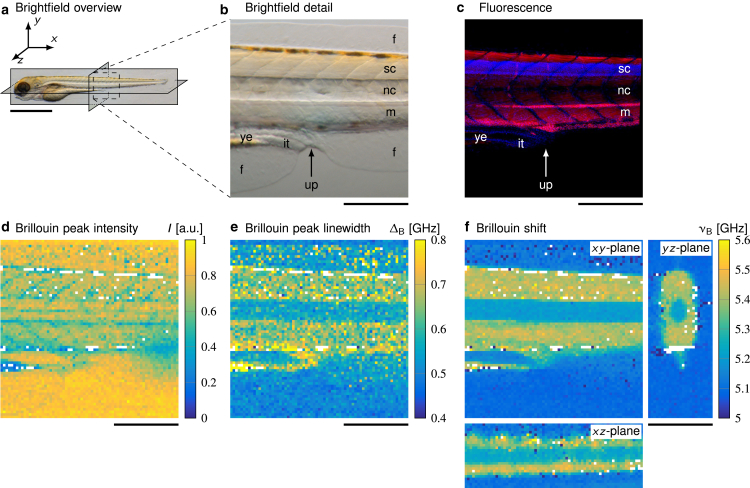
Figure 2.

Images of the same zebrafish larva at four days post-fertilization (dpf). Brightfield and Brillouin images were obtained in a living specimen, and fluorescence microscopy was performed after fixation after Brillouin microscopy. (a) A brightfield image showing the specimen and the three anatomical planes is given. Scale bar, 1 mm. (b) shows an enlarged brightfield image of the region of interest containing the spinal cord (sc), the notochord (nc), muscle segments (m), the fins (f), the yolk extension (ye), the intestinal tissue (it), and the urogenital pore (up). (c) The corresponding fluorescence image depicts the same structures—cell bodies in the spinal cord (nuclei, blue), muscle tissue (actin, red), and the notochord. Brillouin microscopy yields (d) the peak intensity, (e) the peak linewidth given as full width at half maximum, and (f) the Brillouin shift. The peak intensity detects anatomical structures that scatter or absorb light in the beam path. The peak width is indicative of the viscous properties. The Brillouin shift is displayed for the three anatomical planes indicated in (a) and is proportional to the elastic properties of the sample. Scale bars (b–f), 200 μm.

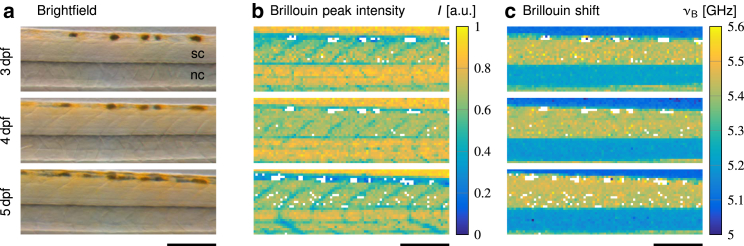
Figure 3.

Brillouin measurements of a representative zebrafish larva during development. (a) Brightfield images show the spinal cord (sc) and the notochord (nc) obtained directly after the Brillouin measurements. (b) Corresponding peak intensities and (c) Brillouin shifts of the same specimen are shown. Scale bars, 150 μm.

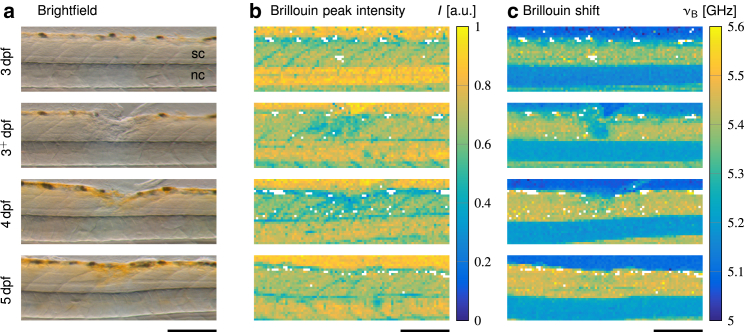
Figure 4.

Brillouin measurements of a representative zebrafish larva after spinal cord injury. Lesioned larvae were probed at 3 dpf immediately before and 1 h after the injury (3⁺ dpf) as well as on the two subsequent days (4 and 5 dpf). (a) Brightfield images showing the spinal cord (sc) and the notochord (nc) obtained directly after the Brillouin measurements are shown. (b) Corresponding peak intensities and (c) Brillouin shifts of the same specimen are shown. Scale bars, 150 μm.

Figure 5.

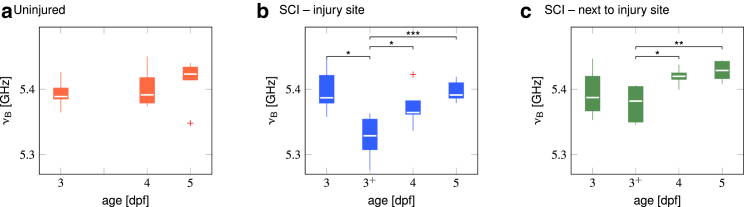
Quantification of the temporal development of the Brillouin shift during development and repair. (a–c) Box plots of the average Brillouin shifts of the respective areas in individual fish are given. The boxes indicate the interquartile ranges, the whiskers extend to the most extreme data still within 1.5 interquartile ranges of the respective quartile (Tukey boxplot), and the medians are depicted as white lines. Outliers are indicated as red crosses. ^∗p < 0.05; ^∗∗p < 0.01; ^∗∗∗p < 0.001.

The laser light is then coupled into a single-mode fiber and guided to a custom-built inverse confocal microscope. The confocal microscope is based on a Zeiss Axiovert 200 M microscope stand (Zeiss, Oberkochen, Germany) equipped with a translation stage. The light emitted from the illumination fiber is collimated, guided to the objective, and focused into the specimen with a total power of 10 mW. Alternatively, a moveable mirror can be shifted into the beam path, guiding the light to a methanol-filled cuvette used as calibration sample. To achieve a sufficient working distance, a Zeiss Plan Neofluar 20×/0.5 NA objective is used, which results in a spatial resolution of 1 μm in the lateral plane and ∼5 μm in the axial direction. For high-resolution images, we apply a Zeiss water-immersion C-Apochromat 40×/1.2 NA objective providing subcellular resolution of 0.4 μm in the lateral plane and ∼1 μm in the axial direction. Similar resolutions have been demonstrated to be possible for Brillouin microscopy in (73, 74) already. However, using high-NA objectives leads to a decrease of the Brillouin shift of 1–2% for the objectives used here (75). The sample is furthermore illuminated with a white light source to acquire a brightfield image after the Brillouin measurement. The Brillouin scattered light is collected in the backscattering direction and separated from the brightfield illumination by a shortpass mirror (DMSP650; Thorlabs, Newton, NJ) with a 650 nm cutoff wavelength. To achieve confocality, a second single-mode fiber guiding the light into the Brillouin spectrometer is used. In the spectrometer, the light is collimated and subsequently filtered by a band pass (FBH780-10; Thorlabs) to block Raman scattered light. The molecular absorption cell (TG-ABRB-I85-Q; Precision Glass Blowing, Englewood, CO) absorbs light with the same frequency as the excitation laser (e.g., Rayleigh scattered and reflected light) (76). After passing the absorption cell, the beam is guided to two VIPA interferometers (OP-6721-6743-4; Light Machinery, Nepean, Canada) with 15.2 GHz free spectral range. The interferometers lead to an angular dispersion of light with different frequencies (70), which allows us to image the Brillouin spectrum of the probed measurement point on the scientific complementary metal-oxide-semiconductor camera (Andor Zyla 4.2 PLUS; Oxford Instruments, Abingdon, England). For this purpose, we recorded two spectra per measurement point with an acquisition time of 500 ms each, which we found optimal to minimize the measurement uncertainty. The resulting random error amounted to 14 MHz, which is similar to values from other publications (51, 73). The standard deviation of the mean value of measurements with independent calibrations was 10 MHz (see also Fig. S2). A spatially resolved map of the Brillouin shift is acquired by automatically translating the specimen with a motorized stage by steps of 7 μm for the images shown in Figs. 2,3, 4, 5, and 6 and by steps of 2 μm for the images in Figs. 7, 8, and S6.

Figure 6.

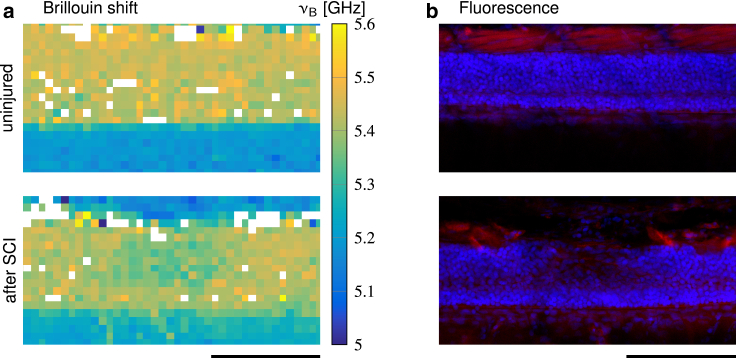
Comparison of (a) the Brillouin shift and (b) the corresponding fluorescence image for an uninjured and a lesioned zebrafish spinal cord at 5 dpf. The fluorescence image shows cell bodies (nuclei, blue) and muscle tissue (actin, red). SCI, spinal cord injury. Scale bars, 100 μm.

Figure 7.

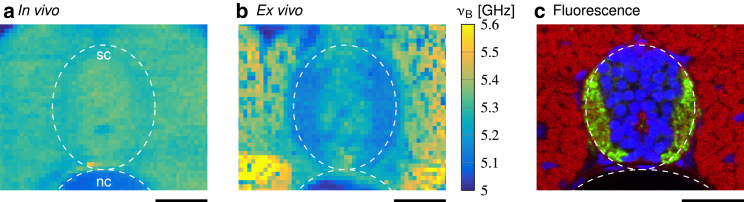
Representative high-resolution Brillouin images of the perispinal area in (a) an anesthetized zebrafish larva and (b) an acute tissue slice from a vibratome-sectioned specimen. (c) Immunohistochemistry of a transverse zebrafish section shows fluorescent labeling of cell bodies (nuclei, blue) and axons (acetylated tubulin, green) in the spinal cord as well as muscle tissue (actin, red) in the surrounding area. The approximate positions of the spinal cords (sc) and the notochords (nc) are indicated by dashed lines. Scale bars, 25 μm.

Figure 8.

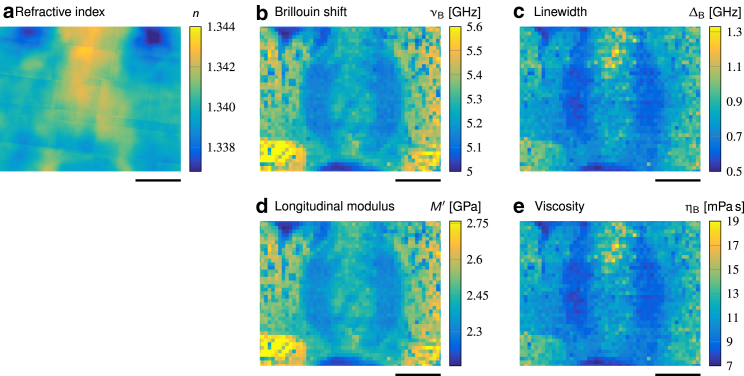
Determination of the longitudinal modulus M′ and the viscosity η_B from the RI n, the Brillouin shift ν_B and the linewidth Δ_B for larval zebrafish tissue. (a) Maps of the RI n obtained by quantitative phase imaging, (b) Brillouin shift, and (c) linewidth obtained with the Brillouin microscope for an acute zebrafish slice are shown. (d) Longitudinal modulus M′ and (e) viscosity η_B determined with Eqs. 1 and 2 from (b) and (c) are shown. Scale bars, 25 μm.

Brillouin imaging

The acquisition of the camera images as well as the control of the translation stage and the objective lens’ z-position is performed using a custom MATLAB (The MathWorks, Natick, MA) program. The acquired raw data are stored as a Hierarchical Data Format 5 file, allowing for efficient data handling (77). The subsequent data analysis also uses a custom MATLAB program and is done in multiple steps. First, the one-dimensional Brillouin spectra are extracted from the two-dimensional camera images. The position, width, and intensity of the Brillouin and Rayleigh peaks are then determined by fitting Lorentzian functions to every peak. To calibrate the frequency axis, a reference measurement of a methanol sample placed in the calibration beam path is acquired every 10 min by moving a mirror into the beam path (Fig. 1). This allows us to obtain an absolute value for the Brillouin shift and compensates for possible drifts of the VIPA setup during the measurement. For every reference measurement, we fit the theoretical, nonlinear frequency axis to the Brillouin spectrum according to (78). Interpolating along the temporal axis yields a calibrated frequency axis for every time point during the measurement, which is used to calculate the Brillouin shift in GHz. Plotting the calibrated Brillouin shift over the position of the translation stage finally leads to a spatially resolved map of the mechanical properties of the sample. All white pixels displayed in the maps correspond to coordinates in which the sample caused strong back reflections due to large refractive index gradients or the Brillouin signal was absorbed because of strong pigmentation (see Supporting Materials and Methods, Note S1). These values were discarded.

Animals

All zebrafish were kept and bred in the fish facility of Biotechnology Center of the TU Dresden as described in (79). Embryos from wild-type zebrafish were incubated in PTU (1-phenyl-2-thiourea, 0.00375% in E3 embryo medium; Sigma-Aldrich, St. Louis, MO) after 1 dpf to prevent melanogenesis (80).

Mounting of zebrafish larvae for in vivo Brillouin and brightfield imaging

Larvae were anesthetized in tricaine (MS222) (0.01% in E3; Sigma-Aldrich) and placed in a lateral position on a 30-μm-thick, flat polyacrylamide gel that had been polymerized on a glass-bottom dish suitable for optical imaging. A drop (200 μL) of low-gelling-point agarose (1% in E3, 30°C; Sigma-Aldrich) was used to immobilize the larvae in this position for subsequent imaging. Immobilized larvae were then immersed in MS222 (0.01% in E3) during imaging. All specimens were released from the agarose embedding between Brillouin measurements and kept under standard conditions (79).

Fluorescence microscopy

After obtaining the final Brillouin image, zebrafish larvae were sacrificed by an overdose of MS222, fixed with paraformaldehyde (4% in phosphate-buffered saline (PBS)), subjected to multiple washing and permeabilization steps using PBSTx (0.8% TritonX-100, 1% dimethyl sulfoxide in PBS), and stained with 4′,6-diamidino-2-phenylindole (DAPI) and phalloidin-tetramethylrhodamine (both 1:1000 in PBS). Larvae were then washed with PBS, incubated in glycerol (75% in PBS) for 3 h, and mounted in 1,4-diazabicyclo[2.2.2]octane (DABCO)-containing mounting medium (2.5% DABCO, 90% glycerol in 50 mM Tris-HCl (pH 8); Sigma-Aldrich).

For immunohistochemistry on vibratome-sectioned zebrafish larvae, 4-day-old specimens were sacrificed and chemically fixed as described above. The larvae were then embedded in 2.5% low-gelling-point agarose and sectioned at 150–200 μm. Thereafter, sections were subjected to multiple washing and permeabilization steps using PBTx for ∼2 h before incubation in blocking buffer (4% bovine serum albumin in PBSTx) for 1 h. Sections were then incubated with a primary antibody against acetylated tubulin (T6793, 1:500 in blocking buffer; Sigma) overnight at 4°C. Afterwards, sections were washed twice in PBSTx for consecutive 5, 10, 15, and 30 min before incubation with phalloidin (conjugated to Alexa Fluor 647, A22287, 1:1000; Invitrogen, Carlsbad, CA) and secondary antibody (goat anti-mouse Alexa Fluor 488, A11001, 1:200; Invitrogen) in blocking buffer overnight at 4°C. The next day, sections were washed twice in PBSTx for consecutive 5, 10, 15, and 30 min before washing twice with PBS, counterstaining with DAPI, and mounting in DABCO-containing mounting medium.

Image acquisition and processing

Brightfield images were obtained using the Olympus Stereomicroscope SZX 16 and the SDF PLAPO 0.8×/0.12 NA and 2.0×/0.3 NA objectives (Olympus, Tokyo, Japan). Confocal fluorescence microscopy was performed to image fixed and stained larvae using the Zeiss LSM700 and a Plan Apochromat 10×/0.45 NA objective. The fluorescence images displayed in this study are maximum z-projections of four optical planes (∼1μm each), which correlate to the section thickness measured by Brillouin microscopy. Brightfield and fluorescence images were adjusted in brightness and contrast using Fiji and assembled with CorelDraw.

Spinal cord lesion

Larvae were anesthetized in MS222 (0.01% in E3) and immobilized as described for Brillouin imaging. Lesions were performed manually at 3 dpf by inserting the broken tip of a pulled injection glass capillary in the most ventral part of the spinal cord at the level of the urogenital pore and moving the tip dorsally in a quick motion. Notochords and major blood vessels remained intact. Larvae were subsequently released from the agarose embedding.

Preparation of zebrafish sections

Zebrafish larvae were sacrificed by an overdose of MS222 (0.2% in PBS; Sigma-Aldrich), embedded in low-gelling-point agarose (2.5% in artificial cerebrospinal fluid; Sigma-Aldrich) and cut into transverse sections using a vibratome. The artificial cerebrospinal fluid (aCSF) contained (in mM) 134 NaCl, 2.9 KCl, 1.2 MgCl₂, 2.1 CaCl₂, 10 HEPES buffer, and 10 glucose, adjusted to pH 7.8 with NaOH (81). A section thickness of 300 μm was used for indentation measurements as well as Brillouin microscopy. Refractive index (RI) measurements were performed using 200 μm sections. Zebrafish sections selected for indentation measurements were immobilized on tissue culture plastic with Histoacryl (B. Braun, Melsungen, Germany), which was sparsely applied between the tissue culture plastic and the agarose embedding at a distance from the zebrafish section. The sections were submerged in cooled aCSF during indentation measurements. For both Brillouin microscopy and RI measurements, the sections were immobilized by sandwiching them between two glass slides suitable for optical imaging and surrounded by aCSF. All vibratome sections were obtained from 4-day-old larvae.

Quantitative phase imaging

Quantitative phase and intensity images were recorded with a commercial phase-imaging camera (SID4-Bio; Phasics, Saint-Aubin, France) attached to an inverted microscope (IX71; Olympus) as described in (82). The imaged zebrafish section was larger than the field of view covered by the camera sensor, and thus we applied an image-stitching approach. Intensity images were recorded manually with a 40–80% overlap and background corrected by division with a reference image. Stitching was performed with an appropriate type of descriptor (83) in the intensity images, applying a translational model, and isolating valid descriptors with a random sample consensus approach. The images were blended using the median value of the individual images. Quantitative phase images exhibit random phase offsets, which were corrected with an iterative approach. In each iteration, the stitched phase image was assembled using the image locations obtained from stitching the intensity data. Then, the mean phase of each individual image (excluding a 10-pixel border around the image) was corrected to match that of the corresponding field of view in the stitched image for the subsequent iteration. A total of 20 iterations were performed. The phase measured corresponds to the difference in the optical path difference through the zebrafish section. By taking into account the thickness of the section, the integral RI n(x, y) at each point of the section can be computed using

$$n\left(x,y\right)=n_{\text{gel}}+\frac{\mathit{\Phi }\left(x,y\right)\mathit{\lambda }}{2\pi d_{\text{sec}}},$$ (3)

where n_gel = 1.3395 is the RI of the hydrogel measured with an Abbe refractometer (2WAJ; Arcarda, St. Charles, IL), Φ(x, y) is the measured quantitative phase, λ = 647 nm is the wavelength used for imaging, and d_sec = 200 μm is the thickness of the zebrafish section.

Statistical analysis

To compare the Brillouin shifts of different regions within the specimens’ spinal cords, the values corresponding to every region had to be identified. For this purpose, all measurement points belonging to the specimen’s spinal cord were selected first. For the injury site, all values in the spinal cord in an area with a width of 100 μm around the center of the lesion were chosen. The region next to the injury site included all values in the spinal cord separated from the injury site by a 25 μm clearance to exclude the transient values between both regions. All Brillouin shifts corresponding to the identified regions were averaged for the individual specimen, yielding N = 6 mean values for every region and for the injured and uninjured zebrafish, respectively. We used the Friedman ANOVA for statistical analyses of repeated measurements on the same specimens (Fig. 5) and the Kruskal-Wallis test for comparisons among different specimens (Fig. S4). These analyses were followed by least-significant-difference post hoc tests. The shown asterisks indicate the significance levels: ^∗p < 0.05, ^∗∗p < 0.01, and ^∗∗∗p < 0.001.

Results

Brillouin microscopy mechanically characterizes anatomical structures in living zebrafish larvae

To identify anatomical structures and assign distinct material properties to various organs and tissues in living zebrafish larva, we compared images acquired with Brillouin microscopy with images from brightfield and confocal fluorescence microscopy of the same specimens at 4 days post-fertilization (dpf) (Fig. 2). For this purpose, individual zebrafish larvae were anesthetized and immobilized using low-gelling-point agarose in a glass-bottom dish suitable for optical imaging. Using Brillouin microscopy, we measured the material properties of the larval tissues in all three anatomical planes. All specimens were subsequently imaged using brightfield microscopy and fixed and stained with tetramethylrhodamine-conjugated phalloidin and DAPI for confocal fluorescence microscopy. Although the formation of melanophores could be suppressed successfully, all zebrafish exhibited the two other types of pigment cells, xanthophores and iridophores. The latter can be observed as dark spots in all brightfield images (Fig. 2, a and b) and caused reflections during the Brillouin image acquisition (Fig. 2, d–f; Supporting Materials and Methods, Note S1). The corresponding values were therefore discarded and displayed as white pixels in the Brillouin images.

In both the brightfield images (Fig. 2, a and b) and the Brillouin peak intensity map (Fig. 2 d), image contrast is governed by absorption and scattering processes in the specimen, which allows us to discern prominent anatomical structures such as the notochord and the diagonal pattern of the muscle segments. The fluorescence image (Fig. 2 c) additionally allows us to distinguish the spinal cord tissue (blue) from the surrounding muscle tissue (red). Although the aforementioned imaging modalities convey information about the presence of certain anatomical features, the Brillouin shift and the linewidth (full width at half maximum) show the material properties of these features. The Brillouin peak linewidth depends on the phonon lifetime and is therefore directly related to the loss modulus and the viscosity of the sample (see Eq. 2). For muscle and spinal cord tissue, the Brillouin peak linewidth (Fig. 2 e) is higher than for the intestinal tissue and the notochord. The Brillouin shift depends on the longitudinal (storage) modulus and is indicative of the elastic, solid-like sample properties (see Eq. 1). Our measurements (Fig. 2 f) revealed a higher Brillouin shift of the yolk extension and the muscle and spinal cord tissue as compared to the intestinal tissue and notochord. The zebrafish notochord is formed by a thin (∼2 μm; value extracted from images in (84)) outer layer of extracellular matrix and sheath cells that surround an inner layer of vacuolated cells (85, 86). Mechanically, the notochord has been described as a rigid, fluid-filled cylinder under pressure (86, 87). Muscle tissue, nervous tissue, and yolk, on the other hand, have all been described as viscoelastic materials exhibiting both fluid-like viscous properties and solid-like elastic properties (13, 88, 89, 90, 91, 92). It is therefore not surprising that the solid-like characteristics displayed in the Brillouin shift maps are the lowest for the notochord as compared to the other types of tissue. The low Brillouin shift values for the intestinal tissue are presumably indicative of the presence of intestinal fluid, which has been described as a Newtonian fluid with a negligible elastic contribution from the intestinal mucus (93). The Brillouin shift map also revealed the diagonal pattern of the muscle segments, and we were able to detect the fins in the yz-plane. After the measurements, the larvae were released from the agarose and behaved normally after cessation of sedation.

Brillouin shifts of the larval zebrafish spinal cord transiently decrease after injury

To detect changes of the material properties of the spinal cord tissue during development, we probed the same specimens (N = 6) on three consecutive days. This allowed us to follow the evolution of the developmental physical phenotype that might serve as a signaling cue for neurons and glial cells residing in the tissue. Both the brightfield image (Fig. 3 a) and the Brillouin peak intensity map (Fig. 3 b) display the position of the spinal cord, notochord, and the regular diagonal pattern of the muscle tissue. The position, contrast, and Brillouin shift (Fig. 3 c) of these structures remained similar during the investigated time interval.

To test the hypothesis that the regenerating zebrafish spinal cord changes its mechanical properties, we acquired Brillouin images after spinal cord transection until 2 days post-injury (Fig. 4). All specimens (N = 6) were imaged immediately before the injury at 3 dpf, 1 h after the injury (3⁺ dpf), and on the two consecutive days (4 and 5 dpf). The disrupted structure of the lesioned spinal cord was visible in both the brightfield image (Fig. 4 a) and the Brillouin peak intensity map (Fig. 4 b), in which the lesion site displayed lower values as compared to neighboring spinal cord tissue. Similarly, the map of the Brillouin shift (Fig. 4 c) showed lower values in the lesion site than in the surrounding tissue parts. It should be noted that the Brillouin shift of the lesioned area (ν_B = (5.33 ± 0.03) GHz) was still higher than that of the surrounding agarose gel (ν_B = (5.09 ± 0.01) GHz). This indicated that there was not just a trivial liquid-filled gap but some sort of tissue with decreased Brillouin shift as compared to the uninjured spinal cord, which could be indicative of a lower elastic modulus. As the repair of the spinal cord progressed, the Brillouin shift increased gradually.

The investigated time interval of lesioned animals coincided with the developmental period of uninjured animals and therefore allowed for direct comparison. To quantify the change of the Brillouin shift, we averaged the Brillouin shift values for three selected regions. The regions of interest in the uninjured animals correspond to the entire spinal cord tissue (Fig. S3, red box). For the lesioned fish, the spinal cord tissue was divided into regions containing the lesion site (Fig. S3, blue box) and regions for the remaining tissue (Fig. S3, green box). We did not find significant differences between the Brillouin shifts of uninjured larvae at different developmental stages (Fig. 5 a, Friedman ANOVA p = 0.31). Spinal-cord-injured larvae displayed a significant decrease of the Brillouin shift immediately after injury at the lesion site (Fig. 5 b, $p_{\left(3,3^{+}\right)}=0.014$), which gradually increased during the two consecutive days to values that remained lower as compared to values in intact adjacent tissue portions (Fig. 5 b, $p_{\left(3^{+},4\right)}=0.025$ and $p_{\left(3^{+},5\right)}=0.0008$, Fig. S4 d, p = 0.015). There, the temporal profile of the Brillouin shift displayed values comparable to uninjured animals immediately after the injury (Fig. 5 c and Fig. S4 b) and an increase thereafter (Fig. 5 c, $p_{\left(3^{+},4\right)}=0.025$ and $p_{\left(3^{+},5\right)}=0.004$).

A decrease of Brillouin shifts coincides with lower cell-body densities

The mechanical properties of nervous tissues have been correlated to local cell-body density and distribution using the presence of nuclei as a proxy for cell bodies (11, 46, 56). To investigate whether the changes of Brillouin shifts observed in our study coincide with an altered tissue structure and cell-body arrangement, we fixed and stained uninjured and lesioned zebrafish after Brillouin microscopy (Fig. 6). Uninjured spinal cord tissue displayed a packing of cell nuclei that was translationally invariant along the anterior-posterior axis of the spinal cord. This highly ordered arrangement corresponded to evenly distributed Brillouin shifts. As described above, the lesion site displayed significantly decreased Brillouin shifts in comparison to uninjured animals. The low values in the lesion site corresponded to a disorganized arrangement of cell nuclei and a lower fluorescence intensity of the DAPI signal as compared to neighboring, structurally intact tissue segments.

Comparison of in vivo and ex vivo measurements

Previous publications addressing the mechanical characterization of muscle and nervous tissue reported greater elasticity values of muscle tissue in comparison to spinal cord tissue (92, 94, 95). Our Brillouin measurements, however, did not reveal a discernible difference between muscle and spinal cord tissue. To investigate this apparent discrepancy, we obtained high-resolution Brillouin images in the yz-plane of the perispinal area in anesthetized zebrafish larvae. These measurements, too, show a similar Brillouin shift of spinal cord and muscle tissue in living zebrafish larvae (Fig. 7 a). Since the aforementioned studies employed contact-based methods to probe mechanical tissue properties and therefore required tissue dissection and possibly tissue sectioning, we suspected that the reason for the reported presence of mechanical differences between muscle and spinal cord tissue might originate from the differing sample preparation. To investigate the influence of sample preparation on the material properties in larval zebrafish tissue, we obtained Brillouin images in the xy-plane of the perispinal area in transverse zebrafish tissue slices. These images showed greater Brillouin shifts in the muscle tissue as compared to the spinal cord tissue (Fig. 7 b). Within the spinal cord tissue, we detected that areas that predominantly comprise cell bodies (Fig. 7 c, blue) displayed higher Brillouin shifts than areas that contain mostly axons (Fig. 7 c, green). The observed difference between spinal cord areas and muscle tissue ex vivo could also be confirmed with AFM indentation measurements (see Fig. S5; Supporting Materials and Methods, Note S2) and might be attributable to multiple factors. First, the acute zebrafish sections were kept in a medium of which the chemical composition was tailored to the nutritional demand of acute zebrafish spinal cord tissue (81, 96) but not muscle tissue. This might lead to the faster onset of decomposition in muscle tissue than spinal cord tissue and thus might serve to explain the relative changes of the Brillouin shift. Second, muscle tissue post-mortem also exhibits a chemically induced stiffening, rigor mortis. To test whether we detected time-dependent changes of muscle tissue post-mortem that might reflect the onset of rigor mortis, we performed Brillouin measurements of the perispinal area in sacrificed, but not sectioned, zebrafish larvae. The data showed that the Brillouin shift of the muscle tissue increased with time post-mortem, whereas spinal cord tissue, under the conditions described here, exhibited only small changes of mechanical tissue properties during the investigated time interval (Fig. S6; Supporting Materials and Methods, Note S3). Third, vibratome sectioning releases tension in both muscle and spinal cord tissue, which might contribute to the differences observed ex vivo. Also, the different observation directions between in vivo and ex vivo measurements could influence the measured Brillouin signals. And finally, neglecting the contribution of the RI could also conceal differences of the mechanical properties when calculating the longitudinal modulus from the measured Brillouin shift.

Relation between Brillouin signals and viscoelastic properties for larval zebrafish tissues

To calculate the actual longitudinal modulus and the viscosity of a transverse zebrafish section from the measured Brillouin shifts and linewidths (see Eqs. 1 and 2 in Materials and Methods), we acquired the RI distribution (Fig. 8 a) using quantitative phase imaging and calculated the density (see Supporting Materials and Methods, Note S4) for the perispinal tissues (for ideal elastic and viscous test samples, see Supporting Materials and Methods, Note S5). The maps of Brillouin shift ν_B and linewidth Δ_B and of the resulting longitudinal modulus M′ and viscosity η_B are shown in Fig. 8, b–e, respectively. Our data show that the longitudinal modulus of the spinal cord is lower as compared to muscle tissue. Within the spinal cord, regions containing axons show a lower modulus than regions that contain mostly cell bodies. In fact, the longitudinal modulus map (Fig. 8 d) reflects the information visible in the Brillouin shift map with a correlation coefficient of 0.9968 (Fig. 8 b), indicating very little, if not negligible, contribution of the RI. The same holds true for the relation between the linewidth (Fig. 8 c) and the viscosity (Fig. 8 e) with a correlation coefficient of 0.9997.

On the assumption that the RI is comparable in living zebrafish larvae and acute sections, we can conclude that the Brillouin shift as well as the Brillouin peak linewidth correlate directly with the longitudinal modulus and the viscosity, respectively. Hence, the Brillouin signals reported in this study constitute viscoelastic properties. Consequently, the changes of the Brillouin shift of the spinal cord tissue during development and regeneration after injury correspond to changes of the viscoelastic tissue properties that potentially present mechanical signals to mechanosensitive cells residing in the respective tissues.

Discussion

In this report, we demonstrated the first systematic investigation of the mechanical properties of larval tissues in living zebrafish to our knowledge. By using a custom-built confocal Brillouin microscopy setup, we were able to measure the mechanical phenotypes of distinct anatomical structures. The measurements show a lower Brillouin shift and a lower Brillouin peak linewidth of the notochord and intestinal tissue as compared to the spinal cord, muscle tissue, and yolk extension. This conforms with previous studies describing the notochord and the intestinal tissue as fluid-filled structures (85) and the spinal cord, muscle tissue, and yolk as viscoelastic materials (13, 88, 89, 90, 91, 92). The presumably higher stiffness of the perinotochordal basement membrane surrounding the notochord is not reflected in the Brillouin microscopy imaging, likely because its thickness is too low (2 μm) compared to the 7 μm step size used here. As for the yolk extension, our measurements yielded comparable values as previously reported for the yolk in zebrafish embryos (60). Our results furthermore showed that developmental and pathological processes of larval zebrafish spinal cords coincide with significant Brillouin shift changes. During development, we detected comparable values of the Brillouin shifts. After injury, the Brillouin shifts measured in the lesion site decreased immediately but gradually increased thereafter.

Similar findings have been reported previously for embryonic murine brain tissue that increases in elasticity during development (14) and rat brain and spinal cord tissue that has been shown to display decreased elasticity after injury as compared to uninjured control animals (17). However, these studies were performed ex vivo using an indentation method, and it is currently unclear how or if in vivo mechanical properties change after the animal has died. For instance, Margulies et al. reported a difference in mechanical properties between in vivo and excised brain tissue only after repetitive but not at the first indentation (97). In contrast, Weickenmeier et al. used magnetic resonance elastography and found that brain tissue rapidly stiffens after death (98). These controversies highlight the need for continuing investigations of mechanical tissue properties across all spatiotemporal scales because their measurements appear greatly dependent on various experimental parameters. For instance, our data also show that the Brillouin shifts of muscle and spinal cord tissue exhibit comparable values in vivo. This seemingly contrasts with previous results using contact-based techniques like AFM-based indentation measurements (92, 94, 95). However, AFM measurements require contact and are therefore performed using ex vivo samples. For vibratome-sectioned zebrafish tissues, Brillouin measurements show different Brillouin shifts for the different types of tissue. In fact, the Brillouin shift of the muscle tissue is higher than the shift of the spinal cord tissue, which compares to the relative mechanical properties assessed by indentation measurements. The parameters that contribute to mechanical tissue properties in vivo as well as ex vivo could be manifold. For instance, indentation measurements require exposed sample surfaces and possibly sample sectioning. This leads to necrosis, apoptosis, the release of tension, and hydrostatic pressure changes, which all may induce alterations of the mechanical tissue properties. On the other hand, the acquisition of high-resolution images of living organisms using confocal microscopy requires sample immobilization and complete lack of muscle twitching. In zebrafish, this sedation is commonly achieved by immersion in tricaine (MS222)-containing media (99). Tricaine might induce acidification in weakly buffered solutions (99). Acidification has been shown to influence the stiffness of rat brain tissue (100) and might similarly act on the mechanical properties of zebrafish tissue. Furthermore, the larval tissue sections were incubated in a solution whose chemical composition was tailored to the nutritional demand of zebrafish nervous tissue but not muscle tissue. This might induce a faster decomposition of the muscle tissue and/or necrosis. A potential alternative explanation for the observed differences between muscle and spinal cord tissue might be presented by the distinct anisotropy of the respective types of tissue. Both nerve fibers in the spinal cord and muscle fibers are ordered structures that may display anisotropic mechanical behavior, as has been demonstrated for murine spinal cord tissue (46). The difference between mechanical differences found ex vivo that were absent in vivo emphasizes the need for methods, such as Brillouin microscopy, to quantitatively map mechanical properties inside living animals.

The Brillouin shift scales with the longitudinal modulus, the RI, and the density of the sample (see Eq. 1). For sectioned tissues, we determined the RI distribution and calculated the longitudinal modulus and viscosity. In fact, the longitudinal modulus map reflects the information visible in the Brillouin shift map, indicating very little, if not negligible, contribution of the RI. Assuming that the amplitude of RI variations within the sample is similar between in vivo and ex vivo measurements, the Brillouin shift directly corresponds to the longitudinal modulus. However, this assumption might not hold true for other samples. Recent advances in RI tomography enable us to measure the three-dimensional RI distributions for thin samples and single cells (66, 101). Hence, by combining RI tomography and Brillouin microscopy, an unambiguous distribution of the density and the elastic and viscous properties could be obtained for these samples as well.

Still, the interpretation of the acquired longitudinal modulus remains challenging. Brillouin microscopy acquires information on very short length and timescales, whereas AFM provides information for larger length and timescales. Hence, longitudinal and Young’s modulus must not necessarily correlate but could complement each other by providing information about different temporal and spatial regimes. It is also unknown how biological processes relate to these regimes and whether cells are equipped to detect mechanical properties therein. Although biological processes range from ms for operating piezo channels (102) to days for axonal regrowth across the lesion site (33), it is currently unknown which timescales are relevant for cellular mechanosensitivity in the larval zebrafish spinal cord. Furthermore, it has been proposed that Brillouin microscopy is largely sensitive to the water content of the probed volume (103). Although we also found a correlation between Brillouin shift and density of cell nuclei, what other constituents of living biological tissue Brillouin scattering is really sensitive to remains an interesting area of exploration in the future. In any case, the changes of the mechanical properties observed in the larval zebrafish may serve as signaling cues for mechanosensitive neural cell types residing in the spinal cord tissue. In fact, the functional recovery of zebrafish after injury and the lack thereof in mammals are associated with cell types and cellular processes that are mechanosensitive both in vitro and in vivo.

Conclusion

This work constitutes a methodical basis to identify key determinants of mechanical central nervous system tissue properties and to test the relative importance of mechanics in combination with biochemical and genetic factors during biologically important processes in vivo. Future insights into the mechanical mechanisms promoting or inhibiting neuronal regrowth, enabled by Brillouin microscopy, might therefore constitute important additions to biochemical or cell and molecular biological analyses and could eventually even provide novel therapeutic strategies for affected humans.

Additional information: Accession codes

The data sets generated and/or analyzed during the current study are available from the corresponding author on reasonable request.

Author Contributions

R.S. realized the Brillouin microscope and evaluated the Brillouin measurements. S.M. prepared the zebrafish specimens, acquired and evaluated the brightfield and fluorescence images, and performed and evaluated the AFM measurements on zebrafish tissues. R.S. and S.M. conducted the Brillouin measurements and wrote the manuscript with contributions from all authors. S.A. helped with sample preparation, prepared the polyacrylamide hydrogels, and performed and evaluated the corresponding AFM measurements. G.C., P.M., and K.K. conducted the RI measurements. C.M. and C.Z. supported the evaluation of the Brillouin measurements. R.S., S.M., J.C., and J.G. designed the experiments. All authors reviewed the manuscript.

Editor: Christopher Yip.