The virtual cone: A novel technique to generate spherical dose distributions using a multileaf collimator and standardized control-point sequence for small target radiation surgery

Abstract

Purpose

The study aimed to develop and demonstrate a standardized linear accelerator multileaf collimator-based method of delivering small, spherical dose distributions suitable for radiosurgical treatment of small targets such as the trigeminal nerve.

Methods and materials

The virtual cone is composed of a multileaf collimator–defined field with the central 2 leaves set to a small gap. For 5 table positions, clockwise and counter-clockwise arcs were used with collimator angles of 45 and 135 degrees, respectively. The dose per degree was proportional to the sine of the gantry angle. The dose distribution was calculated by the treatment planning system and measured using radiochromic film in a skull phantom for leaf gaps of 1.6, 2.1, and 2.6 mm. Cones with a diameter of 4 mm and 5 mm were measured for comparison. Output factor constancy was investigated using a parallel-plate chamber.

Results

The mean ratio of the measured-to-calculated dose was 0.99, 1.03, and 1.05 for 1.6, 2.1, and 2.6 mm leaf gaps, respectively. The diameter of the measured (calculated) 50% isodose line was 4.9 (4.6) mm, 5.2 (5.1) mm, and 5.5 (5.5) mm for the 1.6, 2.1, and 2.6 mm leaf gap, respectively. The measured diameter of the 50% isodose line was 4.5 and 5.7 mm for the 4 mm and 5 mm cones, respectively. The standard deviation of the parallel-plate chamber signal relative to a 10 cm × 10 cm field was less than 0.4%. The relative signal changed 32% per millimeter change in leaf gap, indicating that the parallel-plate chamber is sensitive to changes in gap width.

Conclusions

The virtual cone is an efficient technique for treatment of small spherical targets. Patient-specific quality assurance measurements will not be necessary in routine clinical use. Integration directly into the treatment planning system will make planning using this technique extremely efficient.

Summary.

A standardized, non-patient-specific control point sequence was developed to create a spherical dose distribution that is comparable to that produced by a 4 mm or 5 mm cone. Preclinical testing using film was done with an anthropomorphic skull phantom. The virtual cone achieved the goal of creating a dose distribution that was comparable to a physical cone, can be accurately modeled using a commercial treatment planning system, and is efficient to deliver.

Alt-text: Unlabelled box

Introduction

Historically, radiosurgery delivered with a C-arm linear accelerator has used circular collimators (cones) and multiple noncoplanar arcs to create spherical dose distributions.1, 2 The advent of high-definition multileaf collimators (MLCs) enabled 3-dimensional conformal radiation therapy, dynamic conformal arc, intensity modulated radiation therapy (IMRT), and volumetric modulated radiation therapy techniques for radiosurgery.3, 4, 5, 6, 7, 8, 9 Although these methods have supplanted cones in the treatment of metastases and larger benign targets such as arteriovenous malformations and acoustic schwannomas, cones remain the standard for functional targets, in particular trigeminal neuralgia.10, 11, 12, 13, 14, 15, 16

Cone-based treatment presents several challenges. The first is the need for a cone-specific dose calculation algorithm. The second is the need for geometric quality assurance of the cone collimation system.1, 17 However, creating a small, spherical dose distribution using an MLC is not straightforward. For an MLC with a 2.5 mm leaf width, creation of an aperture approximating a 4 mm circle is not feasible; the smallest square aperture is 5 mm × 5 mm. IMRT and volumetric arc therapy can be used to generate the desired dose distribution; however, this approach adds an additional burden of patient-specific quality assurance to the treatment process.

To mitigate these challenges, we developed a non-patient-specific control point sequence to create a spherical dose distribution comparable to that produced by a 4 mm or 5 mm cone. The standard control point sequence is stored as a template for application to a specific patient, analogous to a dynamic wedge.18, 19 We report on the preclinical testing of the virtual cone as well as the application to patients.

Methods and materials

The coordinate systems used here are described by the International Electrotechnical Commission publication IEC 61217.²⁰ Control point sequences were designed for the 10 MV flattening filter free beam of an Edge linear accelerator (Varian Medical Systems, Palo Alto, CA) equipped with a 120-leaf NDS120HD MLC, having leaf width of 2.5 mm in the central 8 cm and 5 mm in the outer 14 cm.

Control point sequence

For equally spaced table angles, the possible sets of arrangements are given by

$${\theta }_{\mathrm{S}}\in \left\{\begin{array}{l}180\times \mathrm{i}/\left(2\mathrm{N}+\mathrm{m}\right)|\mathrm{i}=-\mathrm{N},-\mathrm{N}+1,\\ \dots 1,0,1,\dots \mathrm{N}-1,\mathrm{N}\end{array}\right\}$$ (1)

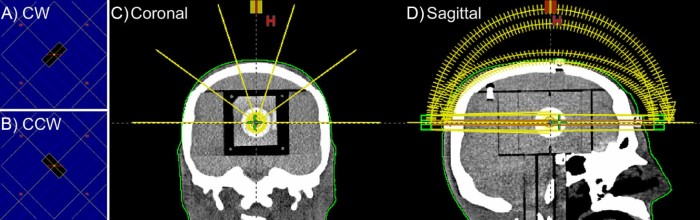
where N is a positive integer and m is either 0 or 1. For m = 0, one of the table angles is 90 degrees, resulting in irradiation directly along the body axis. Control point sequences were developed for N = 2, m = 1, having θ_S = 0, 36, 72, 288, and 324 degrees. For θ_S = 0, a full arc was used; for θ_S ≠ 0, half arcs were used (gantry range, 0-180 degrees). At each table position, clockwise and counter-clockwise arcs were used with collimator angles of 45 and 135 degrees, respectively. The central 2 leaves of the MLC were set to a small gap and the remaining leaves were positioned 3 cm outside of the secondary collimation, which was 1.5 cm × 1.5 cm. Three plans were created with gaps of 1.6, 2.1, and 2.6 mm. The beam geometry is shown in Figure 1.

Figure 1.

Beam geometry for table angles 0, 36, 72, 288, and 324 degrees and leaf gap 2.1 mm. The beams-eye-view of the multileaf collimators aperture is shown for (A) clockwise and (B) counterclockwise arcs at table angles 0, 36, 72, 288, and 324 degrees. Arc geometry is shown in (C) the coronal and (D) sagittal planes.

The dose per degree of the arcs was nonuniform and proportional to the sine of the gantry angle. This weighting was chosen because in the limit of large N, a 2π irradiation, it results in uniform fluence per unit area, which is ideal for creating a spherical dose distribution. The treatment plans were created using MatLab (MathWorks, Natick, MA) and exported as Digital Imaging and Communications in Medicine (DICOM) files that were imported into the Eclipse treatment planning system (Varian Medical Systems, Milpitas, CA). Dose was calculated on a 1 mm × 1 mm × 1 mm grid spacing for the 10 MV flattening filter free beam of an Edge linear accelerator (Varian Medical Systems, Milpitas, CA) using the Eclipse AAA algorithm version 13.6 (Varian Medical Systems). The dose calculation was configured using measured MLC leaf transmission 1.2% and dosimetric leaf gap (DLG) 0.36 mm.

Cone plans

For comparison with the virtual cone, treatment plans were created for 4 mm and 5 mm cones. The plans used the same arc geometry as the virtual cone plans; however, the dose rate was constant, and the noncoplanar arcs started and stopped at 10 degrees from vertical.

Measurement

Measurements of the virtual cone dose distribution in the Stereotactic End-to-End Verification anthropomorphic skull phantom (Computerized Imaging Reference Systems, Norfolk, VA) were obtained using EBT-XD GafChromic film (Ashland Chemical, Covington, KY). A 6.35 × 6.35 × 6.35 cm³ film insert (Computerized Imaging Reference Systems model 038-05) was used to place a film approximately in the center of the skull. The insert could be placed such that the film plane was oriented in either the sagittal, coronal, or transverse planes. A template was used to place 4 fiducial marks on the film. The film plane contained a 3 cm diameter sphere with a contrast 5% higher than the surrounding material to facilitate localization. A computed tomography (CT) scan of the phantom containing the film insert was obtained at 1 mm slice spacing and the isocenter placed in the center of the target sphere. After dose calculation, the plans were normalized to deliver 20 Gy at the isocenter.

Each control point sequence was delivered to the phantom with the film oriented in each plane. Prior to each delivery, the phantom was positioned using a 6 degree-of-freedom robotic couch (PerfectPitch; Varian Medical Systems, Palo Alto, CA) and orthogonal kV images followed by cone beam CT image guidance. The films were digitized using an Epson Perfection V700 scanner (Epson America, Long Beach, CA) at 800 pixels per inch (0.032 mm resolution) and converted to dose using a calibration film with dose values in the range of 2.2 Gy to 22 Gy. A 3-parameter curve was fit to each color channel, and a 3-channel method was used to convert the film to dose.²¹ Measurements in the coronal plane were repeated twice for each plan on separate days with separate calibration films.

Output factor and monitor unit verification

The output $\dot{D}$ of the 2.1 mm gap field was measured at 10 cm depth, 90 cm SSD and 4 cm depth, and 96 cm SSD using EBT-XD film. Five measurements were made at each depth at expected dose values of 1000 cGy. Eleven calibration films were obtained at 10 cm depth by irradiating a 4 cm × 4 cm field to doses in the range of 950 to 1050 cGy. A line was fit to each color channel, and the 3-channel method was used to convert the film to dose.²¹ The dose in a 0.5 mm diameter circle at the center of each film was averaged to obtain the dose.

The measured output at 4 cm and 10 cm was used to compute the expected monitor units using a tissue-phantom ratio (TPR) formalism for which the output $\dot{D}$ at depth d is given by:

$$\dot{D}=\dot{D}\left(10\text{cm}\right)\times TPR\left(d\right)$$ (2)

Assuming depth-independent scatter and beam hardening effects, the TPR can be approximated by an exponential dependence on depth22, 23:

$$TPR\left(d\right)=e^{-\mu \left(d-10\text{cm}\right)}$$ (3)

where µ is obtained from the 4 cm measurement:

$$\mu =\frac{\text{ln}\left(\dot{D}\left(10\text{cm}\right)\right)-\text{ln}\left(\dot{D}\left(6\text{cm}\right)\right)}{6\text{cm}}$$ (4)

For each arc field, the dose was estimated using 2 methods. In the first method, the dose was calculated using:

$$\dot{D}=\dot{D}\left(10\text{cm}\right){\displaystyle {\int }_{{\phi }_{\mathit{start}}}^{{\phi }_{\mathit{stop}}}TPR\left(d\left(\phi \right)\right)d\phi }$$ (5)

where φ is the gantry angle, and the effective radiologic depth at each gantry angle, d(φ), was calculated by ray tracing through the CT volume. The ray tracing and the numerical integration were done using MatLab (MathWorks, Natick, MA). The second method used the average effective radiologic depth computed by the treatment planning system to compute the dose rate:

$$\dot{D}=\dot{D}\left(10\text{cm}\right)\times TPR\left(d_{EqTPS}\right)$$ (6)

Quality assurance

The output constancy of the virtual cone was evaluated using a static field with the same MLC gap and secondary collimator settings as the virtual cone. The ionization was measured using a 2 cm diameter parallel plate ionization chamber (Exradin A11, Standard Imaging, Madison, WI) at 2 cm depth and 100 cm source-to-surface distance in water-equivalent plastic.

Geometric accuracy was verified using a standard Winston-Lutz procedure.1, 17, 24 Additionally, a virtual cone-specific test was developed. Similar to a standard Winston-Lutz test, a tungsten carbide target sphere measuring 6.35 mm in diameter was placed at the isocenter using the onboard kV imager. At each gantry angle, images were obtained using a 3 cm × 3 cm MLC aperture and using the MLC treatment aperture (2.1 mm × 5 mm) at collimator angles of 45 and 135 degrees. Images were obtained at 45 degree gantry angle increments using the MV beam and electronic portal imaging device. The center of the target ball and the 3 cm × 3 cm aperture were obtained by setting a threshold and computing the centroid of the resulting region. The center of the virtual cone apertures was obtained by summing the images obtained at the 2 collimator angles and thresholding and computing the centroid of the resulting region.

Patient treatment

We have treated a patient as part of an institutional review board–reviewed clinical trial for application of the virtual cone to trigeminal neuralgia (ClinicalTrials.gov Identifier: NCT02708810). The purpose of the trial is to determine the feasibility of frameless trigeminal neuralgia radiation surgery using the virtual cone and to measure pain relief after virtual cone radiosurgery utilizing the Barrow Neurologic Institute pain intensity score. The prescription was 80 Gy to the maximum dose. The target was the root entry zone of the trigeminal nerve as identified on a 3-dimensional constructive interference in steady-state (3D-CISS) magnetic resonance image (MRI) set²⁵ that was registered to the treatment planning CT. The isocenter was placed such that the 50% (40 Gy) isodose surface abutted the brainstem.¹⁰

We also have treated a patient for essential tremor using a radiosurgical thalamotomy.²⁶ The isocenter was placed at the ventral intermediate nucleus, which was localized using stereotactic coordinates.²⁷ The prescription was 130 Gy at the maximum dose. The primary organ-at-risk for stereotactic radiation surgery radiosurgical thalamotomy is the internal capsule. To minimize the risk of complications, the isocenter was placed such that the 10% (13 Gy) isodose line of the virtual cone was medial to the internal capsule. To confirm the monitor unit settings, the patient-specific plans were measured using radiochromic film placed in an acrylic block phantom.

Results

Volumes and the equivalent sphere diameters calculated by the treatment planning system for 50%, 25%, and 10% of the maximum dose are shown in Table 1. The mean ratio of the film-to-calculated dose (defined as the ratio of the mean dose inside the 50% area of the calculation) obtained from the 3 coronal plan films was 0.99 (range, 0.96-1.01), 1.03 (range, 1.02-1.04), and 1.05 (range, 1.03-1.07) for the 1.6, 2.1, and 2.6 mm leaf gaps, respectively. The mean offset between the measured and calculated dose distributions in the film plane was 0.3 mm.

Table 1.

Volumes and equivalent diameters calculated by the treatment planning system for 50%, 25%, and 10% of the maximum dose

Plan	Isodose volume/cm3 (Equivalent sphere diameter/mm)
	V50%	V25%	V10%
1.6 mm MLC	0.054	0.210	1.333
	(4.7)	(7.4)	(13.7)
2.1 mm MLC	0.064	0.275	1.552
	(5.0)	(8.1)	(14.4)
2.6 mm MLC	0.087	0.319	1.782
	(5.5)	(8.5)	(15.0)
4 mm cone	0.058	0.187	0.831
	(4.8)	(7.1)	(11.7)
5 mm cone	0.115	0.330	1.437
	(6.0)	(8.6)	(14.0)

MLC, multileaf collimator.

The equivalent diameter is the diameter of a sphere of the given volume.

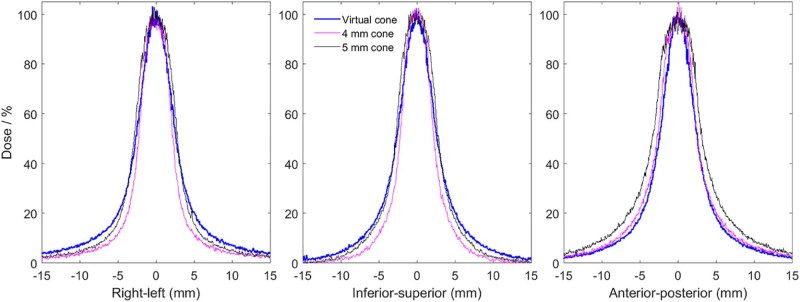
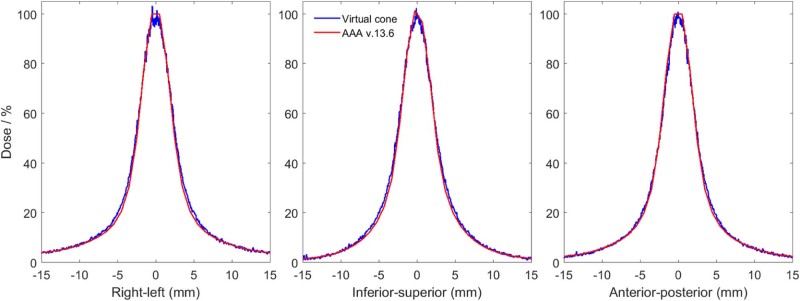
Profiles normalized by the film-to-calculated dose ratio and shifted by the offset are shown in Figure 2 for the 2.1 mm leaf gap and the 4 mm and 5 mm cones. The equivalent diameters of the 50% and 25% isodose areas in the 3 planes for measured and calculated dose distributions are provided in Table 2. The treatment planning system underestimated the diameter of the 50% isodose line by 0.3, 0.2, and 0.1 mm and of the 25% isodose line by 0.8, 0.5, and 0.3 mm for the 1.6, 2.1, and 2.6 mm leaf gaps, respectively. Profiles for the 2.1 mm leaf gap are shown with the treatment planning system calculation in Figure 3.

Figure 2.

Profiles measured using radiochromic film in an anthropomorphic skull phantom for the virtual cone with a 2.1 mm leaf gap, 4 mm cone, and 5 mm cone.

Table 2.

Measured and calculated equivalent diameter of the 50% and 25% isodose lines in each plane

	50% isodose Equivalent diameter (mm)			25% isodose Equivalent diameter (mm)
Plan	Coronal	Transverse	Sagittal	Coronal	Transverse	Sagittal
MLC 1.6 mm
Measured	5.0	4.9	4.9	8.4	8.2	8.3
Calculated AAA 13.6	4.6	4.6	4.6	7.6	7.4	7.5
MLC 2.1 mm
Measured	5.3	5.2	5.2	8.7	8.5	8.5
Calculated AAA 13.6	5.1	5.0	5.1	8.2	8.0	8.1
MLC 2.6 mm
Measured	5.6	5.5	5.5	8.9	8.8	8.8
Calculated AAA 13.6	5.5	5.4	5.5	8.6	8.5	8.5
Cone 4 mm measured	4.5	4.8	4.8	6.7	7.4	7.5
Cone 5 mm measured	5.7	6.0	6.0	8.2	9.1	9.2

MLC, multileaf collimator.

Figure 3.

Profiles calculated using Eclipse AAA version 13.6 and measured using radiochromic film in an anthropomorphic skull phantom.

The parallel plate chamber signal relative to a 10 cm × 10 cm field was measured 9 times over a 15-day period. The mean ratio was 0.305, 0.363, and 0.421 with a standard deviation of 0.3%, 0.2%, and 0.2% for leaf gaps of 1.6 mm, 2.1 mm, and 2.6 mm, respectively. The slope of a linear fit to the relative signal was 0.116 per mm, a change of 32% per mm relative to the 2.1 mm gap. This result indicates that the parallel plate chamber is sensitive to changes in MLC gap width.

The dose rate measured using radiochromic film was 0.420 cGy/MU (range, 0.415-0.430) and 0.322 cGy/MU (range, 0.318-0.325) at 4 cm and 10 cm, respectively, corresponding to a TPR at 4 cm of 1.30. The dose calculated using these values and Equations 5 and 6 are shown in Table 3.

Table 3.

Difference between doses calculated at isocenter by the TPS and estimated using sine-weighted integral of tissue-phantom ratio (Eq. 5) and the average equivalent path length reported by the TPS (Eq. 6)

	Skull phantom		TGN patient plan
Table angle (degrees)	Integral (Eq. 5)	TPS Eq. Path (Eq. 6)	Integral (Eq. 5)	TPS Eq. Path (Eq. 6)
0	5.9%	3.8%	1.7%	0.4%
36	5.2%	2.9%	7.8%	8.9%
72	5.7%	2.8%	9.5%	12.5%
288	5.7%	2.6%	8.4%	9.3%
324	5.2%	2.7%	3.0%	1.6%
Plan	5.6%	3.0%	5.8%	6.1%

Eq, equation; TGN, trigeminal neuralgia; TPS, treatment planning system.

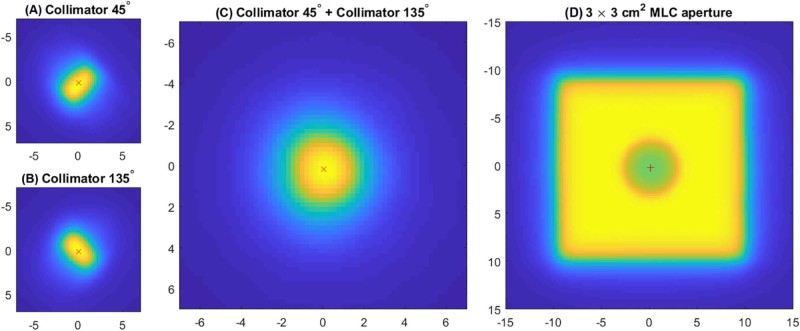
The mean offset between the 3 cm × 3 cm MLC aperture and the center of the target ball was 0.2 mm (range, 0.1-0.4 mm). The mean offset between the sum of the images at 45 and 135 degree collimator angles for a 2.1 mm leaf gap and the center of the target ball was 0.3 mm (range, 0.0-0.6 mm). Example images are shown in Figure 4.

Figure 4.

Electronic portal imaging device images for a 2.1 mm × 5 mm multileaf collimator aperture at collimator angles (A) 45 and (B) 135 degrees. The sum of the images (A) and (B) is shown in (C). The centroid of the high dose region in (A) to (C) is shown with a red x. An electronic portal imaging device image of a 3 cm × 3 cm multileaf collimator aperture is shown in (D). The centroid of the target ball in (D) is shown with a red +.

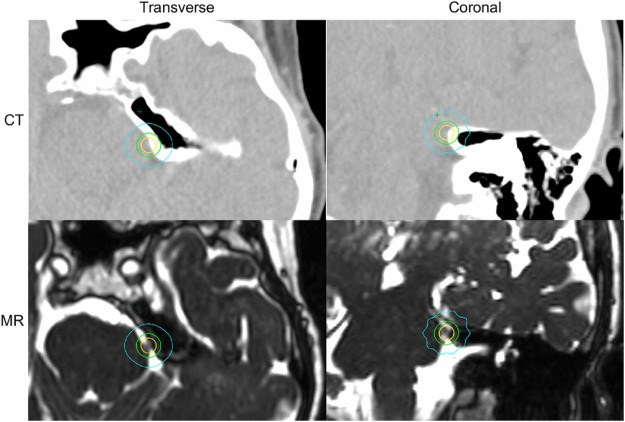
The trigeminal neuralgia patient was treated using the 2.1 mm gap virtual cone. The planned dose distribution is shown in Figure 5. The volume of brainstem receiving ≥10 Gy was 0.31 cm³, and 0.5 cm³ received >7.9 Gy. Pretreatment quality assurance measurements using radiochromic film gave a measurement-to-plan ratio of 1.04, consistent with the preclinical measurements and independent calculation shown in Table 3. The image-guided setup took 7.8 minutes from the first image acquisition to the initiation of treatment, and treatment delivery required 20.3 minutes.

Figure 5.

Dose distribution of virtual cone treatment targeting the root entry zone of the trigeminal nerve. Displayed in the transverse and coronal planes of the treatment planning CT and 3-dimensional constructive interference in steady-state (3D-CISS) magnetic resonance images are isodose lines corresponding to 50% (yellow), 25% (green), and 10% (cyan) of the maximum dose.

The thalamotomy patient was also treated using the 2.1 mm gap virtual cone. Because the maximum dose exceeded the range of the radiochromic film used for quality assurance, the treatment field geometry was duplicated for a total of 20 arcs. Each group of 10 unique fields, delivering half of the planned dose, were delivered for the pretreatment quality assurance measurement and gave measurement-to-plan ratios of 0.98 and 0.99. The treatment delivery time was 33.5 minutes, including approximately 5 minutes for a mid-treatment cone beam CT. Because the gantry rotation speed was limited by the maximum dose rate, the delivery time was not significantly increased by delivering each field twice.

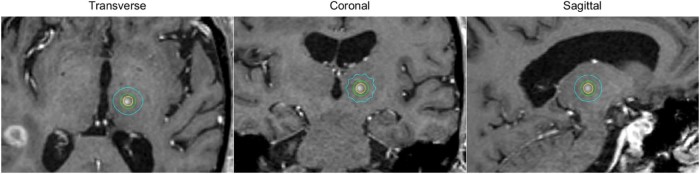
A follow-up T1 MRI scan that was obtained 11 weeks after treatment demonstrated a spherical lesion in the expected location of the ventral intermediate nucleus. The MRI was registered to the treatment planning CT using rigid registration. The planned dose distribution is shown on the follow-up image in Figure 6. The difference between the centroid of the lesion and the isocenter was 0.9 mm, which is similar to that reported elsewhere for frameless, image-guided thalamotomy using a 4 mm cone.²⁸

Figure 6.

Dose distribution of virtual cone treatment targeting the ventral intermediate nucleus of the hypothalamus. Displayed in the principle planes of a T1 magnetic resonance imaging scan obtained 11 weeks after treatment are the isodose lines corresponding to 50% (yellow), 25% (green), and 10% (cyan) of the maximum dose. Note the enhancement encompassed by the 50% isodose volume.

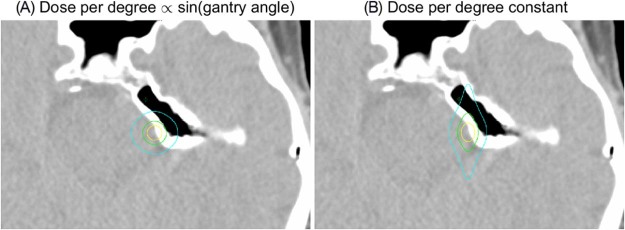
The dose per degree of the arcs was proportional to the sine of the gantry angle to generate a spherical dose distribution. If the dose per degree is constant, the resulting dose distribution is oblate with significant dose spill in the anterior-posterior direction. This effect is illustrated in Figure 7, which shows calculated dose distributions for plans that have dose-per-degree constant and proportional to the sine of the gantry angle calculated for the trigeminal neuralgia patient.

Figure 7.

Dose distribution for a virtual cone treatment plan with a dose per degree (A) proportional to the sine of the gantry angle and (B) constant. The displayed isodose lines correspond to 50% (yellow), 25% (green), and 10% (cyan) of the maximum dose.

The 10 MV flattening filter free beam was chosen because the 2400 monitor unit per minute dose rate minimizes the treatment time. For comparison, the plan for the trigeminal patient was recalculated using the 6 MV flattening filter free beam with a dose rate of 1400 monitor units per minute. The leaf gap was adjusted from 2.1 mm to 2.44 mm to obtain the same prescription (V50%) isodose volume. The resulting volume of low-dose spill was modestly more compact for the 6 MV plan, with the V25% decreasing from 0.27 to 0.24 cm³ and the V10% from 1.55 to 1.15 cm³. The treatment time for the 6 MV plan was 6.1 minutes longer than for the 10 MV plan, an increase of 30%.

The geometry with 5 table angles was chosen to minimize the number of room entries. For comparison, the plan for the trigeminal patient was recalculated using 7 angles (N = 3, m = 1 in Equation 1). The dose distributions were essentially indistinguishable. Seven table angles reduced the low dose volume by more than 0.1 cm³ and 1 cm³ only for dose levels less than 6% and 3% of the maximum dose, respectively.

Discussion

The dose calculation used the DLG determined by direct measurement of the sweeping gap fields.²⁹ However, to minimize the difference between calculation and measurement for volumetric arc therapy and dynamic MLC IMRT plans, the clinical DLG parameter configured in the treatment planning system was 0.86 mm, larger than the measured value by approximately 0.5 mm.³⁰ Therefore, a second MLC was configured in the treatment planning system specifically to support calculations for the virtual cone. Specifically, we configured a second MLC for a different linear accelerator of the same type (TrueBeam, Varian Medical Systems, Palo Alto, CA) that was equipped with a different model of MLC (NDS120 instead of NDS120HD). If the virtual cone–specific MLC configuration was incorrectly selected, the resulting plan would not be deliverable on the target machine because of the mismatch between the planned and equipped MLC models.

Virtual cone plans required a machine override when delivered. At our clinic, all stereotactic radiation surgery is delivered on a single machine, and machine overrides occur only for virtual cone plans, thus providing another layer of quality assurance. In clinical use, having 2 MLC configurations requires careful quality assurance procedures to ensure that the appropriate configuration is used for a given treatment plan. Improvements in modeling of the MLC by the treatment planning system would eliminate the need for a separate MLC configuration for the virtual cone.

Reproducing the virtual cone on a different machine will require consideration of the measured dosimetric leaf gap. Replicating the virtual cone on a machine with a different DLG than reported here will require adjustment of the planned leaf separation by the difference between the DLG of the target machine and 0.36 mm to obtain the same effective dosimetric leaf separation. For example, to replicate the virtual cone with a 2.1 mm separation as reported here on a machine with a 0.5 mm effective leaf gap, the planned leaf separation should be adjusted to 1.96 mm (2.1 mm + 0.36 mm – 0.5 mm).

The measurements using the parallel plate chamber demonstrate that the signal changes significantly with leaf gap, suggesting that this is a sensitive test for both dose output and width of the dose distribution. The measurements presented here demonstrate a high degree of reproducibility over a 2-week period. Measurements over an extended period are necessary to assess the long-term stability of the leaf separation.

The independent dose calculation using the tissue-phantom ratio gave reasonable agreement with measurement and the planning system for both the phantom and clinical plans, overestimating the dose by several percent in both cases. The exponential attenuation coefficient derived from Equation 4 was 0.0443 cm⁻¹, which is in agreement with 0.0441 cm⁻¹ given by Xiao et al for a 10 MV flattened beam; however, the flattening filter free beam has a lower average energy, for which Xiao et al predict a value larger than 0.0441 cm⁻¹.²³ More clinical cases are needed to assess whether the calculation method is sufficiently accurate or needs improvement. Potential refinements include additional measurements of the dose output at 10 cm and the depth dependence of the tissue-phantom ratio. Monte Carlo calculations may prove useful in determining the depth dependence of the tissue phantom ratio.

For the AAA dose calculation, the calculation grid was always positioned such that the isocenter was in the center of a calculation cell in the transverse plane. Furthermore, the calculation grid was aligned with the CT slices. Consequently, the dose distribution was truncated and the calculated dose maximum was not located at the isocenter as would be expected. This dose truncation is evident in the right-left and anterior-posterior profiles of Figure 3. We speculate that this is at least part of the reason why the planning system underestimated the dose by several percent relative to the film measurements. Aligning the dose calculation grid such that a calculation point is located at the isocenter would mitigate this issue.

Because of the small grid size and the number of arcs, the calculation time is not insignificant. We used 10 calculation servers to calculate the control points in parallel and obtained a calculation time of 23.4 minutes. The Acuros XB algorithm is a finite Boltzmann solver and has potential advantages in calculation speed.31, 32 We configured this algorithm using the same beam commissioning data as the AAA algorithm for a comparison of calculation time. The Acuros XB version 13.6 took 2.8 minutes. Acuros XB can be configured to calculate each beam individually or the entire plan (without beam dose). The plan level calculation took 14.8 minutes.

The virtual cone requires room entry for each table rotation. Automated table motion will reduce the treatment delivery time by 2 to 3 minutes. Table rotation during beam delivery could reduce the delivery time further, making the virtual cone a very efficient technique. For comparison, trigeminal neuralgia treatments on a Gamma Knife include approximately 25 minutes of beam time for new sources, which increases as the source decays.

Although the virtual cone dose distribution is similar to a physical cone in the high and intermediate dose regions, the additional collimation of a physical cone results in less volume irradiated at very low dose levels. For the 2.1 mm gap, the 50% isodose volume is approximately the same as a 4 mm cone and the 25% isodose volume is between that for the 4 mm and 5 mm cones. The 10% isodose volume is nearly double that achieved with the 4 mm cone but only 8% larger than that achieved with the 5 mm cone. Therefore, the 2.1 mm gap virtual cone is equivalent to a 4 mm physical cone with respect to prescription volume and similar to a 5 mm physical cone at dose values above 10%. The volumes encompassed by dose values <10% are larger than a 5 mm physical cone, with the relative difference increasing with decreasing dose levels. If very low isodose volumes are of clinical importance, the efficiency and safety advantages of the MLC-based virtual cone technique must be weighed against the reduced low-dose volume of a physical cone.

On the basis of the encouraging preclinical results, a prospective clinical trial of the virtual cone for trigeminal neuralgia radiation surgery has been opened at our institution (ClinicalTrials.gov Identifier: NCT02708810). We have also opened a trial employing the method for radiosurgical thalamotomy for essential tremor (ClinicalTrials.gov Identifier: NCT03305588) modeled after the trial published by Witjas et al.³³ We are exploring the application of the technique to other functional treatments such as anterior capsulotomy for severe, refractory obsessive compulsive disorder.

Conclusions

The virtual cone is an efficient technique to deliver a small spherical dose distribution with excellent accuracy and precision. Direct integration into the planning system, similar to other prestored control point techniques such as a dynamic wedge, along with optimization of the dose calculation time will provide planning times of <10 minutes. The geometric accuracy is equivalent to or better than a physical cone because the MLC is aligned to the machine coordinate system on installation and is not removed.

Periodic geometric quality assurance is necessary, similar to physical cones, but can be completed on a more flexible schedule because the MLC is a permanent component of the linear accelerator. The virtual cone idea can be extended to prestored control point sequences that generate nonspherical dose distributions, such as those produced by 2 cone shots with separate isocenters.