A One-Penny Imputed Genome from Next-Generation Reference Panels

Abstract

Genotype imputation is commonly performed in genome-wide association studies because it greatly increases the number of markers that can be tested for association with a trait. In general, one should perform genotype imputation using the largest reference panel that is available because the number of accurately imputed variants increases with reference panel size. However, one impediment to using larger reference panels is the increased computational cost of imputation. We present a new genotype imputation method, Beagle 5.0, which greatly reduces the computational cost of imputation from large reference panels. We compare Beagle 5.0 with Beagle 4.1, Impute4, Minimac3, and Minimac4 using 1000 Genomes Project data, Haplotype Reference Consortium data, and simulated data for 10k, 100k, 1M, and 10M reference samples. All methods produce nearly identical accuracy, but Beagle 5.0 has the lowest computation time and the best scaling of computation time with increasing reference panel size. For 10k, 100k, 1M, and 10M reference samples and 1,000 phased target samples, Beagle 5.0’s computation time is 3× (10k), 12× (100k), 43× (1M), and 533× (10M) faster than the fastest alternative method. Cost data from the Amazon Elastic Compute Cloud show that Beagle 5.0 can perform genome-wide imputation from 10M reference samples into 1,000 phased target samples at a cost of less than one US cent per sample.

Introduction

Genotype imputation uses a reference panel of phased, sequenced individuals to estimate sequence data in target samples that have been genotyped on a SNP array.^{1, 2} Imputation of ungenotyped markers is a standard tool in genome-wide association studies because it greatly increases the number of markers that can be tested for association with a trait. Genotype imputation also provides a foundation for meta-analysis of genome-wide association studies because it converts data for samples that have been genotyped on different SNP arrays into genotype data for a shared set of sequence variants. Meta-analyses based on genotype imputation have discovered thousands of new genetic associations.³

The reference panel plays the primary role in determining the accuracy of imputed variants. Imputation accuracy for a variant generally increases with increasing reference panel size, and variants must be present in the reference panel in order to be accurately imputed.^{4, 5} Consequently, whenever a significantly larger reference panel becomes available, it is advantageous to re-impute target samples with the larger panel for subsequent analysis.

The value of larger reference panels has led to steadily increasing reference panel size, with the largest reference panels to date having tens of thousands of samples.^{6, 7, 8, 9, 10, 11, 12} Ongoing, large-scale projects, such as the Trans-Omics for Precision Medicine (TopMed) program¹³ and the National Human Genome Research Institute’s Centers for Common Disease Genomics (see Web Resources), are expected to produce reference panels with more than 100,000 individuals.

Increasing reference panel size increases the computational cost of imputation, and this increasing cost has motivated the development of many new computational methods and optimizations. Current imputation methods are able to make use of a rich palette of computational techniques, including the use of identity-by-descent,^{6, 14, 15} haplotype clustering,^{4, 16} and linear interpolation⁵ to reduce the model state space, the use of pre-phasing to reduce computational complexity,^{14, 17, 18} and the use of specialized reference file formats to reduce file size and memory footprint.^{4, 5, 19} The techniques developed thus far have made it possible to provide imputation using reference panels with tens of thousands of individuals as a free web service.⁴

However, the total computational cost of imputation is substantial and increasing. Millions of individuals have been genotyped on SNP arrays and it is probable that millions more will be genotyped in the future. A sample may be re-imputed to a current state-of-the-art reference panel each time it is analyzed or included in a meta-analysis. The increasing size of reference panels increases the per-sample cost of re-imputation. If the past exponential growth in reference panel size continues, reference panels could have ten million individuals within a decade.^{6, 7, 10, 11, 12}

In this paper, we present new methodology that reduces the computational cost of genotype imputation 500-fold when imputing from 10M reference samples, and we use the Amazon Elastic Compute Cloud to show that the new methodology can impute genotypes from 10M reference samples into 1,000 phased target samples for a cost of less than one US penny per sample.

The computational performance of our method is made possible by combining previous advances with several methodological improvements and innovations. Our imputation method uses a Li and Stephens haplotype frequency model,^{2, 20} with a highly parsimonious model state space that is a fraction of the size of the state space of the full Li and Stephens model. We employ a pre-processing step to reduce the full reference panel into a small number of composite reference haplotypes, each of which is a mosaic of reference haplotypes. In addition, we decouple probability calculations at genotyped and ungenotyped markers, which enables us to further reduce the number of state probabilities that must be calculated and stored.

We also make use of recent advances in simulation methods²¹ and inference of historical effective population size²² to generate a simulated dataset that is much larger and more realistic than simulated data used in previous work.⁵ In large reference panels, many markers will be multi-allelic, and our simulation allows for multi-allelic markers, recurrent mutation, and back mutation. We simulate 10M reference samples and 1,000 target samples from a population whose growth rates and demographic parameters are modeled on the UK European population.

Our new imputation method is freely available and implemented in the open source Beagle 5.0 software package (see Web Resources).

Material and Methods

Imputation Methods

We assume that the reference and target genotypes are phased and non-missing. This reduces the computational complexity of imputation from quadratic to linear in the size of the reference panel, and it simplifies the imputation problem to imputing missing alleles on a haplotype.¹⁷

We use the term “reference markers” to refer to markers that are genotyped in the reference panel, the term “target markers” to refer to the markers that are genotyped in the target samples, and the term “imputed markers” to refer to markers in the reference panel that are not genotyped in the target samples. We assume that the target markers are a subset of the reference markers.

Genotype imputation is based on identity by descent (IBD). Two chromosome segments that are inherited from a common ancestor without recombination since the common ancestor are said to be inherited identical by descent. In an IBD segment, the two chromosomes will have identical allele sequences except at sites that have mutated in one of the lineages since the common ancestor. We can use the genotypes at the target markers to identify long IBD segments that a target haplotype shares with the reference haplotypes. If an IBD segment is accurately identified, the ungenotyped alleles in the IBD segment in the target haplotype can be copied from the IBD segment in the reference haplotype. Since there is uncertainty in inferring IBD, a probabilistic model is used to account for the uncertainty and to produce a posterior probability for each possible allele at an imputed marker on the target haplotype. This probabilistic model is typically a hidden Markov model (HMM).²³

Hidden Markov Model

Our imputation method is based on the Li and Stephens²⁰ HMM. Since the Li and Stephens model has been described many times,^{1, 2, 4, 5, 24} we provide only a brief description here.

In the Li and Stephens model, the HMM state space is a matrix of reference alleles, whose rows are reference haplotypes and whose columns are markers. Each HMM state is an entry of the matrix defined by the reference haplotype (row) and marker (column), and each HMM state is labeled with the allele carried by the reference haplotype at the marker.

In imputation with the Li and Stephens model, we assume that the target haplotype corresponds to an unobserved path through the HMM state space from the first marker to the last marker that includes one state at each marker. The HMM and the observed data on the target haplotype determine a probability distribution on the paths. The HMM forward-backward algorithm²³ is used to calculate the probability that the unobserved path passes through a HMM state (the state probability). At each marker, the sum of the probabilities of the states labeled with an allele is the imputed probability for that allele.

A HMM is defined by its state space, initial probabilities, transition probabilities, and emission probabilities. The Li and Stephens HMM state space is the set of all ordered pairs (h, m) whose first element is a reference haplotype and whose second element is a reference marker. We label the reference haplotypes, H, with indices 1, 2, …, $\left|H\right|$, and we label the list of reference markers in chromosome order, M, with 1, 2, …, $\left|M\right|$, where $|\cdot |$ denotes the size of the list.

We assign an initial probability of $1/\left|H\right|$ to each state at the first marker. State transitions are permitted from any state at a marker to any state at the next marker. In the Li and Stephens model used by Impute² and Beagle,⁵ the state transition probabilities between marker m − 1 and marker m are defined in terms of the effective population size N_e, the genetic distance d_m in Morgans between markers m − 1 and m, and the number of reference haplotypes $\left|H\right|$. If the HMM state at marker m − 1 is on reference haplotype h then with probability ${\tau }_m=1-e^{-4N_e{d}_m/\left|H\right|}$, a historical recombination event will cause the HMM state at marker m to be randomly chosen from the $\left|H\right|$ reference haplotypes.² Otherwise (with probability $1-{\tau }_m$), the HMM state at marker m is required to stay on the same reference haplotype. Consequently, the probability that a state (h, m − 1) transitions to state (h, m) is $\left(1-{\tau }_m\right)+{\tau }_m/\left|H\right|$, and the probability that the state (h, m − 1) transitions to state $\left(h^{\text{'}},m\right)$ with $h^{\text{'}}\ne h$ is ${\tau }_m/\left|H\right|$.

We define emission probabilities in terms of an error rate $\epsilon$ (0.0001 by default). Each state (h, m) emits the allele carried by reference haplotype h at marker m with probability $\left(1-\epsilon \right)$ and emits a different allele with probability $\epsilon$.

Our method uses several modifications of this basic Li and Stephens HMM that are used in the Beagle 4.1 imputation method: aggregate markers, restriction of the HMM to the target markers, and a long sliding marker window.⁵ We briefly describe these modifications next.

As in Beagle 4.1, we collapse tightly linked target markers within 0.005 cM into a single aggregate marker whose alleles are the sequences of alleles at the constituent markers. For an aggregate marker comprised of l markers, the genetic map position is the mean genetic position of the first and last markers, and the probability that a HMM state emits a different haplotype is $l\epsilon$ since the emission of a different allele at any of the l constituent markers will cause a different haplotype to be emitted.⁵

We initially include only target markers in the HMM. After computing state probabilities at the target markers, we use linear interpolation on genetic distance to estimate HMM state probabilities at each imputed marker.⁵

Finally, we use a long sliding marker window (40 cM by default), with substantial overlap between adjacent windows (4 cM by default). The sliding marker window limits the data stored in memory when imputing entire chromosomes. Markers in the overlap between two adjacent windows will be imputed twice (once in each window). Since imputation accuracy is expected to increase with distance from a window boundary, we discard the imputed value from the window in which the position is closer to the window boundary.

Computational Methods

Beagle 5.0 also incorporates three additional computational innovations beyond those inherited from Beagle 4.1: composite reference haplotypes, imputation on output, and an improved reference file format (bref3 format).

Composite Reference Haplotypes

One approach to reducing computation time for imputation is to reduce the size of the HMM state space by using only a subset of reference haplotypes when imputing a target haplotype.^{14, 15, 18, 24} If the subset contains the reference haplotypes that share the longest IBD segments with the target haplotype at each position, then the subset can yield the same imputation accuracy as the full set of reference haplotypes.⁶

Previous methods for selecting a target-specific set of reference haplotypes^{6, 14, 15} have required pre-specifying a short marker window (typically with length ≤ 5 cM) and selecting a target-specific set of reference haplotypes for the short window based on Hamming distance between reference and target haplotype in the window,¹⁴ Hamming distance in subintervals of the window,¹⁵ or IBS segment length.⁶ If the marker window is too long, computational efficiency is reduced because the size of the subset must be increased in order to contain additional reference haplotypes that share long IBD segments with the target haplotypes in the larger window. However, if the marker window is too short, imputation accuracy is reduced because IBD segments are truncated by the window boundaries. We present an example of this loss of accuracy in the Results section.

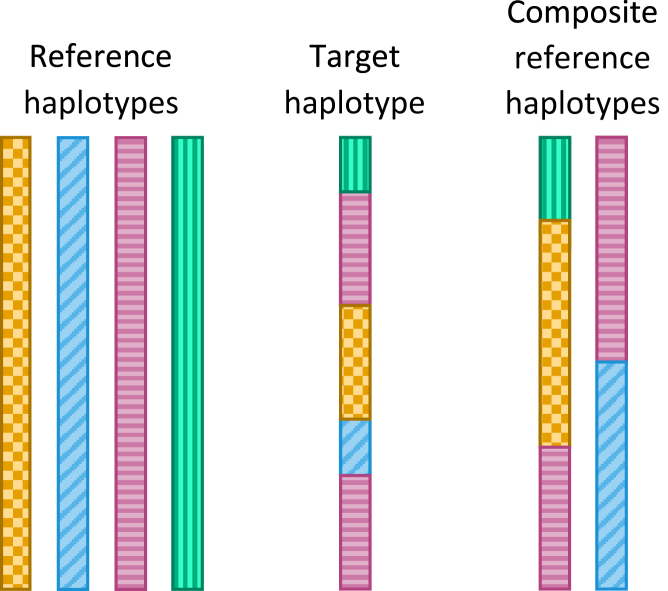
We have developed a method that allows imputation to use long marker windows and a small HMM state space. Instead of a using a target-specific set of reference haplotypes to construct the HMM state space, we use a target-specific set of composite reference haplotypes, where each composite reference haplotype is a mosaic of reference haplotype segments (Figure 1).

Figure 1.

Composite Reference Haplotypes

Long haplotype segments with identical allele sequences are shown with the same color and pattern. The target haplotype shares five segments of identical alleles with the reference haplotypes. The two composite reference haplotypes are each a mosaic of reference haplotypes, with the mosaics chosen so that the target haplotype also shares five segments of identical alleles with the composite reference haplotypes. This permits the two composite reference haplotypes to be used in place of the four original reference haplotypes.

By construction, each haplotype segment in a composite reference haplotype will contain a long interval in which the segment and the target haplotype have identical alleles at the target markers. These intervals are called identity by state (IBS) segments. One can generally expect each long IBS segment to contain at least one long IBD segment. A relatively small number of composite reference haplotypes can be used with large marker windows because each composite reference haplotype contains many long IBS segments.

We give an informal description of composite reference haplotype construction followed by a more precise description using pseudocode. There are a fixed number of composite reference haplotypes (1,600 by default), and we construct these composite reference haplotypes one haplotype segment at a time as we work through the marker window in chromosome order. As each segment is identified, it is added to one of the composite reference haplotypes. As we work through the marker window, we keep track of the staleness of each composite reference haplotype, which is the distance between the current position and the composite reference haplotype’s last IBS segment. When we add a new haplotype segment, we add it to the most stale composite reference haplotype.

Constructing Composite Reference Haplotypes

In order to ensure that the haplotype segments in the composite reference haplotypes cover the entire marker window and to facilitate parallel computation, we divide the marker window into consecutive, non-overlapping intervals I₁, I₂, …, I_K of fixed length (0.1 cM length by default). In each interval I_k, we select a set S_k of reference haplotypes that are identical by state with the target haplotype. Each S_k can contain at most s elements (we describe how s is determined in Appendix A). We want to preferentially select haplotypes for S_k that have longer IBS segments, and we do this by considering seven (by default) consecutive intervals beginning with I_k. We add reference haplotypes to S_k that are IBS with the target haplotype in seven consecutive intervals, six consecutive intervals, and so on, until S_k has size s or until we have added all haplotypes that are identical by state in I_k. All the reference haplotypes and associated IBS segments in the S_k will be included in the composite reference haplotypes.

Pseudocode for construction of the composite reference haplotypes is given in Figure 2. In the pseudocode, the segments comprising each composite reference haplotype are defined by a list of starting markers m_i and a list of haplotypes h_i. The i^th segment will copy haplotype h_i, starting with marker m_i and ending with marker m_i+1 − 1 (or ending with the last marker in the window if the i^th segment is the last segment). We add one segment at a time by adding a starting marker m and a haplotype h to the starting marker and haplotype list of a composite reference haplotype.

Figure 2.

Pseudocode for Constructing Composite Reference Haplotypes

In the pseudocode, L[j] keeps track of the staleness of the j^th composite reference haplotype. L[j] stores the index of the last S_k that contained the most recent haplotype added to the j^th composite reference haplotype. If I_k is the current interval being processed, and we want to add a new segment to the j^th composite reference haplotype, we set the starting point of the segment to a position approximately mid-way between intervals I_L[j] and I_k.

Imputation on Output

Our previous genotype imputation method (Beagle 4.1) calculates imputed allele probabilities for each individual immediately after calculating HMM state probabilities at the target markers.⁵ Beagle 5.0 postpones calculation of imputed allele probabilities until the output VCF file is constructed. This reduces memory requirements because imputation can be performed in short chromosome intervals with the results immediately written to the output VCF file. In our experience, imputing short chromosome intervals has the added benefit of reducing computation time, which may be a consequence of improved spatial and temporal locality of data in memory.

As in Beagle 4.1, we estimate the HMM state probabilities at imputed markers using the two HMM state probabilities at the bounding target markers and linear interpolation on genetic distance, and we combine all reference haplotypes that have identical allele sequences in the interval before performing linear interpolation.⁵ Once the state probabilities are interpolated, the posterior probability for a particular allele is the sum of the state probabilities at the marker for the reference haplotypes that carry the allele. The key point is that the state probabilities at all imputed markers between two genotyped markers are obtained from the state probabilities at the bounding genotyped markers. Consequently, by storing state probabilities at consecutive markers, we can perform imputation as the VCF output file is constructed.

In practice, only a small subset of the state probabilities at consecutive markers needs to be stored. We store state probabilities at consecutive markers for a reference haplotype only if one of the state probabilities is >1/J, where J is the number of composite reference haplotypes, or equivalently the number of HMM states at the marker. If state probabilities at consecutive markers are not stored for a reference haplotype, they are assumed to be 0 when performing imputation.

Bref3 Format

Previously we developed a specialized file format for reference panel data called binary reference (bref) format.⁵ In bref format, a chromosome is broken into consecutive, non-overlapping intervals. If the non-major alleles of a marker are rare, bref format stores the indices of the haplotypes that carry each non-major allele. For all remaining markers in an interval, bref stores the distinct allele sequences and a pointer from each haplotype to the allele sequence carried by the haplotype at these markers. This reduces memory requirements because the number of distinct allele sequences is typically much less than the number of haplotypes.

Beagle 5.0 uses a new version of bref format (bref3) that reduces imputation time relative to the preceding version (bref v2). bref3 uses two bytes to store a haplotype’s allele sequence index in a chromosome interval (bref v2 uses one byte). This permits bref3 to store allele sequences that extend over much longer chromosome intervals, which provides greater compression for large reference panels. In addition, bref3 does not gzip compress the binary reference file (bref v2 files are gzip compressed). This eliminates the computation time required for gzip decompression.

Table 1 reports file size for four reference file formats: gzip-compressed vcf file, gzip-compressed m3vcf,⁴ bref v2,⁵ and bref3 for 10k, 100k, 1M, and 10M simulated UK European reference samples. m3vcf format is similar to bref format, except that m3vcf format stores distinct allele sequences for all markers instead of only higher-frequency markers. These results show that bref3 scales better than bref v2 and gzip-compressed m3vcf with increasing reference panel size, and that bref3 achieves much greater compression than gzip compression.

Table 1.

Memory (GB) Required by Reference File Formats

n	vcf.gz	m3vcf.gz	bref v2	bref3
10k	0.045	0.011	0.006	0.017
100k	0.51	0.12	0.064	0.11
1M	7.9	1.9	0.7	0.7
10M	140.0	–	7.8	4.8

Number of gigabytes required to store 10 Mb of reference sample data for 10k, 100K, 1M, and 10M simulated UK European reference samples stored in vcf.gz, m3vcf.gz, bref v2, and bref3 formats. A dash (–) indicates that the compression could not be performed due to time and memory constraints.

Data

We compared methods using 1000 Genomes Project¹¹ chromosome 14 and chromosome 20 data, Haplotype Reference Consortium¹² chromosome 14 and chromosome 20 data, and simulated data for 10k, 100k, 1M, and 10M reference samples. The average recombination rates on chromosomes 14 and 20 are 1.12 cM/Mb and 1.72 cM/Mb, respectively, in the HapMap genetic map, which span nearly the entire range of average recombination rates for chromosomes (1.09–1.82 cM/Mb) in this map.⁸

Summary statistics for the six reference panels are given in Table 2.

Table 2.

Summary Statistics for Reference Panels Used in This Study

Reference Panel	n	Length (Mb)	Markers	Density (SNVs/kb)	Tri-allelic (%)	Quad-allelic (%)
1000 Genomes (chr 14)	2,452	107.3	2,508,019	23.4	0.0	0.0
1000 Genomes (chr 20)	2,452	62.9	1,718,742	27.3	0.0	0.0
HRC (chr 14)	26,165	107.3	1,236,165	11.5	0.34	0.00049
HRC (chr 20)	26,165	62.9	862,298	13.7	0.23	0.00058
Sim10k	10k	10.0	88,124	8.8	1.1	0.0057
Sim100k	100k	10.0	352,091	35.2	3.6	0.033
Sim1M	1M	10.0	1,210,904	121.1	10.0	0.29
Sim10M	10M	10.0	3,145,425	314.5	19.8	1.4

1000 Genomes Project Data

We downloaded the publicly available 1000 Genomes Project phase 3 version 5a data. The 1000 Genomes data contain 2,504 individuals with phased sequence data from 26 populations.¹¹ We randomly selected two individuals from each population (52 total) to be the imputation target. The remaining 2,452 individuals were the reference panel. We restricted the 1000 Genomes reference and target data to diallelic SNVs having at least one copy of the minor allele in the reference panel. After this marker filtering there were 2,508,019 markers on chromosome 14 and 1,718,742 markers on chromosome 20. In the target samples, we masked markers that were not on the Illumina Omni2.5 array, resulting in 72,973 target markers on chromosome 14 and 54,885 target markers on chromosome 20.

Haplotype Reference Consortium Data

The publicly available Haplotype Reference Consortium (HRC) data were downloaded from the European Genome-Phenome Archive²⁵ at the European Bioinformatics Institute (accession EGAD00001002729). The HRC data include 27,165 individuals with phased SNV genotypes, primarily from low-coverage sequencing. The chromosome 14 HRC data consist of 1,270,436 SNVs at 1,265,969 distinct positions, and the chromosome 20 HRC data consist of 884,983 SNVs at 882,742 distinct positions. Some positions have multiple SNVs because in the publicly available VCF file, multi-allelic markers are represented as multiple diallelic SNV markers at the same position. Since the HRC panel is predominantly European, we randomly selected 1,000 individuals from the constituent UK10K study⁶ to be the imputation target. The remaining 26,165 individuals were the reference panel. We report computation time for imputation into 10, 100, and 1,000 target samples. After excluding monomorphic markers in the reference samples, there were 1,240,379 SNVs at 1,236,165 unique positions on chromosome 14 and 864,376 SNVs at 862,298 unique positions on chromosome 20. In the target samples, we masked markers that were not on the Omni2.5 array or which had more than one ALT allele in the reference samples, resulting in 72,886 target markers on chromosome 14 and 55,013 target markers on chromosome 20.

Simulated Data

We used the msprime program²¹ (Supplemental Data) to simulate 10 Mb of sequence data for 10,001,000 diploid samples with a demographic history modeled on the UK European population. Recent growth rates for the UK European effective population size were obtained from the IBDNe program.⁵ We created four reference panels with 10k, 100k, 1M, and 10M samples by selecting the first 10k, 100k, 1M, and 10M simulated samples. The last 1,000 simulated samples became the imputation target. We report computation time for imputation into 10, 100, and 1,000 target samples.

Since msprime simulates diallellic variants, we devised a strategy for simulating multi-allelic single-nucleotide variants which permits recurrent and back mutation. When running msprime, we increased the length of the 10 Mb simulated region by a factor of 100 and decreased the mutation rate and recombination rate by a factor of 100. After generating data with msprime, we divided the simulated region into non-overlapping 100 base pair windows and collapsed the VCF records in the k^th window into a single genomic position whose position was k. In each 100 base pair window, we reconstructed the phylogenetic binary tree for the haplotypes in the window from the alleles carried by the haplotypes in the window. At each mutation event in the phylogenetic tree, we randomly chose a new allele from the three possible new alleles, and the haplotypes in each leaf of the tree were assigned the allele inherited by that leaf.

We randomly selected 3,333 diallelic variants having minor allele frequency ≥ 0.05 to be the genotyped markers in the imputation target samples. The resulting target marker density (1 marker per 3.3 kb) corresponds to a 1M SNP array in humans.

We also created one chromosome-scale reference panel by making 30 copies of the 10M sample reference panel and shifting each copy by a multiple of 10 Mb. We used this large reference panel to explore the computational performance of our imputation method when imputing a long 300 Mb chromosome from 10M reference samples.

Comparison of Methods

We compared the imputation accuracy and the computation time of our imputation method with four recent versions of three published imputation methods: Beagle 4.1 (27Jan18.7e1),⁵ Impute4 r265.2,^{14, 17, 18, 26} Minimac3 v2.0.1,^{4, 17} and Minimac4 v1.0.0 (S. Das et al., 2015, Am. Soc. Hum. Genet., abstract #1278W).

We used default parameters for each program, except when otherwise noted. When running Impute4, we used the no_maf_align option because strand alignment of reference and target variants was not needed. Impute4 requires specification of the analysis region, which was the entire chromosome or 10 Mb simulated region, except for the HRC reference panel. For the HRC Impute4 analysis, we split chromosome 14 and chromosome 20 into two analysis regions with 250 kb overlap (the default Impute4 buffer parameter) in order to perform imputation within the available computer memory. For Beagle 4.1, we increased the window parameter so that the imputation analysis used a single marker window, except for the simulated 10M reference panel. For the 10M reference panel, Beagle 4.1 used a marker window of 1,400,000 markers ($\approx$4.45 cM) with an overlap of 315,000 markers ($\approx$1 cM) between adjacent windows in order to run within the available computer memory.

Beagle and Impute require a user-specified genetic map. We used the HapMap2 genetic map²⁷ for analyses with real data, and we used the true genetic map for analyses with simulated data. Minimac does not require a genetic map because recombination parameters are estimated and stored when producing the m3vcf format input file for the reference data.^{4, 24}

Beagle 4.1, Beagle 5.0, Minimac3, and Minimac4 were run using their specialized formats for reference panel data: bref v2⁵ for Beagle 4.1, bref3 for Beagle 5.0, and m3vcf⁴ for Minimac3 and Minimac4. We used Minimac3 to construct the m3vcf files. We succeeded in creating an m3vcf reference file for 1M reference samples by borrowing a compute node with 1 TB of memory, but we were unable to create an m3vcf reference file for the largest 10M reference panel due to time and memory constraints.

We report the squared correlation (r²) between the true number of non-major alleles on a haplotype (0 or 1) and the posterior imputed allele probability. Since there is little information to estimate squared correlation for an individual marker when minor allele counts are low, we binned imputed minor alleles according to the minor allele count in the reference panel, and we calculated r² for the imputed minor alleles in each minor allele count bin.

All imputation analyses were run on a dedicated 12-core 2.6 GHz computer with Intel Xeon E5-2630v2 processors and 128 GB of memory, except where otherwise noted. We evaluated one program at a time using 1 and 12 computational threads. For the single-threaded analyses, we report the sum of the system and user time returned by the Unix time command. For multi-threaded analyses, we report the real (wall-clock) time returned by the Unix time command.

Multi-allelic Markers

Beagle is the only program evaluated that permits reference markers to have more than two alleles. For the other programs (Minimac and Impute), triallelic and quadallelic markers in the simulated reference panels were partitioned into two and three diallelic markers, respectively, using the bcftools norm -m command (see Web Resources). The downloaded HRC reference panel represents multi-allelic markers as multiple diallelic markers and was left as is.

Results

Beagle was evaluated using all reference panels. Minimac3 and Minimac4 were run with all reference panels except the largest reference panel (10M) because an m3vcf format file could not be constructed for this reference panel. Impute4 was run with all reference panels except the three largest reference panels (100k, 1M, and 10M). The Impute4 error message for the 100k reference panel indicated that Impute4 is limited to 65,536 reference haplotypes.

Accuracy

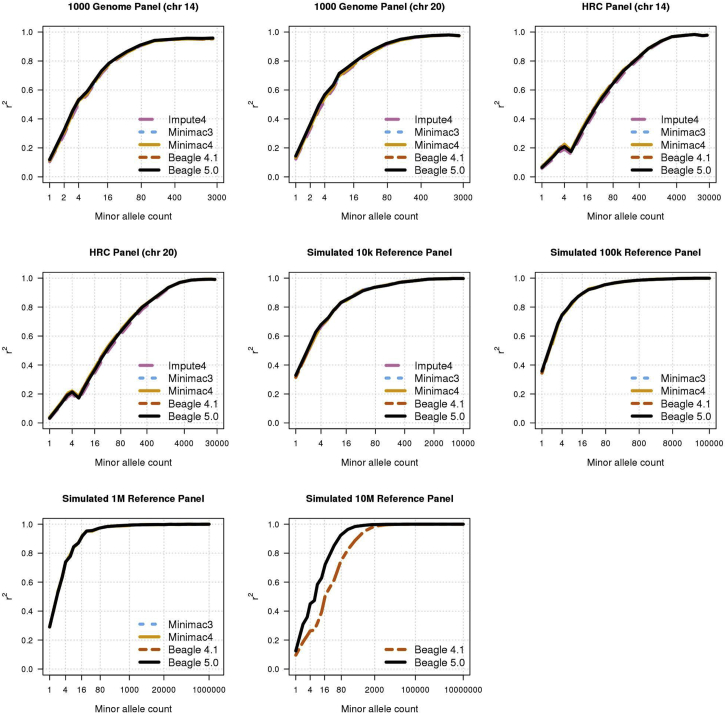
All the genotype imputation methods that we evaluated are based on the Li and Stephens probabilistic model²⁰ and have essentially the same imputation accuracy (Figure 3), which is consistent with previous reports.^{4, 5} The apparent difference in accuracy between Beagle 4.1 and Beagle 5.0 with the 10M reference panel is due to Beagle 4.1 using a short ($\approx$4.45 cM) marker window in order to run within the available computer memory. Experiments with different window and overlap lengths showed that the difference in imputation accuracy for the 10M reference panel is almost entirely explained by the difference in window length (Figure S1).

Figure 3.

Genotype Imputation Accuracy

Genotype imputation accuracy when imputing genotypes from a 1000 Genomes Project reference panel (n = 2,452), a Haplotype Reference Consortium reference panel (n = 26,165), and from 10k, 100k, 1M, and 10M simulated UK-European reference samples. Imputed alleles are binned according to their minor allele count in each reference panel. The squared correlation (r²) between the true number of alleles on a haplotype (0 or 1) and the imputed posterior allele probability is reported for each minor allele count bin. The horizontal axis in each panel is on a log scale. The difference in accuracy for 10M reference samples is due to a difference in length of marker window.

Single-Threaded Computation Time

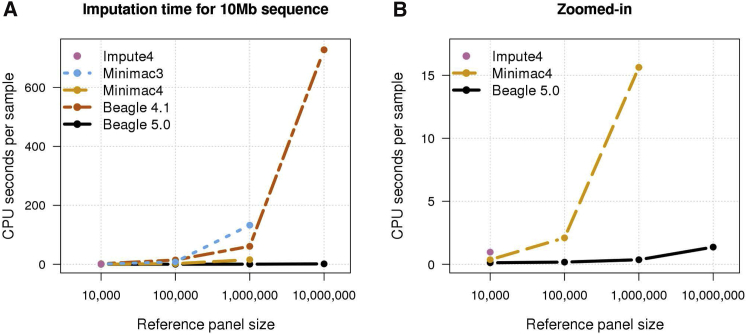
Single-threaded computation times for 10k, 100k, 1M, and 10M reference samples and 1,000 target samples are shown in Figure 4. Beagle 5.0’s computation time was 3 times (10k), 12 times (100k), 43 times (1M), and 533 times (10M) faster than the fastest alternative method. For the 1000 Genomes reference panel with 52 target samples, Beagle 5.0 was 1.6× faster (chromosomes 14 and 20) than the fastest alternative method (Tables S1 and S2). For the HRC reference panel with 1,000 target samples, Beagle 5.0 was 9.5× (chromosome 14) and 8.7× (chromosome 20) faster than the fastest alternative method (Tables S3 and S4). Beagle 5.0 had the lowest computation time in all single-threaded analyses and the best scaling of computation time with increasing reference panel size.

Figure 4.

Single-Threaded Computation Time

Per-sample CPU time when imputing a 10 Mb region from 10k, 100k, 1M, and 10M simulated UK-European reference samples into 1,000 target samples using one computational thread. CPU time is the sum of the system and user time returned by the Unix time command. Impute4 was run with only the 10k reference panel due to software limitations. Minimac3 and Minimac4 were not run with the 10M reference panel due to memory and time constraints.

(A) Results for Impute4, Minimac3, Minimac4, Beagle 4.1, and Beagle 5.0.

(B) Zoomed-in results for Impute4, Minimac4, and Beagle 5.0.

Figure 4A shows that the latest versions of imputation methods have achieved substantial improvements in computational efficiency. Beagle 5.0 is significantly faster than Beagle 4.1, Minimac4 is significantly faster than Minimac3, and a comparison with imputation results in previous studies^{4, 5} for the 1000 Genomes and HRC reference panels shows that Impute4 is significantly faster than Impute2.

One striking feature of Figure 4B is the sublinear scaling of computation time with increasing reference panel size for Minimac4 and Beagle 5.0. This is particularly pronounced for Beagle 5.0. Moving from 10k to 10M reference samples increases the number of reference samples by a factor of 1,000 and the number of imputed markers by a factor of 36, but Beagle 5.0’s imputation time increases by only a factor of 11 (Tables S5 and S8). Sublinear scaling in reference panel size over this range of reference panel sizes is made possible by the use of specialized file formats for the reference panel (bref3 for Beagle 5.0 and m3vcf for minimac4) which scale sublinearly in reference panel size (Table 1).

Multi-threaded Computation Time

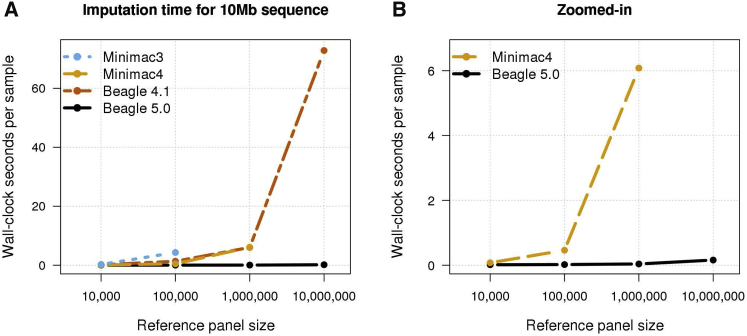
Beagle and Minimac can be run with multiple threads, which reduces wall-clock computation time and permits a single copy of the reference panel data to be stored in memory and used by all CPU cores. Multi-threaded computation times for 10k, 100k, 1M, and 10M reference samples and 1,000 target samples are shown in Figure 5. Beagle 5.0’s computation time was 5 times (10k), 23 times (100k), 156 times (1M), and 458 times (10M) faster than the fastest alternative method. For the 1000 Genomes reference panel, Beagle 5.0 was 3.8× (chromosome 14) and 3.6× (chromosome 20) faster than the fastest alternative method (Tables S9 and S10). For the HRC reference panel with 1,000 target samples, Beagle 5.0 was 12× (chromosome 14) and 11× (chromosome 20) faster than the fastest alternative method (Tables S11 and S12). Beagle 5.0 had the lowest wall-clock time in all multi-threaded analyses and the best scaling of wall-clock time with increasing reference panel size.

Figure 5.

Multi-Threaded Computation Time

Per-sample wall-clock time when imputing a 10 Mb region from 10k, 100k, 1M, and 10M simulated UK-European reference samples into 1,000 target samples using 12 computational threads. Minimac3 was not run with the 1M reference panel using 12 threads due to memory constraints. Minimac3 and Minimac4 were not run with the 10M reference panel due to memory and time constraints.

(A) Results for Minimac3, Minimac4, Beagle 4.1, and Beagle 5.0.

(B) Zoomed-in results for Minimac4 and Beagle 5.0.

Computational Efficiency with Decreasing Target Sample Size

The computation time results in Figures 4 and 5 are for batches of 1,000 target samples. We also examined computation times for batches of 100 and 10 target samples (Tables S3–S8 and S11–S16). In general, the computation time per sample increases as the number of target samples decreases. This is because the time required to read reference panel data from persistent storage is independent of the number of target samples. As the target sample size decreases, this fixed computational cost is shared among fewer target samples.

As the ratio of the number of reference to target samples increases, the time required to read the reference panel into memory will eventually dominate the total computation time. For example, the computation times when imputing from 10M reference samples into 100 or 10 target samples differ by only 20% because most of the computation time in these two analyses is spent reading in the reference panel data (Table S8).

Genome-wide Imputation on the Amazon Compute Cloud

We benchmarked genome-wide imputation time and cost when imputing from 10M reference samples into 1,000 target samples using the Amazon Web Services (AWS) compute cloud. We measured the cost of imputing a long 300 Mb chromosome. We used an AWS Elastic Compute Cloud (EC2) r4.4xlarge server with 16 virtual CPUs, 122 GB of memory, and a 150 GB Elastic Block Store (EBS) general purpose solid state drive. We copied data to the EBS drive via Amazon’s Simple Storage Service (S3), and we used the OpenJDK Java 1.8 runtime environment. We used a 30 cM analysis window to ensure that the memory requirements did not exceed the memory available on the EC2 server. The EC2 server ran for 97 min, which included 2.5 min for status checks and setting up the computing environment, 16 min for copying the program and data files onto the EBS drive, 78 min for genotype imputation, and 0.5 min for copying the imputation output files to our local computer. For comparison, we note that the same analyses can be performed with 40 cM windows on our local compute 12-core server with 128 GB of memory and a wall-clock computation time of 78 min.

The cost of the imputation analysis on the Amazon cloud was $0.63, which is comprised of the cost of the EC2 r4.4xlarge spot instance ($0.24), the cost of the EBS drive ($0.03), the cost of transferring data to S3 storage and briefly storing data there ($0.05), the cost to transfer 3.1 GB of imputed output data from AWS to our local computers ($0.28), and state taxes ($0.02). The per-hour cost of the EC2 r4.4xlarge spot instance was $0.15 per hour on the Ohio region servers, and this cost ranged between $0.1489 and $0.1537 per hour during a 4 month period from January to April, 2018. Since our analysis imputed one-tenth of the human genome, we extrapolate a total cost of $6.30 for imputation of 1,000 target samples, or equivalently a genome-wide imputation cost of less than one penny per sample when imputing from 10M reference samples into 1,000 target samples with Beagle 5.0.

Discussion

We have presented a new genotype imputation method implemented in Beagle 5.0 that has similar accuracy and much faster computation time than the Beagle 4.1,⁵ Impute4,²⁶ Minimac3,⁴ and Minimac4 (Web Resources) imputation methods. The Beagle 5.0 method had the lowest computation time for all reference panel sizes (2.5k–10M) and target sample sizes (10–1,000) considered. Imputation of one tenth of the genome from a reference panel with 10M individuals and one variant per 3 base pairs was performed on the Amazon Web Services compute cloud for $0.00063 per sample, which corresponds to a genome-wide imputation cost of 0.63 cents per sample.

The computational efficiency of Beagle 5.0 is due to several methodological improvements and innovations. The use of composite reference haplotypes permits modeling of arbitrarily large genomic regions with a parsimonious statistical model. An improved reference file format (bref3) reduces the computation time required to read in large reference panels relative to Beagle 4.1. Delaying imputation until output file construction reduces memory use because it permits imputation to be performed incrementally in short genomic intervals with the imputed data written immediately to the output VCF file.

As the size of the reference panel increases, the number of multi-allelic variants in the reference panel also increases. Many genotype imputation programs require multi-allelic markers to be represented as multiple diallelic markers. However, splitting a multi-allelic marker into diallelic markers is problematic because the constraint that posterior allele probabilities must sum to 1.0 cannot be enforced, potentially resulting in a loss of accuracy and inconsistent imputed data. Among the imputation methods evaluated in this study, Beagle was the only method that does not require multi-allelic markers to be represented as multiple diallelic markers.

The Beagle 5.0 genotype imputation method effectively solves the problem of imputing SNV variants in large batches of target samples. However, there is scope for further methodological work to improve computational efficiency when imputing from large reference panels into small batches of target samples, and in the development and evaluation of imputation methods for non-SNV variants, such as HLA alleles,^{28, 29, 30, 31} STR alleles,³² and other structural variants.

When reference panel size is much greater than the target panel size, the time required to read the reference panel from persistent storage dominates the computation time. For a fixed size reference panel, we observed a large increase in Beagle 5.0’s imputation time per sample when the reference panel size is 1,000 or 10,000 times larger than the target sample size (Tables S5–S8). Like many imputation programs, Beagle 5.0 requires all target samples in the same input file to be genotyped for the same set of markers, which limits the number of target samples that can be included in an imputation analysis. One potential approach to reducing imputation time for a small number of target samples would be to modify imputation software to allow multiple input target files to be specified so that the time required to read in the reference panel data can be shared among a larger number of target samples. Although an individual researcher may not have a large number of target samples, an imputation server⁴ could use this approach to impute multiple batches of target samples submitted by different researchers in a single analysis.

The computation time for imputation with Beagle 5.0 scales sublinearly with reference panel size over the range of reference panel sizes considered in this study. A 1,000-fold increase in the number of reference samples and a 36-fold increase in the number of reference markers led to only an 11-fold increase in computation time. Although we have limited our evaluation to reference panels with at most 10M individuals, these results suggest that Beagle 5.0 can analyze much larger reference panels than analyzed here.

Declaration of Interests

The authors declare no competing interests.

Published: August 9, 2018

Appendix A: The Maximal Size of S_k

We enforce a maximal size, s, for each S_k set in order to ensure that each segment in a composite reference haplotype exceeds a minimum length L cM. If the intervals I_k used to define the S_k have length I cM, there are L/I intervals in L cM, and the S_k sets for these intervals will contain ≤sL/I distinct haplotypes. If there are J composite reference haplotypes, we set s to be the largest integer such that sL/I < J. This ensures the number of haplotype segments added in L cM is less than the number of composite reference haplotypes. Consequently, each segment must be at least L cM in length. By default there are J = 1,600 composite reference haplotypes, the interval length is I = 0.1, and the minimum segment length is L = 6 cM, so that $s=\lfloor JI/L\rfloor =26$.

Web Resources

1000 Genomes Project Phase 3 version 5a data, ftp://ftp.1000genomes.ebi.ac.uk/vol1/ftp/release/20130502/

bcftools 1.5, http://www.htslib.org/doc/bcftools.html

Beagle 5.0 and bref3 programs, http://faculty.washington.edu/browning/beagle/beagle.html

Haplotype Reference Consortium data, https://www.ebi.ac.uk/ega/datasets/EGAD00001002729

NIH, RFA-HG-15-001: Centers for Common Disease Genomics (UM1), http://grants.nih.gov/grants/guide/rfa-files/RFA-HG-15-001.html

NIH, RFA-HG-15-026: NHGRI Genome Sequencing Program Analysis Centers (U01), http://grants.nih.gov/grants/guide/rfa-files/RFA-HG-15-026.html