Pulling apart photoexcited electrons by photoinducing an in-plane surface electric field

We make a movie, on the nanometer and femtosecond scale, as we pull apart electrons with a photoinduced surface field.

Abstract

The study and control of spatiotemporal dynamics of photocarriers at the interfaces of materials have led to transformative modern technologies, such as light-harvesting devices and photodetectors. At the heart of these technologies is the ability to separate oppositely charged electrons and holes. Going further, the ability to separate like charges and manipulate their distribution could provide a powerful new paradigm in opto-electronic control, more so when done on ultrafast time scales. However, this requires one to selectively address subpopulations of the photoexcited electrons within the distribution—a challenging task, particularly on ultrafast time scales. By exploiting the spatial intensity variations in an ultrafast light pulse, we generate local surface fields within the optical spot of a doped semiconductor and thereby pull apart the electrons into two separate distributions. Using time-resolved photoemission microscopy, we directly record a movie of this redistribution process lasting a few hundred picoseconds, which we control via the spatial profile and intensity of the photoexciting pulse. Our quantitative model explains the underlying charge transport phenomena, thus providing a roadmap to the more generalized ability to manipulate photocarrier distributions with high spatiotemporal resolution.

INTRODUCTION

The spatial and temporal dynamics of charged particles at the interfaces of materials is of vital consequence to several modern technologies, such as light-harvesting and semiconductor devices. For example, the mobility of carriers (1) and the underlying nature of diffusion (2) raise important questions relevant to semiconductor device technology. In the case of photocatalysis, where light energy is converted to chemical energy at the surface of a semiconductor, spatiotemporal dynamics of the photocarriers directly affects surface chemical reactions (3, 4). To further these scientific and technological aims, over the past few years, a handful of techniques have begun to study the dynamics of photocarriers simultaneously in space and time with high resolution. Ultrafast micro–pump-probe techniques, which interpret the measured, spatially resolved optical response to understand the underlying carrier dynamics, have observed drift and diffusion phenomena in semiconductor nanostructures (5, 6). Scanning ultrafast electron microscopy (SUEM), which uses ultrafast electronic packets to obtain high spatiotemporal resolution, measures the secondary electrons emitted by the probe electron packet to access the photoexcited carrier dynamics (7). As a result, SUEM has recently observed anomalous and anisotropic diffusion phenomena in amorphous silicon (2) and black phosphorous (8), respectively. In contrast, time-resolved photoemission electron microscopy (TR-PEEM) techniques (9) combine the high temporal resolution provided by ultrafast optical pulses with the high spatial resolution provided by photoemitted electrons to study dynamics in metals (10, 11) and semiconductors (12, 13). In semiconductors, TR-PEEM can directly image the density of photoexcited electrons as they evolve in space and time, as exemplified by our recent observation of the motion of electrons in a type II semiconductor heterostructure (14).

Beyond the observation of drift and diffusion phenomena in semiconductor structures, one would like to directly control the distribution of charge densities and local currents in space and time with high resolution. Arguably, one of the most potent examples of manipulating photocarrier distribution for modern technology is the separation of unlike photocharges—electrons and holes—using macroscopic electric fields (15) or energy gradients formed in material heterostructures (16, 17), such as type II heterostructures (18). However, manipulating the distribution of photocarriers of the same charge, for example, only the electrons, can be challenging due to the relatively few ways to separately address subpopulations of the photocarrier. Furthermore, tools to achieve control with both high spatial and temporal resolution remain scarce. Light would provide a natural tool to achieve high speed, but one would need to develop ways to selectively manipulate electrons within the optical spot size to achieve spatial resolution beyond the diffraction limit. A potential tool to manipulating charged carriers with light is the surface photovoltage (SPV) effect, wherein one can alter the surface potential of a doped semiconductor in relation to the light intensity. Previous studies of SPV have demonstrated carrier transport with the SPV effect, including on ultrafast time scales, but have typically studied the response averaged over the entire optical spot (19–21). Being able to manipulate the SPV effect within the optical spot could allow the creation of in-plane electric fields within the optical spot and thus provide control over subpopulation of photocarriers. Ultimately, such an ability to manipulate the distribution of photoexcited electrons and thereby generate local, spatially varying currents with high spatiotemporal resolution would have significant implications for fast, nanoscale opto-electronic devices (22, 23) or for site-specific, temporally gated photocatalytic reactions (24, 25) and many other opto-electronic technologies (26, 27).

Here, using the spatial variations in the intensity of a Gaussian ultrafast optical beam, we generate local electric fields within the optical spot that act to pull apart and separate into two the original Gaussian distribution of photoexcited electrons. Using TR-PEEM, we directly image the evolving electron density with high spatial and temporal resolution and thereby make a movie of the process of separation of the photoexcited electron distribution. By varying the spatial profile and intensity of the ultrafast optical beam, we control the in-plane electric fields and thus the degree and rate of the separation process. Using the high spatial resolution provided by PEEM, we show that the in-plane electric fields are a result of variations in the screening process within the optical spot. We use a model to understand the process, reproduce key features of our experiment, and provide a clear pathway to a more arbitrary manipulation of the photoexcited electron distribution.

RESULTS

Sample preparation and experimental setup

For this study, a p-doped GaAs wafer is cleaved in situ in the ultrahigh vacuum chamber of the PEEM to expose a clean 〈110〉 surface. The sample is photoexcited with a 1.55-eV, 45-fs pump pulse, which creates both photoelectrons in the conduction band and photoholes in the valence band. Then, using a time-delayed, frequency-tripled 4.6-eV probe pulse, we photoemit only electrons from the conduction band, while the photoholes are not directly accessible. The photoemitted electrons are then imaged in the PEEM to form a series of time-delayed images reflecting the evolving spatial distribution of the electrons (Fig. 1). Typically, the field of view and corresponding spatial resolution of the PEEM are set to 75 μm and 40 nm, respectively. The temporal resolution is ~280 fs in our experiment, limited by the frequency-tripled probe pulse. Further details of the setup are described in Materials and Methods.

Fig. 1. Schematic of TR-PEEM and the ultrafast separation of the photoexcited electrons within the optical spot.

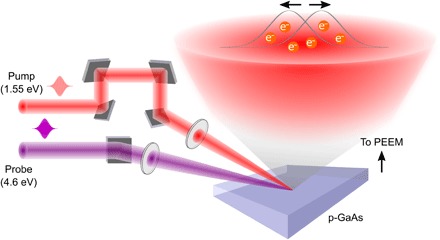
We excite p-doped GaAs with a 1.55-eV pump and photoemit the photoexcited electrons with a 4.6-eV probe. The photoemitted electrons are imaged in a PEEM with high spatial resolution at different pump-probe delays. Assembling the images sequentially provides a movie of our ability to control the redistribution of the photoexcited electrons via optically induced, spatially varying lateral electric fields within the photoexcitation spot.

Ultrafast separation of photoexcited electrons

Using this experimental capability, we first imaged the spatial distribution of the photoexcited electrons at different time delays for both low (1.4 × 10¹⁸ cm⁻³) and high (2.1 × 10¹⁹ cm⁻³) photoexcited carrier densities (Fig. 2). The time-delayed images are normalized individually. We used a grazing angle of incidence of the pump pulse to create an elliptical photoexcitation profile, which provided a strong electric field along the short axis, as explained in more detail below. Three-dimensional (3D) distribution profiles of the photoexcited electrons are plotted, which allows one to easily see the evolution of the original photoexcited Gaussian distribution. The white line in the 2D images projected onto the XY plane marks the boundary of the full width at half maximum (FWHM) of the fitted Gaussian distributions. A normal view of the 2D images is also presented in the Supplementary Materials (fig. S1).

Fig. 2. Pulling apart photoexcited electrons by optically inducing spatially varying electric fields within the photoexcitation spot at high photoexcited carrier densities.

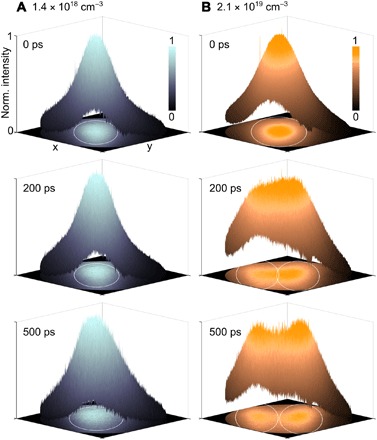
We show snapshots of the normalized spatial distribution of the photoexcited electrons at three different time delays after photoexcitation (0, 200, and 500 ps) for both (A) low and (B) high photoexcited carrier densities. (A) At low carrier density (1.4 × 10¹⁸ cm⁻³), the photoexcited electrons exhibit well-known diffusion phenomena while continuing to retain a Gaussian distribution. (B) At high carrier density (2.1 × 10¹⁹ cm⁻³), the initial Gaussian profile of the photoexcited electrons at 0 ps starts to separate at +200 ps and eventually splits into two distinct distributions with the separation between the two fitted Gaussian peaks greater than the FWHM of the distributions. White elliptical lines in the XY plane demarcate the FWHM of the distributions.

In Fig. 2, we see at the instant of photoexcitation (that is, at 0 ps) the Gaussian distribution profile of the photoexcited electrons inherited from the pump beam. At low photoexcited carrier density (Fig. 2A), the electron distribution profile continues to retain the Gaussian shape as the photoexcited carriers diffuse and recombine over time, as expected in a homogeneous sample. In contrast, for high photoexcited carrier density, we are able to induce a nontrivial redistribution of the photoexcited electrons (Fig. 2B). By +200 ps, the electron distribution profile deviates significantly from a Gaussian and eventually splits into two distinct Gaussian distributions at +500 ps with a separation between the two peaks greater than the FWHM of the two fitted Gaussian profiles (28). Both the time-delayed movies showing the redistribution of the photoexcited electrons can be found in the Supplementary Materials (movies S1 and S2).

Controlling the rate and degree of separation of the photoexcited electrons

The intensity profile of the photoexcitation beam provides a strong degree of control over the rate and degree of separation of the photoexcited electrons. Figure 3A shows the distribution profile of the photoexcited electrons at +500 ps for three different photoexcited carrier densities, that is, 2.8 × 10¹⁸ cm⁻³, 8.4 × 10¹⁸ cm⁻³, and 2.1 × 10¹⁹ cm⁻³. At 2.8 × 10¹⁸ cm⁻³, the distribution profile resembles that of a flat-top Gaussian curve, hinting at the splitting of the photoexcited electron cloud. At 8.4 × 10¹⁸ cm⁻³, the distribution profile now shows two distinct peaks, indicating the presence of two overlapping Gaussian distributions. At 2.1 × 10¹⁹ cm⁻³, the two peaks have now moved even further apart, showing a larger separation between the two distributions of photoexcited electrons. In Fig. 3B, the peak separation is plotted versus time delay for the three different carrier densities as a ratio of the FWHM at +500 ps. The black horizontal line thus marks the point where the separation between the two peaks is equal to the FWHM of the two Gaussian distributions, indicating two resolved Gaussian distributions as per the FWHM criterion (28). We show that the rate of separation and the eventual separation of the photoexcited electron cloud can be controlled by the photoexcitation intensity. We note that at early time delays, in addition to the formation of a lateral electric field that pulls apart the electron distribution, we also have other nonlinear and optoelectronic processes occurring as described in section S1. These processes cause a broadening of the Gaussian distribution at early time delays but culminate by ~10 ps.

Fig. 3. Control of rate of separation of the photoexcited electron clouds.

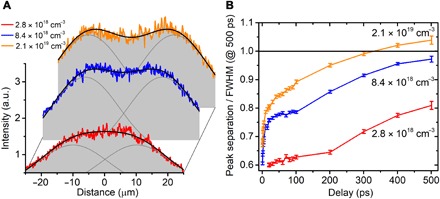
(A) Distribution profile at +500 ps for three different photoexcited carrier densities ranging from a flat-top Gaussian to two overlapping Gaussian distributions with varying amount of separations. For quantitative analysis, the time-delayed distribution profiles are fitted with two Gaussian distributions of the same width and amplitude, leaving the peak positions as free parameters for fitting. The solid black lines show the distribution profiles that arise from the two fitted overlapping Gaussian distributions (solid gray lines). (B) Fitted peak separations as a ratio of the FWHM of their respective profiles at +500 ps for the three different carrier densities. The degree and rate of separation of the quasi-equilibrium distributions can be controlled by tuning the photoexcitation intensities. a.u., arbitrary units.

Formation of lateral electric field

To understand the above phenomena, we first explain the ability to generate in-plane electric fields within the photoexcitation spot due to the intensity variations in the Gaussian pump pulse. Before photoexcitation, a layer of positive charge exists at the surface of a p-doped semiconductor, which is, in turn, balanced by the depletion layer of negatively charged dopants (fig. S2A) and results in the well-known band bending seen in doped semiconductors (19–21, 29, 30). Upon the optical injection of carriers, the photoexcited electrons drift toward the sample surface, while the photoexcited holes drift toward the bulk. The separation of the photoexcited electron-hole pairs leads to the buildup of an opposite field that then screens the preexisting dipoles, causing this built-in surface field to diminish (fig. S2B), surface bands to unbend, and the formation of an SPV. Previously, these phenomena were studied assuming uniform photoexcitation conditions (19–21).

To compare with previous results, we measured the local photoemission intensity only at the center of the photoexcitation spot (fig. S3A), wherein the pump intensity is spatially uniform. At low photoexcited carrier density, we see the vertical transport of the photoexcited electrons to the sample surface, as evidenced by the increase in photoemission intensity. As the photoexcitation carrier density increases, the built-in field begins to be screened and the rise in the photoemission intensity decreases. This measurement agrees very well with previous literature (19), where the measured response was integrated over the entire optical spot. Using the subdiffraction spatial resolution provided by PEEM, we observed spatial variations in the screening process as we moved away from the center of the optical spot, but still within the FWHM (fig. S3B). At the center of the photoexcitation spot where the carrier density is high, the built-in field is largely screened and fewer electrons drift toward the surface. Further away from the center where the photoexcited carrier density is lower and the built-in field is only partially screened, there is an influx of electrons from bulk to the surface, as seen by the huge increase in the photoemission intensity.

In our experiment, under the right intensity conditions, one is left behind with an almost completely screened region at the center of the Gaussian pulse, while regions further away from the center are only partially screened with a finite built-in field. The nonuniformly screened built-in surface field leads to lateral variations in the amount of band bending and, accordingly, a lateral potential difference on the surface (Fig. 4A). The lateral potential difference directly corresponds to an in-plane electric field radiating away from the center that starts to pull apart the photoexcited electrons. By using a grazing angle of incidence corresponding to an elliptical photoexcitation profile, one can weaken the strength of the electric field along the long axis of the ellipse, thereby ensuring that the electrons are pulled apart only in the direction of the short axis (fig. S1).

Fig. 4. The inhomogeneous screening of the built-in fields of a doped semiconductor induces lateral potential differences that pull apart the photoexcited electrons into two distinct distributions.

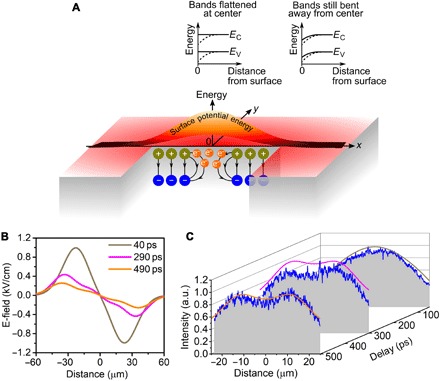
(A) The spatially varying intensity of the Gaussian photoexcitation beam inhomogeneously screens the built-in surface fields of p-doped GaAs. The screening leads to a complete flattening of the bands at the center of the photoexcitation spot (denoted by the origin in Fig. 4A), but only partial flattening away from the center (see section S1 for details). This creates lateral potential differences or local electric fields within the photoexcitation spot that drive spatially varying currents. The dark yellow and blue symbols represent the dipoles and their polarities due to the charges in the depletion layer. The black arrows represent the electric fields from these dipoles. (B) Spatially varying electric field calculated from the evolving distribution of surface dipoles. (C) The calculated (solid lines) evolution of the density of photoexcited carriers closely reproduces the experimental data (blue lines and gray planes), showing the separation of photoexcited electrons into two separate distributions.

To quantitatively model the observed phenomena, we numerically calculate the local electric field and its effect on the photocarrier distribution, both of which evolve in time. The electric field is calculated by taking into account the spatial variation in the local densities of dipoles (Fig. 4A) due to the inhomogeneous screening of the dipoles by the photoexcited carriers. As the photoexcited electrons redistribute in the lateral field (and recombine), the lateral electric fields evolve (and weaken) (Fig. 4B), which, in turn, affects local currents and the evolving distribution of photocarriers. Eventually, for high initial photoexcitation intensities, the photoexcited electrons separate into two Gaussian distributions. Details of our model are discussed in the Supplementary Materials, with Fig. 4C showing that our model correctly reproduces the degree and rate of separation.

DISCUSSION

Our work provides a new paradigm in the spatiotemporal control of charge carriers with high resolution. In general, the ability to alter photoexcited electronic distributions within the optical spot opens up the possibility to go beyond the diffraction limit of light to the nanoscale. Further, using spatial light modulators to imprint other nontrivial intensity patterns on the surface, one could obtain arbitrary control of charge currents on the nanometer, femtosecond scale. These charge currents, in turn, can be used to drive nanoscale opto-electronic devices or for localized, temporally gated photocatalysis with high resolution and unprecedented control. The use of other semiconducting materials, such as transition metal dichalcogenides or Bi₂Se₃, could provide more interesting control of charge currents because of their higher carrier mobilities and the nontraditional dispersion of surface states. Another interesting consequence of the ability to spatially separate and then potentially recombine subpopulations of photoexcited electrons would be to study spatial coherences in the photoelectron population. The ability to study and manipulate spatial quantum coherent effects in photoexcited electron populations would have fundamental and technological value. Lastly, the ability to create lateral energy potential differences at the surface via lateral variations in the amount of band bending could allow the flow of other quasi-particle species such as neutral, tightly bound excitons, thus enabling next-generation excitonic technologies (31, 32).

MATERIALS AND METHODS

The sample was a Zn-doped GaAs 〈100〉 wafer from Semiconductor Wafer Inc. with a sample thickness of 350 ± 25 μm and a dopant concentration of ~10¹⁸ cm⁻³. The sample was heated to 150°C in the ultrahigh vacuum chamber (~10⁻¹⁰ torr) for at least an hour for desorption of gases from the surface. After cooling, the sample was cleaved in situ to expose a fresh 〈110〉 surface and transferred into the main chamber for measurements. The cleaved surface was confirmed with both low-energy electron diffraction (LEED) and photoemission imaging (PEEM) to be clean and free of microscopic ridges. All data were measured at least an hour after the in situ cleaving of the sample to ensure that the surface lattice has relaxed to a stable structure (30). The surface states on the cleaved surface lead to the formation of a depletion layer whose width is estimated to be ~32 nm (33). An exponential fit of the experimental data showed a long-term decay time constant of ~460 ps, denoting the time scale on which the system returns to its ground state.

The TR-PEEM measurements were performed in a LEEM/PEEM system (SPELEEM, Elmitec GmbH) using a femtosecond pump-probe technique. The cathode lens design of the microscope allows nonscanning, high-resolution imaging of the photoemitted electrons with a lateral resolution of ~40 nm. The femtosecond pulses at a central wavelength of 800 nm and a pulse duration of 45 fs were generated by a high-power (2.6 W), high–repetition rate (4 MHz) Ti:sapphire oscillator system. The fundamental pulses were split into two parts: The first part was used as a pump pulse to photoexcite the GaAs sample; the second part was frequency-tripled via β-barium borate crystals to 266 nm and used as a time-delayed probe pulse to photoemit electrons from the sample. Because of the optical penetration depth of the probe and the electron affinity of the sample, only the photoexcited electrons from the top 6 nm were photoemitted from the sample (34, 35). The optical penetration depths of the ultrafast pulses relative to the depletion width are illustrated in fig. S5. Both the pump and the probe pulses were set to p-polarization and focused onto the sample at a grazing angle of 18°. The diameter of the short axis of the pump elliptical spot was ~30-μm FWHM. The probe spot was a few hundred micrometers wide to achieve uniform illumination of the field of view of the sample. The temporal resolution of the measurement was obtained from the rise time of the pump-probe signal to be ~280 fs due to the stretching of the frequency-tripled probe. The LEED pattern of the sample was taken both before and after the measurements to rule out any significant surface change over the course of the measurements.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/9/eaat9722/DC1

Fig. S1. 2D images showing the separation of the photoexcited electrons at the photoexcited carrier density of 2.1 × 10¹⁹ cm⁻³.

Fig. S2. Distribution of dipoles before and after photoexcitation.

Fig. S3. Partial screening of the built-in surface field.

Fig. S4. Origin of the initial fast drop in the photoemission intensity.

Fig. S5. Formation of the in-plane electric field.

Fig. S6. Relative extents of the optical pulse penetration depths and the depletion width of the surface space charge region.

Section S1. Partial screening of the built-in surface space charge field.

Section S2. Formation of lateral electric field.

Movie S1. Gaussian electron distribution profile at low carrier density of 1.4 × 10¹⁸ cm⁻³.

Movie S2. Redistribution of the photoexcited electrons at 2.1 × 10¹⁹ cm⁻³.

Reference (36)