Determination of the Stoichiometry between α- and γ1 Subunits of the BK Channel Using LRET

Abstract

Two families of accessory proteins, β and γ, modulate BK channel gating and pharmacology. Notably, in the absence of internal Ca²⁺, the γ1 subunit promotes a large shift of the BK conductance-voltage curve to more negative potentials. However, very little is known about how α- and γ1 subunits interact. In particular, the association stoichiometry between both subunits is unknown. Here, we propose a method to answer this question using lanthanide resonance energy transfer. The method assumes that the kinetics of lanthanide resonance energy transfer-sensitized emission of the donor double-labeled α/γ1 complex is the linear combination of the kinetics of the sensitized emission in single-labeled complexes. We used a lanthanide binding tag engineered either into the α- or the γ1 subunits to bind Tb⁺³ as the donor. The acceptor (BODIPY) was attached to the BK pore-blocker iberiotoxin. We determined that γ1 associates with the α-subunit with a maximal 1:1 stoichiometry. This method could be applied to determine the stoichiometry of association between proteins within heteromultimeric complexes.

Main Text

BK channels are homotetramers of the pore-forming α-subunit, which is broadly expressed in mammal tissues and its distinctive physiological function is to dampen the effects of the cytosolic increase of Ca²⁺ concentration due to the opening of voltage-dependent Ca²⁺ channels (1, 2, 3, 4). Although BK channels are coded by a single gene (KCNMA1), they display a remarkable functional diversity, largely due to their interaction with accessory subunits. Two families of BK channel accessory subunits, the β-family (β1–β4) (5, 6, 7, 8) and the γ-family (γ1–γ4) (9, 10), confer new and physiological relevant phenotypes to the BK channel. Within the γ-family, the most remarkable effects are produced by the γ1 subunit (9). This accessory subunit greatly increases the allosteric coupling between voltage sensors and pore, shifting the conductance-voltage (G-V) curve >150 mV to the left along the voltage axis (9, 10).

Although the structure of the Aplysia BK channel was determined by the cryo-electron microscopy technique (11, 12), little is known about the detailed structure of the accessory subunits beyond their secondary structure and putative membrane topology (10, 13). Regarding the stoichiometry between the α-subunit and its accessory subunits, it is known that the tetramer formed by α can hold from one to four β1 or β2 subunits (14). However, the stoichiometry between α- and any of the γ-subunits is unknown at present. Interestingly, the γ1 subunit displays an all-or-none effect on the BK channel. However, there is not a definite test of how many γ1 subunits are necessary to cause this effect (15).

Lanthanide resonance energy transfer (LRET) technique, together with symmetric nanopositioning system (SNPS) analysis (16), have been previously used to study conformational changes in ion channels in response to a stimulus like, for example, a change in membrane voltage (16, 17). LRET/SNPS calculates the positions of terbium ions chelated by lanthanide binding tag (LBT) motifs (18), which are strategically inserted in different positions of the protein of interest. In the case of β1, LRET/SNPS was used to determine the structural rearrangements due to the interaction between the α- with β1 subunits (19). Given the tetrameric structure of BK, the LBT-labeled channel contains four LBT-Tb³⁺ donors interacting with a single toxin-BODIPY acceptor. Two alternatives strategies were used to study the (α + β1)BK channel complex (19). In the first approach, the α-subunits were LBT-labeled to explore the Tb³⁺ positions in the absence and the presence of β1 subunit. In the second strategy, β1 was LBT-labeled to determine its position relative to the α-subunit. In both cases, because the acceptor is located outside the center of symmetry of the channel, there are four different donor-acceptor distances. Therefore, one way to analyze the LRET/SNPS results is to describe the decay of the luminescence of the donors in the presence of the acceptor, the sensitized emission (SE), as a set of four different time constants instead of determining Tb³⁺ positions.

Unlike Förster resonance electron transfer, in LRET the acceptor lifetime is several orders-of-magnitude shorter than that of the donor (20), implying that during the time course of donor decay the acceptor can emit and be reexcited many times. This enables the total SE of the acceptor to be the linear combination of the SEs for each donor-acceptor pair. In fact, the SNPS method (16) is based on this idea; the SE of the acceptor is the linear combination of the time constants of the four donors because stoichiometrically each one of the donors is equally represented. Here we extended this idea to a heteromultimeric protein complex by assuming that the kinetics of SE of the double-labeled α/γ1 complex is the linear combination of the kinetics of the SE of the single-labeled complexes.

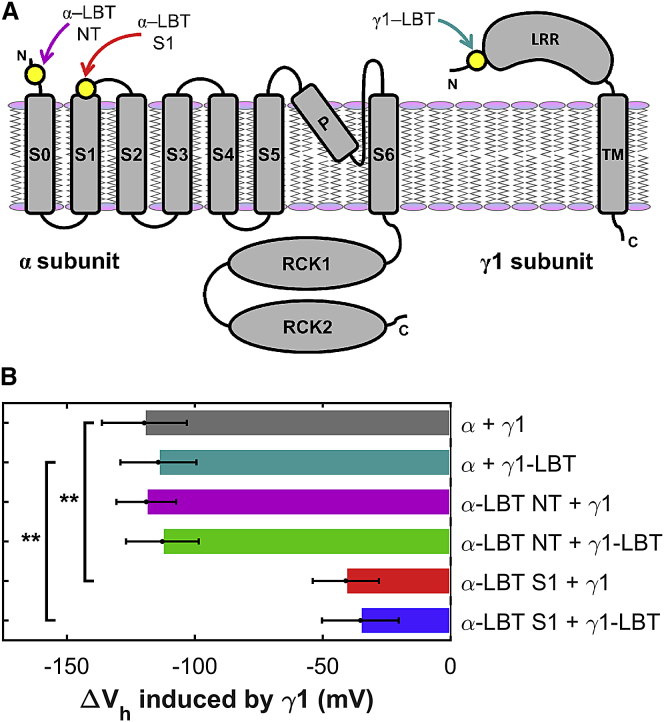
We used two LBT insertion sites in the extracellular face of the α-subunit (Fig. 1 A). One is in the BK N-terminus (between the D15 and S16 residues) and the second is in the C-terminal of the S1 transmembrane segment (between the S134 and the S135). Both constructs were expressed in Xenopus laevis oocytes and tested using the patch-clamp technique to verify their degree of expression and functionality. Both α-LBT constructs displayed robust ionic currents and their activation by voltage was similar to that of the wild-type (wt) α, as previously reported (Fig. S1, A–C, top) (19). In addition, the γ1 subunit was coexpressed with the α (wt) and each α-LBT construct to confirm that γ1 was shifting the G-V curve of the α-LBT channels to the left, as the wt subunit (Fig. S1, A–C, middle). The results showed a large leftward shift of the G-V curve for the α (wt) and the α-LBT NT but not for α-LBT S1 construct (Figs. S1, D–F, and 1 B). Below, we discuss this anomalous behavior of γ1 when coexpressed with the α-LBT S1 construct.

Figure 1.

BK half-activation voltage shifts induced by γ1 (wt) and γ1-LBT construct. (A) Cartoon is given depicting LBT insertion sites in α- and γ1 subunits. (B) Changes in (G/G_max)−V half-activation voltages (ΔV_h) is induced by γ1 wt or γ1-LBT on BK α (wt) and α-LBT NT and S1 constructs. Bar and error bars lengths represent the mean and the mean ± SE (N = 6–13; see Fig. S1), respectively; ^∗∗p < 0.01 (two-tailed Student’s t-test). To see this figure in color, go online.

In γ1, LBT was inserted in the N-terminal of the leucine-rich repeats domain, between the D42 and S43 residues (Fig. 1 A). Robust currents were recorded when this construct was coexpressed with α (wt) and both α-LBT constructs (Fig. S1, A–C, bottom). γ1-LBT produces similar effects than those produced by γ1 (wt) (Figs. S1, D–F, and 1 B), suggesting that the insertion of the LBT did not change the structure and function of the γ1.

All LRET experiments were performed at a holding membrane potential of −80 mV using the two-electrode voltage-clamp technique. The intracellular Ca²⁺ concentration of Xenopus oocytes is submicromolar (20), such as at −80 mV all (α)BK channels are in the closed configuration. Indirect evidence indicates that γ1 does not change the voltage-sensor workings (10), whereby we assumed that, like (α)BK channels, voltage-sensor domains of (α + γ1)BK channels are also in the resting state at −80 mV.

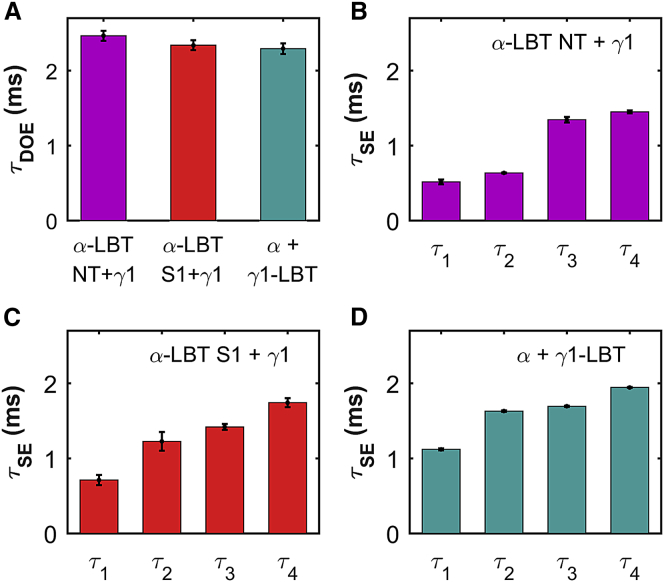
Donor-only emission (DOE) signals from LBT-labeled constructs were obtained as described in the Supporting Materials and Methods. Luminescence decays recorded after a brief light flash were obtained in all cases (Fig. S2, A–C, top, colored traces), whose slowest component had a time constant ∼2.4 ms, which is absent in oocytes expressing nonlabeled α- and γ-subunits (Fig. S2, A–C, top, gray traces). This slowest component has the expected time constant of the decay of excited Tb³⁺ bound to LBT in the absence of the acceptor (τ_DOE) (16, 18, 19). All LBTs constructs tested showed τ_DOE > 2.25 ms, indicating that the LBTs are properly folded after insertion into either protein (Fig. 2 A; Table S1).

Figure 2.

Time constants describing DOE and SE. (A) Largest time constant is shown that was obtained from three-exponential fits to DOE traces. Number of independent DOE experiments (N) was 23, 38, and 19 for (α-LBT NT + γ1), (α-LBT S1 + γ1), and (α + γ1-LBT)BK channels, respectively. (B–D) The four largest time constants are shown that were obtained from Heyduk-constrained (23) SNPS fit from SE traces (α-LBT NT + γ1)BK channels (B, N = 15), (α-LBT S1 + γ1)BK channels (C, N = 5), and (α + γ1-LBT)BK channels (D, N = 12). Bar height represents the mean, and the error-bar length represents the mean ± SE (Table S2). To see this figure in color, go online.

In the presence of 500 nM iberiotoxin-BODIPY, the time-course of the SE of the BODIPY was recorded as described in Supporting Materials and Methods. The acceptor position, out of the symmetry axis of the channel, determines that there are four different donor-acceptor distances and therefore the SE decay may contain up to four exponential decays (16, 19, 21, 22). (α-LBT + γ1)BK channels SE decays, like those in Fig. S2, A–B (bottom), were SNPS-fitted by the equation (19, 23):

$$I\left(t\right)=W_{\alpha }\sum _{i=1}^4{k}_{\alpha ,i}{e}^{-\frac{t}{{\tau }_{\alpha ,i}}}+U\left(t\right)+c,$$ (1)

where W_α is a factor, proportional to the number of α-subunits in the microscope visual field for each experiment; τ_α,i values are the four time constants corresponding to each different donor-acceptor distance; U(t) is the laser-induced fast transient artifact; and c is the offset. In Eq. 1, each preexponential k_α,i is related to each τ_α,i by the Heyduk constraint (23),

$$k_{\alpha ,i}=1/{\tau }_{\alpha ,i}-1/{\tau }_{\text{DOE}},$$ (2)

and the fast transient artifact was described by a two-exponential function

$$U\left(t\right)=A_{1,\text{Art}}{e}^{-t/{\tau }_{1,\text{Art}}}+A_{2,\text{Art}}{e}^{-t/{\tau }_{2,\text{Art}}}.$$ (3)

Similarly, (α + γ1-LBT)BK channels SE decays (Fig. S2 C, bottom) were analyzed using the equation

$$I\left(t\right)=W_{\gamma 1}\sum _{j=1}^4{k}_{\gamma 1,j}{e}^{-\frac{t}{{\tau }_{\gamma 1,j}}}+U\left(t\right)+c,$$ (4)

where W_γ1 is proportional to the number of γ1 subunits present in BK channels in the microscope visual field, and τ_γ1,j are the four time constants corresponding to each different donor-acceptor distance.

The two time constants of the fast transient artifact were always smaller than those from SE (data not shown). From all parameters describing SE decays (Eqs. 1 and 4), only τ values (and therefore k values) are relevant and the rest are artifacts. The set of the four largest time constants obtained from the SNPS fit of several experiments for each preparation were averaged and they are shown in the Fig. 2, B–D, and Table S2.

Interestingly, the SE kinetics of (α + γ1-LBT)BK channels (Fig. S2 C, bottom; Fig. 2 D) is slower than either of the two (α-LBT + γ1)BK channels tested (Fig. S2, A and B, bottom; Fig. 2, B and C; Table S2), indicating that the position of the γ1-LBT is further away from the pore than the NT and S1 segments of the α-subunit.

When both proteins, α and γ1, contain LBTs, it is expected that the SE decay can be described by the linear combination of the first sums in Eqs. 1 and 4, plus the artifact and the offset. Adding Eqs. 1 and 4 and rearranging, we have

$$I\left(t\right)=W_{\alpha }\left[\sum _{i=1}^4{k}_{\alpha ,i}{e}^{-\frac{t}{{\tau }_{\alpha ,i}}}+\frac{W_{\gamma 1}}{W_{\alpha }}\sum _{j=1}^4{k}_{\gamma 1,j}{e}^{-\frac{t}{{\tau }_{\gamma 1,j}}}\right]+U\left(t\right)+c.$$ (5)

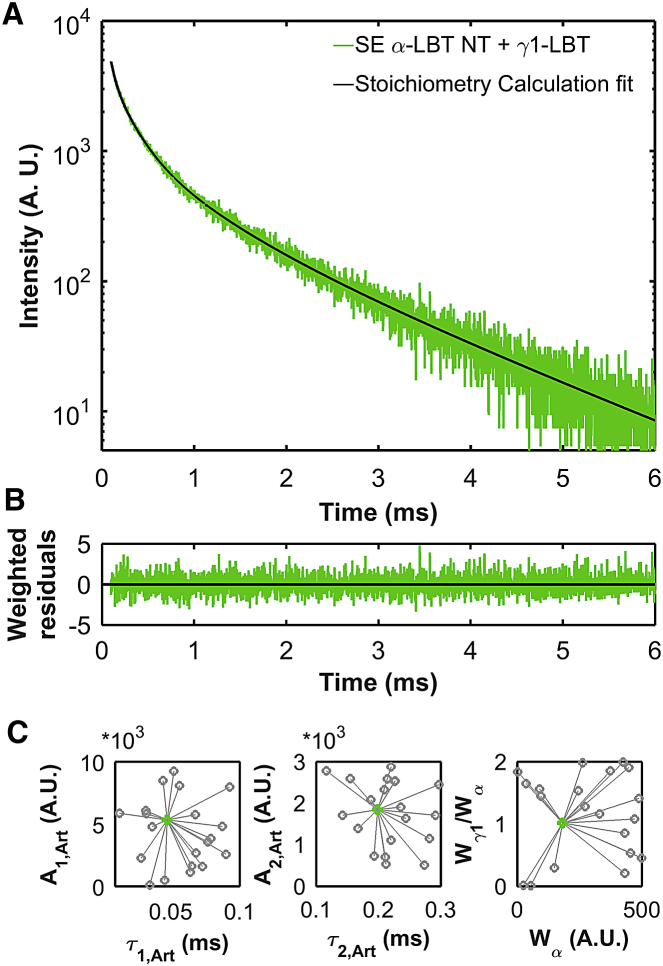
In Eq. 5, W_γ1/W_α is the stoichiometric ratio between the γ1- and α-subunits. To obtain the SE originated by coexpressing α-LBT and γ1-LBT constructs, Xenopus laevis oocytes were coinjected with a mix of mRNA for each one of the α-LBT constructs with γ1-LBT. One representative record of SE obtained from (α-LBT NT + γ1-LBT)BK channels is shown in Fig. 3 A. After the offset subtraction using decay analysis (16), there are only six free parameters in Eq. 5 because both time constants and amplitudes of the exponentials contained in the sums were obtained from experiments in which the SE produced by the pairs (α-LBT + γ1) and (α + γ1-LBT) was fitted using Eqs. 1 and 4. The record shown in Fig. 3 A was fitted using a custom script using the MATLAB function lsqnonlin (the MathWorks, Natick, MA), and the weighted residuals are shown in Fig. 3 B. We started the curve fitting from 100 sets of the six initial adjustable parameters randomly chosen within reasonable limits. This strategy allowed us to minimize the probability that the obtained solution was a local minimum of the sum of the square of the weighted residuals. We found that all 100 fits converged to the same set of final parameters (Fig. 3 C). In the particular case of Fig. 3 A, the W_γ1/W_α ratio was ∼1 (Fig. 3 C, right).

Figure 3.

Stoichiometry determination. (A) SE measurements are given from the α-LBT NT in the presence of γ1-LBT. The SE was fitted using Eq. 5 (black line). The [mRNA_γ1-LBT]/[mRNA_α-LBT NT] ratio was 3:1. The voltage was clamped at −80 mV using the two-electrodes voltage-clamp technique. The SE trace was offset-subtracted. (B) Weighted residuals are given between SE trace and its fit using Eq. 5. (C) One-hundred sets of the six-initial adjustable parameters were randomly generated within reasonably chosen boundaries for the fit of the six parameters from Eq. 5. Pairs of the values of 20 of the 100 sets are shown as open circles (A_1,Art versus τ_1,Art, left; A_2,Art versus τ_2,Art, middle; and W_γ/W_α versus W_α, right). In the 100 fits, all solutions converged to the same value (filled circle). The starting pairs of values and their final solutions are connected by a line. To see this figure in color, go online.

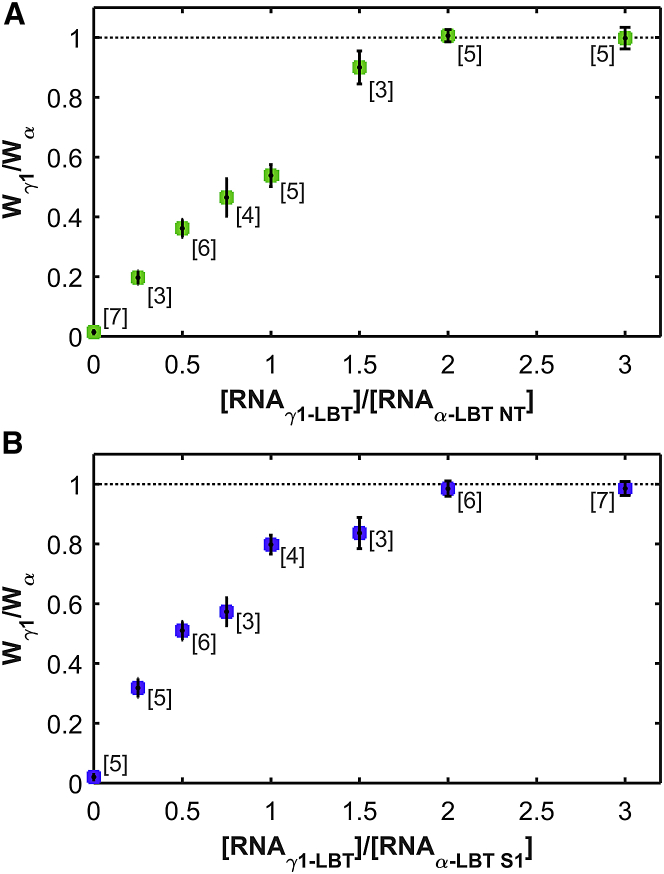
The mRNA for each α-LBT construct and γ1-LBT was coexpressed in different concentration ratios, and their SEs recorded as in Fig. 3 were fitted using Eq. 5. In both cases, the mean value of W_γ1/W_α ratio increases approaching an asymptotic value of ∼1 when the amount of mRNA of γ1-LBT was saturating (Fig. 4, A and B). From results in Fig. 4, we concluded that the maximal stoichiometry of association between the α- and the γ1 subunits of BK channel is 1:1, whereby there are four γ1 subunits per BK channel. This is similar to the maximal stoichiometry of the (α + β1)BK channel complex (14).

Figure 4.

Stoichiometry of the (α + γ1) BK channel complex. (A) Several [mRNA_γ1-LBT]/[mRNA_{α-LBT NT}] and (B) [mRNA_γ1-LBT]/[mRNA_{α-LBT S1}] ratios were injected into Xenopus laevis oocytes and the SE lifetime measurements were fitted with Eq. 5, as described in Fig. 3. In both cases, the stoichiometric ratio tends to an asymptotic value of 1. At each ratio, circles and error bars represent the mean and the mean ± SE, respectively. The number of experiments for each ratio is indicated between square brackets. To see this figure in color, go online.

We recall here that γ1 (wt) and γ1-LBT produce only a modest leftward shift of the G-V curve when they are coexpressed with α-LBT S1, but they produce the full effect when they are coexpressed with α (wt) (Fig. 1). Conversely, α-LBT NT in the presence of γ1 shows a behavior almost identical to the wt α-subunit (Fig. 1). These results suggest that S1, or at least part of this transmembrane segment, participates in the physiological γ1 effect but not in the binding because the α-LBT S1 construct retains the same maximal association stoichiometry as α-LBT NT (Fig. 4, A and B).

Some questions remain to be resolved. The results shown in Fig. 4 cannot answer whether the α-homotetramer can hold fewer than four γ1 subunits, because the W_γ1/W_α ratio as a function of the [RNA_γ1-LBT]/[RNA_α-LBT] ratio only tell us the total proportion of γ1-LBT subunits in relation to the α-LBT. Gonzalez-Perez et al. (15) found that the γ1 effect is all-or-none, but they did not find conclusive evidence on what is γ1:α stoichiometry between both proteins. Thus, a more intriguing question is how many γ1 subunits are needed to cause the all-or-none γ1 effect (15). Also, taking into account the results shown in this letter, it would be interesting to discriminate between two possibilities when there are nonsaturating γ1 expression levels. BK channels could display partial stoichiometries (from 0 to 4 γ1 subunits per channel) or on the contrary, could be expressed as a mix of K channels containing 0 or 4 γ1 subunits without intermediate stoichiometries.

Author Contributions

R.L., F.B., O.A., and W.C.-U. designed the research, analyzed data, and wrote the manuscript. W.C.-U. performed research. F.B. contributed analytic tools.

Editor: William Kobertz.

Supporting Citations

Reference (24) appears in the Supporting Material.