Probing Mitotic CENP-E Kinesin with the Tethered Cargo Motion Assay and Laser Tweezers

Abstract

Coiled-coil stalks of various kinesins differ significantly in predicted length and structure; this is an adaption that helps these motors carry out their specialized functions. However, little is known about the dynamic stalk configuration in moving motors. To gain insight into the conformational properties of the transporting motors, we developed a theoretical model to predict Brownian motion of a microbead tethered to the tail of a single, freely walking molecule. This approach, which we call the tethered cargo motion (TCM) assay, provides an accurate measure of the mechanical properties of motor-cargo tethering, verified using kinesin-1 conjugated to a microbead via DNA links in vitro. Applying the TCM assay to the mitotic kinesin CENP-E unexpectedly revealed that when walking along a microtubule track, this highly elongated molecule with a contour length of 230 nm formed a 20-nm-long tether. The stalk of a walking CENP-E could not be extended fully by application of sideways force with optical tweezers (up to 4 pN), implying that CENP-E carries its cargo in a compact configuration. Assisting force applied along the microtubule track accelerates CENP-E walking, but this increase does not depend on the presence of the CENP-E stalk. Our results suggest that the unusually large stalk of CENP-E has little role in regulating its function as a transporter. The adjustable stalk configuration may represent a regulatory mechanism for controlling the physical reach between kinetochore-bound CENP-E and spindle microtubules, or it may assist localizing various kinetochore regulators in the immediate vicinity of the kinetochore-embedded microtubule ends. The TCM assay and underlying theoretical framework will provide a general guide for determining the dynamic configurations of various molecular motors moving along their tracks, freely or under force.

Introduction

A mechanistic understanding of motor-cargo interactions at the single-molecule level is crucial for unraveling the complexities of intracellular transport and engineering motile biomimetic devices. Members of the kinesin superfamily of ATP-dependent motors contribute to specialized transport functions in cells, moving various cargo along intracellular microtubule (MT) tracks (1). These functions are assisted by the coiled-coil domains, or stalks, which ensure homodimerization and often have additional roles (2, 3). There is marked variability in the length and structure of stalk domains; accordingly, they are likely to form MT-cargo tethers with diverse mechanical and conformational properties. For example, the stalk of the highly processive kinesin-8 Kif18a is formed by a ∼12 nm coiled-coil domain (4), whereas the major transport motor kinesin-1 has two coiled-coil regions separated by a hinge, with a total contour length of ∼80 nm (5). The relationship between the secondary structure of the stalk and the conformational and mechanical properties of the tether it provides for cargo attachment is not well understood. Kinesin-1, for example, is estimated to form a 17 or 57 nm tether, based on two separate studies (6, 7), and apparently its stalk becomes fully extended under a very low force (<1 pN) (8).

Even less is known about the conformation of the actively walking CENP-E, a mitotic kinesin. Defects in this motor are associated with chromosome segregation errors, aneuploidy, and the development of tumors (9, 10, 11). This kinesin-7 subfamily member has an unusually long stalk of 200–230 nm in contour length (12). The highly discontinuous coiled-coil structure of the stalk implies that it is flexible, with an estimated persistence length (PL) of only 26 nm (13). Because the C-terminal tail of CENP-E is likely to be disordered (14), when fully extended this region could add another ∼80 nm to the total contour length. The tail of CENP-E contains an MT-binding site, although its exact location within the tail is not known (13, 15). A CENP-E tail fragment containing an MT-binding site diffuses very rapidly along the MT lattice with an average binding time of <0.5 s, indicating relatively weak MT-binding affinity (13). This site plays an essential role in enabling CENP-E to track the ends of dynamic MTs bidirectionally and processively in vitro, likely contributing to the stability of kinetochore-MT attachments during mitosis. The exact cellular role of the highly elongated CENP-E stalk, however, remains unknown. In the absence of external load, full-length (FL) CENP-E and a truncated (TR) construct with no tail or stalk have very similar transport rates and run lengths in vitro (13). Strikingly, a significantly shortened stalk severely disrupts CENP-E functioning in mitotic cells (16). Therefore, a quantitative understanding of the conformational properties of walking CENP-E as well as how its extension length changes under load is crucial for deciphering its mitotic function.

Despite substantial advances in fluorescence-based imaging techniques, it is not currently possible to visualize the length and conformation of tethering formed by cargo-transporting motors. Notably in this regard, tracking of a microbead transported along the MTs by molecular motor can reveal basic mechanical features of motor-driven movements (17, 18). At the same time, single-particle tracking of the Brownian motion of a microbead tethered to a fixed point provides a powerful tool for gauging the mechanical and conformational properties of the underlying tether. This tethered particle motion (TPM) assay has been successfully used to study the length and flexibility of double-stranded (ds) DNA (19, 20, 21, 22, 23) and to analyze DNA looping and the interactions between nucleic acid chains and proteins in real time (23, 24, 25, 26, 27). A similar approach, the tethered fluorophore motion assay (28), has recently been used to measure the flexural stiffness of single myosin motors stably attached to actin filaments (29). To further adapt these quantitative approaches to moving motors, we constructed and critically analyzed a theoretical model that describes the Brownian motion of a bead carried by a motor stepping with variable velocity on different protofilament tracks of a coverslip-attached MT. We deduced the relationship between the extent of bead excursions and the bead’s tethering and verified it experimentally using a kinesin-1 motor fastened to a microbead by double-stranded DNA (dsDNA) links of known lengths. Unexpectedly, applying the TCM approach to CENP-E kinesin revealed that this motor is not extended to its full contour length when it is walking freely or under a sideways-pulling force applied by laser tweezers. The compact configuration, however, does not change the load-bearing properties of the CENP-E motor, strongly suggesting that the primary role of the CENP-E stalk during chromosome segregation is regulatory rather than mechanical in nature.

Materials and Methods

Experimental procedures

Protein construction and purification

Tubulin was purified from cow brains by thermal cycling and chromatography (30) and then labeled with rhodamine (31). TR kinesin-1 construct labeled with GFP (K560) and TR and FL CENP-E kinesins were purified as in (12, 32). SNAP-GBP construct was prepared by fusing the gene for GBP-6His tag (33) in frame with the SNAP-tag (New England Biolabs (NEB), Ipswich, MA), separated by the flexible linker SGGGGSGGGG in pET28a (Novagen, Madison, WI). Expression was induced at 37°C for 2 h with 1 mM isopropyl β-D-1-thiogalactopyranoside in NEB Express E. coli cells; bacterial pellets were lysed with lysozyme (1 mg ml⁻¹) on ice for 30 min and sonicated in a buffer containing 50 mM NaH₂PO₄ (pH 8.0), 300 mM NaCl, 10 mM imidazole, and 1% phenylmethylsulfonyl fluoride. After centrifugation at 10,000 × g for 20 min, supernatant was incubated with Ni-nitrilotriacetic acid agarose (Qiagen, Hilden, Germany) for 1 h at 4°C. Bound protein was eluted with 250 mM imidazole, loaded onto a Dispo-Biodialyzer unit (pore size 10 kDa molecular weight cutoff; Sigma-Aldrich, St. Louis, MO), and dialyzed in a buffer containing 50 mM NaH₂PO₄ (pH 8.0), 300 mM NaCl, 1 mM dithiothreitol (DTT), and 0.1% Tween-20. Protein fractions were supplemented with 50% glycerol, aliquoted, snap-frozen in liquid N₂, and stored at −80°C.

dsDNA links

Oligonucleotides and primers labeled with biotin or an amino group were purchased from Integrated DNA Technology (Coralville, IA). Amino-group-labeled oligonucleotides were conjugated with benzylguanine (BG) (NEB), as described (34). Short dsDNA links were prepared by complementary pairing of 1 μM biotin-labeled and 5 μM BG-labeled oligonucleotides at room temperature for 1 h in 5× phosphate-buffered saline (PBS) (700 mM NaCl, 13.5 mM KCl, 50.5 mM Na₂HPO₄, 9 mM KH₂PO₄, (pH 7.2)). Long dsDNA links were prepared by polymerase chain reaction (PCR) using one primer labeled with biotin and a second primer labeled with BG, plasmid pET21a as template, and FastStartTaq DNA polymerase (Roche, Basel, Switzerland). The PCR product was purified using the QIAquick PCR Purification kit (Qiagen), diluted to 1 μM in MilliQ H₂O, and stored as aliquots at −20°C. Sequences of PCR primers and the resultant dsDNA are provided in Supporting Materials and Methods.

Preparation of beads coated with kinesin-1 and dsDNA links

Neutravidin was conjugated to 0.5 μm COOH-activated glass beads (Bangs Labs, Fishers, IN), as described (35). Beads were incubated with biotinylated dsDNA (concentrations provided below) in 5× PBS for 2 h, washed extensively by centrifugations at 2600 × g, blocked with 250 μM biotinylated discrete polyethylene glycol (2.5 kDa; Quanta BioDesign, Plain City, OH), and resuspended in 1× PBS containing 4 mg mL⁻¹ bovine serum albumin (BSA) and 2 mM DTT. SNAP-GBP protein (5 μM) was attached to these beads via a covalent bond with dsDNA-bound BG by incubation for 1.5 h at 4°C. Beads were washed three times and stored at −20°C in PBS with 4 mg mL⁻¹ BSA, 2 mM DTT, and 50% glycerol. Before each experiment, the beads were washed in BRB80 buffer (80 mM 1,4-Piperazinediethanesulfonic acid (pH 6.9), 4 mM MgCl₂, 1 mM EGTA) supplemented with 10 μM Mg-ATP, 2 mM DTT, and 4 mg mL⁻¹ BSA; incubated in the same buffer for 1.5–2 h with K560 protein (32); washed; and then used immediately. The amount of dsDNA (per 1 mg of beads) was 2.1–2.8 pmol in group 1, 0.35–1.4 pmol in group 2, 70 pmol in group 3, and 1.4–1.75 pmol in group 4. The amount of K560 was 0.04 pmol in groups 1–3 and 0.4 pmol in group 4. The resultant difference in density of bead coating was confirmed by measurement of bead brightness in the GFP channel and by quantifying the fraction of moving beads; beads with the dense motor coatings were brighter and moved on MTs more frequently (Fig. S4 a).

Preparation of CENP-E-coated beads

We coated 0.5 μm COOH-activated glass beads (Bangs Labs) with streptavidin or neutravidin, as described (35). TR CENP-E kinesin was conjugated by first incubating these beads with biotinylated anti-6His antibody (Abcam, Cambridge, UK) in PBS containing 4 mg mL⁻¹ BSA and 2 mM DTT. The beads were then blocked with 250 μM biotinylated discrete polyethylene glycol, washed extensively, and incubated with TR CENP-E for 2–4 h at 4°C in BRB80 with 100 μM Mg-ATP, 2 mM DTT, and 4 mg mL⁻¹ BSA. Washed beads were kept on ice; before each experiment, beads were sonicated for 3–5 min to reduce clumping. FL CENP-E beads were prepared and used analogously. This protein was conjugated via biotinylated anti-GFP antibodies (Rockland Immunochemicals, Limerick, PA) using the same protocol as for TR CENP-E or a similar procedure described in (13). These methods produced indistinguishable results in the tethered cargo motion (TCM) assay, so small-bead excursions were unlikely to be caused by the CENP-E stalk sticking to the beads. Moreover, CENP-E binding to the beads was specific, as almost no binding was seen in the absence of the antibodies (Fig. S5, b and c). To ensure that beads were predominantly transported by single CENP-E motors, the density of CENP-E coating was reduced until a majority of the beads did not move; only chambers with <30% moving beads were analyzed (7, 36). Run lengths of such beads (Fig. S5 d) were consistent with previously published values for single CENP-E molecules (13, 37).

TCM experimental procedures

Flow chambers were prepared using silanized coverslips and double-sided tape, and solutions were exchanged with a peristaltic pump, as described (38). All assays were performed at 32°C. Taxol-stabilized MTs, polymerized from a mixture containing nine parts of unlabeled tubulin (11 mg mL⁻¹) and one part of rhodamine-labeled tubulin (degree of labeling 0.9; 6 mg mL⁻¹) were immobilized on the coverslip via antitubulin antibodies (Serotec, Hercules, CA). Coverslips were blocked with 1% pluronic F127, and beads were introduced in motility buffer: 80 mM K-1,4-Piperazinediethanesulfonic acid (pH 6.9), 1 mM EGTA, 1–4 mM MgCl₂, 4 mg mL⁻¹ BSA, 2 mM DTT, 6 mg mL⁻¹ glucose, 80 μg mL⁻¹ catalase, 0.1 mg mL⁻¹ glucose oxidase, 0.5% β-mercaptoethanol, 7.5 μM taxol, and Mg-ATP. CENP-E bead motility was assayed at 2 mM Mg-ATP, and kinesin-1 was assayed at 30 or 400 μM Mg-ATP to slow the motor down and collect better statistics. Bead MT-perpendicular excursions did not significantly differ at 30 and 400 μM Mg-ATP (Fig. S4 b), so these data were combined. Less than one-third of beads (groups 1–3) moved along MTs in our experiment.

Our laser-trap instrument has been described previously (39). Some experiments used the upgraded version of this microscopy system, described in (40). With a 1064 nm laser beam (stiffness 0.0025 pN nm⁻¹), a free-floating bead was trapped, brought into contact with an MT, and kept there for 80 s. If directed motion was observed, the trap was switched off immediately, and video recording with differential interference contrast (DIC) was performed using stream acquisition mode (10 ms exposure) using a Photometrics Cascade 650 charge-coupled device camera. In addition, an MT image was taken in the rhodamine channel with 300 ms exposure for subsequent analysis of bead excursions relative to the MT.

Force-clamp and sideways-force experiments

The force clamp was implemented via a feedback control of piezo-stage P-561.3D (Physik Instrumente, Karlsruhe, Germany). A custom-made LabVIEW program triggered the force-clamp regime in response to bead displacement greater than 150 nm from the trap’s center, as detected by a quadrant photodetector (QPD) sampled at 4 kHz and decimated before recording. Laser-trap stiffness was varied (0.008–0.03 pN nm⁻¹) to apply force in a range of 0.1–6 pN. Beads were additionally imaged in DIC to measure displacements beyond the working range of QPD. The piezo stage was controlled at 100 Hz with a feedback coefficient of 0.3–0.5 to maintain constant distance between the centers of the trap and microbead. The MT was recorded with DIC before each experiment, and its orientation relative to the stage axes was measured and used as an input for the force-clamp program. For each bead, optical-trap stiffness calibrations were conducted as in (40) at the end of each experiment. Stage and bead coordinates were recorded at 400 Hz and analyzed using a custom-made MATLAB (The MathWorks, Natick, MA) code. The sideways-force assay was conducted essentially in the same manner as that of the force-clamp assay, except that after the ∼1 pN opposing force was applied, an acoustooptic deflector was additionally used to steer the trap at 1 Hz perpendicular to the MT with an amplitude of 1 μm; laser-trap stiffness was 0.02–0.04 pN nm⁻¹. The fast detachment of CENP-E-coated beads under load prevented us from examining sideways forces larger than 4 pN.

Data analyses

Analysis of experimental TCM data

To extract bead coordinates, recorded stacks of DIC images were tracked using Metamorph (Molecular Devices, San Jose, CA). Bead coordinates were plotted in the X/Y plane using custom-written MATLAB code. The corresponding fluorescence MT image was then used to determine the angle between the MT and X axis in the image plane. A line representing the MT with the same angle was drawn on the X/Y plane such that the average deviation of the bead coordinates from this line was minimal. This procedure was introduced because it was not possible to accurately overlay the DIC and fluorescent channels. The MT-perpendicular bead excursions from the MT-representing line were then calculated for each time point, and the resultant distribution was fitted with a Gaussian function to determine its SD. To estimate variation in this SD value, bootstrapping was performed using a custom-made MATLAB code with 30 independent bootstrap samples; data points from all beads for each tether investigated were pulled together, and 300 random data points were drawn with replacement to calculate SD of Gaussian fit’s SD. To compensate for “blurring” of the bead’s image during camera exposure, the SDs of bead excursions were divided by 0.7, which was the experimentally measured correction factor (see Supporting Materials and Methods). Two-dimensional “cloud” plots were constructed as described in Supporting Materials and Methods.

Analysis of CENP-E displacement during sideways-bead oscillations

Data from the QPD, video recordings with the charge-coupled device camera, and piezo-stage displacement data were analyzed using the MATLAB program. Signals were aligned based on a distinct 1 Hz periodicity introduced by the sideways sweeping of the bead. Bead detachment events were evident from a sudden increase in the oscillation amplitude up to 1 μm and a simultaneous change in the direction of stage motion, indicating disruption of the feedback loop. The sideways force F acting on the bead at each time point was calculated as follows, taking into account the nonlinearity of the optical trap stiffness at large bead displacements (41):

$$F=k\cdot \mathit{\Delta }{y}^{\prime }\cdot e^{-\frac{{\left(\mathit{\Delta }{y}^{\prime }\right)}^2}{2\cdot R^2}}\text{,}$$ (1)

where k is the trap stiffness at the center of the trap, Δy′= y′_bead – y′_trap is the distance between the bead and trap centers, and R = 250 nm is the bead radius.

We took into account the specific geometry of the system (Fig. S5 e) to determine the distance D between the bead surface and the MT for each bead position:

$$D=\sqrt{{y^{\prime }}_{bead}^2+R^2}-R\text{.}$$ (2)

The height of the MT, which is much smaller than R, was neglected. During sweeping, the bead was assumed to remain at a constant distance from the coverslip because changes in the z-position of the laser trap moving 1 μm in the imaging plane are negligible.

Analysis of the force-velocity and force-detachment curves

At saturating ATP concentration, the dependence of motor velocity V on external force F was fitted as follows (42):

$$V\left(F\right)=d\cdot k_{cat}=\frac{d\cdot k_o}{p+q\cdot e^{-\frac{F\cdot \delta }{k_B\cdot T}}}\text{.}$$ (3)

Here, d = 8 nm is the size of a single step of kinesin, k_cat is the catalytic rate constant, k_o is the unloaded rate constant, k_B is the Boltzmann constant, T is the temperature, δ is the characteristic distance over which the load acts, and p and q = (1−p) are the fractions of the unloaded catalytic cycle required for the biochemical and mechanical transitions, respectively. The stalling force was determined using linear fit in the range of −4 to 2 pN.

The dependence of CENP-E kinesin attachment time on applied force was fitted to the following symmetrical exponential function (43):

$$T\left(F\right)=T_o\cdot e^{-\left|\frac{F}{F_d}\right|}\text{.}$$ (4)

Here, T_o is the attachment time of CENP-E kinesin to the MT in the absence of external load, and F_d is the detachment force.

Theoretical modeling

Simulation of bead-fluctuation dynamics

We simulated the MT as a 25 nm cylinder lying on the surface of a plane representing the coverslip. The bead-MT tether was modeled as a worm-like chain of 2 nm segments. The last point of the chain was anchored at the surface of a bead sphere with a radius of 250 nm. This connection was allowed significant flexibility by selecting rotation angles from a Gaussian distribution with SD = 17°. The first chain segment was anchored at the MT surface, and this site coincided with the position of a motor. Orientation of the first segment was fixed perpendicularly to the MT surface. Additional calculations showed that introducing greater rotational mobility of the MT-anchored segment of the chain and the chain’s self-avoidance did not affect major model predictions (see Supporting Materials and Methods; Fig. S1 c). The position of all other chain segments was calculated at each time by randomly selecting the angle at which the next segment deflects from the previous segment from a Gaussian distribution. The variance of this distribution was chosen to provide the desired PL of the chain. Monte Carlo simulations of the “tether-bead” system were carried out as in (21) using a coordinate system in which the motor was stationary. All configurations in which the coordinates of at least one chain segment were found within the bead, MT, or coverslip were discarded. This rule ensured that the tether did not penetrate into these objects. Likewise, configurations in which the bead overlapped with the coverslip were discarded. The presence of the coverslip and bead constrains increases the end-to-end distance of the tether. For example, the 230 nm tether with PL = 26 nm has end-to-end distance 97 ± 1 nm (mean ± SEM, N = 2000) when the tether is modeled with no bead, coverslip or MT, but this distance increases up to 125 ± 1 nm in a system containing all these components. Simulations were implemented using a custom program written in MATLAB (available upon request). Additional details are provided in Supporting Materials and Methods.

Results

Theoretical framework for TCM analysis of a walking motor

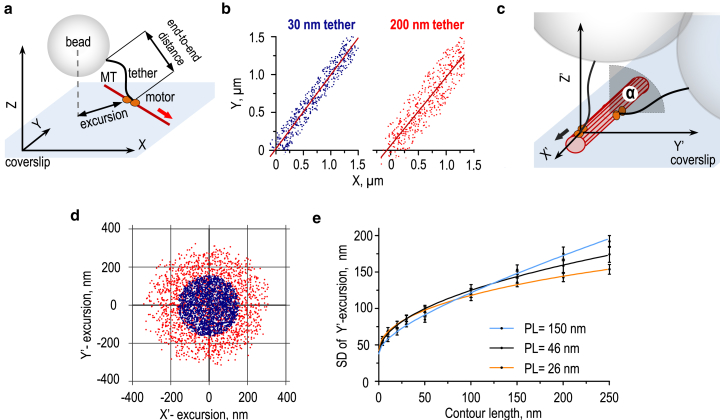
We used a theoretical approach to establish a quantitative framework for analysis of the conformational properties of motor-cargo tethering. Using Monte Carlo simulations, we modeled the motions of microbeads attached via mechanically different tethers to a motor walking along an MT track located in the plane of a coverslip (Fig. 1, a and b; Videos S1 and S2). In the traditional TPM assay, the Brownian motion of a tethered microbead is analyzed relative to the point of the tether’s attachment to the coverslip surface (19, 20, 21, 22, 23). We modified this approach to incorporate two specific features of the motor-MT system. First, to take into account the fact that the kinesin motor walks processively and unidirectionally, Brownian bead motion was analyzed relative to a system of coordinates centered at the moving kinesin (Fig. 1, c and d). The second complexity of the TCM system is that the coverslip-attached MT cylinder provides multiple protofilament tracks for kinesin binding and walking. Because of steric hindrance, the motor binds with different probabilities to different MT protofilaments (Fig. S1). Moreover, when the motor walks along different MT protofilaments, the range and average angle of the kinesin-coupled bead excursions are sterically restricted to different degrees, as illustrated by Figs. S2 and S3. Therefore, experimental results obtained with multiple beads and MTs should correspond to the average behavior on different protofilaments. To accurately represent these complexities in our model, bead coordinates calculated for different protofilaments were averaged using weight coefficients corresponding to the likelihood that the motor would land on a given protofilament (see Supporting Materials and Methods).

Figure 1.

Theoretical predictions for the TCM assay. (a) A schematic of the in vitro motility assay is shown, which uses 0.5 μm beads conjugated to the MT-dependent motor molecule via its natural tail extension or an artificial elongated link. The MT is immobilized on the coverslip; the red arrow indicates the direction of motor walking in the stationary coordinate system XYZ. (b) Predicted XY coordinates are shown for the bead moving on top of the MT at 20 μm min⁻¹ in the stationary coordinate system (500 coordinates for each tether with PL = 46 nm). Lines representing MTs are shown in dark red. (c) A schematic of motor-MT attachment in the moving system of coordinates is shown. Axis X’ points along the MT in the direction of motor walking (black arrow), Y’ and Z’ are perpendicular to the MT, and the origin is located on the surface of the MT at the attachment site for motor domains. Two example attachments to different protofilament tracks are shown. Angle α measures the position of the walking motor relative to the protofilament on top of the MT, for which α = 0°. (d) Two-dimensional “cloud” plots show the predicted bead excursions for 30 nm (blue) and 200 nm (red) tethers in the moving coordinate system. Data are for α = 0°; there is a total of 2000 points for each tether with PL = 46 nm. (e) The predicted relationship between the SD of MT-perpendicular bead excursions along the Y’-axis (Y’-excursion) and contour lengths for different tethers are shown. The lines are empirical fits with the following functions: a + bx + cx^0.5. Data for each tether is based on n = 9000 coordinates. Error bars (SD) were generated by bootstrap analysis; see Materials and Methods. To see this figure in color, go online.

Using this modeling framework, we calculated the predicted range of bead excursions as a function of the length of a mobile tethering molecule. The SD of bead excursions increases nonlinearly with increasing contour length (Fig. 1 e). For flexible tethers, such as the discontinuous coiled-coil stalk of CENP-E (PL = 26 nm (13)) and dsDNA (PL = 46 nm (44)), the SD dependence is best described by a polynomial function of fractional powers. With increasing tether stiffness (e.g., for PL = 150 nm, as in a continuous coiled-coil stalk (45)), this dependence becomes more linear. These calculations reveal the relatively modest impact of tether stiffness within the physiological range of the stalk lengths. Consistent with the theoretical findings in (46), the tether’s stiffness plays more prominent role when the tether length is increased (Fig. S1 c). Importantly, these data show that the range of bead excursions can accurately report the length of a bead tether. Thus, Brownian motion of tethered cargo can be used to gauge the conformational properties of tethering formed by a walking kinesin motor. Accordingly, we called this quantitative method the TCM approach.

Experimental verification of the TCM approach using kinesin-1 with variable dsDNA links

To test these theoretical predictions, we developed an in vitro motility assay to directly measure excursions of a microbead tethered to a kinesin-1 motor via links of known lengths. We designed two dsDNAs of 34 and 557 bp, representing short (12 nm) and long (189 nm) links, respectively. One end of the dsDNA was attached to a 500 nm silica bead via biotin-neutravidin chemistry (Fig. 2 a; see Materials and Methods). The opposite 5′-DNA end was modified to add BG, a substrate for the SNAP (47) enzyme. The BG-labeled dsDNA was then covalently attached to a specially designed protein adaptor, in which SNAP was fused to GBP, a nanobody derived from camelid antibody fragment (48). Beads coated with dsDNA links were incubated with the well-characterized kinesin-1 construct K560 labeled with GFP (32) (Fig. 2 a). This construct contains a fragment of the kinesin-1 coiled-coil stalk and a short neck and consequently has a contour length of just ∼24 nm. Taking into account SNAP-GBP (∼2 nm), the total lengths of the short and long kinesin-1-dsDNA tethers were around 38 and 215 nm, respectively.

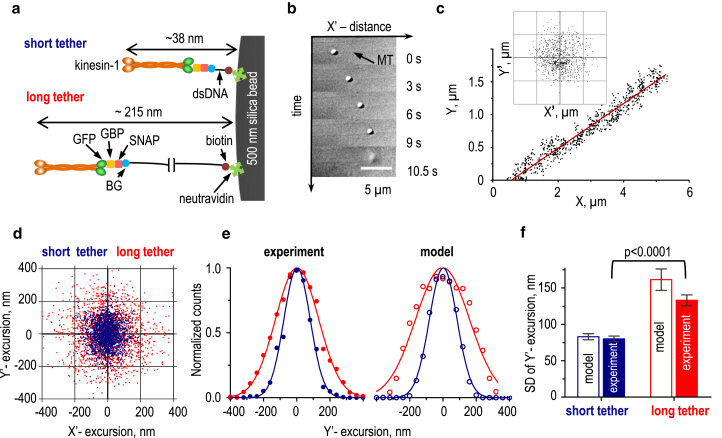
Figure 2.

Verification of the TCM assay using kinesin-1 and dsDNA links. (a) Our strategy for conjugation of kinesin-1 to the surface of a glass bead via dsDNA links of different lengths. The SNAP-GBP protein adaptor enables connection of this GFP-labeled motor to the BG-labeled dsDNA. (b) Selected DIC images are shown of a bead transported by kinesin-1 linked via the long dsDNA link. The bead detached 10.5 s after the start of motion. (c) Experimental coordinates were collected for a bead conjugated to kinesin-1 via the long dsDNA link. The inset shows a cloud of excursions for this bead, calculated as the deviations of the bead’s position from the line representing the MT (MT-perpendicular Y’-excursion) and from the assumed motor attachment site (MT-parallel X’-excursion); see Supporting Materials and Methods. The grid size is 0.2 μm. (d) Experimental cloud plots are shown for microbeads conjugated to kinesin-1 with different dsDNA links; representative data sets are based on the total 12,000 coordinates collected for 29 beads with the short tethers and 15,000 coordinates for 56 beads with the long tethers (for clarity, only 2000 randomly selected coordinates are shown for each tether). MT-parallel X’-excursions for these plots were calculated using the sliding averaging windows of 100–300 time points, corresponding to 1–3 s. (e) Normalized histograms show distributions of experimentally measured versus modeled bead Y’-excursions for the short (blue) and long (red) tethers. Each data set was fitted to a Gaussian function and normalized to its mean value. Each distribution is based on 2000 coordinates. (f) SDs of bead Y’-excursions are shown. Model predictions are based on data in Fig. 1e. Experimental data were obtained from 29 beads with short tethers and 56 beads with long tethers. Error bars are SDs generated by bootstrap analysis; p-values were calculated by unpaired t-test. To see this figure in color, go online.

We then used laser tweezers to bring one such bead to a taxol-stabilized MT attached to a coverslip, as in a traditional bead motility assay (13) (Fig. 2 b; Video S3). With sparse motor coating, less than one-third of the beads walked (Fig. S4 a), implying that the beads were mostly driven by single-motor molecules (7, 36). We recorded bead motions with 10 ms exposure and corrected the data for blurring, as described in Supporting Materials and Methods. Next, we generated two-dimensional bead position clouds, which revealed overall larger excursions of beads tethered via the long dsDNA link (Fig. 2, c and d). The MT-perpendicular components of these excursions were then compared with theoretical predictions. The model and experiment were highly consistent for the short tethers, but the experimental excursions for the long tether were slightly smaller than expected (Fig. 2, e and f).

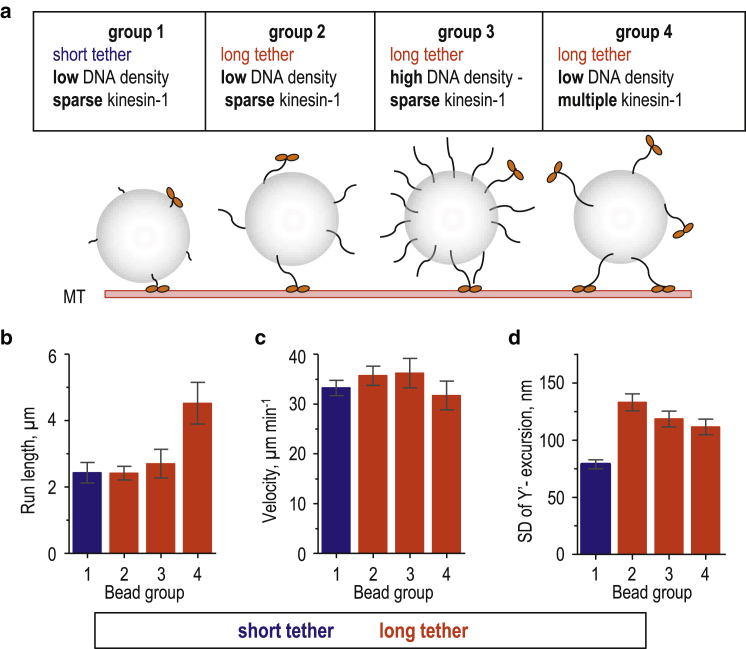
We hypothesized that, on average, lower-than-expected Y’-excursions could arise from stochastic variability in bead coating, leading to some of the beads having a high density of either dsDNA tethers or motors (Fig. 3 a). If several tethered motors are simultaneously engaged with the MT, bead excursions should be restricted (22). Higher dsDNA density could also reduce bead excursions if a single motor containing two GFPs binds two spatially separated dsDNA links, which is more likely to occur when the links are long. It is also conceivable that excessively high dsDNA density could create a dense, mechanically rigid layer around the bead, increasing its effective size and sterically reducing excursions, as illustrated with our theoretical model (Fig. S3, c and d). We tested these predictions by incubating beads with a high concentration of dsDNA (1 μM) and a limiting concentration of kinesin-1 (group 3, Fig. 3) or with a normal concentration of dsDNA (10 nM) and excess kinesin-1 (group 4, Fig. 3). Engagement of multiple kinesins did not change the bead’s velocity, but it did increase the run length as expected (49), whereas denser dsDNA coating had no effect on these parameters (Fig. 3, b and c). In both cases, however, the MT-perpendicular bead excursions decreased by 10–20% (Fig. 3 d), explaining why the model, which used only one dsDNA-motor tether per bead, predicted slightly larger excursions. Importantly, these data show that the TCM method accurately discriminated the long and short tethers linking the walking motor and its microbead cargo.

Figure 3.

Impact of the high density of dsDNA links or motor molecules on bead excursions. (a) A diagram illustrates the four examined groups of kinesin-1 beads, which had different coatings. The length and density of dsDNA links and the density of kinesin-1 were varied to study the impact of these factors on bead excursions measured with the TCM assay. (b and c) Run length (b) and velocity (c) were measured for kinesin-1 beads; see (a). Data show the mean ± SEM measured at 30 μM Mg-ATP; n = 29, 40, 10, and 18 beads for groups 1, 2, 3, and 4, respectively. (d) Experimentally measured SD of Y’-excursions are shown based on n = 29, 56, 20, and 28 beads for groups 1, 2, 3, and 4, respectively. Error bars (SD) were generated by bootstrap analysis. To see this figure in color, go online.

Walking CENP-E kinesin forms a much shorter tether than predicted from its contour length

We then applied this method to examine the conformation of walking CENP-E kinesin. In FL CENP-E, the N-terminal motor domain is connected via a long stalk to the C-terminal tail, which contains a weak MT-binding site (Fig. S5 a) (12, 13). This construct measures 230 ± 25 nm (12) in contour length, whereas the TR CENP-E construct is only ∼10 nm long. These proteins were conjugated to beads via the C-terminal tags (Figs. 4 a and S5, b and c). Only a fraction of these beads moved, and their run lengths were consistent with a single-molecule regime (Fig. S5 d). Using the TCM assay, we observed the motility of beads driven by either of these motors, yielding clouds of bead excursions (Fig. 4 b) and distributions of the MT-perpendicular components (Fig. 4 c). Unexpectedly, these plots revealed only a slight difference between FL and TR CENP-E, suggesting that their effective tether lengths were similar. It seems unlikely that small excursions of the beads carried by FL CENP-E were caused by the nonspecific sticking of CENP-E stalk to bead surface because binding of this C-terminal GFP-labeled protein to the beads was through anti-GFP antibodies (Fig. S5 c; see Materials and Methods).

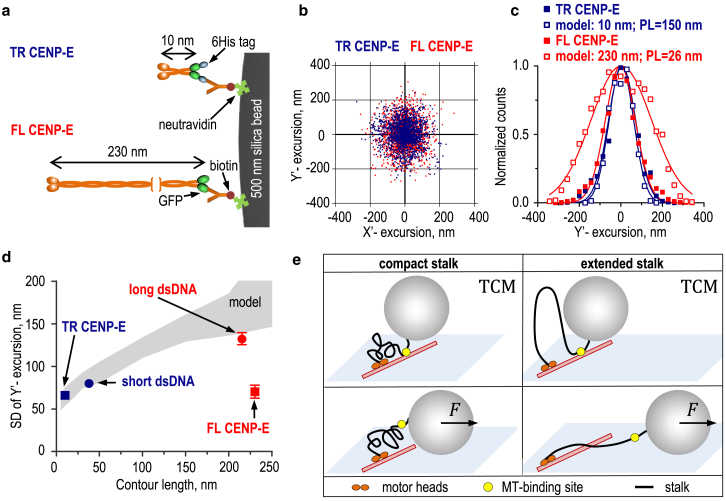
Figure 4.

Analysis of bead excursions for wild-type (full-length (FL)) and truncated (TR) CENP-E kinesins. (a) A strategy is shown for conjugating CENP-E kinesins to microbead cargo. (b) Cloud plots show microbeads carried by different CENP-E kinesin constructs, based on 26 beads for TR CENP-E and 18 for FL CENP-E. For each tether, 2000 randomly selected coordinates are shown. (c) Histograms show distributions of experimentally measured (solid symbols) versus predicted MT-perpendicular (Y’) bead excursions (open symbols). CENP-E tethers were modeled with specified contour lengths and persistence lengths. Each distribution (based on 2000 coordinates) was fitted to a Gaussian function and normalized to its mean value. (d) SDs of bead Y’-excursions are shown versus the contour length of the molecular tether. Squares show experimental measurements for TR and FL CENP-E, and circles show experimental measurements for kinesin-1 with different dsDNA links. The gray area represents the theoretical prediction from Fig. 1e for the range of PL = 26–150 nm, with 95% confidence. (e) Possible models show the FL CENP-E configuration to explain the low SD of the Brownian bead excursions. Upper cartoons show that if the MT-binding site (yellow) within the CENP-E tail is persistently attached to MT, in the TCM assay both compact and extended stalk configurations should lead to similarly small bead excursions limited only by the bead-proximal segment of the unstructured CENP-E tail. In lower cartoons, external sideways force prevents the tail’s MT-binding and stretches CENP-E, limited by the compactness of the stalk (left). In the “extended” stalk model (right), the force-dependent bead displacement should increase up to the total contour length of CENP-E. To see this figure in color, go online.

For TR CENP-E, the experimentally measured SD for MT-perpendicular bead excursions was 66 ± 4 nm, which is close to the theoretically predicted range for a 10 nm contour length (Fig. 4 d). Consistent with this, the TR CENP-E protein had slightly smaller MT-perpendicular excursions than those measured for the short dsDNA tether. By contrast, theoretical simulations for a bead carried via the 230 nm tether with PL = 26 nm, as in FL CENP-E, predicted the average end-to-end distance 125 ± 1 nm (mean ± SEM, N = 2000). Such a tether should generate bead excursions with the SD of ∼150 nm (Fig. 1 e). This is significantly larger than the experimentally measured SD of 70 ± 8 nm for FL CENP-E (Fig. 4 d), implying that despite its very large contour length, CENP-E kinesin forms a short tether with an average end-to-end distance of only ∼20 nm.

Sideways-pulling force cannot fully extend the stalk of a walking CENP-E kinesin

The simplest hypothesis to explain these relatively small bead excursions is that FL CENP-E is compacted, reducing the distance between the bead and the site of motor-domain attachment to the MT (Fig. 4 e, top left panel). However, CENP-E has a second MT-binding site located within the unstructured C-terminal tail (15), so the smaller-than-expected bead excursions may also reflect the short distance between the bead and the tail’s MT attachment site (Fig. 4 e, top right panel). Previous measurements of the tail-MT binding interactions show that it is very transient, lasting <0.5 s, which is significantly shorter than the observation time during TCM assay. However, the estimated rebinding time for the tail and MT is even shorter (<1 ms (13)). Thus, during the TCM assay, the tail should be mostly MT-bound, and CENP-E with either compact or extended stalks would produce similarly small Brownian excursions.

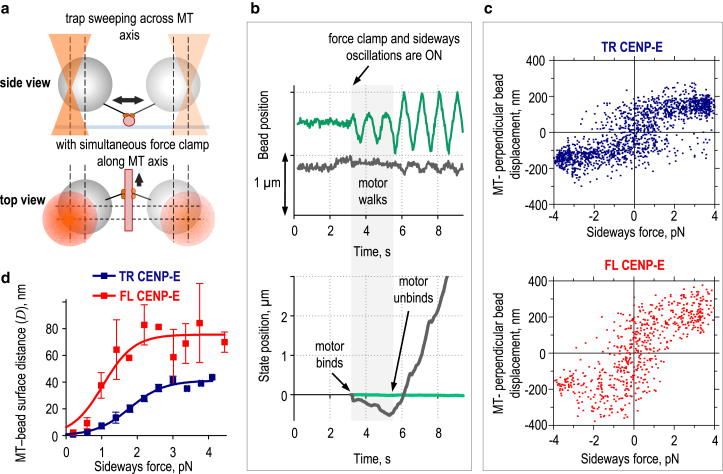
We reasoned that we could discriminate whether the stalk is compact or extended by applying a sideways force on the bead carried by FL CENP-E because force should disrupt CENP-E tail binding to the MT (Fig. 4 e, bottom row). Indeed, even with no force, the tail dissociates from MT very frequently. Because its binding to MT is thermally driven, a small force pulling the tail away from the MT should prevent its rebinding, leaving the motor domains as the only MT attachment site. Moreover, a force acting on the MT-bound tail should also reduce its binding time (50). Using Bell’s equation with a force-dependent transition step of 4 nm, we estimate that a 3 pN force should decrease the tail-MT binding time to 25 ms, and with 8 nm step this time would become only 1.3 ms. Thus, the applied force should dislodge the tail from MT, revealing the natural CENP-E length extension that is not obscured by the second MT binding site in its tail. If the CENP-E stalk is not compacted, the length of the bead-MT tether should increase up to 230 nm, which is much longer than measured from thermal motions in the TCM assay. If the CENP-E stalk is compacted, only a small bead displacement is predicted even in the presence of pulling force. Intermediate tether lengths could also be observed if the compact stalk can be partially extended by force.

To test these predictions, we designed an assay in which the motor-driven bead was pulled with a sideways force, applied by sweeping the optical trap perpendicular to the MT at a frequency of 1 Hz and an amplitude of 0.5 μm (Fig. 5 a; Video S4). The duration of one such cycle is significantly longer than the predicted attachment time of the CENP-E tail to MT under force. To facilitate the unambiguous identification of bead detachment events from the MT due to motor dissociation, we applied an additional small load (1 pN) to a moving bead with the force clamp, implemented via a feedback-controlled piezo stage (see Materials and Methods).

Figure 5.

Probing CENP-E conformation with a sideways force. (a) Schematics show the sideways-force experiment from two different views. The MT cylinder (in red) is attached to the coverslip (blue), shown only from a side view (top image). A bead tethered to the MT-bound motor (small circles) is shown in two extreme positions, corresponding to the amplitude of sideways motion (double-headed arrow). The laser trap, also shown in two extreme positions, is depicted by triangles in the side view and large orange circles in the top view. The bead’s displacement from the trap’s center (broken lines) indicates the presence of the sideways force and the force clamp opposing the motor’s motion along the MT. The arrow in the top view shows the direction of motor walking. (b) An example experiment with the sideways force is shown. The upper graph shows displacement of the bead in the direction across (green) and along (gray) the MT; for clarity, the curves are offset vertically. The bottom graph shows displacements of the piezo stage in the same experiment. The piezo stage starts moving after the force clamp is engaged, indicating that kinesin is walking along the MT. The amplitude of sideways bead displacement (green curve in upper graph) increases up to 1 μm after the motor unbinds from the MT and the bead is no longer tethered to the MT. (c) MT-perpendicular bead displacements under the sideways force are shown, calculated with Eq. 1 for beads carried by TR CENP-E, n = 17, and for FL CENP-E, n = 9. (d) The mean distance D between the MT and bead surface is shown as a function of the sideways force, calculated based on the data in (c) and Fig. S5e, using Eq. 2 in Materials and Methods. Solid lines are fits to sigmoid functions, and bars are SEMs. To see this figure in color, go online.

In Fig. 5 b, changes in the position of the bead (top panel) and stage (bottom) are plotted for one such experiment. Initially, the bead coated with FL CENP-E was brought close to the coverslip-immobilized MT, as in a regular TCM assay. After the CENP-E started walking (3.7 s), the sideways-trap sweeping and force clamp were triggered. Consequently, the MT-perpendicular bead coordinate started to change periodically (green curve in the top panel). The bead continued to move along the MT during the first two cycles of sideways sweeping, as seen from the continuous motion of the stage along the MT axis (gray curve in the bottom panel). When CENP-E unbound from the MT (∼6 s), the direction and velocity of stage motion changed abruptly, as the stage tried to maintain the clamped force on the freed bead. Importantly, the top panel shows that the sideways displacement of the bead under force was relatively small during motor walking, indicating that bead displacement was restricted by the tether. After the bead detached, however, its sideways motion was no longer restricted, and the bead’s position mirrored the trajectory of optical trap, exhibiting a full 1 μm amplitude (top panel, green curve).

We used this assay with CENP-E-coated beads to extract bead displacement in the MT-perpendicular direction as a function of the applied sideways force (Fig. 5 c). Taking into account the bead’s diameter (Fig. S5 e), we calculated the distance from the bead surface to the MT and plotted these binned data as a function of the sideways force (Fig. 5 d). This distance increased with applied sideways force for beads coated with either TR or FL CENP-E. For a TR motor, it reached a plateau of 41 ± 1 nm. This maximal deviation exceeds the total estimated contour length for TR CENP-E, indicating the presence of some additional compliant element. The compliance is likely to result from the slight looping (bending or twisting) of the MT from the sites of coverslip attachment (via antitubulin antibodies) under the sideways force. However, because the MTs were attached to the coverslips using the same antibody concentration in all experiments, such MT looping should be the same for both TR and FL CENP-E. Thus, the offset between the plateau values for the TR and FL CENP-E curves in Fig. 5 d (35 ± 4 nm) corresponds to the difference in the maximal extension lengths of these two proteins. Because the contour length of TR CENP-E does not exceed 10 nm, these data show that FL CENP-E can be extended up to ∼45 nm under sideways force. This is ∼2-fold longer than the average tether length deduced from the TCM assay, suggesting partial FL CENP-E extension under 3–4 pN force. Importantly, the sideways force failed to extend the CENP-E molecule completely, strongly suggesting that walking FL CENP-E kinesin has a compact configuration.

The compact configuration of FL CENP-E does not impede its transport function

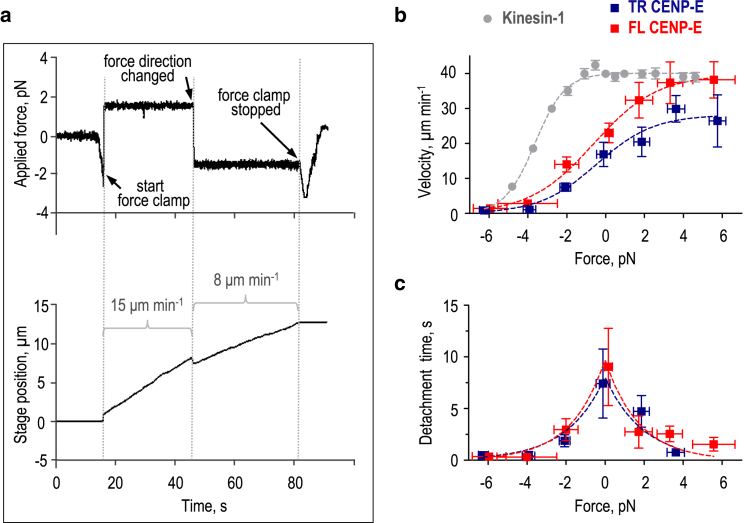
Because walking FL CENP-E kinesin does not behave as an elongated fibrillar tether, we next investigated whether its compact configuration interferes with load-bearing. To test the range of directional loads, we used an optical force clamp along the MT in the absence of the sideways force, as illustrated by recordings from a typical experiment in Fig. 6 a. TR CENP-E, which was used as a control, slowed down significantly under the opposing load and eventually stalled at −4.4 ± 0.8 pN, a slightly smaller stall force than reported previously for artificially dimerized CENP-E motor heads (37). The FL CENP-E kinesin stalled at a similar load of −4.6 ± 0.3 pN (Fig. 6 b). Assisting forces up to 6 pN increased the velocity of TR CENP-E transport by ∼70%. Analogous measurements using beads coated with FL CENP-E revealed that under the assisting load, this motor walked noticeably faster; under the 5–6 pN load, FL CENP-E walked at 38 ± 5 μm min⁻¹, whereas the velocity of TR CENP-E was 26 ± 7 μm min⁻¹ (Fig. 6 b). This is in contrast to conventional kinesin-1, which does not accelerate significantly under assisting force (51).

Figure 6.

Measurement of the response of CENP-E kinesin to mechanical load. (a) An example experiment is shown in which a CENP-E-coated bead moves under the assisting force (2 pN) and then the opposing force (−2 pN), acting along the MT. The upper panel shows the force applied to the bead, and the lower panel shows the motion of the stage, which was programmed to keep a constant distance between the centers of the bead and optical trap. (b) Force-velocity curves show TR and FL CENP-E in comparison with the published data for kinesin-1 (gray (51)). Assisting load is indicated by positive numbers, and opposing force is indicated by negative numbers. Symbols show mean ± SEM based on at least 60 measurements for each CENP-E motor. The lines represent fits to Eq. 3; see Materials and Methods. (c) Force-dependent detachment time for TR and FL CENP-E motors is shown. Lines represent fits to Eq. 4; see Materials and Methods and the legend to (b) for other details. To see this figure in color, go online.

To compare the force-velocity dependencies of the FL and TR CENP-E motors in a more rigorous manner, we fit them with the previously proposed energy-landscape model (42) (see Materials and Methods). Although FL and TR CENP-E had similar fractions of biochemical transitions (p_TR = 0.58 ± 0.10 vs. p_FL = 0.59 ± 0.05), their unloaded catalytic rates were different (k_o,TR = 33.3 ± 3.3 vs. k_o,FL = 48.3 ± 1.6 s⁻¹), which was consistent with a slightly faster velocity of FL CENP-E molecules with no load (13). The characteristic distances associated with the force-dependence of these two constructs were comparable (δ_TR = 2.8 ± 0.8 nm vs. δ_FL = 2.5 ± 0.3 nm), implying that the compact configuration did not significantly alter the response of CENP-E to force. Moreover, with the applied force, the run times decreased similarly for both proteins (Fig. 6 c). Exponential fitting of these dependencies using Eq. 4 in Materials and Methods yielded very similar values for the detachment force: 1.9 ± 0.5 pN for TR vs. 1.7 ± 0.3 pN for FL CENP- E. Thus, the compact configuration of the CENP-E motor limits the range of cargo motion without strongly influencing the ability of the motor to walk under assisting or opposing forces.

Discussion

The predicted structures of nonmotor regions differ dramatically among members of the kinesin superfamily, but little is known about the resultant mechanical properties of cargo tethering in transporting kinesins. The dynamic configurations of stalk- and tail-mediated tethers may affect the ability of motors to move collectively and/or to navigate through complex cytoplasmic environments (29, 52, 53, 54). Potentially, these tethers can also tune the reach from motor-bound cargo to cytoskeletal tracks or serve as tension-sensitive elements to control the motor’s function or conformation in response to load. To begin addressing these issues, we combined experiments and theory to develop the TCM assay. This method is applicable to tethers formed by kinesin nonmotor domains, as we demonstrated for CENP-E (Fig. 4 a), or to tethers engineered using heterologous fibrillar links, such as dsDNA (Fig. 2 a). To our knowledge, our work provides the first experimental and theoretical guide for probing the mechanical properties of motor-bead tethering that takes into account uncertainties arising due to variability of motor velocity and the presence of multiple protofilament tracks. The major advantage of the TCM assay over traditional TPM and tethered fluorophore motion approaches is that it affords a straightforward identification of single, actively walking molecules. Purified kinesins often display heterogeneous behavior; for example, in in vitro preparations of FL CENP-E, only a fraction of motors exhibit directed motility, whereas other molecules fail to bind to MTs (presumably because of autoinhibitory folding (55)) and others bind very transiently or exhibit diffusive motions (13). TCM naturally selects only the motile molecules and consequently reports on the conformation of transporting motors free of intramolecular interactions that modify their activity.

The TCM approach provides important insights into the dynamic configuration of one of the longest kinesin family members, CENP-E. Early in mitosis, this kinesin binds to the kinetochore via a site upstream of the MT-binding site in its C-terminal tail (Fig. S6 a). In the absence of MTs, the kinetochore-bound CENP-E is likely to be fully elongated, contributing to the appearance of a dense and fibrillar kinetochore “corona” (56). This extension is beneficial early in mitosis because it expands the range of MT search and capture by the heads of CENP-E motors tethered to the kinetochore (12). However, the results of this in vitro study reveal that the stalk of CENP-E engaged in active transport along the MT wall does not behave as an elongated fibrillar tether, arguing against the idea that CENP-E is fully extended at the MT-bound kinetochores. Using a laser trap, we applied a 3–4 pN force on a bead attached to the C-terminus of the walking CENP-E, but the tether could not be extended more than twofold (Fig. 5 d). The force pulling on the bead should disrupt binding between the MT and the C-terminal tail of CENP-E, revealing its natural extension length (Fig. 4 e). Thus, the lack of significant elongation of CENP-E under the sideways force suggests that the stalk of the walking CENP-E is compacted. The estimated end-to-end length of transporting CENP-E in vitro is only 20 nm, which is <10% of its contour length and ∼16% of its predicted end-to-end length. In contrast, the tether formed by the K560 kinesin-1 fragment, as measured using a heterologous dsDNA linker, is ∼80% of its contour length, so our finding is specific to CENP-E.

Our conclusion that CENP-E transports in a compact configuration is consistent with the reduced length estimated for kinetochore-bound CENP-E from high-resolution mapping of human kinetochore (57). Importantly, our experiments with laser tweezers argue against the model in which this compact configuration modifies load-bearing by CENP-E. The stall force of FL CENP-E is very similar to that of the CENP-E with no stalk, and both motors increase their velocity to similar degrees under the assisting force. This acceleration and the small detachment force (∼1.8 pN) are in contrast to those of kinesin-1 (Fig. 6 b), which has an almost 1.7-fold greater detachment force (43). Previously, we showed that unlike kinesin-1, CENP-E responds to the opposing load with only a mild increase in backward stepping (40). Together with the findings reported here, these observations imply important differences in the transport functions of these two motor families. The specific force-velocity and detachment characteristics of CENP-E are likely to be responsible for its distinctive collective behavior (58) during chromosome transport, which is an important topic for future investigation.

In summary, our findings using the TCM assay and laser tweezers strongly suggest that the compact CENP-E configuration is regulatory rather than mechanical in nature. Because shortening of the CENP-E stalk leads to severe defects in chromosome segregation (16), the dynamic changes in CENP-E configuration appear to be essential for some function of CENP-E unrelated to transport. The noninhibitory CENP-E folding upon MT capture could serve to ensure that by reaching the MT plus-end, CENP-E motor domains facilitate close encounters between the MT tip and other kinetochore proteins (Fig. S6 b). Direct contact between MT tips and the kinetochore-associated MT-binding proteins is essential for the establishment and maintenance of the MT end-on configuration, and these contacts would be less likely if CENP-E molecules were fully extended. In this respect, it is revealing that CENP-E binds numerous kinetochore and MT regulators, including Mad1, PP1, CENP-F, CLASPs, and SKAP (59, 60, 61, 62, 63). At the dynamic MT tip, the folded CENP-E stalk could provide a mobile molecular platform to bind and translocate these important regulators. Given that the compact CENP-E stalk can be partially extended by force, the association of these regulators with CENP-E could be regulated by tension between the MT-bound CENP-E motor domain and its kinetochore-binding domain (Fig. S6 b). Whether CENP-E helps to localize various kinetochore regulators in a tension-sensitive manner at the kinetochore-embedded MT ends is an interesting question for future cell biological studies.

Author Contributions

N.G., E.V.T., F.I.A., and E.L.G. designed the study. N.G. and E.V.T. performed the experiments and analyzed the data. N.G., V.M., and F.I.A. carried out the theoretical analyses. B.V. and D.W.C. contributed an essential reagent. A.L.D. developed the protocol for dsDNA-bead conjugation. N.G., E.V.T., and E.L.G. wrote the manuscript with input from V.M. and F.I.A.

Editor: Steven Rosenfeld.

Supporting Citations

References (64, 65) appear in the Supporting Material.