Conditional generative adversarial network for gene expression inference

Abstract

Motivation

The rapid progress of gene expression profiling has facilitated the prosperity of recent biological studies in various fields, where gene expression data characterizes various cell conditions and regulatory mechanisms under different experimental circumstances. Despite the widespread application of gene expression profiling and advances in high-throughput technologies, profiling in genome-wide level is still expensive and difficult. Previous studies found that high correlation exists in the expression pattern of different genes, such that a small subset of genes can be informative to approximately describe the entire transcriptome. In the Library of Integrated Network-based Cell-Signature program, a set of ∼1000 landmark genes have been identified that contain ∼80% information of the whole genome and can be used to predict the expression of remaining genes. For a cost-effective profiling strategy, traditional methods measure the profiles of landmark genes and then infer the expression of other target genes via linear models. However, linear models do not have the capacity to capture the non-linear associations in gene regulatory networks.

Results

As a flexible model with high representative power, deep learning models provide an alternate to interpret the complex relation among genes. In this paper, we propose a deep learning architecture for the inference of target gene expression profiles. We construct a novel conditional generative adversarial network by incorporating both the adversarial and ℓ₁-norm loss terms in our model. Unlike the smooth and blurry predictions resulted by mean squared error objective, the coupled adversarial and ℓ₁-norm loss function leads to more accurate and sharp predictions. We validate our method under two different settings and find consistent and significant improvements over all the comparing methods.

1 Introduction

Gene expression profiling is a powerful tool for measuring the expression of thousands of genes under a given biological circumstance. It provides a comprehensive view of cellular status and is therefore the basis for functional gene expression pattern characterization. Gene expression profiling has been widely used in the analysis of various cell conditions and regulatory mechanisms in response to different disturbances, thereby enabling the discovery of cellular functionality and differentiation during the pathogenesis of disease.

The rapid development of high-throughput technologies has contributed to the proliferation of large-scale gene expression profiles. Several public databases have been constructed to archive gene expression data for various biological states. For example, Gene Expression Omnibus (GEO) (Edgar et al., 2002) is a versatile data warehouse storing the gene expression measurement in different cells. The Connectivity Map provides a collection of gene expression profiles from curated human cells. The availability of these databases helps to improve the understanding of gene expression patterns in different cellular situations.

Gene expression analysis has facilitated recent biological studies in various fields, such as cancer classification and subtype discovery (Calon et al., 2015), estrogen-receptor (ER) status determination (Mouttet et al., 2016), drug-target network construction (Y ild ir im et al., 2007), cell type detection (Darmanis et al., 2015) as well as the influenza infection susceptibility and severity analysis (Yan et al., 2015). By assessing global gene expression profiles in colorectal cancer samples, researchers in (Calon et al., 2015) established the connection between elevated expression of mesenchymal genes in stromal cells and poor prognosis and resistance to therapy. On the basis of mRNA expression assay, Mouttet et al., developed a new quantitative assessment of hormone receptor status and HER2 status that characterizes various estrogen-dependent growth mechanisms in different menopausal states of ER-positive breast cancer (Mouttet et al., 2016). By integrating gene expression microarray data, researchers in (Y ild ir im et al., 2007) constructed a bipartite graph to analyze the association between drug targets and disease-gene products, providing a clue to new drug discovery. Moreover, microarray analysis in (Yan et al., 2015) identified significantly altered expression levels of several immune-related genes in mice susceptible to influenza A virus infection.

Despite the rapid advances and widespread application of gene expression profiling, genome-wide profiling remains expensive and difficult when it comes to analyzing numerous cell types in response to different interferences (Nelms et al., 2016). Therefore, how to accurately and efficiently evaluate the entire genome expression is still a key issue. According to previous studies, the expression patterns of different genes are highly correlated (Heimberg et al., 2016; Ntranos et al., 2016; Shah et al., 2016). As is indicated in the cluster analysis of single-cell RNA-seq in (Ntranos et al., 2016) and (Shah et al., 2016), genes from the same cluster exhibited similar expression patterns under different conditions. Given such a high correlation among gene expression profiles, it is reasonable to assume that only a small group of genes can be informative to approximate the overall genome expression. To determine the appropriate small subset of informative genes, researchers in the Library of Integrated Network-based Cell-Signature (LINCS) plan (http://www.lincsproject.org/) performed principle component analysis (PCA) and identified ∼1000 genes that were sufficient to describe ∼80% of the information in the entire transcriptome (Duan et al., 2014). This set of ∼1000 genes, called landmark genes, contains most of the information in the whole genome and can be used to predict the expression of other genes.

Based on the above findings, one credible and cost-effective strategy for large-scale gene expression profiling is to measure the expression profile of only landmark genes and then estimate the remaining target gene expression through an appropriate predictive model. Therefore, it is essential to construct effective computational methods to infer the target gene expression profiles from the landmark genes. The estimation of target gene expression profiles can be naturally formulated as a multi-task regression problem, where the prediction of one target gene can be formulated as one task. The most straightforward model is linear regression, which has been applied in the LINCS program. The LINCS program generated the landmark gene expression of ∼1.3 million profiles using L1000 technology, and adopt the linear regression model to infer the expression of the remaining target genes.

However, the regulatory network among genes is complicated, linear models do not have enough capacity to capture the non-linear relationship of the gene expression profiles (Guo et al., 2014). Kernel models provide a way to introduce flexibility in representing the non-linear relations among gene expression. However, in large-scale scenarios, kernel methods need to calculate an extremely large kernel matrix and therefore suffer from a high computational burden. In contrast, deep learning models are scalable and highly flexible, and have been widely applied to different biological problems, such as protein structure prediction (Lyons et al., 2014), cancer classification (Fakoor et al., 2013) and population stratification detection (Romero et al., 2016). The remarkable predictive power and flexibility of the deep learning model makes it a powerful alternative for effective inference large-scale gene expression profiles.

Chen et al. (2016) applied deep neural networks to the multi-task regression problem for gene expression inference. The authors constructed a fully connected neural network (abbreviated as D-GEX) that outperformed linear models. The success of the D-GEX model proves the prospect of deep learning models in driving the gene expression inference problem. However, D-GEX model uses standard mean squared error (MSE) loss function, which produces smooth and blurry results (Mathieu et al., 2015). In other words, the use of MSE loss makes the model not capable of learning the high-frequency patterns in the data, thus performs poorly when data comes from multi-modal distribution. Also, training D-GEX model using the MSE loss is sensitive to outliers in the data, hence D-GEX is not a robust model. To deal with these problems, we propose a novel conditional generative model for robust and sharp estimation in the regression task. We consider adversarial loss found in generative adversarial networks (GAN) (Goodfellow et al., 2014) to estimate the target gene expression in a sharp and realistic approach. Moreover, we adopt ℓ₁-norm loss to stabilize the adversarial training and make our model robust to outliers. We apply our model for predicting target gene expression profiles from two different gene expression data portal: GEO and genotype-tissue expression (GTEx) (Lonsdale et al., 2013). Our model significantly outperforms previous methods on the inference of gene expression, and also provides insights into the correlation between different genes.

We would like to point out our main contributions as follows:

• Proposing a novel GAN for the problem of gene expression inference.

• Introducing an effective loss function consisting of the adversarial and ℓ₁-norm losses for training the gene regression model.

• Outperforming alternative models with significant margins on two datasets according to different evaluation metrics.

Notation: here we summarize the notations used throughout the whole paper: Unless specified otherwise, upper case letters denote function, e.g. D, G. Bold lower case letters denote vectors, e.g. $x, y, b$. w_i denotes the i-th element of vector w. Plain lower case letters denote scalars, e.g. a, γ, λ. Specially, n denotes the number of gene profiles. l denotes the dimension of the input feature vector, i.e. number of landmark genes. t denotes dimension of the output feature vector, i.e. the number of target genes. $\left|\right|w\left|\right|$ denotes the ℓ₂-norm of w: $\sqrt{{\displaystyle {\sum }_i{w}_i^2}}$.

2 Related work

2.1 Gene expression inference

Despite the progress observed in high-throughput sequencing and analysis techniques, genome-wide gene expression profiles under different perturbations and cellular conditions are still expensive and difficult (Nelms et al., 2016). Therefore, how to keep a low-budget in gene expression profiling while making measurements as informative as possible remains a key issue. According to previous studies, gene expression is highly correlated, and genes with similar function show similar expression patterns in different experimental conditions. With such related structure inherited in gene expression, even a small number of genes can provide abundant information. Shah et al. indicates that a random collection of 20 genes capture ∼50% of the correlation information in the entire genome (Shah et al., 2016). Recent advances in RNA-seq (Heimberg et al., 2016; Ntranos et al., 2016) also support the notion that a small subset of genes are rich enough to depict the overall information throughout the transcriptome.

In order to analyze the gene correlation structure and identify the subset of informative genes, researchers from the LINCS program have assembled the expression profiles from a total of 12 063 genes. They collect the data from GEO database using Affymetrix HGU133A microarrays, and calculate the maximum percentage of expected connections that can be recovered with a specific number of genes. The measurement of recovered connection is based on a comparable rank from the Kolmogorov–Smirnov statistic. According to the LINCS analysis, the researchers find that a set of only 978 genes can recover 82% of the observed connections in the whole transcriptome (Keenan et al., 2017). The set of 978 genes are identified as landmark genes, which can be referenced for inferring the expression of other target genes in various cell types under different chemical, genetic and disease conditions.

2.2 Deep neural networks

In recent years, deep learning has shown impressive performance in wide range of applications, such as computer vision (Krizhevsky et al., 2012), natural language processing (Collobert and Weston, 2008), social network embedding (Wang et al., 2016), speech recognition (Hinton et al., 2012a) and even biological science (Di Lena et al., 2012). The competence of deep models is based on leaning hierarchical representations of data using scalable learning methods. However, learning wide and deep sets of features in multi-layer neural networks is a challenging task. To address this issue, several tricks and techniques are developed in the literature, including regularizations like dropout (Hinton et al., 2012b), normalization layers like batch normalization (Ioffe and Szegedy, 2015) and weight normalization (Salimans and Kingma, 2016), non-saturating activation functions like rectified linear unit (ReLU) (Nair and Hinton, 2010) and leaky rectified linear unit (LReLU) (Maas et al., 2013), clever architectures like Inception model (Szegedy et al., 2015), ResNet (He et al., 2016; Zagoruyko and Komodakis, 2016) and DenseNet (Huang et al., 2017) and advanced optimization algorithms like Adam (Kingma and Ba, 2014) and AdaGrad (Duchi et al., 2011).

In addition to these techniques, a powerful generative model, called GAN, is introduced in (Goodfellow et al., 2014). While GAN is primarily developed to synthesize realistic images with great visual details, it is also widely appreciated due to the learning of loss function instead of manually designing the effective loss for the desired task. In particular, GAN objective includes a two-player minimax game between a generator and a discriminator networks. While the generator aims to fool the discriminator by synthesizing realistic images from arbitrary distribution (i.e. random noise), the discriminator tries to distinguish between the real and synthesized (i.e. fake) images. There are several studies (Denton et al., 2015; Karras et al., 2017), which improved GAN by stabilizing the training process and producing higher quality images. Moreover, some studies enhanced the quality and diversity of synthesized images by conditioning the generation process on the class labels or text descriptions. The conditional GAN models are also successfully applied in image to image translation by learning the mapping function between input and output images (Isola et al., 2016; Zhu et al., 2017). Furthermore, GAN has been adopted in different problems, such as semi-supervised image classification (Salimans et al., 2016), object detection (Li et al., 2017), speech enhancement (Pascual et al., 2017) and drug discovery (Benhenda, 2017).

Although our model falls into the category of conditional GAN models, it is different from the previous works due to the new application of gene expression inference and the challenges in generating large dimension outputs with no spatial structure.

3 Conditional generative adversarial network for gene expression inference

3.1 Motivations

Given a set of gene expression profiles $\Omega ={\{(x_i,y_i)\}}_{i=1}^n$, where ${\left\{x_i\right\}}_{i=1}^n$ denotes n landmark gene expression profiles, and ${\left\{y_i\right\}}_{i=1}^n$ corresponds to target genes, our goal is to learn a multi-task regression model for mapping landmark genes to the corresponding target genes $G:x\to y$, that is appropriate for the inference of each $y_i$ given $x_i$.

Although, the MSE loss is the first objective candidate for learning this mapping function, it suffers from different problems. For instance, if the prediction probability of target genes for a landmark gene x has two equally likely modes y and $y\prime$, then the average value $y_{ave}=(y+y\prime )/2$ will be the estimation with the minimum MSE loss, even if the $y_{ave}$ itself has very low probability. In other words, MSE loss makes the estimation as the average over possible modes, thus leads to blurry and smooth prediction results.

To address the inherently smooth predictions obtained from the MSE loss function, we propose a novel deep generative model, denoted by GGAN, for the inference of target gene expression from landmark genes. In particular, we adopt a conditional adversarial network as our model, where the generator plays the role of conditional distribution of the target genes given the landmark genes, and the discriminator assesses the quality of generated target genes compared to the ground truths. Considering ${\widehat{\mathbf{y}}}_i=G(x_i)$ as the predicted target genes by the generator network, we train the discriminator to distinguish the real pairs $(x,y)$ from the fake pairs $(x,\widehat{\mathbf{y}})$, and learn the generator to synthesize as realistic as possible $\widehat{\mathbf{y}}$ samples to fool the discriminator.

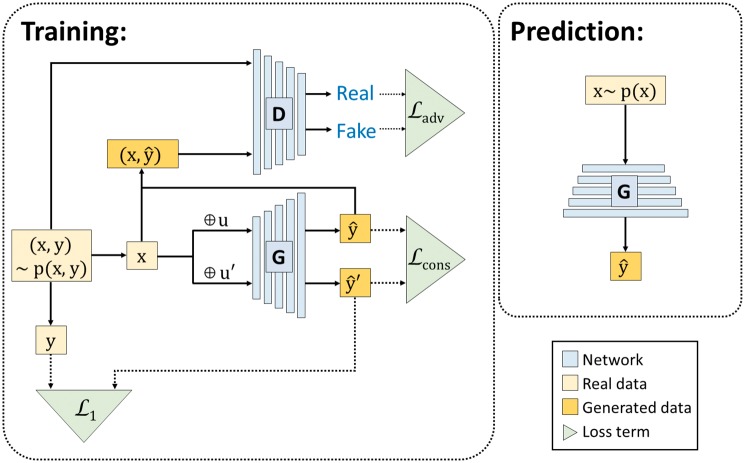
In order to train the generator network, we combine the adversarial loss and ℓ₁-norm loss functions. In contrast to the smoothing effect of MSE loss, adversarial loss selects a single mode and results in sharp predictions. The ℓ₁-norm loss provides robust predictions to the outliers, and is also helpful in stabilizing the adversarial training. In another point of view, ℓ₁-norm loss function captures the low frequency structure of samples, and adversarial loss learns the high-frequency parts of the data. Moreover, to guarantee that the output of our mapping function is stable w.r.t. the perturbation of random noises, we introduce consistency loss in our model such that the output should be similar when the input is added with different random noises. To make the motivation clear, we show the architecture of our model along with the applied loss functions in Figure 1.

Fig. 1.

Illustration of GGAN architecture and its loss functions. We use $(x,y)\in {\mathbb{R}}^{l+t}$ to denote a gene expression profile, where $x\in {\mathbb{R}}^l$ corresponds to the landmark genes and $y\in {\mathbb{R}}^t$ represents the target genes. Our goal is to learn a generator function G which takes x as the input and output $\widehat{\mathbf{y}}$ as the prediction of the target gene expression. To construct an appropriate prediction function G, we consider three loss terms in our model: ${\mathcal{L}}_{cons},{\mathcal{L}}_{adv}$ and ${\mathcal{L}}_1$. ${\mathcal{L}}_{cons}$ measures the consistency of the prediction from G when the input x is perturbed by random noise u and $u\prime$. ${\mathcal{L}}_1$ measures the difference between the prediction vector $\widehat{\mathbf{y}}$ and the ground truth y. For the term ${\mathcal{L}}_{adv}$, we construct a discriminator D which takes both $(x,y)$ and $(x,\widehat{\mathbf{y}})$ as the input. The discriminator D tries to distinguish the real’ sample $(x,y)$ from the ‘fake’ sample $(x,\widehat{\mathbf{y}})$ while the G tries to predict the realistic $\widehat{\mathbf{y}}$ vector to fool the discriminator. ${\mathcal{L}}_{adv}$ measures the adversarial loss in the game between the generator G and discriminator D

3.2 Deep generative model

The min–max adversarial loss for training the generator and discriminator networks in our model has the following form.

$$\underset{G}{\text{min}}\underset{D}{\text{max}}{\mathbb{E}}_{(x,y)\sim p(x,y)}[\log (D(x,y))]+{\mathbb{E}}_{x\sim p(x)}[\log (1-D(x,G(x))].$$ (1)

Note that the input to the discriminator network is the concatenation of landmark and target genes. This formation helps the generator to learn the joint distribution $p(x,y)$, thus produces the corresponding target genes to the landmark genes. It also guides the discriminator to learn the relationship between the landmark and target genes.

The ℓ₁-norm loss function for training the generator network is:

$$\underset{G}{\text{min}}{\mathbb{E}}_{(x,y)\sim p(x,y)}[||y-G(x)|{|}_1].$$ (2)

We also define the consistency loss for training the parameters of the generator as follows.

$$\underset{G}{\text{min}}{\mathbb{E}}_{(x,y)\sim p(x,y)}[||G(x\hspace{0.17em}\oplus \hspace{0.17em}u)-G(x\hspace{0.17em}\oplus \hspace{0.17em}u\prime )|{|}^2],$$ (3)

where u and $u\prime$ are the dropout noises that we add to the input and hidden layers of the generator network.

Training the GAN models to generate the large dimension samples using the adversarial loss is very challenging. There are some studies that propose tricks like patch-GANs (Zhu et al., 2017), in which the discriminator only sees a small patch of input image, or progressive GAN (Karras et al., 2017), in which the generator network is expanded by adding layers during training and the size of generated images is increased as a result. However, we cannot use these tricks, since they are developed for the image data with spatial structure. In order to tackle this issue, we develop the idea of multiplying a binary mask to the inputs of discriminator network. The mask is constructed using the random Bernoulli distribution with probability p_mask, having 0 and 1 elements. We start training using the mask with the high probability (i.e. having more zero elements) to only show the small portion of genes to the discriminator, and then progressively decrease the probability to finally show all the genes to the discriminator at the end of training process. The empirical approximation of the adversarial loss with the incorporated mask has the following form:

$${\mathcal{L}}_{adv}=\frac{1}{n}{\displaystyle \sum _{i=1}^n\log }(D(x_i,y_i{m}_i))+\log (1-D(x_i,G(x_i)m_i)),$$ (4)

where $m_i$ represents the mask. Note that the mask only applies to the target genes in order to simplify the generation task. Also, the masks for $(x_i,y_i)$ and $(x_i,G(x_i))$ in each training step are same in order to show same set of target genes to the discriminator. Besides, we scale up the values of target genes by multiplying by 1∕p_mask during training to keep the output activation intact. This mask not only increases the difficulty level of generation task progressively and stabilize the adversarial learning, but also considers the target genes conditionally independent.

The ℓ₁-norm and consistency loss functions can be also approximated by the following empirical losses.

$${\mathcal{L}}_1=\frac{1}{n}{\displaystyle \sum _{i=1}^n|}|y_i-G(x_i)|{|}_1$$ (5)

$${\mathcal{L}}_{cons}=\frac{1}{n}{\displaystyle \sum _{i=1}^n\left|\right|}G(x\hspace{0.17em}\oplus \hspace{0.17em}u)-G(x\hspace{0.17em}\oplus \hspace{0.17em}u\prime )|{|}^2.$$ (6)

Combining the three loss terms in Equations (4), (5) and (6), we define the joint loss for training the generator network as

$${\mathcal{L}}_{tot}={\mathcal{L}}_1+{\lambda }_{adv}{\mathcal{L}}_{adv}+{\lambda }_{cons}{\mathcal{L}}_{cons}$$ (7)

where λ_adv and λ_cons are the hyper-parameters to balance the role of different loss terms.

To update the parameters in generator G and discriminator D, we adopt gradient-based optimization, which is the most popular method for optimizing neural networks. The stochastic gradient descent (SGD) methods are efficient in calculating the gradient yet introduce high variance in parameter updating thus leads to heavy fluctuation in the objective function. To handle this problem, mini-batch SGD methods propose to update the parameter θ w.r.t. each mini-batch ${\Omega }_m={\{(x_{t_i},y_{t_i})\}}_{i=1}^{n_t}$ given a general cost function $\text{J}(\theta ;\Omega )$ as follows:

$$\theta =\theta -\alpha {\text{▽}}_{\theta }\text{J}(\theta ;{\Omega }_t)$$

where $\Omega ={\displaystyle \underset{t=1}{\overset{T}{\cup }}{\Omega }_t}$ and any two mini-batches are disjoint.

In our gene expression inference problem, we adopt a variant of mini-batch SGD methods to update the parameters in generator G and discriminator D for an efficient and stable update. We summarize the optimization steps in Algorithm 1.

Algorithm 1 Optimization of GGAN via mini-batch SGD method.

Input: Input gene expression profile $\Omega ={\{(x_i,y_i)\}}_{i=1}^n$, where ${\left\{x_i\right\}}_{i=1}^n$ denotes n landmark gene expression profiles, and ${\left\{y_i\right\}}_{i=1}^n$ corresponds to target genes. Hyper-parameter λ_adv and λ_cons.

Output: Generator function G and discriminator function D.

1. Initialize parameters θ_D for D and parameters θ_G for G

2. for number of training iterations do

3.  fort = 1,…, T do

4.   randomly choose mini-batch ${\Omega }_t\subset \{1,\dots ,n\}$ of size b

5.   Update D by ascending along its stochastic gradient:

$${\text{▽}}_{{\theta }_D}{\mathcal{L}}_{adv}(D;{\Omega }_t).$$

• 6.   Update G by descending along its stochastic gradient:

$${\text{▽}}_{{\theta }_G}{\mathcal{L}}_{tot}(G;{\Omega }_t).$$

• 7.  end for

• 8. end for

4 Experimental results

In this section, we apply our model to gene expression data from three different projects, i.e. GEO, GTEx and 1000 Genomes (1000 G). The goal is to correctly predict the expression value of target genes based on the expression of landmark genes. In the meantime, we propose to interpret the role of each landmark gene in the inference of target gene expression, which may provide insights into the information captured by the landmark genes as well as the correlation between different genes.

4.1 Experimental setup

4.1.1 Datasets

We download three different publicly available datasets from https://cbcl.ics.uci.edu/public_data/D-GEX/ for this analysis, which includes: the microarray-based GEO dataset, the RNA-Seq-based GTEx dataset data and the 1000 G RNA-Seq expression data.

The original GEO dataset consists of 129 158 gene expression profiles corresponding to 22 268 probes (978 landmark genes and 21 290 target genes) that are collected from the Affymetrix microarray platform. The original GTEx dataset is composed of 2921 profiles from the Illumina RNA-Seq platform in the format of Reads Per Kilobase per Million (RPKM). While the original 1000 G dataset includes 2921 profiles from the Illumina RNA-Seq platform in the format of RPKM.

We follow the pre-processing protocol in (Chen et al., 2016) for duplicate samples removal, joint quantile normalization and cross-platform data matching. Among the 22 268 genes in the GEO data, there are 10 463 genes having corresponding Gencode annotations in RNA-Seq. In the joint quantile normalization, we map the expression values in the GTEx and 1000 G datasets according to the quantile computed in the GEO data. The expression value has been quantile normalized to the range between 4.11 and 14.97. Finally, the expression value of each gene has been normalized to zero mean and unit-variance. After pre-processing, there are a total of 111 009 profiles in the GEO dataset, 2921 profiles in the GTEx dataset while 462 profiles in the 1000 G dataset. All the profiles correspond to 10 463 genes (943 landmark genes and 9520 target genes).

4.1.2 Baseline methods

In the LINCS program, the gene expression inference is based on the linear regression model:

$$\underset{W,b}{\text{min}}{\displaystyle \sum _{i=1}^n|}|W^T{x}_i+b-y_i|{|}^2$$ (8)

where W is the weight matrix in the regression model. Thus, we include the least square regression (LSR) (8) model in the comparison as the baseline method. We also include two other linear models, which are LSR with ℓ₂-norm regularization (LSR-L2):

$$\underset{W,b}{\text{min}}{\displaystyle \sum _{i=1}^n|}|W^T{x}_i+b-y_i|{|}^2+\lambda \left|\right|W|{|}_F^2$$ (9)

and LSR with ℓ₁-norm regularization (LSR-L1):

$$\underset{W,b}{\text{min}}{\displaystyle \sum _{i=1}^n|}|W^T{x}_i+b-y_i|{|}^2+\lambda \left|\right|W|{|}_1.$$ (10)

The introduction of regularization term in (9) and (10) reduces overfitting of LSR model. We also compare with the k nearest neighbor (KNN) method for regression, where the prediction of a given profile is formulated as the average of its k nearest profiles. Moreover, we compare with a deep learning method for gene expression inference (D-GEX) (Chen et al., 2016) to validate the performance of our GGAN model. The D-GEX model use a multi-task multi-layer fully connected neural network for regression. To the best of our knowledge, D-GEX is the only model that applies deep learning methods to the gene expression inference problem.

4.1.3 Evaluation metrics

The evaluation of the comparing methods is based on two different metrics, which are mean absolute error (MAE) and concordance correlation (CC). Given a set of input data ${\{x_i,y_i\}}_{i=1}^n$, we denote the predicted expression set as ${\left\{{\widehat{\mathbf{y}}}_i\right\}}_{i=1}^n$. The definition of MAE is:

$$MA{E}_j=\frac{1}{n\prime }{\displaystyle \sum _{i=1}^{n\prime }|}{\widehat{y}}_{ij}-y_{ij}|,$$ (11)

where MAE_j indicates the MAE for the j-th target gene, and $n\prime$ is the number of test samples.

The following equation shows the definition of CC:

$$C{C}_j=\frac{2\rho {\sigma }_{y_j}{\sigma }_{{\widehat{\mathbf{y}}}_j}}{{\sigma }_{y_j}^2+{\sigma }_{{\widehat{\mathbf{y}}}_j}^2+{({\mu }_{y_j}-{\mu }_{{\widehat{\mathbf{y}}}_j})}^2},$$ (12)

where CC_j indicates the CC for the j-th target gene, ρ is the Pearson correlation and ${\sigma }_{y_j},{\sigma }_{{\widehat{\mathbf{y}}}_j}$ and ${\mu }_{y_j},{\mu }_{{\widehat{\mathbf{y}}}_j}$ are the mean and standard deviation of $y_j$ and ${\widehat{\mathbf{y}}}_j$ respectively.

Following the experimental protocol in (Chen et al., 2016), we evaluate the methods under two different circumstances. Firstly, we use 80% of the GEO data for training, 10% of the GEO data for validation while the other 10% of the GEO data for testing. Secondly, we use the same 80% of the GEO data for training, the 1000 G data for validation while the GTEx data for testing. In the second scenario, the training, validation and testing comes from different platforms, which is designed to validate if comparing methods are capable of conducting regression models suitable for cross-platform prediction. We use the training data to construct the regression model, validation data for model selection and parameter setting, while the testing data to conduct the evaluation. For each method, we report the overall performance on the testing data. Since we adopt exactly the same setup of the data as in (Chen et al., 2016), for the comparing method D-GEX we directly report the results in the paper (Chen et al., 2016). Moreover, as the CC value is not reported in the original paper of D-GEX, we rerun their released code (https://github.com/uci-cbcl/D-GEX) to get the CC value for comparison in Tables 1 and 3. For D-GEX, we report its best results w.r.t. MAE among different setting of hidden layers and hidden units.

Table 1.

MAE and CC comparison of different methods in the prediction of GEO data

Methods	MAE	CC
LSR	0.3763 ± 0.0844	0.8227 ± 0.0956
LSR-L1	0.3756 ± 0.0841	0.8221 ± 0.0960
LSR-L2	0.3758 ± 0.0842	0.8223 ± 0.0959
KNN-GE	0.5866 ± 0.0698	0.5721 ± 0.3415
D-GEX	0.3204 ± 0.0879${}^{\text{⋆}}$ / 0.3196 ± 0.0877	− / 0.8690 ± 0.0899
GGAN	0.2897 ± 0.0890	0.8785 ± 0.0894

Note: The results of D-GEX is based on a network with three hidden layers and 9000 hidden units in each layer (best structure reported). The results of GGAN is based on the DenseNet architecture. The results of the comparing models are obtained by us running the released codes, except the one marked by ($\text{⋆}$) on top that is reported from the original paper. Better results correspond to lower MAE value or higher CC value.

Table 3.

MAE and CC comparison of different methods in the prediction of GTEx data

Methods	MAE	CC
LSR	0.4704 ± 0.1235	0.7184 ± 0.2072
LSR-L1	0.5669 ± 0.1274	0.6813 ± 0.2188
LSR-L2	0.4682 ± 0.1233	0.7181 ± 0.2076
KNN-GE	0.6520 ± 0.0982	0.3941 ± 0.4124
D-GEX	0.4393 ± 0.1239${}^{\text{⋆}}$ / 0.4380 ± 0.1237	− / 0.7337 ± 0.2072
GGAN	0.4215 ± 0.1264	0.7475 ± 0.2070

Note: The results of D-GEX is based on a network with two hidden layers and 9000 hidden nodes in each layer (best structure reported). The results of GGAN is based on the DenseNet architecture. The results of the comparing models are obtained by us running the released codes, except the one marked by ($\text{⋆}$) on top that is reported from the original paper. Better results correspond to lower MAE value or higher CC value

4.1.4 Implementation details

We use similar architecture for the both datasets, train the networks only using the training sets, tune the hyper-parameters via the validation sets, and report the results on the test sets. For the generator network, we employ a DenseNet (Huang et al., 2017) architecture with three hidden layers, each one containing 9000 hidden units. For the discriminator, we use a fully connected network with one hidden layer including 3000 hidden units. We consider LReLU (Maas et al., 2013) with leakiness ratio 0.2 as the activation function of all layers except the last layer of generator network, which has linear function due to the mean-zero and unit-variance data normalization. Moreover, we set the maximum and minimum learning rates to 5 × 10^–4 and 1 × 10^–5, respectively, and linearly decrease it during training with the maximum epoch 500. Adam algorithm (Kingma and Ba, 2014) is adopted as our optimization method with the default hyper-parameters ${\beta }_1=0.9,{\beta }_2=0.999,\text{\hspace{0.17em}ε}=1e-08$. The batch size is set to 200. We also utilize weight normalization (Salimans and Kingma, 2016) as layer normalization to speed up the convergence of training process. The parameters of all layers are all initialized by Xavier approach (Glorot and Bengio, 2010). We also select dropout, λ_cons, and λ_adv from $dropou{t}^{set}=\{0.05,0.1,0.25\},{\lambda }_{cons}^{set}=\{1,10,50\}$, and ${\lambda }_{adv}^{set}=\{0.1,1,5\}$, respectively. We use Theano toolbox for writing our code, and run the algorithm in a machine with one Titan X pascal GPU.

Furthermore, we replace the original adversarial loss in the GAN models with the least-squares loss in (Mao et al., 2017). We find that this loss leads to more stable training of our model, and paralytically provides better experimental results. In particular, we optimize the generator and discriminator parameters with the following least square loss instead of the sigmoid cross entropy loss function in Equation (4).

$$\begin{array}{c}{\mathcal{L}}_{adv}(D;\Omega )=\frac{1}{2}{\displaystyle \sum _{i=1}^n[}D(x_i,y_i{m}_i)-1{]}^2+{[D(x_i,G(x_i)m_i)]}^2\\ {\mathcal{L}}_{adv}(G;\Omega )={\displaystyle \sum _{i=1}^n[}D(x_i,G(x_i)m_i)-1{]}^2.\end{array}$$ (13)

4.2 Prediction of GEO data

We first present the comparison results on the GEO data in Table 1. The results for GGAN model are obtained from the DenseNet architecture. We can observe apparent improvement of our model over other methods. First of all, deep learning models (D-GEX and GGAN) always performs better than linear models (LSR, LSR-L1 and LSR-L2), which indicates the superiority of deep models in interpreting the non-linear association between different genes. Moreover, we can notice that GGAN model gains significantly better performance than D-GEX, which validates the success of applying the adversarial mechanism in the gene expression inference problem. Compared with D-GEX with MSE loss, our model considers both adversarial loss and ℓ₁-norm loss, thus make more sharp and realistic prediction results.

To show that the major superiority of GGAN over D-GEX comes from the adversarial mechanism in our model design, we further compare D-GEX and GGAN with exactly the same structure (both models use fully connected network with varying number of hidden units and hidden layers). We present the comparison results in Table 2 and we can find GGAN consistently outperforms D-GEX regardless the setting of hidden layers and hidden units. This observation further validates that the use of adversarial loss and ℓ₁-norm loss in GGAN model overcomes the blurry and smooth prediction from D-GEX and make better inference for target genes.

Table 2.

MAE comparison between D-GEX and GGAN model in the prediction of GEO data when varying the number of hidden layers and number of hidden units in each layer

	# Hidden layers
Methods	3000	6000	9000
D-GEX	0.3421 ± 0.0858	0.3337 ± 0.0869	0.3300 ± 0.0874	1	#Hidden layers
	0.3377 ± 0.0854	0.3280 ± 0.0869	0.3224 ± 0.0879	2
	0.3362 ± 0.0850	0.3252 ± 0.0868	0.3204 ± 0.0879	3
GGAN	0.3265 ± 0.0854	0.3165 ± 0.0869	0.3088 ± 0.0862	1
	0.3164 ± 0.0854	0.3037 ± 0.0869	0.2982 ± 0.0868	2
	0.3126 ± 0.0850	0.3015 ± 0.0867	0.2965 ± 0.0868	3

Note: Both models are constructed with the same fully connected neural network structure.

4.3 Prediction of GTEx data

Furthermore, we present the results for the cross-platform prediction, where we use GEO data for training, 1000 G data for validation while GTEx data for testing. We summarize the comparison results in Tables 3 and 4. Our model still gains significant advantage over the comparing methods, which indicates that our GGAN model is capable of capturing the cross-platform information, such that the model constructed on the GEO data predict well for the inference of GTEx data.

Table 4.

MAE comparison between D-GEX and GGAN model in the prediction of GTEx data when varying the number of hidden layers and number of hidden units in each layer

	# Hidden layers
Methods	3000	6000	9000
D-GEX	0.4507 ± 0.1231	0.4428 ± 0.1246	0.4394 ± 0.1253	1	# Hidden layers
	0.4586 ± 0.1194	0.4446 ± 0.1226	0.4393 ± 0.1239	2
	0.5160 ± 0.1157	0.4595 ± 0.1186	0.4492 ± 0.1211	3
GGAN	0.4373 ± 0.1238	0.4351 ± 0.1240	0.4305 ± 0.1245	1
	0.4412 ± 0.1240	0.4323 ± 0.1238	0.4296 ± 0.1241	2
	0.4311 ± 0.1240	0.4294 ± 0.1234	0.4290 ± 0.1240	3

Note: Both models are constructed with the same fully connected neural network structure.

4.4 Visualization

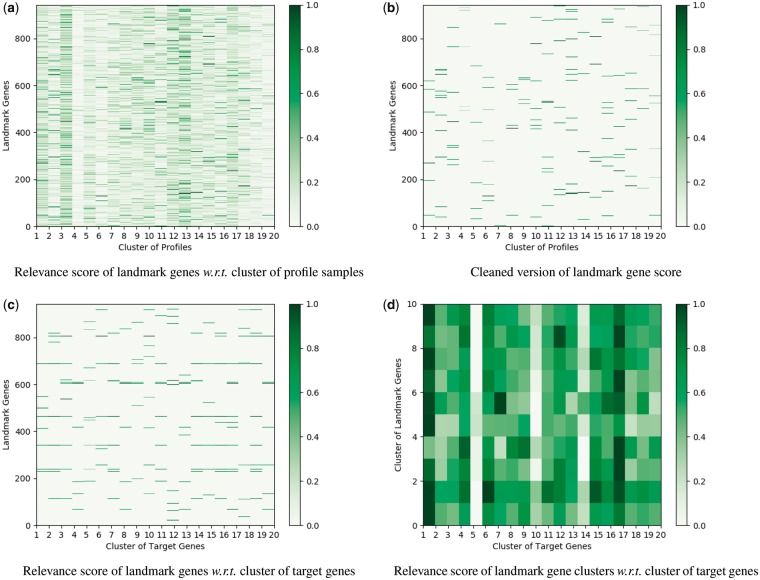
In this subsection, we plot several visualization figures to show the role of different landmark genes in the gene expression inference problem. We adopt the layer-wise relevance propagation (LRP) (Bach et al., 2015) method to calculate the importance of landmark genes. In Figure 2, we look into the results from the fully connected networks (structure for results in Table 2 on the GEO data). Firstly, we divide the gene expression profiles into 20 clusters and then use LRP to calculate the relevance score of landmark genes w.r.t. each profile cluster. Figure 2a and b indicate that the landmark gene expression patterns for various profile groups are different, which replicates the findings in previous cancer subtype discovery and cancer landscape study that different group of samples usually exhibit different expression patterns (Kandoth et al., 2013; Speicher and Pfeifer, 2015). Next, we analyze the relationship between landmark genes and target genes. We cluster the target genes into 20 groups and calculate the overall relevance score of landmark genes in the prediction of each target gene cluster. For a clear visualization, we group the landmark genes into 10 clusters and display the association between landmark gene clusters and target gene clusters in Figure 2d. We can notice apparent difference in the relevance patterns for different target gene clusters, yet some similarity among certain clusters, e.g. cluster (column) 5, 10 and 14. Cluster 5, 10 and 14 show consistent lower relevance value with the landmark genes, while cluster 14 shows higher correlation with the sixth landmark gene cluster than others. This finding has also been validated by previous gene cluster analysis (Medema et al., 2015), where gene cluster information is related to the structure of biosynthetic pathways and metabolites.

Fig. 2.

Illustration of the importance of different landmark genes calculated by fully connected network for the inference of GEO data. (a) The gene expression profiles are divided into 20 clusters using K-means method. The contribution of each landmark gene to different profile clusters is plotted. (b) For each profile cluster, we only show the weights of the top 20 landmark genes with the largest contribution for a clear visualization. (c) The 9520 target genes are grouped into 20 clusters via K-means method. The contribution of each landmark gene to the prediction of different target gene clusters is plotted. (d) The landmark genes in Figure (c) are clustered into 10 groups. The contribution of each landmark gene cluster to the prediction of different target gene clusters is plotted

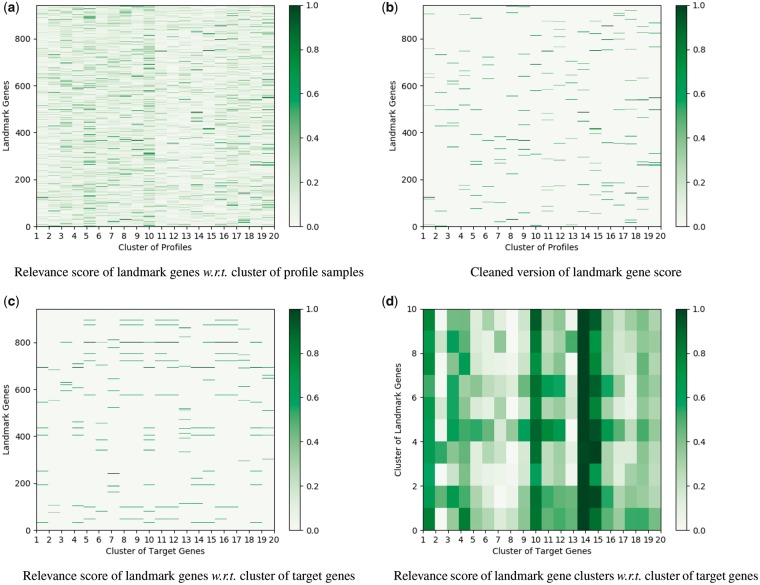
Moreover, we plot the illustration results on the prediction of GTEx data in Figure 3 and find similar result as in GEO data. It is notable that our model for the prediction of GTEx data is training on the GEO data, which validates that our model is able to appropriately capture the relation among genes for the cross-platform prediction.

Fig. 3.

Illustration of the relevance score of different landmark genes calculated by the DenseNet architecture for the inference of GTEx data. (a) The gene expression profiles are divided into 20 clusters using K-means method. The contribution of each landmark gene to different profile clusters is plotted. (b) For each profile cluster, we only show the weights of the top 20 landmark genes with the largest contribution for a clear visualization. (c) The 9520 target genes are grouped into 20 clusters via K-means method. The contribution of each landmark gene to the prediction of different target gene clusters is plotted. (d) The landmark genes in Figure (c) are clustered into 10 groups. The contribution of each landmark gene cluster to the prediction of different target gene clusters is plotted

5 Conclusion

In this paper, we proposed a novel conditional generative model for gene expression inference. Compared with previous deep learning models considering minimum squared error loss that render blurry results, our model employed the coupled adversarial loss and ℓ₁-norm loss to make the regression results sharp and realistic. We validated our model on the inference of two different datasets, GEO and GTEx, and found consistent and significant improvements over all the counterparts. Moreover, we looked into the role of landmark genes in the prediction and identified different relevance pattern, which provided insights into the relations among gene regulatory networks. In the future, we will investigate how to incorporate the profiles with only landmark gene measurement available using semi-supervised framework. Also, it would be interesting to employ the cluster structure among profile samples in the prediction to strengthen the inference of target gene expression.