Understanding the evolution of functional redundancy in metabolic networks

Abstract

Motivation

Metabolic networks have evolved to reduce the disruption of key metabolic pathways by the establishment of redundant genes/reactions. Synthetic lethals in metabolic networks provide a window to study these functional redundancies. While synthetic lethals have been previously studied in different organisms, there has been no study on how the synthetic lethals are shaped during adaptation/evolution.

Results

To understand the adaptive functional redundancies that exist in metabolic networks, we here explore a vast space of ‘random’ metabolic networks evolved on a glucose environment. We examine essential and synthetic lethal reactions in these random metabolic networks, evaluating over 39 billion phenotypes using an efficient algorithm previously developed in our lab, Fast-SL. We establish that nature tends to harbour higher levels of functional redundancies compared with random networks. We then examined the propensity for different reactions to compensate for one another and show that certain key metabolic reactions that are necessary for growth in a particular growth medium show much higher redundancies, and can partner with hundreds of different reactions across the metabolic networks that we studied. We also observe that certain redundancies are unique to environments while some others are observed in all environments. Interestingly, we observe that even very diverse reactions, such as those belonging to distant pathways, show synthetic lethality, illustrating the distributed nature of robustness in metabolism. Our study paves the way for understanding the evolution of redundancy in metabolic networks, and sheds light on the varied compensation mechanisms that serve to enhance robustness.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Biological systems are highly robust against perturbations, which includes loss of gene function (Wagner, 2005). Robustness against null mutations in living systems is carried out by many different mechanisms, one of them being redundancy (Hartman et al., 2001). Redundant genes or functionally redundant pathways tend to cope up for any perturbations in the system. Although there exist a few genes that are indispensable to the survival of the organism, duplicate genes are often retained during evolution in order to combat mutations (Papp et al., 2004). Some genes might be inactive in certain environmental conditions but become active in a different condition to compensate. Even though duplicate genes exist, some alternate metabolic pathways also play a role in establishing robustness (Mahadevan and Lovley, 2008). These perform distinct functional roles and are not redundant in all environmental conditions (Harrison et al., 2007; Ihmels et al., 2004). Adaptation also facilitates the addition of new functional associations, which do not arise to overcome mutational effects per se but are evolutionary by-products and later enable robustness against deleterious mutations (Pál et al., 2005; Wang and Zhang, 2010).

Metabolism forms the core of all cellular processes, building up components required for the growth and survival of organisms. Metabolic networks play a key role in synthesizing components necessary for growth from the nutrients available to the organism. Perturbations to key enzymatic pathways often abolish growth, thus causing lethality. A comprehensive understanding of the metabolic reactions in an organism establishes that some fraction of the reaction functions/pathways is redundant, to enable robustness against single mutations (Wang and Zhang, 2009). Metabolic networks are highly robust against perturbations and utilize the backup reactions/pathways that exist to compensate any lethal damage to the organism (Behre et al., 2008).

Synthetic lethality refers to functional associations that exist between genes/reactions that compensate for one another upon single gene deletions (Hartman et al., 2001). Synthetic lethals refer to a pair of reactions that perform distinct functionalities although they enable organisms to combat lethal perturbations in the system. A synthetic double lethal (DL), therefore, consists of a pair of reactions, which when deleted individually enable the organism to survive, but when deleted together results in lethality. Synthetic DLs enable an organism to survive single mutations/knock-outs, thus enhancing the robustness of the metabolic networks. In a majority of the cases, one reaction involves in a key metabolic pathway and upon deletion of the reaction, fluxes are re-routed through the lethal pair to enable the growth of the organism (Ghim et al., 2005; Güell et al., 2014). Synthetic lethals play an important role in providing backup functions, thus, helps the organism sustain perturbations. Experimental identification of these synthetic lethals through high-throughput techniques is still difficult (Kaelin Jr, 2005). Therefore, many computational methods, based on flux balance analysis (FBA) (Varma and Palsson, 1994; Kauffman et al., 2003), have been developed in the past, viz. SL Finder (Suthers et al., 2009), MCSEnumerator (von Kamp and Klamt, 2014) and Fast-SL (Pratapa et al., 2015). Of these, Fast-SL, developed previously in our laboratory, provides a very efficient way to predict synthetic lethals in a large number of networks, under different growth conditions.

With the above perspective, we aimed to address some of the key questions: How do metabolic networks evolve to acquire new functional redundancies? How do reactions compensate for one another under perturbation? Do the redundancies vary based on the environmental conditions? Does evolution retain native functional redundancies? We build on a previously reported methodology to evolve metabolic networks in silico (Barve and Wagner, 2013) to answer these questions. We generated 2000 metabolic networks in minimal glucose environment and identified single lethals and DLs in these random metabolic networks. We show that across networks, many reactions compensate for one another under various environmental conditions. We observed that key functional reactions evolve to acquire new redundancies and that they tend to partner with a higher number of reactions. We also noticed that real networks possess a significantly higher number of essential reactions and redundant reactions when compared with random networks. We further found that reactions which play very different functional roles can form redundancies in different environmental conditions. Our results also suggest that some of the functional redundancies are environment specific and some compensate for one another in all environmental conditions. Overall, our approach builds towards a much better understanding of the evolution of functional redundancies in metabolism.

2 Methods

2.1 Universe of possible reactions

The ‘universe’ of possible reactions is the set of all the biochemical reactions that are known to occur in organisms. The reaction universe was adapted from a previously described, pruned dataset from Szappanos et al. (2016), which is based on the ModelSEED database (Henry et al., 2010). This universal set of reactions consists of 5162 reactions, including exchange and transport reactions, comprising 2805 metabolites.

2.2 Flux balance analysis

The cornerstone of our analyses is the ability to predict the growth phenotype of any given metabolic network. For this, we employ FBA, which is a widely used constraint-based approach to identify an optimized flux distribution, for a given metabolic network, based on maximizing/minimizing a given (linear) objective function (Varma and Palsson, 1994; Kauffman et al., 2003). FBA solves a linear programming problem to identify a flux distribution, assuming that the network is in steady state. The formulation of FBA is as below:

$$\max \hspace{1em}{\mathbf{c}}^T\mathbf{v}\hspace{1em}s.t.\hspace{1em}\mathbf{S}\mathbf{v}=0$$ (1)

where c denotes the objective function, v is the vector of fluxes of all the biochemical reactions and S corresponds to the stoichiometric matrix, of dimensions m × r that encodes the stoichiometry of all m metabolites in r reactions present in the network. FBA is a reliable method to predict the growth rate of organisms in many conditions (Blank et al., 2005; Papp et al., 2004; Harrison et al., 2007; Szappanos et al., 2016) and has been previously used for studying metabolic network robustness and plasticity (Barve et al., 2012; Almaas et al., 2005; Barve and Wagner, 2013; Güell et al., 2014).

2.3 Generation of random networks

Random networks were generated using a modification of the previously devised method developed by Barve and Wagner (2013). The method uses a Markov-chain Monte Carlo (MCMC) approach to swap a random reaction from a known genome-scale metabolic network with a randomly selected reaction from the universe. At each random swap, an FBA was performed to evaluate the growth of the generated network on a given carbon source. The threshold for identifying growth on a particular carbon source was set to 5% of the wild-type flux, i.e. the biomass flux of E.coli in that particular carbon source. We generated 2000 such random networks starting from the E.coli iAF1260 metabolic network (1983 reactions + 303 exchange reactions), with each random network produced as a result of 5000 such reaction swaps. For each of the random networks, a genotype vector was obtained, which denotes the presence/absence of reactions from the universe. Each of our random networks includes all 553 exchange reactions from the universe, resulting in metabolic networks each having 2536 reactions.

2.4 Growth in different environments

We analysed synthetic lethals and the growth capabilities of the metabolic networks in a set of ten environments, a subset of the fifty environments reported earlier (Barve and Wagner, 2013). These are minimal growth environments that contain oxygen, ammonium, inorganic phosphate, sulphate, sodium, potassium, cobalt, iron, protons, water, molybdate, copper, calcium, chloride, magnesium, manganese and zinc along with a sole carbon source that differs for each environment considered. We considered the 10 different carbon sources based on their biochemical diversity; these included pyruvate (Pyr), D-glucose (Glu), acetate (Ace), D-fructose (Fru), D-galactose (Gal), D-xylose (Xyl), lactose (Lac), inosine (Ino), D-sorbitol (Sor), trehalose (Tre). The random networks generated were analysed for growth in each of the above ten environments using FBA, and a phenotype vector (of length 10) was formed for each of the random networks. The phenotype vector is a bit vector indicating the growth (‘1’)/no growth (‘0’) phenotype of each of the random networks in the ten different environments considered.

2.5 Identification of synthetic lethals

Synthetic lethals in the metabolic networks were identified using Fast-SL (Pratapa et al., 2015). Fast-SL rapidly and efficiently identifies synthetic lethals by pruning the search space followed by a subsequent exhaustive enumeration of all possible combinations in the pruned space. This enables us to perform synthetic lethality studies at a scale not possible before. Overall, we studied synthetic lethals by efficiently evaluating all possible double deletion phenotypes for 2000 metabolic networks in ten different environments $\left(\left(\begin{array}{c}1983\\ 2\end{array}\right)\times 2000\times 10\approx 39\text{billiondoubledeletions}\right)$ using Fast-SL, identifying hundreds of thousands of synthetic lethals. For the purposes of simulation, we defined lethality as the inability to produce 1% of wild-type growth rate (biomass flux).

3 Results

We evolved metabolic networks starting from E.coli iAF1260 and performed exhaustive analyses of the single and DLs in the evolved networks. We analysed how the redundancies are comparable with the E.coli network and how they differ in various environmental conditions. Further, we study how different reactions can form functional redundancies. We also compare the lethals in the universe set of reactions with those in the random networks.

3.1 E.coli harbours a higher level of redundancy compared with random networks

Identification of lethals in random networks establishes the essentiality of reactions for the growth of organisms in particular growth conditions. Identification of reactions that can form DL sets in random networks helps to identify the different possible compensation mechanisms that can occur. In order to figure out the possible single lethals and DL pairs that could exist in metabolic networks, we generated 2000 random networks with a constraint for growth on glucose. For each of the 2000 random networks, single lethals and DLs were identified using Fast-SL (as described in Section 2).

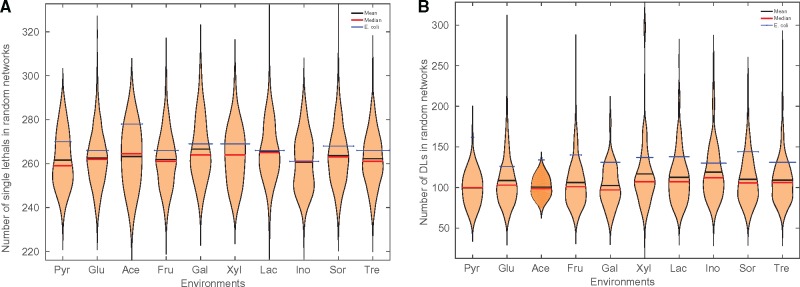
Single and synthetic DL reactions were identified in all 10 environments (Fig. 1). In glucose, the essential reactions in random networks varied from 229 to 319. The mean number of single lethals that existed in random networks was 262, as against 266 lethals in E.coli iAF1260. Around 20% of the random networks had single lethals between 260 and 265. The E.coli iAF1260 model contains essential reactions significantly higher than the mean (and median) of the essential reactions that existed in random networks. Figure 1A also shows the distribution of single lethals for all the environments in random networks.

Fig. 1.

Violin plots showing the distribution of (A) single lethals and (B) double lethals, in random networks across 10 different environments. The ‘violins’ illustrate the distribution of the lethals in each of the environments. The black band denotes the mean number of lethals in random networks, and the red band denotes the median. The number of lethals in the E.coli model iAF1260 is indicated by a blue band

We also analysed the synthetic DLs in random networks and E.coli (Fig. 1B). As an illustration, in glucose environment, observations of DLs in random networks showed that there exist networks which have as low as 48 synthetic DLs. Also, the maximum number of DLs that we observed in a random network was 294 (in glucose environment). The mean number of DLs that were identified in the 2000 random networks was 108. Around 17% of the networks had DLs between 90 and 100. However, the real network, E.coli iAF1260, contains 126 DLs, higher than the average number of DLs in random networks. Figure 1B shows the distribution of the DLs found in all the environments compared with those in E.coli.

Also, the fraction of networks that have single lethals and DLs less than the real network was computed as in Table 1. The results show that, in almost all environments, the fraction is greater than 0.5. This suggests that real networks possess a significantly higher fraction of essential reactions and compensation mechanisms than random networks.

Table 1.

Fraction of random networks with lesser lethals than E.coli in 10 different environments

Growth environments	Pyr	Glu	Ace	Fru	Gal	Xyl	Lac	Ino	Sor	Tre
Fraction of random networks having fewer single lethals than E.coli	0.676	0.619	1.000	0.632	0.633	0.627	0.558	0.495	0.635	0.602
Fraction of random networks having fewer double lethals than E.coli	0.985	0.775	1.000	0.879	0.915	0.779	0.817	0.684	0.867	0.832

To find if the real networks had a higher level of redundancy when compared with random networks, we performed the sign test to compare the number of lethals in E.coli with those that are present in random networks. We found that in the case of single lethals, eight environments had a P-value < 0.05 (Supplementary Table S1), indicating that the number of essential reactions in E.coli is significantly higher than that in random networks, with exceptions in the environments acetate and inosine. As in the case of DLs, the sign test resulted in a P-value < 0.01 (Supplementary Table S1) for nine environments, signifying that the real network has more number of redundant reactions when compared with random networks with the exception being that of lethals in acetate environment. Acetate is an outlier since we could identify only four networks that could show growth out of the 2000 random networks generated on glucose environment.

We further went ahead to identify how many of the DLs in E.coli exist in random networks. Multiple scenarios are possible: first, the DL may exist as is in the random network. In this case, there is no different compensation mechanism that is present (additionally). Second, one of the reactions in the DL may now be singly lethal, owing to the loss of the partner that could compensate. Third, the DL may not show up at all, since there is probably a higher level of redundancy (e.g. a third compensating reaction) that is now present in the network. Here, we investigated for each of the DLs in E.coli, in which networks are the lethals present together in random networks and if present, are they are found as synthetic lethals. Of the lethals that were present together in random networks, 68% of the lethals existed in random networks. The remaining 32% of the DLs were not found as DLs in the random networks, thus could have been compensated by another reaction forming a higher order lethal.

Thus, real networks harbour higher redundancies in comparison with random networks, demonstrating the fact that the real networks are not minimal networks, but evolved to be robust, preserving redundant functions.

3.2 Reactions possess very different functional redundancies

An interesting aspect of identifying synthetic lethals in random networks is that we can find (nearly) all possible functionally redundant reactions that could exist in metabolic networks. Understanding the functional redundancies gives insight into the multiple ways organisms exhibit robustness against perturbations. Thus, we aimed to illustrate the existence of multiple synthetic lethal interactions other than those that are known to exist in nature till date. Through our extensive analysis of DLs in random networks, we are able to illustrate a gamut of possible compensations that can potentially occur in metabolic networks. We show how a single reaction can ‘partner’ with a very large number of different reactions, compensating for single reaction deletions.

We analysed the DLs of the networks that were evolved on glucose, for such partners. Of the 4609 reactions in the universe (excluding the exchange reactions), only 2306 reactions had potential pairs with other reactions. We define a metric for the number of partners that exist for a given reaction as ‘Reaction Compensation Index’ (RCI). Thus, the RCI for a reaction is the number of partners that this reaction can form a synthetic DL. For instance, an RCI of 200 indicates that the reaction has 200 different partners in DLs, across the 2000 random networks that we sampled. We identified the RCI for all the 2306 reactions; Figure 2 shows the histogram of RCI for all reactions. We find that 82 reactions have an RCI $\ge$ 100, 12 of which have an RCI exceeding 200. We also observed that there are 1032 reactions with RCI $\le$ 10. The reaction with the maximum RCI was found to be the formation of ATP from ADP as below:

$$\begin{array}{c}AD{P}_c+Phosphat{e}_c+4H_p^{+}\iff AT{P}_c+H_2{O}_c+3H_c^{+}\\ (c-cytosol;p-periplasm)\end{array}$$

Fig. 2.

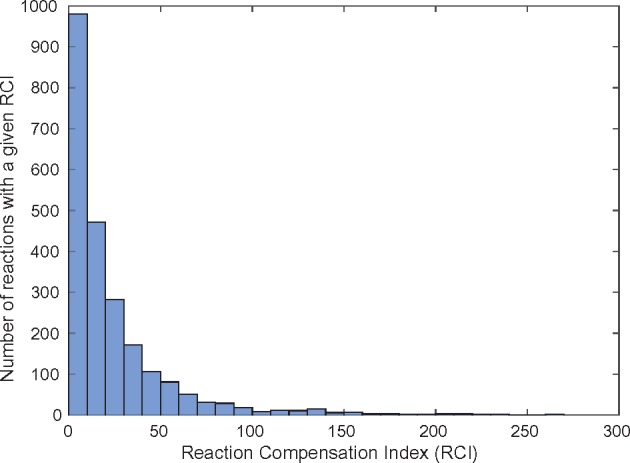
Reaction compensation index of all reactions in glucose environment. The histogram denotes the distribution of the RCI values of reactions in the random networks

The above reaction for the formation of ATP, the key energy currency of the cell, from ADP is a reaction that is absolutely necessary for the organism. This reaction is catalysed by ATP synthase, a key enzyme necessary for organisms to synthesize the energy storage molecule of cells.

Further, we analysed the reactions that compensated for ATP synthase. Of the 266 reactions, 35 reactions involved ATP (Supplementary Table S2B), remaining does not involve ATP (Supplementary Table S2A). When identifying the pathways these compensatory reactions were present in, we found that most of the reactions that compensate for ATP synthase belong to the alternate carbon metabolism, glycolysis/gluconeogenesis, and nucleotide salvage pathway. The reactions that compensated predominantly involve pathways whose end products can in a way be converted to ATP.

Further, we analysed the reactions which had RCI of greater than 200 (Supplementary Table S3). Of these reactions, most of them belonged to the central carbon metabolism, and few to the folate metabolism, methylglyoxal metabolism, and anaplerotic reactions. A closer study of these reactions revealed that glyceraldehyde-3-phosphate production produced in two different reactions one from fructose-6-phosphate and the other from fructose-1, 6-bisphosphate were among the twelve reactions with top RCI. The isomerization of glucose-6-phosphate to fructose-6-phosphate was one among the twelve reactions that had higher compensation mechanisms. Also, the reaction from the citric acid cycle that involves the inter-conversion of fumarate to malate was among the top reactions that had maximum RCI. We also found the reaction involving the conversion of ribulose-5-phosphate to xylulose-5-phosphate belonging to the pentose phosphate pathway was one among the reactions with the top RCI.

The above findings suggest that compensation occurs in a range of ways, thus enabling the network to sustain growth. There exists a high level of redundancy which further enhances the organisms’ robustness to perturbations. It has also been established that compensation can occur in different ways and across different reaction pairs, thus enabling the organism to survive single mutations. Also, a key interesting finding is that most of the reactions that have very high RCI values are absolutely necessary for growth in glucose medium and metabolic networks tend to evolve in a way that has maximum compensation for such reactions.

3.3 How do synthetic lethals vary across environments?

Synthetic lethals across environments has been studied previously in the yeast metabolic network (Harrison et al., 2007). However, a study of synthetic lethals across random networks in different environments helps us to better understand the space of synthetic lethals and how reactions can compensate for one another. We identified DLs in all the 2000 random networks that were evolved on glucose on all 10 different environments under consideration (as described in Section 2).

Figure 3 shows the distribution of DLs in a given number of environments; the DLs are dependent on environments in which the network grows on. There were 163 DLs which were identified in all environments thus, establishing the fact that there are some synthetic lethals which occur irrespective of the environments the networks thrive on. A closer look at the DLs in different environments suggests that there exists DLs which are constrained by the environments the networks grow on. Of the unique DLs that were identified on the networks evolved on glucose, 8043 DLs were unique to environments. This implies that these reaction pairs are present only in one environment and absent in the other nine environments.

Fig. 3.

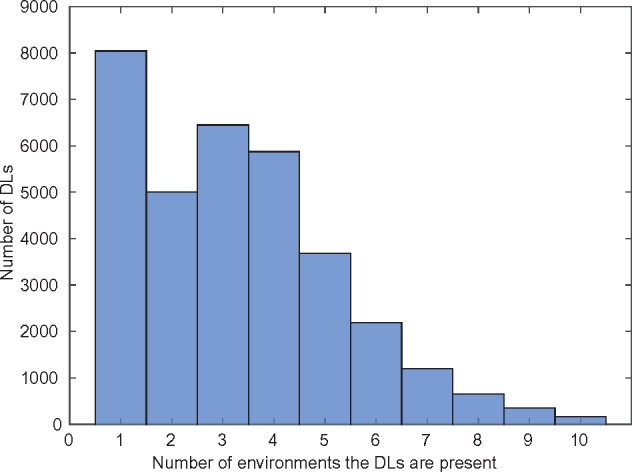
Distribution of DLs across environments. The histogram shows the number of DLs that are present in a given number of environments. For instance, the first bar shows that a large number of lethals (8043) were unique to only one environment, while the last bar shows that a small number of lethals (163) were found in each of the ten environments studied here

The environmentally independent DLs can be regarded as ‘core’ synthetic lethals which tend to compensate for each other under all environmental conditions. On the other hand, there exist lethals that are unique to environments or occur in a few environments that compensate for each other in only a specific growth medium. This is in agreement with the published work on synthetic lethals of yeast on varied environments (Harrison et al., 2007) that establishes two types of synthetic lethals: environmentally independent and environmentally dependent.

On analysis of the 163 DLs present in all environments, seven of these reaction lethals were found as lethals in E.coli in all environments. A surprising finding is that the 163 lethals had reactions non-native to E.coli acquired from the universe as the networks evolved and still are also common in all environments. Thus, it illustrates that metabolic networks could evolve to acquire reactions that can compensate for the existing reactions in the network under multiple environmental conditions.

The number of environmentally dependent DLs was identified as in Table 2. We could observe that inosine medium has the maximum fraction of DLs specific to its environment. The fraction of lethals that are environmentally dependent in acetate environment is the least in comparison to all other environments. This could potentially be since reactions that involve in the growth on inosine environment are different from those networks that assimilate the other carbon sources.

Table 2.

Fraction of environmentally dependent lethals present in each environment

Growth environments	Pyr	Glu	Ace	Fru	Gal	Xyl	Lac	Ino	Sor	Tre
Fraction of lethals that are environmentally dependent	0.04	0.09	0.007	0.03	0.02	0.15	0.06	0.19	0.02	0.06

The distribution of synthetic DLs across different environments begs an interesting question: suppose we were to consider the entire universe of reactions as a giant metabolic network, how do the characteristics of the lethals change? Thus, we went ahead to analyse the lethals in the universe of reactions.

3.4 Identification of higher order lethals in the universe

An analysis of essential reactions in a universe of reactions has been carried out previously (Barve et al., 2012), which illustrates that single lethals in the universe are also essential in any (random) network they are present in. Such reactions were termed superessential, as they are absolutely required for growth on a particular medium. We here extended this idea for synthetic lethals to understand if all the synthetic DLs present in the universe occur in random networks. We thus identified the DLs in the universe for glucose environment.

We identified 102 lethal pairs in the universe of reactions, on a glucose environment. These 102 pairs are constituted by 135 reactions. We analysed the number of times each lethal pair in the universe appears in our random networks. We found that 12 lethal pairs were present in more than 400 random networks. Around 14 DLs were present in less than 10 networks. The 102 lethal pairs can be termed ‘universal double lethals’ since they exist as DLs in the universe, and thus cannot possess further reactions that can compensate for the above reactions.

We then compared the DLs in the universe with those in E.coli. We envisioned three scenarios: first, if both the reactions that form a DL in the universe are present together in E.coli, they would remain a DL. Second, if one of the reactions is blocked, owing to non-availability of reactants, the other would be a single lethal. Third, if only one of them is present in E.coli, the reaction would end up as a single lethal. Of the 102 DLs in the universe, 16 lethals had both reactions present in E.coli. Of these 16, 12 lethal pairs remained as lethals in E.coli, while in four of them, one of the reactions in the pair was singly lethal. In case of the remaining 86 of the DLs from the universe, only one of the reactions in a lethal pair was present in E.coli, and the reaction was single lethal in each of the 86 cases. It would be very interesting to further extend these analyses to all the random networks studied herein, which might point to other interesting compensatory mechanisms.

We further went ahead to analyse the other DLs that were present in the random networks, beyond these 102 DLs, and if it is possible to use the information on higher order lethals that exist in the universe to identify some of these DLs. To this end, we enumerated the triple lethals (TL) in the universe on glucose environment using Fast-SL, which identified 122 TLs. Given any TL set, the loss of one of the reactions would make it a DL set. Thus, there are a potential $\left(\begin{array}{c}3\\ 2\end{array}\right)\times 122=366$ DL sets that could exist across the random networks. Dropping repetitions, we identify that there are 240/366 unique possible DLs. We analysed the overlap of these enumerated lethals with the DLs in each of the random networks and found that only a fraction of the DLs found in random networks could be found using the TLs in the universe. This could possibly illustrate that the additional DLs that exist in random networks are a subset of further higher order lethals present in the universe.

In summary, the universe tends to have varied compensations, which may exist as such in random networks or predominantly result in lower order lethals. The analyses also reveal the layered compensatory mechanisms that exist in different metabolic networks owing to the different set of reactions present in them. We could find many DLs in random networks that neither exist as DLs in the universe nor are a subset of TLs in the universe, thus pointing towards the existence of higher order redundancies in metabolism.

3.5 Random networks illustrate how very diverse reactions can compensate for one another

Compensatory mechanisms are sometimes very straightforward, such as producing the same key metabolite. However, there are instances where the synthetic lethals occur in different pathways, and their compensatory functions are less understood until explored thoroughly. To identify such lethals from the random networks that perform varied functions, we studied some of the lethals identified (in random networks) for their biological significance.

We observed that some widely different reactions, which belong to different pathways, exist as synthetic lethal pairs. For example, the reaction below forms a synthetic lethal pair in random networks while they are absent in E.coli and the universe of reactions. The conversion of chorismate to pyruvate and 4-Hydroxybenzoate, which forms a part of the ubiquinone biosynthesis forms a synthetic lethal pair with the production of 4-Hydroxymandelate from p-hydroxyphenylpyruvate, which is involved in the biosynthesis of antibiotics. When we analysed the enzymes which catalyse these reactions, we found that the former reaction is catalysed by a lyase (EC 4.1.3.40) and the latter by oxidoreductase (EC 1.13.11.46).

Another example of a non-intuitive lethal is the conversion of L-Glutamyl-tRNA from L-Glutamate (ModelSEED: rxn06436) and the reaction which involves in the inter-conversion of succinyl-CoA and glycine to aminolevulinate involved in glycine, serine and threonine metabolism (ModelSEED: rxn00599). The two reactions are catalysed by different types of enzymes, one by a ligase (EC 6.1.1.24) and the other by a transferase (EC 2.3.1.37). A few other examples of such non-intuitive lethals are listed in the Supplementary Table S4.

Thus, we could identify lethals which are absent in E.coli and universe set of reactions but constitute a synthetic lethal pair in random networks. These included many reactions that perform very diverse functions, yet could form a synthetic lethal pair. Our results pave the way to understand how diverse reactions (or pathways) can form functionally redundant pairs.

4 Discussion

Redundancy is a common mechanism employed in cells to achieve robustness. In the context of metabolism, it is interesting to identify how, under different environmental contexts, very different reactions (or, enzymes) within a cell can compensate for one another. In this study, we carry out an extensive analysis of metabolic networks, to understand how redundancy can exist and evolve in metabolism. Beginning with the metabolic network of E.coli, we construct 2000 ‘random’ metabolic networks using a previously established approach (Barve and Wagner, 2013). Each of these metabolic networks has the same size as E.coli and exhibits growth on a minimal glucose medium. These random networks essentially mimic the evolution of E.coli on such an environment. Through a comprehensive study of synthetic lethals across these 2000 random networks in 10 different environments, we shed light on how very diverse reactions (or enzymes) can compensate for one another in metabolic networks. Our results also point towards deep redundancy in the organization of cellular metabolism.

Firstly, we see that E.coli harbours a significantly higher number of single lethals and DLs in nearly all of the environments we considered here. Real networks, thus, are not minimal networks, which merely comprise the least number of reactions necessary for survival in the growth medium but have a high level of redundancy. In other words, the real network tends to retain a larger number of functionally redundant reactions in comparison to random networks. This finding demonstrates that nature preserves redundant functions, enabling survival even when they are subjected to single mutations.

Next, we studied the number of possible different compensations that a single reaction can have. We found that around 12 reactions had an RCI of > 200, showing how a very large number of reactions can form a synthetic lethal pair with a given reaction. Our results show that very important essential reactions necessary for growth on a particular growth medium tend to evolve more functional redundancies. We also noticed that the key enzyme ATP synthase exhibited a higher number of lethal pairs (266) indicating the significance of the reaction for the survival of organisms. Here, it must be noted that while the reactions may not necessarily exactly compensate for one another, in all cases, the cell cannot survive unless at least one of the reactions in the pair is active. These reactions may act as important links in their respective pathways, which compensate for one another in the metabolic network.

Another interesting finding is that synthetic lethals do vary across environments, although there are certain reaction redundancies that tend to exist in all environments. This was in accordance with earlier published work of synthetic lethals in the metabolic network of yeast under different environmental conditions (Güell et al., 2014), but we additionally observe how the synthetic lethals are shaped, across thousands of random networks that show growth in a given environment.

Our analyses of lethal pairs in the universe of reactions give insight into the layered compensations that occur in different metabolic networks. Also, the enumeration of higher order lethals sheds important light on the different compensatory mechanisms that could exist in any metabolic network. Further, we were able to identify lethal pairs which perform very different distinct functions, yet compensate one another to resist perturbations. These reactions, although they do not have any metabolites in common and involve in very different pathways, form a lethal pair, indicating the essentiality of either of the reactions for survival of the organism.

Although we focus primarily on reactions, the ‘unit of deletion’ in the model, it is easy to extend this approach to study genes and construct corresponding genetic interaction networks. Our study generally points towards how genes with very different functions (for example, EC 4.1.3.40 and EC 1.13.11.46) can compensate for one another in an organism’ s metabolism. The reaction universe is also not necessarily complete; but as and when new reactions are discovered, it will enable us to identify even more novel compensation mechanisms. Although we have listed the possible reaction lethals, a closer look into the pathways would enable us to understand the mechanisms involved in the formation of the lethal pairs.

Overall, our work emphasises the adaptive functional redundancies that are acquired, as microbes evolve on a particular environment. We could thus identify novel synthetic lethals and throw light on the wide repertoire of possible functional redundancies, that enhance robustness in metabolic networks.

Funding

Conflict of Interest: none declared.