DeepDTA: deep drug–target binding affinity prediction

Abstract

Motivation

The identification of novel drug–target (DT) interactions is a substantial part of the drug discovery process. Most of the computational methods that have been proposed to predict DT interactions have focused on binary classification, where the goal is to determine whether a DT pair interacts or not. However, protein–ligand interactions assume a continuum of binding strength values, also called binding affinity and predicting this value still remains a challenge. The increase in the affinity data available in DT knowledge-bases allows the use of advanced learning techniques such as deep learning architectures in the prediction of binding affinities. In this study, we propose a deep-learning based model that uses only sequence information of both targets and drugs to predict DT interaction binding affinities. The few studies that focus on DT binding affinity prediction use either 3D structures of protein–ligand complexes or 2D features of compounds. One novel approach used in this work is the modeling of protein sequences and compound 1D representations with convolutional neural networks (CNNs).

Results

The results show that the proposed deep learning based model that uses the 1D representations of targets and drugs is an effective approach for drug target binding affinity prediction. The model in which high-level representations of a drug and a target are constructed via CNNs achieved the best Concordance Index (CI) performance in one of our larger benchmark datasets, outperforming the KronRLS algorithm and SimBoost, a state-of-the-art method for DT binding affinity prediction.

Availability and implementation

https://github.com/hkmztrk/DeepDTA

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

The successful identification of drug–target interactions (DTI) is a critical step in drug discovery. As the field of drug discovery expands with the discovery of new drugs, repurposing of existing drugs and identification of novel interacting partners for approved drugs is also gaining interest (Oprea and Mestres, 2012). Until recently, DTI prediction was approached as a binary classification problem (Bleakley and Yamanishi, 2009; Cao et al., 2014, 2012; Cobanoglu et al., 2013; Gönen, 2012; Öztürk et al., 2016; Yamanishi et al., 2008; van Laarhoven et al., 2011), neglecting an important piece of information about protein–ligand interactions, namely the binding affinity values. Binding affinity provides information on the strength of the interaction between a drug–target (DT) pair and it is usually expressed in measures such as dissociation constant (K_d), inhibition constant (K_i) or the half maximal inhibitory concentration (IC₅₀). IC₅₀ depends on the concentration of the target and ligand (Cer et al., 2009) and low IC₅₀ values signal strong binding. Similarly, low K_i values indicate high binding affinity. K_d and K_i values are usually represented in terms of pK_d or pK_i, the negative logarithm of the dissociation or inhibition constants.

In binary classification based DTI prediction studies, construction of the datasets constitutes a major step, since designation of the negative (not-binding) samples directly affects the performance of the model. As of last decade, most of the DTI studies utilized four major datasets by Yamanishi et al. (2008) in which DT pairs with no known binding information are treated as negative (not-binding) samples. Recently, DTI studies that rely on databases with binding affinity information have been providing more realistic binary datasets created with a chosen binding affinity threshold value (Wan and Zeng, 2016). Formulating the DT prediction task as a binding affinity prediction problem enables the creation of more realistic datasets, where the binding affinity scores are directly used. Furthermore, a regression-based model brings in the advantage of predicting an approximate value for the strength of the interaction between the drug and target which in turn would be significantly beneficial for limiting the large compound search-space in drug discovery studies.

Prediction of protein–ligand binding affinities has been the focus of protein–ligand scoring, which is frequently used after virtual screening and docking campaigns in order to predict the putative strengths of the proposed ligands to the target (Ragoza et al., 2017). Non-parametric machine learning methods such as the Random Forest (RF) algorithm have been used as a successful alternative to scoring functions that depend on multiple parameters (Ballester and Mitchell, 2010; Li et al., 2015; Shar et al., 2016). However, Gabel et al. (2014) showed that RF-score failed in virtual screening and docking tests, speculating that using features such as co-occurrence of atom-pairs over-simplified the description of the protein–ligand complex and led to the loss of information that the raw interaction complex could provide. Around the same time this study was published, deep learning started to become a popular architecture powered by the increase in data and high capacity computing machines challenging other machine learning methods.

Inspired by the remarkable success rate in image processing (Ciregan et al., 2012; Donahue et al., 2014; Simonyan and Zisserman, 2015) and speech recognition (Dahl et al., 2012; Graves et al., 2013; Hinton et al., 2012), deep learning methods are now being intensively used in many other research fields, including bioinformatics such as in genomics studies (Leung et al., 2014; Xiong et al., 2015) and quantitative-structure activity relationship (QSAR) studies in drug discovery (Ma et al., 2015). The major advantage of deep learning architectures is that they enable better representations of the raw data by non-linear transformations in each layer (LeCun et al., 2015) and thus they facilitate learning the hidden patterns in the data.

A few studies employing Deep Neural Networks (DNN) have already been performed for DTI binary class prediction using different input models for proteins and drugs (Chan et al., 2016; Tian et al., 2015; Hamanaka et al., 2016) in addition to some studies that employ stacked auto-encoders (Wang et al., 2017) and deep-belief networks (Wen et al., 2017). Similarly, stacked auto-encoder based models with Recurrent Neural Networks (RNNs) and Convolutional Neural Networks (CNNs) were applied to represent chemical and genomic structures in real-valued vector forms (Gómez-Bombarelli et al., 2018; Jastrzkeski et al., 2016). Deep learning approaches have also been applied to protein–ligand interaction scoring in which a common application has been the use of CNNs that learn from the 3D structures of the protein–ligand complexes (Gomes et al., 2017; Ragoza et al., 2017; Wallach et al., 2015). However, this approach is limited to known protein–ligand complex structures, with only 25 000 ligands reported in PDB (Rose et al., 2016).

Pahikkala et al. (2014) employed the Kronecker Regularized Least Squares (KronRLS) algorithm that utilizes only 2D based compound similarity-based representations of the drugs and Smith–Waterman similarity representation of the targets. Recently, SimBoost method was proposed to predict binding affinity scores with a gradient boosting machine by using feature engineering to represent DTI (He et al., 2017). They utilized similarity-based information of DT pairs as well as features that were extracted from network-based interactions between the pairs. Both studies used traditional machine learning algorithms and utilized 2D-representations of the compounds in order to obtain similarity information.

In this study, we propose an approach to predict the binding affinities of protein–ligand interactions with deep learning models using only sequences (1D representations) of proteins and ligands. To this end, the sequences of the proteins and SMILES (Simplified Molecular Input Line Entry System) representations of the compounds are used rather than external features or 3D-structures of the binding complexes. We employ CNN blocks to learn representations from the raw protein sequences and SMILES strings and combine these representations to feed into a fully connected layer block that we call DeepDTA. We use the Davis Kinase binding affinity dataset (Davis et al., 2011) and the KIBA large-scale kinase inhibitors bioactivity data (He et al., 2017; Tang et al., 2014) to evaluate the performance of our model and compare our results with the KronRLS (Pahikkala et al., 2014) and SimBoost algorithms (He et al., 2017). Our new model that uses two separate CNN-based blocks to represent proteins and drugs performs as well as the KronRLS and SimBoost algorithms on the Davis dataset, and it performs significantly better than both the KronRLS and SimBoost algorithms on the KIBA dataset (P-value, 0.0001). With our proposed model, we also obtain the lowest Mean Squared Error (MSE) value on both datasets.

2 Materials and methods

2.1 Datasets

We evaluated our proposed model on two different datasets, the Kinase dataset Davis (Davis et al., 2011) and KIBA dataset (Tang et al., 2014), which were previously used as benchmark datasets for binding affinity prediction evaluation (He et al., 2017; Pahikkala et al., 2014).

The Davis dataset contains selectivity assays of the kinase protein family and the relevant inhibitors with their respective dissociation constant (K_d) values. It comprises interactions of 442 proteins and 68 ligands. The KIBA dataset, on the other hand, originated from an approach called KIBA, in which kinase inhibitor bioactivities from different sources such as K_i, K_d and IC₅₀ were combined (Tang et al., 2014). KIBA scores were constructed to optimize the consistency between K_i, K_d and IC₅₀ by utilizing the statistical information they contained. The KIBA dataset originally comprised 467 targets and 52 498 drugs. He et al. (2017) filtered it to contain only drugs and targets with at least 10 interactions yielding a total of 229 unique proteins and 2111 unique drugs. Table 1 summarizes these datasets in the forms that we used in our experiments.

Table 1.

Summary of the datasets

	Proteins	Compounds	Interactions
Davis (Kd)	442	68	30 056
KIBA	229	2111	118 254

While Pahikkala et al. (2014) used the K_d values of the Davis dataset directly as the binding affinity values, we used the values transformed into log space, pK_d, similar to He et al. (2017) as explained in Equation (1).

$$\mathrm{p}{\mathrm{K}}_{\mathrm{d}}=-\log 10\left(\frac{{\mathrm{K}}_{\mathrm{d}}}{1e9}\right)$$ (1)

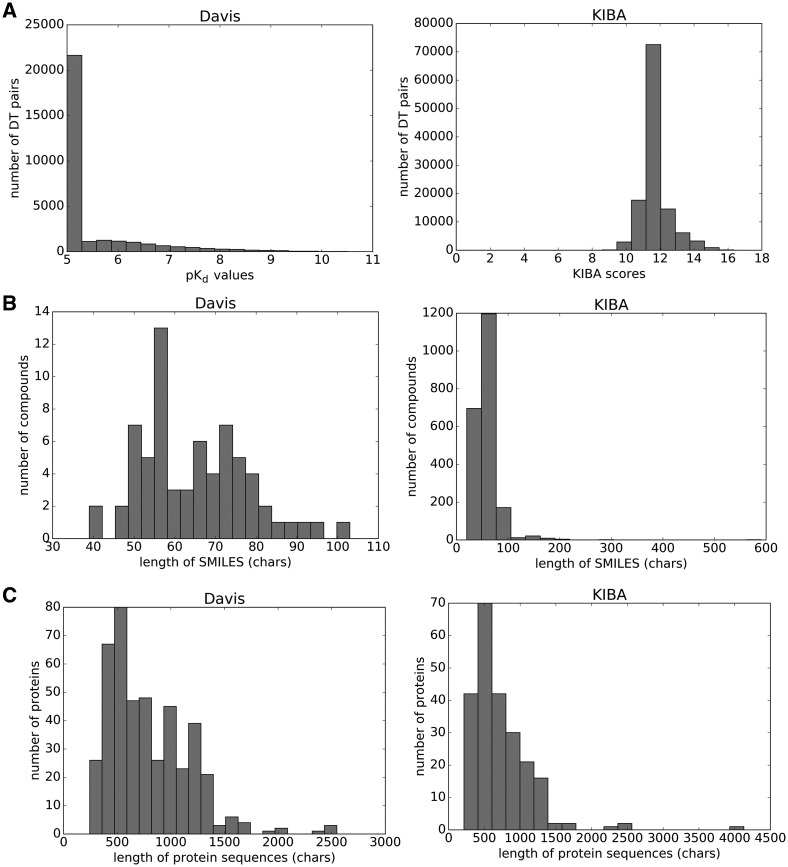
Figure 1A (left panel) illustrates the distribution of the binding affinity values in pK_d form. The peak at pK_d value 5 (10 000 nM) constitutes more than half of the dataset (20 931 out of 30 056). These values correspond to the negative pairs that either have very weak binding affinities (${\mathrm{K}}_{\mathrm{d}}>10000\mathrm{nM}$) or are not observed in the primary screen (Pahikkala et al., 2014). As such they are true negatives.

Fig. 1.

Summary of the Davis (left panel) and KIBA (right panel) datasets. (A) Distribution of binding affinity values. (B) Distribution of the lengths of the SMILES strings. (C) Distribution of the lengths of the protein sequences

The distribution of the KIBA scores is depicted in the right panel of Figure 1A. He et al. (2017) pre-processed the KIBA scores as follows: (i) for each KIBA score, its negative was taken, (ii) the minimum value among the negatives was chosen and (iii) the absolute value of the minimum was added to all negative scores, thus constructing the final form of the KIBA scores.

The compound SMILES strings of the Davis dataset were extracted from the Pubchem compound database based on their Pubchem CIDs (Bolton et al., 2008). For KIBA, first the CHEMBL IDs were converted into Pubchem CIDs and then, the corresponding CIDs were used to extract the SMILES strings. Figure 1B illustrates the distribution of the lengths of the SMILES strings of the compounds in the Davis (left) and KIBA (right) datasets. For the compounds of the Davis dataset, the maximum length of a SMILES is 103, while the average length is equal to 64. For the compounds of KIBA, the maximum length of a SMILES is 590, while the average length is equal to 58.

The protein sequences of the Davis dataset were extracted from the UniProt protein database based on gene names/RefSeq accession numbers (Apweiler et al., 2004). Similarly, the UniProt IDs of the targets in the KIBA dataset were used to collect the protein sequences. Figure 1C (left panel) shows the lengths of the sequences of the proteins in the Davis dataset. The maximum length of a protein sequence is 2549 and the average length is 788 characters. Figure 1C (right panel) depicts the distribution of protein sequence length in KIBA targets. The maximum length of a protein sequence is 4128 and the average length is 728 characters.

We should also note that the Smith–Waterman (S–W) similarity among proteins of the KIBA dataset is at most 60% for 99% of the protein pairs. The target similarity is at most 60% for 92% of the protein pairs for the Davis dataset. These statistics indicate that both datasets are non-redundant.

2.2 Input representation

We used integer/label encoding that uses integers for the categories to represent inputs. We scanned approximately 2 M SMILES sequences that we collected from Pubchem and compiled 64 labels (unique letters). For protein sequences, we scanned 550 K protein sequences from UniProt and extracted 25 categories (unique letters).

Here we represent each label with a corresponding integer (e.g. ‘C’: 1, ‘H’: 2, ‘N’: 3 etc.). The label encoding for the example SMILES, ‘CN=C = O’, is given below.

$$\left[\begin{array}{cccccc}C& N& =& C& =& O\end{array}\right]=\left[\begin{array}{cccccc}1& 3& 63& 1& 63& 5\end{array}\right]$$

Protein sequences are encoded in a similar way using label encodings. Both SMILES and protein sequences have varying lengths. Hence, in order to create an effective representation form, we decided on fixed maximum lengths of 85 for SMILES and 1200 for protein sequences for Davis. To represent the components of KIBA, we chose the maximum 100 characters length for SMILES and 1000 for protein sequences. We chose these maximum lengths based on the distributions illustrated in Figure 1B and C so that the maximum lengths cover at least 80% of the proteins and 90% of the compounds in the datasets. The sequences that are longer than the maximum length are truncated, whereas shorter sequences are 0-padded.

2.3 Proposed model

In this study, we treated protein–ligand interaction prediction as a regression problem by aiming to predict the binding affinity scores. As a prediction model, we adopted a popular deep learning architecture, Convolutional Neural Network (CNN). CNN is an architecture that contains one or more convolutional layers often followed by a pooling layer. A pooling layer down-samples the output of the previous layer and provides a way of generalization of the features that are learned by the filters. On top of the convolutional and pooling layers, the model is completed with one or more fully connected (FC) layers. The most powerful feature of CNN models is their ability to capture the local dependencies with the help of filters. Therefore, the number and size of the filters in a CNN directly affects the type of features the model learns from the input. It is often reported that as the number of filters increases, the model becomes better at recognizing patterns (Kang et al., 2014).

We proposed a CNN-based prediction model that comprises two separate CNN blocks, each of which aims to learn representations from SMILES strings and protein sequences. For each CNN block, we used three consecutive 1D-convolutional layers with increasing number of filters. The second layer had double and the third convolutional layer had triple the number of filters in the first one. The convolutional layers were then followed by the max-pooling layer. The final features of the max-pooling layers were concatenated and fed into three FC layers, which we named as DeepDTA. We used 1024 nodes in the first two FC layers, each followed by a dropout layer of rate 0.1. Dropout is a regularization technique that is used to avoid over-fitting by setting the activation of some of the neurons to 0 (Srivastava et al., 2014). The third layer consisted of 512 nodes and was followed by the output layer. The proposed model that combines two CNN blocks is illustrated in Figure 2.

Fig. 2.

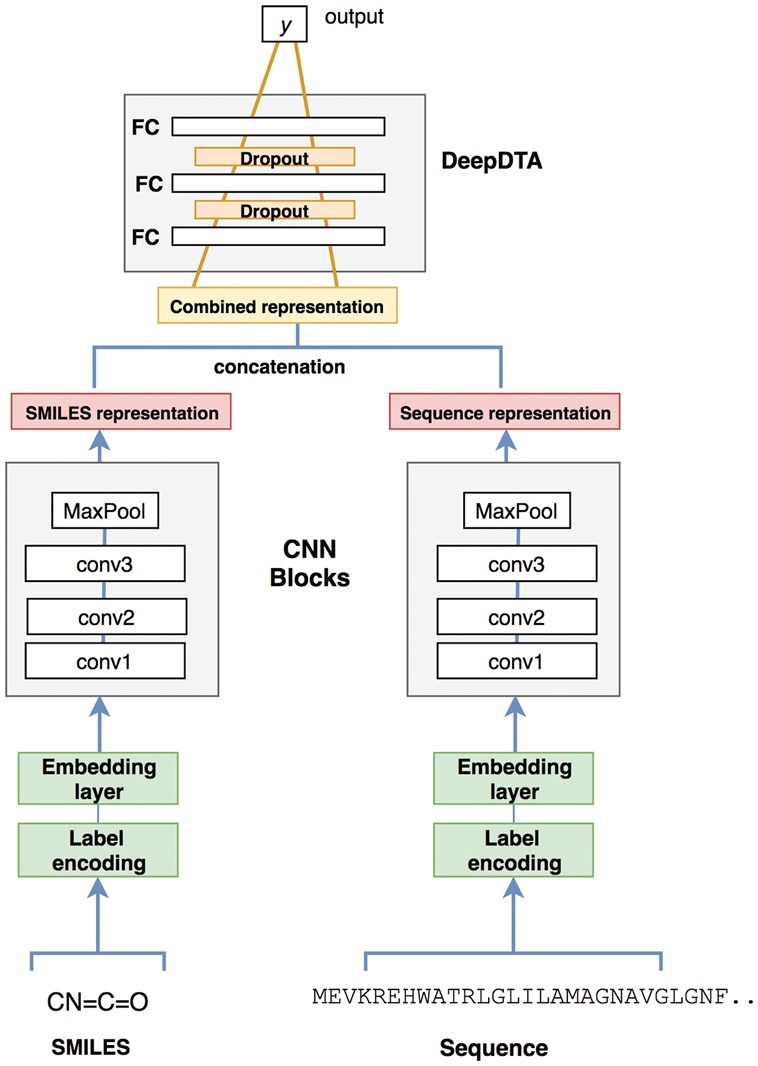
DeepDTA model with two CNN blocks to learn from compound SMILES and protein sequences

As the activation function, we used Rectified Linear Unit (ReLU) (Nair and Hinton, 2010), $g(x)=max(0,x)$, which has been widely used in deep learning studies (LeCun et al., 2015). A learning model tries to minimize the difference between the expected (real) value and the prediction during training. Since we work on a regression task, we used mean squared error (MSE) as the loss function, in which P is the prediction vector, and Y corresponds to the vector of actual outputs. n indicates the number of samples.

$$MSE=\frac{1}{n}{\displaystyle \sum _{i=1}^n{(P_i-Y_i)}^2}$$ (2)

The learning was completed with 100 epochs and mini-batch size of 256 was used to update the weights of the network. Adam was used as the optimization algorithm to train the networks (Kingma and Ba, 2015) with the default learning rate of 0.001. We used Keras’ Embedding layer to represent characters with 128-dimensional dense vectors. The input for Davis dataset consisted of (85, 128) and (1200, 128) dimensional matrices for the compounds and proteins, respectively. We represented KIBA dataset with a (100, 128) dimensional matrix for the compounds and a (1000, 128) dimensional matrix for the proteins.

3 Experiments and results

Here, we propose a novel drug–target binding affinity prediction method based on only sequence information of compounds and proteins. We utilized the Concordance Index (CI) to measure the performance of the proposed model and compared it with the current state-of-art methods that we chose as our baselines, namely a Kronecker Regularized Least Squares (KronRLS) based approach (Pahikkala et al., 2014) and SimBoost (He et al., 2017). We provide more information about these baseline methodologies, our model and experimental setup, as well as our results in the following subsections.

3.1 Baselines

3.1.1 Kron-RLS

KronRLS aims to minimize the following function, where f is the prediction function (Pahikkala et al., 2014):

$$J(f)={\displaystyle \sum _{i=1}^m{(y_i-f(x_i))}^2}+\lambda \left|\right|f|{|}_k^2$$ (3)

$\left|\right|f|{|}_k^2$ is the norm of f, which is related to the kernel function k, and $\lambda >0$ is a regularization hyper-parameter defined by the user. A minimizer for Equation (3) can be defined as follows (Kimeldorf and Wahba, 1971):

$$f(x)={\displaystyle \sum _{i=1}^m{a}_i}k(x,x_i)$$ (4)

where k is the kernel function. In order to represent compounds, they utilized a similarity matrix computed using Pubchem structure clustering server (Pubchem Sim)(http://pubchem.ncbi.nlm.nih.gov), a tool that utilizes single linkage for cluster and uses 2D properties of the compounds to measure their similarity. As for proteins, the Smith–Waterman algorithm was used to construct a protein similarity matrix (Smith and Waterman, 1981).

3.1.2 SimBoost

SimBoost is a gradient boosting machine based method that depends on the features constructed from drugs, targets and drug–target pairs (He et al., 2017). The proposed methodology uses feature engineering to build three types of features: (i) object-based features that utilize occurrence statistics and pairwise similarity information of drugs and targets, (ii) network-based features such as neighbor statistics, network metrics (betweenness, closeness etc.), PageRank score, which are collected from the respective drug–drug and target–target networks (In a drug–drug network, drugs are represented as nodes and connected to each other if the similarity of these two drugs is above a user-defined threshold. The target–target network is constructed in a similar way.) and (iii) network-based features that are collected from a heterogeneous network (drug–target network) where a node can either be a drug or target and the drug nodes and target nodes are connected to each other via binding affinity value. In addition to the network metrics, neighbor statistics and PageRank scores, as well as latent vectors from matrix factorization are also included in this type of network.

These features are fed into a supervised learning method named gradient boosting regression trees (Chen and Guestrin, 2016; Chen and He, 2015) derived from gradient boosting machine model (Friedman, 2001). With gradient boosting regression trees, for a given drug–target pair dt_i, the binding affinity score $\overline{y_i}$ predicted as follows (He et al., 2017):

$$\overline{y_i}=\theta (d{t}_i)={\displaystyle \sum _{m=1}^M{f}_m(d{t}_i)},f_m\in F$$ (5)

in which M denotes the number of regression trees and F represents the space of all possible trees. A regularized objective function to learn the set of trees $f_m$ is described in the following form (He et al., 2017):

$$R(\theta )={\displaystyle \sum _{i}l(y_i,{\overline{y}}_i)}+{\displaystyle \sum _m\alpha }(f_m)$$ (6)

where l is the loss function that measures the difference between the actual binding affinity value yi and the predicted value ${\overline{y}}_i$, while α is the tuning parameter that controls the complexity of the model. The details are described in (Chen and Guestrin, 2016; Chen and He, 2015; He et al., 2017). Similar to Pahikkala et al. (2014), He et al. (2017) also used PubChem clustering server for drug similarity and Smith–Waterman for protein similarity computation.

3.2 Evaluation metrics

To evaluate the performance of a model that outputs continuous values, Concordance Index (CI) was used (Gönen and Heller, 2005):

$$CI=\frac{1}{Z}{\displaystyle \sum _{{\delta }_i>{\delta }_j}h}(b_i-b_j)$$ (7)

where b_i is the prediction value for the larger affinity δ_i, b_j is the prediction value for the smaller affinity δ_j, Z is a normalization constant, h(x) is the step function (Pahikkala et al., 2014):

$$h(x)=\{\begin{array}{ll}1,\hfill & \text{if\hspace{0.17em}}x>0\hfill \\ 0.5,\hfill & \text{if\hspace{0.17em}}x=0\hfill \\ 0,\hfill & \text{if\hspace{0.17em}}x<0\hfill \end{array}$$ (8)

The metric measures whether the predicted binding affinity values of two random drug–target pairs were predicted in the same order as their true values were. We used paired-t test for the statistical significance tests with 95% confidence interval. We also used MSE, which was explained in Section 2.3, as an evaluation metric.

3.3 Experiment setup

We evaluated the performance of the proposed model on the benchmark datasets (Davis et al., 2011; Tang et al., 2014) similarly to (He et al., 2017). They used nested-cross validation to decide on the best parameters for each test set. In order to learn a generalized model, we randomly divided our dataset into six equal parts in which one part is selected as the independent test set. The remaining parts of the dataset were used to determine the hyper-parameters via 5-fold cross validation. Figure 3 illustrates the partitioning of the dataset. The same setting with the same train and test folds was used for KronRLS (Pahikkala et al., 2014) and Simboost (He et al., 2017) for a fair comparison.

Fig. 3.

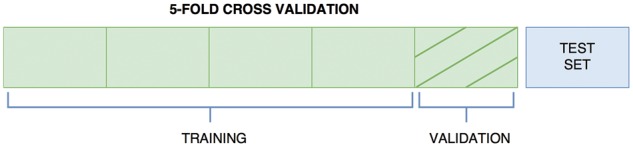
Experiment setup

We decided on three hyper-parameters for our model, namely the number of the filters (same for proteins and compounds), the length of the filter size for compounds, and the length of the filter size for proteins. We opted to experiment with different filter lengths for compounds and proteins instead of a common length, due to the fact that they have different alphabets. The hyper-parameter combination that provided the best average CI score over the validation set was selected as the best combination in order to model the test set. We first experimented with hyper-parameters chosen from a wide range and then fine-tuned the model. For example, to determine the number of filters we performed a search over [16, 32, 64, 128, 512]. We then narrowed the search range around the best performing parameter (e.g. if 16 was chosen as the best parameter, then our range was updated as [4, 8, 16, 20] etc.).

As explained in the Proposed Model subsection, the second convolution layer was set to contain twice the number of filters of the first layer, and the third one was set to contain three times the number of filters of the first layer. 32 filters gave the best results over the cross-validation experiments. Therefore, in the final model, each CNN block consisted of three 1D convolutions of 32, 64, 96 filters. For all test results reported in Table 3, we used the same structure summarized in Table 2 except for the lengths of the pre-fine-tuned filters that were used for the compound CNN-block and protein CNN-block.

Table 3.

The average CI and MSE scores of the test set trained on five different training sets for the Davis dataset

	Proteins	Compounds	CI (std)	MSE
KronRLS (Pahikkala et al., 2014)	S–W	Pubchem Sim	0.871 (0.0008)	0.379
SimBoost (He et al., 2017)	S–W	Pubchem Sim	0.872 (0.002)	0.282
DeepDTA	S–W	Pubchem Sim	0.790 (0.009)	0.608
DeepDTA	CNN	Pubchem Sim	0.835 (0.005)	0.419
DeepDTA	S–W	CNN	0.886 (0.008)	0.420
DeepDTA	CNN	CNN	0.878 (0.004)	0.261

Note: The standard deviations are given in parenthesis.

Table 2.

Parameter settings for CNN based DeepDTA model

Parameters	Range
Number of filters	32*1; 32*2; 32*3
Filter length (compounds)	[4, 6, 8]
Filter length (proteins)	[4, 8, 12]
epoch	100
hidden neurons	1024; 1024; 512
batch size	256
dropout	0.1
optimizer	Adam
learning rate (lr)	0.001

In order to provide a more robust performance measure, we evaluated the performance over the independent test set which was initially left out (blue part). We utilized the same five training sets that we used in 5-fold cross validation to train the model with the learned parameters in Table 2 (note that the validation sets were not used, yielding only four green parts for each training set.) The final CI score was reported as the average of these five results. Keras (Chollet et al., 2015) with Tensorflow (Abadi et al., 2016) back-end was used as development framework. Our experiments were run on OpenSuse 13.2 [3.50 GHz Intel(R) Xeon(R) and GeForce GTX 1070 (8GB)]. The work was accelerated by running on GPU with cuDNN (Chetlur et al., 2014). We provide our source code as well as the train and test folds of the datasets (https://github.com/hkmztrk/DeepDTA/).

3.4 Results

In this study, we propose a deep-learning model that uses two CNN-blocks to learn representations for drugs and targets based on their sequences. As a baseline for comparison, the KronRLS algorithm and SimBoost methods that use similarity matrices for proteins and compounds as input were used. The S–W and Pubchem Sim algorithms were used to compute the pairwise similarities for the proteins and ligands, respectively. We then used these S–W and Pubchem Sim similarity scores as inputs to the FC part of our model (DeepDTA) to evaluate the model. Finally, we used three alternative combinations in learning the hidden patterns of the data and used this information as input to our DeepDTA model. The combinations were (i) learning only compound representation with a CNN block and using S–W similarity as protein representation, (ii) learning only protein sequence representation with a CNN block and using Pubchem Sim to describe compounds and (iii) learning both protein representation and compound representations with a CNN block. We call the last combination used with DeepDTA the combined model.

Tables 3 and 4 report the average MSE and CI scores over the independent test set of the five models trained with the same parameters (shown in Table 2) using the five different training sets for Davis and KIBA datasets.

Table 4.

The average CI and MSE scores of the test set trained on five different training sets for the KIBA dataset

	Proteins	Compounds	CI (std)	MSE
KronRLS (Pahikkala et al., 2014)	S–W	Pubchem Sim	0.782 (0.0009)	0.411
SimBoost (He et al., 2017)	S–W	Pubchem Sim	0.836 (0.001)	0.222
DeepDTA	S–W	Pubchem Sim	0.710 (0.002)	0.502
DeepDTA	CNN	Pubchem Sim	0.718 (0.004)	0.571
DeepDTA	S–W	CNN	0.854 (0.001)	0.204
DeepDTA	CNN	CNN	0.863 (0.002)	0.194

Note: The standard deviations are given in parenthesis.

In the Davis dataset, SimBoost and KronRLS methods perform similarly while the CI values for SimBoost is higher than that for KronRLS in the larger KIBA dataset. When the similarity measures S–W, for proteins, and Pubchem Sim, for compounds, are used with the the fully connected part of the neural networks (DeepDTA), the CI drops to 0.79 for the Davis dataset and to 0.71 for the KIBA dataset. The MSE increases to >0.5. These results suggest that the use of a feed-forward neural network with predefined features is not sufficient to describe drug target interactions and to predict drug target affinities. Therefore, we used CNN layers to learn representations of drugs and proteins to capture hidden patterns in the datasets.

We first used CNN to learn representations of proteins and used the predefined Pubchem Sim scores for the ligands. Using this combination did not improve the results suggesting that use of a CNN architecture is not effective enough to learn from amino acid sequences.

Then we used the CNN block to learn compound representations from SMILES and used the predefined S–W scores for the proteins. This combination outperformed the baselines on the KIBA dataset with statistical significance (P-value of 0.0001 for both SimBoost and KronRLS), and on the Davis dataset (P-value of around 0.03 for both SimBoost and KronRLS). These results suggested that the CNN is able to capture more information than Pubchem Sim in the compound representation task.

Motivated by this result, we tested the combined CNN model in which both protein and compound representations are learned from the CNN layer. This method performed as well as the baseline methods with CI score of 0.878 on the Davis dataset and achieved the best CI score (0.863) on the KIBA dataset with statistical significance over both baselines (P-value of 0.0001 for both). The MSE values of this model were also notably lower than the MSE of the baseline models on both datasets. Even though learning protein representations with CNN was not effective, combination of the two CNN blocks for proteins and ligands provided a strong model.

In an effort to provide a better assessment of our model, we measured the performances of DeepDTA with two CNN modules and two baseline methods with two different metrics as well. $r_m^2$ index can be used to evaluate the external predictive performance of QSAR models where $r_m^2$ values > 0.5 for the test set was determined as an acceptable model. The metric is described in Equation (9) where r² and r₀² are the squared correlation coefficients with and without intercept, respectively. The details of the formulation are explained in (Pratim Roy et al., 2009; Roy et al., 2013).

$$r_m^2=r^2*(1-\sqrt[]{r^2-r_0^2})$$ (9)

The Area Under Precision Recall (AUPR) score is adopted by many studies that utilize binary prediction. In order to measure AUPR based performances, we converted the quantitative datasets into binary datasets by selecting binding affinity thresholds. For Davis dataset we used pK_d value of 7 as threshold (pK_d ≥ 7 binds) similar to (He et al., 2017). For KIBA dataset we used the suggested threshold KIBA value of 12.1 (He et al., 2017; Tang et al., 2014). Tables 5 and 6 depict the performances of DeepDTA with two CNN modules and two baseline methods on Davis and KIBA datasets, respectively.

Table 5.

The average $r_m^2$ and AUPR scores of the test set trained on five different training sets for the Davis dataset

	Proteins	Compounds	$r_m^2$ (std)	AUPR (std)
KronRLS (Pahikkala et al., 2014)	S–W	Pubchem Sim	0.407 (0.005)	0.661 (0.010)
SimBoost (He et al., 2017)	S–W	Pubchem Sim	0.644 (0.006)	0.709 (0.008)
DeepDTA	CNN	CNN	0.630 (0.017)	0.714 (0.010)

Note: The standard deviations are given in parenthesis.

Table 6.

The average $r_m^2$ and AUPR scores of the test set trained on five different training sets for the KIBA dataset

	Proteins	Compounds	$r_m^2$ (std)	AUPR (std)
KronRLS (Pahikkala et al., 2014)	S–W	Pubchem Sim	0.342 (0.001)	0.635 (0.004)
SimBoost (He et al., 2017)	S–W	Pubchem Sim	0.629 (0.007)	0.760 (0.003)
DeepDTA	CNN	CNN	0.673 (0.009)	0.788 (0.004)

Note: The standard deviations are given in parenthesis.

The results suggest that both SimBoost and DeepDTA are acceptable models for affinity prediction in terms of $r_m^2$ value and DeepDTA performs significantly better than SimBoost in KIBA dataset in terms of $r_m^2$ (P-value of 0.0001) and AUPR performances (P-value of 0.0003).

Figure 4 illustrates the predicted against measured (actual) binding affinity values for Davis and KIBA datasets. A perfect model is expected to provide a p = y line where predictions (p) are equal to the measured (y) values. We observe that especially for KIBA dataset, the density is high around the p = y line.

Fig. 4.

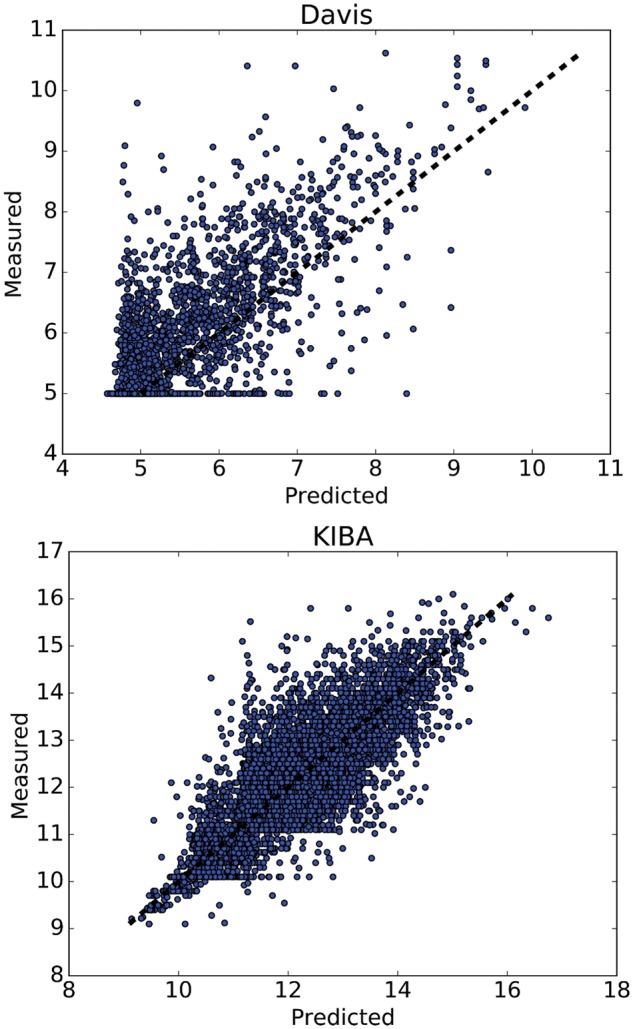
Predictions from DeepDTA model with two CNN blocks against measured (real) binding affinity values for Davis (pK_d) and KIBA (KIBA score) datasets

We also provide plots for two sample targets from KIBA dataset with predictions against actual values in Supplementary Figures S1 and S2.

4 Conclusion

We propose a deep-learning based approach to predict drug–target binding affinity using only sequences of proteins and drugs. We use Convolutional Neural Networks (CNN) to learn representations from the raw sequence data of proteins and drugs and fully connected layers (DeepDTA) in the affinity prediction task. We compare the performance of the proposed model with two recent studies that employed the KronRLS regression algorithm (Pahikkala et al., 2014) and the SimBoost method (He et al., 2017) as our baselines. We perform our experiments on the Davis kinase–drug dataset and the KIBA dataset.

Our results showed that the use of predefined features with DeepDTA is not sufficient to describe protein–ligand interactions. However, when two CNN-blocks that learn representations of proteins and drugs based on raw sequence data are used in conjunction with DeepDTA, the performance increases significantly compared to both baseline methodologies for both KIBA and Davis datasets. Furthermore, the model that uses CNN to learn compound representations from SMILES and S–W similarities of proteins also achieves better performance than the baselines.

We observed that the model that uses CNN-block to learn proteins and 2D compound similarity to represent compounds performed poorly compared to the other methods that employ CNN. This might be an indication that amino-acids require a structure that can handle their ordered relationships, which the CNN architecture failed to capture successfully. Long-Short Term Memory (LSTM), which is a special type of Recurrent Neural Networks (RNN), could be a more suitable approach to learn from protein sequences, since the architecture has memory blocks that allow effective learning from a long sequence. LSTM architecture has been successfully employed to tasks such as detecting homology (Hochreiter et al., 2007), constructive peptide design (Muller et al., 2018) and function prediction (Liu, 2017) that utilize amino-acid sequences. As future work, we also aim to utilize a recent ligand-based protein representation method proposed by our team that uses SMILES sequences of the interacting ligands to describe proteins (Öztürk et al., 2018).

The results indicated that deep-learning based methodologies performed notably better than the baseline methods with a statistical significance when the dataset grows in size, as the KIBA dataset is four times larger than the Davis dataset. The improvement over the baseline was significantly higher for the KIBA dataset (from CI score of 0.836 to 0.863) compared to the Davis dataset (from CI score of 0.872 to 0.878). The increase in the data enables the deep learning architectures to capture the hidden information better.

The major contribution of this study is the presentation of a novel deep learning-based model for drug–target affinity prediction that uses only character representations of proteins and drugs. By simply using raw sequence information for both drugs and targets, we were able to achieve similar or better performance than the baseline methods that depend on multiple different tools and algorithms to extract features.

A large percentage of proteins remains untargeted, either due to bias in the drug discovery field for a select group of proteins or due to their undruggability, and this untapped pool of proteins has gained interest with protein deorphanizing efforts (Edwards et al., 2011; Fedorov et al., 2010; O’Meara et al., 2016). As future work, we will focus on building an effective representation for protein sequences. The methodology can then be extended to predict the affinity of known compounds/targets to novel targets/drugs as well as to the prediction of the affinity of novel drug–target pairs.

Funding

This work was supported by Bogazici University Research Fund (BAP) Grant Number 12304.

Conflict of Interest: none declared.