Generalizing biomedical relation classification with neural adversarial domain adaptation

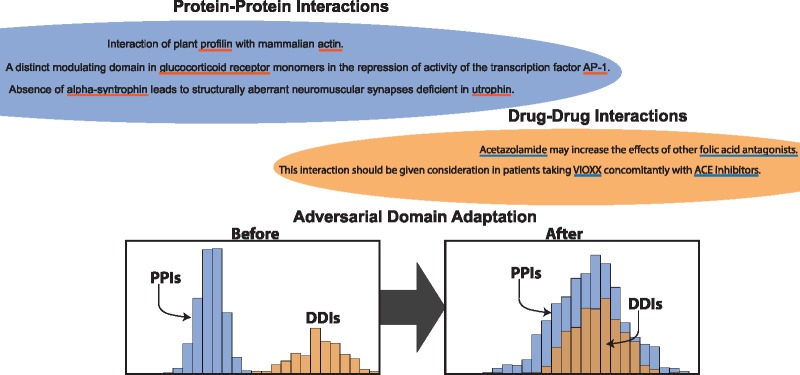
Abstract

Motivation

Creating large datasets for biomedical relation classification can be prohibitively expensive. While some datasets have been curated to extract protein–protein and drug–drug interactions (PPIs and DDIs) from text, we are also interested in other interactions including gene–disease and chemical–protein connections. Also, many biomedical researchers have begun to explore ternary relationships. Even when annotated data are available, many datasets used for relation classification are inherently biased. For example, issues such as sample selection bias typically prevent models from generalizing in the wild. To address the problem of cross-corpora generalization, we present a novel adversarial learning algorithm for unsupervised domain adaptation tasks where no labeled data are available in the target domain. Instead, our method takes advantage of unlabeled data to improve biased classifiers through learning domain-invariant features via an adversarial process. Finally, our method is built upon recent advances in neural network (NN) methods.

Results

We experiment by extracting PPIs and DDIs from text. In our experiments, we show domain invariant features can be learned in NNs such that classifiers trained for one interaction type (protein–protein) can be re-purposed to others (drug–drug). We also show that our method can adapt to different source and target pairs of PPI datasets. Compared to prior convolutional and recurrent NN-based relation classification methods without domain adaptation, we achieve improvements as high as 30% in F1-score. Likewise, we show improvements over state-of-the-art adversarial methods.

Availability and implementation

Experimental code is available at https://github.com/bionlproc/adversarial-relation-classification.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Relation classification has a broad range of applications in biomedical research and healthcare. For example, protein–protein interactions (PPIs) are instrumental in a multitude of biological processes that facilitate the discovery of novel drug targets for treating diseases (Pedamallu and Posfai, 2010). Likewise, adverse drug reactions (ADRs) have detrimental effects on the general populace. In 2009, the Institute of Medicine (IOM) reported at least 1.5 million (Council et al., 2009) adverse drug events occur each year. The IOM estimates that over 4 billion dollars are spent each year in order to treat preventable ADRs. A significant portion of these ADRs are caused by adverse drug–drug interactions (DDIs). Unfortunately, to the best of our knowledge, a single comprehensive source for DDIs is unavailable. While there has been work using natural language processing (NLP) to form a complete knowledge source for DDIs (Ayvaz et al., 2015), this is still an active area of research. Finally, there are many other forms of biomedical relations. For example, gene–disease, chemical–protein and protein–point mutation are all interactions of interest in the biomedical field. Furthermore, there has been a recent focus on ternary relations between entities [e.g. gene–mutation–disease (Singhal et al., 2016)]. But in general it is impractical to develop large manually curated datasets for every type of interaction. Also, creating datasets large enough to cover all domains that may specify biomedical interactions can be prohibitively expensive, especially when medical experts are needed to annotate the data.

Neural networks (NNs) have produced state-of-the-art results in the area of relation classification (dos Santos et al., 2015; Peng and Lu, 2017; Peng et al., 2017). While NNs have shown great promise for relation classification, they are highly susceptible to overfitting (Mou et al., 2016). Moreover, in the domain adaptation or covariate shift setting, issues associated with overfitting are magnified. Researchers have only recently begun exploring the area of domain adaptation with respect to relation classification (Nguyen and Grishman, 2014; Nguyen et al., 2015; Plank and Moschitti, 2013). Unsupervised domain adaptation (i.e. no labeled target data) is of immediate use to biomedical researchers. For example, models trained on patient data collected at a children’s hospital may not generalize well on adult records. Likewise, models trained on colon cancer patient data will not perform well on brain cancer patients records (Bethard et al., 2017). These problems fall under the umbrella term sample selection bias. If unlabeled data are abundant, then unsupervised domain adaptation methods are useful to create generalizable classifiers by providing unbiased data. Finally, we note that our scenario is similar to batch effects encountered in bioinformatics (Leek et al., 2010; Shaham et al., 2017), where issues such as measurement errors caused by variations in conditions between different experimental batches must be handled.

In this paper, we introduce an unsupervised domain adaptation method for relation classification. We focus on two important areas of biomedical relation classification. First, we experiment on adapting complex NNs across different PPI corpora. Figure 1 represents a hypothetical example distribution projected in two dimensions. The blue diamonds and circles represent positive training and test instances, respectively. Likewise, the red stars and triangles represent negative train and test instances. We can see that the test distribution does not match the training distribution [$P\left({\mathit{x}}_{\mathbf{t}\mathbf{r}\mathbf{a}\mathbf{i}\mathbf{n}}\right)\ne P\left({\mathit{x}}_{\mathbf{t}\mathbf{e}\mathbf{s}\mathbf{t}}\right)$]. Because of the biased sample, it is unreasonable to expect our models to generalize well on the test set. This is illustrated in Figure 1 by the linear separator learned on the training dataset (solid line). The classifier does not separate the positive and negative instances in the test dataset. For biomedical relation classification it is likely that the training set could be biased. For example, when a specific knowledge base is used to find sentences that contain PPIs, the knowledge base may be biased toward PPIs of a given species or interaction type within its curation scope. In this paper, we demonstrate how the use of unlabeled data can overcome sampling bias issues. Next, we will show that our method can adapt to other types of interactions, specifically between DDIs and PPIs. We present the intuition behind this through two example sentences:

Fig. 1.

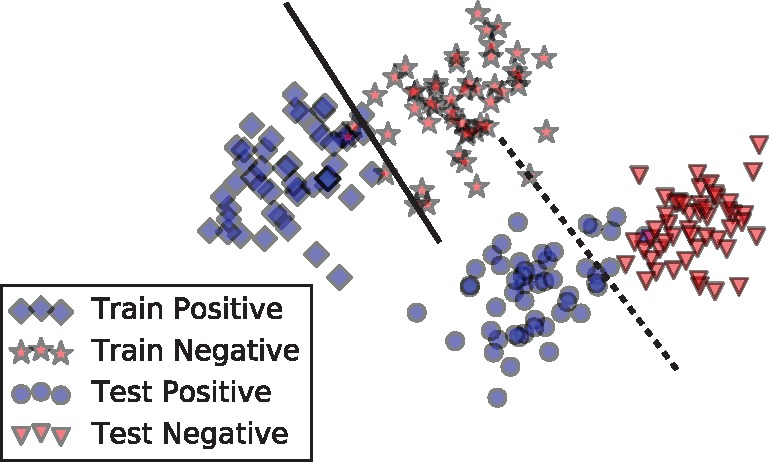
Fictional biased data distribution. The blue diamonds and circles represent train and test instances containing positive interactions. The red stars and triangles represent instances with negative interactions. After adversarial training we would expect the test instances to align with training instances such that it looks like the test dataset was sampled evenly across the training data distribution

• PPI Example: Human cyclin E, a new cyclin that interacts with two members of the CDC2 gene family

• DDI Example: The in vitro interaction between nevirapine and the antithrombotic agent warfarin is complex.

Without any biological expertise, and given two entities, we can understand that there are interactions just by the terms interacts with and interaction between. In general, a model trained to find DDIs (source domain) will not generalize well to PPIs (target domain), because of jargon specific to the source domain. However, through unsupervised adversarial training, we show that we can learn to hide the differences between the source and target datasets.

Overall, we make the following contributions:

• To the best of our knowledge, we introduce the first domain adaptation method of complex NNs for relation classification.

• In order to show that our adversarial training approach is highly generalizable, we experiment with the following state-of-the-art architectures for biomedical relation classification: convolutional NNs (CNNs) and recurrent NNs (RNNs).

• Finally, we perform a detailed quantitative analysis of our method.

We outline the rest of this paper as follows: we discuss related work in Section 2. Next, in Section 3 we explain our method in detail. Experimental results are shown in Section 4. Finally, we conclude this paper and discuss future work in Section 5.

2 Related work

2.1 Relation classification

There has been a large number of relation classification methods proposed over the years. For example, linear models were very popular for relation classification (Bunescu and Mooney, 2005; Rink and Harabagiu, 2010). These methods involved engineering both syntactic and semantic features to be used in the model.

More recently, NNs have been used for relation classification. Zeng et al. (2014) use CNNs to classify relations. The key intuition comes from the use of position vectors, where two vectors are concatenated with each word vector such that the two vectors represent where that word is located in the sentences with respect to the two entities. In dos Santos et al. (2015), a ranking loss is used rather than a softmax output layer in conjunction with a CNN. The use of a ranking loss overcomes issues of class imbalances with the ‘not relation’ class. Also, RNNs have been competitively applied to relation classification tasks, specifically RNNs have been applied along the shortest dependency path (Xu et al., 2015) as well as the full sentence (Zhou et al., 2016). Finally, both CNNs and RNNs have been shown to complement each other when combined (Vu et al., 2016).

The idea of applying NNs to biomedical relation classification has previously been explored by many researchers. Recently, CNNs were used to achieve state-of-the-art results for PPI (Peng and Lu, 2017). Meanwhile, both CNN (Asada et al., 2017; Liu et al., 2016; Matos and Antunes, 2017) and long short-term memory networks (LSTM) have worked well for DDI classification (Kavuluru et al., 2017; Zhang et al., 2017).

2.2 Domain adaptation

Domain adaptation methods are used when the test (target) set differs from the training (source) dataset distribution. In practice, this appears to be a common scenario. For example, sometimes latent temporal dependencies can affect the target data distribution. In the past, researchers have re-weighted source instances such that the source data looks more like the target distribution (Gong et al., 2012; Huang et al., 2006). Besides instance re-weighting, Gong et al. (2012) developed a geodesic kernel method for domain adaptation.

Recently, domain adaptation has also been applied to NNs. First, autoencoders (Chen et al., 2012; Glorot et al., 2011b) have been exploited to learn cross-domain representations. Unfortunately, these methods have been shown to only reduce the cross-domain discrepancies, rather than remove them (Long et al., 2016). Meanwhile, maximum mean discrepancy has been used to minimize the difference between the source and target distributions (Long et al., 2015, 2016). Similar to generative adversarial NNs (Goodfellow et al., 2014) (GAN), adversarial losses (Ganin and Lempitsky, 2015; Ganin et al., 2016) have been explored for domain adaptation. Adversarial domain adaptation works by training a NN that can learn to accurately make predictions for the source task, while ensuring the internal features for both the source and target datasets of the NN are indistinguishable from each other. ReverseGradient (RevGrad) (Ganin et al., 2016) is a recently proposed method for adversarial domain adaptation. RevGrad works by training a discriminator—a simple feed forward NN—to predict the domain (source versus target) of a given instance by minimizing the adversarial loss. At the same time, the base CNN is trained to fool the discriminator by maximizing the adversarial loss while simultaneously minimizing the classification loss. Contrary to RevGrad, the work by Tzeng et al. (2017) (ADDA) works in two stages. First, the NN is trained to minimize the classification loss for the source dataset. Next, ADDA is trained using a GAN loss while ignoring the classification loss. By using a two stage approach with the GAN loss, ADDA is able to generate stronger gradients to update the base NN. The method presented in this paper follows a similar multi-stage approach as described by Tzeng et al. (2017), however our method differs in multiple ways including a specialized NN—involving both learned word and position embeddings—to handle relation classification and additional regularizers to avoid degenerate solutions.

There has been extensive research on the application of domain adaptation to NLP including named entity recognition (Daumé III, 2007), sentiment analysis (Glorot et al., 2011b) and relation classification (Plank and Moschitti, 2013). Similar to our work, researchers have previously studied unsupervised domain adaptation for relation classification (Nguyen and Grishman, 2014; Nguyen et al., 2015). However, our work differs by utilizing recent advances in NNs for relation classification. Specifically, we use both RNNs and CNNs in adversarial settings.

3 Materials and methods

An intuitive visualization of our method is shown in Figure 2. Essentially, given two similar but different datasets, our model encourages the target data distribution, $P\left({\mathit{x}}_{\mathrm{tgt}}\right)$, to look like the source data distribution, $P\left(x_{\text{src}}\right)$. We hypothesize that the model will learn to hide domain specific information such that the source classifier will work better on the target dataset.

Fig. 2.

Intuition of the adversarial domain adaptation process using a fictional data distribution. Given two similar but different datasets, the adversarial training process will try to align the two data distributions. After adversarial training, the distributions should align with one another

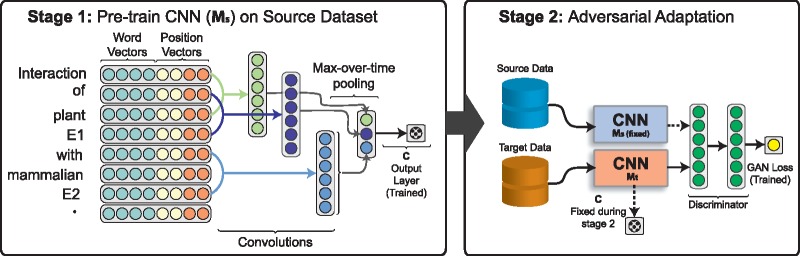
Our method is trained in two stages. First, as shown in Figure 3, we train a standard CNN-based relation classification model, M_s, on the source data. We also experiment with a bi-directional LSTM (Bi-LSTM) model which is not shown in the figure. It is important to note that the target data is not used at this stage. Next, in the second stage we ignore the classification loss, meaning the final output layer from stage 1 is not updated. Moreover, we make two copies of the source classifier, M_s and M_t. We train a new output layer (discriminator) that tries to predict whether each example is from the source or target dataset. The model parameters for M_s are fixed in stage 2. Also, the parameters of the target CNN, M_t, are updated to confuse the discriminator. By this, we mean, we want to update the parameters of M_t such that the discriminator thinks the target instances passed to M_t are from the source dataset. In the context of CNNs, the mid-level features are a vector produced after the convolutional and max-over-time pooling layers. By confusing the discriminator, the mid-level features produced by M_t for the target dataset will be indistinguishable from the features generated on the source data by M_s. This removes bias from the target domain that may cause incorrect predictions. It is important to note that both the discriminator and M_t are continually updated during the training process. Because of the competition between the discriminator and M_t, the discriminator should predict $\sim 0.5$ for target instances after stage 2. This assumes M_t and the discriminator do not overpower each other. Finally, to make predictions at test time, the output layer trained in stage 1 and M_t from stage 2 are combined.

Fig. 3.

The two stage process to our adversarial learning procedure. In Stage 1 either a CNN or Bi-LSTM model is trained on the source dataset. Stage 2 ignores the classification loss and trains a discriminator and the CNN with a new GAN loss instead

Before we discuss the details of our method. We begin by introducing some notation. Throughout this paper we will use s to represent a single instance in the source dataset and S represents the entire source corpus. Likewise, t represents a single target instance and T represents the target dataset. It is important to distinguish different sets of parameters in our model. We let ${\theta }_{M_s},{\theta }_{M_t},\hspace{0.17em}{\theta }_C$ and ${\theta }_D$ represent the parameters for the source base model, target base model, source classification output layer and discriminator, respectively. To simplify notation, we let ${\theta }_{M_t}/{\theta }_{M_s}$ represent the parameters for the CNN or the Bi-LSTM given both models are interchangeable in our algorithm.

3.1 Preprocessing and feature representation

Independent of the base model we use, the input to our models is the same. For relation classification, each instance is composed of a sentence and two entities in that sentence. The task is then to predict if there is an interaction between the two entities given the sentence. In order to improve generalizability, we replace the entities in each sentence with special word vectors representing the tokens E1 and E2, respectively. Replacing the entity words with special tokens ensures our model generalizes to unseen entities, rather than memorizing certain relations between entities in the training dataset. Also, all tokens which occur <5 times in the source dataset are replaced with the unknown token UNK.

Word embeddings preserve both syntactic and semantic information in a low dimensional vector (Mikolov et al., 2013). In our model, each instance is represented as a sequence of word vectors, $[{\mathbf{w}}_1,\dots ,\mathbf{e}1,\dots ,\mathbf{e}2,\dots ,{\mathbf{w}}_N]$, where ${\mathbf{w}}_i\in {ℝ}^d$ represents the word vector for the i-th word in the sequence. It is important to note that $\mathbf{e}1$ and $\mathbf{e}2$ are learned just like any other word vector in the sentence. Furthermore, we use position embeddings to compliment the word vectors. Position embeddings have been show to improve NNs for the task of relation classification (Zeng et al., 2014; Zhao et al., 2016). Specifically, for each word in a sentence, we measure the relative distance between both E1 and E2. Similar to the word embeddings, we also embed each location as a vector, ${\mathbf{p}}_{e1\left(j\right)}$ and ${\mathbf{p}}_{e2\left(j\right)}$ where ${\mathbf{p}}_{e1/2}\left(j\right)\in {ℝ}^e$, which is the position embedding representing the position of the j-th word relative to one of the two respective entities. Finally, we represent each word in a sentence as a single vector

$${\mathbf{x}}_i={\mathbf{w}}_i\left|\right|{\mathbf{p}}_{e1\left(i\right)}\left|\right|{\mathbf{p}}_{e2\left(i\right)},$$ (1)

such that ${\mathbf{x}}_i$ is the concatenation of the word embedding and the two position embeddings.

3.2 Models

One of the goals of this paper is to show that our adversarial learning method can be applied to both modern CNNs and RNNs for relation classification. We begin by giving a brief overview of both CNN and the RNN architectures.

Convolutional neural networks: Intuitively, CNNs learn to extract informative n-grams from text with a set of convolution filters (CFs). The basic architecture is shown in Figure 3. Given a sequence $[{\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_n]$, representing a sentence, which is a sequence of word representations described in Equation (1). First, we zero-pad both the beginning and end of the sentence with s – 1 zero vectors, where s is the number of words our filters span. The CFs are defined as $\mathbf{W}\in {ℝ}^{q\times s(d+2e)}$, where q is the number of feature maps we wish to generate. For example, a CF spanning three words would try to capture informative tri-grams from the sentence. In this work, we use architectures previously described by Nguyen and Grishman (2015). We begin by concatenating each window spanning s words, ${\mathbf{x}}_{i-s+1}\left|\right|\dots \left|\right|{\mathbf{x}}_i$, into a local context vector ${\mathbf{c}}_j\in {ℝ}^{s(d+2e)}$. Next, using a non-linear function [rectified linear unit (Glorot et al., 2011a; Nair and Hinton, 2010)] f, we convolve over each context vector,

$${\widehat{\mathbf{c}}}_j=f(\mathbf{W}{\mathbf{c}}_j+\mathbf{b}),\hspace{0.17em}\hspace{0.17em}\text{where}\hspace{0.17em}\hspace{0.17em}\mathbf{b}\in {ℝ}^q.$$

Given the convolved context vectors $[{\widehat{\mathbf{c}}}_1,{\widehat{\mathbf{c}}}_2,\dots ,{\widehat{\mathbf{c}}}_{n+s-1}]$, we map them into a fixed size sentence representation using max-over-time pooling

$$\begin{array}{c}M(\mathbf{s};{\theta }_M)=[{\widehat{c}}_{\text{max}}^1,{\widehat{c}}_{\text{max}}^2,\dots ,{\widehat{c}}_{\text{max}}^q],\hspace{0.17em}\text{where}\\ {\widehat{c}}_{\text{max}}^v=max({\widehat{c}}_1^v,{\widehat{c}}_2^v,\dots ,{\widehat{c}}_{n+s-1}^v)\end{array}$$

such that ${\widehat{c}}_{\text{max}}^v$ represents the max value across the v-th feature map.

Recurrent neural networks: While CNNs only extract informative n-grams from text, RNNs are able to capture long term dependencies between words. For our RNN method, we use LSTM (Gers et al., 2000), specifically we use a variant introduced by Graves et al. (2012),

$$\begin{array}{c}{\mathbf{i}}_i=sigmoid({\mathbf{x}}_i{\mathbf{W}}_i+{\mathbf{b}}_i+{\mathbf{h}}_{i-1}{\mathbf{U}}_i)\hfill \\ {\mathbf{f}}_i=sigmoid({\mathbf{x}}_i{\mathbf{W}}_f+{\mathbf{b}}_f+{\mathbf{h}}_{i-1}{\mathbf{U}}_f),\hfill \\ {\mathbf{o}}_i=sigmoid({\mathbf{x}}_i{\mathbf{W}}_o+{\mathbf{b}}_o+{\mathbf{h}}_{i-1}{\mathbf{U}}_o),\hfill \\ {\mathbf{p}}_i=\text{tan}\hspace{0.17em}h({\mathbf{x}}_i{\mathbf{W}}_c+{\mathbf{b}}_c+{\mathbf{h}}_{i-1}{\mathbf{U}}_c),\hfill \\ {\mathbf{h}}_i={\mathbf{o}}_i*\hspace{0.17em}\text{tan}\hspace{0.17em}h({\mathbf{f}}_i*{\mathbf{m}}_{i-1}+{\mathbf{i}}_i*{\mathbf{p}}_i),\hfill \end{array}$$

where ${\mathbf{i}}_i,\hspace{0.17em}{\mathbf{f}}_i,\hspace{0.17em}{\mathbf{o}}_i$ represent the input, forget and output gates.

For relation classification, we use a Bi-LSTM to capture contextual information on both sides of each word. We use the Bi-LSTM model proposed in Kavuluru et al. (2017). Specifically,

$$\begin{array}{c}{\vec{\mathbf{h}}}_i={\text{LSTM}}^{\to }\left({\mathbf{x}}_i\right),\hspace{0.17em}\hspace{0.17em}{\overleftarrow{\mathbf{h}}}_i={\text{LSTM}}^{\leftarrow }\left({\mathbf{x}}_i\right),\hspace{0.17em}\hspace{0.17em}\text{and}\hfill \\ {\mathbf{h}}_i={\vec{\mathbf{h}}}_i\left|\right|{\overleftarrow{\mathbf{h}}}_i\hspace{0.17em}\hspace{0.17em}\text{for}\hspace{0.17em}\hspace{0.17em}i=1,\dots ,n\hfill \end{array}$$

where ${\vec{\mathbf{h}}}_i,{\overleftarrow{\mathbf{h}}}_i\in {ℝ}^z$ and ${\mathbf{h}}_i\in {ℝ}^{2z}$. Here, ${\mathbf{h}}_i$ represents the bi-directional contextual information for word i.

Next, we produced a fixed size vector using max-over-time pooling. Given $[{\mathbf{h}}_1,{\mathbf{h}}_2,\dots ,{\mathbf{h}}_n]$, we generate the sentence representation

$$M(\mathbf{s};{\theta }_M)=[h_{\text{max}}^1,h_{\text{max}}^2,\dots ,h_{\text{max}}^{2z}],$$

which can be passed to the output layer such that $h_{\text{max}}^i$ is the max value across dimension i.

3.3 Classification loss

In this paper, we only consider the binary classification task of predicting if two entities interact or not. Given $M(\mathbf{s};{\theta }_M)$, the output from either the Bi-LSTM or CNN, we can generate a probability estimate of whether the two entities in s interact. Specifically,

$$C\left(M\right(\mathbf{s};{\theta }_M\left)\right)=\frac{1}{1+\text{exp}(-(M(\mathbf{s};{\theta }_M){\mathbf{w}}_c+b_c\left)\right)}$$

where ${\mathbf{w}}_c\in {ℝ}^{2z}$ or ${\mathbf{w}}_c\in {ℝ}^q$ depending if M is a Bi-LSTM or CNN, and $b_c\in ℝ$. Next, we can define the classification loss as the binary cross-entropy loss,

$${\mathbb{E}}_{(\mathbf{s},y)\sim \mathbf{S}}[-y\hspace{0.17em}\hspace{0.17em}\text{log}(C\left(M\right(\mathbf{s}\left)\right))-(1-y)\hspace{0.17em}\hspace{0.17em}\text{log}(1-C\left(M\right(\mathbf{s}\left)\right)\left)\right],$$ (2)

where $\mathbb{E}$ represents the expected value and y is the true label for s.

3.4 Adversarial learning

After training on the source dataset, we make two copies of the classifier, M_s and M_t. During adversarial training we fix the parameters of M_s and fine-tune the model M_t. Given the feature representation from the source and target model, we define a discriminator $D\left(M_{\mathrm{s}}\right(\mathbf{s}\left)\right)/D\left(M_{\mathrm{t}}\right(\mathbf{t}\left)\right)$, which learns to predict whether an instance, $\mathbf{s}/\mathbf{t}$, comes from the source or target dataset. For the discriminator, we use a three-layer feed forward NN. The final layer of the discriminator has a single output which is passed through a sigmoid squashing function. The output represents the probability whether a given instance belongs to the source dataset.

Intuitively, with adversarial learning, the discriminator competes with the feature generator such that M_t tries to confuse D. In our model, we accomplish this competition using two loss functions. First, the discriminator weights are trained using a standard supervised loss

$$-{\mathbb{E}}_{\mathbf{s}\sim \mathbf{S}}\hspace{0.17em}\left[\text{log}\right(D\left(M_{\mathrm{s}}\right(\mathbf{s}\left)\right)\left)\right]-{\mathbb{E}}_{\mathbf{t}\sim \mathbf{T}}\hspace{0.17em}\left[\text{log}\right(1-D\left(M_{\mathrm{t}}\right(\mathbf{t}\left)\right)\left)\right],$$ (3)

such that the discriminator tries to learn to predict which dataset each instance comes from. Likewise, the parameters of model M_t are updated by flipping the label for the target class,

$$-{\mathbb{E}}_{\mathbf{t}\sim \mathbf{T}}\hspace{0.17em}\left[\text{log}\right(D\left(M_{\mathrm{t}}\right(\mathbf{t}\left)\right)\left)\right]$$ (4)

compared to Equation (3). The model, M_t, is trained to produce features for target instances such that the discriminator thinks they come from the source dataset. We note that the gradient reversal layer (Ganin et al., 2016) could also be used instead of the two competing loss functions, however the discriminator is known to converge quickly causing the gradient to vanish when using RevGrad.

3.5 Historical regularization

Without constraining $M_{\mathrm{t}}\left(\mathbf{s}\right)$ during adversarial training, the loss function can oscillate (Salimans et al., 2016) hindering learning, or worse, converge to a degenerate solution. To avoid these issues with the GAN loss, we use historical regularization,

$$\left|\right|{\theta }_{M_{\mathrm{t}}}-\frac{1}{V}\sum _i^V{\theta }_{M_{\mathrm{t}}}^i|{|}_F^2,$$ (5)

where ${\theta }_{M_{\mathrm{t}}}^i$ represents the target base model parameters at the i-th training iteration and V is the total number of updates that have been made thus far.

3.6 Label smoothing

Label smoothing has been useful as a regularizer in NNs (Szegedy et al., 2016) and for label calibration (Guo et al., 2017). Here, we use one-sided label smoothing (Goodfellow, 2016; Szegedy et al., 2016;), a technique used to stabilize generative adversarial networks,

$$-.9\hspace{0.17em}{\mathbb{E}}_{\mathbf{s}\sim \mathbf{S}}\hspace{0.17em}\left[\text{log}\right(D\left(M_{\mathrm{s}}\right(\mathbf{s}\left)\right)\left)\right]-{\mathbb{E}}_{\mathbf{t}\sim \mathbf{T}}\hspace{0.17em}\left[\text{log}\right(1-D\left(M_{\mathrm{t}}\right(\mathbf{t}\left)\right)\left)\right],$$ (6)

where the expectation of the source data is down weighted. Intuitively, this technique is used to soften the predictions returned by the discriminator. If the discriminator predicts 1 for the source data, then the loss will learn to reduce the score to a smaller value.

Algorithm 1 Mini-batch stochastic gradient descent algorithm to train our adversarial domain adaptation method

1: for max number of stage 1 training iterations do

2:  Sample mini-batch of m source instances $\{{\mathbf{s}}^1,{\mathbf{s}}^2,\dots ,{\mathbf{s}}^m\}$ from S

3:  Minimize the classification loss and update the parameters according to the gradient:

  ${\nabla }_{{\theta }_{M_{\mathrm{s}}},{\theta }_C}[\frac{1}{m}\sum _i^m\hspace{0.17em}{y}^i\hspace{0.17em}\hspace{0.17em}\text{log}(C\left(M_{\mathrm{s}}\right({\mathbf{s}}^i\left)\right))-(1-y^i)\hspace{0.17em}\hspace{0.17em}\text{log}(1-C\left(M_{\mathrm{s}}\right({\mathbf{s}}^i\left)\right)\left)\right]$

4: end for

5: for max number of stage 2 training iterations do

6:  Sample mini-batch of k source instances $\{{\mathbf{s}}^1,{\mathbf{s}}^2,\dots ,{\mathbf{s}}^k\}$ from S

7:  Sample mini-batch of k target instances $\{{\mathbf{t}}^1,{\mathbf{t}}^2,\dots ,{\mathbf{t}}^k\}$ from T

8:  Update the discriminator parameters using the following gradient:

  ${\nabla }_{{\theta }_D}[\frac{1}{k}\sum _i^k\hspace{0.17em}.9\hspace{0.17em}\hspace{0.17em}\text{log}(D\left(M_{\mathrm{s}}\right({\mathbf{s}}^i\left)\right))-\text{log}(1-D\left(M_{\mathrm{t}}\right({\mathbf{t}}^i\left)\right)]$

9:  Sample a new batch of k target instances $\{{\mathbf{t}}^1,{\mathbf{t}}^2,\dots ,{\mathbf{t}}^k\}$ from T

10:  Update the base model parameters using the following gradient:

  ${\nabla }_{{\theta }_{M_t}}[\frac{1}{k}\sum _i^k\hspace{0.17em}\hspace{0.17em}\text{log}(D\left(M_{\mathrm{t}}\right({\mathbf{t}}^i\left)\right)+\left|\right|{\theta }_{M_t}-\frac{1}{V}\sum _j^V{\theta }_{M_{\mathrm{t}}}^j\left|{|}_F^2\right]$

11: end for

3.7 Training

We train the model in two phases. First, the model is trained on the source data by first optimizing the parameters ${\theta }_{M_{\mathrm{s}}}$ and ${\theta }_C$ according to Equation (2). In stage 2, the model parameters, ${\theta }_{M_{\mathrm{t}}}$, and discriminator parameters, ${\theta }_D$, are updated using Equations (4), (5) and (6). Both the source and target datasets are used in stage 2. The training procedure is formally presented in Algorithm 1. In stage 2, we emphasize that only the discriminator parameters, θ_D, are updated in step 8 of Algorithm 1, while only the target model parameters, ${\theta }_{M_{\mathrm{t}}}$, are updated at step 10. Intuitively, the discriminator and model are competing with each other. It is the discriminator’s job to learn to predict which dataset each instance comes from. Likewise, the model wants to learn to represent target instances such that they look like source examples. Finally, we note that the updates can be made using any learning rule. In this work, we use the Adam optimizer (Kingma and Ba, 2015).

4 Experiments

4.1 Model configuration

During stage 1 of our adversarial training procedure, both the CNN and Bi-LSTM models are trained using the Adam optimizer with a learning rate set to 0.001, beta1 set to 0.9 and beta2 set to 0.999. For stage 1, we train for a maximum of 25 epochs. Likewise, we used a mini-batch size of 16. To avoid overfitting, we use both dropout and l2 regularization, where the dropout value is set to 0.5 and the l2 regularization parameter is set to 0.00001. For the CNN model, we used filter widths of size 3, 4 and 5, with 300 filters learned for each size. In the Bi-LSTM model, we use a hidden state size of 256. In stage 2, for both the CNN and Bi-LSTM, we use a mini-batch size of 128 and train using Adam with a learning rate of 0.0001. We train for a total of 10 000 updates in stage 2. Finally, for our discriminator we use a three-layer feed-forward NN. The first two layers have 512 nodes each combined with the ReLU activation function. The final layer has a single output node which is passed through a sigmoid activation.

4.2 Datasets and comparison methods

In this paper, we conduct two sets of experiments. First, we study cross-corpora generalization with three datasets: BioInfer (Pyysalo et al., 2007), AIMed (Bunescu et al., 2005) and DDI (Segura-Bedmar et al., 2014). The basic statistics for each dataset can be found in Table 1. In all of our experiments, we use 80/20 train and test splits for evaluation. It should be noted that while the DDI dataset contains multiple relation types, we merge all relation types into a single positive class. We defer classifying relation types for future work. The use of these three datasets allow us to compare different scenarios in which we may want to use unsupervised domain adaptation for relation classification. For example, both BioInfer and AIMed are PPI datasets, however sampling bias causes poor cross-corpora performance. Hence, we can analyze how well adversarial domain adaptation can overcome sampling bias. Likewise, we also use the DDI dataset such that we can transfer the knowledge learned on either of the PPI datasets to find DDIs.

Table 1.

The counts for the number of sentences, positive and negative relations in each of the datasets

	# Sentences	# Positive	# Negative
AIMed	1955	1000	4834
BioInfer	1100	2534	7132
DDI	4579	4999	28 509

Next, we compare our method against the top systems on track 4 of the 2017 BioCreative shared task dataset (http://www.biocreative.org/tasks/biocreative-vi/track-4/). Unlike the other three datasets which have mention-level annotations, the BioCreative dataset contains relation annotations at the document level. In order to apply our adversarial method, we must pre-process the dataset such that it is similar to sentence-level relation classification. We assume if a document contains a relationship between two gene entities, then every sentence in the document that mentions the two genes express that relationship. Furthermore, the entities are not given for the test data, so we annotate genes using GeneNormPlus (Wei et al., 2015). Each document is split into sentences and instances are generated using pairs of genes that co-occur in a sentence. Finally, at test time, if we predict a relationship between two entities in any sentence, then we assume that relationship should be predicted at the document level. The BioCreative dataset contains 5546 articles and 1682 relations. We use the official train and test splits for evaluation.

We also compare against the 2017 task 5 BioCreative Chemprot dataset (http://www.biocreative.org/tasks/biocreative-vi/track-5/). Unlike the previous datsets, Chemprot finds interactions between two entities of different types: proteins and chemicals. In our experiments, we only consider relations that occurred in the same sentence which results in 6534 positive relations across 1632 documents. Finally, like the BioCreative dataset, we use the official test split for evaluation.

In this work, we compare two NNs for relation classification. Specifically, we use the CNN architecture proposed by Nguyen and Grishman (2015) and the word Bi-LSTM in Kavuluru et al. (2017). In order to see how our method works in the context of other adversarial domain adaptation methods, we compare against RevGrad (Ganin et al., 2016) applied both to the CNN and Bi-LSTM models. For all of these methods, we use the model specific parameters described in Section 4.1.

4.3 Evaluation measure

For the task for relation classification, we use the F1-score as our evaluation measure. F1-score is defined as the harmonic mean between precision (P) and recall (R) such that

$$P=\frac{\text{TP}}{\text{TP}+\text{FP}},\hspace{0.17em}R=\frac{\text{TP}}{\text{TP}+\text{FN}},\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}F1-score=\frac{2\hspace{0.17em}P\hspace{0.17em}R}{P+R},$$

where TP, FP and FN are the true positives, false positives and false negatives, respectively.

4.4 Results

The pairwise performances between the AIMed, BioInfer and DDI datasets are presented in Table 2. In this table, we report the mention-level F1-score. Overall, we make two observations. First, we observe that adversarial training always improves the cross-corpora generalization for the CNN and Bi-LSTM models. Moreover, our adversarial training unanimously outperforms the RevGrad adversarial domain adaptation method. For RevGrad, when the cross-corpora performance without adversarial training performs well (BioInfer ⇒ AIMed), then RevGrad can reduce the performance compared to not using adversarial learning.

Table 2.

F1-score for all pair wise combinations (source ⇒ target) of the three datasets

	BioInfer ⇒ AIMed	AIMed ⇒ BioInfer	BioInfer ⇒ DDI	DDI ⇒ BioInfer	AIMed ⇒ DDI	DDI ⇒ AIMed	AVG
CNN	0.4522	0.3672	0.3975	0.2213	0.1583	0.2793	0.3126
Bi-LSTM	0.4688	0.2959	0.4087	0.1721	0.1858	0.2580	0.2982
CNN RevGrad	0.4731	0.4255	0.4196	0.3611	0.3131	0.3072	0.3833
Bi-LSTM RevGrad	0.4641	0.4011	0.3941	0.3720	0.2772	0.3529	0.3769
Adv-CNN (Ours)	0.4879	0.5413	0.4419	0.4853	0.4596	0.4471	0.4772
Adv-Bi-LSTM (Ours)	0.4851	0.5654	0.4447	0.4490	0.4657	0.4344	0.4746

Bold entries indicate best results.

Second, when comparing the CNN versus Bi-LSTM, we observe in Table 2 that the CNN performs better with and without adversarial training. In Table 3, we compare the CNN and Bi-LSTM models when trained and tested on the same corpus. When there is no domain shift, the Bi-LSTM outperforms the CNN across all three datasets. We hypothesize that because the Bi-LSTM model is more complex than the CNN model, the Bi-LSTM is more prone to domain overfitting compared to the CNN. However, we see that after adversarial training both models perform comparably. Therefore, we suspect that there is an upper bound to the performance that can be obtained on these datasets with unsupervised domain adaptation techniques. While we suspect there is still room for improvement, without utilizing domain specific information, the datasets may differ in ways we cannot account for with our method.

Table 3.

The F1-score when training and testing on the same dataset (source ⇒ source). Specifically, these are the results of training on the 80% split and testing on the 20% split

	AIMed	BioInfer	DDI
CNN	0.5335	0.6079	0.7392
Bi-LSTM	0.6152	0.6562	0.7804

There are three main aspects to our model: adversarial learning, label smoothing and historical regularization. In Table 4, we perform an ablation study to understand how each of these factors affect performance. Here, we focus on the CNN results, given it had the best overall performance. We trained our model 10 times on the same train/test split using different random seeds each time. By repeating the training process, we analyze the average F1-score loss caused by removing each of the factors. We also look at the standard deviation to understand the stability they provide to the adversarial training process. First, we observe that both label smoothing and historical averaging have a large impact on the F1-score. More importantly, we see that removing historical regularization makes the training process unstable with a SD of 0.112. We believe that this regularization term grounds the learning process. Specifically, we hypothesize that it is easy for the word embeddings to converge to a degenerate solution.

Table 4.

Ablation study on the effects of label smoothing and historical regularization

	BioInfer ⇒ AIMed	AIMed ⇒ BioInfer	BioInfer ⇒ DDI	DDI ⇒ BioInfer	AIMed ⇒ DDI	DDI ⇒ AIMed
ADV-CNN	0.4820 ± 0.003	0.5433 ± 0.004	0.4389 ± 0.005	0.4844 ± 0.019	0.4507 ± 0.007	0.4386 ± 0.007
One-sided label smoothing	0.4722 ± 0.012	0.4626 ± 0.037	0.4116 ± 0.021	0.4320 ± 0.029	0.3676 ± 0.054	0.4081 ± 0.007
Historical regularization	0.4345 ± 0.022	0.3919 ± 0.112	0.4212 ± 0.016	0.4052 ± 0.084	0.4376 ± 0.022	0.3586 ± 0.065

Next, in Table 5, we compare our unsupervised domain adaptation method (with the CNN base model) against the top systems on the BioCreative dataset. We want to emphasize that we report document-level F1-score in Table 5. Because the competition involved PPI prediction, we evaluate using both AIMed and BioInfer as source datasets. Compared to the top systems, our method achieves state-of-the-art performance without training on the competition’s labeled dataset. Training on AIMed achieves an F1-score of 0.36. Moreover, we see improvements using the adversarial training across both the AIMed and BioInfer datasets. We get a 4% improvement applying adversarial learning on the BioInfer dataset. The improvement is enough to move from third to first place compared to the competition rankings. We believe our performance can be attributed to difficulty of developing document-level relation classification methods using the official training dataset. Likewise, we note that the F1-score is still rather low. We attribute this to the cascading errors caused by using GeneNormPlus for named entity recognition on the test set.

Table 5.

The F1-score compared with the top participants on task 4 of the 2017 BioCreative shared task

Team #/method	Precision	Recall	F1-score
375	0.3890	0.3010	0.3394
379	0.0981	0.5059	0.1643
391	0.2269	0.1910	0.2074
405	0.0693	0.0245	0.0362
420	0.3653	0.2561	0.3011
433	0.0581	0.2006	0.0901
AIMed	0.3423	0.3799	0.3601
BioInfer	0.2271	0.4344	0.2983
AIMed ⇒ BioCreative	0.4398	0.3159	0.3677
BioInfer ⇒ BioCreative	0.3829	0.3052	0.3397

Bold entries indicate best results.

4.5 Limitations and discussion

We report the F1-scores on the Chemprot dataset in Table 6. Without adversarial learning, we observe that the BioInfer dataset generalizes best on the Chemprot dataset. Moreover, unlike Table 2, the DDI dataset provides better generalizability than the AIMed dataset after adversarial domain adaptation. Both the AIMed ⇒ Chemprot and DDI ⇒ Chemprot experiments improve using adversarial learning. However, our methods do not improve the BioInfer score. The main reason adversarial learning does not work is because the proportion of positive to negative relations is very different in BioInfer (35%) compared to Chemprot (10%). The problem of class imbalance between datasets is a known problem for unsupervised domain adaptation methods (Ming Harry Hsu et al., 2015). In future work, we plan to research how to handle this problem with adversarial learning methods.

Table 6.

Results on the Chemprot dataset

Method	F1-score
AIMed	0.1683
BioInfer	0.3324
DDI	0.2927
AIMed ⇒ Chemprot	0.3127
BioInfer ⇒ Chemprot	0.2538
DDI ⇒ Chemprot	0.4007

We want to briefly touch on why we do not use historical regularization and label smoothing on with our RevGrad method. Specifically, RevGrad suffers from a vanishing gradient problem while our method (without historical regularization and label smoothing) suffers from instability during stage 2 of training. RevGrad works by flipping the sign of the gradient of the adversarial loss to update the CNN/Bi-LSTM parameters. Thus, the discriminator and network parameters are trained at the same time. However, if the adversarial loss is small, then the gradient will be small, causing the adversarial loss to have little impact on the CNN/Bi-LSTM parameters. Our method avoids this by splitting the adversarial loss into two components [Equations (3) and (4)]. To test this, we added both historical regularization and label smoothing to the CNN RevGrad method for the AIMed ⇒ BioInfer experiment and repeated it three times. The average F-score is 0.4234 which is similar to the result in Table 2.

Finally, we analyze changes in the model before and after adversarial training as presented in the Supplementary Material.

5 Conclusion

In this paper, we proposed an unsupervised adversarial domain adaptation approach to relation classification. We first experimented on three benchmark corpora: AIMed, BioInfer and DDI. We have shown an average improvement over 17% in F1-score compared to not using domain adaptation. Likewise, we demonstrated that our model shows superior performance compared to RevGrad. Next, on the BioCreative dataset, we achieve state-of-the-art results without using labeled training data. The following are some of the future avenues we wish to explore:

• While we have demonstrated the ability to adapt models between pairs of biomedical relation datasets, we believe multiple sources could be used during the training process to further improve on the results.

• We believe there is an upper bound to the knowledge that is usable between models trained on different relation datasets. This is evident when the entity types are different (e.g. DDI versus PPI). We believe that combining distance supervision with adversarial domain adaptation could provide significant improvements. While distantly supervised datasets are inherently noisy with the combination of adversarial domain adaptation we think the two methodologies will complement each other.