Evaluating statistical approaches to leverage large clinical datasets for uncovering therapeutic and adverse medication effects

Abstract

Motivation

Phenome-wide association studies (PheWAS) have been used to discover many genotype-phenotype relationships and have the potential to identify therapeutic and adverse drug outcomes using longitudinal data within electronic health records (EHRs). However, the statistical methods for PheWAS applied to longitudinal EHR medication data have not been established.

Results

In this study, we developed methods to address two challenges faced with reuse of EHR for this purpose: confounding by indication, and low exposure and event rates. We used Monte Carlo simulation to assess propensity score (PS) methods, focusing on two of the most commonly used methods, PS matching and PS adjustment, to address confounding by indication. We also compared two logistic regression approaches (the default of Wald versus Firth’s penalized maximum likelihood, PML) to address complete separation due to sparse data with low exposure and event rates. PS adjustment resulted in greater power than PS matching, while controlling Type I error at 0.05. The PML method provided reasonable P-values, even in cases with complete separation, with well controlled Type I error rates. Using PS adjustment and the PML method, we identify novel latent drug effects in pediatric patients exposed to two common antibiotic drugs, ampicillin and gentamicin.

Availability and implementation

R packages PheWAS and EHR are available at https://github.com/PheWAS/PheWAS and at CRAN (https://www.r-project.org/), respectively. The R script for data processing and the main analysis is available at https://github.com/choileena/EHR.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Post-market drug analysis is increasingly applied for uncovering rare or subtle effects and also may uncover novel therapeutic applications for a drug. These investigations are facilitated by the maturation of large, longitudinal databases such as electronic health records (EHRs), which can be used to identify novel adverse drug events (ADEs), study long-term drug safety, investigate the effect of drugs in special populations such as women and children and uncover new indications for existing drugs (Rastegar-Mojarad et al., 2015; Trifirò et al., 2009). However, an important limitation of EHRs is that data are observational and contain systematic biases; hence there is great need for tools that enable efficient and more comprehensive assessment of medication effects in EHRs and attenuate these biases.

The Phenome-wide association study (PheWAS) is a hypothesis-generating method to systematically test associations between a genetic variant or clinical factor of interest and a compendium of clinical outcomes or phenotypes, generally represented by individual billing codes or groupings of billing codes (Denny et al., 2010). PheWAS analyses have successfully replicated known genotype-phenotype associations, discovered new phenotype associations for genetic variants and been adapted to identify associations with non-genetic biomarkers (e.g. laboratory findings, clinical diagnoses, environmental exposures and seasonality; Boland et al., 2015; Denny et al., 2011; Denny et al., 2013; Hebbring, 2014; Krapohl et al., 2016; Liao et al., 2013; Neuraz et al., 2013; Rastegar-Mojarad et al., 2015; Ritchie et al., 2013; Ryan et al., 2013).

The application of PheWAS methods to the discovery of drug effects introduces several important statistical challenges. First, as with all observational (non-randomized) studies, subjects in the exposed group are often systematically different from those in the unexposed control group. In contrast to traditional PheWAS of a genetic variant, where the genetic ‘exposure’ precedes any outcomes and is assumed to be randomly distributed within a specified population, drug exposures are not randomly distributed. The indications for a particular drug may yield significant, systematic differences in the baseline and outcome status of medication exposed versus unexposed individuals. In order to determine the effect of the exposure of interest on outcomes, methods must be in place to account for these systematic differences. When there are a large number of covariates to be adjusted relative to the sample size and the number of cases, as there may be in PheWAS and other EHR-based studies, performing traditional covariate adjustment is unreliable or even infeasible. In cases such as these, propensity score (PS) methods are useful to adjust for an estimated probability of exposure based on a large number of covariates (Rosenbaum and Rubin, 1983). Several methods using PS have been developed, including PS matching (Rosenbaum and Rubin, 2012a), PS stratification (Rosenbaum and Rubin, 2012b) and inverse probability of treatment weighting (Rosenbaum, 1987). Matching on PS and adjusting for PS are the most commonly used approaches in traditional epidemiological and population-based EHR studies (Gagne et al., 2015; Hayes et al., 2016; Rosenbaum, 1987; Zhou et al., 2015).

A second challenge in using PheWAS to study drug effects is that many of the phenotypes are not common in any given population. With such sparse binary outcomes, complete separation is an obstacle for logistic regression (Ali et al., 2015). For example, when binary outcome and exposure variables are classified in a 2 x 2 table, complete separation occurs if no case is observed in one of the exposure groups––that is all cases are perfectly predicted by one exposure status. When complete separation occurs, the standard logistic regression method cannot provide reasonable results, since the estimate of the coefficient [i.e. the maximum likelihood estimate (MLE)] is infinite and P-value obtained from the default method of Wald test is meaningless. Instead of a Wald-type method, the conditional likelihood ratio test and the likelihood interval provide a better solution for complete separation (Albert and Anderson, 1984; Choi, 2011; Choi et al., 2015; Dupont and Plummer, 2016) if the goal of study is solely to test associations, but they cannot provide a finite MLE. Among several likelihood-based methods, the penalized maximum likelihood (PML) method [often called Firth’s penalized-likelihood logistic regression in genetics (Firth, 1993)], which was originally proposed to correct bias of the MLE, is a potential solution to the problem of complete separation since it can provide a finite MLE even for complete separation (Heinze and Schemper, 2002).

A third statistical challenge to this application of PheWAS is maintenance of adequate power without excessive Type I error. Since PheWAS involves testing thousands of outcome phenotypes for association to the exposure of interest, a substantial proportion of phenotypes will be falsely identified as associated at a nominal P-value threshold with each drug exposure (Type I error). At the same time, as a hypothesis-generating method, it is important to avoid large Type II errors which can lead to the inappropriate exclusion of potentially real drug effects, as can happen with conservative methods such as Bonferroni correction. Thus, an ideal PheWAS method maximizes power while controlling Type I error rates within an acceptable range.

The performance of various statistical methods for mitigating selection bias in the context of a high dimension, sparse phenotype matrix in order to use PheWAS analyses for the purpose of identifying drug effects has not been rigorously assessed. In this study, we performed Monte Carlo simulations with known true associations between exposure and outcome phenotypes and compared the two most commonly used methods for addressing confounding: matching on PS and adjusting for PS. We also evaluated logistic regression with two methods, the default (Wald test) and PML, the latter being a potential method to address complete separation. We assessed Type I error, power and bias for both methods. In addition, we suggest a standardized procedure for data pre-processing and analysis for PheWAS. We illustrate the application of our proposed methods to identify potential latent effects of medication exposure using pediatric patients exposed to two commonly used antibiotics, gentamicin and ampicillin.

2 Materials and methods

2.1 Data for case studies

The data for this study were extracted from a de-identified version of the Vanderbilt University Medical Center EHR called the Synthetic Derivative (SD; Roden et al., 2008). The SD is a research database where HIPPA safe harbor identifiers have been removed to create a non-human subjects resource for research.

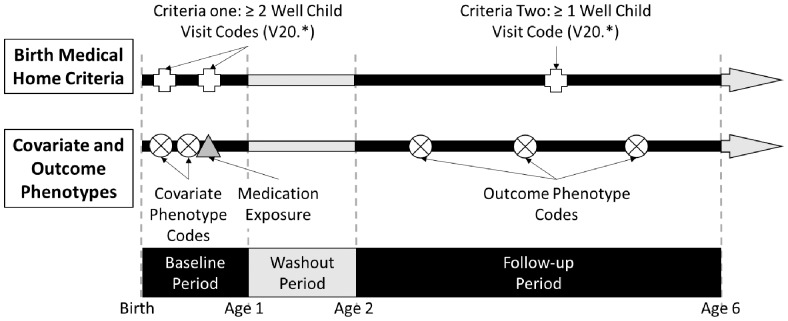
For the case studies, the hypothesis was that PheWAS-based methods and EHR data could be used to identify candidate novel latent drug effects, evident in children years after exposure to a drug during infancy. To test this hypothesis, we identified a set of individuals that met criteria to be a part of a ‘birth medical home’ cohort. Inclusion criteria are two health maintenance (‘well child’) visits at least 7 days apart within their first year of life (age = 0) and another well child visit between ages 2–5 years, defined by the presence of one of the V20 ICD-9 CM codes (‘Health supervision of infant or child’) in the patient’s EHR. Figure 1 demonstrates the two criteria for the birth medical home cohort. Each individual was classified as exposed or unexposed to gentamicin and ampicillin based on medication extraction using the MedEx tool applied to electronic order entry and clinical note text (Xu et al., 2010). Exposure was defined as one or more mentions of the drug name with dose, route, strength or frequency, occurring within the first year of life, with all other individuals defined as ‘unexposed’.

Fig. 1.

Cohort and phenotype definitions. The baseline period was defined as the first year of life and the follow-up period as 2–5 years of age. The top of the figure illustrates the inclusion criteria for the birth medical home cohort, where codes for health maintenance (‘well child’) visits are required in the baseline and follow-up periods. The center of the figure shows the covariate phenotype codes for the PSs, obtained from the baseline period and the outcome phenotype codes, obtained from the follow-up period. Also shown is the medication event; when present for the drug of interest, the individual is classified as ‘exposed’, and when absent, the individual is classified as ‘unexposed’

For the cohort, all ICD-9 CM codes were extracted for a baseline period of age = 0 and an outcome period of ages 2–5 years (Fig. 1), with translation of codes from the baseline and outcome periods to 1814 possible phecodes for PheWAS analysis using the v1.2 phecode map (Denny et al., 2013). Single instances of each phecode defined a case for the corresponding phenotype, race, sex and current age were extracted for use as covariates. Race was coded as a binary variable for EHR recorded race of ‘white’. Current age (on the date of data extraction) in our analysis acts as a measure of era, as each individual’s baseline and outcome data were extracted from age 0 and age 2–5 years, respectively. The baseline data were used in the case study as well as the simulation study.

2.2 Data pre-processing

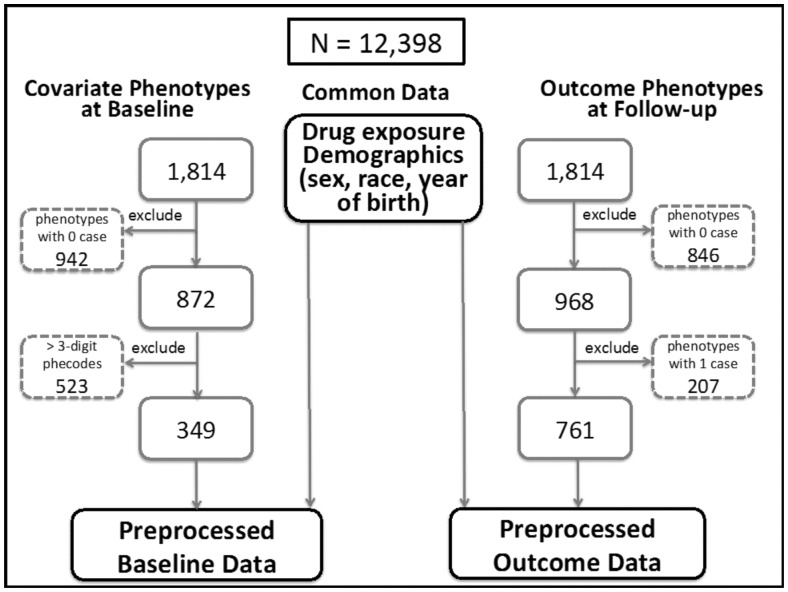
Figure 2 summarizes the data pre-processing procedure for PheWAS data obtained from the birth medical home population, with an emphasis on pre-processing covariate phenotypes at the baseline (left) and outcome phenotypes at the follow-up (right). The demographic features (sex, race and year of birth) are the same for the baseline and outcome data. From all of the possible phenotypes, first we excluded phenotypes with no observed cases: 942 phenotypes in the baseline data and 846 in the follow-up data. For the outcome phenotypes, we excluded an additional 207 phecodes with only one case (21% of the 968 with any observed cases). Due to the hierarchical nature of phecodes (Denny et al., 2013), the more specific 4 and 5-digit phecodes are often highly correlated with their parent 3-digit codes as cases in the lower level codes are also cases in the higher level codes. For example, ‘381: Otitis media and Eustachian tube disorders’ (n = 4, 790 at baseline) is almost identical to ‘381.1: Otitis media’ (n = 4772 at baseline). However, another child code of 381, ‘381.2: Eustachian tube disorders’, has only 97 individuals at baseline. The inclusion of highly correlated covariate phecodes may not provide much valuable information as a covariate when building a PS model, while inducing collinearity in the regression analysis, which should be avoided. Decreasing the number of covariate phecodes also helps build more stable PS model while reducing analysis and simulation times. Thus, we only included 3-digit phecode phenotypes for the baseline data, excluding 523 lower level phecodes. For the outcome data, all codes (3-, 4- and 5-digit phecodes) were evaluated. This data pre-processing yielded 349 covariate phenotypes in the baseline period and 761 outcome phenotypes in the follow-up period for the pediatric dataset.

Fig. 2.

Diagram of data pre-processing

2.3 PS model and generation of PS matched exposure-control datasets

A PS model was developed for PS matching or PS adjustment. The PS is the probability of being exposed conditional on observed covariates, obtained using a logistic regression with the exposure variable as the outcome. Age was included as a continuous variable, and baseline phenotypes, race and sex as binary variables. Most of the covariates are very sparse and the expected exposure rates are low (e.g. 10% for gentamicin), and hence a logistic regression could not be reliably performed with 352 covariates (349 phenotypes, age, sex and race), even with a large sample size (N = 12 398). Regularized regressions such as ridge regression or lasso have been proven very useful when the number of covariates, k, is greater than the sample size, n, (i.e. k > n). Although PheWAS data are k < n typically with very large sample size, regularized regression methods are still useful with sparse binary outcomes, which can shrink coefficients toward zero, most of which are likely to be zero (i.e. no effect). Thus, we adopted a regularized logistic regression with elastic-net penalty (Zou and Hastie, 2005) to obtain PS in logit scale using the predicted probability of being exposed, which was implemented using an R package glmnet (Friedman et al., 2010). The elastic-net penalty parameter, α, ranges from 0 to 1, from which we used two extreme values of α = 0.1 and 0.9, closer to ridge regression (equivalent to α = 0) and lasso (equivalent to α = 1), respectively, to examine sensitivity to the choice of penalty.

Using the generated PS, matched exposure-control datasets were constructed by selecting control subjects whose PS values were matched to exposed subjects, with matching ratios of exposure to control, 1–1, 1–2 and 1–4, using an R package Matching (Sekhon, 2011) with a caliper of 0.2 as suggested in Austin (Austin, 2011) and without allowing replacement and ties to speed up simulations. Since the PS for some subjects were very extreme (more than 5% had greater than ±3 in logit scale), we also generated trimmed datasets consisting of subjects within the 5th to 95th percentiles of PS, in order to evaluate sensitivity of the analysis results to the subjects with extreme PS values. Datasets for an alternate strategy using PS adjustment analyses were also generated, which include all individuals (the full dataset) as either exposed cases or unexposed controls, and their PS.

2.4 Outcome model

For each outcome phenotype, a logistic regression was performed using each of the PS matched datasets without adjusting for any covariates as well as the full data with adjustment of PS only. Two estimation methods in logistic regression were employed. First, the associations between drug exposure and outcome phenotypes were tested using the Wald test, the default test method in logistic regression. When complete separation occurs, a logistic regression model does not converge, yielding extremely large coefficients (in absolute value) and P-values that are not meaningful. This occurs regardless of how many cases are observed in the exposed or control group, although some of these phenotypic associations could be real. For example, if 100 cases are observed in exposed group with no case in control group for a given phenotype, this phenotype can be potentially important, yet will be missed. To handle complete separation, we applied the PML method using an R package logistf (Heinze and Ploner, 2016) that can provide a finite estimate for the regression coefficient and a reasonable P-value that can be useful to identify potentially important phenotypes when complete separation occurs.

2.5 Simulation study

A typical dataset for a PheWAS examining the effect of an exposure on outcome phenotypes includes a fixed set of data at a given time. Based on our pediatric cohort of 12 398 individuals, we used the baseline data to simulate datasets for outcome phenotypes with known associations between the exposure and outcome phenotypes, while approximately preserving the distribution of case frequency for outcome phenotypes. We assumed three scenarios for exposure effects on outcome phenotypes in terms of odds ratio (OR): the null hypothesis (OR = 1), moderate effect (OR = 2) and strong effect (OR = 3). We expect that only few latent ADEs, if any, will be associated with drug exposure in real life—thus, a small percent (1.5%) of outcome phenotypes were assumed to be truly associated with drug exposure and the majority (98.5%) to be the null—i.e. only 11 out of 761 outcome phenotypes are expected to be associated under each alternative. Specific simulation steps for outcome phenotypes are summarized in Figure 3 and described in detail as follows.

Fig. 3.

Summary of simulation steps

In order to mimic the distribution of case frequency for the observed outcome phenotypes data, for each observed outcome phenotype, y_j, j = 1, …, 761, we performed a logistic regression with regularization using elastic-net penalty of α = 0.5 on the covariate matrix, X, which includes all baseline covariates except the exposure variable, and obtained the jth set of coefficient estimates (ß_j) (i.e. a vector length of 353 for the intercept, age, race, sex and 349 covariate phenotypes). For the outcome phenotypes with extremely low case frequency (e.g. ≤ 3), for which the analysis did not converge, all coefficients were assumed to be zero except for the coefficient for intercept that was estimated using its observed frequency to mimic the observed data. To account for uncertainty, we simulated ß_j* from normal distribution with the mean of the estimated coefficients, ß_j and the SD of 0, 0.05, 0.5 and 0.5 for the intercept, age, race and sex, respectively, and 0.1 for all covariates phenotypes. Then, ß_j* were used to simulate the jth outcome phenotype as follows.

We set the known associations between the exposure and outcome phenotypes (i.e. OR = 1, 2 and 3), by randomly assigning these three values of log ORs to each of outcome phenotypes, denoting γ_exp,j. Considering sparsity of most phenotypes, when assigning the coefficients for alterative hypotheses, we ensured that they were assigned to outcome phenotypes with relatively high case frequency (i.e. upper 85 percentile of frequency distribution) with higher probability, while still allowing them to be assigned to those with low case frequency using a ratio of 20 to 1 in probability; this ensured that the majority of outcome phenotypes assigned to the alternatives can remain in the analysis after excluding no case during the data pre-processing. Let Z be the baseline data including the exposure variable, E, mimicking from ampicillin case study (i.e. Z = X + E), and θ_j = ß_j* + γ_exp,j be the vector of simulation coefficients (i.e. the length of 354) including the hypothesized exposure coefficient, γ_exp,j for the jth outcome phenotype. With the linear predictor, Zθ_j, the probability of being case for the jth outcome phenotype, p_j = 1/[1 + exp(–Zθ_j)], was calculated, which was used to simulate binary outcomes for the jth outcome phenotype, y_j* from Bernoulli distribution with probability p_j. Combining these 761 simulated outcome phenotypes with the exposure and three demographic variables (i.e. age, race and sex), the final simulated dataset was constructed.

With each of 1000 simulated datasets, the associations between exposure and outcome phenotypes were tested at significance level of 0.05 and the coefficients were estimated using the methods described above. For each hypothesis, the proportion of outcome phenotypes yielding P < 0.05 (i.e. positive rate) was calculated, and bias was estimated using the mean squared errors (MSEs) defined by the mean of squared differences between the estimate and the hypothesized value. Then, the Type I error rate and power as well as the mean bias were calculated using the mean of positive rates and bias across 1000 simulations with and without exclusion of outcome phenotypes that yielded complete separations. The simulation studies were conducted using R Statistical Software (version 3.2.1; R Core Team, 2017).

2.6 Case studies

We performed PheWAS using the data with gentamicin and ampicillin exposures as case studies using the methods described above. A PS for exposure to each antibiotic in the first year of life was created for all individuals meeting the birth medical home criteria. A PheWAS was performed for each drug, with phecode phenotypes as the outcome in a PML logistic regression model predicted by gentamicin or ampicillin exposure adjusting for the PS using an R package PheWAS (Carroll et al., 2014). For comparison to the typical PheWAS approach employed in most genetic studies, models adjusting only for demographic variables (age, sex and race) were also tested. To limit to only those phenotypes that are clinically reasonable, we removed codes for congenital conditions for the case study analyses.

3 Results

3.1 Simulation studies

3.1.1 Comparison between PS matched and PS adjustment analyses

Table 1 presents the simulation results based on PS generated with elastic-net penalty of α = 0.1, which compares the analyses that were performed using PS matched datasets and the full dataset with PS adjustment. Of note, when the analyses were performed with the full dataset without use of a PS, Type I error rates were as high as 0.3 (data not shown). With the PS, the sample size was larger for the full versus matched datasets, with respect to both the number of individuals (e.g. 12 398 for full data versus 2818 for 1:1 matching) and the average number of phenotypes tested (e.g. 720 for full data versus 536 for 1:1 matching) after excluding those with no cases. The results under the null hypothesis reveal that the Type I error rates from all analyses ranged from 0.01 to 0.04, indicating that Type I error was well controlled at the significance level of 0.05 in all scenarios. PS matched analyses had lower Type I error rates, which may be due to the elimination of phenotypes with smaller case counts due to smaller overall population size. Results under the alternative hypotheses demonstrated that the full data analysis with PS adjustment resulted in greater power compared to the PS matched analyses: 62% versus 41–52% for OR = 2 and 83% versus 70–78% for OR = 3. The number of phenotypes under the alternative hypotheses was sometimes 10, smaller than originally hypothesized 11, for the PS matched analyses, since candidate phenotypes were excluded before the analysis as part of data pre-processing. The reduction of tested outcome phenotypes likely contributed to the decreased Type I error rates for the PS matched analyses, when compared to the PS adjusted analyses. As expected, the power was greater for the larger effect size of OR = 3 compared to OR = 2, regardless of PS method used.

Table 1.

Type I error rate and power based on simulation results for PS matched data analysis (1–1, 1–2 and 1–4) and PS adjusted data analysis

	PS matched	PS matched	PS matched	PS adjustment (N =12 398)
	(1–1)	(1–2)	(1–4)
	(N = 2818)	(N = 4227)	(N = 7045)
Null hypothesis (Type I error)
OR = 1	0.02	0.01	0.02	0.04
# phenotypesa	536	575	617	720
Alternative hypotheses (Power)
OR = 2	0.41	0.48	0.52	0.62
# phenotypesa	10	10	11	11
OR = 3	0.70	0.75	0.78	0.83
# phenotypesa	11	11	11	11

Note: All PS generated with elastic-net penalty of α = 0.1.

^aAverage number of outcome phenotypes remaining in the simulated datasets.

3.1.2 Comparison between the default and PML methods in logistic regression

On average, 27% of the outcome phenotypes resulted in complete separation (i.e. no case in either the exposed group or the unexposed control group). As expected, complete separation yielded unreasonable extreme estimates for coefficients from the standard logistic regression and P > 0.99 with its default Wald test method due to infinite MLEs for these outcomes. On the other hand, the analyses where models were fit with the PML approach and tested using those penalized likelihoods yielded reasonable estimates of coefficients and P-values for the outcomes with complete separation. To examine how the instances of complete separation would affect the results, we excluded outcomes with complete separation and compared average results for the remaining 526 outcomes. For both methods, the Type I error rates were well controlled at level of 0.05 and the power was similar (Table 2). The reason for similar power for both methods was due to the fact that complete separation occurred very rarely in the analyses for the outcome phenotypes simulated under the alternative hypotheses by our simulation design (i.e. their case frequency was relatively high, which prevented complete separation) as evidenced in almost same average number of outcome phenotypes remaining in the simulated datasets. On the other hand, the mean bias was much smaller with the PML compared to the default method, even for the analyses without complete separation (Table 3).

Table 2.

Type I error rate and power based on simulation results comparing the conventional maximum likelihood method (Wald) and the PML method

	All outcome phenotypes			Excluding complete separation
	Wald	PML	# phenotypesa	Wald	PML	# phenotypesa
Null hypothesis (Type I error)
OR = 1	0.04	0.04	720	0.05	0.04	526
Alternative hypotheses (Power)
OR = 2	0.62	0.61	11	0.65	0.65	10
OR = 3	0.83	0.83	11	0.86	0.86	11

Note: Logistic regressions performed with PS adjustment, using PS generated with elastic-net penalty of α = 0.1.

^aAverage number of outcome phenotypes remaining in the simulated datasets.

Table 3.

Mean bias (i.e. MSE) based on simulation results comparing the conventional maximum likelihood method (Wald) and the PML method

	All outcome phenotypes			Excluding complete separation
	Wald	PML	# phenotypesa	Wald	PML	# phenotypesa
Null hypothesis (Type I error)
OR = 1	170.1	1.4	720	0.85	0.76	526
Alternative hypothesis (Power)
OR = 2	15.3	0.4	11	0.21	0.18	10
OR = 3	10.2	0.3	11	0.19	0.16	11

Note: Logistic regressions performed with PS adjustment, using PS generated with elastic-net penalty of α = 0.1.

^aAverage number of outcome phenotypes remaining in the simulated datasets.

3.1.3 Sensitivity to regularization penalty parameters for PS model

The elastic-net penalty parameter, α, for the PS model had little effect on predicting PS, although the analyses using PS generated with α = 0.9 resulted in very slight increase in power for the analyses with matched datasets, compared to those using PS generated with α = 0.1 (Supplementary AppendixTable A1).

3.1.4 PS trimmed data analysis

The Type I error rates from PS trimmed data analyses were similar compared to those without trimming, but the power was decreased as expected, due to the decreased sample size (Supplementary AppendixTable A2).

3.2 Case studies: latent effects of gentamicin and ampicillin in pediatric patients

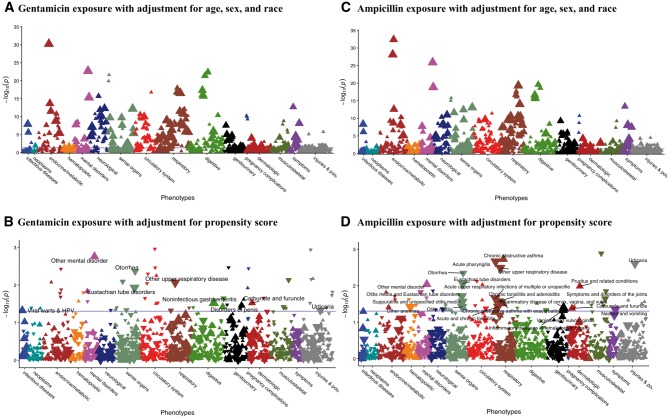
The summary of demographics and exposure variables is presented in Table 4. For gentamicin exposure in the first year of life, PheWAS of outcomes at ages 2–5 years adjusting for only demographic variables and not PS using the PML method indicated 302 phenotypes with P < 0.05 (Fig. 4A). In contrast, only 57 were significant when adjusting with the PS (Fig. 4B). The blue horizontal lines in Figure 4 represent a nominal significance level of 0.05, without multiple testing correction. Of those, 17 have OR > 1, indicating increased risk associated with gentamicin exposure. The phecodes with the most abundant case counts, representing those most likely to have clinical relevance, are ‘non-infectious gastroenteritis’ (OR = 1.31, P = 0.03); ‘other mental disorder’ (OR = 1.86, P = 0.002); ‘viral warts and HPV’ (OR = 1.71, P = 0.047); ‘disorders of penis’ (OR = 1.73, P = 0.035) and ‘carbuncle and furuncle’ (OR = 1.91, P = 0.03). A total of 40 phenotypes had OR < 1, indicating a potential protective effect from early gentamicin exposure. Phecodes with the most abundant case counts in this category included ‘Eustachian tube disorders’ (OR = 0.67, P = 0.012); ‘other upper respiratory disease’ (OR = 0.66, P = 0.009) and ‘urticaria’ (OR = 0.65, P = 0.047). All results from the PS adjusted analysis of gentamicin are presented in Supplementary AppendixTable A3.

Table 4.

Demographic data for ampicillin and gentamicin case studies

		Ampicillin			Gentamicin
	All	Exposed	Unexposed		Exposed	Unexposed
N	13 642	1462	10 289		1263	11 205
N Female	6660	647	5092		539	5552
%	48.8%	44.3%	49.5%		42.7%	49.5%
Mean age	10.3	7.9	9.1		8.8	11.1
SD	5.1	3.3	4.0		3.6	4.9
N White	4965	505	3668		449	4114
%	36.4%	34.5%	35.6%		35.6%	36.7%

Fig. 4.

PheWAS Manhattan plot of latent outcomes effects of gentamicin and ampicillin exposures during infancy. For all plots, phenotypes are grouped along the x-axis by category, and the y-axis is the –log10 of P-value. The blue line indicates a nominal 0.05 significance level. The direction of each triangle indicates the direction of effect, with upward triangles for ORs (OR) > 1 and downward triangles for OR < 1. The size of each triangle indicates the number of total cases for each phecode, with the smallest triangles for < 50, then < 100 and < 200 cases and the largest triangles for ≥ 500 cases. (A) Phenotypes ascertained at age 2–5 associated with gentamicin exposure in infancy, with adjustment for age, sex and race. (B) Phenotypes ascertained at age 2–5 associated with gentamicin exposure in infancy, with adjustment for PS for gentamicin exposure. (C) Phenotypes ascertained at age 2–5 associated with ampicillin exposure in infancy, with adjustment for age, sex and race. (D) Phenotypes ascertained at age 2–5 associated with ampicillin exposure in infancy, with adjustment for PS for ampicillin exposure

For ampicillin, adjusting for only demographic variables and not PS resulted in 439 phenotypes with P < 0.05 associated with early exposure (Fig. 4C), and PS adjustment reduced this number to 58 (Fig. 4D). Of those, 23 have OR > 1. The phecodes with the most abundant case counts include ‘inflammatory diseases of female pelvic organs’ (OR = 1.4, P = 0.047); ‘other mental disorder’ (OR = 1.66, P = 0.009) and ‘chronic obstructive asthma’ (OR = 1.91, P = 0.002). The 35 phenotypes with OR < 1, indicating an association of exposure to decreased incidence of the phenotype, included ‘acute upper respiratory infections’ (OR = 0.85, P = 0.022); ‘Eustachian tube disorders’ (OR = 0.68, P = 0.009) and ‘nausea and vomiting’ (OR = 0.83, P = 0.045). All results from the PS adjusted analysis of ampicillin are shown in Supplementary AppendixTable A4.

4 Discussion

Initially introduced as a way to use EHR data to identify the clinical impact of genetic variation, PheWAS is increasingly used to generate hypotheses around a variety of exposures. For many types of exposures, the appropriate statistical methods have not been rigorously studied. Specifically, the best methods to control for confounding factors and maximize power to detect potential signal such as drug effects have not been identified. In this study, we compared two methods most commonly used to account for potential confounding, PS adjustment and PS matching. Our main finding from the simulation study was that the Type I error rates for both methods were well controlled at 0.05, while the method of PS adjustment resulted in greater power compared to the matched data analyses due to reduced sample size in the matched analyses.

Within our datasets, the majority of outcome phenotypes are very sparse, leading a high rate of complete separation, namely an average of 27% of outcome phenotypes in simulated datasets and 31% and 30% in gentamicin and ampicillin case study, respectively. With the standard logistic regression approach, each of these outcomes with complete separation had not yielded meaningful results. The use of the PML method generated P < 0.05 in some of these instances (10 and 8 phenotypes for gentamicin and ampicillin, respectively), demonstrating that we were able to recover significant results, potentially due to true association with the exposure. Given the hypothesis-generating goal of PheWAS analysis (with subsequent validation in independent datasets), it is important to be able to identify candidate phenotypes, even in instances of complete separation. The PML method provided reasonable P-values with well controlled Type I error rates (without requiring multiple testing corrections). In addition, PML in logistic regression can reduce bias in the parameter estimates and provide reasonable estimates even for complete separation, for which those from the standard logistic regression diverge to ± infinity.

Although PheWAS data typically have very large sample sizes such that the number of covariates is less than the sample size (i.e. k < n), a logistic regression to generate PS using the many sparse binary phecodes commonly observed in PheWAS could not be reliably performed. Our simulation study supported the use of regularized regression methods in this circumstance, and the choice of regularization penalty parameter in PS model had little effect on the results, although it would be good practice to perform sensitivity analysis using at least two extreme penalty parameters as demonstrated in the simulation study. When performing PheWAS on drug exposures, particularly for those that are not commonly used, we do not recommend trimming data based on the PS, which resulted smaller power in our simulations. Based on our simulation studies, we recommend PS adjustment over PS matched data analysis to gain more power, while controlling for the Type I error rate at reasonable level. These characteristics are important for a PheWAS, as they permit obtaining the most complete set of candidate phenotypes for further studies without a large increase in the false discovery rate. In addition, we recommend using PML instead of the default method in logistic regression to identify phenotypes with complete separation which may be truly associated with the exposure. We also recommend standardizing the data pre-processing as we described in this study, as summarized in Figure 2. The R script for data pre-processing and the main analysis as well as the major part of simulation codes are available at https://github.com/choileena/EHR and the functions used for the analysis are freely available as an R package EHR (Choi and Beck, 2017) and an R package PheWAS at https://github.com/PheWAS/PheWAS. Although the simulation studies were based on data obtained from pediatric population, the statistical approach we suggest would be applicable to other types of PheWAS with diverse populations.

The case studies using pediatric exposures to gentamicin and ampicillin show a dramatic reduction in the number of candidate associations after adjustment for PS, many of which were likely false positive results and appropriately removed. The PS adjusted results provide a much more reasonable list of interesting observed associations without correcting multiple testing. Renal damage is a known ADE of gentamicin. Among the phenotypes associated with gentamicin exposure during infancy is ‘disorders resulting from impaired renal function’, (n = 64 individuals, OR = 6.49, P = 0.004). This association may serve as a positive control for this study. For the identification of possible latent effects of early antibiotic exposures in infants, both ampicillin and gentamicin were associated with increased risk for ‘other mental disorder’. In this cohort, the most frequent specific billing code included in this phecode is V40.3, other behavioral problems. There are no known associations between early antibiotic exposure and later childhood behavior problems. If replicated in an independent dataset, this may represent a novel sequela of early exposure to these drugs. However, causality cannot be determined based on this retrospective, observational dataset. This association may be observed due to residual confounding and not a direct manifestation of drug exposure. Knowing the patterns of risk for outcomes after drug exposures can be of value to clinicians who follow patients long-term, as it may facilitate focused screening, early detection and modification of risk factors. Furthermore, since the majority of individuals were exposed to both gentamicin and ampicillin, the associations identified may be driven by exposure to either antibiotic, or represent a drug-drug-interaction. There are not enough individuals with exposure to one, but not the other, antibiotic for further investigation of these possibilities.

We do not recommend an additional adjustment of demographic covariates in the analyses, which were already incorporated into the PS. The inclusion of additional covariates may lead unreliable results for sparse phenotypes, likely increasing the false discovery rate. However, after selecting list of candidate phenotypes, the analyses with additional adjustment of demographic covariates could be performed post-hoc. As we have demonstrated in case study, clinically unreasonable or irrelevant phenotypes (e.g. congenital conditions) can be removed. Another common strategy is to filter based on number of cases to exclude rare conditions (e.g. exclude phenotypes with < 20 cases), which may be statistical artifacts and/or clinically irrelevant.

Our data analysis approach has several limitations. Even though the statistical approach we recommend would be applicable to other medications, other types of PheWAS data and/or other analytical approaches than PheWAS, our simulation findings would need to be confirmed in other datasets and for other applications. In addition, while the PS adjusted analysis demonstrated greater power than PS matched analysis in simulation and more reasonable results than adjustment for demographics alone in our case studies, residual confounding not captured by the PS may still impact the results and lead to false positive associations. All PheWAS results require replication in external datasets, including those generated with the methods we propose and the results of the case studies. Furthermore, the limitations inherent to observational studies and EHR-based research would not be precluded through the application of our methods. For example, incomplete ascertainment of exposures (e.g. individuals may have received antibiotic therapy at another facility, not captured in our EHR), and ascertainment bias (e.g. children exposed to gentamicin may have increased screening for kidney function, due to the known nephrotoxic danger of the drug) are persistent limitations in all studies using EHR data. PheWAS using phecodes is a powerful hypothesis generation and discovery tool, but using presence and absence of billing codes has inherent limitations. Some individuals have missing (false negative) billing codes, i.e. individuals appear to be controls but are actually cases, which increases the false negative rate. Other individuals have billing codes for conditions they do not have, due to misdiagnosis or errors in assigning billing codes, causing false positives. We expect these misclassifications not to differ between exposed and non-exposed groups in our cohort. This type of misclassification (called non-differential misclassification) produces a bias toward the null, increasing the likelihood a true association may be missed (Rothman et al., 2015). However, depending on exposure, it is possible that differential misclassification (i.e. the misclassification differs between exposed and non-exposed groups) may occur, which could yield a bias in either direction. Potential differential misclassification should be judged case-by-case. Another concern would be correlated phecodes that may be also misclassified, which would have similar impact on the results as discussed above. In addition, a causal relationship between drug exposure and outcome cannot be proven based on association in observational data.

5 Conclusion

PheWAS analysis of longitudinal EHR datasets is one method for hypotheses generation, but investigators must be mindful of issues of confounding by indication and low event rates. Based on our simulation studies, PS adjustment provides greater power than PS matching and controls Type I error. The PML regression approach, rather than the conventional logistic regression approach, results in reasonable P-values and well controlled Type I error. Combining these methods of PS adjustment and PML regression yielded an effective tool for applying PheWAS that avoids some common pitfalls.