Femtosecond Hydration Map of Intrinsically Disordered α-Synuclein

Abstract

Protein hydration water plays a fundamentally important role in protein folding, binding, assembly, and function. Little is known about the hydration water in intrinsically disordered proteins that challenge the conventional sequence-structure-function paradigm. Here, by combining experiments and simulations, we show the existence of dynamical heterogeneity of hydration water in an intrinsically disordered presynaptic protein, namely α-synuclein, implicated in Parkinson’s disease. We took advantage of nonoccurrence of cysteine in the sequence and incorporated a number of cysteine residues at the N-terminal segment, the central amyloidogenic nonamyloid-β component (NAC) domain, and the C-terminal end of α-synuclein. We then labeled these cysteine variants using environment-sensitive thiol-active fluorophore and monitored the solvation dynamics using femtosecond time-resolved fluorescence. The site-specific femtosecond time-resolved experiments allowed us to construct the hydration map of α-synuclein. Our results show the presence of three dynamically distinct types of water: bulk, hydration, and confined water. The amyloidogenic NAC domain contains dynamically restrained water molecules that are strikingly different from the water molecules present in the other two domains. Atomistic molecular dynamics simulations revealed longer residence times for water molecules near the NAC domain and supported our experimental observations. Additionally, our simulations allowed us to decipher the molecular origin of the dynamical heterogeneity of water in α-synuclein. These simulations captured the quasi-bound water molecules within the NAC domain originating from a complex interplay between the local chain compaction and the sequence composition. Our findings from this synergistic experimental simulation approach suggest longer trapping of interfacial water molecules near the amyloidogenic hotspot that triggers the pathological conversion into amyloids via chain sequestration, chain desolvation, and entropic liberation of ordered water molecules.

Introduction

Protein hydration layer has a profound influence on the structure, dynamics, binding, assembly, and function of proteins (1, 2, 3, 4, 5, 6, 7). The water molecules present in the vicinity of the polypeptide chain exhibit unique dielectric and dynamical characteristics that are fundamentally different from those of the bulk water (1). Water is believed to drive the hydrophobic collapse during the protein-folding process (8). A broad range of techniques, such as neutron scattering, nuclear magnetic resonance (NMR), vibrational, terahertz, and femtosecond fluorescence spectroscopy, and molecular dynamics (MD) simulations, have been employed to investigate the unique properties of hydration water in globular proteins (9, 10, 11, 12, 13). These studies have shown that the mobility of interfacial hydration water is significantly restrained compared to that of bulk water. The hydration water in proteins is termed as “biological water” (5, 7). However, unlike in globular proteins, the behavior of water in an emerging class of proteins known as intrinsically disordered proteins (IDPs) remains elusive. IDPs lack the ability to undergo autonomous folding under the native condition and exist as dynamic ensembles of interconverting structures (14, 15). The dynamic nature of IDPs confers them the flexibility to adopt a diverse range of conformations that expand the functional repertoire of proteins (14, 15, 16, 17, 18). The conformational plasticity of IDPs is also responsible for protein misfolding that results in aberrant protein aggregation yielding cytotoxic amyloids associated with a number of debilitating neurodegenerative diseases (19, 20, 21). The amino acid composition and the intricate balance between chain-chain and chain-solvent interactions is conjectured to play a pivotal role in determining the conformational ensemble of IDPs (22). However, little is known about the nature and the role of hydration water in functional and pathological consequences of IDPs.

In our work, we have chosen α-synuclein (α-syn), which is believed to play a central role in the pathogenesis of Parkinson’s disease (23). The aggregates of α-syn are the main component of Lewy bodies, which epitomize the characteristic histological feature of Parkinson’s disease (23). Although α-syn belongs to the class of expanded IDP devoid of any significant collapse (24, 25), there are transient long-range interactions that make α-syn marginally more compact than an archetypal random-coil in solution (26, 27, 28). The precise cellular function of α-syn has remained largely unclear; however, it has been implicated in synaptic plasticity, learning, neurotransmitter release, dopamine metabolism, and vesicular trafficking (29). α-syn consists of 140 amino acid residues and can be broadly divided into three distinct domains based on the amino acid composition: 1) the positively charged N-terminal domain [aa 1–60], which is crucial for the protein-membrane interaction; 2) the hydrophobic and amyloidogenic nonamyloid-β component (NAC) domain [aa 61–95]; and 3) the negatively charged, proline-rich C-terminal domain [aa 96–140] with chaperone-like activity (30).

In this work, we monitored the behavior of hydration water in different regions of monomeric α-syn using highly sensitive femtosecond time-resolved fluorescence spectroscopy. Additionally, we performed atomistic MD simulations of solvated α-syn to identify the molecular origin of such region-specific dynamics of hydration water. The results from this synergistic experimental simulation approach suggest that the distinct water rearrangements governed by the local amino acid composition and conformation are likely to translate into specific functional and pathological roles for α-syn.

Materials and Methods

Site-directed mutagenesis, protein expression, purification, and labeling

The plasmid construct used for the recombinant expression of α-syn in Escherichia coli BL21 (DE3) pLys S strain was the same as reported previously (31). The cysteine mutations at 9, 18, 56, 78, 90, and 140 were created using the QuikChange site-directed mutagenesis kit (Stratagene, San Diego, CA). The primer sequences are shown in Table S1. The expression and purification of the mutants was same as that of wild-type α-syn with some modification (31). The buffer used for dialysis was pH 7.4 with 20 mM Tris buffer containing 1 mM dithiothreitol (DTT) and 50 mM NaCl. Labeling of the cysteine variants was carried out with a 5 M excess of acrylodan under denatured condition (6 M GdmCl in pH 7.4 with 20 mM Tris buffer containing 1 mM DTT and 50 mM NaCl). The labeled proteins were then passed through a PD-10 column to remove excess dye. For all the experiments, the buffer exchange with the native buffer (pH 7.4) (20 mM Tris buffer containing 1 mM DTT and 50 mM NaCl) was performed on a PD-10 column. The proteins were filtered through AMICON ultra (50 KDa cutoff; Millipore, Burlington, MA) immediately before the experiments. The concentration of the labeled protein was estimated using ε₃₆₅ = 12,800 M⁻¹ cm⁻¹ (32). The concentration of the labeled proteins used for all our fluorescence measurements was ∼40 μM. All the spectroscopic measurements were carried out at room temperature.

Steady-state fluorescence

The steady-state fluorescence measurements were carried out in a Fluoromax-4 spectrometer (HORIBA Jobin Yvon, Edison, NJ). The samples were excited at 380 nm wavelength. The steady-state fluorescence anisotropies were measured at 525 nm. The steady-state fluorescence anisotropy (r_ss) is given by the following:

$$r_{ss}=\left(I_{\parallel }-I_{\perp }G\right)/\left(I_{\parallel }+2I_{\perp }G\right)\text{,}$$ (1)

where I_|| and I_⊥ are fluorescence intensities collected using parallel and perpendicular geometry, respectively. The perpendicular components were always corrected using a G-factor.

Femtosecond fluorescence up-conversion

A second harmonic light of mode locked 100 fs Ti:Sapphire laser (1 W, 80 MHz repetition rate; Tsunami; Spectra Physics, Santa Clara, CA) was used as the excitation source for up-conversion measurements. For generating 800 nm light, the self-mode-locked Ti:Sapphire laser was pumped by continuous wave second harmonic light of Nd:YVO4 laser (Millenia Pro; Spectra Physics) that was pumped by an electrically pumped diode laser. Finally, 380 nm light (∼25 mW) was used to excite the samples housed in a rotating cell. The excitation light polarization was set at the magic angle (54.7°) with respect to the gate light. The emission light was up-converted using 800 nm gate light in 1-mm-thick β-barium borate (type I) crystal. The resulting up-converted light was passed through an ultraviolet bandpass filter and then through a double monochromator (DM2100; CDP, Moscow, Russia). Finally, a photon-counter photomultiplier tube (having dark noise <5 cps) was used for signal counting. The decays were collected from 450 to 560 nm after every 10 nm until 300 ps. We carried out similar measurements using 400 nm as the excitation wavelength and a 475–585 nm emission scan range to establish that the time-resolved emission spectra (TRES) results were independent of excitation wavelength. The correlation function plots corresponding to 380 nm excitation are shown in Fig. 3 (see below for construction of TRES). The instrument response function was measured by measuring the cross correlation between the gate light and the Raman signal of buffer, and the full width at half-maximum was ∼250 fs. The emission decay traces were fitted by reconvolution in a desired number of exponentials in a homebuilt program in Igor Pro 6.37 (33). The data were then plotted in Origin Pro 8.5.

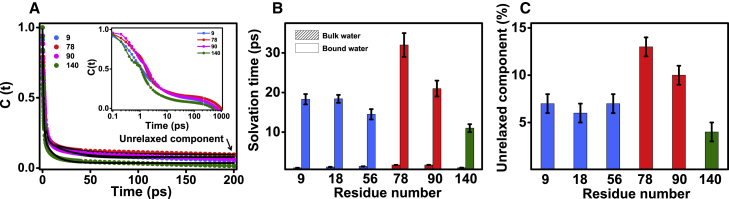
Figure 3.

(A) The hydration correlation function [C(t)] from 0 to 200 ps for residues 9, 78, 90, and 140 of α-syn are shown for comparison (inset shows the complete C(t)). (B) The solvation times recovered from the analysis of femtosecond data (C) and the unrelaxed component (bound water type-II) are shown for all the acrylodan-labeled single cysteine positions of α-syn (N-domain: blue; NAC domain: red; C-domain: olive). See Table S2 for the recovered solvation parameters along with the errors. To see this figure in color, go online.

Time-resolved fluorescence anisotropy measurements

Time-resolved fluorescence anisotropy measurements were carried out using time-correlated single photon counting (TCSPC) and femtosecond fluorescence up-conversion. For anisotropy measurements in femtosecond up-conversion setup, the fluorescence was collected at 525 nm, and the orientation of the excitation light was 0 and 90° with respect to the gate light for parallel (I_‖) and perpendicular (I_⊥) fluorescence intensities, respectively. For TCSPC, the emission wavelength was fixed at 525 nm with a bandpass of 4 nm, and a 375 nm laser diode was used as the excitation source for acrylodan. The full width at half-maximum of the instrument response function with TCSPC setup was found to be ∼250 ps. The anisotropy decays were analyzed by globally fitting I_ǁ(t) and I_⊥(t), as described previously (34).

Construction of TRES

The recovered fluorescence lifetime parameters were used to construct the fluorescence decays at different emission wavelengths using I_λ(t) = ∑_i α_i exp (−t/τ_i), where α_i and τ_i represent the contributions and lifetimes of different components, respectively. The TRES were then constructed using

$$I\left(\lambda ,t\right)=I_{\lambda }^{SS}{I}_{\lambda }\left(t\right)/{\sum }_i{\alpha }_i{\tau }_i,$$ (2)

where I_λ^SS represents the steady-state fluorescence intensity at a fixed emission wavelength λ, and I_λ(t) is the same as mentioned above. All the spectra (obtained at different time points) were fitted using log-normal functions to extract the peak frequency ν(t) as a function of time and were then normalized to account for the overall extent of frequency shift. The solvation correlation function is

$$C\left(t\right)=\left(\mathit{v}\left(t\right)-v\left(\infty \right)\right)/\left(v\left(0\right)-v\left(\infty \right)\right),$$ (3)

where ν(0), ν(t), and ν(∞) are the emission peak frequencies at times 0, t, and ∞, respectively. The recovered ν(0) from our measurements was ∼21,300 ± 150 cm⁻¹, which is close to the ν(0) reported previously (35). The recovered ν(2 ns) (from TCSPC measurements) for all the mutants was similar (∼19,000 cm⁻¹). Therefore, 19,000 cm⁻¹ was used as ν(∞). The correlation function was fitted using the following sum of exponentials:

$$C\left(t\right)={\alpha }_{bulk}\mathit{exp}\left(-t/{\tau }_{bulk}\right)+{\alpha }_{type-I}\mathit{exp}\left(-t/{\tau }_{type-I}\right),$$ (4)

where τ_bulk and τ_type-I represent the solvation times, and α_bulk and α_type-I represent the contributions of the different solvation components, respectively. The amplitude of the (unrelaxed) residual solvation component is denoted as α_type-II and is equal to [1 − (α_bulk + α_type-I)]. The errors in the solvation parameters were estimated from the data obtained from three independent sets of experiments.

MD simulations

The initial structures for MD simulation were taken from the protein ensemble database (PeDB: 9AAC). Four different α-syn structures with radius of gyration Rg = ∼30–35 Å and solvent-accessible surface area SASA = 140–160 nm² were selected (Fig. S1). This selection criterion was based on the earlier simulation results (27). The ensemble MD simulations with strict ensemble-averaged NMR paramagnetic relaxation enhancement restraints revealed that the most populated ensemble of α-syn structures corresponds to low Rg (30–35 Å) and high SASA (140–160 nm²) (27). The protein structure was then solvated in a 100 × 100 × 100 Å³ cubic box filled with preequilibrated ∼32,275 water molecules (Fig. S1 A). Simulations were performed using the OPLS-AA force field parameters for the protein (36) and the SPC/E water model (37). The choice of force field is crucial in simulating IDP sequences (38, 39, 40, 41). The all-atom optimized potentials for liquid simulations (OPLS-AA) force field was chosen, as previous studies showed that this force field generated IDP conformations that are in good agreement with experimental data (41, 42, 43, 44, 45, 46). The extended simple point charge (SPC/E) water model was selected because of its ability to correctly reproduce the dynamics of water at room temperature in bulk and near proteins (37, 38, 47, 48, 49, 50). The OPLS-AA+SPC/E parameter combination has been also used in a number of recent studies to simulate the structure and binding of IDPs (51, 52, 53, 54), including α-syn (42), and generated the ensembles consistent with experimental results. Two separate recent studies have further confirmed that the generated ensemble of disordered Aβ_21–30 as well as Aβ₄₀ and Aβ₄₂ is highly similar between OPLS-AA+SPC/E and OPLS-AA+TIP3P (transferable intermolecular potential with three points) (52, 53). The protonation states of the acidic and basic residues of the peptide were set at pH 7. We added 39 Na⁺ and 30 Cl⁻ ions to the system, randomly placing them in the box, resulting into a charge-neutralized system with 50 mM salt concentration in bulk. The system was energy minimized using steepest descent algorithm for ∼50,000 steps. The resulting structure was used as the starting point for a 100-ns-long MD. All simulations were performed with a 1 fs time step in an NPT ensemble at 300 K and 1 atm. Temperature was kept constant using velocity rescaling with a stochastic term (55). Pressure was maintained using the Berendsen algorithm (56). The particle-mesh Ewald method was used to calculate the long-range electrostatics (57) with a Fourier spacing of 0.12 nm, whereas the short-range electrostatic interactions and van der Waals interactions were treated with a cutoff distance of 1 nm. Neighbor lists were updated every 10 fs with a cutoff of 1 nm. The bonds were constrained using the Linear Constraint Solver (58) and SETTLE (59) algorithms. Simulations were performed using the Groningen Machine for Chemical Simulations 4.5 software (60). All MD simulations were run using International Business Machines BlueGene/Q supercomputers. Fig. S1, B and C shows the evolution of Rg and SASA of the peptide chain for the four 100-ns-long trajectories. The peptide chain collapses to an Rg of 20 Å in runs 1 and 4 at ∼50 ns and then remains stable around that value. In runs 2 and 3, more extended structures are populated during the 100 ns duration with Rg values ≥30 Å. For dynamical characterization of hydration shell water, short 10-ns-long MD runs were performed starting from the structures populated at 50 and 100 ns (Fig. S1 D) of each of the four runs using the MD protocol stated above. At least two independent runs were performed from a single initial configuration. The structures were saved every 200 fs. Thus, all structural and dynamical attributes of hydration water reported in this study are estimated by averaging over multiple 10-ns-long trajectories starting from different initial configurations and initial velocity distributions.

Simulation analysis

To define the hydration shell around a specific residue i of the peptide chain, all surface water molecules within 4 Å (considering distance between nonhydrogen atoms only) of residues i − 4 to i + 4 were considered. The timescale of the existence within the defined hydration shell for those water molecules was determined by estimating the normalized survival probability, C_S(t), which is defined as (61)

$$C_S\left(t\right)=\raisebox{1ex}{$\sum _{i=1}^{N_{wat}}<P_i\left(t0\right)P_i\left(t0+t\right)>$}\!\left/ \!\raisebox{-1ex}{$<P_i\left(t0\right)P_i\left(t0\right)>$}\right.,$$ (5)

where $P_i\left(t0+t\right)$ is equal to 1 if the water molecule i that was within the defined hydration shell at time t0 still remains there at time t0 + t, which otherwise is equal to 0. N_wat is the number of water molecules within the hydration shell at time t0. The angular brackets denote averages over all time origins. Therefore, C_S(t) corresponds to the average fraction of water molecules that still remain within the hydration shell after a time t. It is assumed that the time interval (i.e., 200 fs) between snapshots is small enough for significant displacement of water molecules.

The self-diffusion coefficients were calculated from the mean-square displacement (MSD) of all oxygen atoms using the following Einstein relationship:

$$\underset{\text{t}\to \text{f}\infty }{\lim }\langle {\left|r\left(t^{\prime }+t\right)-r\left(t^{\prime }\right)\right|}^2\rangle =6Dt,$$ (6)

where r(t) is the position of the water oxygen at time t, D is the self-diffusion coefficient, and the brackets denote averaging over all water molecules and all time origins t′.

The reorientational dynamics of hydration shell water was evaluated by measuring the second-order Legendre polynomial time-correlation functions (TCFs) of both O-H bond vectors as follows:

$$C_{O-H}\left(t\right)=<P_2\left[u\left(0\right).u\left(t\right)\right]>,$$ (7)

where u is the unit O-H bond vector. The angular brackets denote the ensemble average over all the water molecules and all time origins.

A hydrogen bond (H-bond) was considered to be present if the distance between the H-bond donor D and acceptor atom A, R_DA ≤0.35 nm, and the angle between the DA and the DH vectors, θ_ADH ≤30°. Here, either the donor or the acceptor atom can belong to the protein or to water. To probe the protein-water hydrogen-bond kinetics, we have calculated the correlation function expressed as follows:

$$C_{HB}\left(t\right)=<h\left(0\right)h\left(t\right)>.$$ (8)

The function h(t) is equal to 1 if an H-bond is formed at time t, which otherwise is 0. The angular brackets denote averaging over all protein-water H-bonds and over all time origins. Thus, the correlation function C_HB(t) corresponds to the survival probability of the H-bond at time t, given that it is formed at t = 0. A hydration water molecule was considered to be confined if at least three protein side-chain carbon atoms were found within 3.5 Å of the O_w atom. All protein structures were rendered using visual MD software (62).

To further ensure that the choice of water model had minimal influence on the main results of this study, we have rerun the 10-ns-long simulations using the OPLS-AA protein force field and the TIP3P water model. The OPLS-AA+TIP3P combination has emerged as a popular combination in IDP simulations recently (41, 44, 46, 63). The results were then compared with the ones generated using the OPLS-AA+SPC/E combination. The survival probability function [C_S(t)] of SPC/E hydration water overall decays slightly faster compared to the TIP3P water, which likely stems from the enhanced mobility of TIP3P water compared to SPC/E water (37). Nevertheless, the overall trend of C_S(t) decay across the different sites is independent of water models. These studies confirmed that the choice of water model does not affect our major conclusion.

Results and Discussion

Residue-specific hydration dynamics from femtosecond time-resolved fluorescence

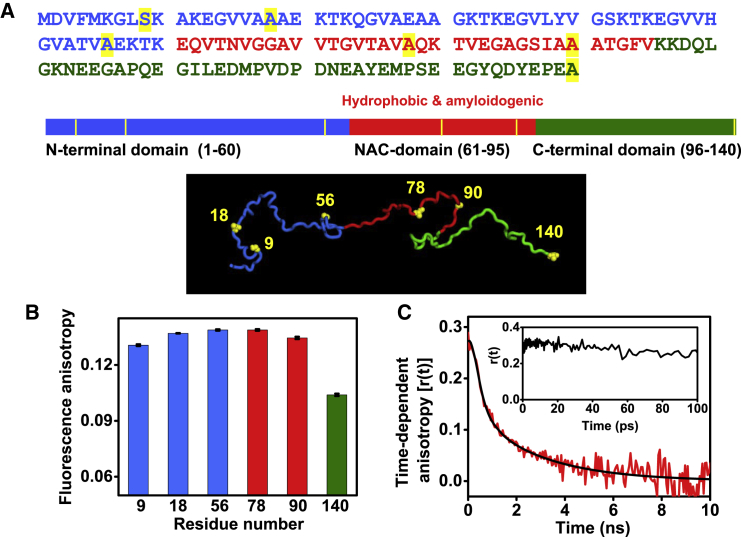
We took advantage of the fact that α-syn is devoid of cysteine (Cys) and created six single Cys mutations encompassing the entire polypeptide length. Considering the significance of all three domains of α-syn in function and disease, we incorporated Cys at residue positions 9, 18, and 56 (N-domain); positions 78 and 90 (NAC domain); and position 140 (C-domain) (Fig. 1 A). The Cys residues were then covalently labeled with a highly environment-sensitive fluorophore, namely acrylodan, which is suitable for hydration dynamics studies (64, 65). To ensure that incorporation of Cys and acrylodan labeling did not induce any perturbation in the structural attributes of α-syn, we monitored the circular dichroism signal for all Cys variants. The circular dichroism spectra for all the variants overlapped and showed signature of a typical disordered monomeric protein similar to the wild-type α-syn (Fig. S2 A). To probe ultrafast hydration, it is important to first confirm that the fluorophore is sufficiently exposed to water. Therefore, as a prelude to the ultrafast hydration studies, we carried out steady-state fluorescence experiments with acrylodan-labeled Cys variants. Highly red-shifted emission maxima (∼525 nm) confirmed that acrylodan is completely solvent exposed at all locations (Fig. S2 B). Additionally, the low steady-state fluorescence anisotropy indicated high conformational flexibility at all locations (Fig. 1 B). The anisotropy at C-terminal residue 140 was even lower because of the end effect. These results together indicated that the microenvironment is similar for all of the positions in the monomeric state of α-syn. Next, to directly monitor the local flexibility of the fluorophore, we performed picosecond fluorescence depolarization measurements. A typical biexponential fluorescence anisotropy decay with a significant amplitude (∼60%) of local motion was observed, suggesting that acrylodan is flexible, as expected (Fig. 1 C). We also carried out the femtosecond time-resolved anisotropy measurements (Fig. 1 C, inset), which revealed no significant rotational mobility on the sub-100-ps timescale (see later).

Figure 1.

(A) The amino acid sequence of α-syn and the schematic representation of its domains along with one of the NMR structures taken from the protein ensemble database (PeDB: 9AAC, conformation #147) generated using PyMOL (Schrödinger, New York, NY) are shown (N-domain: blue; NAC domain: red; C-domain: olive). The single cysteine mutation positions are highlighted in yellow. (B) The steady-state fluorescence anisotropy is shown for all acrylodan labeled at different Cys positions of α-syn (highlighted in (A)). The SE was estimated from three measurements. (C) Fluorescence anisotropy decay of acrylodan labeled at position 78 (black line: fit; recovered parameters: ϕ_fast ∼0.8 ns, β_fast ∼0.6 and ϕ_slow ∼2.3 ns, β_slow ∼0.4) is shown, with the inset showing its femtosecond time-resolved fluorescence anisotropy decay from 0 to 100 ps. To see this figure in color, go online.

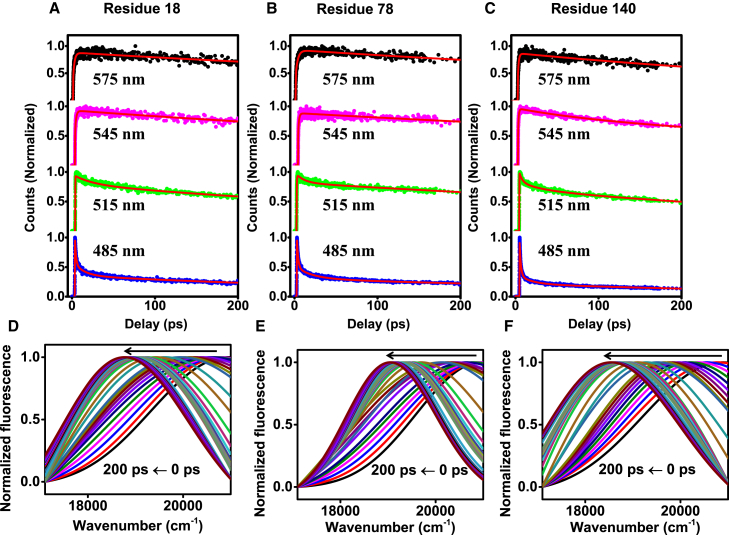
After confirming that all of the chosen locations are flexible and solvent exposed, we carried out the ultrafast hydration dynamics studies using the femtosecond fluorescence up-conversion technique to probe the hydration dynamics around the different domains of α-syn. Using this technique, we can probe the dielectric response of proteins by monitoring the time-dependent fluorescence Stokes shift (TDFSS) of the fluorophore that is covalently linked to the protein. The reorganization of the hydration water network around the excited state of fluorophore results in an emission shift to a longer wavelength (lower energy) due to progressive stabilization of an instantaneously created (excited-state) dipole (6, 7). This shift in the emission spectra (expressed in wavenumber) during the process of solvent reorganization is the measured TDFSS (6, 7). The TDFSS within a given experimental time window is a measure of solvent relaxation around the fluorophore transition dipole with respect to the initial unrelaxed excited state. Thus, the TDFSS is critically dependent on how water molecules are organized and how fast/slow H-bond rearrangements occur in the vicinity of the fluorophore. To estimate the TDFSS and the hydration timescales, we constructed the TRES and the hydration correlation function [C(t)] using the femtosecond-resolved fluorescence up-conversion transients collected at different wavelengths spanning the entire emission spectral range of the acrylodan fluorescence (for details, see Materials and Methods). The representative transients at four different wavelengths and TRES for three residue positions—18 (N-domain), 78 (NAC domain), and 140 (C-domain)—are shown in Fig. 2. The signal was found to decay at the blue edge and rise at the red edge, which is an archetypal feature of solvent relaxation (65). The TDFSSs within 200 ps were found to be ∼2200, ∼2100, and ∼2300 cm⁻¹ for the N-domain (positions 9,18, and 56), NAC domain (positions 78 and 90), and C-domain (position 140), respectively. The C(t) plots for four residue positions are shown in (Fig. 3 A). The time-zero frequency [ν(0)] recovered from our femtosecond experiments for all the mutants was close to ν(0), as estimated previously (35) using a method described for estimation of the time-zero spectrum (66). It is interesting to note that the extent of TDFSS observed for all acrylodan-labeled variants of α-syn is similar to the typical shift observed for highly solvent-exposed locations in the unfolded state of proteins and is significantly different from globular proteins (65). However, the timescales of hydration dynamics recovered are appreciably different from the bulk and are similar to the timescales reported for other proteins (see below) (7, 65).

Figure 2.

The femtosecond up-conversion transients using an excitation wavelength of 400 nm (with fits shown in red) at four typical emission wavelengths from 0 to 200 ps for acrylodan labeled at (A) 18, (B) 78, and (C) 140 α-syn and the time-resolved emission spectra (TRES), with the arrow indicating the time-dependent Stokes shift (in wavenumber) (D–F). The spectra are shown in different colors for clarity. To see this figure in color, go online.

Resolving hydration water in α-syn

Using femtosecond time-resolved studies, we were able to separate bulk water and surface bound (hydration) water in monomeric α-syn around the chosen locations. The analyses of the hydration correlation functions revealed contributions from three distinct hydration components: 1) ∼1 ps; 2) tens of picoseconds ranging between 10 and 40 ps; and 3) an unrelaxed (ultraslow) component within the time window of 200 ps. The recovered solvation parameters for all the residue positions are given in Table S2 and are depicted in the form of bar plots in Fig. 3, B and C. Several theoretical and experimental investigations have revealed that the solvation time for bulk water relaxation spans from 100 fs to ps (1, 7). In contrast, the hydration water has considerably slower relaxation time, ranging between 10 and 100 ps. Thus, the ultrafast component (∼1 ps) represents the bulk water, and the slower component (of tens of picoseconds), which we refer to as “bound water type I,” can be assigned to the hydration water or the so called “biological water” (1, 5, 7). It is important to emphasize here that the rotational dynamics of the fluorophore alone did not contribute to the solvation on the picosecond timescale because the femtosecond time-resolved anisotropy decay did not exhibit any significant drop within 100 ps (Fig. 1 C, inset). The third component of solvation was much slower, and C(t) did not decay completely to zero within 200 ps (Fig. 3 A). We refer to this residual (unrelaxed) component of solvation as “bound water type II,” which relaxes only on the timescale of hundreds of picoseconds to nanoseconds.

The presence of restrained water molecules in amyloidogenic NAC domain

The TDFSS data allowed us to infer the following: 1) the contribution of the bulk water is similar for all the variants (∼75%) (Fig. S3). This observation signifies that the ultrafast component dominates the slower component of hydration for all the locations of α-syn. This finding is in agreement with a previous report on the unfolded state of a globular protein, in which the bulk water contribution was found to be ∼75% (65). 2) Although the extent of steady-state Stokes shift is similar for all the variants (Fig. S2 B), the reorientational timescales of bound water type I are different along the polypeptide chain (Fig. 3 B). The NAC domain locations have slightly longer hydration times, suggesting slower water motion around this region (Fig. 3 B). The hydration time for type I water follows this order: 78 (NAC) > 90 (NAC) > 9 (N) ≈ 18 (N) ≈ 56 (N) > 140 (C). 3) The contribution (amplitude) of the unrelaxed component of hydration that corresponds to type II water was found to be the most for 78 (∼15%) and the least for 140 (<5%) (Fig. 3 C). In the case of the N-domain (9, 18, 56), the solvation with respect to ν(∞) was ∼95% complete within 200 ps. The C-terminal residue at 140 also showed >95% decay in C(t). In contrast, for the NAC domain residues, especially 78, the solvation was found to be <90% complete within 200 ps (>10% of unrelaxed component; Fig. 3 C). Therefore, our femtosecond time-resolved data indicate that both hydration water (type I) and ultraslow water (type II) are retarded near the NAC region (see Fig. S4 for C(t) plots for all residues and Table S2 for the recovered solvation parameters).

Taken together, our results suggest that the contribution and timescale of bulk water is similar for all of the residue positions, indicating that the polypeptide chain is nearly homogeneously solvated and is devoid of any persistent structure in the native state. However, bound water type I around 78 (NAC domain) is associated with a longer reorientation time, and hence, these water molecules are more ordered compared to water molecules present in the N- and C-domains. Additionally, the contribution of (ultraslow) type II water is more prominent in the NAC domain of α-syn. Our femtosecond time-resolved TDFSS results therefore allowed us to construct a hydration map of intrinsically disordered α-syn. We would like to point out that observed TDFSS is a net result of a variety of complex mechanisms of water dynamics often associated with the chain dynamics (1, 6, 7). The motions that contribute to TDFSS could involve rotational and translational motions, breaking and making of H-bonds between water-water and protein-water, exchange between various types of water, coupling of water and chain dynamics, and so forth. TDFSS provides a convoluted effect of some or all of those dynamics. Therefore, to discern the different dynamic components as well as to determine the molecular origin of the dynamical heterogeneity of water in α-syn, we next performed all-atom MD simulations.

MD simulations support heterogeneous hydration water

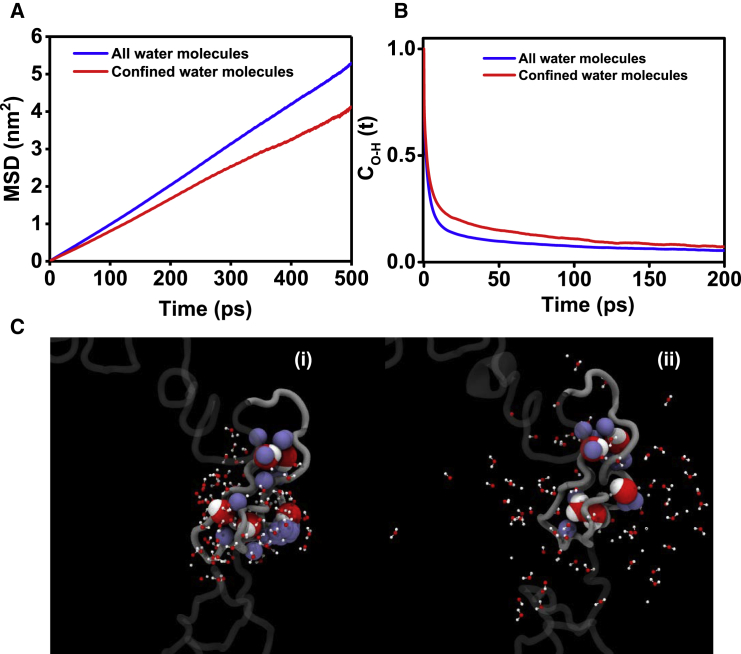
To decipher the molecular factors leading to the dynamical heterogeneity of hydration water around α-syn, we performed multiple atomistic MD simulations of α-syn monomer with OPLS-AA force field explicit in SPC/E water (Fig. S4; see also Materials and Methods). The resulting ensemble was composed of structures with a radius of gyration (R_g) of ∼20–35 Å and SASA of 100–130 nm² (Fig. S1), suggestive of a combination of compact and extended structures and in line with earlier reports (67, 68). These protein conformations lack any major secondary structure, which is consistent with the reported disordered nature of α-syn (24, 26, 28). Fig. 4 A shows the residence time or the survival probability function [C_S(t)] of the hydration shell water molecules near different sites of α-syn, as estimated from the simulations (see Materials and Methods). The decay of the correlation function C_S(t) is site dependent (Fig. 4 A; see also Fig. S5, A and B) and is in good agreement with our TDFSS experiments. Multiple runs from a single initial configuration as well as from different initial configurations were performed to ensure that the simulated C_S(t) profiles are robust. The multiphasic form of the survival probability implies the existence of various types of water with distinct timescales of survival near the protein surface. Table S3 summarizes the fitted parameters for simulated correlation functions around different sites. The ultrafast component near all sites represents ∼50% of hydration shell water with <1 ps residence time, which corresponds to the contribution from bulk water. Another ∼30–40% exhibited a slower residence time of 12–16 ps, akin to bound water type I. The remaining 10–20% hydration shell water molecules displayed a much longer residence time similar to bound water type II, which remains bound on the timescale of hundreds of picoseconds. The longer residence time component is slowest (>180 ps) near the NAC domain residues (positions 56, 78, and 90). We also performed simulations of α-syn using the TIP3P water model and compared them with the SPC/E simulations (Fig. S5 C). These results confirmed that the choice of water model does not affect our main conclusion i.e., hydration water around the NAC domain exhibits the longest residence times. Taken together, the presence of three distinct components is likely to correspond to bulk-like, type I bound, and type II bound within hydration water of α-syn. Our simulations further confirmed the more sluggish nature of type II bound water near the NAC domain seen in our experiments.

Figure 4.

(A) Survival probability functions C_s(t) of water molecules in the α-syn hydration shell around different sites, as estimated from MD. (B) A linear-log plot of second-order reorientational time correlation function C_O-H(t) for all O-H bonds of hydration shell waters is shown. (C) The mean-square displacement (MSD) (in nm²) is shown as function of time (in picoseconds) of hydration shell water around different residues. The black lines in (B) and (C) represent data corresponding to bulk water. (D) A linear-log plot of protein-water (PW) H-bond time correlation functions, C_HB-PW(t), is shown. See Fig. S5 for all residue positions and Tables S3–S5 for the parameters recovered upon fitting C_s(t), C_O-H(t) and C_HB-PW(t), respectively. To see this figure in color, go online.

Molecular origin of dynamical heterogeneity in hydration shell

Next, we characterized the reorientation dynamics of hydration water by estimating the second-order Legendre polynomial TCF of O_w-H_w bond, C_O-H(t). The reorientation TCF has been linked to anisotropy curves obtained from polarization-resolved femtosecond infrared spectroscopy and also to orientation relaxation times recovered from magnetic relaxation techniques (69). Fig. 4 B shows C_O-H(t) averaged over all water molecules that are initially located within the hydration shell of a residue of interest. The reorientation dynamics of hydration water across all sites within α-syn was found to be slower compared to the bulk (Fig. 4 B). Further inspection of Fig. 4 B suggested the presence of significant heterogeneity in reorientation dynamics of surface water, the dynamics being slowest near residue 78 and fastest near residue 140. The reorientational dynamics of surface water was further quantified by fitting C_O-H(t) to a triexponential decay function (70) (Table S4). The three characteristic relaxation times that were recovered consisted of an ultrafast subpicosecond component (<1 ps), an intermediate component (1–5 ps), and a slow component >20 ps (Table S4). The ultrafast decay represents the liberation of water molecules, whereas the intermediate and slow relaxation times are attributed to water H-bond exchange (1). The intermediate relaxation time is ∼1.5 times slower in hydration shell compared to the bulk (Table S4), and ∼10–15% of hydration water displayed ultraslow reorientation dynamics, which was completely absent in bulk water. We next characterized the translational dynamics of hydration water by estimating the MSD of water oxygen (Fig. 4 C). The self-diffusion constants of the hydration water at different sites are given in Table S4 and are comparable with the overall diffusion constant of hydration water around α-syn reported earlier (47). Overall, the hydration water appears translationally more restricted compared to bulk water and is more sluggish near the NAC domain. Taken together, the hydration water within α-syn appears to be dynamically restricted compared to the bulk, the effect being strongest near the NAC domain. Because the hydration water is under the strong influence of protein, we have also quantified the relaxation kinetics of protein-water (PW) H-bonds (Fig. 4 D). The PW H-bond relaxation kinetics can be fitted to a triexponential function (71). These results are outlined in Table S5 and indicate that the water molecules directly interacting with the polypeptide chain exist in diverse forms. Given that the lifetime of H-bonds in bulk water is ∼5 ps, the water molecules H-bonded to α-syn can be classified as bulk (τ₁^PW of the order of 1–10 ps), surface (τ₂^PW 10–100 ps), and trapped (τ₃^PW 100–1000 ps). Longer τ₃^PW near residue positions 78 and 90 thus imply stronger trapping of water molecules near the NAC domain.

Earlier work on folded proteins has attributed such variation of water residence times primarily to surface topology (72, 73, 74). Water present in the vicinity of buried or concave sites is characterized by long residence time (order of 100 ps), whereas water at the exposed or convex sites displays relatively shorter residence time (order of 10 ps). Because local solute environment is known to play a crucial role in the slowdown of water dynamics, we have analyzed the local environment of hydration water at different sites of α-syn. These results are summarized in Table 1. The number of hydration water molecules per amino acid is lowest near the NAC domain, which is consistent with its strong hydrophobic character (Fig. S6 A; Table 1). The NAC domain also remained less solvent exposed compared to rest of the protein in our simulations (Fig. S6 B). Table 1 also shows that at weakly hydrated sites (i.e., at residues 78 and 90), each hydration water molecule forms fewer water-water (WW) H-bonds on average. At the same time, those water molecules display slightly higher propensity to form PW H-bonds. To account for the effect of local topology, we have estimated from the simulations the average number of side-chain carbon atoms in vicinity (within 4.5 Å of O_w) of a hydration water molecule (N_c) that decreases in the following order: 78 > 90 > 9 > 140. The probability distribution of N_c at different α-syn sites confirms this trend (Fig. S6 C). In fact, nearly half of the hydration water molecules were found to be surrounded by at least three side-chain carbon atoms near residue position 78 (Table 1). This fraction of hydration water (f_c) is defined as “confined water.” When we limit our analysis to only f_c, we find that water molecules belonging to f_c form an even larger number of PW H-bonds (with almost equal probability of polypeptides acting as H-bond acceptors or donors) and a lower number of WW H-bonds when compared to all hydration water molecules. This trend is observed for water molecules belonging to f_c at all sites.

Table 1.

Local Hydration Properties around Residues of Interest, as Recovered from MD Simulations

Residue Position	Nh	SASA (nm2)	NHB (PW)	NHB (WW)	NC	fc	NHB(WW)C	NHB (PW)C
9	6.55 (1.06)	0.84 (0.15)	0.05 (0.02)	2.73 (0.06)	2.36 (0.19)	39.80 (3.47)	2.66 (0.11)	0.09 (0.05)
78	5.06 (0.21)	0.55 (0.12)	0.09 (0.02)	2.68 (0.05)	2.68 (0.22)	46.20 (4.53)	2.59 (0.07)	0.16 (0.05)
90	4.80 (0.64)	0.55 (0.10)	0.09 (0.07)	2.68 (0.08)	2.44 (0.30)	40.00 (6.72)	2.59 (0.13)	0.17 (0.13)
140	8.86 (1.60)	1.22 (0.19)	0.03 (0.01)	2.77 (0.04)	2.17 (0.39)	32.83 (9.41)	2.75 (0.38)	0.04 (0.02)

N_h, number of hydration water molecules per amino acid; SASA, solvent-accessible surface area per residue; N_HB(PW), average number of protein-water hydrogen bonds per hydration water molecule; N_HB(WW), average number of water-water hydrogen bonds per hydration water molecule; N_c, average number of protein side-chain carbon atoms within 4.5 Å of a hydration water molecule; f_c, percentage of hydration water molecules confined by at least three protein side-chain carbon atoms; N_HB(PW)^c and N_HB(WW)^c are the average number of protein-water and water-water hydrogen bonds, respectively, per confined water molecule. Numbers within the parentheses correspond to the SDs of the estimates obtained from different simulation trajectories.

These results can be explained in light of the extended jump model that connects water dynamics with H-bond partner exchange. The extended jump model considers sudden large-amplitude jumps during H-bond acceptor exchange as the primary factor governing reorientation dynamics of water (75, 76). The proposed mechanism is found to be valid in bulk as well as near solutes. Two factors contribute to water slowdown: 1) the restricted approach of the new H-bond partner and 2) the initial H-bond strength, with the former playing the primary role (77, 78, 79). A direct relationship has been established between the approach of a new H-bond acceptor and the excluded volume effect induced by local confinement and/or the presence of hydrophobic groups. Accordingly, it has been suggested that PW H-bonds near convex protein sites break via angular jump mechanism, whereas near the concave (buried) sites, the breaking of H-bonds is likely to occur via diffusion (70, 80). In line with these previous studies, our analysis revealed an association between the stronger confinement and the restrained dynamics of hydration water near the NAC domain. The confined hydration water molecules appear isolated, as they form fewer WW H-bonds (Table 1). The ones that are initially H-bonded with the polypeptide chain remain so for a longer period of time (Fig. 4 D). This stronger confinement near the NAC domain is a result of the local composition (a mix of hydrophobic and polar amino acids) and conformation (concave site). The trapped water molecules experience stronger excluded volume effect from nearby amino acid residues. The confined water molecules consistently displayed more retarded translational and reorientation dynamics when compared to all hydration water molecules, as depicted in Fig. 5, A and B. Fig. 5 C shows two simulation snapshots of the NAC domain hydration shell that were collected 160 ps apart (also see Video S1). It is evident that the stronger confinement of water molecules near residues 78 and 90 hinders H-bond partner access, thereby hindering the reorientation of a few water molecules.

Figure 5.

(A) Mean-square displacement (MSD) (in nm²) and (B) second-order reorientational time correlation function [C_O-H(t)] as function of time (in picoseconds) for hydration shell water molecules (in red) and all water molecules (in blue) around residue 78, as estimated from MD. (C) Two simulation snapshots of hydration shell (160 ps apart) near residues 78 and 90 of α-syn show the trapped water molecules with longer residence times within the NAC domain. The protein chain is shown in gray using a ribbon representation. For clarity, only the NAC domain is shown as opaque. The water molecules that were initially within the hydration layer are shown using CPK representation (oxygen in red and hydrogen in white). The trapped water molecules and protein side-chain carbon atoms (in ice blue) surrounding them are shown using vdW spheres. Also, see Video S1, which shows the time trajectory and trapping of five hydration water molecules within the NAC domain in the time range of 200 ps. To see this figure in color, go online.

Compared to both residues 78 and 90 (NAC domain), N-terminal residues 9, 18, and 56 exhibited much faster bound water relaxation, which, however, was slower than that of the C-terminal residue 140. This difference in the bound water solvation time for N-terminal residues can be explained again in terms of the local composition, solvent exposure, N_c, and the average number of PW H-bonds per hydration water molecule (N_HB(PW)). The N-terminal domain is rich in amino acids that are H-bond donors (K and R). Additionally, the N-terminal domain contains a small stretch of hydrophobic residues, although the hydrophobicity of this region is lower than that of the NAC domain (Figs. 1 A and S6 A). The local SASA values around these residues are also larger compared to those around the NAC domain residues (Fig. S6 B; Table 1), whereas N_c and N_HB(PW) are smaller. These effects together yield weaker trapping of bound water at N-terminal residues, accounting for the less retarded water dynamics in the N-domain when compared to the NAC domain. The fastest bound water relaxation dynamics is demonstrated by extreme C-terminal residue 140. This site is the most hydrated and corresponds to the smallest N_c. Additionally, this region is also strongly solvent-exposed. These factors account for the weaker trapping of bound water molecules, leading to faster water dynamics at the C-terminal end.

Amyloid formation and pathological implications of hydration layer of α-syn

Hydration water molecules critically contribute to various protein functions and control the protein side-chain fluctuations on the picosecond timescale (4, 81). Given the inherent unstructured and dynamic nature of the IDP sequences, one might conjecture that the behavior of hydration water around IDP is different than that of globular proteins. In fact, the overall hydration dynamics of α-syn was earlier compared with that of a globular protein using atomistic simulations (38), which suggested the somewhat higher mobility of the hydration water around disordered regions. A recent neutron-scattering and molecular simulation study has further revealed coupling between water dynamics and functional motions in another amyloidogenic IDP, namely tau (10). Therefore, the contrasting nature of water molecules within different domains of α-syn might as well have important biological consequences. The N-terminal domain is homologous to the lipid-binding domain of apolipoproteins and is known to form amphipathic α-helices in the presence of synthetic lipids. The markedly different timescale of bound water dynamics at the N-terminal domain might play a specific role during α-syn membrane interactions because the hydration water is known to play a significant role in mediating protein-ligand binding, intermolecular interaction, and specificity (1, 2, 3, 82, 83). The interaction of α-syn with membranes is associated with the physiological function as well as the misfolding and aggregation (29, 84). The NAC domain being hydrophobic in nature is known to play a crucial role in α-syn aggregation (85). Studies have shown that the NAC domain forms the core of α-syn amyloid fibrils and can independently form aggregates that are cytotoxic. Moreover, there was a recent report that emphasized the importance of a stretch from 68 to 78 of the NAC domain in the context of the cytotoxicity of α-syn aggregates (86). The hydration water mobility was found to be more locally enhanced around the core domain in τ fibers than in nonaggregated tau (9, 87). We propose that the presence of confined water molecules can contribute to the amyloidogenicity of the NAC domain. Water around this region can affect the rate of intramolecular backbone reconfiguration, which has been earlier proposed to facilitate the critical oligomer formation via intermolecular association (88). We observed a considerable blue shift of ∼40 nm in the acrylodan emission at the NAC domain upon amyloid formation, indicating chain desolvation during aggregation (S.A., K.B., and S.M., unpublished data). Therefore, the intermolecular association of α-syn is likely to be driven by contact formation and water exclusion, resulting in the sequestration into obligatory oligomers via entropic liberation of confined water molecules into the bulk milieu, which has been proposed to drive the amyloid assembly process (46, 64, 89, 90, 91, 92).

Author Contributions

S.A., A.D., P. Das, and S.M. conceived the research and designed the study. S.A., A.K.S., K.B., and P. Dogra performed the experiments. S.A. analyzed the data. K.B. created the mutants and expressed the protein constructs. P. Das carried out and analyzed the MD simulations. S.A., P. Das, and S.M. wrote the manuscript. All authors discussed the results and commented on the manuscript.

Editor: Elizabeth Komives.