Abstract
Using fluorescence correlation spectroscopy in single-plane illumination microscopy, we investigated the dynamics of chromatin in interphase mouse adult fibroblast cell nuclei under the influence of the intermediate filament protein lamin A. We find that 1) lamin A-eGFP and histone H2A-mRFP show significant comobility, indicating that their motions are clearly interconnected in the nucleus, and 2) that the random motion of histones H2A within the chromatin network is subdiffusive, i.e., the effective diffusion coefficient decreases for slow timescales. Knocking out lamin A changes the diffusion back to normal. Thus, lamin A influences the dynamics of the entire chromatin network. Our conclusion is that lamin A plays a central role in determining the viscoelasticity of the chromatin network and helping to maintain local ordering of interphase chromosomes.
Introduction
The function of the genome in the cell depends strongly on its three-dimensional structure and dynamics (1, 2). Recent simulation results suggest that the dense random chromatin network alone cannot account for the observed elastic modulus of the nucleus (3, 4) and that other constituents of the cell nucleus must contribute to its mechanical properties. In this context, the connection between the viscoelastic properties of the cell nucleus and gene function have become a recent focus of interest (5, 6). Lamins, which are intermediate filament proteins first found in the nuclear lamina, were thought to fulfill mainly structural functions in the nucleus, such as providing shape and mechanical stability (7). Recent findings show that they also play important roles in essential cellular processes such as transcription, DNA replication, cell cycle progression, and chromatin organization (8, 9, 10, 11, 12, 13). Thus, there is an intimate connection between lamins and genome function. Single-particle tracking of telomers in live cells (14, 15) indicated that knockout of lamin A strikingly alters the dynamics, inducing a transition from anomalous diffusion to normal diffusion. However, the depletion of LAP2α, a protein that interacts with lamin A and chromatin, has no effect on the anomaly of diffusion. This suggested the prominent role of interconnections mediated by lamin A in chromatin in controlling its dynamics. Therefore, our goal is to investigate possible connections between histone diffusion and lamin A as they can be singled out in cell nuclei.
Dynamics of chromatin and proteins in the cell nucleus have been visualized by modern light microscopy techniques. Fluorescence correlation spectroscopy (FCS) offers submillisecond time resolution but so far it was mostly limited to single-point measurements in a laser focus. Spatially resolved FCS in live cells has been pioneered by Wachsmuth et al. (16); later, Dross et al. collected protein mobility maps by point-to-point FCS (17), and Garini et al. employed direct particle tracking on telomeres to ascertain diffusion anomaly in nuclei (14, 15). However, such measurements are extremely time-consuming and impractical for extensive studies on live cells. A major advance in the analysis of dynamical processes in live cells was achieved by parallel acquisition of FCS data across entire lines or regions (18, 19). Specifically, combining FCS with single-plane illumination microscopy (SPIM-FCS) (20) allows mobility imaging of entire two-dimensional cross sections, providing diffusion coefficients, flow velocities, and concentrations of fluorescent proteins. Two-color fluorescence cross correlation spectroscopy (FCCS) (SPIM-FCCS) also allows imaging of molecular interactions on live cell images (21). Recently, we could show that the mobility of a heterodimeric transcription factor strongly correlated with the degree of dimerization, spatially localizing specific binding to DNA in the dimer form using this method (22, 23, 24).
Materials and Methods
Preparation of cells
We used mouse adult fibroblast (MAF) adherent cells (25) (provided by H. Herrmann, German Cancer Research Center, Heidelberg, Germany) grown in phenol-red-free Dulbecco’s modified eagle medium (Invitrogen Life Technologies, Carlsbad, CA), supplemented with 10% fetal calf serum and 1% glutamine and incubated at 37°C in a 5% CO2 atmosphere. Transiently, transfection with lamin A-eGFP, eGFP-tetramer, H2A-mRFP1, or combinations of these was done with FuGENE HD or Lipofectamine transfection kits, depending on the cell line (Promega, Mannheim, Germany). The cells were plated and transfected in a 35 mm petri dish 24–48 h before the measurement. They were either grown on small glass pieces (size: , thickness: ) or embedded in 2% agarose gels made of phenol-red-free Hank’s balanced salt solution (PAN Biotech, Aidenbach, Germany) inside 0.3 mL U-100 insulin syringes (Becton Dickinson France SAS, Le Pont-de-Claix, France) to halt the cell movements.
Cells selected for measurements showed a healthy shape (no blebs, a recognizable nucleus, and typical flattened shape) and were not obviously in mitosis. For each condition, several cells were acquired on different days. Cells that moved during the measurement, in which the bleach correction did not succeed because of slow large-scale fluctuations, or that showed other unusual artifacts (e.g., large internal rearrangements or aggregates) were excluded. This way, ∼30% of the cells were removed from further evaluations. To reduce cell movements, all measurements were performed at room temperature .
SPIM-FCS and SPIM-FCCS
The SPIM-FCS device has recently been described (21). A modulated diode laser at 488 nm and a diode-pumped laser at 561 nm (Cobolt AS, Solna, Sweden) were combined colinearly, and a vertical light sheet was formed by a horizontally oriented cylindrical lens in front of a 10×/NA0.3 illumination objective (Nikon, Tokyo, Japan). The light sheet was focused into a sample chamber filled with cell culture medium, into which the observation objective lens was immersed at a working distance of 2.3 mm from the center of the light sheet. Light sheet alignment, calibration, and characterization were done as in (21).
Cells were mounted vertically from above into the sample chamber filled with FluoroBright Dulbecco’s modified eagle medium, which is a clear, nonfluorescent, nonscattering cell culture medium that sustains the cells over the duration of the measurements (typically 30–90 min per sample). The glass slip was typically positioned under an angle of with respect to the light sheet to avoid light being reflected into the detection objective and to optimize the width of the cross section.
Image series were collected with a 128128 pixel Andor BI860 electron-multiplying charge-coupled device (EMCCD) camera (Andor, Belfast, Ireland). A spectral splitter in front of the camera created two simultaneous 12864 pixel images for the two-color channels corresponding to GFP and RFP. The images were aligned as described in (21). Images were acquired at a rate of 2000 frames/s and subjected to autocorrelation analysis. System alignment and calibration, sample positioning, data acquisition, and analysis were all controlled by our own software package Quickfit3 (26), a modular data acquisition, analysis, and model-fitting system.
Data analysis
The general autocorrelation function for pixel {x,y} on an image sensor is defined as:
| (1) |
where operator is defined as a time average, and the lag time τ is given in the unit of . For SPIM-FCCS, the dual-view optics images the two-color channels side-by-side on the sensor, yielding two separated image series (green channel) and (red channel). Then, the two-color cross correlation function (CCF) becomes
| (2) |
Image series were corrected for background and bleaching, and correlation functions were computed as described in (21). Diffusion models were fitted to the correlation data using the known pixel geometry and point-spread function of the optics (21). We assumed either a multicomponent normal diffusion model or a one-component anomalous diffusion model.
Normal diffusion
The most common dynamics in FCS is free Brownian motion, characterized by a mean-square displacement that is linear in time:
| (3) |
where is the diffusion coefficient of species χ, which is moving in a d-dimensional space.
The normalized FCS autocorrelation function for particles with diffusion coefficient D undergoing normal Brownian motion in a light sheet, imaged by an objective lens onto a detector with square pixels, is as follows (21):
| (4) |
Here, a is the pixel size of the image in the observation plane, the index denotes the color channel of the microscope, is the lateral width of the objective point-spread function, is the thickness of the light sheet, and is the mean number of particles of species χ in the observation volume . Assuming that all the species have the same molecular brightness, the multicomponent diffusion model would be written in terms of an overall concentration , where and the relative concentration is for each species:
| (5) |
Anomalous diffusion
When the random motion of particles is hindered by the surrounding medium, the mean-square displacement is no longer a linear function of time. Hence,
| (6) |
It has been demonstrated in different sources that in this case, can be described by a power law as follows (27, 28, 29, 30, 31, 32):
| (7) |
Here, α is the anomaly parameter, and is the generalized or anomalous diffusion coefficient ( inherently depends on α, as its unit is ). Equation 7 implies that a crowded environment does not simply reduce the diffusion coefficient but leads to significantly different behavior of the particles. The propagator for such anomalous transport process is assumed to be a Gaussian function with a sublinear time dependence :
| (8) |
which results in a normalized correlation function similar to Eq. 4, with τ replaced by :
| (9) |
Correlation and model fitting
The data analysis typically was done on an image series of frames. Those regions in the image series to be analyzed were selected, and the correlation functions were computed for each pixel or pair of pixels. Next, the correlation functions were fitted by the selected diffusion model. All these steps were implemented in an automatic procedure in the Quickfit3 software. Results of the correlation fits could be displayed as color-coded parameter images, averaged correlation fits, or histograms over the fitted pixels.
Results
Imaging FCCS shows that lamin A and chromatin are diffusing together
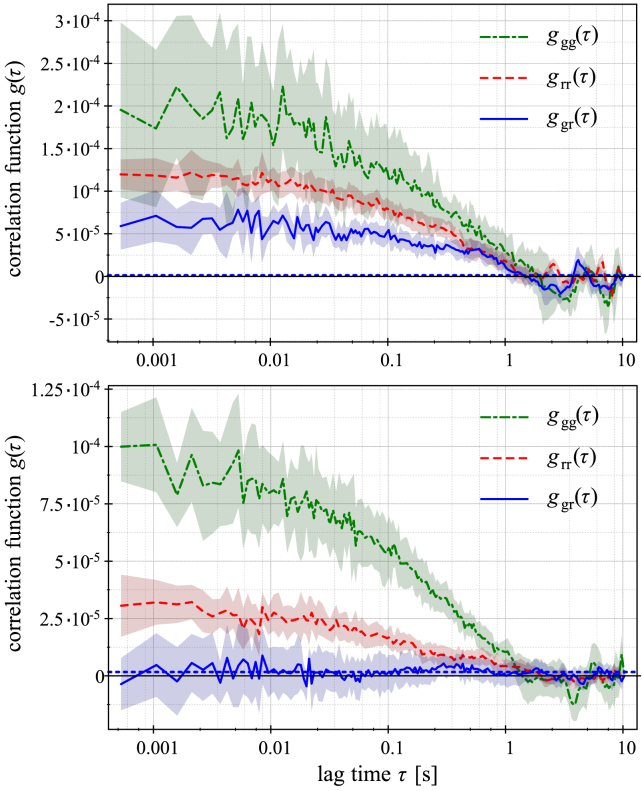
We applied SPIM-FCCS to investigate how lamin A interacts with chromatin using a lamin A knockout MAF cell line stably transfected with H2A-mRFP1 (LMNA−/− MAF-H2A-mRFP) and then transiently cotransfected with lamin A-eGFP. The replacement of endogenous lamin A proteins with fluorescently labeled ones enables us to study the comobility between lamin A and histones. The cells were either grown on small coverslides or embedded in 2% agarose gels to halt cellular movement. The measurements on coverslides and in gels were cross-validated and proven to be mutually consistent (see Table 1 for a comparison). For better statistics, pixel binning was used on the image series. For the sake of brevity, we refer to binned pixels as pixels throughout this article unless otherwise mentioned. As a negative control, we transiently transfected LMNA−/− MAF-H2A-mRFP with eGFP tetramer (eGFP-4x), which does not interact with chromatin and should therefore show only negligible cross correlation (CC). Fig. 1 displays autocorrelation and CC curves for a sample cell (upper panel) and a control (lower panel). The amplitude of the CC of the control is not larger than the cross talk indicated by the horizontal dashed line. In the sample cell, the nonzero autocorrelation function (ACF) amplitude demonstrates that the dynamics of both lamin A and histones has a stochastic character, and the nonzero CC demonstrates that lamin A and histones are diffusing together, indicating that there is a form of interconnection between the two species. We also notice that the decay of the two ACFs is very similar, indicating similar diffusive motion of the two species.
Table 1.
Statistical Overview of the Relative Cross Correlation Function Amplitude
| Coverslips |
2% Agarose Gel |
|||
|---|---|---|---|---|
| Control | Sample | Control | Sample | |
| q | ||||
LMNA−/− MAFs transiently expressing eGFP4x as control cells and LMNA−/− MAFs transiently expressing lamin A-eGFP as sample cells. They were measured on coverslips and also they were embedded in 2% agarose gel made of phenol red-free Hank's balanced salt solution.
Figure 1.
Examples of typical auto- (green dashed/red dotted lines) and cross correlation (blue solid lines) curves. The lines are the averages, and the shadowed polygons show the SD of the correlation function calculated at each pixel. The upper panel shows the average cross correlation and SD of laminA-eGFP with H2A-mRFP together with their respective ACFs corresponding to one nonbinned pixel selected in a sample cell. The lower panel reports the cross correlation function and the SD of eGFP4x with H2A-mRFP next to the ACFs of each of them at a selected single pixel (a pixel) of a control cell. Both sample cells and controls are LMNA−/− MAF-H2A-mRFP transiently transfected with lamin A-eGFP and GFP-4x, respectively. The horizontal dashed line indicates the cross talk level between green and red channels. To see this figure in color, go online.
To quantify the interaction between lamin A and histone proteins, the relative CCF amplitude was calculated for all pixels of each acquisition. For this reason, first a two-component normal diffusion model was fitted to the autocorrelation curves of all different pixels in image series for each channel. The quicker ones represent the freely moving histones or lamin As, whereas the slower diffusion means binding to a larger structure e.g., chromatin. Then, the CC curves corresponding to each pixel were fitted with a single-component normal diffusion model in which and have been replaced. This modification is necessary because we are cross correlating signals collected over different spectral bands, with slightly different optical resolution. To fit the CCF with a single-component model and retrieve a diffusion coefficient, we assume an average value of the optical resolution. Because the dwell time is linearly proportional to the square of the linear size of the observation volume, we recalculate the resolution in the sample plane and along the optical axis as follows:
| (10) |
Finally, the amplitude of each model was extracted. The relative CCF amplitude, then, is defined as follows:
| (11) |
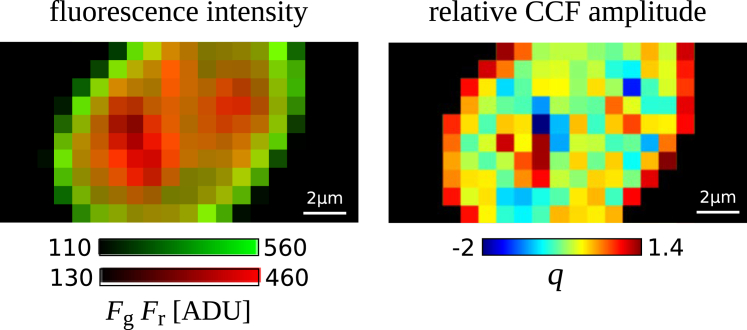
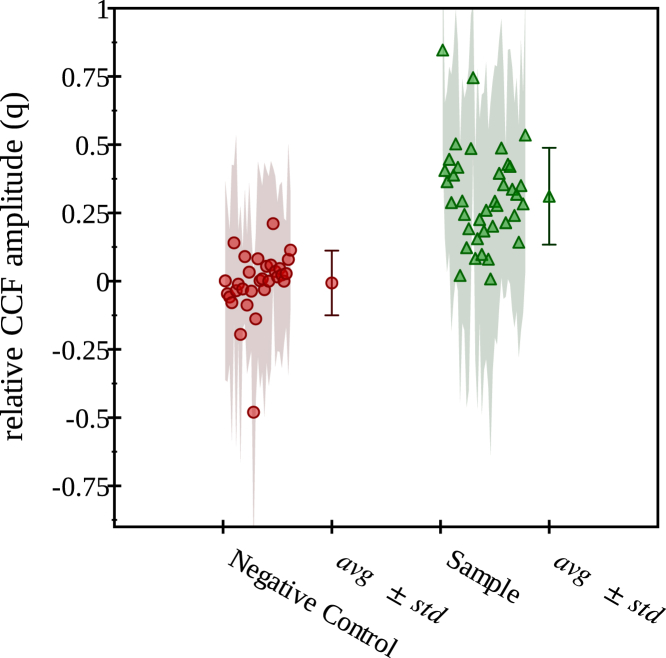
In Eq. 11, we are considering on equal footing lamin A proteins and histones and evaluating the number of less-abundant objects that are codiffusing with the more abundant ones. Fig. 2 shows a representative map of the relative CCF amplitude (q) obtained from a cell expressing lamin A-eGFP and H2A-mRFP. Fig. 3 summarizes the relative FCCS amplitude over all measured cells. These results demonstrate that a considerable fraction (more than 30%) of lamin A is codiffusing with histone proteins. A one-component normal diffusion fit to the CCF averaged over all pixels in the cell yields a diffusion coefficient on coverslips and for the cells embedded in agarose gels, which is compatible with the slow component of the histone motion (Table 2). This suggests that lamin A is associated with chromatin-bound histones only.
Figure 2.
Parameter images of SPIM-FCCS measurement of lamin A-eGFP and H2A-mRFP. The distribution of the lamin A (green) and the H2A (red) fluorescence signals can be seen in the left panel (the analog-to-digital converter unit (ADU) is the output unit of the EMCCD camera). The map of the relative CCF amplitude in the nucleus of LMNA−/− MAF-H2A-mRFP transiently transfected with lamin A-eGFP is shown in the right panel. Negative values of q are originated by the instrumental noise.
Figure 3.
Statistical summary of the relative FCCS amplitude in LMNA−/− MAF-H2A-mRFP expressing eGFP4x, as negative control, and lamin A-eGFP using SPIM-FCCS. The medians of the relative FCCS amplitudes for 31 negative control cells are pooled together and shown with small filled circles. For 39 sample cells, the medians are displayed as small filled triangles. The average and SD of these medians can be found next to them as a filled circle with error bars for negative control and a filled triangle with error bars for sample. To see this figure in color, go online.
Table 2.
Averages and SD of the Fit Parameters over 75 MAF and 75 LMNA−/− MAF Cells that Express H2A-eGFP
| MAF | LMNA−/− MAF | |
|---|---|---|
| α | ||
| [ms] | ||
The parameters in the first two rows are the result of the anomalous diffusion fit model, and the rest are obtained from the two-component normal diffusion fit model.
Imaging FCS shows that chromatin diffuses anomalously in wild-type but not in lamin A knockout cells
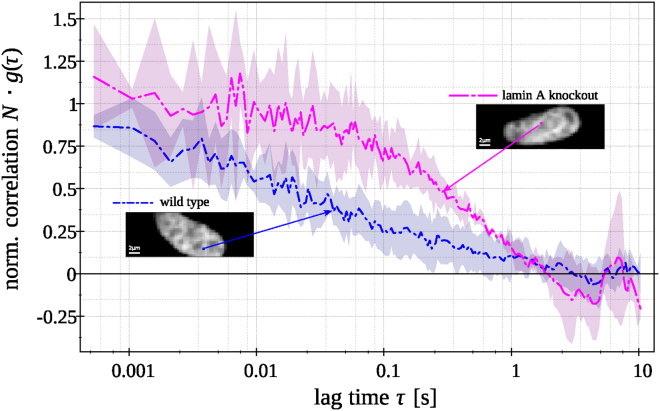
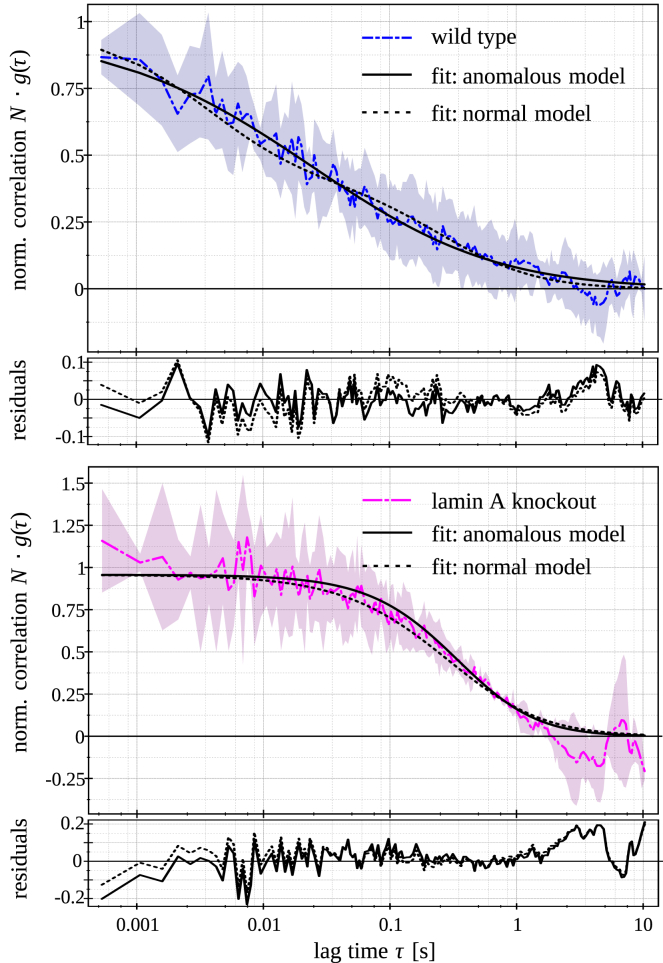
Fig. 4 shows the fluorescence intensity images of a wild-type cell and a lamin A knockout cell, both expressing H2A-eGFP together with two typical autocorrelation curves at the single pixels ( pixels) highlighted in the fluorescence images. A clear effect is evident by comparing the curves. Contrary to the curve in the lamin A knockout cell, the autocorrelation curve in the wild-type cell demonstrates a shorter correlation time, and its overall shape is substantially different. To describe this effect, two different SPIM-FCS models were fitted to the autocorrelation curves (Eq. 1): an anomalous diffusion model (Eq. 9), assuming the diffusion is anomalous and the fraction of freely diffusing particles and internal chromatin dynamics are negligible, and a two-component normal diffusion model (Eq. 4), in which the diffusion is normal and two different diffusing particles are expected. The slower ones are assumed to be chromatin-bound histones, and the faster ones can account for either unbound histones or faster internal dynamics of chromatin. Fig. 5 shows typical fits for both models that do not differ significantly in fit quality. Thus, these are more or less equally valid ways to account for the crowded environment in live cells.
Figure 4.
Typical FCS ACFs taken at the single pixels, as indicated in the corresponding SPIM images of the MAF wild-type and lamin A knockout cells. To see this figure in color, go online.
Figure 5.
FCS ACFs against different fit models and their corresponding residuals: autocorrelation curves, two different fits, and residuals were calculated at nonbinned pixels in fluorescence image series acquired from MAF cells expressing H2A-eGFP as wild-type (upper panel) and LMNA−/− MAF cells expressing H2A-eGFP (lower panel). To see this figure in color, go online.
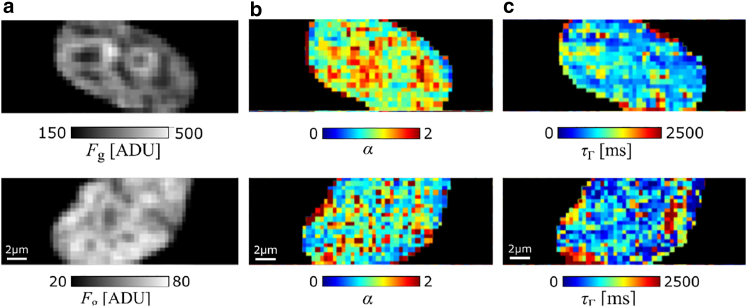
The two-component normal diffusion model has four fit parameters (number of particles in a focal volume N, fast-diffusion coefficient , slow-diffusion coefficient , and the fraction of particles diffusing slowly ), whereas the anomalous diffusion model has only three (number of particles in a focus N, anomaly parameter α, and anomalous diffusion coefficient ). For the two-component normal diffusion fit, the fast-diffusion coefficient was fixed to ensure better convergence of the algorithm. This fast component is usually interpreted as the diffusion coefficient of free histones, and it is in the same range as those obtained for inert tracer proteins (17, 33). The slow component corresponded to the motion of chromatin-bound histones. For all pixels in each cell image series, a two-component normal diffusion fit with all parameters free is performed, and the median of the distribution is calculated. Then, this value is fixed, and the autocorrelation curve of each pixel is fitted again with the same model. Fig. 5 shows fluorescence images and fit results for a typical wild-type and a lamin A knockout cell expressing H2A-eGFP. A random motion in the cell can be defined as motion whose correlation function (measured on a signal collected through a high numerical aperture objective lens) is described by a hyperbolic decay. The good result of the fitting procedure indicates that the fluctuations can be described by random motion statistics. From the anomaly parameter maps (Fig. 6), it is visually apparent that histone diffusion is more anomalous in the wild-type than in the lamin A knockout cells. Moreover, the fraction of the slow component in the two-component normal diffusion fit increases for the knockout cells (Table 2).
Figure 6.
Maps of fluorescence intensity, diffusion anomaly, and dwell time in an LMNA−/− MAF (upper row) and MAF wild-type (lower row). (a) Fluorescence intensity images show an LMNA−/− MAF and MAF wild-type expressing H2A-eGFP represented in the analog-to-digital converter unit (ADU), which is the output unit of the EMCCD camera. For each cell, (b) the map of anomaly parameter α and (c) the dwell time obtained from the anomalous diffusion model are shown in their corresponding columns.
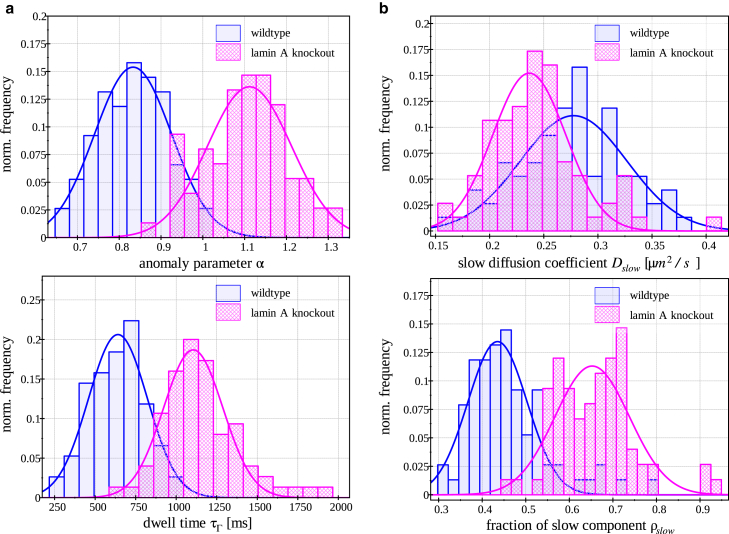
In most cases, the histograms of the fit parameters over all the pixels of the same cell contain a certain number of outliers and often feature broad distributions. Therefore, robust statistical estimators, such as the median, are used for any further evaluation. Fig. 7 summarizes the fit results for the anomaly parameter and the dwell times of all pixels in all measured cell nuclei (160 MAFs and 153 LMNA−/− MAFs).
Figure 7.
The distributions of fit parameters over all measured cells. (a) Fit results obtained with the anomalous diffusion model. The distribution of anomaly parameters α (upper panel) shows an apparent shift to the normal diffusion by knocking out lamin A protein. The distribution of the dwell time (lower panel) obtained from all measured cells represents a longer time to leave the observed volume in the absence of lamin A protein. (b) Using the two-component normal diffusion model, we extracted the distibution of slow diffusion coefficient (upper panel) and the fraction of slow component (lower panel). The bound histones are evidently more dominant in the absence of lamin A. A statistical summary of the fit results is reported in Table 2. To see this figure in color, go online.
The statistical averages over all pixels in all cells confirm that histone mobility in the wild-type fibroblasts is well described by anomalous subdiffusion . In MAFs lacking A-type lamins, the anomaly of this motion is no longer observed, and a normal diffusion model is enough to explain the data . These results agree with the recent findings about telomere motion (14). Furthermore, we detect a significant slowing down of histone mobility when lamin A is missing, indicated by an increased dwell time. Similar conclusions can be reached from the two-component model as the fraction of slow component increases when passing from the wild-type cells to the lamin A knockout ones .
Discussion
Chromatin in the cell nucleus is highly ordered yet dynamic. The principles of its organization, crucial for proper cell function, still remain unclear (34, 35). Here, to get further insight into these mechanisms, we focused on the effect of lamin A on chromatin dynamics. Evidence is growing that nuclear lamins form a filamentous scaffold throughout the nucleus that not only determines its shape and mechanical properties but also serves as a docking site for chromatin and for many proteins that participate in chromatin organization (14). Besides the extensive lamin structures located within the nuclear lamina, smaller and more dynamic lamin polymers may form protein complexes involved in a wide range of nuclear housekeeping functions, such as DNA replication, DNA repair (8, 10), and RNA pol II transcription (36).
To characterize chromatin dynamics in live cells, we use FCS and FCCS in SPIM-FCS/FCCS. FCS yields mobility parameters through an autocorrelation analysis of fluorescence fluctuations measured inside a small observation volume. Two-color FCCS, in addition, provides information about the interactions between differently labeled particles. SPIM-FCS allows such an autocorrelation analysis on fast image series for hundreds of thousands of contiguous pixels, thereby providing two-dimensional mobility and interaction maps in live cells (20).
We applied SPIM-FCS to study the influence of lamin A on the mobility of chromatin fluorescently labeled with H2A-eGFP. Earlier experimental studies on transport processes inside the cells have demonstrated that the intranuclear diffusion of particles is anomalous (3, 6, 16, 29, 31). This is likely because of macromolecular crowding and/or the viscoelasticity of the nuclear microenvironment, which hinders the random motions of particles. There are different polymer models to describe these anomalous dynamics. Guigas et al. studied the diffusion of gold nanospheres in cells and found out that their anomalous diffusion is in agreement with the Rouse model for polymer dymanics (6). This indicates that the intranuclear environment resembels a polymeric sponge. However, Erdel et al. have shown that a more detailed model, namely the porous medium model, is needed to explain the subdiffusivity of chromatin. They summarized different polymer models and deduced that a porous medium or random obstacle network for diffusing particles can better characterize the nucleoplasm (4). Brownian dynamics simulations also showed that the chromatin chain alone would not display anomalous diffusion; this requires, in addition, the presence of a viscoelastic matrix around the polymer (3). We show that the diffusion anomaly parameter α of chromatin-bound histones in MAFs is , indicating this subdiffusion is in good compliance with the results presented in Erdel et al (4). In the lamin A knockout cell line, on the other hand, diffusion reverted to normal but significantly slowed down. This change in chromatin dynamics suggests that the lamin network is the source of the nucleoplasmic viscoelasticity. In the absence of lamin A, the nucleoplasm loses its viscoelastic behavior, reducing diffusion obstruction. Furthermore, the loss of the elastic lamin A interconnections reduces the overall speed of chromatin motion, as indicated by the longer residence time in the focal volume. This can be also seen from the two-component model because the fraction of slowly diffusing histones in lamin A knockout cells increases. This agrees with the theoretical predictions of Chakrabarti, who showed that the loop closure time for an elastic polymer chain is accelerated by viscoelasticity (37). It is noteworthy that our findings agree with recent findings by Garini’s group on telomere motion in the cells lacking lamin A proteins (14).
To understand better how lamin A affects the viscoelasticity of the nuclear interior, we analyzed the diffusion of an inert probe, eGFP tetramer((eGFP)-4x), with the same technique (data not shown). In lamin-A-deficient cells, the mobility of free eGFP-4x is significantly slowed down (from in the wild-type cells to in the knockout ones). This result supports the view that lamin A is responsible for the viscoelasticity of the nuclear interior.
We also examine the interactions between lamin A and chromatin, performing SPIM-FCCS measurements on mouse cells in which lamins and histones are labeled with different colors. The significant CC amplitude (Fig. 1) demonstrates that a relatively large fraction of lamin A is moving together with histones. Because the decay time of the CC curves is comparable to the residence time of histones bound to chromatin, we can infer that lamin A and chromatin are codiffusing.
To conclude, because lamin A depletion strikingly changes chromatin dynamics, we suggest that molecular regulation of chromatin diffusion by lamin A in the nuclear interior is critical for the maintenance of genome organization.
Author Contributions
J.L. came up with the original idea and conceived the project. F.T. and B.I. performed the measurements with contributions from J.W.K. and J.L. F.T. and B.I. analyzed the data and F.T. prepared the figures with contributions from J.W.K., G.C., J.L., and K.T. G.M. prepared the samples and worked out a protocol to embed the cells. F.T. and J.L. wrote the article with input from J.W.K., G.C., and K.T.
Acknowledgments
This article is dedicated to the memory of J.L., who initiated and passionately promoted this project until his sudden loss on the 6th of May 2017.
We acknowledge Giulia Marcarini for performing the initial experiments and data analysis. We also thank Yuval Garini, Mickey Schurr, and György Vámosi for inspiring discussions; Harrald Hermann and Kendra Maaß for providing the cell lines; and Tabea Krieger, Ralf Metzler, and Andrey Cherstvy for critical reading of the manuscript and useful comments.
The project was funded by the Heidelberg Graduate School of Mathematical and Computational Methods for the Sciences, founded by Deutsche Forschungsgemeinschaft grant GSC 220 in the German Universities Excellence Initiative in the form of a doctoral fellowship to F.T.
Editor: Tamar Schlick.
Footnotes
Jörg Langowski, deceased on May 6th, 2017.
References
- 1.Paul R., Heil P., Schwarz U.S. Propagation of mechanical stress through the actin cytoskeleton toward focal adhesions: model and experiment. Biophys. J. 2008;94:1470–1482. doi: 10.1529/biophysj.107.108688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wang N., Tytell J.D., Ingber D.E. Mechanotransduction at a distance: mechanically coupling the extracellular matrix with the nucleus. Nat. Rev. Mol. Cell Biol. 2009;10:75–82. doi: 10.1038/nrm2594. [DOI] [PubMed] [Google Scholar]
- 3.Fritsch C.C., Langowski J. Chromosome dynamics, molecular crowding, and diffusion in the interphase cell nucleus: a Monte Carlo lattice simulation study. Chromosome Res. 2011;19:63–81. doi: 10.1007/s10577-010-9168-1. [DOI] [PubMed] [Google Scholar]
- 4.Erdel F., Baum M., Rippe K. The viscoelastic properties of chromatin and the nucleoplasm revealed by scale-dependent protein mobility. J. Phys. Condens. Matter. 2015;27:064115. doi: 10.1088/0953-8984/27/6/064115. [DOI] [PubMed] [Google Scholar]
- 5.Bronstein I., Israel Y., Garini Y. Transient anomalous diffusion of telomeres in the nucleus of mammalian cells. Phys. Rev. Lett. 2009;103:018102. doi: 10.1103/PhysRevLett.103.018102. [DOI] [PubMed] [Google Scholar]
- 6.Guigas G., Weiss M. Sampling the cell with anomalous diffusion - the discovery of slowness. Biophys. J. 2008;94:90–94. doi: 10.1529/biophysj.107.117044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Dechat T., Pfleghaar K., Goldman R.D. Nuclear lamins: major factors in the structural organization and function of the nucleus and chromatin. Genes Dev. 2008;22:832–853. doi: 10.1101/gad.1652708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Mahen R., Hattori H., Venkitaraman A.R. A-type lamins maintain the positional stability of DNA damage repair foci in mammalian nuclei. PLoS One. 2013;8:e61893. doi: 10.1371/journal.pone.0061893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Gonzalo S. Springer; New York: 2014. DNA Damage and Lamins; pp. 377–399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Gibbs-Seymour I., Markiewicz E., Hutchison C.J. Lamin A/C-dependent interaction with 53BP1 promotes cellular responses to DNA damage. Aging Cell. 2015;14:162–169. doi: 10.1111/acel.12258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Swift J., Ivanovska I.L., Discher D.E. Nuclear lamin-A scales with tissue stiffness and enhances matrix-directed differentiation. Science. 2013;341:1240104. doi: 10.1126/science.1240104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Irianto J., Pfeifer C.R., Discher D.E. Nuclear lamins in cancer. Cell. Mol. Bioeng. 2016;9:258–267. doi: 10.1007/s12195-016-0437-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Cho S., Irianto J., Discher D.E. Mechanosensing by the nucleus: from pathways to scaling relationships. J. Cell Biol. 2017;216:305–315. doi: 10.1083/jcb.201610042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bronshtein I., Kepten E., Garini Y. Loss of lamin A function increases chromatin dynamics in the nuclear interior. Nat. Commun. 2015;6:8044. doi: 10.1038/ncomms9044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Vivante A., Brozgol E., Garini Y. Genome organization in the nucleus: from dynamic measurements to a functional model. Methods. 2017;123:128–137. doi: 10.1016/j.ymeth.2017.01.008. [DOI] [PubMed] [Google Scholar]
- 16.Wachsmuth M., Waldeck W., Langowski J. Anomalous diffusion of fluorescent probes inside living cell nuclei investigated by spatially-resolved fluorescence correlation spectroscopy. J. Mol. Biol. 2000;298:677–689. doi: 10.1006/jmbi.2000.3692. [DOI] [PubMed] [Google Scholar]
- 17.Dross N., Spriet C., Langowski J. Mapping eGFP oligomer mobility in living cell nuclei. PLoS One. 2009;4:e5041. doi: 10.1371/journal.pone.0005041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wohland T., Shi X., Stelzer E.H. Single plane illumination fluorescence correlation spectroscopy (SPIM-FCS) probes inhomogeneous three-dimensional environments. Opt. Express. 2010;18:10627–10641. doi: 10.1364/OE.18.010627. [DOI] [PubMed] [Google Scholar]
- 19.Capoulade J., Wachsmuth M., Knop M. Quantitative fluorescence imaging of protein diffusion and interaction in living cells. Nat. Biotechnol. 2011;29:835–839. doi: 10.1038/nbt.1928. [DOI] [PubMed] [Google Scholar]
- 20.Krieger J.W., Singh A.P., Langowski J. Dual-color fluorescence cross-correlation spectroscopy on a single plane illumination microscope (SPIM-FCCS) Opt. Express. 2014;22:2358–2375. doi: 10.1364/OE.22.002358. [DOI] [PubMed] [Google Scholar]
- 21.Krieger J.W., Singh A.P., Wohland T. Imaging fluorescence (cross-) correlation spectroscopy in live cells and organisms. Nat. Protoc. 2015;10:1948–1974. doi: 10.1038/nprot.2015.100. [DOI] [PubMed] [Google Scholar]
- 22.Brazda P., Krieger J., Vámosi G. Ligand binding shifts highly mobile retinoid X receptor to the chromatin-bound state in a coactivator-dependent manner, as revealed by single-cell imaging. Mol. Cell. Biol. 2014;34:1234–1245. doi: 10.1128/MCB.01097-13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Szalóki N., Krieger J.W., Vámosi G. Evidence for homodimerization of the c-Fos transcription factor in live cells revealed by fluorescence microscopy and computer modeling. Mol. Cell. Biol. 2015;35:3785–3798. doi: 10.1128/MCB.00346-15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Pernuš A., Langowski J. Imaging Fos-Jun transcription factor mobility and interaction in live cells by single plane illumination-fluorescence cross correlation spectroscopy. PLoS One. 2015;10:e0123070. doi: 10.1371/journal.pone.0123070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Sullivan T., Escalante-Alcalde D., Burke B. Loss of A-type lamin expression compromises nuclear envelope integrity leading to muscular dystrophy. J. Cell Biol. 1999;147:913–920. doi: 10.1083/jcb.147.5.913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Krieger, J. W., and J. Langowski. 2012. QuickFit 3.0: a data evaluation application for biophysics. Technical report, DKFZ Heidelberg. http://www.dkfz.de/Macromol/quickfit/.
- 27.Metzler R., Klafter J. The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Phys. Rep. 2000;339:1–77. [Google Scholar]
- 28.Metzler R., Klafter J. The restaurant at the end of the random walk: recent developments in the description of anomalous transport by fractional dynamics. J. Phys. Math. Gen. 2004;37:R161. [Google Scholar]
- 29.Höfling F., Franosch T. Anomalous transport in the crowded world of biological cells. Rep. Prog. Phys. 2013;76:046602. doi: 10.1088/0034-4885/76/4/046602. [DOI] [PubMed] [Google Scholar]
- 30.Weiss M., Hashimoto H., Nilsson T. Anomalous protein diffusion in living cells as seen by fluorescence correlation spectroscopy. Biophys. J. 2003;84:4043–4052. doi: 10.1016/S0006-3495(03)75130-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Weiss M., Elsner M., Nilsson T. Anomalous subdiffusion is a measure for cytoplasmic crowding in living cells. Biophys. J. 2004;87:3518–3524. doi: 10.1529/biophysj.104.044263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Horton M.R., Hofling F., Franosch T. Development of anomalous diffusion among crowding proteins. Soft Matter. 2010;6:2648–2656. [Google Scholar]
- 33.Vámosi G., Mücke N., Tóth K. EGFP oligomers as natural fluorescence and hydrodynamic standards. Sci. Rep. 2016;6:33022. doi: 10.1038/srep33022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Fraser P., Bickmore W. Nuclear organization of the genome and the potential for gene regulation. Nature. 2007;447:413–417. doi: 10.1038/nature05916. [DOI] [PubMed] [Google Scholar]
- 35.Wachsmuth M., Caudron-Herger M., Rippe K. Genome organization: balancing stability and plasticity. Biochim. Biophys. Acta. 2008;1783:2061–2079. doi: 10.1016/j.bbamcr.2008.07.022. [DOI] [PubMed] [Google Scholar]
- 36.Brody Y., Neufeld N., Shav-Tal Y. The in vivo kinetics of RNA polymerase II elongation during co-transcriptional splicing. PLoS Biol. 2011;9:e1000573. doi: 10.1371/journal.pbio.1000573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Chakrabarti R. Dynamics of end-to-end loop formation for an isolated chain in viscoelastic fluid. Physica A. 2012;391:5326–5331. [Google Scholar]