Redox-coupled quinone dynamics in the respiratory complex I

Significance

Complex I is the primary energy-converting enzyme of aerobic respiratory chains. By reducing quinone to quinol, this gigantic enzyme pumps protons across its membrane domain, which in turn powers ATP synthesis and active transport. Despite the recently resolved molecular structures of complex I, the quinone dynamics and its coupling to the pumping function remains unclear. Here we show by large-scale molecular simulations that the quinone reduction leads to ejection of the quinol molecule from the active site into a second binding site near the proton-pumping membrane domain of complex I. The identified region has been linked with human mitochondrial disorders. Our work suggests that the quinone dynamics provides a key coupling element in complex I.

Abstract

Complex I couples the free energy released from quinone (Q) reduction to pump protons across the biological membrane in the respiratory chains of mitochondria and many bacteria. The Q reduction site is separated by a large distance from the proton-pumping membrane domain. To address the molecular mechanism of this long-range proton-electron coupling, we perform here full atomistic molecular dynamics simulations, free energy calculations, and continuum electrostatics calculations on complex I from Thermus thermophilus. We show that the dynamics of Q is redox-state-dependent, and that quinol, QH₂, moves out of its reduction site and into a site in the Q tunnel that is occupied by a Q analog in a crystal structure of Yarrowia lipolytica. We also identify a second Q-binding site near the opening of the Q tunnel in the membrane domain, where the Q headgroup forms strong interactions with a cluster of aromatic and charged residues, while the Q tail resides in the lipid membrane. We estimate the effective diffusion coefficient of Q in the tunnel, and in turn the characteristic time for Q to reach the active site and for QH₂ to escape to the membrane. Our simulations show that Q moves along the Q tunnel in a redox-state-dependent manner, with distinct binding sites formed by conserved residue clusters. The motion of Q to these binding sites is proposed to be coupled to the proton-pumping machinery in complex I.

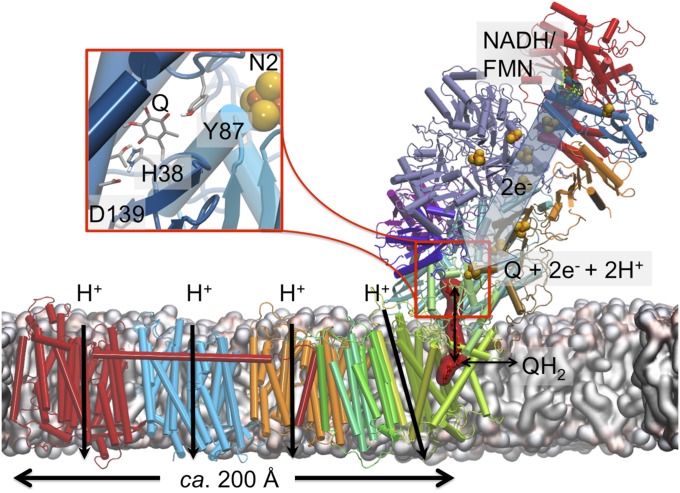
Complex I (NADH:ubiquinone oxidoreductase) functions as an important member of the aerobic respiratory chains of many organisms. This gigantic (0.5–1 MDa) redox-driven proton pump receives electrons from the oxidation of foodstuffs, via reduced NADH, and transfers them to quinone (Q), a reaction that is coupled to proton translocation across the membrane (1–5). The electrochemical proton gradient thus established drives synthesis of ATP and active transport (6). Structural studies (7–12) show that the electron transfer module of complex I is located exclusively in the hydrophilic domain of the protein, whereas the proton-pumping activity takes place in the antiporter-like membrane subunits (13–15), located as far as ca. 200 Å from the Q reduction site (Fig. 1). Despite many mechanistic suggestions (2, 4, 5, 7, 8, 10–12, 16, 17), it remains currently unclear how the coupling between the electron and proton transfer reactions is achieved across such large distances.

Fig. 1.

Structure and function of complex I from T. thermophilus (PDB ID code 4HEA). Reduction of Q (shown in red surface representation) by electron transfer from NADH/FMN in the hydrophilic arm of complex I drives proton pumping in the membrane domain, up to 200 Å away from the site of Q reduction. (Inset) The Q-reduction site near the N2 center, where Q interacts with residues Tyr-87_Nqo4 and His-38_Nqo4.

In contrast to most Q reductases, the Q-binding site in complex I is located ∼20–30 Å above the membrane plane, in a tight tunnel (11, 12) that ends at around 12 Å from the iron–sulfur center, N2, which serves as the immediate electron donor for Q (Fig. 1, Inset) (18). It has been suggested that the reduction of Q is coupled to the proton-pumping machinery in complex I (19–22). More specifically, Euro et al. (14) proposed that it is the initial negative charge on Q deposited upon reduction that triggers proton translocation via an electrostatic/conformational change mechanism. This idea was subsequently adopted and extended in the mechanisms proposed by Sazanov and coworkers (10, 11) Brandt (20), Verkhovskaya and Bloch (23), Kaila (17), and Wikström and Hummer (24, 25). Recently, we showed (26) that the reduction of Q is coupled to a local proton transfer from Tyr-87_Nqo4 and His-38_Nqo4, forming QH₂. This in turn triggers a charge redistribution cascade that propagates into the membrane-bound NuoH/Nqo8 subunit. It was also suggested that the coupling is mediated by conformational and electrostatic rearrangements, which lead to increased pK_a values of several conserved residues in the Nqo8 subunit, thereby activating the proton pump (26).

We recently proposed that there might be two preferred Q-binding positions within the Q tunnel (4) (see also ref. 24), a low (Q_L) and a high (Q_H) potential site. The Q_L site is near center N2 that was initially characterized biochemically (27–29) and later confirmed computationally (26, 30). The Q_H site could be located somewhere in the Q tunnel, albeit its precise location as well as its molecular architecture remains undescribed (Fig. 1). To date, however, a bound Q molecule has not been resolved in any of the crystal or recent cryo-EM structures of complex I (11, 12, 31, 32). Two conformations have been reported for Q bound to the conserved Tyr-87_Nqo4 (30), and recent studies also show that the mammalian complex I can operate with different numbers of isoprene units, Q₁–Q₁₀ (33). Earlier reports from labeling experiments (34, 35) also support the existence of multiple Q-binding sites in complex I. Moreover, it was suggested that the Q molecule could itself act as a piston in the proton-pumping mechanism of complex I, thereby functioning as a dynamic redox transducer that shuttles between the two sites (4). This model has some mechanistic similarities to the two-stroke model by Brandt (20), in which two sequential proton-pumping steps are coupled to affinity variations of Q between high- and low-affinity sites.

Here we identify by large-scale atomistic molecular dynamics (MD) simulations and Poisson–Boltzmann (PB) continuum electrostatic calculations, as well as by free energy simulations and Bayesian diffusion models, putative Q-binding sites in complex I and show how the dynamics of Q may be coupled to the proton-pumping process in complex I. Our combined simulation data provide molecular insight into how complex I may employ the Q dynamics to serve a piston function that transduces the redox energy into a proton-pumping activity.

Results and Discussion

Q Dynamics near the N2 Iron–Sulfur Center.

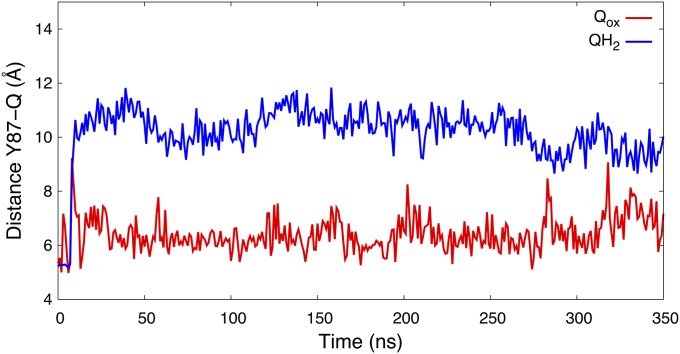
To probe the dynamics of Q in its binding site near the N2 center, we performed atomistic MD simulations of complex I with oxidized Q (Q_ox), and reduced and doubly protonated quinol (QH₂). Data from 350-ns MD simulations suggest that the Q_ox remains bound at the site near N2 (Fig. 2). In contrast, we find that the reduced quinol species (QH₂) moves 8–10 Å away from Tyr-87_Nqo4, when Tyr-87_Nqo4 is deprotonated and His-38_Nqo4 is neutral, corresponding to a state after electron transfer from N2 and proton transfer from His-38_Nqo4 and Tyr-87_Nqo4 (26). We also observed similar redox- and protonation-state-dependent Q dynamics in multiple short MD simulations, as well as by using independent simulation setups of complex I (SI Appendix, Table S1), suggesting that the obtained overall behavior of Q_ox and QH₂ is robust (SI Appendix, Fig. S1). It has been shown earlier that QH₂ formation triggers a conformational change in the active site, in which the anionic Asp-139_Nqo4 dissociates from the neutral His-38_Nqo4, and the latter residue approaches the functionally important Tyr-87_Nqo4 (26, 29). Structural rearrangement in this region was also observed in the crystal structures of complex I (11, 12). These protein motions are likely factors responsible for the observed difference between the dynamics of the two neutral species, Q_ox and QH₂ (Fig. 2).

Fig. 2.

Distance of the Q headgroup from the active site Tyr-87_Nqo4 for oxidized Q (Q_ox, in red) and reduced/protonated QH₂ (in blue) states obtained from 350-ns MD simulations of each state.

To probe the relative effects of conformational and protonation changes on the dynamics of Q near the N2 site, we performed additional ca. 150-ns MD simulations of structures in which we replaced Q_ox with QH₂, and vice versa (see also ref. 26). Starting from the Q_ox position, QH₂ remained bound to the Q_ox site (SI Appendix, Fig. S2). Note that in this simulation, Tyr-87_Nqo4 and His-38_Nqo4 were protonated, and the His-38_Nqo4/Asp-139_Nqo4 ion pair remained intact. Similarly, Q_ox starting from the QH₂ position, with Tyr-87_Nqo4 deprotonated and His-38_Nqo4 neutral, did not relax to the position seen in the Q_ox simulation with Tyr-87_Nqo4 and His-38_Nqo4 modeled in their protonated states (SI Appendix, Fig. S2). Hence, our data are consistent with the hypothesis that conformational changes in the protein linked to deprotonation of the His/Asp pair are partly responsible for the lowered affinity for QH₂ near Tyr-87_Nqo4.

Free Energy of Redox-State-Dependent Q Dynamics.

To explore the energetics driving the Q dynamics that take place beyond time scales accessible by our unbiased MD simulations, we performed free energy calculations using umbrella sampling (US) (36) in combination with the weighted histogram analysis method (WHAM) (37) (Methods). Due to sampling problems of a long-tailed Q₆–Q₁₀, we employed a short-tailed Q₁ in the US/WHAM calculations, which can also function as a substrate of complex I (33).

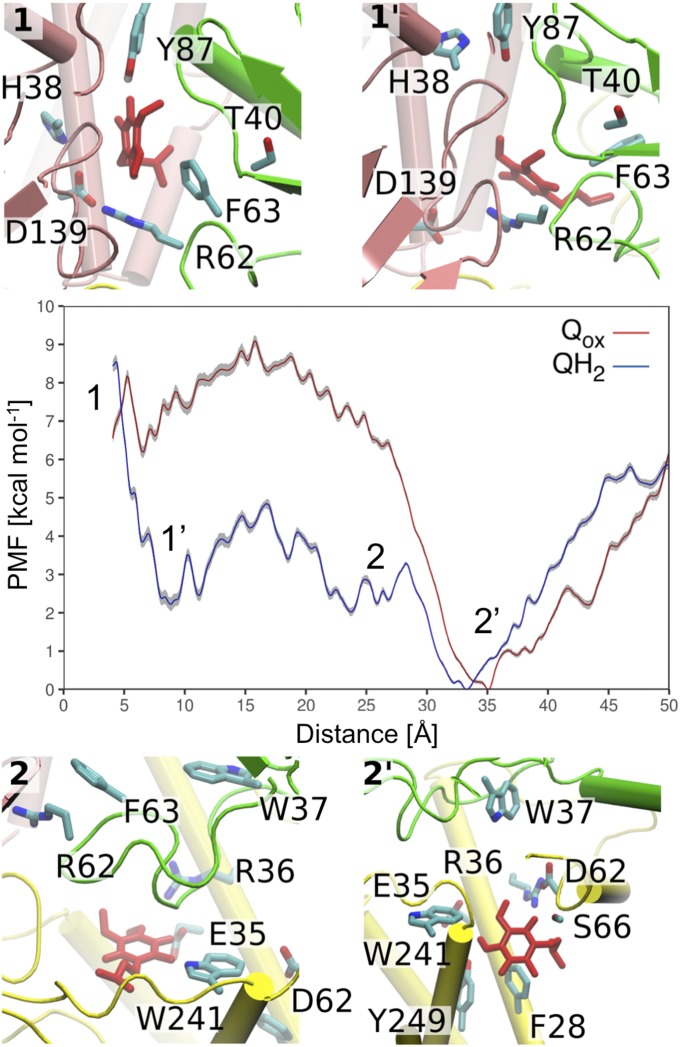
Fig. 3 shows the resulting potentials of mean force (PMFs) for the Q_ox and QH₂ motions in the Q tunnel as functions of the Tyr-87_Nqo4–Q distance. The PMF profiles suggest that the oxidized Q (Q_ox) in a membrane milieu has to surpass an activation energy barrier of ca. 5–8 kcal⋅mol⁻¹ to reach the site near N2 (Fig. 3), where we observe a local plateau in the free energy surface. The PMF profile also indicates that Q binds weakly relative to the membrane Q pool, with a global minimum at around 30 Å from Tyr-87_Nqo4 and a ca. 5 kcal⋅mol⁻¹ barrier to reach the membrane environment (Fig. 3).

Fig. 3.

The free energy (PMF) profiles (in kilocalories per mole) obtained from US simulations for oxidized (Q_ox, red) and reduced (QH₂, blue) short-tailed Q₁ species. The PMF shows the standard deviation of the statistical error (in gray), which was estimated by bootstrap analysis. (Insets) Structural snapshots corresponding to transient binding sites 1, 1′, 2, and 2′ in the PMF profile. See also SI Appendix, Fig. S3 for a close-up of site 2′. Overlaps in the sampled reaction coordinates are shown in SI Appendix, Fig. S19.

The US/PMF profile for QH₂ shows a minimum at site 1′, ca. 8–10 Å from Tyr-87_Nqo4, which roughly corresponds to the equilibrium position of the QH₂ headgroup observed in the free MD simulations (Fig. 2 and SI Appendix, Fig. S1). Between 10 and 30 Å, the PMFs for both Q and QH₂ are quite flat, indicating relatively unhindered back-and-forth motion. Interestingly, site 1′ for QH₂ coincides with the crystallographically refined position of a Q analog in the structure of mitochondrial complex I from Yarrowia lipolytica (12). The free energy profile suggests that upon formation of QH₂ at the site close to N2 (site 1), the species relaxes to a new position, site 1′, 8–10 Å away from Tyr-87_Nqo4. The relaxation to the new position may have functional relevance in preventing reverse electron transfer, as the distance to the N2 center increases to >14 Å, a typical distance threshold for biological electron transfer processes (38).

Importantly, the US/PMF calculations also suggest for the QH₂ species a second minimum, site 2, at ca. 25 Å, which is next to a conserved set of acidic residues that have been suggested to play an important role in redox-coupled proton pumping (17, 26, 39) (discussed below). We also observe a second minimum 2′ at around 33–35 Å away from Tyr-87_Nqo4 (Fig. 3) within Nqo8 at the opening to the membrane (SI Appendix, Fig. S3). To reach site 1 near N2 from site 2′, Q has to surpass an activation energy barrier of ca. 5–8 kcal⋅mol⁻¹. To further probe this putative second Q-binding site we explored the dynamics of QH₂ and Q_ox using equilibrium MD simulation analyzed with a Bayesian diffusion model (40) (discussed below).

Q Dynamics in the Tunnel and a Putative Second Q-Binding Site.

To probe how Q₁₀ moves within the long Q tunnel, we ran multiple equilibrium MD simulations starting from different positions of Q_ox and QH₂ obtained from nonequilibrium steered MD (SMD) simulations (Methods and SI Appendix, Figs. S4 and S5). From the equilibrium simulations, we extracted the time series of the Tyr-87_Nqo4(OH)–Q distance, a reaction coordinate also used in the US simulations (SI Appendix, Fig. S5). In a Bayesian analysis (40) (Methods), we then used these time series to estimate local diffusion coefficients and free energy profiles for the Q_ox and QH₂ motions along the tunnel.

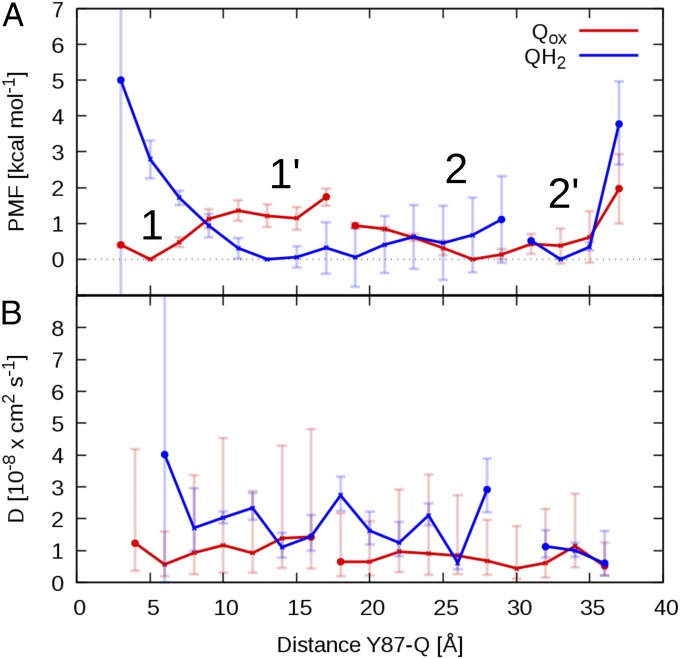
The free energy profiles are shown in Fig. 4A. For Q_ox, we find a local minimum (site 1) at ca. 4 Å from Tyr-87_Nqo4 and edge-to-edge distance of ca. 14 Å of the Q headgroup to the iron–sulfur cluster N2. This site is stabilized further by a hydrogen bond to protonated His-38_Nqo4 (Fig. 5B), consistent with previous studies (30), and our equilibrium MD simulations. A shoulder in the PMF (site 1′) indicates a metastable site at a distance of ∼10–15 Å to Tyr-87_Nqo4, where the Q headgroup forms interactions with Phe-63_Nqo6 (Fig. 5B and SI Appendix, Fig. S6). We also observe a distinct second binding site (2 and 2′) at a distance of around 25–35 Å from Tyr-87_Nqo4 (Fig. 4), which coincides with the global minimum in the PMF profiles obtained by US/WHAM (Fig. 3). In site 2, the aromatic side chains of Trp-37_Nqo6, Trp-241_Nqo8, and Tyr-249_Nqo8 (Fig. 5 B and C and SI Appendix, Fig. S6) stabilize the Q headgroup, which is also surrounded by two conserved ion pairs, Arg-36_Nqo8/Asp-62_Nqo8 and Arg-62_Nqo6/Glu-35_Nqo8 (Fig. 5B). In site 2′, the Q headgroup interacts mainly with Trp-241_Nqo8, at the opposite side from site 2 (SI Appendix, Fig. S6), and with the backbone carbonyl group of Ser-66_Nqo8 (Fig. 5B and SI Appendix, Fig. S6). Moreover, the Q headgroup is located near the entrance of the Q tunnel, and its hydrophobic tail is in contact with the membrane milieu. Exit of Q to the membrane is hindered by a free energy barrier of >3 kcal⋅mol⁻¹, consistent with the US/WHAM profiles for the short-tailed Q. The transient binding sites obtained from our Bayesian analysis are overall similar to those obtained for the short-tailed Q₁ by US (Fig. 3).

Fig. 4.

Free energy (PMF) profile and diffusion coefficient of Q_ox (red) and QH₂ (blue) in the Q tunnel. (A) Free energy profiles as a function of Tyr-87_Nqo4(OH)–Q distance and (B) corresponding position-dependent diffusion coefficient profiles extracted from unbiased equilibrium MD simulations from system setup 2 by a Bayesian analysis using a 1D diffusion model. The two PMF profiles are shifted vertically with their global minimum set to zero. In A 1, 1′, 2, and 2′ indicate local minima in the Q-binding cavity for the Q_ox and QH₂ headgroup, respectively. Marked gaps in the profiles indicate unresolved free energy differences in rarely sampled areas of the reaction coordinate (SI Appendix, Fig. S5). Error bars in the PMF indicate standard errors of the mean, which were estimated by block averaging (Methods).

Fig. 5.

(A) Structure of the Q tunnel, with Q_ox (in red) and QH₂ (in blue) at transient binding sites 1, 1′, 2, and 2′ obtained from the 1D diffusion model (Fig. 4). (B and C) Close-ups of the Q-binding sites. Sites 1/1′ and 2/2′ correspond to the site close to N2 and the site at the entrance of the Q tunnel, respectively.

We also find four local minima for the QH₂ headgroup (Fig. 5C), which are near the corresponding local minima for the oxidized Q_ox (Fig. 5B). Moving away from Tyr-87_Nqo4 toward the opening of the tunnel, the PMF profile for QH₂ smoothly decreases toward the site 1′ at ca. 13 Å (Fig. 4A). At site 1′, QH₂ forms hydrogen bonds with the backbone of Thr-40_Nqo6, Gly-42_Nqo6, and Thr-54_Nqo6 (Fig. 5C). The PMF profile for QH₂ is flat in the range of 10- to 28-Å distance to Tyr-87_Nqo4 (see SI Appendix, Fig. S5 for the projected reaction coordinate), which includes sites 1′ and 2 (Fig. 4A). At site 2, QH₂ interacts with the aromatic amino acid residues Trp-241_Nqo8, Tyr-249_Nqo8, and Trp-37_Nqo6 (SI Appendix, Fig. S7), similarly as for the oxidized Q. Two ion pairs, Arg-36_Nqo8/Asp-62_Nqo8 and Arg-62_Nqo6/Glu-35_Nqo8, strongly interact with the quinol headgroup in site 2 (Fig. 5C and SI Appendix, Fig. S7). The dispersion of the trajectories (SI Appendix, Fig. S5) indicates that sites 2 and 2′ for QH₂ are separated by a significant free energy barrier, which leads to a sampling gap between 28 and 32 Å of the distance reaction coordinate (see SI Appendix, Fig. S5 for the projected reaction coordinate). At site 2′, QH₂ interacts with Trp-241_Nqo8 on the side opposite minimum 2, and with the aromatic side chain of Phe-28_Nqo8. QH₂ is further stabilized by hydrogen bonds with the backbone carbonyl group of Ser-66 _Nqo8 (Fig. 5C and SI Appendix, Fig. S7; see also SI Appendix, Table S3 and sequence alignments in SI Appendix, Figs. S8–S10). Note that site 1, in which QH₂ forms a contact with Tyr-87_Nqo4 (Fig. 5C), is only resolved in the PMF profiles with projected reaction coordinate and is not connected to the rest of the PMF (SI Appendix, Fig. S5). Interestingly, apart from three MD trajectories, which end up in this site, all other trajectories move to site 1′, consistent with the equilibrium MD simulations (Fig. 2). Similarly, we observe a sampling gap for Q between sites 1′ and 2. Overall, the Q tunnel can be divided into a part connecting sites 1, 1′, and 2 and the tunnel entrance around site 2′, which is separated by a cluster of aromatic residues, including Trp-241_Nqo8, and salt bridges (Figs. 3 and 5). In the channel connecting sites 1′ and 2, the quinol can diffuse quite freely, whereas the passage between the two sections is at least partially hindered.

The PMF profiles extracted from the Bayesian models are somewhat shallower than the PMFs calculated using US/WHAM simulations, but they nevertheless show a qualitatively similar behavior. For QH₂, both models indicate that the quinol moves away from Tyr-87_Nqo4 to a distance of about 10 Å, to a site that coincides with the location of a Q analog in the complex I structure of Y. lipolytica (12), and from 10 to 25 Å both PMFs are quite flat. The steep drop in the US/WHAM PMF at about 30 Å coincides with the sampling gap in the unrestrained QH₂ simulations. Also for Q_ox, the PMFs exhibit similar features and local minima, with one notable exception: the US/WHAM PMF for Q shows a sharp (ca. 7 kcal⋅mol⁻¹) drop at 30 Å, where the diffusion model is quite flat and the unrestrained simulations (SI Appendix, Fig. S5) do not indicate any distinct features. As discussed above, we attribute these differences, on one hand, to local structural changes in the protein around the Q tunnel, and, on the other hand, to differences in the Q-tail length, which in the case of Q₁₀ is almost entirely in the membrane at a Tyr-87_Nqo4–Q distance of ca. 30 Å. In addition to differences in the simulation protocol, we expect significant statistical uncertainties in both profiles, in reflection of the large system and complex Q motion. Our statistical analyses and estimated error bars (SI Appendix, Fig. S5) suggest that the overlap in the sampled reaction coordinate during the MD simulations is good, which forms the basis for employing the diffusion model, but the relative barriers are somewhat sensitive to the employed parameters in the diffusion model (SI Appendix, Fig. S5 E and F). Importantly, however, the diffusion model calculations predict, consistent with the results obtained from the US/WHAM simulations, that a second Q-binding site is located 25–35 Å from Tyr-87_Nqo4.

In Fig. 4B, we show the position-dependent diffusion coefficients for Q_ox and QH₂. We obtained values in the range of D = 1–4 × 10⁻⁸ cm²⋅s⁻¹ for the back-and-forth diffusion of Q in the Q tunnel of complex I. Despite large statistical uncertainties, these values are about one order of magnitude slower than the diffusion coefficients of a lipid in a typical fluid membrane environment and of ubiquinone in vesicles (41). As a rough estimate of the Q exit time in the absence of significant barriers, we obtain τ_exit ∼ (30 Å)²/D ∼ 0.01 ms. An Arrhenius correction for a barrier of 3 kcal⋅mol⁻¹ would slow down this time to about 1 ms, which is in the range of the experimental turnover rate of complex I (4).

Three main findings emerge from the MD simulations: (i) that the reduced and protonated QH₂ moves away from Tyr-87_Nqo4 to a site occupied by a Q analog in a structure of Y. lipolytica complex I (12); (ii) that a distinct second binding site emerges close to the opening of the Q tunnel to the membrane, where the Q headgroup forms tight interactions with a cluster of aromatic and charged amino acids; and (iii) that the motion of Q₁₀ along the tunnel is relatively facile, with a diffusion coefficient lower by about a factor 10 compared with free dynamics in a membrane and relatively modest free energy barriers.

Q Dynamics-Triggered Redox and Protonation Shifts.

We counted 183 ion pairs in subunits Nqo4 and Nqo6-Nqo10 of complex I, which may be of functional relevance for the proton-pumping process. To probe the coupling of the Q dynamics and the conformation of these ion pairs, we select seven pairs (SI Appendix, Table S2), which are in the vicinity of the Q-binding cavity or close to the antiporter-like subunits Nqo8/Nqo7 of the membrane domain of complex I (SI Appendix, Fig. S11). Interestingly, we find that the conformational state of these ion pairs depends on the Q-binding position (SI Appendix, Figs. S11 and S12): For example, the Asp-139_Nqo4/His-38_Nqo4 ion pair is closed in all simulations with Q_ox, and more open in the QH₂ state (SI Appendix, Fig. S11), consistent with earlier findings (26). We observe the largest difference in the opening dynamics between Q_ox and QH₂, when Q_ox is bound at the first binding site (1/1′) and QH₂ is bound in the second binding site (2/2′). Many of the studied ion pairs remain close in simulations with Q_ox (SI Appendix, Fig. S11), whereas in the simulations with QH₂ these ion pairs open up, with the exception of the Asp-62_Nqo8/Arg-36_Nqo8 ion pair (SI Appendix, Fig. S11). Our analysis also indicates that these ion pairs dissociate when the Q moves from site 2 to 2′ in the SMD pulling simulation (SI Appendix, Fig. S13). The Asp-62_Nqo8/Arg-36_Nqo8 ion pair is of special interest, as it is has been found to affect the assembly and function of complex I (42).

To further probe how these dynamical changes affect the redox potential of Q in the putative second binding site near Trp-241_Nqo8, and protonation events that may couple to occupation of this site, we performed PB continuum electrostatics calculations of Q along snapshots of structures obtained from the MD simulations. We find that the movement of Q, from the site 1 to site 2, is linked to an increase in the redox potential by ca. 200 mV (Q_ox/SQ^•/− couple; SI Appendix, Fig. S14), which arises from differences in local protein surroundings, especially by interaction or proximity to positively charged residues (Arg-62_Nqo6, Arg-36_Nqo8, and Lys-69_Nqo8), and dissociation from the N2 center (30). Moreover, approximate electrostatic binding free energies further suggest that the motion of the Q_ox/QH₂ toward the second binding site is coupled with an energy release of ca. 5 kcal⋅mol⁻¹ (SI Appendix, Fig. S15), which could account in part for the increase in redox potential and the overall shape of the PMF profiles. Our PB calculations also suggest that Q binding at site 2 may trigger protonation changes of nearby residues His-233_Nqo8 and Asp-72_Nqo7 (SI Appendix, Fig. S16), an event that could be involved in the proton-pumping process (discussed below).

While some negatively (positively) charged residues remained deprotonated (protonated) through the simulation trajectories, the PB calculations suggest that certain specific residues might undergo protonation changes that are linked with the Q position. To this end, Asp-72_Nqo7 and Glu-74_Nqo7 prefer to be deprotonated when Q_ox is in the binding site 1 and protonated when Q_ox is approaching these residues. In contrast, Glu-130_Nqo8 is initially protonated when Q_ox is in binding site 1, but it deprotonates when the Q_ox approaches binding site 2/2′. We find that His-38_Nqo4 is predicted to be protonated with Q_ox and neutral (δ- or ε- tautomer on His) with QH₂, but interestingly the PB calculations suggest that Tyr-87_Nqo4 would prefer to reprotonate also in the simulation trajectory with QH₂/His/TyrO⁻. The reason for the latter finding might be that QH₂ moves rapidly to the second binding site, which is expected to increase the proton affinity of Tyr-87_Nqo4. The reprotonation of Tyr-87_Nqo4 might, however, be kinetically limited by formation of a water contact to the N-side of the membrane or by conformational changes of nearby residues (39). To this end, His-34_Nqo4 is located at the interface between the active site and the N-side, and the residue could thus act as an intermediate proton donor during reprotonation of the active site. The PB calculations suggest that His-34_Nqo4 remains deprotonated when Q is in site 1, but it protonates when the Q_ox moves away or is reduced and protonated into QH₂. Moreover, consistent with our earlier work (26), Glu-35_Nqo8, Glu-248_Nqo8, Glu-223_Nqo8, and Glu-235_Nqo8 are deprotonated when Q_ox residues in binding site 1, but they show a strong upshift in their pK_a values when the Q_ox moves approaches bindings site 2/2′ (SI Appendix, Fig. S16). Some of these acidic residues were recently modeled in their protonated states by studying multiple redox/protonation states of a Q molecule in the middle of the Q tunnel (39), in line with the Q-shuttle proposal (4), and were found to be conformationally flexible depending upon their protonation states. The observed pK_a shifts correlate with the ion-pair dynamics (SI Appendix, Fig. S12). For example, the increase in the pK_a of Glu-225_Nqo8 correlates well with the distance to Lys-40_Nqo7 and Arg-73_Nqo8 (SI Appendix, Fig. S12), and similar correlations are observed for Glu-35_Nqo8 and Glu-235_Nqo8 and their nearby ion pairs. Importantly, the predicted Q-binding sites and surrounding ion pairs can form valuable input for future site-directed mutagenesis and labeling experiments (SI Appendix, Table S4).

Mechanistic Implications.

Experimental data (43) suggest that the complex I from Escherichia coli comprises one tightly bound Q with a ratio of 1.3 (± 0.1) per FMN molecule. However, it remains entirely unknown where the Q molecule is bound in the complex I structure. Based on the data from our PMF calculations, we suggest that Q can bind at or near the site of reduction, and at a site close to the entrance of the Q tunnel, formed by two highly tilted and one horizontal helix of the Nqo8 subunit (SI Appendix, Fig. S3). This second site, located at a distance of around 30 Å away from Tyr-87_Nqo4, is lined with aromatic and charged groups that offer favorable interactions for the Q_ox and QH₂ headgroups. The equilibrium redox titration shows that the tightly bound Q gets reduced to quinol at potentials <−300 mV (43), which according to our calculations would correspond to the Q bound at a site ca. 4 Å from Tyr-87_Nqo4. At the second binding site near the tunnel opening, the calculated redox potential is substantially higher, shifted up by the interactions with nearby positively charged residues. Interestingly, such a shift in redox potential coupled to Q motion has been proposed (4) as an explanation of redox titration experiments (43).

Upon electron transfer from N2 to the Q bound at site 1, leading to the formation of semiquinone (SQ), our calculations indicate that the significant work linked to dissociating SQ could kinetically trap the latter (SI Appendix, Fig. S17). A similar kinetic trapping of an SQ has also been suggested in cytochrome bc₁ (44). Arrival of the second electron from the iron–sulfur chain leads to formation of the two-electron reduced QH₂ species by coupled proton transfer from His-38_Nqo4 and Tyr-87_Nqo4, followed by structural rearrangement (26). This process reduces the binding free energy of the quinol by 2–3 kcal⋅mol⁻¹, suggesting that the species is released to Q-binding site 1′. Our calculations suggest that the diffusion of quinol toward the latter site is exergonic, a process that may thus comprise a primary energy transduction step in complex I that the enzyme employs for driving the proton-pumping machinery (17). Diffusion of the QH₂ from site 1′ away from N2 also appears to be barrierless until it reaches site 2, found based on our free energy calculations. Our electrostatic calculations suggest that the Q bound at the second site at the entrance of the Q tunnel may alter the protonation probability of nearby titratable residues (SI Appendix, Figs. S16 and S18). To this end, previous MD simulations (16, 45) suggest that the protonation states of buried residues in the membrane domain of complex I may control the formation proton-conducting water wires between the bulk.

In the standard single-Q model, Q molecules exchange with the membrane pool. Since the N2 cluster is the primary electron donor to Q, a newly arriving Q species bound initially at Q-binding site 2/2′ will need to diffuse toward the active site 1 close to N2, become reduced and travel back to site 2/2′, and finally diffuse into the membrane. We roughly estimated a minimum round-trip time in the range of tens of microseconds, in the absence of free energy barriers, which would move into the millisecond regime for barriers as low as 3 kcal⋅mol⁻¹. Indeed, the barriers in our simulations appear to be higher than this, but we caution against overinterpretation of these values, which may reflect in part the difficulties in equilibrating and sampling the motions of such a large and complex protein.

Nevertheless, it is worth noting that even under the most ideal circumstances of a large Q pool in the membrane and completely unrestricted motion of Q in the ca. 35-Å tunnel with a diffusion coefficient D, that is 1/10 of free diffusion, and a barrier of only 3 kcal⋅mol⁻¹, the round-trip time is already around 1 ms. Any further increase in the barrier height would thus limit the overall turnover. As a possible alternative, binding of a second Q has been occasionally discussed in the literature (4) (see also refs. 17 and 46). Interpreting our simulation results also in such a framework, one Q molecule would continuously shuttle between two binding sites 1 and 2, and function as a redox transducer. From site 2 (or 2′) the electrons would have to be transferred to a secondary Q in the membrane or in site 2′. To contribute to the Q pool, the quinol at the second Q-binding site, ca. 30 Å away from Tyr-87_Nqo4, has to further reduce a membrane-bound Q if the former is restricted to the piston motion between the two sites, as possibly supported by the obtained high free energy barrier for QH₂ to exit the membrane. The oxidation of quinol at this site by a membrane-bound Q requires the latter to be within ca. 14 Å of the former to allow for an efficient electron transfer according to biological electron transfer theories (38). A putative membrane bound site, Q_M (M for membrane) on the surface of the Nqo8 subunit would have to fulfill this criterion. This site would need to have a protonic connectivity with the aqueous N-phase or to the QH₂ species at second Q-binding site, which is required to stabilize the negatively charged species (Q^•/− or QH⁻) that forms upon reduction, and the coupled oxidation of quinol. The putative double-Q-piston model is consistent with some previous experimental and computational suggestions, for example the redox-state-dependent conformational fluctuation of E-quartet glutamates in subunit Nqo8 (26), conformational changes of residues in the two crystal structures, in particular Glu-213_Nqo8 (11, 12), and data from labeling studies (35), that allow us to construct a basic architecture of this putative third Q-binding site.

The possibility of multiple Q-binding sites in complex I is indirectly also supported by the recent reinterpretation of EPR data of SQ species in complex I from E. coli (47). In addition to already well-known fast- and slow-relaxing SQ signals (SQ_Nf and SQ_Ns, respectively) (19, 28) that fit well with the two proposed sites, with distances of ∼10 Å and 35 Å from the N2 center, respectively, a third very-slow-relaxing SQ signal (SQ_Nvs) has been proposed (47). It was suggested that the latter signal originates from a Q bound at a membrane–protein interface (47). In the context of our model, the latter location would correspond to the Q_M site, whereas SQ_Nf and SQ_Ns would be analogous to the sites ca. 4–10 Å and ca. 25–35 Å from Tyr-87_Nqo4, respectively.

After reoxidation of QH₂ bound at the second site, its protons are either released to the N- or P-sides of the membrane, transferred to the Q_M molecule, or a combination of these scenarios. Moreover, reprotonation of the residues that served as initial proton donors in the Q reduction step (Tyr-87_Nqo4 and His-38_Nqo4) is required for complex I to restore its ground state for the next reaction cycle.

Conclusions

Our molecular simulations on complex I in states that occur immediately before and after the Q reduction suggest that a single Q molecule shuttles between the hydrophilic and membrane domains of complex I within a tight tunnel. This remarkable diffusion process spans a distance of ca. 30 Å and is likely to be important for establishing a strong coupling between the spatially distant proton and electron transfer activities in complex I. Based on our molecular simulations, we have described here the molecular structure of a putative second Q-binding site, hoping to stimulate new site-directed mutagenesis and labeling experiments (SI Appendix, Table S4). The studied Q piston motion is suggested to comprise an elementary energy transduction step in complex I that is responsible for activating the long-range controlled proton-pumping machinery.

Methods

MD Simulations.

The crystal structure of complex I from Thermus thermophilus was taken from the Protein Data Bank (PDB ID code 4HEA) (11). Following the protocol described in our earlier work (26), we constructed an atomistic model system of complex I immersed in a lipid–solvent environment. The model system consisted of 809,314–823,699 atoms, including the entire complex I, POPC lipids, TIP3P water molecules, and Na⁺ and Cl⁻ ions, mimicking a 150 mM salt concentration. We performed simulations in various redox/protonation states of Q using Q₁, Q₆, and Q₁₀ (see text and SI Appendix, Table S1). Force-field parameters for the ubiquinone substrates and iron–sulfur centers were derived from density functional theory calculations from our previous work (26, 30, 33). Our previous calculations (30) suggest that the derived parameters reproduce experimental redox potentials. The simulations were performed with NAMD2 (48), using the CHARMM27 and CHARMM36 force fields for protein, lipids, water, and ions (49, 50) at constant temperature (T) and pressure (P), with T = 310 K and P = 1 atm. The time step was 1–2 fs, long-range electrostatics was treated with particle mesh Ewald method, and all hydrogen bonds are restrained by the ShakeH algorithm as implemented in NAMD. The equilibrium properties of our simulation models were monitored with different indicators (e.g., the lipid equilibration is shown in SI Appendix, Fig. S20). Simulation trajectories were analyzed using Visual Molecular Dynamics (51). All simulation setups are summarized in SI Appendix, Table S1.

SMD Simulations.

We performed two independent SMD simulations (52, 53) of bound Q and quinol in the first binding site in hydrogen-bonding distance to Tyr-87_Nqo4, with a constant pulling velocity of 0.5 Å⋅ns⁻¹ and a force constant of 100 kcal⋅mol⁻¹⋅Å⁻², applied to the center of mass of Q in the direction of the exit of the binding pocket. To keep the protein and the lipid membrane stable in the box, we fixed the Cα atoms in the transmembrane helices of Nqo10 with a force constant of 2 kcal⋅mol⁻¹⋅Å⁻². No temperature or pressure controls were used in the SMD simulations, which were performed using NAMD2 (48). We also performed a second set of SMD simulations with higher pulling velocities, by pulling the last carbon atom (C34) of the Q₆ tail at a constant velocity of 5 Å⋅ns⁻¹ in various redox/protonation states of Q (Q_ox, QH₂, and SQ). After multiple tests, the value of the force constant (k) was chosen to be 8 kcal⋅mol⁻¹⋅Å⁻². The snapshots along the pulling trajectories were used to perform equilibrium US simulations (discussed below). Due to the slow convergence (54), we did not calculate the PMF from the SMD simulations. However, our preliminary calculations show that it is energetically costly to pull a negatively charged SQ out of the Q tunnel in comparison with neutral Q_ox and QH₂ species (SI Appendix, Fig. S17).

PMF from Diffusion Model.

Based on snapshots extracted every 2 ns from the SMD trajectory of Q and QH₂, we initiated multiple unrestrained equilibrium MD simulations starting from different positions of the Q_ox and QH₂. For Q_ox, we performed initially 38 such MD simulations, each 11 ns long, and to improve the sampling in rarely visited regions of the reaction coordinate we initiated 23 additional 11-ns MD simulations. We completed the dataset of Q by adding 4 × 11-ns MD simulations in which the Q headgroup was initially in hydrogen-bonded contact with His-38_Nqo4 and Tyr-87_Nqo4, using a starting structure obtained from previous work (26). For the quinol simulations, we initially performed 38 × 11-ns MD simulations and to improve the sampling in rarely visited regions, we initiated 14 additional 11-ns MD simulations. We completed the dataset of QH₂ by adding 5 × 11-ns MD simulation in which the Q headgroup was initially in hydrogen-bonded contact with His-38_Nqo4 and Tyr-87_Nqo4, starting from the same structure as the QH₂ SMD, but with QH₂ replaced by Q. From the complete 65 × 11-ns and 57 × 11-ns equilibrium MD simulations of Q_ox and QH₂, respectively, the last 10 ns were used for the analysis. In addition to the Tyr-Q distance reaction coordinate, we also projected the shortest distance between Tyr-87_Nqo4 and a carbonyl oxygen of the Q/ol headgroup on the SMD pulling vector (SI Appendix, Fig. S4). Results for these PMF calculations are shown in Fig. 4 and SI Appendix, Fig. S5.

One-Dimensional Diffusion Model.

The rate constant for the overall Q release by diffusion along the Q tunnel is exponentially sensitive to the free energy barrier heights and linearly proportional to the diffusion coefficient. The position-dependent diffusion coefficient $D\left(q\right)$ along the reaction coordinate $q$ describes the local dynamics on the free energy surface $F\left(q\right)$. Several 1D coordinates $q$ were considered to monitor the motion of Q through the Q-binding cavity, each discretized into bins $q_i$ (0 ≤ i ≤ N) of width $\mathrm{\Delta }q=\left|q_{i+1}-q_i\right|$ = 2 Å. Error bars in the PMF indicate standard errors of the mean, which were estimated by block averaging, dividing the trajectories into three blocks of equal length.

From the observed bin transitions in the MD trajectories, we estimated $D\left(q\right)$ and $F\left(q\right)$ self-consistently by using a 1D diffusion model as described in ref. 40. The MD simulation reports on the local “propagators” along the reaction coordinate $q$. One can compare the observed bin transitions in the MD trajectories with those expected from the diffusive dynamics. A likelihood function is constructed that gives the probability of observing exactly the motion along $q$ seen in the simulations.

The likelihood $L$ between transitions given the rate model is

$$\text{log}\hspace{0.17em}L={\displaystyle \sum }_{i,j}{N}_{ji}\text{log}\left(p\left(j,\mathrm{\Delta }t\vee i,0\right)\right),$$ [1]

where N_ji is the number of observed transitions from state $i$ to $j$ with the lag time Δt. N_ji was computed from MD trajectories with coordinates saved every 10 ps. The lag times of 1.5, 2, and 2.5 ns were used. $p\left(j,\mathrm{\Delta }t\vee i,0\right)$ is the conditional probability that the system is in the state j at the time t + Δt given that it is in the state $i$ at time $t$. The log (L) is maximized with a Monte Carlo search by varying $F_i$ and D_i ± 1/2. All kinetic constants k of the local propagator in the diffusion model enter into the rate matrix K.

The rate constant from state $i$ to state $i\pm 1$ is

$$k_{i\to i\pm 1}=\frac{D_{i\pm \frac{1}{2}}}{\mathrm{\Delta }{q}^2}exp\left[\frac{-F_{i\pm 1}-F_i}{2k_{B}T}\right].$$ [2]

$F_i$ is the free energy at the center of bin $q_i$, and $D_{i\pm \frac{1}{2}}=D\left(q_i+q_{i\pm 1}/2\right)$ is the diffusion coefficient between bin i and i ± 1. Because the local propagator is moving on a 1D reaction coordinate, direct transitions occur only between neighboring bins. The rate matrix K thus adopts the following form:

$$K_{ij}=\{\begin{array}{cc}{k}_{i\leftarrow j}& \text{if\hspace{0.17em}}\left|i-j\right|=1\\ -k_{j\to j+1}-k_{j\to j-1}& \text{if}\hspace{0.17em}i=j\\ 0& \text{otherwise}\end{array}.$$ [3]

US Simulations.

US simulations (36) were performed using the colvar module in NAMD2 (48). Smaller model systems of complex I consisting of ca. 180,000 atoms were constructed from the SMD simulation trajectories. Each model system consisted of Nqo4–Nqo10 and Nqo15 complex I subunits, immersed in lipid–solvent surroundings. US simulations were performed by constraining the distance between Tyr-87_Nqo4 and the headgroup of Q by a half-harmonic potential of 5 kcal⋅mol⁻¹⋅Å⁻². The distance sampled was in the range of [4 Å, 50 Å] with a 0.5-Å spacing, simulating in total 61 umbrella windows. At d = 4 Å, the Q headgroup is hydrogen bonding with Tyr-87_Nqo4, whereas at a distance of 50 Å it is almost out in the lipidic milieu, such that the entire Q-tunnel region was explored.

The US simulations were performed for two states of Q (Q_ox and QH₂), using a short-tailed Q₁. A sufficient overlap between the neighboring histograms was observed for each Q-state simulation (SI Appendix, Fig. S19), and convergence was analyzed by calculating the time evolution of PMF profiles. The PMF was calculated using WHAM (37), as implemented in ref. 55, with a convergence threshold of 0.00001 kcal⋅mol⁻¹, and after discarding the first 5 ns of data. The bootstrap error analysis, as implemented in ref. 55, showed a statistical uncertainty of ±0.1 kcal⋅mol⁻¹ (see also Fig. 3).

Our analysis revealed that closely spaced US windows (with shorter simulations timescales) allow better coverage of the reaction coordinate and faster convergence of PMF profiles. However, despite these and using a smaller ligand (Q₁), the very high complexity of the protein–substrate system results in minor oscillations in PMF profiles, thereby representing limited sampling.

PB Continuum Electrostatics.

Redox potentials and pK_a values were computed based on electrostatic potentials obtained by solving the linearized PB equation using APBS (56) and Monte Carlo titration sampling (57, 58). The protein was described using atomic partial charges, embedded in an inhomogeneous dielectric continuum with dielectric constants of ε_p = 4 for the protein and ε_w = 80 for the water, a probe radius of 1.4 Å, and ionic strength of 100 mM potassium chloride. The redox potential was computed as a difference of electrostatic free energy shifts between a model compound in water and the model compound in the protein. Charges for Q and iron–sulfur clusters as well as redox potentials of model compounds in water were obtained from ref. 30. Due to limited experimental data available for complex I, benchmarking the accuracy of the PB calculations is outside the scope of the present work. However, previous studies (59) suggest that PB calculations can reproduce experimental data in proteins with a mean error of ca. 1 pK unit (59) or 60 mV (60, 61). Redox potentials of iron–sulfur cluster are computationally challenging (62), but we found (30) that some experimental redox potentials for complex I are indeed reproduced within a 100- to 200-mV error bar. However, we expect the complexity of the simulation system is likely to introduce larger overall errors but nevertheless to qualitatively capture electrostatic effects linked to Q dynamics. Results from the PB calculations are shown in SI Appendix, Figs. S14–S16.