On the importance of accounting for nuclear quantum effects in ab initio calibrated force fields in biological simulations

Significance

In molecular modeling the motion of nuclei, especially hydrogen, cannot be described using the laws of classical mechanics. The importance of nuclear quantum effects has long been appreciated by the ab initio molecular dynamics and by the water simulation communities. However, the vast majority of simulations of biological systems performed at ambient conditions treat atomic motion classically. Even in the new-generation force fields parameterized from quantum mechanics these effects are thought to be minor compared with other inaccuracies at room temperature and pressure. We show that a force field in excellent agreement with quantum mechanical energies and forces will not produce acceptably inaccurate predictions at ambient conditions unless the nuclear motion and interaction are accounted for in the simulation.

Abstract

In many important processes in chemistry, physics, and biology the nuclear degrees of freedom cannot be described using the laws of classical mechanics. At the same time, the vast majority of molecular simulations that employ wide-coverage force fields treat atomic motion classically. In light of the increasing desire for and accelerated development of quantum mechanics (QM)-parameterized interaction models, we reexamine whether the classical treatment is sufficient for a simple but crucial chemical species: alkanes. We show that when using an interaction model or force field in excellent agreement with the “gold standard” QM data, even very basic simulated properties of liquid alkanes, such as densities and heats of vaporization, deviate significantly from experimental values. Inclusion of nuclear quantum effects via techniques that treat nuclear degrees of freedom using the laws of classical mechanics brings the simulated properties much closer to reality.

Historically, simulation of biomedically important systems has been done with the empirical force fields (FFs) pioneered 50 years ago (1, 2). As computer power has increased and quantum mechanical energy calculations have become more accurate than experiment, FFs derived from this quantum mechanical data have become feasible. In future quantum mechanics (QM) parameterized FFs are likely to be much more important than empirical FFs as they can be applied to new systems without needing experimental data for calibration. Being able to accurately reproduce experimental data with QM-based FFs is essential. The aim of this paper is to assess the need to include nuclear quantum effects (NQEs) in simulations. Here we show that they must be included if a QM parameterized FF is to correctly reproduce bulk properties.

Molecular mechanics (3, 4) bridges the precise calculation of interactions of a few atoms at rest by ab initio methods (QM) (4, 5) with the larger numbers of atoms and dynamic simulations over long time scales essential to predict measured bulk properties of matter. The starting component of molecular mechanics is an effective Newtonian interaction model, or FF (4, 6). In this work we employ a FF parameterized by agreement with QM-derived energies, forces, and monomer properties (we expand on this choice in Discussion). Once the interaction energies and forces have been adequately described, the quantities of interest are obtained by sampling the potential surface of a large molecular ensemble via various means, usually Monte Carlo or Newtonian molecular dynamics (MD) (3, 4, 7). The sampling machinery encompasses many critical parts such as proper maintenance of ensemble temperature and pressure, careful integration and truncation practices, enhanced sampling techniques that overcome energy barriers, limitations of machine precision, and many others (3, 7–13).

In Monte Carlo and MD sampling, the Born–Oppenheimer approximation (14) decouples the electron degrees of freedom from nuclear motion: the former are treated as instantaneous and the latter, conventionally, as classical Newtonian point masses. Atoms and nuclei, however, do not behave classically (3, 15–18) and quantum uncertainty in atomic position may significantly impact the structure and properties of the ensemble. The importance of these NQEs is widely known and accepted by researchers working on, for example, path integral MD (PIMD) and ab initio MD (15), as well as by the community working on water models. The focus on water is natural since water, due to its importance, ubiquity, and anomalies is the traditional starting point for FF development. However, water simulations can actually obscure the importance of NQEs because the various effects oppose and thus partially cancel each other (19). At this time the widely used FFs and simulation packages rarely, if ever, consider NQEs. There are two reasons for this. First, these FFs are empirical and thus fitted to reproduce experimental results; they therefore contain the NQE corrections implicitly. Second, as the vast majority of investigations of NQE have concentrated primarily on water (15, 20) or systems with extreme physical conditions that enhance NQE (21, 22), the errors caused by leaving them out are thought to be minor compared with the accuracy of the FFs themselves, and hence with the expected accuracy of predictions made for biological systems at room temperature and pressure.

Valuable exceptions are the works of Martyna and coworkers, who investigated NQEs for weakly interacting species: the noble gases helium and xenon (17) and alkanes (16, 23). These researchers discovered that the NQE, as modeled by PIMD (17, 23), significantly alters the molar volume of weakly interacting liquid alkanes (16, 23). Since alkanes are literally the backbone of all organic molecules (16), this work emphatically suggests that the inclusion of NQE should not be limited to strongly interacting systems. Some of the effects may, in fact, be more prominent in weaker interactions such as those occurring in nonpolar environments. However, as Martyna and coworkers used a relatively simple empirical FF which did not closely agree with QM energies, the question of whether simulations with a quantum mechanically parameterized FF must include NQE remained open.

The ArrowFF is InterX’s medium-precision polarizable FF. Agreement with QM properties and energies is only one of many several guiding principles in ArrowFF design. Some of the other considerations are, for example, transferability, economy of parameters, and computational tractability. Consequently, for some functional groups and atoms, we allow the ArrowFF to deviate from QM benchmarking in a carefully restrained way.

However, as the aim of this study is to highlight the contribution NQEs make to a QM-faithful FF, we will narrow our focus to a chemical subset ArrowFF describes very well: the alkanes. Alkanes are generally easier to describe than many other chemical species because they are fairly isotropic, nonpolar, and have low three-body interaction energy. In fact, even coarse-grained united-atom representations (24, 25) describe alkanes fairly well. This does not narrow our conclusions because alkanes are ubiquitous and important in biological molecules and the drugs that target them. We first confirm that the ArrowFF does indeed represent alkanes faithfully, making them a perfect system on which to demonstrate the contribution of NQE for prediction of ensemble properties. We then show that although the ArrowFF of alkanes is in excellent agreement with high-level QM, NQE must be included for accurate calculation of very basic bulk properties such as densities and heats of vaporization.

Methods

We use the ArrowFF with the following features: nonbonded terms are dipole-polarizable multipolar exchange-repulsion and electrostatics that suitably describe charge penetration and delocalization, as well as Tang–Toennies-damped (26) spherical C6 and C8 dispersion terms. The functional form of the bonded interactions is taken from MMFF94 (27), with force constants and equilibrium values fitted to QM energies at the MP2/aug-cc-pVTZ level of theory. Multibody effects are modeled by polarization; there are no explicit three-body terms [e.g., Axilrod–Teller (28)] for alkanes. More details can be found in refs. 29–31. The ArrowFF alkanes’ parameters are not specifically designed for alkanes but are a part of the FF broadly covering protein and ligand functional groups. Nevertheless, as we show below, the ArrowFF describes the alkanes particularly well.

We model NQEs via PIMD (13, 16), which is based on the Feynman path integral formulation of QM (32). In PIMD, a quantum system is mapped onto an extended classical system consisting of multiple replicas of the original classical system with harmonic springs linking adjacent replicas of each atom of the system (17). As the number of replicas increases, the ensemble averages of the observables of the extended classical system converge to those of the quantum system (3, 17, 33). Simulation is performed on an isothermal–isobaric ensemble (NPT) modeled using a Nosé–Hoover chain thermostat (12) and a Martyna–Tuckerman–Tobias–Klein barostat (34). Electrostatic interactions are truncated with multipolar PME (35) at the cutoff of 9 A. A multiple time step technique (36) with primitive integration is used to speed up PIMD calculations. Bonded and interreplica harmonic interactions, which are easier to compute, are sampled with the time step of 0.25 fs, while the more expensive nonbonded interactions are sampled with the time step of 2 fs. Multiple time steps and PIMD are implemented in our Arbalest MD simulation software. In Arbalest the nonbonded interactions are computed efficiently on NVIDIA graphical processing units.

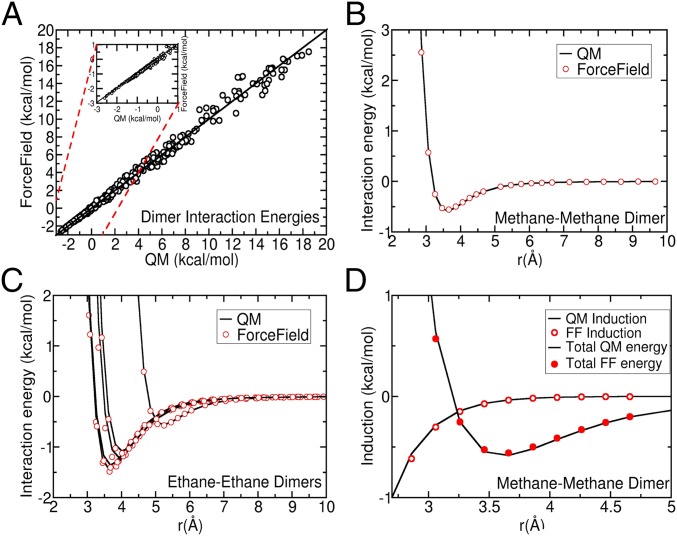
To ensure that the simulation discrepancies do not arise from the imprecision of the FF or the underlying QM calculations, we require both a high level of theory and a good agreement between FF and QM energies. We calculate QM dimer energies at the highest QM level reasonable for large-scale calculations: MP2/CBS [based on Helgaker two-point extrapolation (37) from aug-cc-pVTZ to aug-cc-pVQZ basis sets] + CCSD(T)/aug-cc-pVTZ - MP2/aug-cc-pVTZ basis sets. This level of theory is known as the “gold standard” (38) and is commonly used as a benchmark in the computational chemistry community. The ArrowFF is fitted to these gold-standard energy values. In Fig. 1A we plot energy values for the ArrowFF with corresponding QM energies for a diverse set of alkane dimers. In Fig. 1 B and C we show the agreement between ArrowFF and QM along the dissociation curves for the minima of methane–methane and ethane–ethane dimers.

Fig. 1.

A shows that dimer ArrowFF interaction energies agree well with the corresponding QM energies for a representative set of four alkanes combined in six alkane dimer species (2,526 poses total). The Inset magnifies the important attractive region. The agreement between ArrowFF and QM is good as shown by (B) the dissociation curves for the minimal methane dimer, (C) the dissociation curves of five local minima of the ethane–ethane dimer, and (D) the induction energy of the methane dimer along the dissociation curve.

As seen from Fig. 1 A–C the agreement between ArrowFF and QM dimer energies is excellent everywhere, including the high-energy regions of significant electron overlap.

A direct proof that many-body ArrowFF energies also agree with their QM counterparts is difficult because precise determination of QM energies of large clusters is computationally costly. For alkanes, however, we can infer this indirectly. Using a high level of theory [the level of theory for the trimer is HF(aug-cc-pV5Z) + df-MP2/(aug-cc-pVQZ ->aug-cc-pV5Z) + CCSD(T)/(aug-cc-pVTZ ->aug-cc-pVQZ)-MP2/(aug-cc-pVTZ ->aug-cc-pVQZ)] we calculate the nonadditive trimerization energy of the optimal methane trimer to be 0.014 kcal/mol. This small value for the optimal trimer (much less than, for example, the intermolecular dimerization zero-point vibration energy of 0.26 kcal/mol) means that many-body corrections arise almost exclusively from the nonadditivity of the induction term. The agreement of this term with QM is illustrated in Fig. 1D, where we display the correspondence of the QM and ArrowFF induction energies along a dissociation curve for the methane–methane dimer. We therefore believe that ArrowFF reproduces the molecular interactions in bulk liquid alkanes well enough for the current investigation.

Results

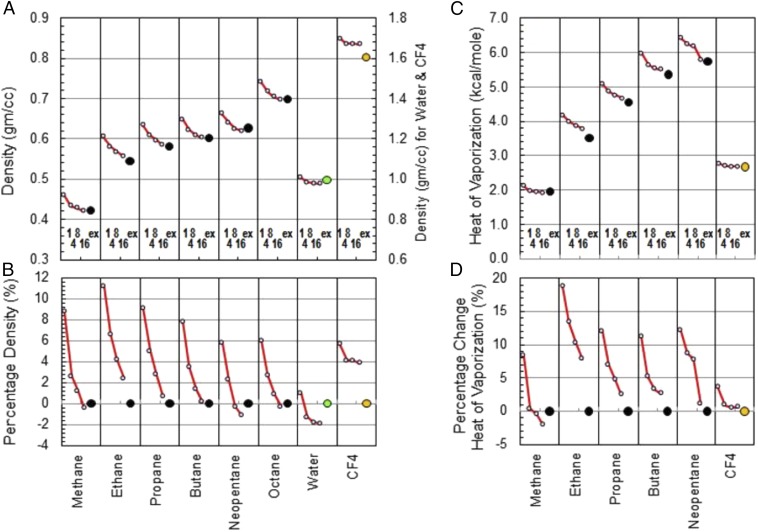
Having shown that our alkane model is accurate, we proceed to calculate the densities and heats of vaporization of several alkane systems. Fig. 2 A and B show the deviations between the calculated and experimental densities for alkanes and water using n = 1, 4, 8, or 16 PIMD beads. Although the results have not converged fully with 16 beads, we consider this range of bead numbers (n) sufficient for the conclusions of this paper. As a precaution, we computed methane properties with 32 and 64 beads with a further reduced time step. The results presented in SI Appendix confirm that truncating at 16 beads is reasonable.

Fig. 2.

A and B show the densities and their percentage errors for representative alkanes (methane, ethane, propane, butane, octane, and neopentane) as well as for water and CF₄. C and D show the heats of vaporization values and their percentage errors for methane, ethane, propane, butane, neopentane, and CF₄. The error decreases as the number of PIMD beads increases (1, 4, 8, and 16). The experimental value is shown as a large black dot for alkanes, a green dot for water, and an orange dot for CF₄. The simulation temperatures for the systems were 112, 184, 231, 272, 298, 298, 298, and 145 K for methane, ethane, propane, butane, neopentane, octane, water, and CF₄, respectively. The simulation box is a 32-Å cube; each system was run for 500 ps at a pressure of 1 bar. The error bars for density are within 0.01 g/cm³ and for heat of vaporization within 0.02 kcal/mol and smaller than the symbol size in the figures.

The computed classical (n = 1) densities deviate by as much as 11% from the experimental values. This is a disturbingly large discrepancy: the community traditionally expects predicted densities to be at most within 3–4% of experiment (24, 39, 40). Similar deviations are seen in heat of vaporization values (Fig. 2 C and D). It is unlikely that deficiencies in the ArrowFF are responsible for the errors because the models reproduce the QM energies well (Fig. 1). It is also unlikely that we have significant bond-length errors as we use the minimized QM ground-state geometries.

Once the NQEs are incorporated by having more than one bead per atom, the discrepancies gradually decrease to below 2%, which is very acceptable for a purely QM parameterization. Note that due to several opposing subeffects mentioned above the systematic NQE shift for water is much smaller than that for alkanes (Fig. 2 A and B).

The magnitudes of the density reductions we find here as the number of beads increases are consistent with the changes in effective volume observed by Martyna and coworkers (16) and Martyna et al. (23) with Amber95 (41): ∼3% for octane and ∼9% for butane. The volume changes reported by Martyna and coworkers (16) and Martyna et al. (23) also differ slightly between Amber95 and CHARMM22, thus making the imperfect agreement with the ArrowFF here reasonable.

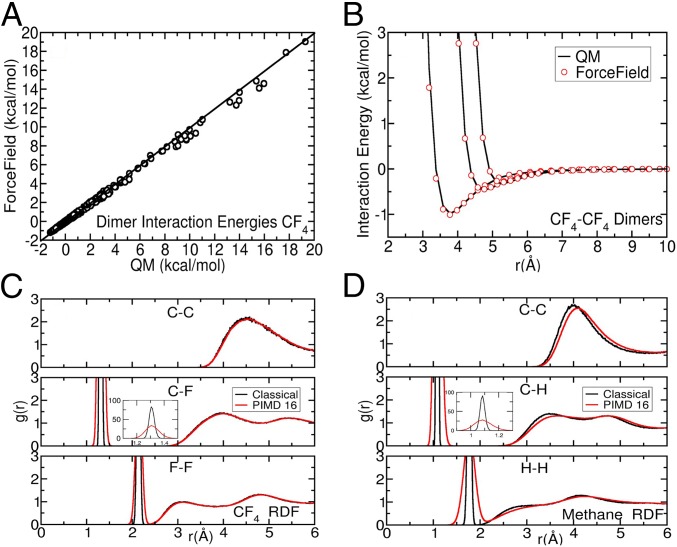
To confirm that the above results were caused by the hydrogen-related NQE we damped the effects by substituting hydrogen with a much heavier fluorine. The FF parameters for CF₄ were constructed via exactly the same procedure we use for parameterization of alkanes and, indeed, all other atom types. The model accuracy for CF₄ (Fig. 3 A and B) is good and similar in quality to the alkane models. The simulation results (Fig. 2) show that in the classical approximation of just one bead the density of CF₄ is much closer to experiment than the density of methane. Also, as expected, the calculated density of CF₄ does not decrease appreciably with the number of PIMD beads. Fig. 3 C and D show the radial distribution functions (RDFs) for CH₄ and CF₄ for classical (n = 1) and PIMD simulations (n = 16). Again, the structure of CH₄ is significantly altered by PIMD, whereas the structure of CF₄ remains almost the same. To ensure that our conclusions are not influenced by the differences in the center-of-mass fluctuations between CH₄ and CF₄ we also constructed a fictitious CH₄ molecule where the weight of the central carbon was increased to 84 a.u. The results, presented in SI Appendix, do not alter our conclusions. The much smaller deviations from experiment and the relative insensitivity to the number of beads in CF₄ compared with CH₄ affirms our assertion that NQEs are the primary cause of deviation from experiment of alkane density and heat of vaporization values.

Fig. 3.

A shows agreement between ArrowFF and QM energies for CF₄ dimers. B shows that ArrowFF and QM energies are very similar along the dissociation curves of the three minimum energy dimer geometries of CF₄ (similar to Fig. 1B). We also show the RDFs for (C) CF₄ and (D) CH₄. The RDF of CH₄ is significantly shifted when we include NQE with 16 beads, whereas that of CF₄ remains largely unchanged.

Discussion

We have shown that NQEs significantly change ensemble predictions made by molecular mechanics simulations of biological systems. We have further shown that when the FF is a good fit to QM energies these changes are needed to bring the results of calculations closer to experimental values. The important conclusion from these results is that QM-parameterized FFs, carefully parameterized to reproduce accurate QM data, give substantial errors unless NQEs are included.

Whether or not one should include the NQE in simulations, via PIMD, centroid MD (42, 43), or other available methods is contingent on several factors. Clearly, if one is interested in investigating the isotope effect, one has no choice but to include NQEs in the simulation. The recommendation to the practitioner seeking predictive values for ensemble properties (e.g., energies of solvation, etc.) depends on the choice of parameterization paradigm, the computational priorities, and the available expertise. Properly implementing PIMD is nontrivial (15–17, 23), but much guidance is available, and so the primary drawback of PIMD is computational cost. Recently, several promising bead truncation methods (44–48) reduce the amount of computational overhead needed to sufficiently capture the NQE corrections to approximately four times that of the classical simulation. This leaves the nature of the FF parameterization as the main factor in deciding whether to include NQE in the simulations.

All current wide-coverage FFs infer some of their parameters empirically by requiring that the computed ensemble properties agree with experimental values such as heats of evaporation, densities, solvation energies, dielectric constants, and so on (24, 39, 49–51). If one follows this parameterization paradigm, one can fold the NQE into the framework of fitting to experiment as is done for other unaccounted-for effects. After all, the corrections to computed properties due to NQEs are of the same order of magnitude as other frequently neglected effects such as polarization, penetration effect, functional form choices, three-body dispersion, multipole truncation, and so on (6, 52). For example, the approach taken by the AMOEBA FF (51, 53, 54) of getting some parameters (e.g., electrostatics) from QM calculations and others (van der Waals, vdW) from judicious fitting to experimental values makes good sense. Such implicit inclusion of NQEs (and other factors) into the vdW parameterization is reminiscent of how the first-generation classical FFs [e.g., GROMOS (24, 55), Merck (27, 40), GAFF (50), OPLS (25, 39, 40, 56), and CFF (8, 57)] implicitly included polarization by increasing partial charges in the liquid phase (58, 59).

Although the experimentally fitted FFs can and do achieve good agreement with the training set measurements, they encounter serious transferability issues. One of the reasons for this is the difficulty of properly choosing which parameters to adjust and by how much. The problem is illustrated by Hobza and coworkers (60), Sherrill et al. (61), and Demerdash et al. (62), who showed that although the agreement of the total energy for parameterized molecules is rather good, the individual components can contain significant deviations from their QM counterparts. These deviations then trigger a chain of transferability failures and total energy errors once the model is extended to new chemical species or even to pair interactions not considered in the training set.

The other choice of FF development is to design the FF to agree either in toto or componentwise with some or all of the following QM derived quantities: the intramolecular energies (“bonded terms”) (63), the intermolecular two-body and higher energies (“nonbonded terms”) (6, 63), nonadditive energies (e.g., polarization) (52), and the properties of single molecules (e.g., multipole moments, ESP-fitted charges) (6, 64) and small clusters. FF parameterization by QM calculations started in 1970s (65–68) and because of dramatic increases in computational resources has become fully feasible today. As QM computations are limited only by molecular size, the QM parameterized approach can be directly applied to molecules that have not had their properties measured, or, especially, have not yet been synthesized. Furthermore, recent computational advances, for example symmetry adapted perturbation theory (SAPT) (69, 70) or density functional theory (DFT)-SAPT (71–73) help the transferability of FFs based on QM data. DFT-SAPT decomposes the interactions into individual components which can then be accurately fitted by suitable FF functional forms and then subsequently extended by their corresponding appropriate transferability rules. Because of these advantages the current generation of advanced FFs (18, 29–31, 51, 53, 54, 74, 75) are increasingly adopting the QM–FF correspondence as a guiding principle. To aid in this development, we have shown here that if an FF is parameterized solely by fitting ab initio QM data (or is itself solely ab initio) (47), NQEs must be accounted for in the simulation.