Rapid diffusion-state switching underlies stable cytoplasmic gradients in the Caenorhabditis elegans zygote

Significance

Intracellular concentration gradients regulate essential processes including the organization of the mitotic spindle, cytokinesis, and cell polarity. Unlike tissue-scale gradients, little is known about how intracellular gradients form. We used single-particle tracking to characterize the behaviors of individual molecules that sculpt gradients in the cytoplasm of the Caenorhabditis elegans zygote. Our findings suggest that MEX-5 and PIE-1 rapidly switch between fast- and slow-diffusing states with kinetics that vary along the axis of the cell. As a consequence, slow-diffusing MEX-5 and PIE-1 particles are highly polarized, giving rise to their respective gradients. Using mathematical modeling, we show that rapid diffusion-state switching can quickly pattern gradients across a range of temporal and spatial scales.

Abstract

Protein concentration gradients organize cells and tissues and commonly form through diffusion away from a local source of protein. Interestingly, during the asymmetric division of the Caenorhabditis elegans zygote, the RNA-binding proteins MEX-5 and PIE-1 form opposing concentration gradients in the absence of a local source. In this study, we use near-total internal reflection fluorescence (TIRF) imaging and single-particle tracking to characterize the reaction/diffusion dynamics that maintain the MEX-5 and PIE-1 gradients. Our findings suggest that both proteins interconvert between fast-diffusing and slow-diffusing states on timescales that are much shorter (seconds) than the timescale of gradient formation (minutes). The kinetics of diffusion-state switching are strongly polarized along the anterior/posterior (A/P) axis by the PAR polarity system such that fast-diffusing MEX-5 and PIE-1 particles are approximately symmetrically distributed, whereas slow-diffusing particles are highly enriched in the anterior and posterior cytoplasm, respectively. Using mathematical modeling, we show that local differences in the kinetics of diffusion-state switching can rapidly generate stable concentration gradients over a broad range of spatial and temporal scales.

Concentration gradients encode spatial information that can be used to organize cells and tissues. At the tissue level, morphogen gradients form through protein diffusion away from a local source of protein synthesis along with protein disappearance into a distributed sink (for example, through protein uptake or degradation) (1, 2). While such mechanisms generate robust and persistent gradients over long length scales and timescales, they cannot generate gradients over subcellular length scales where diffusion rapidly dissipates asymmetries (3). Because subcellular gradients regulate essential processes including spindle assembly, the positioning and timing of cell division and cell polarity (4–6), elucidating the mechanisms that give rise to subcellular gradients is central to understanding the spatial organization of cells.

The polarization of the cytoplasm in the Caenorhabditis elegans zygote provides a dramatic example of how subcellular gradients can spatially organize cells. Shortly following fertilization, the zygote undergoes a ∼10-min polarization process during which conserved cell polarity regulators, the PAR proteins, concentrate in opposing cortical domains containing aPKC kinase in the anterior and PAR-1 kinase in the posterior (7, 8). Concurrently, the cytoplasmic RNA-binding proteins MEX-5 and MEX-6 (MEX-5/6 hereafter) segregate into the anterior cytoplasm (9, 10) while PIE-1 and POS-1 segregate into the posterior cytoplasm, forming opposing gradients that span the anterior/posterior (A/P) axis (11–14). These gradients persist until the cell divides ∼10 min later and contribute to defining the distinct identities of the anterior and posterior daughter cells (Fig. 1A) (15, 16).

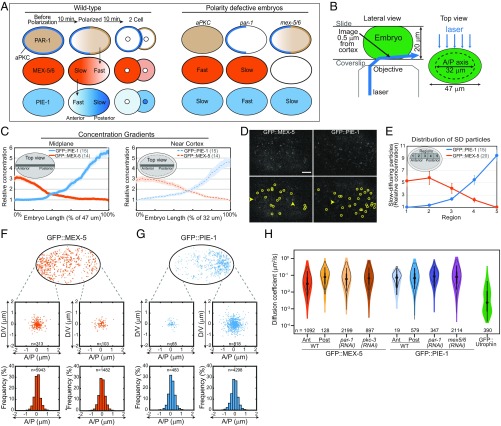
Fig. 1.

(A) Distribution of cortical and cytoplasmic proteins in WT and polarity defective embryos. In WT, all factors are symmetric before polarization, segregate along the A/P axis during polarization, and are inherited asymmetrically upon cell division. The ensemble mobilities of MEX-5 and PIE-1 are indicated (Fast or Slow). PAR-1 increases MEX-5/6 mobility in the posterior, and MEX-5/6 increase PIE-1 mobility in the anterior. PAR-1 also inhibits MEX-5/6 activity, such that PIE-1 mobility is fast in par-1 mutant embryos and slow in aPKC mutant embryos. (B) Schematic of near-TIRF imaging. An inclined laser was used to image in the cytoplasm, ∼0.5 μm from the cell cortex. The dotted line (Top view) indicates the region imaged. (C) The relative GFP::MEX-5 and GFP::PIE-1 gradients along the A/P axis at the cell midplane (47 μm long) and near the cortex (32 μm long). The gray bar indicates where the gradients were measured. The dashed black line (Right) indicates the portion of the embryo imaged near the cortex. (D) Representative single frames from near-TIRF movies of GFP::MEX-5 and GFP::PIE-1 (50-ms exposures). Particles detected by single-particle tracking are circled (Bottom). Arrows indicate examples of blurred FD particles. See Movies S4 and S5. (Scale bar: 5 μm.) (E) Relative number of SD particles in the indicated regions along the A/P axis (normalized to region 5 for GFP::MEX-5, region 1 for GFP::PIE-1). Error bars indicate SEM in this and all subsequent figures, and n is indicated in parentheses. (F and G) Tracks of GFP::MEX-5 and GFP::PIE-1 SD particles in WT. (Top) All tracks >250 ms from a 10-s movie are shown. (Middle) Displacement of SD particles along the A/P axis and perpendicular to the A/P axis (labeled dorsoventral, D/V). For each track, the starting point is at the plot origin and the dot indicates the final point. Tracks are from regions 1 and 5 of WT. (Bottom) Frequency of particle displacements along the A/P axis. Tracks >250 ms from 100-s movies are analyzed (20 embryos for GFP::MEX-5; 15 embryos for GFP::PIE-1). (H) Violin plot (log scale) of estimated D_c of GFP::MEX-5 SD particles, GFP::PIE-1 SD particles, and GFP::Utrophin speckles. Black circles, median; box, 25th and 75th percentiles; whiskers, 1.5× the interquartile range from the 25th and 75th percentiles. The empty gray violin shapes represent estimates from simulated tracks of pure Brownian motion. See SI Appendix, Fig. S1.

Fluorescence recovery after photobleaching (FRAP), photoconversion, and fluorescence correlation spectroscopy (FCS) studies showed that MEX-5 (17–20), POS-1, and PIE-1 mobility vary along the A/P axis (20, 21). Variation in mobility has been proposed to reflect the accumulation of MEX-5 and PIE-1 in slow-diffusing complexes in the anterior and posterior, respectively (18–21). MEX-5 mobility appears to be controlled by differences in the balance of kinase and phosphatase activities along the A/P axis: MEX-5 mobility is increased in the posterior by PAR-1 (17, 19) and decreased by the uniformly distributed phosphatase PP2A (19). PLK-1 and PLK-2 kinases (PLK1/2) act with their binding partners MEX-5/6 to increase POS-1 and PIE-1 mobility in the anterior, suggesting that differences in the balance of kinase and phosphatase may control their segregation to the posterior (refs. 20–23 and this study).

In principle, several mechanisms could generate stable gradients by controlling the redistribution of proteins from regions of high diffusivity into regions of low diffusivity. For example, gradients could form through gradations in the association of a protein with anchoring structures across the cell axis. These interactions could either stably immobilize the protein or transiently retard its mobility (24). Additionally, binding sites could either be broadly distributed within a cytoplasmic domain or be in a limited number of foci from which a protein disperses into the surrounding cytoplasm, as has been proposed for PIE-1 in the cytoplasm (20) and aPKC/PAR-6 at the cell cortex (25). An additional, nonexclusive possibility is that directed transport, even with a weak directional bias, could contribute to the progressive segregation of slow-diffusing complexes along the A/P axis (26). Previous studies have not distinguished between these models because they relied on measurements of the collective dynamics of ensembles of proteins that obscure the behaviors of individual molecules.

Single-particle tracking provides a uniquely powerful way to access how control over the behaviors of individual molecules sculpts gradients. In this study, we use single-particle tracking and mathematical modeling to characterize the microscale reaction–diffusion dynamics that give rise to the MEX-5 and PIE-1 gradients. Our findings suggest that individual particles of MEX-5 and PIE-1 interconvert between fast- and slow-diffusing states on timescales that are much shorter than the timescale of gradient formation and maintenance. We provide evidence that upstream polarity regulators locally control the kinetics of diffusion-state switching along the polarity axis, which in turn maintains the MEX-5 and PIE-1 gradients. Additionally, we use mathematical modeling to show that rapid diffusion-state switching can generate gradients across a broad range of temporal and spatial scales.

Results

To characterize the dynamics that underlie the maintenance of the GFP::MEX-5 and GFP::PIE-1 gradients, we used near-TIRF imaging to follow their behaviors at the single-particle level (Fig. 1B) (27). Both GFP::PIE-1 and GFP::MEX-5 were expressed from transgenes, and partial RNAi directed against GFP was used to reduce their expression levels to facilitate single-particle tracking (27). Imaging was performed in the cytoplasm at a depth of ∼0.5 μm from the cell cortex in polarized embryos in which the MEX-5 and PIE-1 gradients were already established (maintenance phase). Embryos were gently compressed between a coverslip and slide separated by 20-μm polystyrene bead spacers, which allowed us to image along ∼32 μm of the A/P axis (the A/P axis is ∼47 μm long at the cell midplane under these mounting conditions). Using spinning-disk confocal microscopy, we determined that the amplitude of the anterior-rich GFP::MEX-5 gradient is 3.2-fold at the cell midplane and 3-fold near the cell cortex. The amplitude of the posterior-rich GFP::PIE-1 gradient is 5.8-fold at the cell midplane and 4.7-fold near the cell cortex (Fig. 1C). Therefore, near-TIRF imaging near the cortex allows access to the dynamics that shape the MEX-5 and PIE-1 gradients.

Using relatively fast acquisition rates (18-ms exposures; ∼55 fps), we observed that GFP::MEX-5 and GFP::PIE-1 were present in both highly dynamic fast-diffusing particles and in relatively static slow-diffusing particles (Movies S1 and S2). We observed the frequent appearance and disappearance of individual GFP::MEX-5 and GFP::PIE-1 slow-diffusing particles, which we interpret to reflect rapid switching between fast- and slow-diffusing states, presumably through binding and dissociation. The slow-diffusing state could reflect either the stable interaction of GFP::MEX-5 and GFP::PIE-1 with a slow-diffusing binding partner or the slow diffusion of GFP::MEX-5 and GFP::PIE-1 on an unknown cytoplasmic compartment. GFP::MEX-5 slow-diffusing particles are highly enriched in the anterior, whereas the GFP::PIE-1 slow-diffusing particles are highly enriched in the posterior. In contrast, the fast-diffusing particles of both GFP::MEX-5 and GFP::PIE-1 appear to be uniform. These initial qualitative observations suggest that local accumulation of slow-diffusing particles gives rise to the GFP::MEX-5 and GFP::PIE-1 gradients and motivated us to characterize their dynamics in a more rigorous manner using single-particle tracking analysis. While this study focuses on GFP::MEX-5 and GFP::PIE-1, we found that the dynamics of GFP::POS-1 are qualitatively similar to those of GFP::PIE-1 (Movie S3), suggesting similar single-particle dynamics may underlie the segregation of PIE-1 and POS-1.

Although we could readily observe the appearance and disappearance of slow-diffusing particles, we could not reliably track GFP::MEX-5 and GFP::PIE-1 fast-diffusing particles during these transitions. Therefore, we focused our single-particle analysis on the dynamics of the slow-diffusing particles using relatively slow acquisition rates (50-ms exposures; ∼20 fps), at which slow-diffusing particles (SD particles hereafter) have high signal-to-noise ratio while the fast-diffusing particles (FD particles hereafter) are blurred such that they are no longer detectable as discrete particles (Fig. 1D and Movies S4 and S5).

Dynamics of Slow-Diffusing Particles.

GFP::MEX-5.

We performed single-particle tracking to characterize the dynamics of GFP::MEX-5 SD particles. Strikingly, we find that the concentration of GFP::MEX-5 SD particles is 5.3-fold higher in the anterior than in the posterior (Fig. 1E). To begin to distinguish between the multiple kinetic processes that could contribute to the anterior enrichment of GFP::MEX-5 SD particles (see Introduction), we first characterized the displacement of GFP::MEX-5 particles in the SD state. The displacement of SD particles is isotropic in both the anterior and posterior of wild-type (WT) embryos, with no bias in movement toward the anterior (Fig. 1F). Additionally, GFP::MEX-5 moves only short distances in the SD state (<2 μm) relative to the length of the cell (Fig. 1F). We conclude that neither lateral diffusion nor the directed transport of GFP::MEX-5 in the SD state contribute to the anterior accumulation of GFP::MEX-5 SD particles.

To characterize the mobility of GFP::MEX-5 SD particles, we measured mean-square displacement (MSD) versus lag time τ on trajectories with lifetimes >20 frames (SI Appendix, Fig. S1 A and B). The first five lag times of the trajectories were fit to the equation MSD = 4D_ct^α to estimate a short-term diffusivity D_c and an anomaly exponent α (α = 1 for free diffusing particles and α < 1 for subdiffusive particles) (SI Appendix, Fig. S1 A′ and B′). These values were compared with simulated Brownian diffusion trajectories with the same distribution of track lengths (SI Appendix, Fig. S1 A″ and B″). In the posterior, the motion of SD particles is well described by Brownian motion with a D_c of 0.11 μm²/s and an α = 0.97 (Fig. 1H and SI Appendix, Fig. S1 B′ and B″). In the anterior, ∼75% of SD particles exhibit similar Brownian motion (α = 0.97, D_c = 0.11 μm²/s) and ∼25% of SD particles are more subdiffusive (α = 0.53; D_c = 0.01 μm²/s) (Fig. 1H and SI Appendix, Fig. S1 A′ and A″). The heterogeneity in the mobilities of SD particles in the anterior suggests there may be heterogeneity in the interactions that retard MEX-5 mobility in the anterior. However, because the displacement of GFP::MEX-5 in the SD state is <2 μm, we posit that this heterogeneity does not contribute to MEX-5 segregation (see also the FRAP analysis of GFP::MEX-5 and GFP::PIE-1 and Fig. 4M).

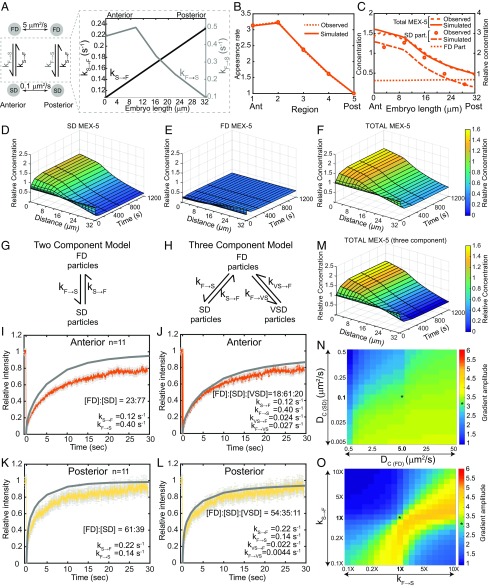
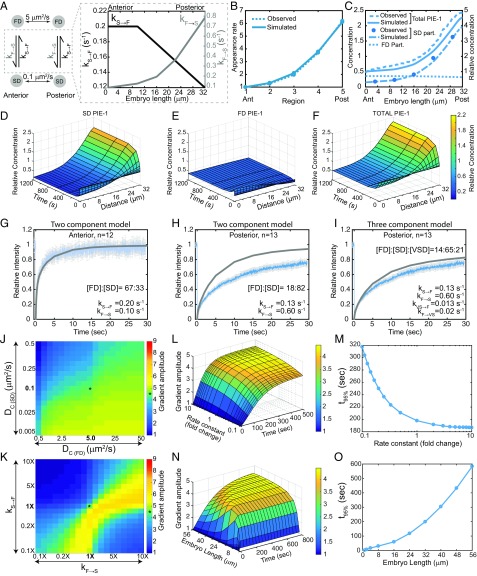
Fig. 4.

Simulation of MEX-5 gradient formation (32-μm-long A/P axis). (A) Schematic of the MEX-5 simulation parameters indicating the D_c of FD and SD particles and k_F→S and k_S→F along the A/P axis. (B) Simulated and observed MEX-5 appearance rates in the five regions along the A/P axis. (C) Concentrations of FD (simulated), SD, and total (observed and simulated) MEX-5 molecules (left axis, absolute concentrations in simulations; right axis, concentrations relative to the total MEX-5 at the posterior boundary). (D–F) Surface plots of MEX-5 SD particles (D), FD particles (E), and total MEX-5 (F) along the A/P axis from base simulations. (G–L) FRAP analysis of GFP::MEX-5. (G and H) Schematic of two- and three-component FRAP simulations. (I–L) Simulated FRAP curves in gray (I and K are two-component, and J and L are three-component models) overlaid with the experimental curves. Relative particle concentrations and rate constants are indicated. (M) Surface plot of total MEX-5 along the A/P axis over time in a three-component model. (N) Sensitivity of the base MEX-5 simulation to changes in the D_c of FD and SD particles. (O) Sensitivity of the base MEX-5 simulation to changes in k_F→S and k_S→F (2×k_S→F means k_S→F is doubled at all points relative to the base values). (N and O) Heat maps, gradient amplitude at the anterior boundary; asterisk (*), result of base simulations. See SI Appendix, Figs. S4 and S6.

We next examined the role of PAR-1 in controlling the distribution and dynamics of GFP::MEX-5 SD particles. In par-1(RNAi) embryos, the MEX-5 gradient fails to form because its ensemble mobility is uniformly slow (17, 19). In pkc-3(RNAi) embryos, PAR-1 is delocalized, which results in uniformly fast GFP::MEX-5 ensemble mobility (Fig. 1A) (17, 19). Similar to WT, the movements of GFP::MEX-5 SD particles are local (<2-μm displacement) (SI Appendix, Fig. S1G), isotropic, and have identical diffusion coefficients (0.10 μm²/s) in par-1(RNAi) and pkc-3(RNAi) embryos (Fig. 1H and Movies S6 and S7). Importantly, however, GFP::MEX-5 SD particles are uniformly distributed in both par-1(RNAi) and pkc-3(RNAi) embryos (SI Appendix, Fig. S1E). While we cannot directly compare the concentration of SD particles between different embryos due to variability in expression levels and illumination, the proportion of GFP::MEX-5 particles in the SD state appears to be lower in pkc-3(RNAi) embryos than in par-1(RNAi) embryos (Movies S6 and S7). We conclude that PAR-1 drives GFP::MEX-5 segregation by regulating the distribution of GFP::MEX-5 SD particles and that this regulation does not involve control of the displacement of GFP::MEX-5 in the SD state.

GFP::PIE-1.

PIE-1 segregation depends on MEX-5/6, which act to increase GFP::PIE-1 mobility in the anterior (9, 21). In mex-5/6(RNAi) embryos, the ensemble mobility of GFP::PIE-1 is slow throughout the cytoplasm, and in par-1(RNAi) embryos, the uniform distribution of MEX-5/6 results in uniformly fast GFP::PIE-1 ensemble mobility (Fig. 1A) (21). PLK-1/2 are also required for PIE-1 segregation and are recruited to the anterior by MEX-5/6 (22). mex-5(T186A) disrupts the interaction between MEX-5 and PLK-1/2 (22). GFP::PIE-1 fails to segregate in mex-5(T186A);mex-6(RNAi) embryos (SI Appendix, Fig. S3 A and B), consistent with the possibility that MEX-5/6 may act through PLK-1/2 to drive PIE-1 segregation.

The concentration of GFP::PIE-1 SD particles is 9.4-fold higher in the posterior than in the anterior of WT embryos (Fig. 1E) and is uniform in mex-5/6(RNAi) and par-1(RNAi) embryos (SI Appendix, Fig. S1F). In WT, mex-5/6(RNAi) and par-1(RNAi) embryos, GFP::PIE-1 SD particles appear and disappear from roughly the same position in the cytoplasm (<2-μm displacement), do not move with a directional bias toward the posterior (Fig. 1G, SI Appendix, Fig. S1H, and Movies S8 and S9), and exhibit similar mean short-term diffusivities (Fig. 1H and SI Appendix, Fig. S1 C–C" and D–D"). We conclude that MEX-5/6 regulate the distribution of GFP::PIE-1 SD particles and that this regulation is not through control of the directed transport or mobility of GFP::PIE-1 in the SD state. We note that single-molecule speckles of the actin filament-binding domain of Utrophin (GFP::Utrophin) have a very different mobility signature than GFP::MEX-5 and GFP::PIE-1 SD particles (D_c = 0.012, α = 0.56; Fig. 1H), suggesting that the reduced mobility of GFP::MEX-5 and GFP::PIE-1 SD particles is not due to static interactions with actin filaments.

We conclude that upstream polarity regulators control the polarized distribution of GFP::MEX-5 and GFP::PIE-1 SD particles along the A/P axis, which underlies the differences in the ensemble mobility of GFP::MEX-5 and GFP::PIE-1. We next sought to determine whether the local differences in the kinetics of switching between the FD and SD states enrich GFP::MEX-5 and GFP::PIE-1 SD particles in the appropriate cytoplasmic domain.

Kinetics of Diffusion-State Switching.

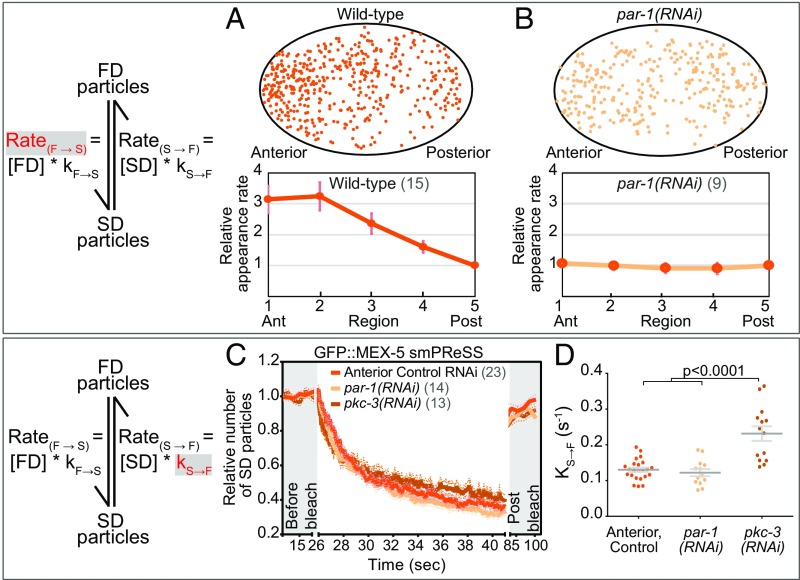
In the following analysis, we assume that the appearance of an SD particle during near-TIRF imaging reflects the switch of a particle from the FD to the SD state and that the disappearance of an SD particle reflects the switch of a particle from the SD to the FD state. The kinetics of these transitions are described by the rate constants k_F→S and k_S→F, respectively.

GFP::MEX-5.

We first characterized the kinetics of GFP::MEX-5 conversion from the FD to the SD state by quantifying the rate at which new GFP::MEX-5 SD particles appear at different positions along the A/P axis (Rate_F→S). Note that because the concentration of GFP::MEX-5 FD particles is not measured in these experiments, we cannot determine the rate constant k_F→S from the Rate_F→S (see Mathematical models of MEX-5 and PIE-1 differential diffusion for estimates of k_F→S). We find that the Rate_F→S of GFP::MEX-5 is 3.1 times higher in the anterior than in the posterior of WT embryos (Fig. 2A and Movie S4) and is uniform along the A/P axis of par-1(RNAi) embryos (Fig. 2B and Movie S6), consistent with the idea that PAR-1 inhibits the transition of MEX-5 from the FD to the SD state. The sites where SD particles appear are broadly dispersed throughout the cytoplasm, suggesting that GFP::MEX-5 does not initially bind to a limited number of foci from which it disperses to the surrounding cytoplasm (Fig. 2 A and B).

Fig. 2.

Kinetics of GFP::MEX-5 switching between the FD and SD states. (A and B) Appearance rate (Rate_F→S) of new GFP::MEX-5 SD particles (red in the schematic) along the A/P axis of WT and par-1(RNAi) embryos. (Top) Each dot marks the appearance of a new SD particle with trajectory >250 ms during a 10-s acquisition. The same WT embryo was analyzed in Fig. 1F. (Bottom) Mean appearance rate within five regions along the A/P axis (normalized to region 5). We cannot directly determine k_F→S from Rate_F→S because [FD particles] under near-TIRF is unknown. (C) smPReSS curves of SD GFP::MEX-5 particles in the anterior of WT and along the entire A/P axis of par-1(RNAi) and pkc-3(RNAi) embryos. SD particle number is normalized to the mean of “before bleach” for each embryo and averaged among embryos. “Post bleach” is following a 45-s recovery. Dotted lines indicate SEM. (D) Apparent k_S→F estimated from the smPReSS curves in C. Each dot represents an individual embryo. See SI Appendix, Fig. S2.

We next estimated the kinetics of GFP::MEX-5 switching from the SD to the FD state (k_S→F). The disappearance of GFP::MEX-5 SD particles during imaging reflects both k_S→F and photobleaching at a rate k_ph. To estimate k_S→F, we performed smPReSS analysis in which the change in the density of SD particles before (k_S→F only) and during photobleaching (k_S→F + k_ph) is used to estimate k_S→F (27). In WT, the apparent k_S→F for GFP::MEX-5 is 0.12 s⁻¹ in the anterior (Fig. 2 C and D, SI Appendix, Fig. S2A, and Movie S10). Similarly, the apparent k_S→F of GFP::MEX-5 is 0.12 s⁻¹ in “anteriorized” par-1(RNAi) embryos (Fig. 2 C and D, SI Appendix, Fig. S2B, and Movie S11) (17, 19). Because we could not perform smPReSS analysis on GFP::MEX-5 in the posterior due to the low density of SD particles, we analyzed “posteriorized” pkc-3(RNAi) embryos. The apparent k_S→F of GFP::MEX-5 in pkc-3(RNAi) embryos (0.22 s⁻¹) is significantly higher than in the anterior of WT (Fig. 2 C and D, SI Appendix, Fig. S2C, and Movie S12), indicating that GFP::MEX-5 SD particles are more persistent in the anterior than in the posterior. Importantly, the observed 5.3-fold enrichment of GFP:MEX-5 SD particles in the anterior can be accounted for by the differences in GFP::MEX-5 Rate_F→S (∼3.1-fold higher in the anterior) and k_S→F (∼1.8-fold higher in the posterior), which predict a ∼5.7-fold anterior enrichment of SD particles.

We previously demonstrated that reducing MEX-5 affinity for RNA reduces the amplitude of its gradient by increasing its ensemble mobility in the anterior (19). The apparent k_S→F of the MEX-5 RNA-binding mutant GFP::MEX-5(ZFmut) is 0.16 s⁻¹ in the anterior (SI Appendix, Fig. S2 D and E and Movie S13), indicating that its increased ensemble mobility can be attributed, at least in part, to the decreased persistence of GFP::MEX-5(ZFmut) SD particles.

GFP::PIE-1.

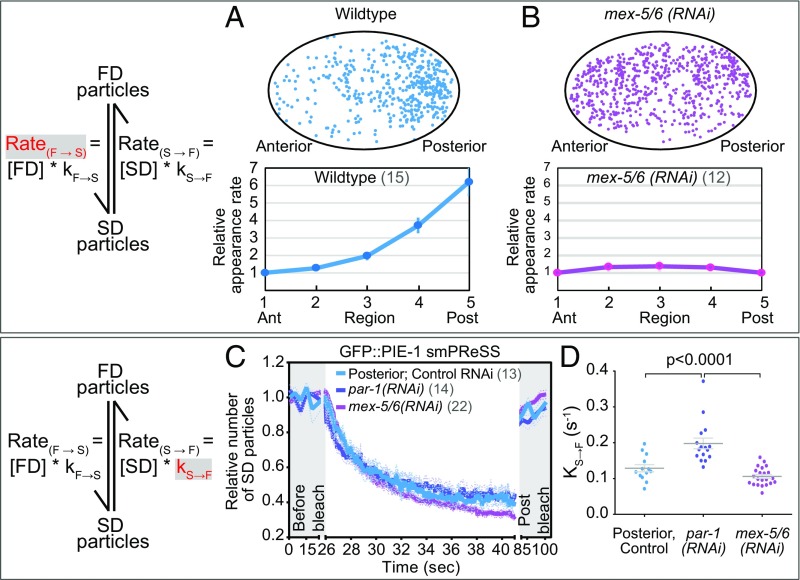
We performed similar analyses to characterize the kinetics of GFP::PIE-1 switching between SD and FD states. The appearance rate of GFP::PIE-1 SD particles (Rate_F→S) is 6.2-fold higher in the posterior than in the anterior of WT (Fig. 3A and Movie S5) and is symmetric in mex-5/6(RNAi) embryos (Fig. 3B and Movie S8). Similarly, in mex-5(T186A);mex-6(RNAi) embryos, both the distribution and Rate_F→S of GFP::PIE-1 are symmetric (SI Appendix, Fig. S3 C and D).

Fig. 3.

Kinetics of GFP::PIE-1 switching between the FD and SD states. (A and B) Appearance rate (Rate_F→S) of new GFP::PIE-1 SD particles in WT and mex-5/6(RNAi) embryos (as in Fig. 2A except the Bottom was normalized to region 1). The same WT embryo was analyzed in Fig. 1G. (C) smPReSS curves of SD GFP::PIE-1 particles in the posterior of WT embryos and along the entire A/P axis of mex-5/6(RNAi) and par-1(RNAi) embryos (as in Fig. 2C). (D) Apparent k_S→F estimated from the smPReSS curves in C. See SI Appendix, Figs. S2 and S3.

Using smPReSS, we find that the apparent k_S→F of GFP::PIE-1 in the posterior of WT is 0.13 s⁻¹ (Fig. 3 C and D, SI Appendix, Fig. S2F, and Movie S14) and is 0.11 s⁻¹ in “posteriorized” mex-5/6(RNAi) embryos (Fig. 3 C and D, SI Appendix, Fig. S2G, and Movie S15). In “anteriorized” par-1(RNAi) embryos, the apparent k_S→F of GFP::PIE-1 is significantly higher (0.2 s⁻¹) than in the posterior of WT, indicating that GFP::PIE-1 particles are more persistent in the posterior than in the anterior (Fig. 3 C and D, SI Appendix, Fig. S2H, and Movie S16). The observed 9.4-fold enrichment of SD particles in the posterior can be accounted for by the differences in GFP::PIE-1 k_F→S (6.2-fold higher in the posterior) and k_S→F (∼1.5-fold higher in the anterior), which predict a 9.5-fold posterior enrichment of SD particles.

Taken together, the findings described above indicate that the reaction/diffusion dynamics of GFP::MEX-5 and GFP::PIE-1 are remarkably similar. Both proteins interconvert between approximately symmetrically distributed FD particles and asymmetrically distributed SD particles. GFP::MEX-5 and GFP::PIE-1 switch to the SD state more frequently and remain in the SD state longer in the anterior and in the posterior, respectively. We conclude that the differences in the kinetics of diffusion-state switching along the A/P axis give rise to the MEX-5 and PIE-1 gradients.

Mathematical models of MEX-5 and PIE-1 differential diffusion.

We next used mathematical modeling to test whether the reaction–diffusion dynamics described above are sufficient to give rise to the MEX-5 and PIE-1 gradients. We generated two separate 1D reaction–diffusion models [derived from a previous model of MEX-5 reaction–diffusion dynamics (19)] for MEX-5 and for PIE-1 in which molecules diffuse along the A/P axis in either the FD or SD state and locally switch between diffusive states with simple first-order kinetics (schematized in Figs. 4A and 5A). For simplicity, our simulations consider an idealized situation in which all SD particles have a D_c of 0.1 μm²/s, although we note that this single value does not reflect the observed heterogeneity in the mobility of GFP::MEX-5 SD particles in the anterior. The D_c of the FD particles was estimated to be 5 μm²/s based on previous FCS analysis of GFP::MEX-5 (19). The change in the concentration of FD and SD molecules over time is described by the following differential equations:

$$\frac{\partial \left[\mathrm{FD}\right]}{\partial t}=k_{\text{S}\to \text{F}}\hspace{0.17em}\left[\mathrm{SD}\right]-k_{\text{F}\to \text{S}}\hspace{0.17em}\left[\mathrm{FD}\right]+D_{c\left(\mathrm{FD}\right)}\frac{{\partial }^2\left[\mathrm{FD}\right]}{\partial x^2},$$

$$\frac{\partial \left[\mathrm{SD}\right]}{\partial t}=-k_{\text{S}\to \text{F}}\hspace{0.17em}\left[\mathrm{SD}\right]+k_{\text{F}\to \text{S}}\hspace{0.17em}\left[\mathrm{FD}\right]+D_{c\left(\mathrm{SD}\right)}\frac{{\partial }^2\left[\mathrm{SD}\right]}{\partial x^2},$$

where t is time in seconds, [FD] and [SD] are the local concentrations of FD molecules and SD molecules, D_C(FD) and D_C(SD) are the diffusion coefficients of FD and SD molecules, k_S→F is the rate constant of a molecule transitioning from the SD to FD state, k_F→S is the rate constant of a molecule transitioning from the FD to SD state, and x is the spatial coordinate in a 1D Cartesian coordinate system (see SI Appendix, Supplemental Methods for further details).

Fig. 5.

Simulation of PIE-1 gradient formation (32-μm-long A/P axis). (A) Schematic of the PIE-1 simulation indicating the D_c of the FD and SD particles and the gradients of k_F→S and k_S→F along the A/P axis. (B) Simulated and observed PIE-1 appearance rates in the five regions along the A/P axis. (C) Concentrations of FD (simulated), SD, and total (observed and simulated) PIE-1 molecules (as in Fig. 4C except normalized to the anterior). (D–F) Surface plots of PIE-1 SD particles (D), FD particles (E), and total PIE-1 (F) along the A/P axis from base simulations. (G–I) FRAP analysis of GFP::PIE-1 as in Fig. 4 I–L. (J) Sensitivity of the base PIE-1 simulation to changes in the D_c of FD and SD particles. (K) Sensitivity of the base PIE-1 simulation to changes in k_F→S and k_S→F, as in Fig. 4N except normalized to the anterior. (L) Surface plot of gradient amplitude as a function of diffusion-state switching kinetics. (M) Time required to reach 95% maximal gradient amplitude as a function of kinetics (from simulations in L). (N) Surface plot of gradient amplitude as a function of embryo length. (O) Time required to reach 95% maximal gradient amplitude as a function of embryo length (from simulations in N). See SI Appendix, Figs. S4–S7.

For both the MEX-5 and PIE-1 simulations, we assume that k_S→F varies along the A/P axis between the observed values for k_S→F in the anterior and posterior (Figs. 4A and 5A). To estimate k_F→S values for MEX-5, we first estimated the relative concentration of FD and SD particles in the anterior and posterior. Based on the assumption that FD particles are approximately uniformly distributed and that the total MEX-5 gradient (Fig. 1C) reflects the sum of the SD particle (Fig. 1E) and the FD particle concentrations (unknown), we calculated the relative FD particle concentration. From these values and the measured Rate_F→S, we estimated k_F→S along the A/P axis (Fig. 4B) (SI Appendix, Supplemental Methods). We estimated k_F→S values for PIE-1 using the same approach (Fig. 5B). We refer to these values as the base MEX-5 and PIE-1 simulation values.

Importantly, the base MEX-5 and PIE-1 simulations give rise to gradients of the observed amplitude (Figs. 4C and 5C). Simulations approached steady state within ∼4 min with a 32-μm length scale (cell length near the cortex) (Figs. 4 D–F and 5 D–F) and ∼6 min with a 50-μm length scale (cell length at the midplane) (SI Appendix, Fig. S4), which are within the timescale of gradient formation. Based on these initial simulations, we conclude that the differences in the kinetics of diffusion-state switching described in this study are sufficient to give rise to the MEX-5 and PIE-1 gradients.

FRAP analysis of GFP::MEX-5 and GFP::PIE-1.

One limitation of single-particle imaging is that photobleaching may limit our ability to track particles that exchange very slowly. To test for the presence of relatively immobile particles, we compared GFP::MEX-5 and GFP::PIE-1 FRAP recovery curves with simulated FRAP recovery curves (SI Appendix, Fig. S5A and Supplemental Methods) using the base simulation parameters described above, which we refer to as two-component simulations (Fig. 4G). With the exception of PIE-1 in the anterior (Fig. 5G and SI Appendix, Fig. S5B), the two-component simulations overestimated the percent FRAP recovery (Figs. 4 I and K and 5H), suggesting that the base simulations do not reflect a relatively static component that is present in the embryo. We therefore modified our simulation to allow FD particles to switch to either the SD state or to a very slow-diffusing state (VSD) (Fig. 4H). We estimated VSD particles to have a D_c of 0.01 μm²/s based on our analysis of short-term diffusivity of GFP::MEX-5 in the anterior (SI Appendix, Fig. S1A′). We estimated the exchange rate of VSD particles to be ∼10-fold slower than the SD particles because such slow exchange rates would not have been reflected in the smPReSS analysis. We then altered the proportion of VSD particles in our FRAP simulation until the simulated recovery curves reasonably fit the observed curves.

Using this approach, we estimated the proportion of GFP::MEX-5 VSD particles to be ∼20% in the anterior and 11% in the posterior (Fig. 4 J and L). For PIE-1, we estimated the concentration of VSD particles to be ∼21% in the posterior (Fig. 5I and SI Appendix, Fig. S5C). VSD particles presumably reflect the relatively stable association of MEX-5 and PIE-1 with an unknown cytoplasmic structure. We tested whether GFP::PIE-1 VSD particles in the posterior cytoplasm reflects the association of GFP::PIE-1 with P granules by comparing the FRAP recovery of GFP::PIE-1 in the posterior cytoplasm of WT and pgl-1(RNAi);pgl-3(bn104) embryos, in which we no longer detect GFP::PIE-1 granules in the posterior cytoplasm (SI Appendix, Fig. S5D). The GFP::PIE-1 FRAP recovery profile is identical to WT and pgl-1(RNAi);pgl-3(bn104) embryos (SI Appendix, Fig. S5E), indicating that the GFP::PIE-1 VSD particles are not likely to be due to P granule association. Because inclusion of the VSD particles in the MEX-5 simulation did not significantly alter the dynamics of gradient formation (Fig. 4M), we did not include VSD particles in our subsequent simulations.

Critical parameters for gradient formation.

We tested the sensitivity of the base MEX-5 and PIE-1 simulations to changes in the diffusion coefficient of the SD and FD particles. In both base simulations, the D_c of the FD and SD particles differ by roughly 50-fold. Changes that increased the difference in particle diffusivity (for example, decreasing the D_c of SD particles) resulted in a slight increase in gradient strength (Figs. 4N and 5J). In contrast, changes that decrease the difference in particle diffusivity (for example, increasing the D_c of SD particles) resulted in a significant decreased in gradient strength (Figs. 4N and 5J). We conclude that a wide range of SD and FD diffusivities could result in differential diffusion as long as they are sufficiently different (approximately greater than 10-fold) in diffusivity (see also refs. 19 and 24).

For both MEX-5 and PIE-1, coordinately increasing or decreasing k_F→S and k_S→F had little effect on the amplitude of gradient formation (Figs. 4O and 5K), indicating that a broad range of kinetic switching rates can generate subcellular gradients. We next analyzed the effect of varying reaction kinetics on the timescale of gradient formation. Because the MEX-5 and PIE-1 simulations are very similar, we focused on the PIE-1 simulation. Interestingly, coordinately decreasing both k_F→S and k_S→F slows the formation of the PIE-1 gradient such that a 10-fold decrease in switching kinetics roughly doubled the time required to approach steady state. In contrast, coordinately increasing k_F→S and k_S→F did not increase the rate of gradient formation (Fig. 5 L and M), indicating that the kinetics of MEX-5 and PIE-1 diffusion-state switching are optimal for their rapid gradient formation. Additionally, these results indicate that only at very fast diffusion-state switching kinetics does the maximal rate of gradient formation become limited by the mobility of the gradient-forming protein (19).

We next analyzed the effect of varying the gradient length scale from 1 to 56 μm on the behavior of our base PIE-1 simulation. For gradients between 16 and 56 μm, the steady-state gradient amplitude was similar but the time required to reach steady state increased as a function of gradient length (Fig. 5 N and O). Gradient amplitudes progressively weaken for length scales below 16 μm such that essentially no gradient is formed at length scales of <4 μm. At short length scales, the mobility of the SD particles is sufficient for them to spread roughly one-half the length of the gradient, which effectively dissipates the gradient. We conclude that the type of reaction diffusion mechanisms described here can generate gradients at a wide range of temporal and spatial scales, and that the rate of gradient formation is controlled by both the kinetics of diffusion-state switching and the length scale of gradient formation.

We next tested the individual contribution of the gradients in k_S→F and k_F→S and found that the differences in k_F→S along the A/P axis account for the majority of both the MEX-5 and the PIE-1 gradients (SI Appendix, Figs. S6 A–C and S7 A–C). Modulating only k_F→S or only k_S→F while maintaining the base values for the other parameters dramatically altered gradient amplitude. For example, decreasing k_F→S relative to k_S→F progressively decreased gradient amplitude as the proportion of particles in the symmetrically distributed FD state increased (Figs. 4O and 5K, SI Appendix, Figs. S6 D and E and S7 D and E). In contrast, decreasing k_S→F relative to k_F→S increased the proportion of particles in the asymmetrically distributed SD state, and therefore increased gradient amplitude (SI Appendix, Figs. S6 D and F and S7 D and F). However, when k_F→S >> k_S→F, essentially all particles in the anterior and posterior were in the SD state, and gradients no longer formed (SI Appendix, Figs. S6 D and G and S7 D and G). Taken together, these simulation results suggest that the segregation of MEX-5 and PIE-1 requires a balance between the mechanisms that control their switching between fast- and slow-diffusing states.

Discussion

In this study, we characterize the reaction–diffusion dynamics that maintain the MEX-5 and PIE-1 gradients. We find that GFP::MEX-5 and GFP::PIE-1 frequently interconvert between fast- and slow-diffusing states with kinetics that are highly asymmetric along the A/P axis due to regulation by upstream polarity regulators. As a result, the distributions of GFP::MEX-5 and GFP::PIE-1 slow-diffusing particles are strongly polarized, which provides the basis of the GFP::MEX-5 and GFP::PIE-1 gradients. The continuous flux between uniformly distributed fast-diffusing particles and asymmetrically distributed slow-diffusing particles occurs on timescales that are much shorter (seconds) than that of gradient formation and maintenance (minutes). Therefore, the seeming stability of these maintenance phase gradients belies the rapid underlying single-particle dynamics.

The reaction–diffusion dynamics of MEX-5 and PIE-1 are analogous in some ways to the reaction–diffusion dynamics of the PAR proteins. PAR-3, PAR-6, and PAR-2 continuously exchange between a symmetrically distributed, fast-diffusing cytoplasmic pool and an asymmetrically distributed cortical pool (27–31). The kinetics at which the PAR proteins bind to and dissociate from the cortex differs significantly along the A/P axis, leading to their concentration in the appropriate cortical domains. Maintenance of the cortical PAR domains is controlled by a network of redundant, mutually antagonistic interactions between the anterior and posterior PAR proteins that restrict them to the appropriate cortical domain (8). In contrast, the regulatory interactions in the cytoplasm appear to be hierarchical: MEX-5/6 regulate PIE-1 and POS-1 segregation, but POS-1 and PIE-1 do not regulate MEX-5/6 segregation (9). Additionally, whereas the anterior PAR domain appears to be maintained through the dynamic clustering and dispersion of the aPAR/PAR-6 at the cell cortex (25, 31–33), MEX-5 and PIE-1 appear to bind to distributed sites within the cytoplasm, suggesting that their gradients do not form through clustering and dispersion. Clustering is thought to increase the avidity of the PAR proteins for the cortex, which may explain why the association of the PAR proteins with the cortex is significantly more stable [k_off < 0.008 s⁻¹ for PAR-6 and PAR-2 (27, 28, 30)] than the association of MEX-5 and PIE-1 with their cytoplasmic binding partner/s (k_off ∼ 0.1–0.2 s⁻¹).

How do upstream polarity regulators control variation in the kinetics of MEX-5 and PIE-1 diffusion-state switching? Our current model is that MEX-5 diffusivity is increased by PAR-1 phosphorylation in the posterior and decreased throughout the cytoplasm by PP2A dephosphorylation (19). Because the spatial segregation of opposing kinases and phosphatases can generate phosphorylation-state gradients (34, 35), we consider it likely that a gradient in the phosphorylation status of MEX-5 gives rise to local differences in the kinetics of binding/dissociation of MEX-5 from its slow-diffusing substrate. While the mechanisms by which MEX-5/6 control the diffusion-state switching of PIE-1 are not fully understood, it has been shown that (i) the interactions between MEX-5/6 and PLK-1/2 are required to increase the PIE-1 and POS-1 diffusivity in the anterior cytoplasm (refs. 22 and 23 and SI Appendix, Fig. S3), and (ii) PLK-1 phosphorylation increases POS-1 diffusivity (23). These observations raise the possibility that an analogous phosphorylation cycle may underlie POS-1 and PIE-1 differential diffusion. In the future, incorporating the MEX-5/6 phosphorylation cycle (and, if warranted, PIE-1 and POS-1 phosphorylation cycles) into mathematical models of gradient formation will be critical for understanding how these coupled reaction–diffusion mechanisms transduce patterning information through the cytoplasm.

Some intracellular gradient-forming mechanisms appear to rely on reactions that occur at the cell boundary/cell pole. For example, in Schizosaccharomyces pombe, the kinase Pom1p is loaded onto the cell cortex at the cell poles. Pom1p dissociates from the cortex as it diffuses from the pole, giving rise to gradients that decrease toward the middle of the cell (5). Two central features of the Pom1 gradient-forming mechanism are that (i) binding/association with the cell pole provides the critical asymmetry that underlies gradient formation, and (ii) because the binding reaction occurs at the cell boundary, the rate of gradient formation will be limited by the mobility of Pom1 as it moves away from the pole. In contrast, the MEX-5 and PIE-1 binding reactions appear to be distributed throughout the cytoplasm, such that the formation of their gradients are relatively insensitive to the mobility of their slow-diffusing particles. While we presume that reactions involving the PAR proteins at the cell cortex initiate the cytoplasmic polarization pathway, our findings indicate that these reactions are likely acting upstream of the control of MEX-5 or PIE-1 mobility.

In the classic formulation of the morphogen hypothesis (36), gradations in morphogen concentration cause gradations in morphogen binding interactions, for example to cell surface receptors or to chromatin binding sites. In this view, the protein gradient gives rise to differences in the levels of protein interactions across space. Interestingly, this cause and effect relationship is inverted in the mechanism described in this study: The MEX-5 and PIE-1 gradients arise as a consequence of regulated differences in their binding interactions across space. In principle, gradient formation through rapid diffusion-state switching could provide a general means by which gradients are rapidly patterned across a wide range of temporal and spatial scales. Therefore, it will be interesting to learn to what extent other gradients are a cause or a consequence of a protein’s spatially graded binding activity.

Materials and Methods

C. elegans strains, culturing, and gene editing are described in SI Appendix. In addition, mathematical modeling, FRAP simulations, smPReSS, single-particle tracking, and estimates of short-term diffusivity are described in SI Appendix.

Near-TIRF Imaging

Embryos were dissected into M9 on a coverslip. Approximately 100 20-μm polystyrene microspheres were added (Bangs Laboratories), and the coverslip was mounted on a slide and sealed with Vaseline. Slides were placed on a stage with a rotating insert, and embryos were oriented with the A/P axis perpendicular to the plane of the illumination laser.

Near-TIRF imaging was performed on a Nikon Ti-E inverted microscope equipped with TI-TIRF illuminator, a 100×/1.49 N.A. APO TIRF objective with the temperature correction collar set to 23 °C, a 50-mW 488-nm laser housed in an Andor Laser Combiner and a 488/561-nm dual-bandpass filter. Images were collected on one of the two Andor iXon 897 cameras (17-MHz readout speed; gain, 3; intensification, 300) mounted on an Andor Tucam. A 1.5× magnifier was used for all experiments. Using Perfect Focus, the imaging plane was set at ∼0.5 μm from the embryo cortex. The laser illumination angle was chosen empirically to maximize the signal-to-noise ratio. This microscope was driven by NIS Elements software (Advanced Research 4.50.00 Build 1117 Patch 03). With the exception of the smPReSS experiments, all time-lapse imaging was performed under continuous imaging for 2,000 frames with either 18-ms exposures (∼55 fps) at 60% laser power or 50-ms exposures (∼20 fps) at 100% laser power. All movies were started during PN centration.

Spinning-Disk Confocal Microscopy

Gradient quantification and FRAP analysis was performed at nuclear envelope breakdown on a Marianas spinning-disk confocal microscope controlled by the Slidebook software package (3I) and built around a Zeiss Axio Observer Z.1 with a Zeiss Plan-Apochromat 63×/1.4 N.A. oil-immersion objective, a CSU-X1 spinning disk (Yokogawa), an Evolve 512 × 512 EMCCD camera (Photometrics), and a 50-mW 488-nm solid-state laser.

The GFP::PIE-1 and GFP::MEX-5 gradients were quantified using spinning-disk confocal microscopy. The same embryo was imaged at the cell cortex and midplane with 60% laser power, 1-s exposures, and camera intensification of 300 and gain of 1. Intensity values were corrected for the camera background. To correct for zygotic autofluorescence, the average fluorescence intensity of 12 N2 zygotes was subtracted before calculation of the normalized GFP::PIE-1 and GFP::MEX-5 concentration gradients. Line scan analysis was performed as described (20).

FRAP imaging was performed with continuous imaging with 20-ms exposures (intensification, 300; gain, 2; 75% laser power for both photobleaching and imaging). Photobleaching was performed with a Phasor unit using the 488-nm laser, 20-ms bleach time, and a 4-μm diameter circular region of interest positioned at ∼15% (anterior) or 85% (posterior) embryo length. FRAP curves were normalized as described (22).