Significance
Animals in natural environments necessarily come into contact with surfaces having differing orientations and materials. However, not much is known about how their feet contribute to friction, particularly in the case of dual-attachment mechanisms and passive mechanics (morphological intelligence). We study the desert locust’s (Schistocerca gregaria) morphology, spines and adhesive pads, and jumping behavior to extract traits that contribute to enhancing friction. Our results demonstrate the potential contribution of morphological intelligence to solving complex dynamic locomotion problems. We anticipate that this study will inspire further research of the strategies used by animals to interact dynamically with diverse surfaces. Furthermore, the concepts presented can be easily adapted to, for the enhancement of, existing simple miniature and state-of-the-art large-legged terrestrial robots.
Keywords: locust, robot, slip, friction, jump
Abstract
During dynamic terrestrial locomotion, animals use complex multifunctional feet to extract friction from the environment. However, whether roboticists assume sufficient surface friction for locomotion or actively compensate for slipping, they use relatively simple point-contact feet. We seek to understand and extract the morphological adaptations of animal feet that contribute to enhancing friction on diverse surfaces, such as the desert locust (Schistocerca gregaria) [Bennet-Clark HC (1975) J Exp Biol 63:53–83], which has both wet adhesive pads and spines. A buckling region in their knee to accommodate slipping [Bayley TG, Sutton GP, Burrows M (2012) J Exp Biol 215:1151–1161], slow nerve conduction velocity (0.5–3 m/s) [Pearson KG, Stein RB, Malhotra SK (1970) J Exp Biol 53:299–316], and an ecological pressure to enhance jumping performance for survival [Hawlena D, Kress H, Dufresne ER, Schmitz OJ (2011) Funct Ecol 25:279–288] further suggest that the locust operates near the limits of its surface friction, but without sufficient time to actively control its feet. Therefore, all surface adaptation must be through passive mechanics (morphological intelligence), which are unknown. Here, we report the slipping behavior, dynamic attachment, passive mechanics, and interplay between the spines and adhesive pads, studied through both biological and robotic experiments, which contribute to the locust’s ability to jump robustly from diverse surfaces. We found slipping to be surface-dependent and common (e.g., wood 1.32 1.19 slips per jump), yet the morphological intelligence of the feet produces a significant chance to reengage the surface (e.g., wood 1.10 1.13 reengagements per jump). Additionally, a discovered noncontact-type jump, further studied robotically, broadens the applicability of the morphological adaptations to both static and dynamic attachment.
Terrestrial locomotion emerges from interaction with one’s environment (1), which is further complicated by the diversity of surface materials and dynamic timescales. Locomotion studies have explored dynamics with point-contact feet (2–10), rigid, rough (11–13), mesh (14), and smooth (15, 16) surfaces, deformable (17) surfaces, granular (18–25) surfaces, and obstructed environments (26, 27) elucidating traversing behaviors, optimal strategies, and new environmental material models (28). However, interactions tend to dissipate energy, which is well studied for granular surfaces [environmental dissipation (28)], but not for rigid surfaces (body dissipation) which, through slipping, tend to dissipate energy in the tissues (29). Scansorial robots using either spines (30–32) or gecko-inspired dry adhesives (33–36) have demonstrated the frictional properties of each of these attachment mechanisms on rigid surfaces. However, the diversity of surfaces in the environment sometimes necessitates multiple attachment mechanisms, and, whereas humans have developed shoes for ice, grass, wood, rock, track, slip, and stick, animal feet must be multifunctional.
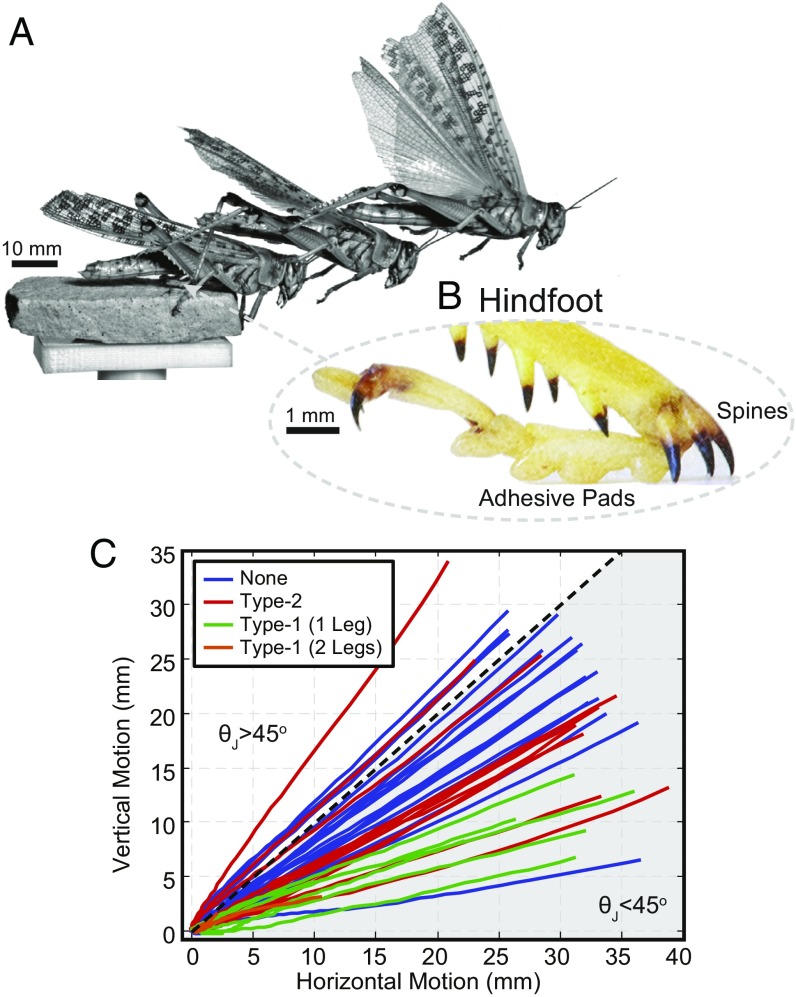
Desert locusts (1, 37–40) [Schistocerca gregaria; female, 2.32 0.31 g; male, 1.67 0.14 g; t(30) = 10.0, P = 0.00] escape-jumped (41) from an elevated platform in response to a rapid approach from behind by the experimenter (Fig. 1A, Movie S1, and Animals and Statistics). The surface material is one of five selected, including hydrophobic glass (contact angles of 94.7°/84.0°, n = 119), hydrophilic glass (contact angles of 32.6°/21.6°, n = 111), wood (sawn pine, n = 113), sandstone (n = 112), and mesh (steel, n = 95), where n represents the number of trials (Fig. 2, Table 1, and Surface Preparation). These materials were selected to both challenge and isolate the two major attachment mechanisms of the locust: the spines, whose contribution to surface friction is unknown, and wet adhesive pads (Fig. 1B). We proposed that the glass would sufficiently isolate the adhesive pad behavior and the change in wettability would challenge the wet adhesion, whereas the wood, sandstone, and mesh would sufficiently isolate the spine behavior, and the change in surface roughness and cohesion would challenge the spine friction (42). We recorded the foot behavior for each material with a high-speed camera; further details are presented in Locust Experiments. Initial observations of the jumping angles (Fig. 1C) and accelerations (Fig. 3A) suggest that the locust’s feet exhibit frictional properties beyond that predicted by the traditional Coulomb friction model.
Fig. 1.
The desert locust’s jumping behavior. (A) Side-view video snapshots of a desert locust (S. gregaria) jumping trial. (B) Photo of the locust’s hindfoot. (C) Body -motion during jumping trials where the locust had either no (none), type-2, type-1 (one leg), and type-1 (two legs) slips (males only; Trial Details). Tracking stops when the last foot leaves the surface. Jumping angles, (gray region), require friction coefficients >1, which are generally not achievable in the traditional Coulomb friction model.
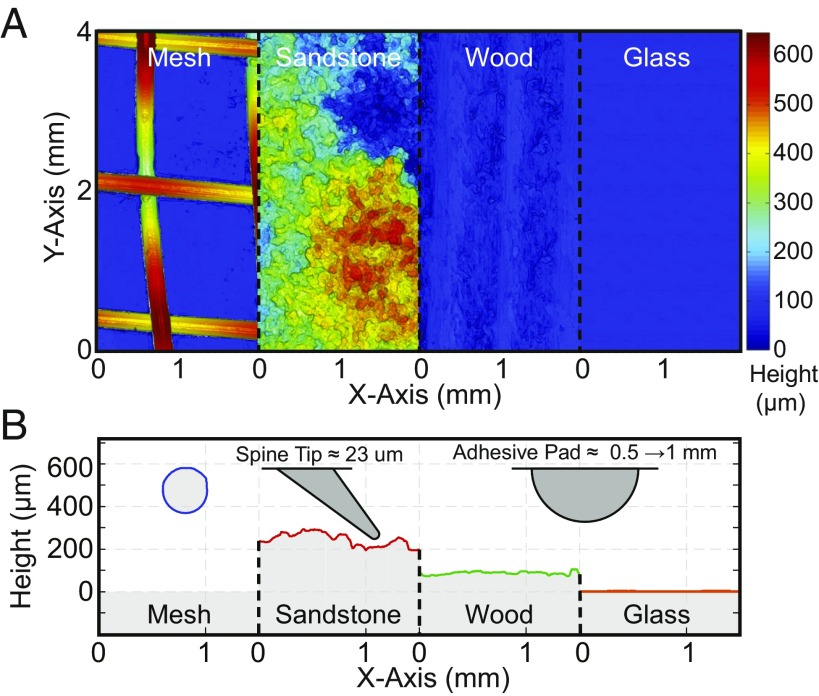
Fig. 2.
Experiential surfaces compared with the locust. (A) Surface materials (3D surface profilometer micrographs). (Magnification: 100.) (B) Surface cross-sections compared with the locust’s spines and adhesive pads.
Table 1.
Summary of surface roughness properties
| Material | , m | , m | Maximum height, m |
| Glass* | 0.02 | 0.01 | 0.19 |
| Wood (pine) | 10.60 | 0.68 | 212.07 |
| Sandstone | 75.13 | 1.16 | 581.12 |
| Mesh (steel) | 174.26 | 1.15 | 665.39 |
The arithmetic mean area roughness, Sa (asperities), arithmetic mean line roughness discretized by the average spine tip radius of 23 _m, Ra (friction), and height range of each material.
The transparency and reflectivity may have added noise to the measurements.
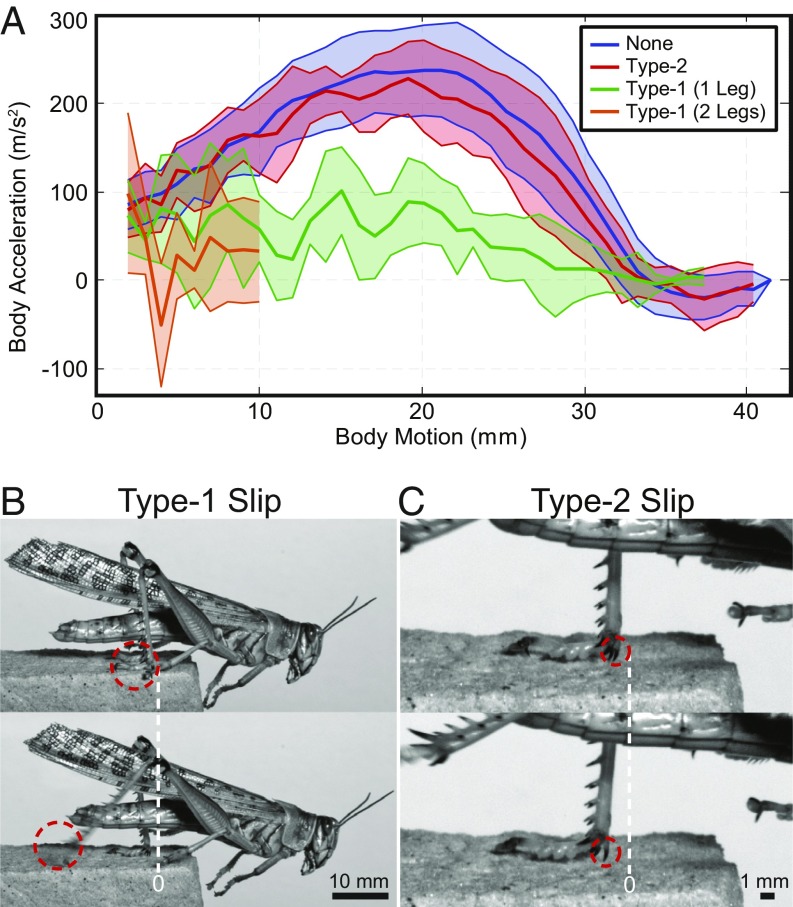
Fig. 3.
Locust slipping behavior. (A) Body accelerations during jumping trials where the locust had no (none), type-2, type-1 (one leg), and type-1 (two legs) slips (males only; Trial Details). Here, the shaded regions represent a SD around the mean. (B) Type-1 slip: two video snapshots where the foot does not reengage and leaves the surface. (C) Type-2 slip: two video snapshots where the foot reengages with a single spine. In B and C, motion of the red circle represents the approximate motion of the feature in the two images.
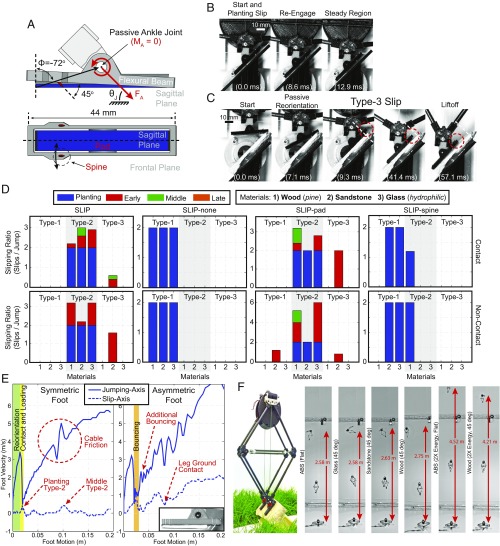
To quantify the performance of the locust’s feet on each surface, individual slipping events were counted and categorized by whether the foot reengaged the surface after the slip as (type 1 or 2) slips and the potential energy lost as (planting, early, middle, or late) slips (Fig. 4). The slip-type categories include type-1 slips, where all remaining energy is lost, and type-2 slips, where a slip and reengagement occur, resulting in minimal energy lost (Fig. 3 B and C); reengaging the surface occurs when the foot comes to rest after a slip event. The potential energy lost divides the slip events into four energy ranges, defined by knee angle, , ranges at the onset of the slip, which represent the potential energy loss of [0]100%, [0, 45] = [100, 38]%, [45, 135]° = [38, 0.6]%, and [135, 180] = [0.6, 0]%, respectively, where the potential energy fractions come from the kinematics of the robotic platform. Late slips will henceforth be excluded from analyses, as the remaining energy is minimal, and the robotic platform dynamics predict lift-off within this region. The planting slip comes from the discovery that locusts occasionally initiate a jump without their feet in contact (noncontact jump) with the surface, or without sufficient contact, and sometimes a slip occurs before the foot comes to rest, compared with a jump in which the foot begins in contact with the surface (contact jump). To investigate the importance and modification of morphological traits difficult to investigate on the locust, robotic feet were developed for the robotic platform [MultiMo-Bat (43, 44)], which uses a similar catapult-type jump and leg structure to that of the locust (Fig. 6A, Robotic Foot, and Movie S2).
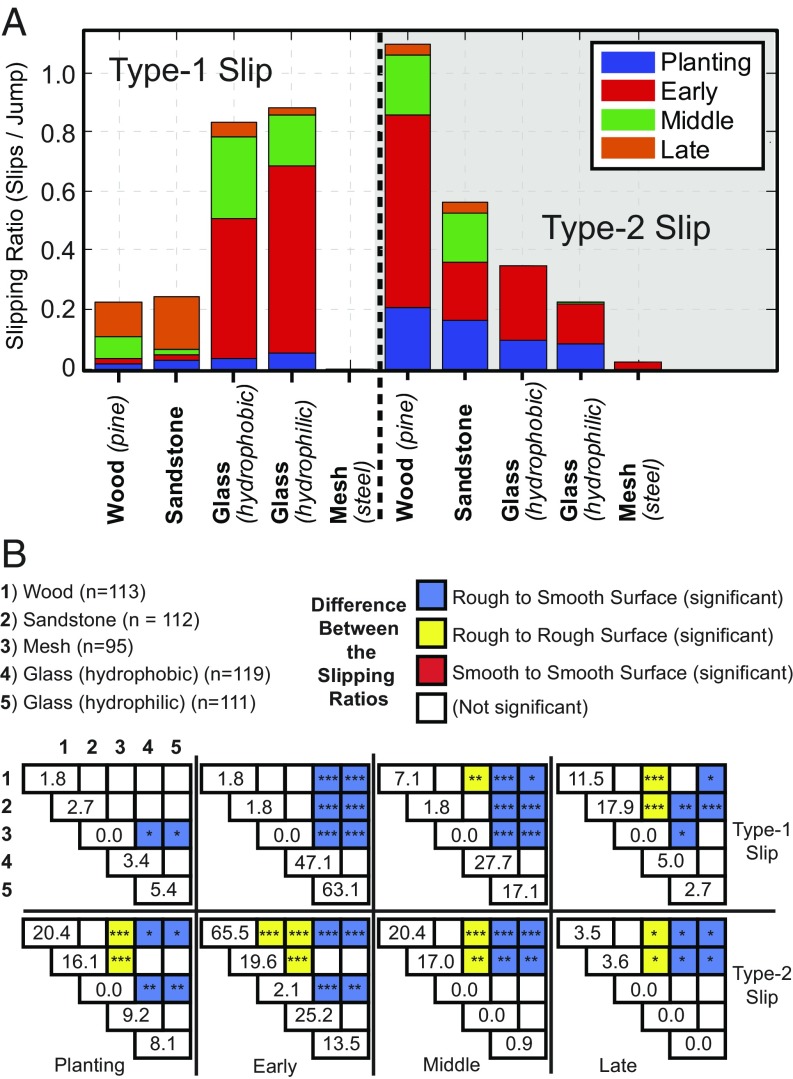
Fig. 4.
Locust experimental results per jump (per-leg rates are half), divided into slip type (type 1 or 2) and energy regions (planting, early, middle, or late). (A) Average slipping ratios (slips/jump) for each slip type on each material. (B) Material significance matrix, which compares the slipping ratios of each material within a single slip type and energy region of A, to determine significance of the differences in the means [e.g., type-1 slip and planting (upper left quadrant) presents the 10 unique significance measures between all five materials]. The diagonal values represent the slipping ratios (slips/jump), where zero values indicate that no slipping events were observed. *P 0.05; **P 0.01; ***P 0.001. n represents the number of trials on each material.
Fig. 6.
Robot experimental results of the SLIP foot. (A) Robotic SLIP foot diagram. (B) Contact jump (glass), where the foot preload is zero (high-speed video snapshots). (C) Noncontact jumps (sandstone), where the foot preload is zero (high-speed video snapshots). A type-3 slip, where the foot loading is greater than the surface friction but does not leave the surface, is shown. Motion of the red circle represents the approximate motion of the feature in the images. (D) Experimental results per jump (per leg rates are half) for the SLIP foot and each constituent part separated into contact and non-contact-type jumps. Feet include: SLIP, complete foot; SLIP-none, no pad or spines (3D-printed ABS pad base); SLIP-pad, no spines; and SLIP-spine, no pad. (E) Robot foot tracking of noncontact jumps, presenting the jumping-axis velocity, slip-axis velocity, and behaviors of symmetric and asymmetric feet, such as reorientation, contact, planting, bouncing, and mechanism traits such as variable cable friction. (F) Robot experiments, for flat and 45° surface angles, showing no loss of jumping performance. Robot experiments at twice the energy (80% increase in energy density due to an additional 13.2 g), comparing the flat performance to that of type-3 slipping on wood at a 45° surface angle, are shown (superimposed high-speed video snapshots).
Results and Discussion
We reasoned that slipping would be common, yet the high probability would suggest very low robustness if not for the discovered possibility to reengage the surface (overall behavior, Fig. 4A; statistical data, Fig. 4B). This discovery, along with that of the noncontact jump behavior (SI Appendix, Fig. S2A), suggests that the morphological adaptations of the locust’s feet are designed for both static and dynamic surface interactions. The lower chance of type-1 slips on the rough surfaces (wood, 0.22 ± 0.44; sandstone, 0.24 ± 0.47; and mesh, 0.0 ± 0.0) compared to the smooth surfaces (hydrophobic glass, 0.83 ± 0.66; and hydrophilic glass, 0.88 ± 0.70) further suggest specialization for spine-based friction. However, whereas early and middle type-1 slips showed pervasive significant differences between the rough and smooth surfaces, the planting type-1 slips did not, suggesting that the two friction mechanisms have equal difficulty interacting dynamically with surfaces (Fig. 4B).
Spines.
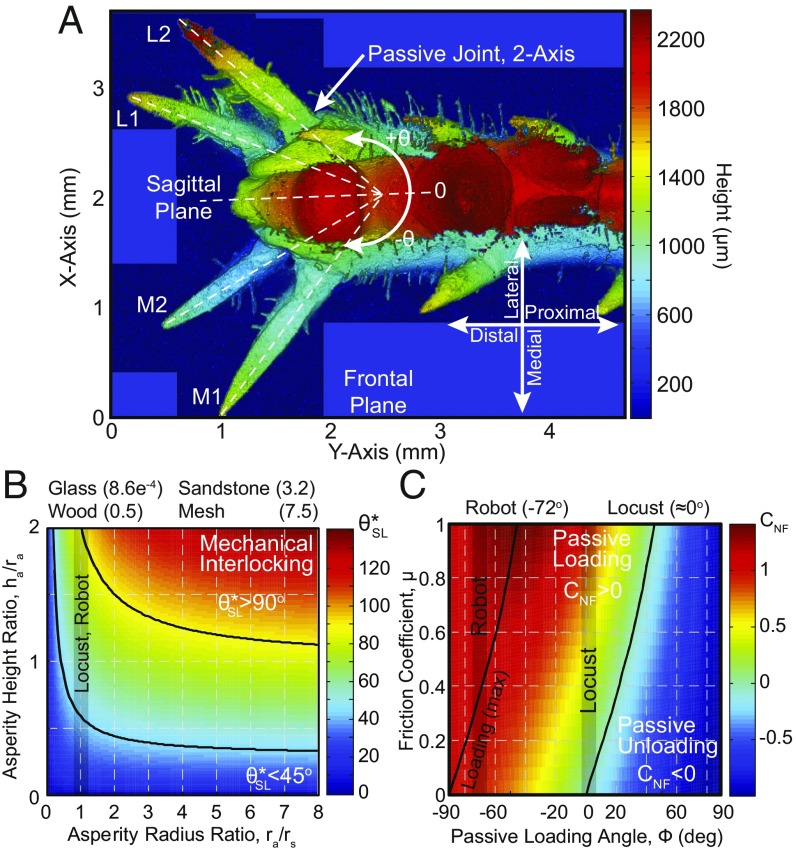
The locust’s spines protrude from the distal end of the tibia, defined by two characteristic angles measured from the leg’s sagittal and frontal planes (Fig. 5A, SI Appendix, Fig. S1 A and B, and Table 2), potentially adapted from those seen on the forefeet (SI Appendix, section S1) and used for rapid running on challenging surfaces (14). Spines are able to enhance friction by interacting with asperities, which have differing angles than that of the overall surface, effectively increasing the loading angle, , to a more surface-perpendicular orientation. We developed a nondimensional model of the spine tip ( = 23.3 13.4 m) and asperity radii, , which predicted that smaller asperities (mean area roughness: wood, m; sandstone, m) should be less stable (Fig. 5B and Spine Interaction), which we reasoned would result in higher slip rates and was confirmed by the locust experiments, in which a significant difference was observed between the mean type-2 slips for wood (1.10 1.13) and sandstone (0.56 0.89), t(212) = 4.0, P = 0.00 (Fig. 4). However, the similar chance of type-1 slips on wood (0.22 0.44) and sandstone (0.24 0.47), t(222) = 0.3, P = 0.74, suggested that the locust’s spines are well developed to find and hold asperities on a broad range of roughnesses and dynamic conditions, resulting in minimal loss of jumping energy.
Fig. 5.
Locust friction mechanisms. (A) The locust’s foot with spines and adhesive pads (3D surface profilometer micrograph). The passive two-axis joint allows for nearly 180° in the sagittal plane and a difference of −10° in the frontal plane. (Magnification: 100.) (B) Spine-asperity interaction plot which determines the potential increases in the effective loading angle as a function of the spine tip radius, , asperity radius, , and asperity height, . The average asperity radius ratios, , of the tested materials are listed above the plot. (C) Adhesive pad interaction plot, which determines the passive loading coefficient, .
Table 2.
Spine characteristics
| Angles to leg planes* | ||
| Spine | Sagittal plane, ° | Frontal plane, ° |
| M1 | −136.8 9.1 | 41.0 ± 7.9 |
| M2 | −155.3 ± 9.5 | 42.6 ± 12.6 |
| L2 | 144.1 8.0 | 47.7 ± 8.4 |
| L1 | 126.3 10.1 | 51.2 8.8 |
L, lateral; M, medial.
The angles are measured from the specified planes.
The spines may be able to penetrate the soft surface of the wood to enhance or create an asperity; however, the decreasing slip rates on increasingly rough surfaces [wood, 1.17 1.17, vs. sandstone, 0.59 0.90, t(210) = 4.2, P = 0.00; sandstone vs. mesh, 0.02 0.14, t(118) = 6.6, P = 0.00] and failure to identify any spine indentations on the wood surface using a 3D surface profilometer suggested that the spines are instead adapted to hold existing asperities. This conclusion was further supported by the discovery of a two-axis passive joint (Fig. 5A), which connects the spine to the tibia. This joint introduces compliance into each spine, allowing each to locate the valley of an asperity through changing its sagittal-plane angle up to 180° and increasing its contact angle by 10°, thus enhancing its hold (45).
Adhesive Pads.
The locust’s first tarsal segment contains three separate adhesive pads (Fig. 1B) which rely on preloading to generate friction (46). However, the spines, attached to the tibia and positioned more distally than the ankle joint, limit the deformation of the relatively soft adhesive pads [effective modulus of 300 kPa (47)] and thus the direct loading (Fig. 5A). The maximum deformation force (45 mN), assuming spherical hertzian contact and complete deformation of the hemispherical pads, is only 32.3% of the maximum load per foot. We therefore reasoned that the foot morphology may indirectly enhance the loading of the pads. This was confirmed by analysis of the torque on the first tarsal segment, where the model (Adhesive Pad Interaction) produced a loading coefficient, , which suggested that the locust can indirectly enhance its pad loading as a function of the friction coefficient (Fig. 5C). The low margin predicted in the model and transition between static and dynamics regimes during slipping, which tends to reduce the interaction strength, would suggest, contrary to our observations (Fig. 4), that reengagement is impossible. The solution may be in the leg structure and jumping behavior of the locust, similar to that of the robotic platform, which produces an increasing force over approximately the first half of the jumping cycle (Fig. 3A). This increase in applied force may be compensating for the reduced interaction strength, making the observed reengagements of the adhesive pads possible.
The desert locust’s adhesive pads secrete an emulsion of “lipidic nano-droplets dispersed in an aqueous liquid” (48) passively during the deformation of its sponge-like cuticle, as with other insects (49). However, the wet adhesion of the locust showed no specialization for hydrophobic or hydrophilic surfaces (natural examples in refs. 50–52), as evidenced by the similar chance of type-1 [hydrophobic glass 0.83 0.66 and hydrophilic glass 0.88 0.70, t(224) = 0.6, P = 0.57] and type-2 [hydrophobic glass 0.34 ± 0.66 and hydrophilic glass 0.23 ± 0.46, t(212) = 1.6, P = 0.11] slips (Fig. 4). This corroborated results for climbing aphids (53) and confirmed a supposition for locusts (48), which suggests that the emulsion can tolerate changes in surface wettability without affecting its overall adhesive properties. Furthermore, as unstable (coalescing) emulsions lead to surface films (demulsification) that may reduce friction (54), the result suggests that either that the locust’s emulsion is stable (dispersed) or renewed sufficiently often to remain dispersed until use. The dispersed droplets each create a lipid–water interface allowing a number of capillary bridges (55, 56) between the foot and surface to form, thereby enhancing friction through contact pinning and viscous forces.
Coupled Attachment Mechanisms.
The difference in the loading behavior corresponds well with the particular needs of each attachment mechanism. Spines effectively increase the contact angle between the foot and surface, reducing the necessary friction coefficient, but still relying on the applied load. Conversely, pad-based friction is a function of both the applied load and the adhesion; however, the normal load required for adhesion is typically at least an order of magnitude less than the frictional force produced for flat adhesives and greater than that for structured adhesives (46, 57, 58). In this way, the locust has developed a strategy, whereby the spines receive the majority of the force to maximize their friction and chance of interlocking, and the adhesive pads rely instead on passive loading to saturate the adhesion and enhance friction.
Balancing the performance of the attachment mechanisms is achieved by changing the configuration, magnitude, and distribution of the locust’s applied forces (applied 200 mN, adhesive pads 45 mN, spines 86 mN; maximum per foot), where the robot (applied 10.8 N, adhesive pads 4.7 N, spines 2.8 N; maximum per foot) had 54 times more force than the locust (Foot Forces), where is the force perpendicular to the surface. First, the robotic “multi-Surface Locust-Inspired Passively-adaptable” (SLIP) foot had both the spines and adhesive pad mounted on the first tarsal segment, allowing both to maintain a prescribed orientation throughout all leg angles, eliminating the loss of spine interaction at low jumping angles and high knee angles (SI Appendix, Fig. S1B). Second, whereas the locust’s 66% of the perpendicular force was not sufficient for penetration of the wood surface, the robot easily penetrated the surface at 37%, allowing for stable mechanical interlocks on the soft wood surface. Finally, the remaining force was then redistributed to the adhesive pads to enhance surface friction on both smooth and rough surfaces. This was confirmed by robotic experiments (Fig. 6 B and C and Robot Experiments) which resulted in no type-1 slips (Fig. 6D, SLIP, and Movie S4). Foot tracking also related much of the type-2 slips to the zero initial foot loading (preload = 0 N), causing planting type-2 slips during the contact and loading period, and variation in mechanism friction, causing early and middle type-2 slips (e.g., Fig. 6E, symmetric, and Robot Experiments).
The non-contact-type jumps, observed in the locust, suggest that the attachment mechanisms are developed for both static and dynamic attachment. This was verified by robotic experiments where the noncontact jumps were accentuated to a misalignment angle of 45° and impact velocities of approximately 3.4 m/s (Fig. 6 C and E, symmetric), resulting in no type-1 slips (Fig. 6D, noncontact); type-2 and -3 (Type-3 Slip) slipping behaviors were slightly increased by the increased dynamics. Furthermore, the constituent parts of the SLIP foot, tested independently (Fig. 6D, SLIP-none, -pad, and -spine), showed the adhesive pad as the primary attachment mechanism on all surfaces and jump conditions, as it was essential in reducing the spine loading, facilitating spine friction on surfaces with low cohesion.
Type-3 Slip.
First observed in the locust (SI Appendix, Fig. S2B and Movie S3), type-3 slips are that of continuous slipping (Fig. 6C), which occurs when the surface-interaction strength is less than the applied load. Only a few occurrences were observed in the locust and only on the glass surfaces, whereas the robot showed a much higher chance of type-3 (contact, 0.60 ± 1.05; noncontact, 1.60 ± 0.84) slips, albeit only on the sandstone surface (Fig. 6D). This suggests that while the maximum forces on the locust’s spines and adhesive pads were both within the limits of the surface materials’ interaction strength, the significant increase in the foot forces of the robot were not. Therefore, requiring the robot to share the load between several spines (30, 45) to reduce the individual interaction forces to that supported by the cohesion of the sandstone grains.
Detachment.
Detachment from the surface is accomplished passively for both mechanisms in the locust and robot. Nonembedded spines simply escape the asperities (e.g., sandstone), whereas embedded spines [e.g., wood (robot only)] have been observed to perturb the foot slightly at liftoff, indicating that a small force was required for removal of the spines. The adhesive pads of both the locust and robot, unlike the gecko’s highly discretized fibrillar adhesives (46), have relatively large, continuous surfaces, limiting intimate surface contact and the adhesive’s ability to resist the propagation of cracks through the interface. The locust was observed to use circumferential peeling of the approximately spherical pads (Fig. 5A), whereas the robot’s large rectangular pad (Fig. 6A) was observed to peel from front to back. In both cases, once peeling was initiated, it quickly propagated through the entire surface, passively separating the two, unlike the gecko, which must actively detach its feet (35).
Foot Asymmetry.
We posited that the locust’s asymmetric foot, while working well for contact jumps, would have difficulty reorienting to significantly misaligned surfaces during noncontact jumps (Fig. 6 C and E, symmetric). This was confirmed by robotic experiments (SI Appendix, Fig. S3), where the initial misalignment was set at 45°, and the foot was not only observed to slip, but also bounced off the surface after the initial contact (Fig. 6E, asymmetric). This was due to a shorter lever-arm, which resulted in increased foot rotational rates (symmetric ≈160 deg/s, asymmetric ≈370 deg/s). This suggests that, although the locust’s foot can plant from short distances, the orientation must be similar to that of the surface, whereas the robot’s symmetric foot morphology can tolerate much greater misalignment.
Rotational Decoupling.
The positioning of the spines and adhesive pads on separate segments, thus decoupling their rotational motions, is integral to the performance of the combined attachment mechanisms. This was confirmed by robotic experiments of several feet where the spines and adhesive pad rotations were coupled and showed significant type-1 slipping (coupled, SI Appendix, Fig. S4; decoupled, Fig. 6). This was potentially caused by the passive loading torque of the adhesive pad, which tends to pull the spines away from the surface; in this case, stiffer thermal plastic pads were used to minimize foot rotation during loading. The locust’s spine orientations were coupled to the leg angle (SI Appendix, Fig. S1B), whereas the robotic SLIP foot had further decoupled the spines, adhesive pad, and leg. This allowed both the spines and adhesive pad to continuously and independently reorient to maintain a desired configuration (Fig. 6F) to passively support dynamic terrestrial locomotion on diverse surfaces.
Jumping Performance.
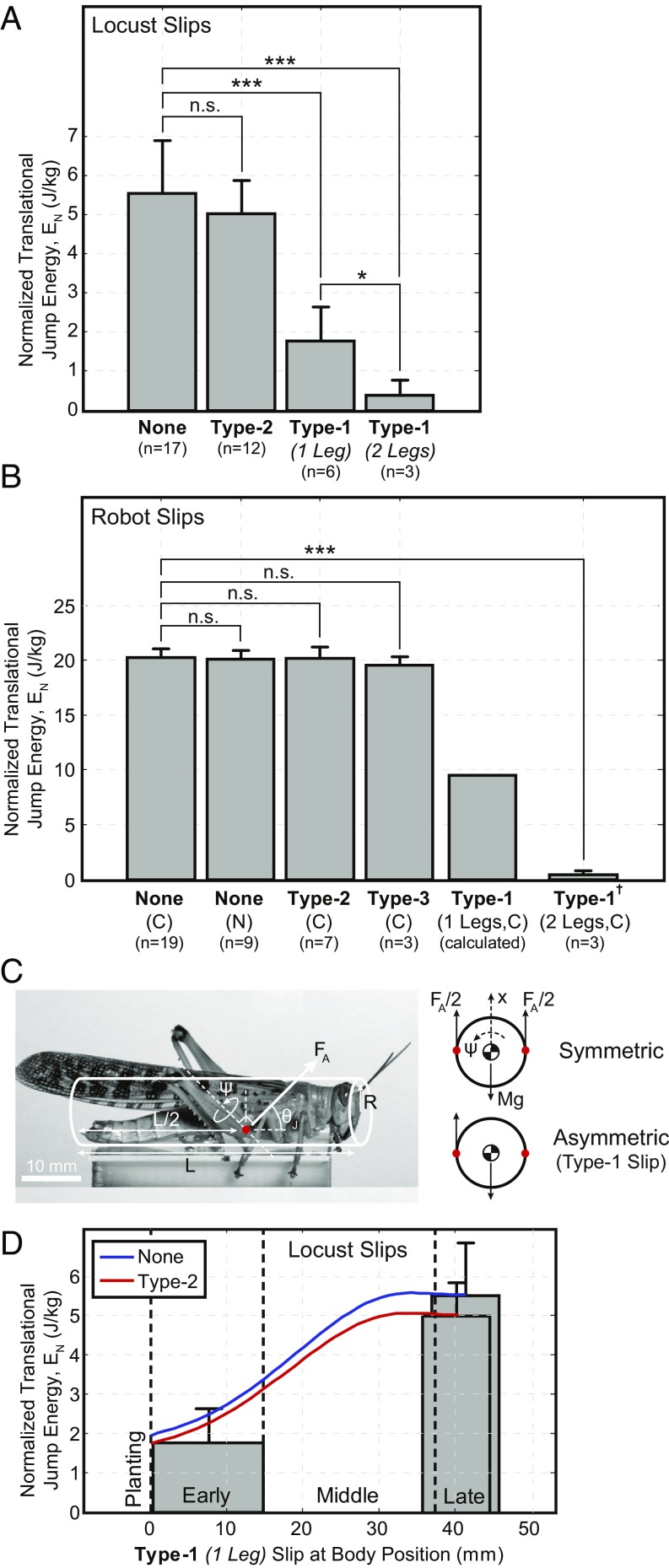
Type-2 slips result in minimal energy loss (Fig. 7 A and B, type-2), as evidenced by the similar normalized translational jumping energies () of the no-slip (none) and type-2 slip cases of the locust, t(27) = 1.26, P = 0.22, and robot, t(9) = 0.09, P = 0.93. Type-3 slips showed similar minimal energy loss in the robot, t(3) = 1.47, P = 0.24; however, these results represented relatively slow foot-sliding velocities, whereas higher velocities may remove significant energy and are left as future work. Unlike the previous, single type-1 slips resulted in significant energy loss [Fig. 7 A and B, type-1 (one leg)], as evidenced by the significant difference in the of the no-slip (none) and type-1 (one leg) slip cases of the locust, t(14) = 7.86, P = 0.00, and robot (calculated, Slip Energy).
Fig. 7.
Mass normalized translational jumping energy () for different types of slips (Trial Details and Slip Energy). (A) Locust: males only. (B) Robot: SLIP foot at a 45° surface angle. † Data are from the SLIP-none foot. (C) Simplified model (Slip Energy) for determining the ratio of translational and rotational energies in the event of a type-1 slip. (D) Locust: estimated as a function of the position, within the jumping cycle, in which a type-1 slip occurs. Assumed jumping angle is 45°. Energy regions (planting, early, middle, or late) are shown for an approximate leg length of 20 mm. Approximate position for the included type-1 (one leg) slip data from A is shown. Notes: Work is measured from jump initiation to foot separation, where each slip type is composed of slips from approximately the early knee angle region, to accentuate the energy losses, and covers all materials in which the behavior was observed. *P 0.05; **P ≤ 0.01; ***P 0.001; n.s., not significant. Variables: number of trials, n; contact-type jump, C; and non-contact-type jump, N.
Type-1 slips may also have an added effect on the jumping performance as they break the sagittal-plane symmetry, common to most animals, introducing a torque on the body (Fig. 7C), as only a single leg is in contact. This was experimentally confirmed by the >50% reduction in the locust’s , observed between the early stage type-1 (one leg) and no-slip (none) cases (Fig. 7A). A simplified model (Fig. 7 C and D and Slip Energy) captured the performance degradation and demonstrated the significance of the slip’s position in the jumping cycle. Earlier slips resulted in not only more energy loss, but more energy converted into rotational, instead of translational, motion, the effect of which was further accentuated by the distance between the leg and center of mass ( body width/2).
In total, each of the locust’s feet can support an average shear force of 149 mN ( 131 mN), whereas the robotic SLIP foot was verified to an average shear force of 7.7 N ( 7.7 N) on the rough and smooth surfaces. The robot experiments verified the attachment mechanisms to a misalignment, or jump, angle of 45°, at which point attachment must rely on more than Coulomb friction. However, with decreasing jump angle ( 45°) comes increasing burden on the attachment mechanisms (), captured by the adhesive and spine-interaction models, requiring enhanced adhesion and spine interaction to maintain attachment.
Summary
This study highlights slipping not as an anomaly, but as part of the dynamic locomotion of the desert locust, yet, in the absence of control, morphological intelligence encoded into the physical system can reduce the severity of many of the slipping events and preserve robust locomotion on diverse surfaces.
Materials and Methods
Animals.
The desert locusts (S. gregaria) were obtained from a local pet store and housed in a terrarium with heat lamp and plentiful food supply. Any stress or nutritional deficiency was abated by a acclimation period of no less than 5 d, where no experimental trials were conducted. Grass was the main source of food provided to the locusts.
Locust Experiments.
The desert locusts were transferred from their main terrarium to an empty acrylic terrarium with a heat lamp and thermometer. The locusts, being cold-blooded, were warmed up to an average temperature of 30.5 °C before being transferred to the testing terrarium. This process also allowed them to clean their adhesive pads, especially important before smooth-surface trials.
An acrylic box was constructed to contain the locusts after each jump, while allowing unrestricted viewing of the event. In the center, a small platform was placed, on which the surface could be modified for testing various parameters of the locust’s jump. The platform dimensions were specifically selected to encourage the locust to align itself perpendicular to the viewing direction. The high-speed digital camera (VisionResearch, Phantom v641) recorded the jumping trials at 1,400 frames per second.
Surface Preparation.
The hydrophilic glass was prepared by cleaning a glass slide with varying polarity solvents; the sequence was as follows: acetone, isopropyl alcohol, deionized water, and argon gas for drying. To fabricate the hydrophobic glass, the surface chemistry of some of the cleaned glass slides was altered through a silanization process as follows: air plasma, immersion in butylamine and methoxy(dimethy) octadecylsilane, and condensation at 80 °C. The advancing and receding contact angles were measured by using a Krüss-Drop Shape Analyzer. The wood, sandstone, and steel mesh were purchased from a local hardware store and cut to proper size. The wood was smooth-cut pine, chosen for its relative softness.
Imaging.
The surface and locust foot morphology plots were generated with a high-resolution 3D surface profilometer (Keyence VK-X200) with and resolutions of 1,390 nm and resolutions of 0.1 nm.
Trial Details.
The selected jump trials each had only a single slip event occurring in the planting or early knee angle ranges, as these would produce the most observable and similar effects in the jumping energy for a given singular slip event. These approximated the worst case for each slip type, where n represents the number of trials.
Figs. 1C, 3A, and 7A had the following surface breakdown per slip type: none: hydrophilic glass (n = 5), sandstone (n = 6), and mesh (n = 6); type 2: hydrophobic glass (n = 1), hydrophilic glass (n = 2), wood (n = 10), and sandstone (n = 3); and type 1 (one leg): hydrophilic glass (n = 4) and sandstone (n = 2), including planting (n = 1), early (n = 3), and middle (n = 2). The middle trials were just after the transition from the early region: type-1 (two leg): hydrophilic glass (n = 6).
Fig. 7B had the following surface breakdown per slip type: none (C): hydrophilic glass (n = 6), wood (n = 9), and sandstone (n = 4); none (N): hydrophilic glass (n = 4), wood (n = 4), and sandstone (n = 1); type 2: hydrophilic glass (n = 5), wood (n = 1), and sandstone (n = 1); type 3: sandstone (n = 3); and type-1 (one leg): hydrophilic glass (n = 1), wood (n = 1), and sandstone (n = 1).
Statistics.
The reported statistical values were obtained from two-sample, two-tailed t tests, where significance, , was defined as P 0.05 with a null hypothesis of equal mean values. The effective degrees of freedom were approximated with the Welch–Satterthwaite equation, and all reported values represent a SD. All reported statistical data follow the following template: t(n1) = n2, P = n3, where is the effective degrees of freedom, is the t-critical value, and is the significance or P value.
Spine Orientation.
Comparing the sagittal-plane angles of the corresponding medial (M) and lateral (L) spines, M1, L1, t(18) = 2.44, P = 0.03, and M2, L2, P = 0.03 and t(17) = 2.86, P = 0.01, showed low significant differences in the angles, whereas the frontal-plane angles only showed a significant difference, albeit low, between M1 and L1, t(18) = 2.85, P = 0.01, indicating only a minor probability of spine asymmetry. However, the angles did indicate that all of the spine would be oriented to interact with the surface during jumping (Table 2).
SI Appendix, Fig. S1B shows the relationship between leg, , spine, , jumping, , and spine loading, , angles, where indicates that the spine tip is no longer able to interact with the surface. The passive joints which connect the spines to the tibia give them the freedom to change their sagittal-plane angle from the initial positions (Table 2) to nearly 180° (SI Appendix, Fig. S1B, SP = 180°). This suggests that the spines can passively locate stable positions on the surface as they are loaded. These joints also allow for approximately −10° of rotation in the frontal plane (SI Appendix, Fig. S1B, FP-10°). Therefore, as the spines are loaded, their effective spine angle is reduced, broadening the leg angle range over which they can interact with the surface. This joint will also include some damping, which can be used to reduce the impulse caused by the spine reengaging after a slip, increasing the chance of a successful reengagement. In all, locusts have developed spines that can interact with the surface even in extreme cases; for example, a horizontal jump ( and initial ) resulted in spine angles of , permitting strong surface interaction. Spine placement, however, typically only allows the more distal medial and lateral spines to interact with the surface.
Spine Interaction.
The performance of spines is strongly related to the roughness characteristics of the surface, spine angle , and spine loading angle . We have included surfaces with overhanging asperities and, for our purposes, will calculate an effective increase to the spine loading angle for round asperities as:
| [1] |
where is the asperity radius ratio, , and is the asperity height ratio, , with asperity radius, , asperity height, , and spine radius, (Fig. 5B). Mechanical interlocking occurs at , whereas reduces the required friction coefficient; for example, results in effective increase in the spine loading angles of and requiring a friction coefficient and , respectively, for a horizontal jump (). A friction coefficient of is within generally achievable limits, demonstrating that even at extreme jumping angles, the locust’s spines greatly enhance the surface friction. We expect the spines to find asperities with increasing likelihood on the wood, sandstone, and mesh. The glass, however, does not produce any usable asperities, and therefore the adhesive pad performance can be isolated.
Adhesive Pad Interaction.
Using the morphology (SI Appendix, Fig. S1A) and summing the torques about pad yields an expression for the torque on segment as follows,
| [2] |
where is the applied ankle force, is the applied ankle torque, and is the distance between and the ankle joint . Then, is the reaction force at pad , is the reaction force at pad , and and are the -distances between pads - and -, respectively. The frictional, , and adhesive, , forces have been substituted in for the applied horizontal force to limit it to that supported by the surface friction. The left side is then related to the applied loads, and the right side, the passive loading of the adhesive pads, where the jumping angle range , - angle range ( is in the -direction), and the friction coefficient determine the loading behavior.
The adhesive force, , can be approximated by the pulloff adhesive force of a flat punch from a flat surface. The maximum force is given by (59),
| [3] |
where the effective pad radius, , effective work of adhesion, , and the elastic moduli and Poisson’s ratios of glass, , and the adhesive pad, , respectively, determine the behavior. The effective work of adhesion of the locust’s pads (6 J/m2) (47) is greater than five times that of the SLIP foot’s adhesive pad material (Ecoflex 00-20, 1.17 0.13 J/m2, Work of Adhesion).
For Eq. 2 to produce a negative torque, unloading the adhesive pads, the normal vs. frictional load coefficient, , must be less than zero, , assuming the adhesion is always attractive. Fig. 5C presents the relationship between the friction coefficient, , and the - angle, , where the optimal - angle is and the transition between loading and unloading is governed by . The highly deformable adhesive pads makes exact measurement of the angle difficult; however, under load, approaches zero. Applied ankle torque, , can be used to increase the pad loading for additional adhesion, whereas pads and will generally not contribute.
Work of Adhesion.
The work of adhesion was calculated directly from measured pull-off force-displacement curves of the soft elastomer foot pads (Smooth-On, Ecoflex 00-20) by using a 4-mm hemispherical indenter. Three separate sites on the material were tested, where an initial set of trials were conducted to allow the adhesion to stabilize before the measurements were taken. Finally, the work of adhesion was calculated by using the measured adhesive force-displacement curve and contact area. The resulting work of adhesion values are as follows: Ecoflex 00-10 = 1.207 0.036 J/m2, Ecoflex 00-20 = 1.168 ± 0.128 J/m2, and thermal plastic = 0.142 ± 0.015 J/m2, whereas from literature, the locust’s work of adhesion was measured as ∼6 J/m247 The locust, however, was measured in a much more idealized configuration. Therefore, the actual value achieved during locomotion may have been much lower, as evidenced by the locust’s poor permanence on smooth surfaces.
Robotic Foot.
The SLIP foot, Fig. 6A, incorporates all of the features extracted from the locust’s foot. The spines are steel pins mounted at a 45° angle and attached to flexural beams [cross-section 1×3 mm ()]—material modulus experimentally determined in SI Appendix, section S3—which allow sufficient freedom to move both horizontally ( mm) and vertically, , to find asperities and strong enough to penetrate soft surfaces to create its own asperities. The elastomeric adhesive pads (Smooth-On, Ecoflex 00-20) are dry, using instead van der Waals forces to eliminate the difficultly of maintaining a fluid on the feet. The pad is symmetric about the ankle joint, with , thus ensuring passive pad loading. The rotational dynamics of the adhesive pad, , and spines, , are decoupled from each other as well as the leg, , allowing each to passively orient to the surface throughout the jump, including during slipping. The loading of the spines and adhesive pad is similar to that of the locust, where the pad must be deformed for the spines to engage the surface. However, as the adhesive pad has a thickness of 1 mm and 100% tensile modulus of 55.2 kPa, initial deformation of the distal region opposite the spines requires little force, allowing the spines to interact immediately. Finally, inspiration is taken from planthopper (Issus) nymphs, which use biologically created gears (60), to synchronize the two sides of the robot’s legs, ensuring the force produced is along the center-of-mass axis (SI Appendix, Fig. S5 B and C).
Foot Forces.
The robot’s spines and adhesive pad forces are determined from the kinematics,
| [4] |
where each is modeled as simple spring and distance before full pad contact, , distance before backing material engagement, , and applied load, , dictate the total foot displacement, . The spring constants are,
| [5] |
where the lever arm parameters, including elastic modulus, MPa, moment of area, m4, and length, m, and the adhesive pad parameters including, elastic modulus, kPa, area, m2, and thickness, m, define the relationships. Finally, the robot’s spine, , and adhesive pad, , forces are defined as,
| [6] |
The locust’s adhesive pad force is determined by the hertz contact model of two elastic spheres,
| [7] |
where the radii, m and , Poisson’s ratios, and , and tensile moduli, kPa and , for the adhesive pad and surface, respectively, and the assumed full hemisphere deformation, , determine the pad loading. Then, subtraction from the total applied force, , determines the locust’s spine loading.
The applied force, , during jumping is calculated through feature tracking (custom Matlab software) for the locust and robot.
Robot Experiments.
To experimentally characterize the performance of the SLIP foot, a specific series of trials were conducted at a jumping angle of , at which point the necessary friction coefficient is difficult to achieve using the traditional Coulomb friction model. A dynamically similar jumping rig, SI Appendix, Fig. S5A, was used to facilitate observation (VisionResearch, Phantom v641) of the foot and uniform testing (Dynamics). The testing sequence was as follows: glass, sandstone, wood, and glass, where 10 trials were conducted for, first, the noncontact and, then, contact-type jumps on each surface in the sequence, where the approximate foot impact velocity was 3.4 and 0 m/s, respectively. The order was designed to challenge the SLIP foot, as no modifications or cleaning were conducted between trials; the glass and sandstone could dull or damage the spines, whereas the sandstone and wood could contaminate and damage the adhesive. The order ensured that each material was tested after the SLIP foot had undergone jumps which could reduce the performance of the primary attachment mechanism.
The robot showed much more deterministic jumping behavior than that of the locust (SLIP foot, Fig. 6; coupled foot, SI Appendix, Fig. S4). As the preloading of the locust’s foot is unknown, the contact jump experiments were conducted at zero preload to simulate the most difficult situation. However, as both attachment mechanisms required some applied load to create friction, an initial slip (planting type 2) was regularly observed during the period before sufficient friction had been created to resist slipping. Type-3 slips were only observed in the sandstone, with higher occurrence in the more dynamic noncontact jumps. These produced a slip of approximately 1.5–2.5 cm, observed as approximately linear scratches in the sandstone, resulting in only a minor loss of energy.
The high occurrence of early type-2 slips for noncontact jumps (Fig. 6) is caused by the energy storage mechanism and not the foot morphology. Fig. 6E demonstrates the typical sudden drop-off in foot velocity which precedes the slip event; this is observed as the foot pulling away from the surface. It is caused by nonuniform friction in the cable mechanism which is accentuated by the sudden velocity changes of the non-contact-type jump, as evidenced by the higher early type-2 slip rates of noncontact jumps. This further challenges the SLIP feet to interact with the surface, and we would expect improved results if the legs were locked and the cable unwound before the jump.
Finally, the SLIP feet were tested on the MultiMo-Bat (Fig. 6F) to validate the system integration and performance. The MultMo-Bat was tested first on a flat Acrylonitrile butadiene styrene (ABS) surface and then on angled () glass, sandstone, and wood surfaces, where the behavior matched that of the constrained jumping rig trials (Fig. 6F). Body posture on the angled surface, as with the locust, was maintained through a combination of foot and body contacts. The MultiMo-Bat produced a maximum jumping height of 2.75 m, with similar jumping heights for all cases, where the jumping energy density (J/kg) is approximately equal to the jumping rig. Increasing the jumping energy density by 80% (Fig. 6F) propelled the MultiMo-Bat up to the maximum height of 4.52 m. Continued slipping was observed on the angled wood surface due to the significant increase in tip loading; however, the passive confirmation of the SLIP foot allowed the MultiMo-Bat to extract sufficient energy to propel itself up to heights >4 m.
Dynamics.
To analyze the robotic foot’s interaction with the surface, a jumping rig was developed which simulates the dynamics of the robot, but within a more observable configuration. The configuration, SI Appendix, Fig. S5 A and B, was designed to be dynamically similar to that of the robot, SI Appendix, Fig. S5C, which is governed by
| [8] |
whereas the jumping rig is governed by
| [9] |
where and represent to position of the two masses, main body, g, and foot, g. The robot’s N/m and mm are the stiffness of the main power spring and the leg length, respectively. The ground interaction is governed by N/m and Ns/m, which are the stiffness and damping coefficient, respectively. Note that all values represent half of the robot, as only one leg is being tested. The ground stiffness was chosen to be arbitrarily large compared with , whereas the damping coefficient was calculated from the experimentally determined coefficient of restitution, , of the 3D-printed ABS material (Stratasys uPrintSE Plus, ABSplus), discussed in SI Appendix, section S3. The gravitational potential contributed little to the jumping dynamics, as the accelerations were an order of magnitude greater over short periods ([25,50] ms) (Fig. 3A). Therefore, the orientation of the trials played an insignificant role in the dynamics during the foot contact.
A comparison of the dynamics, SI Appendix, Fig. S5D, showed good agreement between the magnitude and damping responses of the testing rig and the robot, with only a small variation in the bouncing frequency of the foot (SI Appendix, section S2).
Slip Energy.
The mass normalized translational jump energies, presented in Fig. 7 A and B, were calculated by numerical integration (trapezoidal rule) from the acceleration data. To ensure uniformity, only male trials were included (Trial Details).
Assuming the locust as a uniform cylinder, the rotational inertia () as a function of jumping angle () is calculated as follows,
| [10] |
where the length of the body (), effective radius (), jumping angle (), effective density (), and mass () define the relationship. The variation in the rotational inertia comes from the assumption that a type-1 slip would hinder the locust’s ability to properly align its body. The ratio of the translational to total energy, , caused by a type-1 slip, for the locust is then,
| [11] |
and the robot, having constant rotational inertia (), is then,
| [12] |
where the translational energy (), rotational energy (), applied force (), and the gravitational constant ( m/s2) define the ratios. These allow for estimation of the effects of a type-1 slip (locust, Fig. 7B) at different points of the jumping cycle, from the no-slip (none) cases presented in Fig. 7 A and C as,
| [13] |
where the body position at the onset of the type-1 slip (), body position at liftoff (), and body position along motion axis () define the behavior. Comparing the normalized translational jumping energy of the predicted and actual type-1 (one leg) slips of the locust shows good agreement (Fig. 7D), which allows for approximation of the effect to the robotic platform [Fig. 7B, type-1 (one leg)].
Supplementary Material
Acknowledgments
We thank Byung-Wook Park for creation of the hydrophobic glass surfaces, Dirk Drotlef for work of adhesion measurements, and Davide Bray for assistance with the biological experiments. This work is supported by the Max Planck Society.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1804239115/-/DCSupplemental.
References
- 1.Dickinson MH, et al. How animals move: An integrative view. Science. 2000;288:100–106. doi: 10.1126/science.288.5463.100. [DOI] [PubMed] [Google Scholar]
- 2.Noh M, Kim SW, An S, Koh JS, Cho KJ. Flea-inspired catapult mechanism for miniature jumping robots. IEEE Trans Rob. 2012;28:1007–1018. [Google Scholar]
- 3.Kovac M, Fuchs M, Guignard A, Zufferey JC, Floreano D. A miniature 7g jumping robot. IEEE International Conference on Robotics and Automation. 2008:373–378. [Google Scholar]
- 4.Beck A, et al. Jump stabilization and landing control by wing-spreading of a locust-inspired jumper. Bioinspiration Biomimetics. 2017;12:066006. doi: 10.1088/1748-3190/aa8ceb. [DOI] [PubMed] [Google Scholar]
- 5.Zhao J, et al. MSU jumper: A single-motor-actuated miniature steerable jumping robot. IEEE Trans Rob. 2013;29:602–614. [Google Scholar]
- 6.Lambrecht BGA, Horchler AD, Quinn RD. A small, insect-inspired robot that runs and jumps. IEEE/RSJ International Conference on Intelligent Robots and Systems. 2005:40–45. [Google Scholar]
- 7.Spröwitz A, et al. Towards dynamic trot gait locomotion: Design, control, and experiments with cheetah-cub, a compliant quadruped robot. Int J Rob Res. 2013;32:932–950. [Google Scholar]
- 8.Ananthanarayanan A, Azadi M, Kim S. Towards a bio-inspired leg design for high-speed running. Bioinspiration Biomimetics. 2012;7:046005. doi: 10.1088/1748-3182/7/4/046005. [DOI] [PubMed] [Google Scholar]
- 9.Seok S, et al. Design principles for energy-efficient legged locomotion and implementation on the MIT cheetah robot. IEEE/ASME Trans Mechatronics. 2014;20:1117–1129. [Google Scholar]
- 10.Raibert M, Blankespoor K, Nelson G, Playter R. BigDog, the rough-terrain quadruped robot. IFAC Proc Vol. 2008;17:10822–10825. [Google Scholar]
- 11.Pearson K, Franklin R. Characteristics of leg movements and patterns of coordination in locusts walking on rough terrain. Int J Rob Res. 1984;3:101–112. [Google Scholar]
- 12.Goldman DI, Chen TS, Dudek DM, Full RJ. Dynamics of rapid vertical climbing in cockroaches reveals a template. J Exp Biol. 2006;209:2990–3000. doi: 10.1242/jeb.02322. [DOI] [PubMed] [Google Scholar]
- 13.Sponberg S, Full RJ. Neuromechanical response of musculo-skeletal structures in cockroaches during rapid running on rough terrain. J Exp Biol. 2008;211:433–446. doi: 10.1242/jeb.012385. [DOI] [PubMed] [Google Scholar]
- 14.Spagna JC, Goldman DI, Lin PC, Koditschek DE, Full RJ. Distributed mechanical feedback in arthropods and robots simplifies control of rapid running on challenging terrain. Bioinspiration Biomimetics. 2007;2:9–18. doi: 10.1088/1748-3182/2/1/002. [DOI] [PubMed] [Google Scholar]
- 15.Autumn K, Dittmore A, Santos D, Spenko M, Cutkosky M. Frictional adhesion: A new angle on gecko attachment. J Exp Biol. 2006;209:3569–3579. doi: 10.1242/jeb.02486. [DOI] [PubMed] [Google Scholar]
- 16.Autumn K, et al. Evidence for van der Waals adhesion in gecko setae. Proc Natl Acad Sci USA. 2002;99:12252–12256. doi: 10.1073/pnas.192252799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Spence AJ, Revzen S, Seipel J, Mullens C, Full RJ. Insects running on elastic surfaces. J Exp Biol. 2010;213:1907–1920. doi: 10.1242/jeb.042515. [DOI] [PubMed] [Google Scholar]
- 18.Li C, Umbanhowar P, Komsuoglu H, Koditschek D, Goldman D. Sensitive dependence of the motion of a legged robot on granular media. Proc Natl Acad Sci USA. 2009;106:3029–3034. doi: 10.1073/pnas.0809095106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Marvi H, et al. Sidewinding with minimal slip: Snake and robot ascent of sandy slopes. Science. 2014;346:224–229. doi: 10.1126/science.1255718. [DOI] [PubMed] [Google Scholar]
- 20.Li C, Hsieh ST, Goldman DI. Multi-functional foot use during running in the zebra-tailed lizard (Callisaurus draconoides) J Exp Biol. 2012;215:3293–3308. doi: 10.1242/jeb.061937. [DOI] [PubMed] [Google Scholar]
- 21.Li C, Zhang T, Goldman DI. A terradynamics of legged locomotion on granular media. Science. 2013;339:1408–1412. doi: 10.1126/science.1229163. [DOI] [PubMed] [Google Scholar]
- 22.Mazouchova N, Umbanhowar PB, Goldman DI. Flipper-driven terrestrial locomotion of a sea turtle-inspired robot. Bioinspiration Biomimetics. 2013;8:026007. doi: 10.1088/1748-3182/8/2/026007. [DOI] [PubMed] [Google Scholar]
- 23.Maladen RD, Ding Y, Li C, Goldman DI. Undulatory swimming in sand: Subsurface locomotion of the sandfish lizard. Science. 2009;325:314–318. doi: 10.1126/science.1172490. [DOI] [PubMed] [Google Scholar]
- 24.Dorgan KM, Jumars PA, Johnson B, Boudreau BP, Landis E. Burrow extension by crack propagation. Nature. 2005;433:475. doi: 10.1038/433475a. [DOI] [PubMed] [Google Scholar]
- 25.Dorgan KM. The biomechanics of burrowing and boring. J Exp Biol. 2015;218:176–183. doi: 10.1242/jeb.086983. [DOI] [PubMed] [Google Scholar]
- 26.Li C, et al. Terradynamically streamlined shapes in animals and robots enhance traversability through densely cluttered terrain. Bioinspiration Biomimetics. 2015;10:046003. doi: 10.1088/1748-3190/10/4/046003. [DOI] [PubMed] [Google Scholar]
- 27.Jayaram K, Full RJ. Cockroaches traverse crevices, crawl rapidly in confined spaces, and inspire a soft, legged robot. Proc Natl Acad Sci USA. 2016;113:E950–E957. doi: 10.1073/pnas.1514591113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hosoi A, Goldman DI. Beneath our feet: Strategies for locomotion in granular media. Annu Rev Fluid Mech. 2015;47:431–453. [Google Scholar]
- 29.Bayley TG, Sutton GP, Burrows M. A buckling region in locust hindlegs contains resilin and absorbs energy when jumping or kicking goes wrong. J Exp Biol. 2012;215:1151–1161. doi: 10.1242/jeb.068080. [DOI] [PubMed] [Google Scholar]
- 30.Desbiens AL, Asbeck AT, Cutkosky MR. Landing, perching and taking off from vertical surfaces. Int J Rob Res. 2011;30:355–370. [Google Scholar]
- 31.Paul S, Mckenzie C, Parness A. Video summary of D.R.O.P. the durable reconnaissance and observation platform. 2012 IEEE International Conference on Robotics and Automation. 2012:3535–3536. [Google Scholar]
- 32.Pope MT, et al. A multimodal robot for perching and climbing on vertical outdoor surfaces. IEEE Trans Rob. 2016;33:38–48. [Google Scholar]
- 33.Birkmeyer P, Gillies AG, Fearing RS. Dynamic climbing of near-vertical smooth surfaces. IEEE/RSJ International Conference on Intelligent Robots and Systems 2012 [Google Scholar]
- 34.Hawkes EW, Eason EV, Asbeck AT, Cutkosky MR. The gecko’s toe: Scaling directional adhesives for climbing applications. IEEE/ASME Trans Mechatronics. 2013;18:518–526. [Google Scholar]
- 35.Kim S, et al. Smooth vertical surface climbing with directional adhesion. IEEE Trans Rob. 2008;24:65–74. [Google Scholar]
- 36.Murphy MP, Kute C, Menguc Y, Sitti M. Waalbot II: Adhesion recovery and improved performance of a climbing robot using fibrillar adhesives. Int J Rob Res. 2011;30:118–133. [Google Scholar]
- 37.Bennet-Clark HC. The energetics of the jump of the locust Schistocerca gregaria. J Exp Biol. 1975;63:53–83. doi: 10.1242/jeb.63.1.53. [DOI] [PubMed] [Google Scholar]
- 38.Heitler WJ. The locust jump III. Structural specializations of the metathoracic tibiae. J Exp Biol. 1977;67:29–36. [Google Scholar]
- 39.Pearson KG, Stein RB, Malhotra SK. Properties of action potentials from insect motor nerve fibres. J Exp Biol. 1970;53:299–316. doi: 10.1242/jeb.53.2.299. [DOI] [PubMed] [Google Scholar]
- 40.Hawlena D, Kress H, Dufresne ER, Schmitz OJ. Grasshoppers alter jumping biomechanics to enhance escape performance under chronic risk of spider predation. Funct Ecol. 2011;25:279–288. [Google Scholar]
- 41.Gabriel JM. The development of the locust jumping mechanism II. Energy storage and muscle mechanics. J Exp Biol. 1985;118:327–340. [Google Scholar]
- 42.Dai Z, Gorb SN, Schwarz U. Roughness-dependent friction force of the tarsal claw system in the beetle Pachnoda marginata (Coleoptera, Scarabaeidae) J Exp Biol. 2002;205:2479–2488. doi: 10.1242/jeb.205.16.2479. [DOI] [PubMed] [Google Scholar]
- 43.Woodward MA, Sitti M. Design of a miniature integrated multi-modal jumping and gliding robot. IEEE/RSJ International Conference on Intelligent Robots and Systems. 2011:556–561. [Google Scholar]
- 44.Woodward MA, Sitti M. MultiMo-Bat: A biologically inspired integrated jumping-gliding robot. Int J Rob Res. 2014;33:1511–1529. [Google Scholar]
- 45.Asbeck AT, Kim S, Cutkosky MR, Provancher WR, Lanzetta M. Scaling hard vertical surfaces with compliant microspine arrays. Int J Rob Res. 2006;25:1165–1179. [Google Scholar]
- 46.Murphy MP, Aksak B, Sitti M. Gecko-inspired directional and controllable adhesion. Small. 2009;5:170–175. doi: 10.1002/smll.200801161. [DOI] [PubMed] [Google Scholar]
- 47.Goodwyn PP, Peressadko A, Schwarz H, Kastner V, Gorb S. Material structure, stiffness, and adhesion: Why attachment pads of the grasshopper (Tettigonia viridissima) adhere more strongly than those of the locust (Locusta migratoria) (Insecta: Orthoptera) J Comp Physiol A. 2006;192:1233–1243. doi: 10.1007/s00359-006-0156-z. [DOI] [PubMed] [Google Scholar]
- 48.Vötsch W, et al. Chemical composition of the attachment pad secretion of the locust Locusta migratoria. Insect Biochem Mol Biol. 2002;32:1605–1613. doi: 10.1016/s0965-1748(02)00098-x. [DOI] [PubMed] [Google Scholar]
- 49.Dirks JH, Federle W. Mechanisms of fluid production in smooth adhesive pads of insects. J R Soc Interface. 2011;8:952–960. doi: 10.1098/rsif.2010.0575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Koch K, Barthlott W. Superhydrophobic and superhydrophilic plant surfaces: An inspiration for biomimetic materials. Philos Trans R Soc. 2009;367:1487–509. doi: 10.1098/rsta.2009.0022. [DOI] [PubMed] [Google Scholar]
- 51.Koch K, Bhushan B, Barthlott W. Multifunctional surface structures of plants: An inspiration for biomimetics. Prog Mater Sci. 2009;54:137–178. [Google Scholar]
- 52.Feng L, et al. Super-hydrophobic surfaces: From natural to artificial. Adv Mater. 2002;14:1857–1860. [Google Scholar]
- 53.Dixon AFG, Croghan PC, Gowing RP. The mechanism by which aphids adhere to smooth surfaces. J Exp Biol. 1990;152:243–253. [Google Scholar]
- 54.Dresselhuis DM, van Aken GA, de Hoog EHA, Cohen Stuart MA. Direct observation of adhesion and spreading of emulsion droplets at solid surfaces. Soft Matter. 2008;4:1079–1085. doi: 10.1039/b718891a. [DOI] [PubMed] [Google Scholar]
- 55.Bibette J, Mason TG, Gang H, Weitz DA, Poulin P. Structure of adhesive emulsions. Langmuir. 1993;9:3352–3356. [Google Scholar]
- 56.Lee M, Kim B, Kim J, Jhe W. Noncontact friction via capillary shear interaction at nanoscale. Nat Commun. 2015;6:7359. doi: 10.1038/ncomms8359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Kim S, Aksak B, Sitti M. Enhanced friction of elastomer microfiber adhesives with spatulate tips. Appl Phys Lett. 2007;91:89–92. [Google Scholar]
- 58.Gravish N, Wilkinson M, Autumn K. Frictional and elastic energy in gecko adhesive detachment. J R Soc Interface. 2008;5:339–348. doi: 10.1098/rsif.2007.1077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Aksak B, Murphy MP, Sitti M. Adhesion of biologically inspired vertical and angled polymer microfiber arrays. Langmuir. 2007;23:3322–3332. doi: 10.1021/la062697t. [DOI] [PubMed] [Google Scholar]
- 60.Burrows M, Sutton G. Interacting gears synchronize propulsive leg movements in a jumping insect. Science. 2013;341:1254–1256. doi: 10.1126/science.1240284. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.