Abstract
Outcome-dependent sampling (ODS) scheme is a cost-effective way to conduct a study. For a study with continuous primary outcome, an ODS scheme can be implemented where the expensive exposure is only measured on a simple random sample and supplemental samples selected from 2 tails of the primary outcome variable. With the tremendous cost invested in collecting the primary exposure information, investigators often would like to use the available data to study the relationship between a secondary outcome and the obtained exposure variable. This is referred as secondary analysis. Secondary analysis in ODS designs can be tricky, as the ODS sample is not a random sample from the general population. In this article, we use the inverse probability weighted and augmented inverse probability weighted estimating equations to analyze the secondary outcome for data obtained from the ODS design. We do not make any parametric assumptions on the primary and secondary outcome and only specify the form of the regression mean models, thus allow an arbitrary error distribution. Our approach is robust to second- and higher-order moment misspecification. It also leads to more precise estimates of the parameters by effectively using all the available participants. Through simulation studies, we show that the proposed estimator is consistent and asymptotically normal. Data from the Collaborative Perinatal Project are analyzed to illustrate our method.
Keywords: biased sampling, estimating equation, missing data, secondary analysis, semiparametric estimation, validation sample
1 | INTRODUCTION
In many epidemiology studies, the primary outcome variable is easy to obtain, while some exposure variables are expensive or difficult to measure. This motivates statisticians to develop outcome-dependent sampling (ODS) designs, in which the selection probability depends on the primary outcome variable. The main idea of such ODS designs is to concentrate resources on those participants that are more informative in explaining the outcome/exposure relationship. The case-control design has been widely used for studies with a binary primary outcome.1 Prentice2 proposed a case-cohort study design for failure time regression analysis. Zhou et al3 considers an ODS design for data with a continuous primary outcome: In their design, in addition to a simple random sample (SRS) from the full cohort, 2 supplemental SRSs are drawn from 2 tails of the outcome distribution. The initial SRS from the entire cohort provides information about the overall population, and supplemental samples allow investigators to oversample those participants that are more informative about the exposure-response relationship. One example of such ODS design is the Collaborative Perinatal Project (CPP).3,4 The main purpose of CPP is to study the relationship between in utero exposure to polychlorinated biphenyls (PCBs) and multiple neurological outcomes, including children’s IQ performance. As PCB level is expensive to ascertain, an ODS scheme is adopted: An SRS is taken, and 2 supplemental samples are chosen from 2 tails of the IQ distribution. Related works on ODS to evaluate the association between expensive exposure and the primary outcome variable include Zhou et al,3,10,11 Weaver and Zhou,5 Wang and Zhou,6,8 Song et al,7 and Qin and Zhou.9
In any real studies, it is typical that there are more than 1 endpoint of interest. As such, investigators would like to reuse the ODS data to study the association between a secondary outcome and the obtained exposure variable. For example, in the CPP data, investigators are also interested in examining the relationship between PCB level and children’s birth weight. Many prior studies have tried to assess the association between these 2 measures, and yet so far have failed to reach a consistent conclusion.12–18 With CPP data collected in the first place using an ODS design to evaluate children’s IQ and PCB level, we are interested in adding some evidence to this research problem by developing a valid and precise method for secondary analysis under ODS designs.
In this paper, we develop a method for conducting secondary analysis under continuous outcome ODS design described by Zhou et al.3 As the data obtained from ODS design is not a random sample of the overall population, performing secondary analysis is not straightforward. Ignoring the biased sampling nature of the data could yield an invalid estimate of the true parameters in the general population. The analysis restricted to the participants in the SRS portion is clearly inefficient as it underuses the available data. A significant amount of work was done on secondary analysis in case-control data. This includes the likelihood-based methods,19–21 inverse probability weighting (IPW),22,23 and estimating equation.24,25 However, to the best of our knowledge, there has been no research conducted on the secondary regression analysis in the continuous outcome ODS design framework.
We propose estimating equation approaches to analyze a secondary outcome for data obtained from an ODS design with a continuous primary outcome. The advantage of our approach is that no additional model assumptions are specified. The augmented estimating equation utilizes the available information in the full cohort, and hence increases estimation precision. In addition, our method is computationally stable and fast. The organization of the paper is as follows. In Section 2, we present some notations, data structure and our model under ODS designs. In Section 3, we propose two estimating equations, IPW estimating equation and augmented IPW estimating equation. We give the corresponding asymptotic properties in Section 4. In Section 5, we present the simulation results that compare our proposed estimator to other competing estimators. In Section 6, we apply our methods to CPP data to study the relationship between children’s birth weight and maternal PCB level. We conclude this paper by a brief discussion in Section 7.
2 | DATA STRUCTURE AND MODEL
To fix notation, let Y1 be the primary continuous outcome variable that the ODS sampling scheme is based on. Let X be the expensive exposure, which is only observed for some participants, and Z be the vector of other covariates that are easy to obtain. Furthermore, let Y2 denote a continuous secondary response. Our interest lies in inference of the secondary response Y2 with respect to X adjusting for other covariates Z for data obtained from continuous outcome ODS design.
We partition the domain of Y1 into a union of 3 mutually exclusive intervals: A1∪A2∪A3 = (−∞, a]∪(a, b]∪(b, +∞). We assume that the underlying data {(Y1, Y2, X, Z), i = 1, …, N} are independent and identically distributed random vectors, with N be the size of the full cohort. The ODS design proposed by Zhou et al3 can be regarded as a 2-phase design: In the first phase, information on primary outcome, secondary outcome, and inexpensive covariates are observed for each member of the full cohort. That is, we observe {(Y1i, Y2i, Zi), i = 1, …, N}. In the second phase, the expensive exposure X is measured on an SRS of size n0 from the full cohort and 2 supplemental SRSs drawn from 2 tails of the distribution of Y1, ie, supplemental sample of size n1 from {Y1∈A1} and supplemental sample of size n3 from {Y1∈A3}. Let V0, V1, V3 be the index set of SRS, supplemental sample taken from {Y1 ≤ a}, and supplemental sample taken from {Y1 > b}, respectively. That is to say, we observe {Xi, i ∈ V0∪V1∪V3} in the second phase. Here, the sample sizes n0, n1, and n3 are fixed by design. Note that we use fixed-size sampling (sampling without replacement) for both the initial SRS and the supplemental samples. When stratum sizes (ie, number of participants in A1 and A3) are very large, it is equivalent to independent Bernoulli sampling, as the stratum specific sampling probabilities are effectively fixed.
Let V = V0∪V1∪V3, and let nV be the size of V. Then, nV = n0+ n1 + n3. Using terminology from measurement error literature, these nV observations are called validation sample. In addition, we let . We refer to the observations as the nonvalidation sample because expensive exposure X is not measured for these individuals. Let represent the index set of the nonvalidation sample, and ri be the indicator variable of observing X for participant i, then V={i : r=1} and .
The data structure for the ODS design can be summarized as the following:
| (1) |
Let μ1i = E(Y1i | Xi, Zi) and μ2i = E(Y2i | Xi, Zi) denote the conditional expectation of Y1i and Y2i given the covariates, respectively. In most problems, we are interested in estimating the regression coefficients (β, γ) from the following 2 models:
| (2) |
where g1(·) and g2(·) are specified link functions, such as g(x) = x for linear regression. Without loss of generality, we use the identity link g1(x) = g2(x) = x to illustrate our ideas throughout the paper. It is also worth mentioning that no distributional assumptions are made about y1i and y2i. Since analysis on secondary outcome is our primary goal, we focus on developing an inference procedure for (γ0, γ1, γ2).
3 | ESTIMATING EQUATION APPROACH
3.1 | Inverse probability weighted estimating equation
Let ξ = (β, γ). Since we do not make any parametric assumptions about Y1 and Y2, no likelihood-based approaches are available. Let ei = (e1i, e2i)′ = (Y1i − μ1i, Y2i − β2)′. Following the ideas from Horvitz and Thompson, Liang and Zeger, and Zhao et al,26–28 we first propose an IPW estimating equation that uses the validation sample only:
| (3) |
where Q is the covariance matrix of (Y1, Y2), ie, Q = Cov(Y1, Y2), πi is the probability of being selected into the validation sample for each participant i, and
The selection probability πi is a function of the observed outcome value Y1i. Let V0,k be the index set of the observations in the SRS that belongs to the kth stratum Ak. That is, V0 = V0,1 ∪ V0,2 ∪ V0,3. Then, πi can be expressed as follows:
For complex sampling designs, such as the ODS design described in this paper, it is difficult to express πi in explicit forms. We cannot directly solve Equation 3 as the covariance matrix Q, and the selection probability π is unknown. Hence, the general idea is to plug in consistent estimators of Q and π into S1(ξ, Q, π) to get and then solve the equation Ŝ1(ξ) = 0.
Because Y1 and Y2 are observed for each member of the full cohort, a consistent estimator of the covariance matrix Q is the sample covariance derived from the full cohort. That is,
where and are sample means for Y1 and Y2, respectively.
Let Nk, k = 1, 2, 3 be the number of observations in the full cohort that belong to the kth stratum Ak. Similarly, let n0,k, k = 1, 2, 3 be the number of observations in the SRS that belong to stratum Ak. That is, N = N1+N2+N3, n0 = n0,1+n0,2+n0,3. Then for each participant, the observed probability of being sampled within its respective strata Ak can be written as
It is straightforward to show that is a consistent estimator for πi. Hence, our first proposed estimator satisfies the following estimating Equation 4 and can be obtained using Newton-Raphson algorithm.
| (4) |
3.2 | Augmented inverse probability weighted estimating equation
The weighted estimating equation 4 described above may not be precise as it uses only the information contained in the validation sample where the expensive exposure X is observed. Following the ideas from Robins et al,29 an augmented estimating equation can be used. Let ui be any kernel function, and let h(y1i, y2i, zi) be any function, then
is an augmented estimating equation. Any choice of h(·) would lead to a consistent estimate of the parameters. This comes from the fact that
However, an optimal choice of h(·) would improve the estimation precision. From Robins et al,29 it is shown that the optimal h(·) should be the conditional expectation of the kernel function given the observed data, ie, h(y1i, y2i, zi) = E(ui|y1i, y2i, zi).
Following this line of reasoning, we propose the following augmented IPW (AIPW) estimating equation based on estimating equation 3:
| (5) |
Notice that the augmented estimating equation 5 incorporates all the information available in the full cohort, including those observations in the nonvalidation sample. To use estimating equation 5, one needs to assume a form of the conditional moments, ie, E(Xi | Y1i, Y2i, Zi) and . As the expensive exposure variable is often on a continuous scale, it is reasonable to assume that
and
Then, the second-order moment can be expressed through the conditional mean and conditional variance as .
Let ϕ = (ϕ0, ϕ1, ϕ2, ϕ3). We notice that S2(ξ, Q, π, ϕ, σ2) has several components, in which ξ is the parameter of interest and (Q, π, ϕ, σ2) are nuisance parameters. The following summarizes the steps on how to conduct the analysis:
Fit a linear regression to obtain parameter estimates for (ϕ, σ2) based on the SRS portion of the data.
As outlined in Section 3.1, obtain the consistent estimator , for Q and π.
- Plug into S2 to obtain . Our second proposed estimator is the solution to the following augmented IPW estimating equation:
(6)
Note that how to estimate (Q, π, ϕ, σ2) does not influence the asymptotic distribution of as long as the nuisance parameter estimates are root-N consistent. In Appendix A, we use a lemma from Yuan and Jennrich30 to show why this is the case.
4 | ASYMPTOTIC RESULTS
In this section, we will present theorems regarding the consistency and asymptotic normality for our proposed estimators and . Let ξ* be the true values of the parameters of interest, and let (Q*, π*, ϕ*, ) denote the true values of the nuisance parameters (Q, π, ϕ, σ2). In addition, we let Ek denote the conditional expectation given Y1 ∈ Ak. That is, for any function f(·), Ek[f(Y1, Y2, X, Z)] = E[f(Y1, Y2, X, Z) | Y1∈Ak]. Under regularity conditions outlined in Appendix A, assuming that n0/nV→ρ0>0 and nk/nV→ρk≥0 for k = 1, 3, the following theorems hold for and :
Theorem 1
and converge in probability to ξ*.
Theorem 2
Let θ denote the nuisance parameters (Q, π), then has the following asymptotic distributional properties:
| (7) |
where
and
Replacing the population quantities with the sample quantities, a consistent estimator for the asymptotic variance-covariance matrix can be obtained as
where and .
Theorem 3
Let n = (Q, π, ϕ, σ2) denote all the nuisance parameters. has the following asymptotic distributional properties:
| (8) |
where , and .
Replacing the population quantities with the sample quantities, a consistent estimator for the asymptotic variance-covariance matrix can be obtained as:
where and .
Outline of the proofs are in Appendix A. We will apply a result of Foutz31 to prove the consistency of our estimator and use Taylor expansion together with Slutsky theorem to prove asymptotic normality.
5 | SIMULATION STUDIES
In this section, we conduct extensive simulation studies to evaluate the finite sample performance of our proposed estimators. There are 5 competing estimators: (1) denotes the regression estimator based on SRS portion of validation sample. (2) denotes the regression estimator from an SRS of the same size as the validation sample. Notice that this estimator is not available in practice, because when the existing data are obtained from an ODS design, it is impossible to obtain a SRS of the same size of the ODS sample. We include in the table for comparison purpose only. (3) denotes the estimate from our inverse probability weighted estimating equation proposed in Section 3.1. (4) denotes the estimate from our proposed augmented IPW estimating equation in Section 3.2. (5) denotes a semiparametric maximum likelihood estimator similar to Jiang et al.20 In deriving , we assume that (Y1, Y2) is bivariate normal and use estimated likelihood technique to deal with the nuisance functions. The details are shown in Appendix B.
The data are generated from the following models:
| (9) |
where X ~ N(0, 1), Z ~ Bernoulli(0.45) and (e, ε) follows a bivariate normal distribution with , , cov(e,ε) = ρσ1σ2. The true parameter values are β0 = 1, β2 = − 0.5, γ0 = 1, γ2 = − 0.5, σ1 = σ2 = 1, and ρ = 0.8. We allow β1 and γ1 to take value 0 or 0.5.
Let and be the sample mean and standard deviation for the primary outcome Y1 observed in the full cohort. In continuous outcome ODS design, we first select an SRS of size n0, then a supplemental sample of size n1 is chosen from and a supplemental sample of size n3 chosen from . The validation sample has size nV = n0 + n1 + n3. We consider the following 2 settings: (1) n0 = 200, n1 = n3 = 100. (2) n0 = 300, n1 = n3 = 50. In addition, we also vary the cutoff points of the strata by considering different values of a, ie, a = 1 or 1.5.
Tables 1 and 2 show the simulation results based on 1000 independent replications. The full cohort size is N = 3000. In Table 1, (n0, n1, n3) = (200, 100, 100). In Table 2, (n0, n1, n3) = (300, 50, 50). The average of parameter estimates (Mean), empirical variance of parameter estimates across all simulations (VAR), average of the variance estimator , and 95% CI coverage are reported. In addition, we show the sample relative efficiency of all estimators relative to in terms of estimating γ1. The sample relative efficiency is defined as the ratio of empirical variance, ie, .
TABLE 1.
Simulation results based on 1000 simulations with n0 = 200, n1 = n3 = 100, the validation sample size is nV = 400, the full cohort size is N = 3000
| α | β1 | γ1 | Methods |
|
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | VAR |
|
CI | Mean | VAR |
|
CI | SRE | ||||||
| 1.0 | 0 | 0 | ξSRS | −0.002 | 0.0049 | 0.0050 | 0.948 | −0.001 | 0.0046 | 0.0050 | 0.966 | 0.58 | ||
| ξR | 0.000 | 0.0024 | 0.0025 | 0.958 | 0.001 | 0.0026 | 0.0025 | 0.950 | 1.04 | |||||
| ξIPW | −0.001 | 0.0020 | 0.0021 | 0.947 | 0.002 | 0.0027 | 0.0027 | 0.947 | 1.00 | |||||
| ξAIPW | 0.000 | 0.0021 | 0.0021 | 0.946 | 0.002 | 0.0027 | 0.0027 | 0.945 | 1.00 | |||||
| ξSPML | 0.001 | 0.0015 | 0.0014 | 0.954 | 0.001 | 0.0019 | 0.0018 | 0.940 | 1.42 | |||||
| 0.5 | ξSRS | 0.002 | 0.0048 | 0.0050 | 0.956 | 0.502 | 0.0049 | 0.0050 | 0.955 | 0.53 | ||||
| ξR | 0.001 | 0.0026 | 0.0025 | 0.949 | 0.501 | 0.0026 | 0.0025 | 0.950 | 1.00 | |||||
| ξIPW | 0.003 | 0.0020 | 0.0020 | 0.952 | 0.502 | 0.0026 | 0.0026 | 0.947 | 1.00 | |||||
| ξAIPW | 0.003 | 0.0014 | 0.0014 | 0.956 | 0.504 | 0.0016 | 0.0016 | 0.938 | 1.63 | |||||
| ξSPML | 0.002 | 0.0010 | 0.0010 | 0.950 | 0.500 | 0.0013 | 0.0013 | 0.955 | 2.00 | |||||
| 0.5 | 0 | ξSRS | 0.501 | 0.0053 | 0.0050 | 0.944 | 0.001 | 0.0049 | 0.0050 | 0.952 | 0.55 | |||
| ξR | 0.501 | 0.0026 | 0.0025 | 0.943 | 0.001 | 0.0026 | 0.0025 | 0.939 | 1.04 | |||||
| ξIPW | 0.503 | 0.0023 | 0.0025 | 0.958 | 0.003 | 0.0027 | 0.0028 | 0.947 | 1.00 | |||||
| ξAIPW | 0.503 | 0.0018 | 0.0018 | 0.936 | 0.000 | 0.0018 | 0.0018 | 0.942 | 1.50 | |||||
| ξSPML | 0.499 | 0.0017 | 0.0017 | 0.942 | 0.002 | 0.0014 | 0.0014 | 0.944 | 1.93 | |||||
| 0.5 | ξSRS | 0.499 | 0.0052 | 0.0050 | 0.949 | 0.499 | 0.0050 | 0.0050 | 0.948 | 0.56 | ||||
| ξR | 0.500 | 0.0025 | 0.0025 | 0.947 | 0.498 | 0.0026 | 0.0025 | 0.950 | 1.08 | |||||
| ξIPW | 0.501 | 0.0022 | 0.0025 | 0.960 | 0.500 | 0.0028 | 0.0028 | 0.952 | 1.00 | |||||
| ξAIPW | 0.502 | 0.0020 | 0.0020 | 0.951 | 0.502 | 0.0025 | 0.0023 | 0.943 | 1.12 | |||||
| ξSPML | 0.500 | 0.0016 | 0.0017 | 0.958 | 0.500 | 0.0017 | 0.0018 | 0.955 | 1.65 | |||||
| 1.5 | 0.5 | 0 | ξSRS | 0.500 | 0.0048 | 0.0052 | 0.968 | 0.002 | 0.0046 | 0.0052 | 0.960 | 0.67 | ||
| ξR | 0.498 | 0.0024 | 0.0025 | 0.956 | −0.001 | 0.0024 | 0.0025 | 0.940 | 1.29 | |||||
| ξIPW | 0.504 | 0.0027 | 0.0029 | 0.955 | 0.004 | 0.0031 | 0.0033 | 0.953 | 1.00 | |||||
| ξAIPW | 0.505 | 0.0022 | 0.0022 | 0.947 | 0.001 | 0.0022 | 0.0022 | 0.949 | 1.41 | |||||
| ξSPML | 0.504 | 0.0017 | 0.0017 | 0.948 | 0.006 | 0.0014 | 0.0014 | 0.947 | 2.21 | |||||
| 0.5 | ξSRS | 0.496 | 0.0050 | 0.0050 | 0.947 | 0.500 | 0.0049 | 0.0050 | 0.956 | 0.61 | ||||
| ξR | 0.502 | 0.0025 | 0.0025 | 0.953 | 0.502 | 0.0025 | 0.0025 | 0.950 | 1.20 | |||||
| ξIPW | 0.501 | 0.0028 | 0.0029 | 0.954 | 0.504 | 0.0030 | 0.0032 | 0.955 | 1.00 | |||||
| ξAIPW | 0.503 | 0.0025 | 0.0025 | 0.944 | 0.505 | 0.0027 | 0.0027 | 0.947 | 1.11 | |||||
| ξSPML | 0.501 | 0.0017 | 0.0018 | 0.950 | 0.501 | 0.0018 | 0.0018 | 0.953 | 1.67 | |||||
Abbreviation: SRE, sample relative efficiency. Results are based on the model Y1=β0+β1X+β2Z+e, Y2=Y0+Y1X+Y2Z+ε, where X~N(0, 1), Z~Bernoulli(0.45) and (e, ε) follow a bivariate normal distribution with , , cov(e, ε)=ρσ1σ2; the true parameter values are β0=1, β2=−0.5, γ0=1, γ2=−0.5, σ1=σ2=1, ρ=0.8. The cutoff points for the outcome-dependent sampling design are and . ξSRS denotes the regression estimator based on simple random sample portion of the validation sample. ξR denotes the regression estimator from a simple random sample of the same size as the validation sample. ξIPW denotes the estimate from our inverse probability weighted (IPW) estimating equation. ξaipw denotes the estimate from augmented IPW (AIPW) estimating equation. ξSPWL is a semiparametric maximum likelihood (SPML) estimator similar to Jiang et al,20 which models (Y1, Y2) parametrically using a bivariate normal distribution.
TABLE 2.
Simulation results based on 1000 simulations with n0 = 300, n1 = n3 = 50, the validation sample size is nV = 400, the full cohort size is N=3000
| α | β1 | γ1 | Methods |
|
|
|||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | VAR |
|
Mean | VAR |
|
SRE | ||||||
| 1.0 | 0 | 0 | ξSRS | 0.000 | 0.0034 | 0.0034 | −0.001 | 0.0036 | 0.0034 | 0.69 | ||
| ξR | 0.000 | 0.0024 | 0.0025 | 0.000 | 0.0025 | 0.0025 | 1.00 | |||||
| ξIPW | 0.001 | 0.0021 | 0.0020 | 0.000 | 0.0025 | 0.0023 | 1.00 | |||||
| ξAIPW | 0.001 | 0.0021 | 0.0020 | 0.000 | 0.0025 | 0.0023 | 1.00 | |||||
| ξSPML | 0.001 | 0.0018 | 0.0018 | 0.000 | 0.0021 | 0.0021 | 1.19 | |||||
| 0.5 | ξSRS | −0.004 | 0.0034 | 0.0034 | 0.496 | 0.0034 | 0.0034 | 0.65 | ||||
| ξR | −0.001 | 0.0023 | 0.0025 | 0.500 | 0.0024 | 0.0025 | 0.92 | |||||
| ξIPW | −0.001 | 0.0020 | 0.0020 | 0.498 | 0.0022 | 0.0023 | 1.00 | |||||
| ξAIPW | −0.001 | 0.0013 | 0.0014 | 0.500 | 0.0014 | 0.0014 | 1.57 | |||||
| ξSPML | 0.001 | 0.0012 | 0.0012 | 0.498 | 0.0013 | 0.0014 | 1.69 | |||||
| 0.5 | 0 | ξSRS | 0.501 | 0.0032 | 0.0034 | 0.001 | 0.0034 | 0.0034 | 0.62 | |||
| ξR | 0.499 | 0.0024 | 0.0025 | 0.000 | 0.0025 | 0.0025 | 0.84 | |||||
| ξIPW | 0.502 | 0.0018 | 0.0022 | 0.001 | 0.0021 | 0.0024 | 1.00 | |||||
| ξAIPW | 0.502 | 0.0014 | 0.0015 | 0.000 | 0.0016 | 0.0015 | 1.31 | |||||
| ξSPML | 0.500 | 0.0014 | 0.0015 | 0.001 | 0.0014 | 0.0014 | 1.50 | |||||
| 0.5 | ξSRS | 0.500 | 0.0032 | 0.0034 | 0.498 | 0.0032 | 0.0033 | 0.66 | ||||
| ξR | 0.499 | 0.0025 | 0.0025 | 0.499 | 0.0025 | 0.0025 | 0.84 | |||||
| ξIPW | 0.502 | 0.0018 | 0.0022 | 0.501 | 0.0021 | 0.0024 | 1.00 | |||||
| ξAIPW | 0.503 | 0.0017 | 0.0017 | 0.502 | 0.0019 | 0.0018 | 1.11 | |||||
| ξSPML | 0.500 | 0.0016 | 0.0016 | 0.499 | 0.0016 | 0.0018 | 1.31 | |||||
| 1.5 | 0.5 | 0 | ξSRS | 0.500 | 0.0036 | 0.0034 | 0.001 | 0.0035 | 0.0034 | 0.74 | ||
| ξR | 0.498 | 0.0025 | 0.0025 | −0.001 | 0.0026 | 0.0025 | 1.00 | |||||
| ξIPW | 0.501 | 0.0023 | 0.0022 | 0.000 | 0.0026 | 0.0024 | 1.00 | |||||
| ξAIPW | 0.502 | 0.0018 | 0.0016 | 0.000 | 0.0018 | 0.0017 | 1.44 | |||||
| ξSPML | 0.500 | 0.0014 | 0.0014 | 0.002 | 0.0014 | 0.0014 | 1.86 | |||||
| 0.5 | ξSRS | 0.499 | 0.0035 | 0.0034 | 0.499 | 0.0034 | 0.0034 | 0.68 | ||||
| ξR | 0.502 | 0.0026 | 0.0025 | 0.501 | 0.0027 | 0.0025 | 0.85 | |||||
| ξIPW | 0.500 | 0.0021 | 0.0022 | 0.500 | 0.0023 | 0.0024 | 1.00 | |||||
| ξAIPW | 0.501 | 0.0018 | 0.0018 | 0.501 | 0.0019 | 0.0019 | 1.21 | |||||
| ξSPML | 0.499 | 0.0014 | 0.0015 | 0.499 | 0.0017 | 0.0017 | 1.35 | |||||
Abbreviation: SRE, sample relative efficiency. Results are based on the model Y1=β0+β1X+β2Z+e, Y2=γ0+γ1X+γ2Z+ε, where X~N(0, 1), Z~Bernoulli(0.45) and (e, ε) follow a bivariate normal distribution with , , cov(e,ε)=ρσ1σ2; the true parameter values are β0=1, β2=−0.5, γ0=1, γ2=−0.5, σ1=σ2=1, ρ=0.8. The cutoff points for the outcome-dependent sampling design are and ξSRS denotes the regression estimator based on simple random sample (SRS) portion of the validation sample. ξR denotes the regression estimator from an SRS of the same size as the validation sample. ξIPW denotes the estimate from our inverse probability weighted (IPW) estimating equation. ξAIPW denotes the estimate from augmented IPW (AIPW) estimating equation. ξSPMI is a semiparametric maximum likelihood (SPML) estimator similar to Jiang et al,20 which models (Y1, Y2) parametrically using a bivariate normal distribution.
From Tables 1 and 2, we have the following observations: (1) All 5 estimators yield virtually unbiased estimates. (2) ξSPML has the most precise estimate. However, as later shown in the simulation studies, the validity of depends heavily on the correctness of bivariate normal assumption and is hence not robust. (3) Among , , and , the augmented estimating equation estimator is the most precise in all settings except for when β1 = y1 = 0, where the performance of and are similar. For example, when (n0, n1, n3) = (200, 100, 100), a = 1, β1 = 0, γ1 = 0.5, the empirical variance estimating γ1 is 0.0016 for , which is smaller than 0.0026 for and 0.0049 for . The precision gain comes from the fact that and use more participants than . (4) For all estimators, averages of the variance estimator is very close to the empirical variance (ie, is close to VAR). (5) The 95% CI coverage is close to 0.95, which implies that the asymptotic normal approximation works well in these finite sample size settings. (6) When the cutoff points are further out (ie, a = 1 versus a = 1.5), the precision gains of and over are slightly lower (Table 1). The ODS sample is more enriched with a=1.5. However, this more enriched study design is offset by the highly variable IPW weighting distribution that results in precision loss. (7) Comparing the results across Tables 1 and 2 in terms of estimating γ1, we find that, for a given validation sample size (nV = 400), when SRS sample size is larger (ie, n0 = 200 versus n0 = 300), the variance of and decreases. However, the variance of has a faster decreasing rate. That is, the precision gains of and over is smaller when the SRS sample size is larger.
We investigate the scenario where the error term ε is not normally distributed. The simulation set up is the same as Table 1 except for the error term. We assume that e ~ N(0, 1), ε is a gamma distribution with shape parameter 2, rate parameter 1, then normalized to have mean 0 and variance 1. This error term is right skewed. From Table 3, we see that our proposed estimators are more robust to model misspecification than . When true γ1 = 0.5, the 95% CI coverage rate is poor for . also has larger empirical variance than and as it misspecified the distribution of Y2. Another limitation of is that it is subject to “curse of dimensionality” as nonparametric method is used to estimate the nuisance function. Therefore, the method cannot be directly applied when the dimension of Z is relatively high, ie, > 3. In addition, the method does not have a natural extension when Z has both discrete and continuous components.
TABLE 3.
Simulation results when ε is not normal. The full cohort size is N=3000, (n0, n1, n3)=(200, 100, 100)
| α | β1 | γ1 | Methods |
|
||||
|---|---|---|---|---|---|---|---|---|
| Mean | VAR |
|
CI | |||||
| 1.0 | 0 | 0 | ξIPW | 0.003 | 0.0038 | 0.0036 | 0.941 | |
| ξAIPW | 0.003 | 0.0039 | 0.0036 | 0.926 | ||||
| ξSPML | 0.001 | 0.0027 | 0.0026 | 0.960 | ||||
| 0.5 | ξIPW | 0.499 | 0.0038 | 0.0037 | 0.946 | |||
| ξAIPW | 0.502 | 0.0037 | 0.0035 | 0.932 | ||||
| ξSPML | 0.493 | 0.0055 | 0.0041 | 0.871 | ||||
| 0.5 | 0 | ξIPW | 0.002 | 0.0036 | 0.0034 | 0.933 | ||
| ξAIPW | 0.001 | 0.0032 | 0.0030 | 0.930 | ||||
| ξSPML | −0.001 | 0.0021 | 0.0021 | 0.953 | ||||
| 0.5 | ξIPW | 0.501 | 0.0031 | 0.0032 | 0.954 | |||
| ξAIPW | 0.505 | 0.0026 | 0.0027 | 0.940 | ||||
| ξSPML | 0.494 | 0.0038 | 0.0029 | 0.899 | ||||
Results are based on the model Y1=β0+β1X+β2Z+e, Y2=γ0+γ1X+γ1Z+ε, where X~N(0, 1), Z~Bernoulli(0.45), and e~N(0, 1), ε is a gamma distribution with shape parameter 2, rate parameter 1, normalized to have mean 0 and variance 1. The true parameter values are β0=1, β2=−0.5, γ0=1, γ2=−0.5. The cutoff points for the outcome-dependent sampling design are and . ξIPW denotes the estimate from our inverse probability weighted (IPW) estimating equation; ξaipw denotes the estimate from augmented IPW (AIPW) estimating equation; ξSPML is a semiparametric maximum likelihood (SPML) estimator similar to Jiang et al,20 which models (Y1, Y2) parametrically using a bivariate normal distribution.
We further investigate the performance of our proposed estimators in estimating γ1 under different combinations of the SRS sample and supplemental samples. The simulation set up is as follows: a = 1.0,β0 = 1,β1 = 0.5,β2 = −0.5,γ0 =1,γ1 = 0.5,γ2 = −0.5,σ1 = σ2 = 1,ρ = 0.8. The full cohort has size N=3000. We fix the validation sample to have size nV =400 and vary (n0, n1, n3). Figure 1 shows the sample relative efficiency of and relative to over a wide range of proportion of the SRS sample in the validation sample (n0/nV). We confirm that when SRS size is larger, there is larger precision gain of over , while the precision gain of and over is smaller.
FIGURE 1.
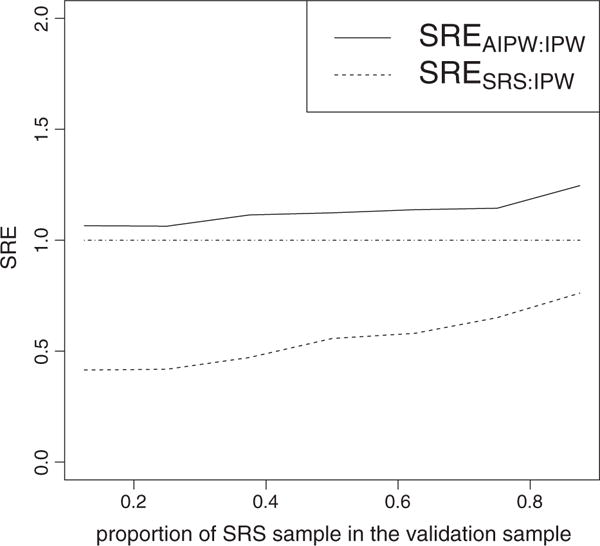
Sample relative efficiencies (SREs) comparing and to in terms of estimating γ1, under various combinations of simple random sample (SRS) and supplemental samples. The SRE is defined as . The X-axis is the fraction of SRS in the validation sample: n0/nV
We also evaluate the precision gain of our proposed estimators for different values of ρ, where ρ is the correlation coefficient between 2 error terms e and e in (9). Figure 2 shows the corresponding sample relative efficiency. When correlation changes from 0 to 1, the precision gain of over is relatively stable for different ρ values. On the other hand, the precision gain of over is decreasing when γ1 >0, and increasing when γ1<0.
FIGURE 2.
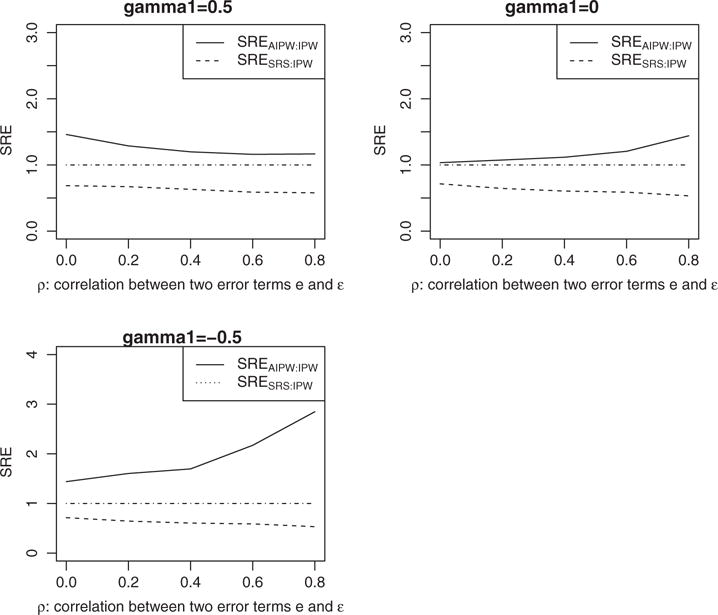
Sample relative efficiencies (SREs) comparing and to in terms of estimating γ1, under different values of ρ. The sample relative efficiency is defined as . AIPW, augmented IPW; IPW, inverse probability weighted
6 | COLLABORATIVE PERINATAL PROJECT DATA
In this section, we applied our method to analyze the CPP data set. The CPP is originally conducted as a cohort study to evaluate the risk factors for birth defects and other neurological disorders of childhood.32 The study involved 12 hospitals/universities located across the United States. In all, 55 908 pregnancies were registered, representing the experience about 44 000 women. The children born during the study were followed up until 8 years old. One hypothesis is that maternal PCB levels are related to children’s IQ performance at 7 years of age.4 Because the exposure variable PCB levels are very expensive to measure, ODS design is conducted on the basis of CPP data. An SRS of 849 individuals is selected, and then 2 supplemental samples are selected based on the children’s IQ score. One supplemental sample of size 81 is selected from the lower tail of the IQ distribution, defined by 1 standard deviation below the mean IQ score in the CPP population. The other supplemental sample of size 108 is chosen from 1 standard deviation above the mean IQ score.
Many researchers have made efforts to assess whether there is association between PCB level and child’s birth weight, but the findings from these studies are not consistent. Some indicate an inverse association,12,16,18 while other indicates a positive association13 or no association at all.14,15,17 We use our available CPP data to perform the secondary outcome analysis. In our analysis, we use the Weschler Intelligence Scale for children at 7 years old (IQ) as the primary outcome, and child’s birth weight (in grams) to be the secondary outcome. Other confounding variables include parent’s education level (EDU), social economic status of the child’s family (SES), race ethnicity of the child (RACE), and gender of the child (GENDER).
Table 4 shows the parameter estimates, standard error, and 95% CIs for the secondary outcome model, which regresses birth weight over PCB level adjusting for other covariates. Simple random sample denotes the regression analysis based on the SRS portion of the data. Inverse probability weighted denotes the inverse probability weighted estimating equation we proposed in Section 3.1, which uses the validation sample only. Augmented IPW denotes the augmented inverse probability weighted estimating equation proposed in Section 3.2. The semiparametric maximum likelihood estimator is excluded from the analysis, as it does not have a natural extension when the covariates contain both discrete and continuous components.
TABLE 4.
Analysis for a secondary outcome: child’s birth weight in CPP study
| Variables | SRS | IPW | AIPW | |
|---|---|---|---|---|
| Int | Estimate | 3208.14 | 3209.44 | 3089.24 |
| SE | 86.54 | 79.49 | 21.97 | |
| 95% CI | (3038.52, 3377.76) | (3053.64, 3365.24) | (3046.18, 3132.30) | |
| PCB | Estimate | −0.67 | −5.44 | −5.49 |
| SE | 9.20 | 8.41 | 8.46 | |
| 95% CI | (−18.70, 17.36) | (−21.92, 11.04) | (−22.07, 11.09) | |
| EDU | Estimate | −8.97 | −8.81 | 1.70 |
| SE | 9.10 | 8.39 | 1.36 | |
| 95% CI | (−26.81, 8.87) | (−25.25, 7.63) | (−0.97, 4.37) | |
| SES | Estimate | 13.94 | 16.06 | 13.58 |
| SE | 10.77 | 10.33 | 2.16 | |
| 95% CI | (−7.17, 35.05) | (−4.19, 36.31) | (9.35, 17.81) | |
| RACE | Estimate | 204.10 | 206.16 | 189.84 |
| (WHITE = 1) | SE | 38.13 | 37.93 | 6.29 |
| 95% CI | (129.37, 278.83) | (131.82, 280.50) | (177.51, 202.17) | |
| GENDER | Estimate | −147.69 | −145.65 | −119.25 |
| (FEMALE = 1) | SE | 34.72 | 31.96 | 5.33 |
| 95% CI | (−215.74, −79.64) | (−208.29, −83.01) | (−129.70, −108.80) |
The response variable is child’s birth weight in grams. The expensive exposure is mother’s polychlorinated biphenyl (PCB) level. Other confounding variables include: parent’s education level (EDU), social economic status of the child’s family (SES), race ethnicity of the child (RACE), and gender of the child (GENDER). The results under simple random sample (SRS) are the regression analysis using the SRS portion of the outcome-dependent sampling sample. Inverse probability weighted (IPW) is the inverse probability weighted estimating equation, and augmented IPW (AIPW) is the augmented inverse probability weighted estimating equation we proposed. SE, standard error.
All 3 analyses confirm that maternal PCB concentration is not significantly associated with child’s birth weight. However, the proposed IPW and AIPW estimator provide more precise estimates of the effects, evidenced by the reduced standard error and narrower CI. For example, the standard error for the PCB effect is 8.41 for IPW and 8.46 for AIPW, which is smaller than 9.20 for the standard regression analysis based on the SRS portion of the data. All 3 analyses confirm that being White has a positive impact on child’s birth weight, while AIPW analysis shows that social economic status has a positive impact on birth weight. In addition, girls have lower birth weight compared with boys as we expected. Note that there seems to be some difference between AIPW and IPW estimator for the EDU effect. We conducted additional simulation studies to show that such difference is merely due to sampling variability, and the observed difference is not that large if we take into account of the magnitude of the standard error. The details are shown in the Supporting Information.
7 | DISCUSSION
Investigators would all like to use the availability of expensive exposure that is already measured in a previous study. Most studies have multiple endpoints beside the primary outcome. This means that we often need to reuse the already collected data to analyze a secondary outcome in relation to the expensive exposure. However, when the original data are collected via an outcome-dependent fashion, secondary outcome analysis can be challenging as the ODS sample is no longer an SRS of the general population. As more studies are conducted using ODS designs, there is ever increasing needs for performing secondary analysis correctly and precisely for data from these studies. Our research is intended to fill these gaps and is the first attempt to develop precise inference procedure for a secondary outcome under the continuous outcome ODS design. We proposed IPW and AIPW estimating equations, in which only the form of the regressions are specified. Our proposed approach has the advantage of making no parametric distribution assumptions on (Y1, Y2) and thus is robust to model misspecification. Yet our proposed estimators are able to improve estimation precision relative to the naive analysis using SRS sample only.
Recall that r is the indicator variable of being selected into the validation sample. The expensive exposure X and r are conditionally independent given Y1. This means that in the Step 1 of AIPW analysis, we could actually use the whole validation sample (nV participants) to estimate the nuisance parameters (ϕ, σ2). As we mentioned before, how to estimate the nuisance parameter (ϕ, σ2) does not influence the asymptotic distribution of as long as the nuisance parameter estimates are consistent. However, in small sample scenarios, there could be some difference. For instance, when full cohort has size 3000, (n0, n1, n3) = (50, 175, 175), the proposed estimator could have some bias (mean of parameter estimates is 0.515 while the true value for γ1 is 0.5), if we only used SRS (50 participants) to estimate the nuisance parameters. On the other hand, the bias is reduced to 0.07, if we use the validation sample (400 participants) to estimate the nuisance parameters and then solve the AIPW estimating equation. When SRS sample size is larger, such as (n0, n1, n3) = (200, 100, 100), the results between these 2 approaches are almost identical.
We found that our proposed estimators have the same asymptotic variance regardless of whether we are using fixed-size sampling (sampling without replacement) or independent Bernoulli sampling in choosing the initial SRS and the supplemental samples. This is because even though (r1, ⋯, rN) are correlated under fixed-size sampling, it can be proved that for different participants i and j. For case-cohort design, the difference between 2 subcohort sampling methods have been studied.33,34 They found that the variance under fixed-size SRS is always smaller than or equal to the variance under Bernoulli sampling. There is equivalence when the corresponding covariance parts equal to 0 (see the comparison between and ΣH in Kulich and Lin33).
In our paper, when we implemented our AIPW estimator, we specified the form of the conditional moments, E(X | Y1, Y2, Z) and E(X2 | Y1, Y2, Z) using a linear regression model. In practice, the expensive exposure X might be discrete, then a generalized linear model could be adopted. We could also use some nonparametric techniques to estimate these conditional moments. Interest rises to see if there exists any difference between parametric and non-parametric methods. In addition, we used the observed selection probability in both IPW and AIPW estimators. In some ODS designs, the true selection probability is known based on the design structure and can be calculated. It would be interesting to see whether using the true probability or observed probability makes any difference in statistical efficiency. Furthermore, we are looking for a flexible parametric family to jointly model the primary and secondary outcome. Copula seems to be a natural way to achieve the goal. This is another possible area of future research.
Supplementary Material
Acknowledgments
This research is part of Yinghao Pan’s PhD dissertation. It is partially supported by grants R01 ES021900 and P30 ES010126 from the National Institute of Environmental Health Sciences, P01 CA142538 from the National Cancer Institute, and the Intramural Research Program of the NIEHS/NIH. The authors thank editors and 2 referees for their suggestions to improve the paper.
Funding information
National Cancer Institute, Grant/Award Number: P01 CA142538; National Institute of Environmental Health Sciences, Grant/Award Numbers: R01 ES021900 and P30 ES010126
APPENDIX A
PROOFS
We provide the outline of the proofs for the augmented IPW estimator . The proof for follows the similar arguments and thus omitted here. Let η = (Q, π, ϕ, σ2) denote all the nuisance parameters. We make the following regularity conditions:
The parameter space of ξ, Ξ, is a compact subspace of Rp, and that the true underlying value ξ* lies in the interior of the parameter space; the covariate space, is a compact subset of R; and the covariate space, , is a compact subset of Rq for some q≥ 1.
For all (Y1, Y2, X, Z), s2(ξ, η) is continuous for all ξ ∈ Ξ; the partial derivatives , for i = 1, …, p, exist and are continuous for all ξ ∈ Ξ.
Interchanges of differentiation and integration are valid for s2(ξ, η) and its first-order partial derivatives with respect to ξ.
- The following expected value matrix is finite and negative definite at (ξ*, η*):
The supremum of in the neighborhood of ξ* is bounded by a function g that has finite expectation. (Outline of the proof for consistency):
By law of larger numbers, it is straightforward to show that
| (A1) |
Using the fact that is a consistent estimator of η*, and , it can be shown that
| (A2) |
Combining (A1) and (A2), we know that
Furthermore, using Assumptions 1-3 and consistency of , we can show that
| (A3) |
holds uniformly for ξ in parameter space. Also, by law of large numbers,
| (A4) |
Combining (A3) and (A4), we have
uniformly for ξ ∈ Ξ. From Assumption 4, we know that is negative definite and hence invertible at (ξ*, η*). Hence, we can apply a result of Foutz31 that uses the inverse function theorem to prove that our proposed estimator is a consistent and unique solution to the estimating equations.
(outline of the proof for asymptotic normality):
Let us denote
Using lemma 2 from Yuan and Jennrich,30 we have
| (A5) |
Let A and B be the limit of AN and BN, respectively. By law of large numbers, we know that
That is, A = −I2(ξ*, η*) and B = 0. Rearrange (A5) and using the fact that , we have
B = 0, is bounded in probability. Hence, we know that
By the proposition in appendix 1 of Kulich and Lin,33
where Σ2(ξ, η) = E[s2(ξ, η)s2(ξ, η)T. Then, using Slutsky theorem, we know that
Notice that B=0 implies that the asymptotic distribution of does not influence the asymptotic distribution of as long as is root-N consistent.
APPENDIX B: BRIEF DESCRIPTION OF THE ESTIMATED LIKELIHOOD APPROACH
To develop the semiparametric maximum likelihood estimator , we need to assume that (Y1, Y2) is bivariate normal. That is,
where (ei, εi) follows a bivariate normal distribution with , , cov(ei, εi) = ρσ1σ2.
For a participant in V(validation sample), the contribution to the likelihood is (Y1, Y2, X, Z). For a participant in (nonvalidation sample), the contribution is (Y1, Y2, Z). Hence, the likelihood corresponding to (1) is proportional to
where fξ(Y1, Y2 | X, Z) is the density function of a bivariate normal distribution and GX|Z(·|·) represents the conditional distribution function of X given Z. The log-likelihood is
Notice that GX|Z is a nuisance function. Using ideas from Weaver and Zhou,5 we propose to work with the following estimated log-likelihood function:
where we nonparametrically estimate GX|Z using the SRS sample. For discrete Z, let
For continuous Z, we use the kernel method, ie,
where KH(·) = |H|−1/2K(H−1/2·) is a kernel with a bandwidth matrix H. Then, the proposed semiparametric maximum likelihood estimator is the solution to the following estimating equation:
Footnotes
SUPPORTING INFORMATION
Additional Supporting Information may be found online in the supporting information tab for this article.
CONFLICT OF INTEREST
None declared.
ORCID
Yinghao Pan http://orcid.org/0000-0002-4022-1815
References
- 1.Cornfield J. Method of estimating comparative rates from clinical data. Application to cancer of the lung, breast, and cervix. J Natl Cancer Inst. 1951;11(6):1269–1275. [PubMed] [Google Scholar]
- 2.Prentice R. A case-cohort design for epidemiologic cohort studies and disease prevention trials. Biometrika. 1986;73(1):1–11. [Google Scholar]
- 3.Zhou H, Weaver M, Qin J, Longnecker M, Wang M. A semiparametric empirical likelihood method for data from an outcome-dependent sampling scheme with a continuous outcome. Biometrics. 2002;58(2):413–421. doi: 10.1111/j.0006-341x.2002.00413.x. [DOI] [PubMed] [Google Scholar]
- 4.Longnecker M, Klebanoff M, Zhou H, Wilcox A, Berendes H, Hoffman H. Proposal to Study in Utero Exposure to DDE and PCBs in Relation to Male Birth Defects and Neurodevelopmental Outcomes in the Collaborative Perinatal Project. Washington, DC: Study Proposal, National Institute of Environmental Health Sciences; 1997. [Google Scholar]
- 5.Weaver M, Zhou H. An estimated likelihood method for continuous outcome regression models with outcome-dependent sampling. J Am Stat Assoc. 2005;100(470):459–469. [Google Scholar]
- 6.Wang X, Zhou H. A semiparametric empirical likelihood method for biased sampling schemes with auxiliary covariates. Biometrics. 2006;62(4):1149–1160. doi: 10.1111/j.1541-0420.2006.00612.x. [DOI] [PubMed] [Google Scholar]
- 7.Song R, Zhou H, Kosorok M. A note on semiparametric efficient inference for two-stage outcome-dependent sampling with a continuous outcome. Biometrika. 2009;96(1):221–228. doi: 10.1093/biomet/asn073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wang X, Zhou H. Design and inference for cancer biomarker study with an outcome and auxiliary-dependent subsampling. Biometrics. 2010;66(2):502–511. doi: 10.1111/j.1541-0420.2009.01280.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Qin G, Zhou H. Partial linear inference for a 2-stage outcome-dependent sampling design with a continuous outcome. Biostatistics. 2011;12(3):506–520. doi: 10.1093/biostatistics/kxq070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zhou H, Qin G, Longnecker MP. A partial linear model in the outcome-dependent sampling setting to evaluate the effect of prenatal PCB exposure on cognitive function in children. Biometrics. 2011;67(3):876–885. doi: 10.1111/j.1541-0420.2010.01500.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zhou H, Wu Y, Liu Y, Cai J. Semiparametric inference for a 2-stage outcome-auxiliary-dependent sampling design with continuous outcome. Biostatistics. 2011;12(3):521–534. doi: 10.1093/biostatistics/kxq080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Fein G, Jacobson J, Jacobson S, Schwartz P, Dowler J. Prenatal exposure to polychlorinated biphenyls: effects on birth size and gestational age. J Pediatr. 1984;105(2):315–320. doi: 10.1016/s0022-3476(84)80139-0. [DOI] [PubMed] [Google Scholar]
- 13.Dar E, Kanarek M, Anderson H, Sonzogni W. Fish consumption and reproductive outcomes in Green Bay, Wisconsin. Environ Res. 1992;59(1):189–201. doi: 10.1016/s0013-9351(05)80239-7. [DOI] [PubMed] [Google Scholar]
- 14.Vartiainen T, Jaakkola JJ, Saarikoski S, Tuomisto J. Birth weight and sex of children and the correlation to the body burden of PCDDs/PCDFs and PCBs of the mother. Environ Health Perspect. 1998;106(2):61–66. doi: 10.1289/ehp.9810661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Grandjean P, Bjerve K, Weihe P, Steuerwald U. Birthweight in a fishing community: significance of essential fatty acids and marine food contaminants. Int J Epidemiol. 2001;30(6):1272–1278. doi: 10.1093/ije/30.6.1272. [DOI] [PubMed] [Google Scholar]
- 16.Karmaus W, Zhu X. Maternal concentration of polychlorinated biphenyls and dichlorodiphenyl dichlorethylene and birth weight in Michigan fish eaters: a cohort study. Environ Health. 2004;3(1):1. doi: 10.1186/1476-069X-3-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Longnecker M, Klebanoff M, Brock J, Guo X. Maternal levels of polychlorinated biphenyls in relation to preterm and small-for-gestational-age birth. Epidemiology. 2005;16(5):641–647. doi: 10.1097/01.ede.0000172137.45662.85. [DOI] [PubMed] [Google Scholar]
- 18.Murphy L, Gollenberg A, Louis G, Kostyniak P, Sundaram R. Maternal serum preconception polychlorinated biphenyl concentrations and infant birth weight. Environ Health Perspect. 2010;118(2):297–302. doi: 10.1289/ehp.0901150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lee A, Mcmurchy L, Scott AJ. Re-using data from case-control studies. Stat Med. 1997;16(12):1377–1389. doi: 10.1002/(sici)1097-0258(19970630)16:12<1377::aid-sim557>3.0.co;2-k. [DOI] [PubMed] [Google Scholar]
- 20.Jiang Y, Scott A, Wild CJ. Secondary analysis of case-control data. Stat Med. 2006;25(8):1323–1339. doi: 10.1002/sim.2283. [DOI] [PubMed] [Google Scholar]
- 21.Lin D, Zeng D. Proper analysis of secondary phenotype data in case-control association studies. Genet Epidemiol. 2009;33(3):256–265. doi: 10.1002/gepi.20377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Richardson D, Rzehak P, Klenk J, Weiland S. Analyses of case-control data for additional outcomes. Epidemiology. 2007;18(4):441–445. doi: 10.1097/EDE.0b013e318060d25c. [DOI] [PubMed] [Google Scholar]
- 23.Monsees G, Tamimi R, Kraft P. Genome-wide association scans for secondary traits using case-control samples. Genet Epidemiol. 2009;33(8):717–728. doi: 10.1002/gepi.20424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wei J, Carroll RJ, Muller UU, Keilegom IV, Chatterjee N. Robust estimation for homoscedastic regression in the secondary analysis of case-control data. J R Stat Soc Series B Stat Methodol. 2013;75(1):185–206. doi: 10.1111/j.1467-9868.2012.01052.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ma Y, Carroll RJ. Semiparametric estimation in the secondary analysis of case-control studies. J R Stat Soc Series B Stat Methodol. 2016;78(1):127–151. doi: 10.1111/rssb.12107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Horvitz D, Thompson D. A generalization of sampling without replacement from a finite universe. J Am Stat Assoc. 1952;47(260):663–685. [Google Scholar]
- 27.Liang K, Zeger SL. Longitudinal data analysis using generalized linear models. Biometrika. 1986;73(1):13–22. [Google Scholar]
- 28.Zhao L, Lipsitz S, Lew D. Regression analysis with missing covariate data using estimating equations. Biometrics. 1996;52:1165–1182. [PubMed] [Google Scholar]
- 29.Robins J, Rotnitzky A, Zhao L. Estimation of regression coefficients when some regressors are not always observed. J Am Stat Assoc. 1994;89(427):846–866. [Google Scholar]
- 30.Yuan K, Jennrich R. Estimating equations with nuisance parameters: theory and applications. Ann Inst Stat Math. 2000;52(2):343–350. [Google Scholar]
- 31.Foutz R. On the unique consistent solution to the likelihood equations. J Am Stat Assoc. 1977;72(357):147–148. [Google Scholar]
- 32.Niswander K, Gordon M. The women and their pregnancies. Washington, D. C.: U.S. Government Printing Office; 1972. (U.S. Department of Health, Education, and Welfare Publication (NIH) 73-379). [Google Scholar]
- 33.Kulich M, Lin DY. Additive hazards regression for case-cohort studies. Biometrika. 2000;87(1):73–87. [Google Scholar]
- 34.Nan B, Yu M, Kalbfleisch J. Censored linear regression for case-cohort studies. Biometrika. 2006;93(4):747–762. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


