Abstract
It has been extremely difficult for conventional computational approaches to reliably predict the properties of multi-reference systems (i.e., systems possessing radical character) at the nanoscale. To resolve this, we employ thermally-assisted-occupation density functional theory (TAO-DFT) to predict the electronic and hydrogen storage properties of Li-terminated linear boron chains (Li2Bn), with n boron atoms (n = 6, 8, …, and 16). From our TAO-DFT results, Li2Bn, which possess radical character, can bind up to 4 H2 molecules per Li, with the binding energies in the desirable regime (between 20 and 40 kJ/mol per H2). The hydrogen gravimetric storage capacities of Li2Bn range from 7.9 to 17.0 wt%, achieving the ultimate goal of the United States Department of Energy. Accordingly, Li2Bn could be promising media for storing and releasing H2 at temperatures much higher than the boiling point of liquid nitrogen.
Introduction
Hydrogen (H2) is a clean energy carrier, because only water vapor is emitted when converted into energy. Besides, hydrogen is quite plentiful on Earth in compound form (e.g., water (H2O)). Moreover, in terms of mass, the energy content of hydrogen is approximately three times that of gasoline. Hence, hydrogen can be a clean and green fuel, and has the potential to replace fossil fuels. Nonetheless, in terms of volume, the energy content of hydrogen is extremely low, when compared with that of gasoline. Therefore, efficient, economical, and safe hydrogen storage methods need to be developed for adopting hydrogen as a fuel in fuel cell vehicles1–6. The conventional high-pressure method where hydrogen is stored in carbon fiber reinforced plastic (CFRP) tanks at rather high pressures (e.g., between 350 and 700 bar) and the cryogenic method where hydrogen is stored at temperatures below the boiling point of H2 (about 20 K) are both unsuitable for onboard vehicle applications, due to the safety issues and high energy costs, respectively. Accordingly, it remains very difficult to efficiently store hydrogen in a lightweight and safe container6.
Presently, metal-organic frameworks (MOFs) and metal hydrides are adopted for storing hydrogen. As far as MOFs are concerned, the hydrogen storage capacities can be large due to the pore structure and high surface area of MOFs. Nevertheless, the hydrogen desorption temperatures for MOFs are rather low. On the other hand, in spite of their large hydrogen storage capacities, the hydrogen desorption temperatures for metal hydrides (e.g., MgH2, AlH3, LiBH4, and NaAlH4) can be very high, and the kinetics can be very slow (due to the formation/breaking of covalent and/or ionic bonds during the adsorption/desorption of hydrogen). Based on simple thermodynamic arguments, the hydrogen binding energy on a hydrogen storage material (HSM) has to lie between 20 and 40 kJ/mol per H2, for hydrogen uptake and release at near-ambient conditions7–9. However, among existing MOFs and metal hydrides, none can satisfy all the required conditions in order to use as an efficient HSM in onboard vehicles. Furthermore, on the basis of the ultimate goal of the United States Department of Energy (USDOE), a hydrogen gravimetric storage capacity of 6.5 wt% is required for a driving range of about 500 km6. Consequently, finding a HSM with all desirable properties has been very challenging.
Recently, carbon nanostructures have emerged as the potential materials for technological applications. The flexible bond formation (sp1, sp2, and sp3 hybridization) of carbon yields a very wide range of nanostructures which possess unique properties10. These nanostructures have been the test ground for studying many exotic phenomena. Especially, the discovery of C60 fullerene and the one-dimensional (1D) carbon nanotubes has revealed the potential of nanomaterial applications in diverse fields. Later, the discovery of graphene, the first ever two-dimensional (2D) material, has unlocked new possibilities in nanoscience and nanotechnology. This yields other 2D and quasi-2D materials, such as silicene, phosphorene, boron nitride nanomaterials, transition-metal dichalcogenides, single layers of metal oxides, and very recently, boron nanomaterials11,12. Since graphene is a semimetal or zero-gap semiconductor, its applications in electronics are impossible, unless a band gap can be opened by means of doping, defect formation, functionalization, and so on. Therefore, searching for other nanomaterials with better properties than graphene is in full swing.
In this pursuit, boron nanostructures are currently under intensive investigation to explore their electronic properties and potential applications. Due to recent advances in theoretical methods and experimental techniques, several boron nanostructures have been predicted and/or synthesized, and some of their basic properties and potential applications have been reported13–21. The observation of the Dirac cone22 in β12 boron sheet grown on Ag(111) has increased interest in these boron nanomaterials, due to their potential applications in electronics and possible exotic properties. The clusters and exhibit fluxional behavior, which has the potential for molecular Wankel motors15. Theoretical predictions have shown that B40 is a potential anode material for Li-ion battery applications23. Apart from their interesting electronic properties, these boron nanostructures can potentially be promising HSMs, because of their lightweight and high surface area. However, as carbon nanostructures are known to bind H2 molecules very weakly with the hydrogen binding energies typically less than 10 kJ/mol per H2 (primarily due to van der Waals (vdW) interactions), it is likely that most boron nanostructures also bind H2 molecules with insufficient binding energies. To increase the hydrogen binding energy to the desirable regime (between 20 and 40 kJ/mol per H2), the boron nanostructures can be suitably decorated/functionalized with some selective atoms (e.g., Li, Al, Ca, light transition metals, etc.)2.
However, transition metals are highly prone to clustering, and hence, the hydrogen storage capacities can easily decrease. Also, the first few H2 molecules can be adsorbed dissociatively (i.e., undesirable for applications at ambient conditions)24. Therefore, the dopant or decorating atoms should be rationally chosen with the following characteristics: a) they should be lightweight, b) they should not form clusters, and c) they can bind hydrogen molecularly. The element lithium (Li) seems to be ideal, as it can easily satisfy these conditions. When adsorbed or decorated, the 2s electron from the Li atom can be transferred to nanostructures (due to the difference between their electronegativity values), and hence, the Li atom can become a cation (i.e., a positively charged ion). The electric field from the dipole that is produced by the charge transfer is capable of polarizing the incoming H2 molecules (around the Li), and binding the H2 molecularly with the aforementioned desirable regime. This mechanism is referred to as charge-transfer induced polarization2,25,26. Therefore, Li-modified boron nanomaterials can potentially be HSMs.
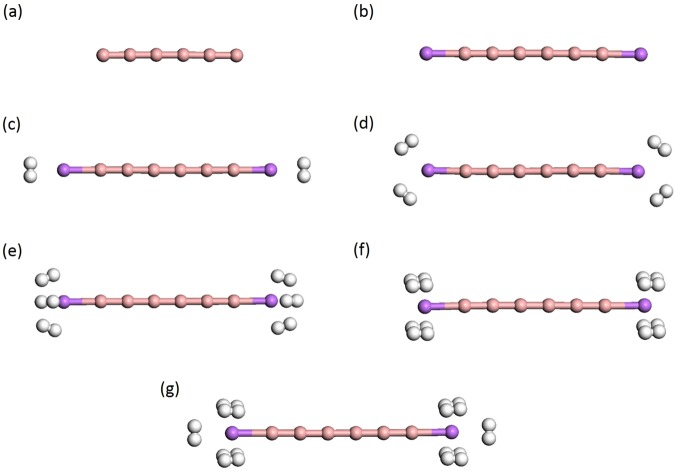
Among boron materials, there has recently been considerable interest in linear boron chains (Bn), containing n boron atoms bonded with sp1 hybridization (see Fig. 1(a)), because of their promising electronic and mechanochemical properties. Their mechanochemistry studies have revealed that, under tension, boron atoms can form linear chains27. These boron chains show an interesting reversible structural phase transition between linear two-atom-wide narrow ribbons and single-atom chains under tension. The chains and narrow ribbons are linked by a tension-driven transformation and reported to be the stable structures. Understandably, linear boron chains can potentially be HSMs, if the chains are terminated with Li atoms. Note that Li-terminated linear boron chains (Li2Bn) can be promising HSMs (see Fig. 1(b–g)), as they are lightweight materials associated with the aforementioned polarization mechanism2,25,26. However, it remains very challenging to synthesize Li2Bn, as they can possess radical character (prevalent in low-dimensional systems because of quantum confinement effect28). Therefore, predicting the electronic and hydrogen storage properties of Li2Bn could pave the way for the progress in this field, and also play an important role in selecting ideal materials for nanoelectronics and optoelectronics applications.
Figure 1.
Structures of (a) linear boron chain (B6), (b) Li-terminated linear boron chain (Li2B6), and (c–g) Li2B6 with x H2 molecules (x = 1–5) adsorbed on each Li, obtained with TAO-BLYP-D. Here, pink, purple, and white balls represent B, Li, and H atoms, respectively. For the longer Li2Bn (n = 8, 10, …, and 16), the H2 adsorption patterns remain similar.
Currently, electronic structure calculations on systems at the nanoscale are mainly performed using Kohn-Sham density functional theory (KS-DFT)29 with approximate exchange-correlation (XC) density functionals30. However, KS-DFT with traditional XC density functionals, such as BLYP-based (e.g., BLYP31,32, B3LYP33,34, and B2-PLYP35), PBE-based (e.g., PBE36, PBE037, PBE0-238, PBE0-DH39, and PBE-QIDH40), and ωB97-based (e.g., ωB9741, ωB97X41, ωB97X-D342, and ωB97X-243) functionals, may not be reliable in predicting the properties of multi-reference systems (i.e., systems possessing radical character), wherein ab initio multi-reference electronic structure methods, such as the density matrix renormalization group (DMRG) approach and multi-reference configuration interaction (MRCI) methods, are usually required44,45. Despite their high predictive accuracy, calculations based on ab initio multi-reference electronic structure methods can however be computationally infeasible for systems at the nanoscale (particularly for geometry relaxation). Consequently, the study of multi-reference systems at the nanoscale remains extremely difficult for conventional computational approaches.
Aiming to achieve a decent balance between accuracy and efficiency for the study of multi-reference systems at the nanoscale, thermally-assisted-occupation density functional theory (TAO-DFT)46 and its extensions47–49 have recently been proposed. On the basis of the physical arguments given in Section III.E of ref.46 and the numerical investigations presented in Section IV of ref.46, the static correlation energy of a system can be properly described by the entropy contribution (i.e., a function of the fictitious temperature and orbital occupation numbers (an implicit density functional)), even when a local or semilocal XC density functional is employed in TAO-DFT. Similar to the static correlation energy of a system, the entropy contribution in TAO-DFT is always nonpositive, yielding insignificant contributions for a single-reference system, and significantly lowering the total energy of a multi-reference system. Note that the inclusion of fractional occupation numbers in electronic structure calculations has been recently explored in some directions. For example, the fractional occupation number weighted electron density (FOD) analysis has been recently developed for a real-space measure and visualization of static correlation effects50,51, yielding promising applications to carbon nanoforms52.
Note that TAO-DFT is similar to KS-DFT in computational efficiency. Moreover, TAO-DFT reduces to KS-DFT when the static correlation energy of a system is insignificant, enabling a well-balanced description for both systems possessing non-radical character and systems possessing radical character53–57. In our previous TAO-DFT studies, Li-adsorbed acenes55 and Li-terminated linear carbon chains (Li2Cn)57 were found to be promising HSMs at near-ambient conditions, showing that the search for promising HSMs can be extended to large systems possessing radical character. Although Li2Cn and Li2Bn look similar in structure, their electronic and hydrogen storage properties are distinctly different. In particular, Li2Cn were found to exhibit oscillatory diradical behavior with increasing chain length57, while Li2Bn exhibit increasing polyradical character with the increase of chain length (as will be seen below). Owing to its reasonable accuracy in predicting the properties of multi-reference systems at the nanoscale, we employ TAO-DFT to predict the electronic and hydrogen storage properties of Li2Bn (n = 6, 8, …, and 16) in the present study.
Computational Details
We perform all calculations with Q-Chem 4.458. Results are obtained from TAO-BLYP-D47 (i.e., TAO-DFT employing the Becke-Lee-Yang-Parr XC density functional with dispersion corrections (BLYP-D)59 and the θ-dependent density functional based on the local density approximation (LDA)) with the fictitious temperature θ = 7 mhartree46,47, using the 6–31 G(d) basis set and the numerical grid containing 75 radial points in the Euler-Maclaurin quadrature and 302 angular points in the Lebedev grid.
Results and Discussion
Electronic Properties
To begin with, we perform spin-unrestricted TAO-BLYP-D calculations to obtain the lowest singlet and lowest triplet states of Li2Bn (n = 6, 8, …, and 16), with the respective geometries being fully relaxed57. Subsequently, we calculate the singlet-triplet energy gap of Li2Bn as
| 1 |
where ES and ET are the lowest singlet and lowest triplet energies, respectively, of Li2Bn. As presented in Fig. 2, Li2Bn (n = 6, 8, …, and 16) has a singlet ground state (i.e., similar to Li2Cn57). As n increases, EST changes drastically, implying that the electronic properties of Li2Bn can be properly tuned by changing the length of Li2Bn.
Figure 2.
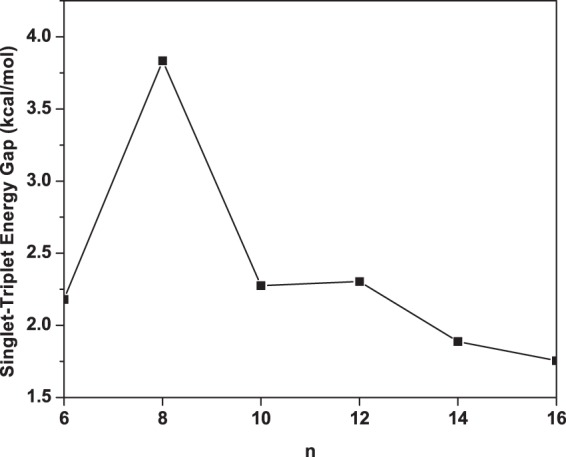
Singlet-triplet energy gap of Li2Bn, obtained with TAO-BLYP-D.
For the exact theory, the lowest singlet energies of Li2Bn obtained with spin-restricted and spin-unrestricted calculations should be identical, due to the symmetry constraint46–48,60. To see if this property remains valid here, spin-restricted TAO-BLYP-D calculations are additionally performed for the lowest singlet energies on the corresponding optimized geometries. It is found that the lowest singlet energies of Li2Bn obtained with spin-restricted and spin-unrestricted TAO-BLYP-D calculations are numerically identical, indicating that our spin-unrestricted TAO-BLYP-D calculations do not yield unphysical symmetry-breaking solutions.
Strong binding of terminating Li atoms in Li2Bn is essential for reversible hydrogen storage applications. In order to know if the terminating Li atoms are stable, we calculate the Li binding energy on Bn using57
| 2 |
where , ELi, and are the total energies of Bn, Li, and Li2Bn, respectively. Subsequently, the standard counterpoise method61 is employed to correct the basis set superposition error (BSSE) associated with Eb(Li). As can be seen in Fig. 3, the Li atoms can strongly bind with the Bn chain (and form Li2Bn) with binding energies ranging from 282 to 295 kJ/mol per Li. Such high binding energies are desirable for reversible applications, as the dopant atoms should remain bound to Bn during the desorption of hydrogen molecules. The bonding of Li to Bn should be ionic due to the electronic charge transfer from Li to Bn, which is expected to enhance the H2 adsorption to the Li atoms (as will be shown and discussed later).
Figure 3.
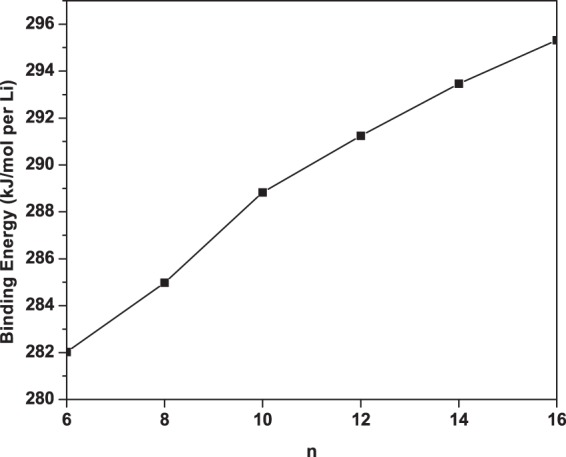
Li binding energy on Bn, obtained with TAO-BLYP-D.
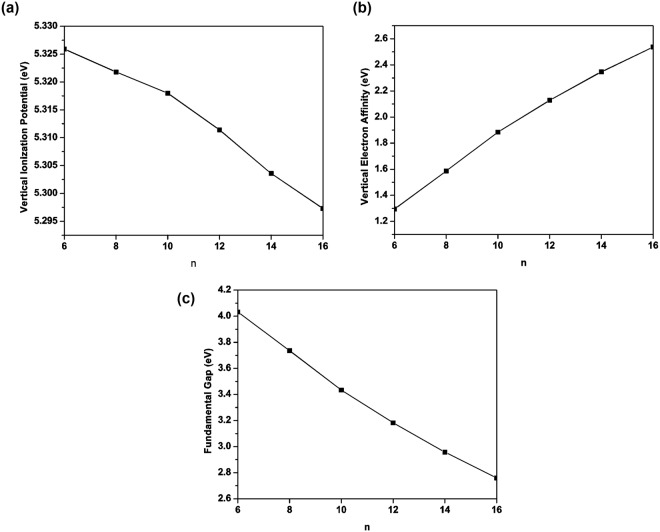
The possibility of Li2Bn for photovoltaic applications is assessed here. At the optimized geometry of the lowest singlet state (i.e., the ground state) of Li2Bn, spin-unrestricted TAO-BLYP-D is employed to calculate the vertical ionization potential (i.e., the energy difference between the cationic and neutral charge states)
| 3 |
vertical electron affinity (i.e., the energy difference between the neutral and anionic charge states)
| 4 |
and fundamental gap
| 5 |
via the Δ self-consistent field (ΔSCF) approach. As the chain length of Li2Bn increases, IPv monotonically decreases, and EAv monotonically increases, yielding a monotonically decreasing Eg (see Fig. 4). The IPv value is found to be less sensitive to the chain length of Li2Bn than the EAv and Eg values. Note also that the Eg value of Li2Bn (n = 14 and 16) is within the most interesting range (1 to 3 eV), giving promise for applications of Li2Bn in nanophotonics. Note that our theoretical results may guide further experimental studies on Li2Bn.
Figure 4.
(a) Vertical ionization potential, (b) vertical electron affinity, and (c) fundamental gap for the ground state of Li2Bn, obtained with TAO-BLYP-D.
Here, we assess the multi-reference character of Li2Bn by calculating the symmetrized von Neumann entropy47,48,53,55–57,60
| 6 |
for the ground state of Li2Bn. In Eq. (6), the occupation number of the ith orbital calculated by TAO-BLYP-D (denoted as fi), which takes a value between zero and one, is close to the ith natural orbital occupation number46–48. For a single-reference system ({fi} are approximately equal to either zero or one), SvN is negligible. However, for a multi-reference system ({fi} are distinctly different from either zero or one for active orbitals, and are approximately equal to either zero or one for other orbitals), SvN raises with the number of fractionally occupied orbitals (i.e., active orbitals). As presented in Fig. 5, SvN increases with the chain length of Li2Bn, implying that the multi-reference character of Li2Bn should generally increase with the chain length.
Figure 5.
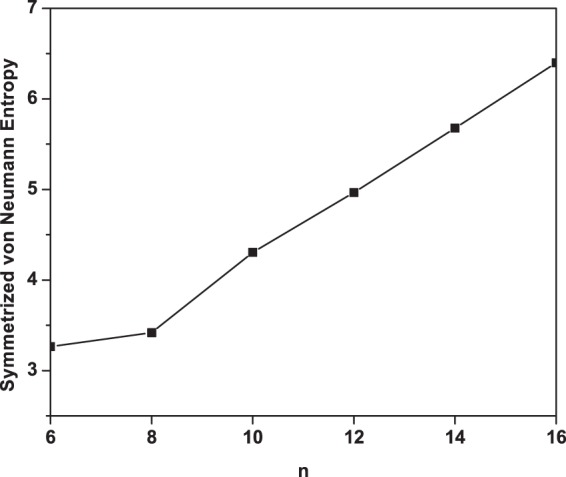
Symmetrized von Neumann entropy for the ground state of Li2Bn, obtained with TAO-BLYP-D.
To further illustrate the reasons of the increase of SvN with n, the active orbital occupation numbers for the ground state of Li2Bn, obtained with TAO-BLYP-D, are plotted in Fig. 6. For Li2Bn (containing N electrons), the highest occupied molecular orbital (HOMO) is given by the (N/2)th orbital, and the lowest unoccupied molecular orbital (LUMO) is given by the (N/2 + 1)th orbital46,48,53,56,57. As shown, the number of fractionally occupied orbitals oscillatorily increases with the chain length of Li2Bn, implying that the multi-reference character of Li2Bn should generally increase with n (see Table S1 in Supplementary Information).
Figure 6.
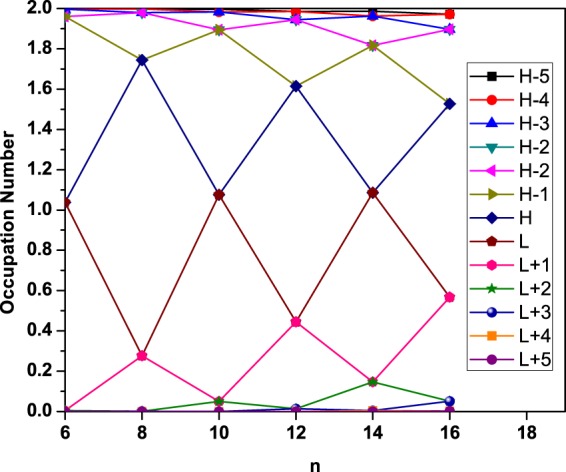
Active orbital occupation numbers (H−5, …, H−1, H, L, L+1, …, and L+5) for the ground state of Li2Bn, obtained with TAO-BLYP-D. For brevity, HOMO and LUMO are denoted as H and L, respectively.
Based on the above results, the longer Li2Bn, which have the smaller EST values, smaller Eg values, larger SvN values, and more significant polyradical character, are expected to possess stronger static correlation effects than the shorter Li2Bn. Since KS-DFT employing traditional XC density functionals cannot reliably predict the properties of systems possessing radical character, and calculations based on ab initio multi-reference electronic structure methods are computationally infeasible for systems at the nanoscale (e.g., the longer Li2Bn), it is well justified to employ TAO-DFT in the present study.
Hydrogen Storage Properties
To begin with, we first examine the potential of Bn for hydrogen storage applications. Our preliminary TAO-BLYP-D results show that Bn can only adsorb H2 molecules with very weak binding energies (i.e., less than 5 kJ/mol per H2), mainly governed by vdW interactions. Therefore, Bn can be useful for hydrogen storage only at very low temperatures. Besides, Bn can only bind very few H2 molecules, since the interactions between the adsorbed H2 molecules at short separation distances are repulsive. Therefore, the average hydrogen binding energy on Bn should decrease, as the number of the adsorbed H2 molecules increases. Accordingly, Bn should be modified to realize a promising HSM at ambient conditions.
In the following, the hydrogen storage properties of Li2Bn (n = 6, 8, …, and 16) are studied using TAO-BLYP-D. At the optimized geometry of the lowest singlet state (i.e., the ground state) of Li2Bn, we initially put x H2 molecules (x = 1–5) at several locations on the chain, and subsequently optimize the structures to get the most stable geometry. However, it is found that the H2 molecules are adsorbed at the Li sites. All the H2 molecules can be adsorbed molecularly to the Li atoms, and this molecular adsorption is preferable for practical hydrogen storage applications. Here, we calculate the average hydrogen binding energy on Li2Bn using57
| 7 |
where , , and are the total energies of H2, Li2Bn, and Li2Bn with x H2 molecules adsorbed on each Li, respectively. Necessarily, to account for BSSE, the aforementioned counterpoise method is used61. The BSSE associated with Eb(H2) is estimated to range from 2.16 to 2.69 kJ/mol per H2 for x = 1–5 (see Tables S2 and S3 in Supplementary Information). There is a significant error due to BSSE, which denotes the importance of BSSE correction in H2 adsorption binding energy calculations. As presented in Fig. 7, Eb(H2) ranges from 21 to 26 kJ/mol per H2 for x = 1–4, and ranges from 18 to 19 kJ/mol per H2 for x = 5, lying in (or very close to) the aforementioned desirable binding energy regime (between 20 and 40 kJ/mol per H2).
Figure 7.
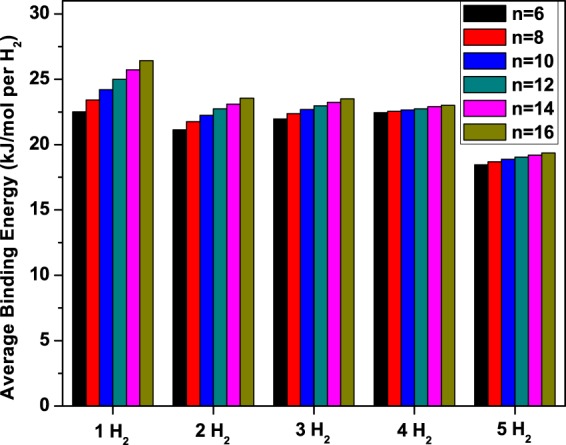
Average hydrogen binding energy on Li2Bn (n = 6, 8, …, and 16) with x H2 molecules (x = 1–5) adsorbed on each Li, obtained with TAO-BLYP-D.
Besides the average hydrogen binding energy, the successive hydrogen binding energy should also be computed to assess the actual hydrogen storage capacity. Here, we calculate the successive hydrogen binding energy on Li2Bn using57
| 8 |
Here, Eb,y(H2) is the binding energy of the yth H2 molecule (y = 1–5) on Li2Bn. Here also, the aforementioned counterpoise method61 is adopted to correct the BSSE associated with the binding energies. The BSSE associated with Eb,y(H2) is estimated to range from 1.39 to 3.18 kJ/mol per H2 for y = 1–5 (see Tables S4 and S5 in Supplementary Information). There is a significant error due to BSSE, which also denotes the importance of BSSE correction in such studies. As shown in Fig. 8, Eb,y(H2) ranges from 20 to 26 kJ/mol per H2 for y = 1–4, and ranges from 3 to 5 kJ/mol per H2 for y = 5. This denotes that only the first four H2 molecules (on each Li) are adsorbed in the desirable binding energy regime, and the fifth H2 molecule is adsorbed weakly (possibly due to vdW interactions and this is useful for hydrogen storage only at ultra low temperatures).
Figure 8.
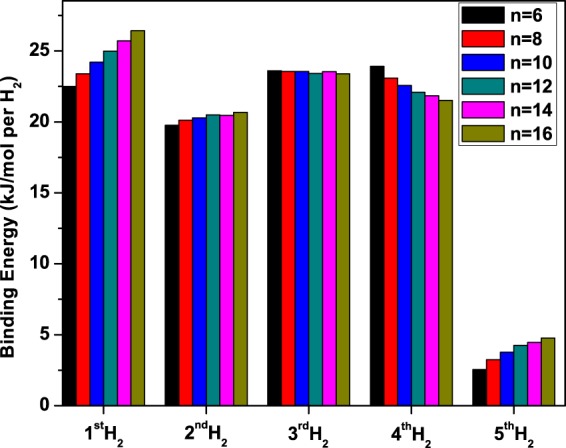
Binding energy of the yth H2 molecule (y = 1–5) on Li2Bn (n = 6, 8, …, and 16), obtained with TAO-BLYP-D.
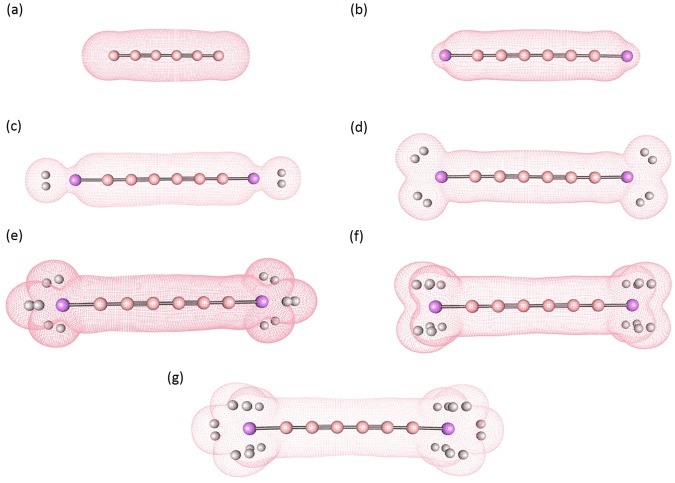
To examine the nature of the hydrogen binding energies on Li2Bn, the Li atomic charge for Li2Bn (n = 6, 8, …, and 16) with x H2 molecules (x = 0–5) adsorbed on each Li (see Fig. 9), is calculated by the CHELPG (CHarges from ELectrostatic Potentials using a Grid based method) scheme62. In addition, the isosurfaces of charge density for B6 and Li2B6 with x H2 molecules (x = 0–5) adsorbed on each Li are also plotted (see Fig. 10). For the longer Li2Bn, the isosurfaces of charge density remain similar. The charge transfer is from Li to Bn in Li2Bn due to the difference between their electronegativity values, yielding 0.6–0.7 |e| on each Li for Li2Bn. This is also evidenced by the depleted charge around each Li. While the charge depleted Li is able to bind more than one H2 molecule, the Li atomic charge reduces with the number of the adsorbed H2 molecules (x = 0–3). This kind of adsorption should be due to that the charge depleted Li can polarize the incoming H2 molecules (i.e., governed by the aforementioned charge-induced dipole interactions2,25,26), yielding the enhanced hydrogen binding energy and high hydrogen storage capacity for Li2Bn. However, when there are many H2 molecules adsorbed on each Li (e.g., x = 4), the charge densities of the Li atom and the adsorbed H2 molecules can be substantially overlapped, which can enhance orbital interactions3,7. Therefore, when there are many H2 molecules adsorbed on each Li, orbital interactions are expected to be important for the hydrogen binding energies as well. Because of the enhanced orbital interactions, when the fourth H2 molecule is adsorbed on the Li atom, some electronic charge can be moved from the Li atom to the adsorbed H2 molecules, yielding a slight increase in the positive charge on Li. As the fifth H2 molecule is adsorbed very weakly (primarily due to vdW interactions), there is no significant change in the charge on Li. Consequently, the hydrogen adsorption in Li2Bn can be due to not only charge-induced dipole interactions, but also orbital interactions and vdW interactions.
Figure 9.
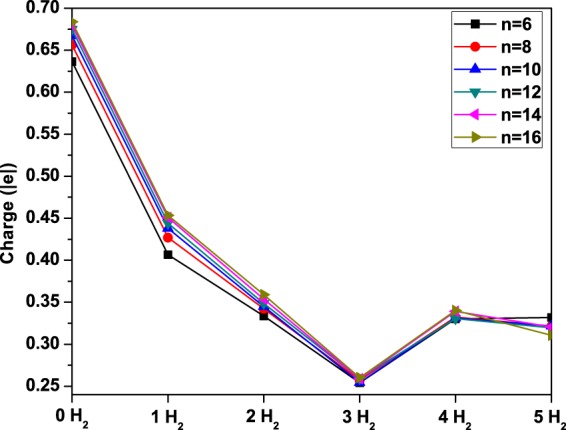
Li atomic charge for Li2Bn (n = 6, 8, …, and 16) with x H2 molecules (x = 0–5) adsorbed on each Li, obtained with TAO-BLYP-D. Here, the CHELPG scheme is employed to calculate the Li atomic charge.
Figure 10.
Isosurfaces of charge density (the isovalue is 0.02 e/Å3) for (a) B6 and (b–g) Li2B6 with x H2 molecules (x = 0–5) adsorbed on each Li, obtained with TAO-BLYP-D. Here, pink, purple, and white balls represent B, Li, and H atoms, respectively.
For practical applications, we estimate the desorption temperature, TD, of the adsorbed H2 molecules by
| 9 |
Note that Eq. (9) is the van’t Hoff equation55,57,63,64, where Eb(H2) is calculated using Eq. (7). As suggested by previous studies55,57, the total entropy change before and after the hydrogenation, ΔS, is approximated by the change in hydrogen entropy from gas to liquid phase (ΔS = 13.819R65). Besides, p0, peq, kB, and R are the standard atmospheric pressure (1 bar), the equilibrium pressure, the Boltzmann constant, and the gas constant, respectively. As listed in Table 1, TD for Li2Bn (n = 6, 8, …, and 16) with x H2 molecules (x = 1–4) adsorbed on each Li, is calculated by Eq. (9) at peq = 1.5 bar8 and at peq = 1 bar. Since the Eb(H2) values range from 21.13 to 26.42 kJ/mol per H2 for x = 1–4, the respective TD values range from 179 to 223 K at peq = 1.5 bar, and range from 184 to 230 K at peq = 1 bar. These desorption temperatures are all well above 77 K (i.e., the boiling point of liquid nitrogen), which can be easily achieved. Therefore, Li2Bn (n = 6, 8, …, and 16) can be promising HSMs for storing and releasing H2 at temperatures much higher than the boiling point of liquid nitrogen.
Table 1.
Hydrogen desorption temperature TD (K) [calculated using Eq. (9) at peq = 1.5 (bar) and at peq = 1 (bar)] and hydrogen gravimetric storage capacity Cg (wt%) [calculated using Eq. (10)] for Li2Bn (n = 6, 8, …, and 16) with x H2 molecules (x = 1–4) adsorbed on each Li, obtained with TAO-BLYP-D.
| n | T D | C g | |||||||
|---|---|---|---|---|---|---|---|---|---|
| peq = 1.5 | peq = 1 | ||||||||
| 1 H2 | 2 H2 | 3 H2 | 4 H2 | 1 H2 | 2 H2 | 3 H2 | 4 H2 | ||
| 6 | 190 | 179 | 186 | 190 | 196 | 184 | 191 | 195 | 17.0 |
| 8 | 198 | 184 | 189 | 191 | 204 | 189 | 195 | 196 | 13.8 |
| 10 | 205 | 188 | 192 | 192 | 211 | 194 | 197 | 197 | 11.7 |
| 12 | 211 | 192 | 194 | 192 | 218 | 198 | 200 | 198 | 10.1 |
| 14 | 218 | 195 | 197 | 194 | 224 | 201 | 202 | 199 | 8.9 |
| 16 | 223 | 199 | 199 | 195 | 230 | 205 | 204 | 200 | 7.9 |
Here, Cg is calculated only for x = 4.
Since Li2Bn (n = 6, 8, …, and 16) is able to adsorb a total of 8 H2 molecules (i.e., 4 per Li), where both the average hydrogen binding energies and successive hydrogen binding energies are in the aforementioned desirable regime, we calculate the respective hydrogen gravimetric storage capacity using57
| 10 |
where is the mass of Li2Bn, and is the mass of H2. As shown in Table 1, Cg ranges from 7.9 to 17.0 wt%, achieving the USDOE ultimate goal of 6.5 wt%. It can be inferred from the H2 adsorption patterns of Li2Bn that Li2Bn is able to adsorb up to a total of 8 H2 molecules with both the average hydrogen binding energies and successive hydrogen binding energies being in the desirable regime, independent of the value of n. Accordingly, the Cg value of Li2Bn should decrease with increasing chain length. Nevertheless, it may not be justified to directly compare the Cg values presented in this work with the USDOE ultimate goal of 6.5 wt%, as the latter is for the entire system of hydrogen storage (which includes the HSM, surrounding container, insulation equipment, and so on)6. However, the Cg values of Li2Bn presented in this work are rather high (particularly for the smaller n), when compared with the USDOE ultimate goal. Therefore, the entire systems of hydrogen storage via Li2Bn can still be promising HSMs for storing and releasing H2 at temperatures much higher than the boiling point of liquid nitrogen.
Conclusions
In conclusion, because of the recent developments of TAO-DFT, calculations on large systems possessing radical character are now feasible. Accordingly, it is now possible to look for desirable HSMs among multi-reference systems at the nanoscale (i.e., extremely difficult systems for conventional computational approaches). In this work, the electronic properties (e.g., Eb(Li), EST, IPv, EAv, Eg, SvN, and the occupation numbers of active orbitals) and hydrogen storage properties (e.g., Eb(H2), Eb,y(H2), TD, and Cg) of Li2Bn (n = 6, 8, …, and 16) have been studied using TAO-DFT. As the ground states of Li2Bn exhibit multi-reference character, KS-DFT with traditional XC functionals may not reliably predict the properties of Li2Bn, and calculations based on ab initio multi-reference electronic structure methods can be computationally infeasible due to the large electronic systems considered here. Therefore, it is well justified to adopt TAO-DFT in the present study. From our TAO-DFT results, Li2Bn is able to adsorb a total of 8 H2 molecules, where both the average hydrogen binding energies and successive hydrogen binding energies are in the desirable regime (between 20 and 40 kJ/mol per H2). Hence, the Cg values of Li2Bn range from 7.9 to 17.0 wt%, achieving the USDOE ultimate goal of 6.5 wt%. Accordingly, Li2Bn could be promising HSMs for storing and releasing H2 at temperatures much higher than the boiling point of liquid nitrogen, which can be easily achieved.
Because of recent advances in the synthesis of nanomaterials, it may be feasible to practically realize hydrogen storage via Li2Bn. For example, Li2Bn can be adopted as building blocks. As proposed by Liu et al.66, we can connect Li-coated fullerenes with Li2Bn, which may be promising HSMs as well. It will then be necessary to comprehensively study the relevant properties of these systems, which can be a possible future study. Furthermore, as the syntheses of Pt-terminated linear carbon chains have been feasible67, the syntheses of Li2Bn may be feasible in near future, and are now open to experimentalists.
Electronic supplementary material
Acknowledgements
This work was supported by the Ministry of Science and Technology of Taiwan (Grant Nos MOST107-2628-M-002-005-MY3; MOST104-2628-M-002-011-MY3), National Taiwan University (Grant Nos NTU-CC-107L892906; NTU-CCP-106R891706; NTU-CDP-105R7818), and the National Center for Theoretical Sciences of Taiwan.
Author Contributions
This work was initiated and designed by S.S. and J.-D.C. The calculations were performed by S.S. The data analysis was performed by S.S. and J.-D.C. The manuscript was written by S.S. and J.-D.C.
Competing Interests
The authors declare no competing interests.
Footnotes
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Supplementary information accompanies this paper at 10.1038/s41598-018-31947-9.
References
- 1.Schlapbach L, Züttel A. Hydrogen-storage materials for mobile applications. Nature. 2001;414:353–358. doi: 10.1038/35104634. [DOI] [PubMed] [Google Scholar]
- 2.Jena P. Materials for hydrogen storage: past, present, and future. J. Phys. Chem. Lett. 2011;2:206–211. doi: 10.1021/jz1015372. [DOI] [Google Scholar]
- 3.Park N, et al. Progress on first-principles-based materials design for hydrogen storage. PNAS. 2012;109:19893–19899. doi: 10.1073/pnas.1217137109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Dalebrook AF, Gan W, Grasemann M, Moret S, Laurenczy G. Hydrogen storage: beyond conventional methods. Chem. Commun. 2013;49:8735–8751. doi: 10.1039/c3cc43836h. [DOI] [PubMed] [Google Scholar]
- 5.Durbin D, Malardier-Jugroot C. Review of hydrogen storage techniques for on board vehicle applications. Int. J. Hydrogen Energy. 2013;38:14595–14617. doi: 10.1016/j.ijhydene.2013.07.058. [DOI] [Google Scholar]
- 6.U. S. Department of Energy. Target explanation document: onboard hydrogen storage for light-duty fuel cell vehicles. Technical report. Available at: https://www.energy.gov/eere/fuelcells/hydrogen-storage (Accessed: March 2018) (2017).
- 7.Lochan RC, Head-Gordon M. Computational studies of molecular hydrogen binding affinities: the role of dispersion forces, electrostatics, and orbital interactions. Phys. Chem. Chem. Phys. 2006;8:1357–1370. doi: 10.1039/b515409j. [DOI] [PubMed] [Google Scholar]
- 8.Bhatia SK, Myers AL. Optimum conditions for adsorptive storage. Langmuir. 2006;22:1688–1700. doi: 10.1021/la0523816. [DOI] [PubMed] [Google Scholar]
- 9.Sumida K, et al. Impact of metal and anion substitutions on the hydrogen storage properties of M-BTT metal-organic frameworks. J. Am. Chem. Soc. 2013;135:1083–1091. doi: 10.1021/ja310173e. [DOI] [PubMed] [Google Scholar]
- 10.Georgakilas V, Perman JA, Tucek J, Zboril R. Broad family of carbon nanoallotropes: classification, chemistry, and applications of fullerenes, carbon dots, nanotubes, graphene, nanodiamonds, and combined superstructures. Chem. Rev. 2015;115:4744–4822. doi: 10.1021/cr500304f. [DOI] [PubMed] [Google Scholar]
- 11.Geim AK, Grigorieva IV. Van der Waals heterostructures. Nature. 2013;499:419–425. doi: 10.1038/nature12385. [DOI] [PubMed] [Google Scholar]
- 12.Tan C, et al. Recent advances in ultrathin two-dimensional nanomaterials. Chem. Rev. 2017;117:6225–6231. doi: 10.1021/acs.chemrev.6b00558. [DOI] [PubMed] [Google Scholar]
- 13.Zhai H-J, Kiran B, Li J, Wang L-S. Hydrocarbon analogues of boron clusters–planarity, aromaticity and antiaromaticity. Nat. Mater. 2003;2:827–833. doi: 10.1038/nmat1012. [DOI] [PubMed] [Google Scholar]
- 14.Arvanitidis AG, Tai TB, Nguyen MT, Ceulemans A. Quantum rules for planar boron nanoclusters. Phys. Chem. Chem. Phys. 2014;16:18311. doi: 10.1039/C4CP02323D. [DOI] [PubMed] [Google Scholar]
- 15.Sergeeva AP, et al. Understanding boron through size-selected clusters: structure, chemical bonding, and fluxionality. Acc. Chem. Res. 2014;47:1349–1358. doi: 10.1021/ar400310g. [DOI] [PubMed] [Google Scholar]
- 16.Piazza ZA, et al. Planar hexagonal B36 as a potential basis for extended single-atom layer boron sheets. Nat. Commun. 2014;5:3113. doi: 10.1038/ncomms4113. [DOI] [PubMed] [Google Scholar]
- 17.Zhai H-J, et al. Observation of an all-boron fullerene. Nat. Chem. 2014;6:727–731. doi: 10.1038/nchem.1999. [DOI] [PubMed] [Google Scholar]
- 18.Sergeeva AP, et al. B22− and B23−: all-boron analogues of anthracene and phenanthrene. J. Am. Chem. Soc. 2012;134:18065–18073. doi: 10.1021/ja307605t. [DOI] [PubMed] [Google Scholar]
- 19.Mannix AJ, et al. Synthesis of borophenes: anisotropic, two-dimensional boron polymorphs. Science. 2015;350:1513–1516. doi: 10.1126/science.aad1080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Feng B, et al. Experimental realization of two-dimensional boron sheets. Nat. Chem. 2016;8:563–568. doi: 10.1038/nchem.2491. [DOI] [PubMed] [Google Scholar]
- 21.Tian J, et al. One-dimensional boron nanostructures: prediction, synthesis, characterizations, and applications. Nanoscale. 2010;2:1375. doi: 10.1039/c0nr00051e. [DOI] [PubMed] [Google Scholar]
- 22.Feng B, et al. Dirac fermions in borophene. Phys. Rev. Lett. 2017;118:096401. doi: 10.1103/PhysRevLett.118.096401. [DOI] [PubMed] [Google Scholar]
- 23.Moradi M, Bagheri Z, Bodaghi A. Li interactions with the B40 fullerene and its application in Li-ion batteries. Physica E. 2017;89:148–154. doi: 10.1016/j.physe.2017.02.018. [DOI] [Google Scholar]
- 24.Sun Q, Wang Q, Jena P, Kawazoe Y. Clustering of Ti on a C60 surface and its effect on hydrogen storage. J. Am. Chem. Soc. 2005;127:14582–14583. doi: 10.1021/ja0550125. [DOI] [PubMed] [Google Scholar]
- 25.Niu J, Rao BK, Jena P, Manninen M. Interaction of H2 and He with metal atoms, clusters, and ions. Phys. Rev. B. 1995;51:4475. doi: 10.1103/PhysRevB.51.4475. [DOI] [PubMed] [Google Scholar]
- 26.Froudakis GE. Why alkali-metal-doped carbon nanotubes possess high hydrogen uptake. Nano Lett. 2001;1:531–533. doi: 10.1021/nl0155983. [DOI] [Google Scholar]
- 27.Liu M, Artyukhov VI, Yakobson BI. Mechanochemistry of one-dimensional boron: structural and electronic transitions. J. Am. Chem. Soc. 2017;139:2111–2117. doi: 10.1021/jacs.6b12750. [DOI] [PubMed] [Google Scholar]
- 28.Brus L. Size, dimensionality, and strong electron correlation in nanoscience. Acc. Chem. Res. 2014;47:2951–2959. doi: 10.1021/ar500175h. [DOI] [PubMed] [Google Scholar]
- 29.Kohn W, Sham LJ. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965;140:A1133–A1138. doi: 10.1103/PhysRev.140.A1133. [DOI] [Google Scholar]
- 30.Seenithurai S, Kodi Pandyan R, Vinodh Kumar S, Saranya C, Mahendran M. Li-decorated double vacancy graphene for hydrogen storage application: a first principles study. Int. J. Hydrogen Energy. 2014;39:11016–11026. doi: 10.1016/j.ijhydene.2014.05.068. [DOI] [Google Scholar]
- 31.Becke AD. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A. 1988;38:3098–3100. doi: 10.1103/PhysRevA.38.3098. [DOI] [PubMed] [Google Scholar]
- 32.Lee C, Yang W, Parr RG. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B. 1988;37:785–789. doi: 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
- 33.Becke AD. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993;98:5648–5652. doi: 10.1063/1.464913. [DOI] [Google Scholar]
- 34.Stephens PJ, Devlin FJ, Chabalowski CF, Frisch MJ. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem. 1994;98:11623–11627. doi: 10.1021/j100096a001. [DOI] [Google Scholar]
- 35.Grimme S. Semiempirical hybrid density functional with perturbative second-order correlation. J. Chem. Phys. 2006;124:034108. doi: 10.1063/1.2148954. [DOI] [PubMed] [Google Scholar]
- 36.Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996;77:3865–3868. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- 37.Adamo C, Barone V. Toward reliable density functional methods without adjustable parameters: the PBE0 model. J. Chem. Phys. 1999;110:6158–6170. doi: 10.1063/1.478522. [DOI] [Google Scholar]
- 38.Chai J-D, Mao S-P. Seeking for reliable double-hybrid density functionals without fitting parameters: the PBE0-2 functional. Chem. Phys. Lett. 2012;538:121–125. doi: 10.1016/j.cplett.2012.04.045. [DOI] [Google Scholar]
- 39.Brémond E, Adamo C. Seeking for parameter-free double-hybrid functionals: the PBE0-DH model. J. Chem. Phys. 2011;135:024106. doi: 10.1063/1.3604569. [DOI] [PubMed] [Google Scholar]
- 40.Brémond E, Sancho-García JC, Pérez-Jiménez AJ, Adamo C. Communication: double-hybrid functionals from adiabatic-connection: the QIDH model. J. Chem. Phys. 2014;141:031101. doi: 10.1063/1.4890314. [DOI] [PubMed] [Google Scholar]
- 41.Chai J-D, Head-Gordon M. Systematic optimization of long-range corrected hybrid density functionals. J. Chem. Phys. 2008;128:084106. doi: 10.1063/1.2834918. [DOI] [PubMed] [Google Scholar]
- 42.Lin Y-S, Li G-D, Mao S-P, Chai J-D. Long-range corrected hybrid density functionals with improved dispersion corrections. J. Chem. Theory Comput. 2013;9:263–272. doi: 10.1021/ct300715s. [DOI] [PubMed] [Google Scholar]
- 43.Chai J-D, Head-Gordon M. Long-range corrected double-hybrid density functionals. J. Chem. Phys. 2009;131:174105. doi: 10.1063/1.3244209. [DOI] [PubMed] [Google Scholar]
- 44.Mizukami W, Kurashige Y, Yanai T. More π electrons make a difference: emergence of many radicals on graphene nanoribbons studied by ab initio DMRG theory. J. Chem. Theory and Comput. 2013;9:401–407. doi: 10.1021/ct3008974. [DOI] [PubMed] [Google Scholar]
- 45.Gryn’ova G, Coote ML, Corminboeuf C. Theory and practice of uncommon molecular electronic configurations. WIREs Comput. Mol. Sci. 2015;5:440–459. doi: 10.1002/wcms.1233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Chai J-D. Density functional theory with fractional orbital occupations. J. Chem. Phys. 2012;136:154104. doi: 10.1063/1.3703894. [DOI] [PubMed] [Google Scholar]
- 47.Chai J-D. Thermally-assisted-occupation density functional theory with generalized-gradient approximations. J. Chem. Phys. 2014;140:18A521. doi: 10.1063/1.4867532. [DOI] [PubMed] [Google Scholar]
- 48.Chai J-D. Role of exact exchange in thermally-assisted-occupation density functional theory: a proposal of new hybrid schemes. J. Chem. Phys. 2017;146:044102. doi: 10.1063/1.4974163. [DOI] [PubMed] [Google Scholar]
- 49.Lin C-Y, Hui K, Chung J-H, Chai J-D. Self-consistent determination of the fictitious temperature in thermally-assisted-occupation density functional theory. RSC Adv. 2017;7:50496–50507. doi: 10.1039/C7RA10241K. [DOI] [Google Scholar]
- 50.Grimme S, Hansen A. A practicable real-space measure and visualization of static electron-correlation effects. Angew. Chem. Int. Ed. 2015;54:12308–12313. doi: 10.1002/anie.201501887. [DOI] [PubMed] [Google Scholar]
- 51.Bauer CA, Hansen A, Grimme S. The fractional occupation number weighted density as a versatile analysis tool for molecules with a complicated electronic structure. Chem. Eur. J. 2017;23:6150–6164. doi: 10.1002/chem.201604682. [DOI] [PubMed] [Google Scholar]
- 52.Pérez-Guardiola A, et al. The role of topology in organic molecules: origin and comparison of the radical character in linear and cyclic oligoacenes and related oligomers. Phys. Chem. Chem. Phys. 2018;20:7112–7124. doi: 10.1039/C8CP00135A. [DOI] [PubMed] [Google Scholar]
- 53.Wu C-S, Chai J-D. Electronic properties of zigzag graphene nanoribbons studied by TAO-DFT. J. Chem. Theory Comput. 2015;11:2003–2011. doi: 10.1021/ct500999m. [DOI] [PubMed] [Google Scholar]
- 54.Yeh C-N, Chai J-D. Role of Kekulé and non-Kekulé structures in the radical character of alternant polycyclic aromatic hydrocarbons: a TAO-DFT study. Sci. Rep. 2016;6:30562. doi: 10.1038/srep30562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Seenithurai S, Chai J-D. Effect of Li adsorption on the electronic and hydrogen storage properties of acenes: a dispersion-corrected TAO-DFT study. Sci. Rep. 2016;6:33081. doi: 10.1038/srep33081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Wu C-S, Lee P-Y, Chai J-D. Electronic properties of cyclacenes from TAO-DFT. Sci. Rep. 2016;6:37249. doi: 10.1038/srep37249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Seenithurai S, Chai J-D. Effect of Li termination on the electronic and hydrogen storage properties of linear carbon chains: a TAO-DFT study. Sci. Rep. 2017;7:4966. doi: 10.1038/s41598-017-05202-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Shao Y, et al. Advances in molecular quantum chemistry contained in the Q-Chem 4 program package. Mol. Phys. 2015;113:184–215. doi: 10.1080/00268976.2014.952696. [DOI] [Google Scholar]
- 59.Grimme S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006;27:1787–1799. doi: 10.1002/jcc.20495. [DOI] [PubMed] [Google Scholar]
- 60.Rivero P, Jiménez-Hoyos CA, Scuseria GE. Entanglement and polyradical character of polycyclic aromatic hydrocarbons predicted by projected Hartree“-Fock theory. J. Phys. Chem. B. 2013;117:12750–12758. doi: 10.1021/jp401478v. [DOI] [PubMed] [Google Scholar]
- 61.Boys SF, Bernardi F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970;19:553–566. doi: 10.1080/00268977000101561. [DOI] [Google Scholar]
- 62.Breneman CM, Wiberg KB. Determining atom-centered monopoles from molecular electrostatic potentials. The need for high sampling density in formamide conformational analysis. J. Comput. Chem. 1990;11:361–373. doi: 10.1002/jcc.540110311. [DOI] [Google Scholar]
- 63.Qiu N-X, Zhang C-H, Xue Y. Tuning hydrogen storage in lithium-functionalized BC2N sheets by doping with boron and carbon. Chem Phys Chem. 2014;15:3015–3025. doi: 10.1002/cphc.201402246. [DOI] [PubMed] [Google Scholar]
- 64.Durgun E, Ciraci S, Yildirim T. Functionalization of carbon-based nanostructures with light transition-metal atoms for hydrogen storage. Phys. Rev. B. 2008;77:085405. doi: 10.1103/PhysRevB.77.085405. [DOI] [Google Scholar]
- 65.Lemmon, E. W. In Handbook of Chemistry and Physics 96th edn (eds Haynes, W. M. et al.) Section 6, 21–37 (CRC Press, 2016).
- 66.Liu C-S, An H, Guo L-J, Zeng Z, Ju X. Theoretical realization of cluster-assembled hydrogen storage materials based on terminated carbon atomic chains. J. Chem. Phys. 2011;134:024522. doi: 10.1063/1.3526744. [DOI] [PubMed] [Google Scholar]
- 67.Kano E, Takeguchi M, Fujita J-I, Hashimoto A. Direct observation of Pt-terminating carbyne on graphene. Carbon. 2014;80:382–386. doi: 10.1016/j.carbon.2014.08.077. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.