The origin and early evolution of life in chemical composition space

Abstract

Life can be viewed as a localized chemical system that sits in the basin of attraction of a metastable dynamical attractor state that remains out of equilibrium with the environment. To explore the implications of this conception, I introduce an abstract coordinate system, chemical composition (CC Space), which summarizes the degree to which chemical systems are out of equilibrium with the bulk environment. A system’s chemical disequilibrium (CD) is defined to be proportional to the Euclidean distance between the composition of a small region of physical space, a pixel, and the origin of CC space. Such a model implies that new living states arise through chance changes in local chemical concentration (“mutations”) that cause chemical systems to move in CC space and enter the basin of attraction of a life state. The attractor of a life state comprises an autocatalytic set of chemicals whose essential (“keystone”) species are produced at a higher rate than they are lost to the environment by diffusion, such that spatial growth of the life state is expected. This framework suggests that new life states are most likely to form at the interface between different physical phases, where the rate of diffusion of keystone species is tied to the low-diffusion regime, whereas food and waste products are subject to the more diffusive regime. Once life nucleates, for example on a mineral surface, it will tend to grow and generate variants as a result of additional mutations that find alternative life states. By jumping from life state to life state, systems can eventually occupy areas of CC space that are too far out of equilibrium with the environment to ever arise in a single mutational step. Furthermore, I propose that variation in the capacity of different surface associated life states to persist and compete may systematically favor states that have higher chemical disequilibrium. The model also suggests a simple and predictable path from surface-associated life to cell-like individuation. This dynamical systems theoretical framework provides an integrated view of the origin and early evolution of life and supports novel empirical approaches.

All cellular life that we know of is organized in cells that depend upon biopolymers to transfer information across generations and to fulfill the essential chemical functions of life. However, just because our experience is limited to such life forms does not mean that this is the only way of being alive. For one thing, we do not know if there might be other kinds of entities that can evolve adaptively, justifying them being called alive, that do not form discrete cells and/or do not contain informational biopolymers. For another, if we wed ourselves too strongly to the notion that living systems must be composed of discretely individuated genetically-encoded units in order to evolve adaptively, then we close off the possibility that some or all of these attributes could have arisen via a prior adaptive process (Baum, 2015). Thus, constructive research into the origin of life needs a general conceptual framework for thinking about life and its evolution within which cellular life is a special case.

In this paper I explore such a generic description of life and use it to explain how life forms that we see today can have come to be so chemically weird. After all, one thing that is striking about life is its apparent ability to overcome the second law of thermodynamics and become more out of equilibrium with its environment over evolutionary time. The key is to craft a conceptual framework in which tendencies (if present) can readily be understood in relation to the expected environmental equilibration point. Here, I propose that living systems correspond to metastable attractor states that tend to remain out equilibrium with the environment and then use this framework to explore the earliest emergence of life from non-life, its evolutionary path towards complexification, and the causes and consequences of cellular encapsulation.

Chemical composition space

Stipulating that life is a spatially localized, chemical phenomenon that uses fluxes of energy and chemical foods to overcome entropic decay and/or to grow, it is ideal to visualize an abstract space that is conditioned upon the expected concentrations of chemical species in the absence of life-like processes. We will achieve this by considering the concentrations of all chemical species in a small but finite area of physical space, a pixel¹, relative to these same chemicals’ concentrations in the surrounding environment.

Suppose that we had complete knowledge of the kinetics of all possible chemical reactions. In such a case, given the concentrations of all chemical species (X₁, X₂, X₃…X_N) in a single physical pixel, p, surrounded by pixels that are at equilibrium with the environment, at a certain time, t, we would be able to calculate the expected changes in concentration of all species in p:$d{[X_{1-N}]}_p/dt$.

Imagine a bulk environment whose average chemical composition, [X_1-N]_e, remains constant regardless of the presence or absence of life states. The current state of a certain pixel in this environment can be summarized by placing its composition into an abstract multidimensional space in which each axis² is the difference between the concentration of a certain chemical species X in p, [X]_p, and in the environmental flux, [X]_e, weighted by the internal chemical energy of that chemical, _Ux (the reasoning behind this weighting will be explained shortly). Thus, the coordinate of p in this abstract space is: $U_{x1}({[X_1]}_{\text{p}}–{[{\text{X}}_1]}_e),U_{x2}({[{\text{X}}_2]}_{\text{p}}–{[{\text{X}}_2]}_e),U_{x3}({[{\text{X}}_3]}_{\text{p}}–{[{\text{X}}_3]}_e)\dots U_{xN}({[{\text{X}}_N]}_{\text{p}}–{[{\text{X}}_N]}_e)$.

By summarizing concentration differences between the pixel and the environment, chemical composition (CC) space allows us to capture the notion that a living pixel is one that is far from being in equilibrium with the environment that it lives in. Weighting by energy content is needed, however, since we are not equally concerned with the local concentration of all chemical species, but specifically of high-energy species that would be unlikely to be present at high concentrations by chance. Finding a pixel of concentrated water in an environment rich in dihydrogen and dioxygen would hardly be remarkable. But finding peptides in an environment through which ammonia and carbon dioxide flow might be suggestive of life-like activity. To capture this factor, I propose weighting the coordinate system such that the position of a pixel on an axis is proportional to the probability that this chemical species would be formed and then concentrated to such an extent by chance (i.e., without living systems). I recognize that the summation over the bond energies of chemical species, its internal energy, is not a practical (i.e., measurable) attribute in most cases, but I believe that using it as a weighting function is sufficient for the conceptual exploration we will be conducting here.

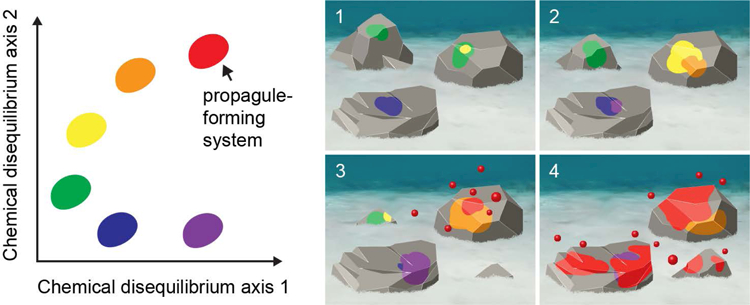
Consider a physical pixel, p, that is surrounded by pixels that are at equilibrium with the environmental flux. The concentrations of a certain chemical species, X, at p may be lower than in its surrounding pixels if the chemical reactions occurring at p use more of X than they produce. This means that on some axes of CC space, p may be to the left of the origin. However, given that life’s novelty entails maintaining certain chemicals at high local concentration, my illustrative figures will focus only on those dimensions for which p has positive values. Viewing the environmental flux as food, chemicals in p whose current concentrations exceed that in the flux, the non-food chemicals³, must have been produced in p. Figure 1 represents an idealized sketch of CC space (not physical space), compressed onto two arbitrary axes.

Fig. 1.

Illustration of chemical composition (CC) space, where each point corresponds to the difference in concentration of all chemical species between a pixel in physical space, [X_i]_p, and its environment, [X_i]_e, weighted by the internal energy of that chemical species U_i. CC space has as many axes as there are chemical species, but just two axes are shown for illustrative purposes. The streaks depict the expected change in chemical compositions of a pixel in physical space as a consequence of chemical reactions occurring in the pixel, in the absence of noise or interactions with other pixels. The shaded areas correspond to the zones of attraction around three different metastable attractors, here interpreted as life states.

The origin of this coordinate system corresponds to a pixel that is in complete equilibrium with the environmental flux. Even in an idealized environment with constant flux, individual pixels will not all sit exactly on the origin. Microscale stochasticity ensures that any given pixel is likely to deviate from the environmental mean. However, if all that is at play is chance, then the probability of a pixel being at a certain CC coordinate will decline with the distance of that coordinate to the origin: points distant from the origin cannot be found by chance but require some long-term, adaptive process. Taking the view that one of the most important challenges for origin of life theory is to explain how life comes to be exceedingly out of chemical equilibrium with the environment, an important feature of chemical composition space is a pixel’s Euclidean distance (see, Intoy et al., 2016) from the origin, which can be interpreted as a measure of chemical disequilibrium (CD):

$$C{D}_p=\sqrt{{(U_{{\text{X}}_1}([{\text{X}}_1]p–[{\text{X}}_1]e))}^2+{(U_{{\text{X}}_2}([{\text{X}}_2]p–[{\text{X}}_2]e))}^2}+{(U_{{\text{X}}_3}([{\text{X}}_3]p–[{\text{X}}_3]e))}^2+\dots +{(U_{{\text{X}}_N}([{\text{X}}_N]p–[{\text{X}}_N]e))}^2$$ (1)

To a first approximation, changes in the chemical composition of a pixel, dCC/dt will depend on four factors: (a) reactions occurring among the chemicals currently at p, as governed by their current concentrations and the kinetic rules of the full dynamical system,(b) the diffusive exchange of chemicals between p and the bulk environment, (c) the diffusive exchange of chemicals between p and physically adjacent pixels⁴, and (d) chance fluctuations. The first three factors can be represented as expected vectors of change in the position of p in CC space. The first factor yields a vector that could point in any direction in any axis depending on the kinetics of all reactions in the dynamical system. The second factor provides a constant vector pointing towards the origin, whose magnitude is proportional to the distance from the origin, scaled by the rate of diffusion. The third factor yields a vector pointing towards the concentrations in the adjacent pixel(s), scaled by diffusion (if adjacent pixels are at equilibrium with the environment, then this vector will be identical to the preceding). The magnitude and direction of the streaks shown in Figure 1 represent the expected changes in a pixel’s chemical composition over time, which would be a summation over the three deterministic factors just listed. However, the actual change in chemical composition experienced by a pixel would also be affected by the fourth factor, chance. Such chance fluctuations can result in either increases or decreases in concentration of each chemical species, with the expected change in any one chemical’s concentration being zero. While the distribution of expected concentration changes by chance is not simple (Debenedetti, 1987), it stands to reason that greater changes in concentration are less likely than smaller fluctuations.

Considering a focal pixel in physical space, and assuming (for now) that adjacent pixels are in equilibrium with the environment, a few generalities are worth highlighting. In the absence of chemical reactions occurring in p, p will move towards the origin of abstract CC space, the point of zero disequilibrium. This aligns with intuition: unless active processes are at play, chemical systems will equilibrate with the environment. However, p’s movement towards the origin in CC space can be deflected or reversed by chemical reactions occurring in p. This occurs because kinetic blocks can combine with continuous chemical inputs from the environmental flux to prevent rapid equilibration.

CC space as a whole can be imagined as being covered by a field of vectors that correspond to the expected changes chemical composition in an isolated pixel subjected to the specified environmental flux. In such a space a preponderance of vectors will point towards the origin (Fig. 1). An alternative way to visualize this is as a landscape in which vectors due to equilibration with the environment correspond to the expected gravitational pull on a ball, corresponding to a pixel’s chemical state. As shown in Fig. 2, every point in CC space has higher altitude than the origin, meaning that the overall tendency of pixels is to fall towards the origin.

Fig. 2.

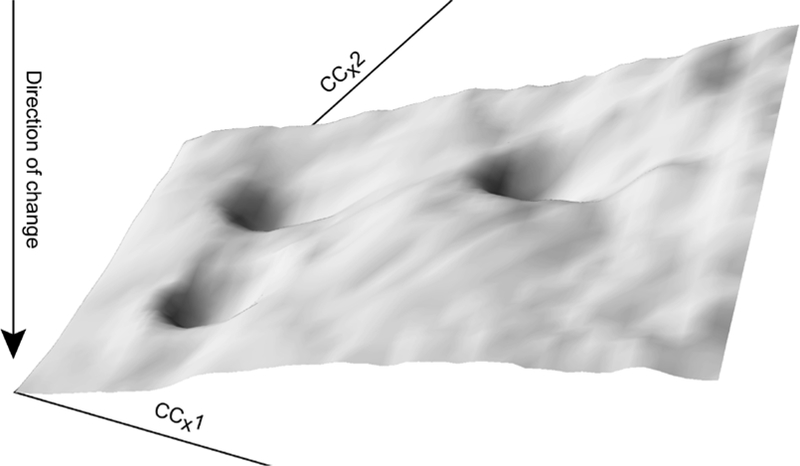
Illustration of chemical composition (CC) space with expected changed in chemical concentration of a pixel depicted in terms of the expected position of a ball responding to gravity. The three wells correspond to three metastable equilibria and their zones of attraction (as in Fig. 1)

We know that within the real (but incompletely charted) chemical dynamical system, some pixels, most notably those corresponding to living cells, persist far from environmental equilibrium. The best way to understand this is to equate a living state with a metastable attractor in CC space⁵. In reality these attractors could be of various kinds (fixed point, limit cycle, strange, etc.), but for simplicity let us visualize each metastable attractor as a point surrounded by a basin of attraction. By definition, a pixel in the basin of attraction will tend to move towards the attractor and then remain there until a stochastic event knocks the pixel out of the basin of attraction or CC space itself changes, for example due to a change in the physical environment (altering the kinetics of chemical reactions within the dynamical system) or a change in the environmental flux.

How can a pixel remain at an attractor and avoid falling to equilibrium? This is only possible if the reactions in p use energy to prevent entropic decay (as famously pointed-out by Schrödinger, 1945). That is to say, the second law of thermodynamics means that, in order to prevent or delay the fall towards the origin, the net reactions in p must use free energy and release heat⁶. Additionally, since all the non-food chemical species in p are susceptible to dilution by environmental flux and/or chemical degradation, we can also conclude that if p sits at a metastable attractor, all non-food species must be produced by reactions within p at a rate equaling their rate of dilution/decay. If the rate of production were lower, p would not be sitting directly on an attractor, and would drop towards the origin (which also may be towards the closest attractor if the pixel is in a basin of attraction). Alternatively, if the rate of production is higher than the flux, p will move further away from the origin until it sits on the actual attractor.

As an aid to visualization, Fig. 3 shows a set of chemical reactions whose kinetics might allow them, in an environment rich in a replenishing supply of food species, F₁, F₂, and F₃, to manifest a metastable state corresponding to high concentrations of the non-food catalytic species, C₁, C₂, and C₃, and non-food waste species, W1, W2, and W3. A pixel that had a high concentration of C₁, C₂, and C₃ but was surround by pixels in equilibrium with the environment might produce these non-food species at a rate equaling their loss to the environment (and adjacent pixels) by diffusion. Such a system⁷ would contain an ensemble of chemicals that make more of one another over time, meaning that we can refer to the system as autocatalytic (Hordijk et al., 2010; Kauffman, 1986), autopoietic (Varela et al., 1974) or self-sustaining (Joyce, 1994). Pixels in the basin of attraction of a metastable state could also be autocatalytic, although the rates of production of each functional chemical would not exactly match the rates of dilution until the attractor point was reached.

Fig. 3.

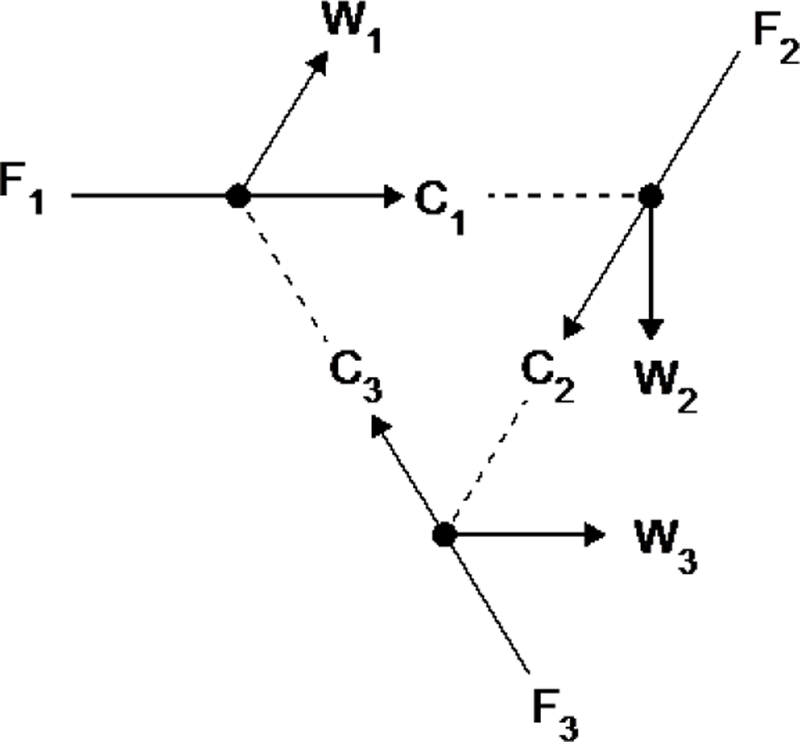
Example of a simple 3-member autocatalytic set. Three kinds of food chemicals, F₁, F₂, and F₃, are converted to three catalytic species, C₁, C₂, and C₃, respectively, with the simultaneous production of three waste products, W₁, W₂, and W₃, respectively. The chemical conversion of food to catalyst plus waste is represented with solid arrows, while dotted lines indicated catalysis.

Life as a metastable chemical system

Within the framework just presented life corresponds to a localized ensemble of chemical species that sits at a metastable state in CC space or in the basin of attraction around such a metastable state. In contrast, pixels that sit at the origin are dead, whereas pixels that sit neither at the origin nor in the gravitational pull of a metastable state (alive) are on a trajectory towards the origin, i.e., towards death⁸.

The ensemble of chemicals that comprises the life system includes all non-food species with elevated local concentration. It is not obviously necessary that there be subsystems playing informational or boundary-forming roles, as assumed by the chemoton model (Gánti, 1975; Gánti, 1997). Likewise, self-propagating systems need not include specific catalysts (Virgo and Ikegami, 2013) and, even if they do, there is no logical distinction between catalysts and metabolites (Cornish-Bowden et al., 2013). At minimum, a chemical system sitting near an attractor in CC space need only comprise a local concentration of a set of chemical species (probably both organic and inorganic) with the collective property of self-propagation.

It is worth asking at this point whether the notion of life as a localized chemical system in the basin of attraction of a metastable attractor captures the important features of more conventional definitions of life, of which the most widely cited is NASA’s working definition: “a self-sustained chemical system capable of undergoing Darwinian evolution” (Joyce, 1994). Chemical systems occupying the zones of attraction around metastable states are self-sustaining in the sense that, to remain near the attractor state, the chemicals in p must produce enough of the self-same chemicals to compensate for those lost by diffusive exchange with the environment.

Self-sustenance also implies the capacity for growth, another hallmark feature of prototypical life. Consider a pixel in physical space, p, that sits at a metastable state in CC space and is surrounded by other pixels, p’, that are in equilibrium with the environment and, hence, at the origin of CC space. Diffusive equilibration of p with the environment will lead p’ to become enriched (relative to the environment) in the non-food chemical that characterize p. Consequently, p’, will come to have chemical concentrations that place it on the downhill side of p in space (Fig. 4). If the chemical composition of p’ places it within the zone of attraction around the living state occupied by p, then p’ will tend to move to the same state as p. This implies expansion of the life state from p to p+p’, which is growth. Furthermore, assuming environmental constancy, p’ will convert its adjacent pixels, p’’ to the life state, and so forth. Such behavior is not dependent on my heuristic quantization of space into pixels, and would still be possible even in a spatially continuous model. Thus, defining life as a chemical system that occupies a metastable attractor state captures an important feature of prototypical life, the capacity for open-ended growth through physical space in a permissive environment9.

Fig. 4.

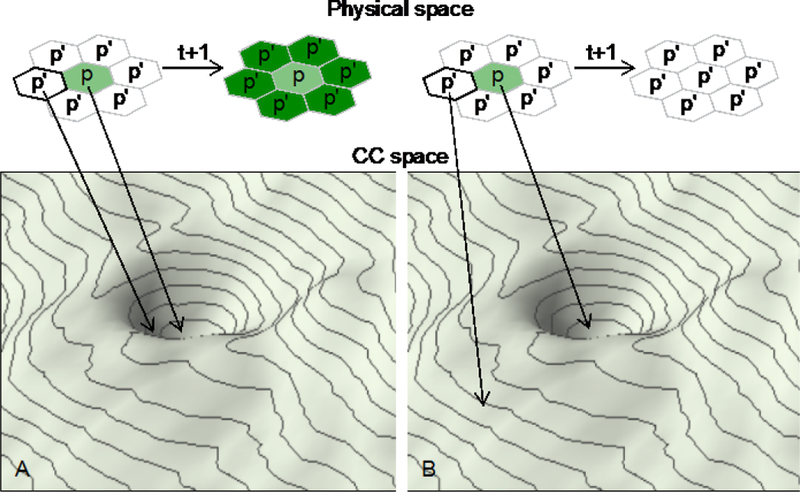
The viability of a life state in an explicit spatial context depends on the state expected for a pixel, p’, that is physically adjacent to a pixel that sites on the attractor of a life state. A. If p’ receives sufficient influx of chemicals from p to situate p’ in the zone of attraction, the life state will grow from p to encompass all adjacent pixels. In this case the life state is viable. B. If p’ sits outside of the zone of attraction, for example because dilution of chemicals enriched at p is too rapid, p’ will not be converted to the life state. In this case the life state is not viable and the area in the life state will shrink over time. Note, the lowest point of the basin of attraction shown is (and must be) above the origin of CC space.

What about the final key feature of “life,” the capacity for Darwinian evolution or, as I would prefer, “adaptive evolution”?¹⁰ At small physical scales, chemical kinetics is shaped by molecular stochasticity as much as by mass action kinetics. As a result, a chemical system sitting at one position in CC space has a finite probability of experiencing a stochastic jump to a new set of chemical concentrations, which is to say a different position in CC space. Given that such jumps involve changes in chemical concentration, and smaller changes in concentration are more likely than large ones, it follows that the expected position of p after undergoing such a stochastic “mutation” is centered on its current position and declines with distance in CC space. Mutational jumps have the potential to instantaneously move p from near one attractor state into the basin of attraction of another. Many chemical networks have the potential to manifest multiple metastable equilibria (Piedrafita et al., 2010; Wagner et al., 2017; Wynveen et al., 2014). This means that a mutation can result in a chemical system adopting a new life state, with an expectation that it will remain in the derived state until perturbed by a change in the environment or by a further mutation. Thus, it is in principle always possible (if in some cases vanishingly improbable) for a spatially localized chemical system to evolve from one metastable life state to another.

The movement in CC space just described might be discounted as “just” change since there is no adaptive process entailed. However, as discussed more fully below, adaptive evolution would be in effect if life states differ in their expected longevity such that pixels in robust chemical states become more abundant than pixels in less stable life states. For example, all things being equal, life states with large basins of attraction will tend to persist for longer because pixels in these states are less likely to leave the life state by chance. Additionally, the ways that life states interact could cause some to win at the expense of others. For example, if adjacent pixels in physical space occupy alternative life states, properties of the two states could result in one “winning,” for example by converting space formerly occupied by the other state into its state. Consequently we should expect, a selective process to occur in which certain life states, which may be classified as fitter in that environment, tend to become more frequently realized than less fit alternatives. These phenomena will be discussed in more detail later. For now, all that needs to be noted is that life as I have defined it has the potential for self-sustenance, growth and adaptive evolution.

The reader might object that there are some chemical dissipative structures that correspond to metastable states but differ greatly from life, as conventionally defined. For example, a pixel inside a candle flame¹¹ receives a flux of long-chain hydrocarbons delivered by the wick and oxygen delivered by convection, which result in a local enrichment of a different set of species in the flame, for example shorter-chain hydrocarbons, carbon monoxide, and carbon dioxide. However, while a flame has the key properties of self-sustenance and growth, for example, along a wick or to a second wick, we do not usually consider it to be alive. A flame can change over time as a result of changes in the environment or in the flux of fuel and oxygen, but adaptive evolution is not seen. There are two, possible explanations for this. First, because all the chemical species that constitute a flame cycle through the system at about the same rate (on the same time frame as energy dissipation), a flame lacks a class of chemical species that can store “memories” of past conditions. In contrast, a prototypical living chemical system has a set of non-food species whose residence time, though finite, is much greater than the rate at which food is digested and waste is released. The identity and concentration of these non-food species is influenced not just by the current environment, but also by the recent history. As a result these non-food species give the system the potential to build progressively on past evolution in a way that is impossible in systems showing equivalent rates of flux of all species. Second, perhaps because of the first explanation, we have no evidence that there are additional metastable states close enough to the flame system in CC space to be accessible by a stochastic mutation. Thus, whether or not one views a flame as a kind of (simple) living system, it seems that canonical life corresponds to a subset of dissipative structures which have some long lived chemical species that allow them to evolve adaptively further and further away from the origin of CC space.

The spontaneous appearance of surface-associated life

Before going on to explore adaptive evolutionary processes in more detail, it will be helpful to develop a sense for where evolvable life states are most likely to arise in the first place. A new self-propagating chemical state needs both food, which is to say the components that will make the chemical species in the autocatalytic set, and energy to drive a set of thermodynamically uphill reactions. However, neither factor is likely to have been infrequent on the early Earth, on other planetary bodies, or even in many natural and human-made Earth environments today. Even if we restrict our attention to organic life, we have known since the Miller-Urey experiments and investigations of cometary material that potential food species form spontaneously in many situations. Furthermore, there are many natural energy sources. In addition to high-energy bonds in organic foodstuffs energy can be obtained from light and chemical disequilibria (redox or pH) maintained by solar-and/or radioactively-driven geochemical processes. Under what circumstances can an environment that experiences flux in food chemicals, with or without additional source of chemical energy, transition to an evolvable living state?

The main factor determining whether a life state is viable in a spatially explicit model is diffusion, and particularly the relative rates of diffusion for food and non-food chemical species. Diffusion of food chemicals into the system is needed for self-propagation, with higher rates of diffusion supporting potentially higher rates of production of non-food chemicals. Likewise, diffusion of waste species out of the system will often be needed to sustain high rates of autocatalysis. At the same time, it is essential that diffusion not result in excessive loss of those non-food chemicals that are needed for self-propagation, the keystone species¹². A potential life state is not viable if its keystone chemicals (e.g., catalysts C₁, C₂, and C₃ in Fig. 3) diffuse away from one another faster than they are produced. While formal analysis is needed, I will conjecture that life cannot easily arise unless food and waste all diffuse at an appreciably higher rate than the keystone species. It is possible that all keystone chemical species might have lower intrinsic diffusion rates, for example by being larger molecules or tending to aggregate spontaneously (Shenhav et al., 2003). However, it seems a priori easier to achieve the life state if the keystone chemical species are configured such that they have a low rate of diffusing away from each other while still having access to rapidly diffusing food species.

One setting that seems especially conducive to differential diffusion is at the interface between two different phases: solid-liquid, solid-gas, or liquid-gas. The interface between two liquid phases, for example on the surface of oil microdroplets (Sharov, 2009), is also worth considering, although I am not aware of any strictly geochemical mechanisms for the sustained generation of oils or lipids. At such interfaces an autocatalytic set of chemicals could persist and grow if the diffusion of the keystone species were governed by the less diffusive phase while food was provided by the more diffusive phase. Indeed, the origin of life field has been focused on the solid-liquid interface at least since Wächtershäuser (1988). This setting seems well suited to the origin of life because we know that in realistic geological settings the liquid phase, for example, an ocean or volcanic pool, can become enriched in diverse chemical species, some of which will be adsorbed selectively onto specific kinds of mineral surface. Additionally, some mineral surfaces can serve as keystone species themselves, for example by serving as direct catalysts of one or more reactions in an autocatalytic set. Thus, for the purposes of exposition I will focus hereafter on the scenario of solid mineral surfaces submerged in a constantly replenishing, food-rich solution.

Under this model life could begin when a set of keystone species became attached, by chance, to the same pixel of a surface. For example, in the hypothetical autocatalytic set shown in Fig. 3, if the keystone catalysts, C1, C2, and C3, can become immobilized on a particular mineral surface, while the food and waste species cannot, a life state might nucleate and then grow over the surface as more catalyst molecules were formed and then retained in close proximity by adsorption onto adjacent surface. Provided diffusion of food and waste is fast enough relative to the rate at which keystone species are lost from the surface, open-ended growth of the life state over the surface would be possible. Consequently, mineral surfaces could serve as sites for de novo life states to nucleate spontaneously and then propagate themselves.

The reader might wonder why a surface associated initial life state is more plausible than a protocell, vesicle, coacervate droplet, or some such individuated chemical system. This might be especially surprising given the extensive body of literature built around the idea that the first replicating entity was a protocell that contained an autocatalytic system capable of using resources in the environment to collectively replicate its internal contents and create more bounding membrane (Chen and Nowak, 2012; Chen et al., 2005; Fontanari et al., 2006; Kamimura and Kaneko, 2010; Luisi and Varela, 1989; Mavelli and Ruiz-Mirazo, 2013; Morowitz et al., 1988; Ruiz-Mirazo et al., 2017; Szostak et al., 2001). While these models have the pleasing feature that adaptive evolution can begin even in the absence of any kind of genetic encoding (Shenhav et al., 2003; Vasas et al., 2012), their plausibility depends on the claim that a dividing and evolvable protocell can arise spontaneously without any prior adaptive process. Such a spontaneous origin is hard to imagine. In particular, a de novo protocell with a bounding membrane would need to enclose an autocatalytic metabolism in which the keystone chemical species tend to remain within the protocell, while food diffuses in, and waste diffuses out. Furthermore, this protocell would have to have a preexisting ability to divide – and to do so with sufficient regularity to show exponential growth dynamics and overcome the (analog) error threshold (see, Vasas et al., 2010). These demands are rather stringent. Given that self-propagation (autopoiesis) does not require compartmentalization (Virgo et al., 2009), it seems easiest to infer that protocells are late-evolving products of living chemical systems whose spatial structure arises by means other than enclosure in a membrane (Szathmáry, 2015). While I will focus on mineral surfaces, the principles should equally apply to other possible interfaces.

Mutations in CC Space

The abstract CC space contains many potential metastable attractor states. Imagine that one such life state, not too far from the origin, has been found by the spontaneous formation of an autocatalytic system at one physical point on a mineral surface. How will evolution proceed from there? In particular, how might new attractor states uphill from the initial life state, that is further from the environmental equilibrium, be found?

As already indicated, some exploration of CC space can be achieved by chemical mutations. Thus far I have emphasized chance changes in concentration at small spatial scales, which can move a pixel in any direction in CC space, with the probability of a distant move being lower than that for a near move. Now we need to add another kind of mutation: rare chemical reactions, such as ones requiring the simultaneous interaction of multiple, low-concentration reactants. As discussed by (Vasas et al., 2012), rare chemical reactions can introduce a new chemical species into a system¹³, which amounts to opening a new dimension in CC space.

Such chemical novelty is illustrated in Fig. 5, which represents an extension to the autocatalytic core shown in Fig. 3. In this case, if either of two new chemical species C₄ or C₅ formed spontaneously on a surface already rich in C₁, C₂, and C₃, for example by a rare spontaneous reaction between a waste product from the original set and a food compound, then C₄ and C₅ would be added to the original set representing a shift to a new metastable equilibrium. Furthermore, this innovation would be expected to spread through the spatially extended system that occupied the ancestral metastable state, representing an example of neighborhood selection (Baum, 2015).

Fig. 5.

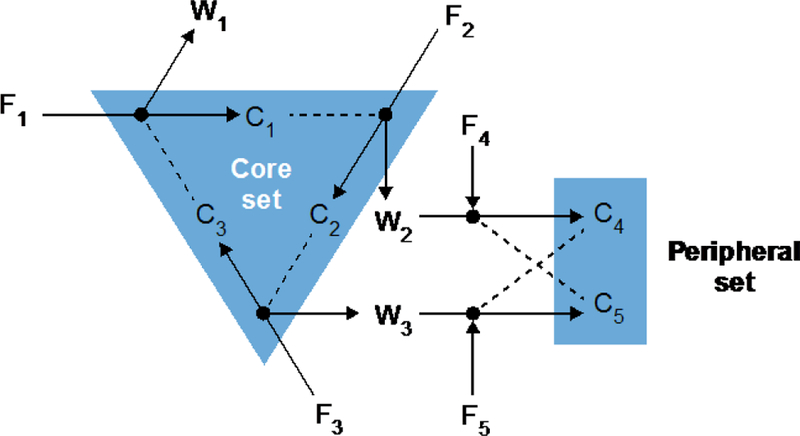
Example of how rare chemical reactions, such as the localized production of C₄ or C₅ by a rare reaction between waste products from the original catalytic set and low-abundance food species, could expand the self-propagating system, resulting in movement of a pixel to a new metastable state (with high concentrations of C₄ and C₅). It is supposed that the newly formed non-food species C₄ and C₅ cross-catalyze one another formation and tend to attach to the same mineral surface as C₁, C₂ and C₃. The chemical conversion of food to catalyst plus waste is represented with solid arrows, while dotted lines indicated catalysis.

Whereas chance fluctuations in concentration would be random with respect to the dimensions of CC space, with jumps away from the origin being about as likely as ones towards the origin, the production of new species might be expected to generally increase disequilibrium. Although this is not guaranteed – a new species’ production could cause flux changes such that chemical disequilibrium is actually lowered – this mutational process has the potential to continually generate higher CD states, some of which might be favored during adaptive evolution.

In addition to chemical mutations, CC space can also be explored by changes in environmental fluxes or in the physical environment. These changes can push living systems into new states, some of which could be self-propagating. Furthermore, it is possible that a sudden change back to the prior environmental parameters could result in a living system being stranded in the zone of attraction of a different attractor state than it started at. As with the conventional evolutionary history of cellular life, such historically contingent environmental buffeting is unpredictable and not readily explained by general laws, but no less real or important for this unpredictability.

Evolution to greater chemical disequilibrium

Each potential life state, whether or not it is occupied, corresponds to a dip or divot in CC space – an attractor state surrounded by a basin of attraction. The disequilibrium of each potential life state, namely the minimum Euclidean distance from the origin to a point within the basin, varies greatly. The first life state occupied in an evolutionary sequence arises via chance chemical changes meaning that it must be of low disequilibrium, which can also be understood as being low complexity or high entropy. Thus, life will always start close to the origin. The fact that even the simplest known living systems are far too complex to have arisen spontaneously, implies that life began at lower levels of disequilibrium and, over time, leap-frogged through a series of life-states that were sequentially further and further from the origin. How and why did this happen?

Some evolutionary biologists, most famously Stephen Jay Gould believed that the fact that life must begin at the left wall of a complexity graph is sufficient to create an illusion that there is a drive to complexity (Gould, 1988). In other words there is no bias towards higher complexity just a constraint to begin simple. This case might be defensible when it comes to cellular life, but if you believe (as I do) that a cell is too out of equilibrium with the environment to arise without the prior existence of a living and evolving system (Baum,2015) then the lack of life systems sitting in the chasm between cells and the origin of CC space suggests that the left-wall artifact is insufficient to explain the observed pattern. This is, I think, why many scientists (e.g., Krakauer, 2011) take it as a given that the remarkably intricate life forms around us today point to some intrinsic evolutionary drive to higher complexity¹⁴. Could adaptive evolutionary processes acting on surface-associated systems provide a ratchet towards high CD life states?

First we need to consider if elevated disequilibrium might tend to enhance the long-term persistence of self-propagating systems living on mineral surfaces. Self-propagating systems can always be bounced out of the life stated by chance changes in the concentrations of chemical species. On average, might higher CD states be more robust to death-by-mutation than lower CD states? I would conjecture that the answer is yes, based on the following argument.

Since the flux through chemical reactions is driven by relative concentrations, it seems likely that the distance between an attractor and the rim of its basin of attraction, which represents the tolerance of the autocatalytic system to perturbations of chemical concentrations, should scale with relative chemical concentration. For example, we might suppose that the relative concentrations of each pair of species need to remain within 10% of their optimal values for the autocatalytic system to remain viable. What is interesting is that a system where the chemical species are at low concentrations (i.e., few molecules per unit volume) would be much more likely to exceed the 10% threshold through a chance fluctuation than a system where chemical species are at a much higher local concentration¹⁵. Thus, while a system with high CD might be more difficult to “find” by chance, once it has arisen it should persist for longer than a low CD state. This implies that, all things being equal, we might imagine a tendency to see more high CD states over time. This mechanism may be similar to that explored by (England, 2015) when systems sit in a strongly-driven environment, which is to say there are abundant free energy sources, but each energy source is difficult to access due to kinetic blocks. In such cases, life states that can exploit richer energy sources gain stability because they dissipate energy locally, which makes it more difficult for a random process to take them back out of the life state.

While the foregoing argument is attractive, many other factors could swamp the mutational robustness advantage of high CD states. For a start, differences in growth rate among life states might be expected to be a major factor affecting the evolution of surface-associated systems and might easily overwhelm the mutational stability advantage of high CD states. However, I cannot see a good reason to assume that high growth rate of a life state would correlate with its CD¹⁶.

A further important driver of CD change might reside in the outcomes of interactions of adjacent pixels that are in different life states. When a pair of unbounded, growing life states come into contact on a physical surface (Fig. 6) there are three possible outcomes: Annihilation: The life states cancel each other out, meaning that the pixels are both moved out of the life state; (2) Coexistence: The states merge, meaning that both chemical states coexist in each pixel – they grow through one other; (3) Replacement: One state wins, meaning that it grows through the other state converting pixels from the losing to the winning state.

Fig. 6.

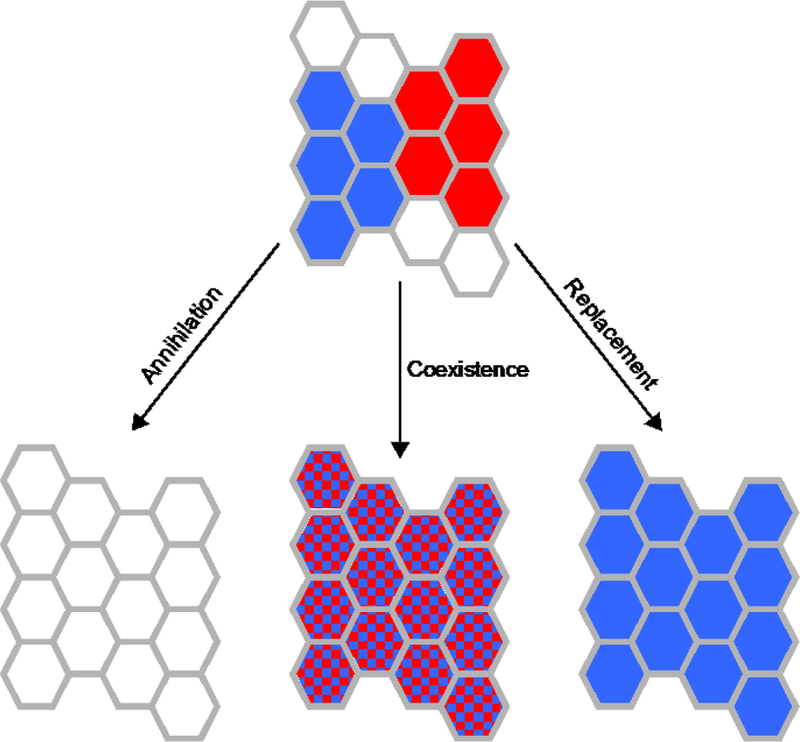
Possible outcomes of interactions among two different life states, depicted in blue and

Annihilation is an expected outcome when the systems each depend on a certain flux of the same food chemical, which is insufficient to support either autocatalytic set above its rate of diffusive loss. Alternatively, interactions among non-food chemicals could produce poisonous or parasitic products. However, since annihilation removes two life-states, it can play only a minimal role in the CD of the life states that do exist.

Coexistence increases the number of chemical species that have elevated concentration, thereby raising the CD of a physical pixel – moving it further from the environmental equilibrium point. This outcome is facilitated by cases in which the non-food chemicals enriched in the two autocatalytic sets do not compete for food or attachment points on the surface and do not cross-react. Coexistence could be passive, in the sense that neither products nor reactants are shared, such that the original autocatalytic systems neither compete nor cooperate. Sometimes, however, coexistence might entail commensalism, as when the waste products of one are used and/or degraded passively by the other (see Fig. 5), or mutualism, where each network produces a waste product of value to the other. It seems reasonable to assume that mutualistic systems would be more robust in the long run, but, while there has been some prior theoretical work (Hordijk et al., 2012; Vasas et al., 2012), more research is needed to evaluate the evolutionary consequences of passive or cooperative coexistence as a means of complexification.

Replacement also has the potential to systematically increase CD, since it entails one life state replacing another. Although formal modeling is needed, consideration of some simple cases leads me to conjecture that there ought to be a general tendency for more complex autocatalytic states to replace less complex ones.

The first case to consider involves a high CD state, H, in pixel p interacting with a lower CD state, L, in a physically adjacent pixel, p’, were H and L lie on the same diagonal through the origin of CC space. That is to say, the H and L states contain exactly the same species in the same proportion but at different absolute concentrations. Let us assume that L and H are both self-propagating in the absence of interactions with other life states, which is to say that they can convert an adjacent pixel from a state in equilibrium with the environment (i.e., with non-food species at concentration 0) into L or H, respectively. It stands to reason that if H can convert an adjacent pixel lacking any keystone species to the H state, then it could almost surely also convert p’ in state L, which has the same keystone species at an intermediate concentration (0 > [X_i]_L< [X_i]_H). This implies that H would grow into an L pixel and convert the latter to state H.

The same reasoning can be generalized to suggest that H will replace L in all cases where H and L are different growing life states and where all chemical species satisfy the inequality, [X_i]_L≤ [X_i]_H. For example, suppose that L and H have identical concentrations of all chemicals except for some chemical species that are part of the autocatalytic set acting in H (with a non-zero concentration) but absent from L. For example, let L be the autocatalytic set depicted in Fig. 3 and H be the one in Fig. 5, which also includes C₄ and C₅. It seems inescapable that H will replace L, meaning that the additional chemical species (C₄ and C₅) will be spread throughout the areas previously occupied by the L state.

These simplistic examples do not provide an explicit guide for cases in which some chemicals are at higher concentration in H and others are at higher concentration in L, even in the case that H has higher CD (a greater Euclidean distance from the origin of CC space). That being said, I will conjecture that this should typically be so. Higher CD chemical states can only succeed in growing (i.e., converting adjacent pixels to their state) by having high enough productivity to flood those adjacent pixels with molecules for each keystone species. This would seem to predict a general tendency for higher CD states to replace lower CD states, which might provide a general explanation for why lower entropy dissipative structures tend to accumulate over evolutionary time. That being said formal mathematical models would be needed to validate this intuition and assess whether it holds just for chemical concentration or also applies to the internal energy term of chemical composition.

Boundaries and cell formation

It is generally held that the cellular habit, which results in the existence of populations of bounded vesicles that compete for representation in future generations, can make adaptive evolution more efficient (Chen and Nowak, 2012). However, such an advantage for future evolution cannot be used as a direct explanation for the transition from the unbounded state (surface-associated chemical ensembles) to bounded protocells¹⁷ (Szathmáry, 2015). Nonetheless, I will now argue that adaptive evolution on surface life states, framed by the concept of CC space, suggests a plausible evolutionary path to the cell. This model is similar to that proposed by Wächtershäuser (1988; 2007), but framed in terms of ecology and evolution rather than chemistry.

One potential class of non-keystone chemicals gained during a living system’s evolution are those that self-organize to form a membrane between the system and the overlying solution (Fig. 7 A-B). Such chemicals might first form as waste products (Nghe et al., 2015), but could then become enriched if their presence, directly or indirectly, promotes the rate of their own production in the system (for example by elevating the local concentration of reactants). If membrane-forming species inhibited diffusion of an essential food species into the system, or toxic waste product out of the system, they would be disfavored and could never spread through an entire living system. However, if the membrane allowed sufficient flux of food and waste chemicals for its own production, it could spread over an entire evolving ensemble.

Fig. 7.

Scenario for the origin of membranes and the cell habit. A. The ancestral surface-associated life state is composed of a set of keystone chemical species (red, orange, yellow) that are weakly attached, directly or indirectly, to the underlying mineral surface. B. A new amphiphilic chemical species (blue) is formed and self-organizes to form an overlying membrane. The presence of a membrane allows the accumulation of novel chemical species (pink). C. The membrane is stabilized by the production of a further bridge species (light blue) that can associate with the membrane and the underlying mineral. D. Physical disruption can release a stable cell-like vesicle that would initially be capable of reestablishing the surface state through the actions of the bridge species.

In the context of a surface receiving a flux of food species from an overlying solution, there are good reasons to expect that a membrane-bearing life state that arose, M, would tend to replace any non-membrane-bearing life state that it encountered, N. The logic behind this claim is that a membrane could only have come to characterize M if the membrane were permeable to all chemicals needed for M to survive, yet there is no a priori reason to think that this membrane would also allow rapid diffusion of the food species needed for N to survive. As a result, should a patch of M come into contact with a patch of N, the membrane would be likely to render N non-viable, making it that much harder for N to outcompete M for shared food or attachment points. As a result, over time we might expect to see a higher and higher proportion of living systems that produce overlying membranes.

In addition to providing a competitive advantage in pairwise interactions among life states, the addition of a selectively permeable membrane over a living system significantly changes that system’s evolutionary potential. This follows because many dissolved chemical species could now become locally enriched between the membrane and the surface. Because the rate at which these chemicals are expected to equilibrate with the environment has slowed, the threshold productivity for autocatalytic systems is also lowered, effectively increasing the number of potentially viable metastable states. Thus, insofar as the vectors in CC space are scaled by diffusion, the addition of a membrane (or any other factor changing rates of diffusion for some or all species) could greatly change the expected dynamical behavior¹⁸.

The formation of an overlying membrane requires some chemical connection, probably non-covalent, between the membrane and the underlying mineral surface, likely via bridging molecules (Fig. 7C). Such systems would be well suited to long-distance dispersal of the life state to a new mineral surface. Physical agitation could generate a membrane vesicle that included all the keystone species of the life state as well as the bridging molecules that confer an affinity to the natal mineral on which the system evolved. As a result, such vesicles could serve as propagules, allowing the system to colonize all patches of natal mineral within some broad area (Fig. 7D). As argued previously (Baum, 2015), propagules of this sort provide a natural step towards the evolution of the cellular habit. At first the autocatalytic system might only have been metabolically active when interacting with the mineral, but selection would tend to favor variants that could grow and divide while dispersing in the liquid phase (Baum, 2015). Thus, selection for dispersal ability can be seen as the key evolutionary driver of the origin of the cellular habit.

The formation of protocells changes the evolutionary dynamics in many ways, but especially by disadvantaging parasitic chemical species (Vasas et al., 2012). Whereas the spatial organization accorded by a two-dimensional surface can help prevent parasitic species from driving a living system to extinction and even foster adaptive evolution (Boerlijst and Hogeweg, 1995; Konnyu et al., 2008; Könnyű et al., 2008; Virgo et al., 2013), it is still not for easy living systems to drive parasites to extinction – they tend to persist in a dynamic equilibrium with their host. However, once life becomes compartmentalized into protocells, selection for cellular viability and replication ability allows many (but not all) parasitic species to be exterminated.

Even after compartmentalized living systems arise, we might expect it to take time for protocells to function as autonomous, clonal lineages. The same tradeoff that drives modern life to experience varied frequencies of sexual reproduction would apply. Traits promoting fusion might be favored by group selection because frequent sharing of chemical species among protocells of the same evolving population would keep the population from drifting away from its optimum chemical composition. This follows because the average concentrations of chemicals in two protocells would, on average, tend to be closer to the attractor than either protocell will be individually. Conversely there are two major downsides to the promiscuous fusion of protocells, which might favor the evolution of barriers to fusion. First, fusion of protocells that sit close to different attractors will tend to average the concentration of all chemical species and thereby move the fused protocell out of the zone of attraction of either attractor. In other words, fusion of two living protocells can immediately yield a non-living protocell¹⁹. Second, fusion exposes each protocell to the risk of picking-up a parasitic species. Thus, mechanisms that prevent fusion among protocells or between protocells and surface-associated relatives are likely to eventually arise.

It is worth highlighting that although the evolutionary transition to a population of individuated protocells with little if any fusion would alter evolutionary dynamics (e.g., the frequency of parasites), the new system can still be accommodated within the dynamical systems view of life proposed here. In one sense, the CC space concept works better for protocells than for uncompartmentalized, surface-associated systems because, in contrast to “pixels,” protocells are objectively individuated. Thus, it is reasonable to view the axes of protocellular CC space as corresponding to the concentrations of each chemical species in a protocell relative to that chemical’s concentration in the environment (weighted by the chemical’s internal energy). On the other hand CC space does a poor job of capturing overall disequilibrium when protocells contain organelles or supramolecular structures that are actively assembled (as opposed to self-assembled), since organelles (etc.) add an extra layer of disequilibrium that is not captured by the chemical composition of the protocell as a whole.

The evolutionary invention of autonomous protocells entailed the gradual weaning of living systems from dependence on their natal mineral surface and the stepwise acquisition of mechanisms to limit protocell-surface and protocell-cell fusion. Multiple protocells in a population might sit in the zone of attraction of the same metastable attractor, implying that they will tend to converge to the same point (the attractor) given enough time. These can be thought of as protocells with the same genotype but with phenotypes that have been altered by environmental noise. Other protocells, though, may have experienced a history of chemical mutation that results in them sitting in a different life state – one that might confer higher or lower fitness (i.e., potential for survival and reproduction). Thus, many of the essential aspects of conventional speciation genetics arise as soon as populations of bounded living systems arise, even prior to the origin of a digital genetic encoding system.

Future work

I have proposed that viewing life as a localized, metastable chemical system that avoids equilibration with the environment through the use of environmentally provided matter and energy helps clarify the origin and early evolution of life. Such a conception points to surfaces as the most likely milieu for self-propagating chemical systems (i.e., life) to originate and suggests that there may be a general tendency for complexification through neighborhood selection within surface-associated systems and competition among them. It also lends credence to the idea that the cell habit is an expected innovation related to dispersal. However, while these verbal and conceptual arguments are tantalizing, I think the reader will agree that they need to be formalized. For example, formal models are needed to help us understand conditions conducive to the spontaneous emergence of autocatalytic, self-propagating chemical systems, how such systems can move among multiple metastable equilibria, how competing states on a single surface will interact, and how surface associated states can generate membranes and cells. Nonetheless, while I recognize that many readers will wish to suspend acceptance of this framework until rigorous, quantitative models have been developed, let me end by arguing that we should not let the lack of formal demonstration discourage us from making use of this conceptual framework to guide empirical research.

Historically, research into the origin of life has been premised on the idea that life cannot get going until there exists some entity capable of self-replication. Whether we envisage the first self-replicator as a membrane-bounded protocell (Mavelli and Ruiz-Mirazo, 2013; Morowitz et al., 1988; Szostak et al., 2001), a droplet (Segre et al., 1998; Sharov, 2009; Shenhav et al., 2003), or a very talented RNA molecule (Gilbert, 1986; Joyce, 2002), the first replicator would have been very complicated, which can only make us pessimistic about ever seeing the spontaneous origin of new life in the lab. Consequently, empirical origin of life research has, primarily focused on the historical problem of explaining how certain distinctive chemical features of cellular life arose, especially nucleic acids and proteins. The ahistorical problem of how, in general, living systems originate and what features they must have has barely been studied empirically. After all, if you believe there is no hope of being able to generate a new living system in the lab how could you make progress except through theoretical modeling?

Taking the view that an autocatalytic set of chemicals growing over a mineral surface is an adaptively evolvable system changes the calculus greatly. If the high degree of chemical disequilibrium (= high complexity) of extant life is not a primordial feature but, rather, the consequence of disequilibrium/complexity accreting from the moment an autocatalytic set first nucleated on a lump of rock, then one can be much more hopeful about the possibility of studying new living systems in the lab. Such a perspective allows that the earliest stages of life might arise easily enough to be seen in the lifetimes of today’s scientists. Indeed, the outline of a research program for detecting de novo surface-associated life-like chemical systems has already been proposed (Baum and Vetsigian, 2016) and is being acted upon by several research groups, including my own. Thus, by conceptualizing life in the CC framework we may hope that a new generation of empirical origin of life research will begin that may finally clarify how life, as a general phenomenon, emerges and what factors are required for this to occur. Then and only then will we be able to determine which features of extant life are necessary attributes of all living systems and which were the result of chance occurrences on the ancient Earth.