Abstract
Purpose
Epidermal growth factor receptor (EGFR) is thought to play a role in the regulation of cell proliferation; with its activation stimulating tumour growth. EGFR inhibitors have shown promise in the treatment of cancer, particularly in non-small cell lung cancer, however, resistance is observed in the majority of patients. A tumour growth model was developed aiming to explain this resistance.
Methods
The model incorporating populations of both sensitive and resistant cells were fitted to data from a study of EGFR inhibitor AZD3759 in brain metastasis mouse models. The observed regrowth of tumours in higher dose groups suggested the development of resistance to treatment. The bioluminescence observations were highly variable, covering many orders of magnitude, so to assess how reliable the model was, the parameter estimates were compared to those found in less noisy subcutaneous mouse models.
Results
The fitted model suggested that resistance was mainly due to a proportion of cells being resistant at baseline, and the contribution of mutations occurring during the study leading to resistance was negligible. Estimated growth rate and dose–response was found to be comparable between brain metastasis and subcutaneous mouse models.
Conclusions
The developed model to describe resistance suggests that the resistance to EGFR-inhibition seen in these xenografts is best described by assuming a small percentage of cells are resistant to treatment at baseline. This model suggests changes to dosing and dosing schedule may not prevent resistance to treatment developing, and that additional treatments would need to be used in combination to overcome resistance.
Keywords: Bioluminescence, Resistance, Brain metastasis, Xenograft, EGFR inhibitor
Introduction
The targeting of epidermal growth factor receptor (EGFR), a cell-surface receptor in the ErbB family, has shown anti-tumour activity and has been seen as a promising therapy in oncology [1]. There are different classes of EGFR inhibitors, small molecules, such as gefitinib and erlotinib, that inhibit the tyrosine kinase inhibitors (TKIs) as well as monoclonal antibodies (mAbs) such as cetuximab and panitumumab [2, 3]. EGFR is thought to play a role in the regulation of cell proliferation [4], its activation stimulates tumour growth and progression, promotes proliferation, angiogenesis, invasion, metastasis and inhibition of apoptosis [1].
Despite the early promise of EGFR-inhibition in the treatment of cancer, the development of resistance to treatment is observed in the majority of patients [3, 5, 6]. The mechanisms of resistance are not fully understood, but a number have been proposed, such as secondary mutations, activation of alternate signalling, impairment of the apoptosis pathway, histological transformation [3, 5, 7–10] and brain metastasis that are protected from treatment by the blood–brain barrier [11]. Resistance can more broadly be described as being due to pre-existing resistant cells or de novo evolution [12–14].
A mathematical model to describe resistance to EGFR inhibitors has previously been developed in cell lines, describing two populations of cells, sensitive and resistant, which were found to exhibit different growth kinetics. The model was used to optimise the dosing schedule to prevent resistance [15]. A further model assuming acquired resistance has been fitted to both gefitinib and erlotinib in patient-derived xenografts, however, the possibility that a fraction of the cells are resistant at baseline was not considered [16]. A general framework has been proposed to model resistance to EGFR-inhibition, when used in combination with a cytotoxic treatment. The framework again suggests describing separate populations of sensitive and resistant cells, which both exhibit exponential growth, although the model was not fitted to experimental data [17].
Here we present a simple mathematical model to describe the developed resistance to treatment with EGFR inhibitors, which can then be used to assess the impact of different treatment regimens. The model was tested on data arising from a complex brain metastasis mouse model following treatment with AZD3759, an EGFR inhibitor designed to effectively cross the blood–brain barrier (BBB). The estimated dose–response curve developed in the brain metastasis mouse model was then compared to the dose–response estimated from standard subcutaneous xenograft mouse models.
Materials and methods
Pharmacokinetic (PK) and tumour growth inhibition data were available from two preclinical studies investigating the use of EGFR inhibitor AZD3759, which is ATP competitive, similar to gefitinib. However, is has been designed to cross the BBB to tackle central nervous system (CNS) metastasis in patients with activating mutations of EGFR in non-small cell lung cancer (NSCLC) [18, 19]. AZD3759 is now being tested in early clinical trials. One preclinical study was carried out in subcutaneous xenografted mice and the other in brain metastasis mouse models.
The study in brain metastasis models had longer follow-up and resistance was observed within several weeks. A model of resistance to treatment with EGFR inhibitors was developed using this dataset. Due to the highly variable nature of the bioluminescence observations in the brain metastasis models, the estimated model parameters were compared to those found in the less variable subcutaneous mouse models to assess reliability.
Subcutaneous xenograft mouse models
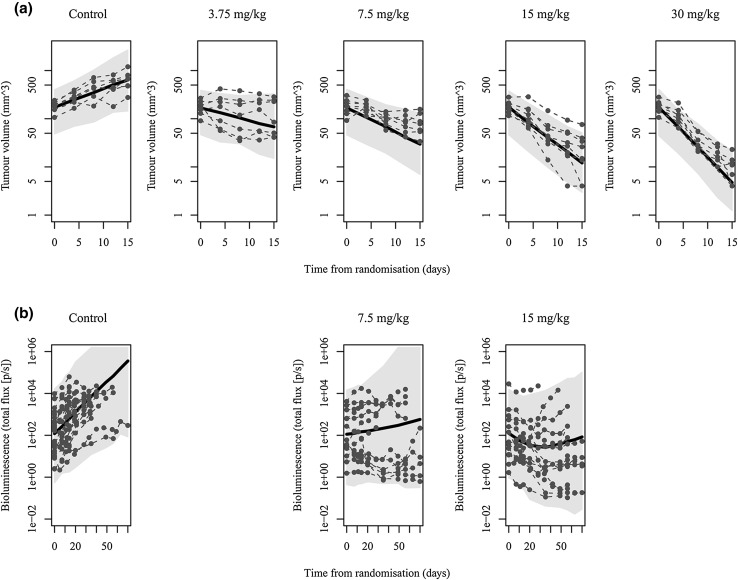
Data were available from a study in subcutaneous xenografted mice, where AZD3759 was tested at four dose levels (3.75, 7.5, 15 and 30 mg/kg dosed daily), a clear dose–response was observed. Approximately 15 mm3 of cells were initially implanted, tumour size at the start of dosing was approximately 180 mm3, then measured roughly every 4 days using callipers, tumour volume was then calculated as V = (length × width2)/2. In total, 38 animals were included in the study, 7 control animals, and 7 or 8 animals in each dose group. A number of tumour growth models were tested but due to the relatively short follow-up time of 15 days and no resistance to AZD3759 treatment or slowing of growth due to competition between cells for resources such as oxygen [20, 21] being observed, a simple exponential growth model was found to sufficiently describe the data. The dose–response was assumed to be proportional to the tumour volume, both linear and Emax dose–response models (Eq. 1) were tested, with an Emax model found to better describe the data. Treatment was assumed to cause cell death rather than causing a decrease in the proliferation rate, in line with [22], as reductions in tumour size from baseline are observed. The response to treatment was assumed to remain constant throughout the study as dosing was daily.
The model described by Eq. (1) was fitted to the data using the first-order conditional estimation method (FOCE with interaction) in NONMEM 7.3 [23], inter-individual variation (IIV) and residual error were assumed to be log-normally distributed. The magnitude of IIV was expressed as a coefficient of variation (CV%), the square root of the variance. IIV was initially assumed on all parameters, but was not included in the final model if there were difficulties in estimation or if it was estimated to be small:
| 1 |
where is the volume of the tumour, is the maximum effect of treatment, is the dose and is the dose at which 50% of the maximum effect is achieved. Visual predictive checks (VPCs) were used to assess the model fit, 1000 datasets were simulated from the model and 95% prediction intervals were calculated by taking the 2.5th and 97.5th centiles.
Brain metastasis mouse models
Additional data were available in brain metastasis mouse models, where the human NSCLC cell line PC9 (exon 19 deletion) was transfected with the GL4.50[luc2/CMV/Hygro] vector containing the luciferase gene (PC9_Luc) using lipofectamine LTX. The cells were implanted into 51 immunodeficient nude mice, 25 controls and 13 in each dose group. Due to the location of the tumours bioluminescence imaging was used to quantify tumour burden, bioluminescence signals were measured using a Xenogen imaging system [24]. The bioluminescence data were extremely variable; both at baseline, which covered many orders of magnitude, and in growth rate (Fig. 1 left); however, a clear dose–response can be seen with two doses (7.5 and 15 mg/kg) when considering change from baseline (Fig. 1 right).
Fig. 1.

Raw bioluminescence measurements for brain metastasis data (left) with fold change from baseline (right)
The follow-up time in this study was up to 70 days and evidence that tumours stopped responding to treatment was observed, particularly in the higher dose group where the tumours begin to regrow despite continuous daily dosing. Therefore, in the model, the tumour was assumed to be made up of two populations of cells, those sensitive to treatment and those which were resistant (Fig. 2). Growth was assumed to be exponential, as has previously been used in bioluminescence tumour growth data [25]. It was assumed that sensitive and resistant cells could both be described using separate exponential growth terms. In the brain metastasis data, it was not possible to fit an Emax model for dose–response, as only two doses were tested, so a linear model with cell death rate () was assumed (response = , see Eq. 2).
Fig. 2.
Structure of model for resistance to treatment, the total tumour volume consists of both sensitive and resistant cells with proliferation rates and , rate constant describes the conversion of sensitive cells to resistant cells and describes cells death due to treatment
The differential equations used to describe the resistance model are given in Eqs. (2–4). Two different hypotheses for the mechanism of how resistance occurs were considered.
Hypothesis 1 Due to heterogeneity within the tumour, a fraction of cells are resistant to treatment at baseline.
Hypothesis 2 The tumour is composed solely of sensitive cells and these can become mutated during the study leading to resistance [13, 14].
Both hypotheses were tested independently and then together. When cells were assumed to be resistant at baseline the initial conditions were: and where is the proportion of cells which are sensitive at baseline; and a logit transformation was used to constrain between 0 and 1. The treatment was assumed to act on sensitive cells only and, as in the subcutaneous model, was assumed to cause cell death. The treatment effect was assumed to be proportional to dose and the effect on sensitive cells was assumed to be constant over the course of the study:
| 2 |
| 3 |
| 4 |
The model was fitted to raw bioluminescence data using FOCE with interaction in NONMEM 7.3, inter-individual variation and residual error were again assumed to be log-normally distributed.
Results
Subcutaneous xenograft mouse models
The parameter estimates for the exponential growth model fitted to the subcutaneous xenografted mice are given in Table 1. The visual predictive checks in Fig. 3a as well as other diagnostic checks indicate that the model describes the dose–response well, and the inter-individual variation is well captured.
Table 1.
Parameter estimates from exponential model fitted to the subcutaneous xenograft data, with relative standard errors from bootstrapping
| Parameters | Estimate (RSE%) | IIV CV% |
|---|---|---|
| λ (proliferation rate constant, 1/day) | 0.0855 (10.8) | 34.9 |
| E max (mm3/day) | 0.519 (27.8) | – |
| ED50 (mg/kg) | 21.5 (83.2) | – |
| Gamma (–) | 0.617 (45.2) | – |
| Baseline (mm3) | 175 (5.5) | 30.5 |
| Residual error (%) | 12.7 |
Fig. 3.
Visual predictive check for a the subcutaneous models and b brain metastasis models by dose, with population model fit (solid line), maximum tumour size (horizontal dashed line) and 95% prediction intervals (shaded)
Brain metastasis mouse models
The resistance to treatment observed in the brain metastasis models was found to be best explained by hypothesis 1; assuming a proportion of cells were resistant at baseline. This hypothesis was preferred based on a number of factors including the AIC (4029.19 for hypothesis 1, 4028.59 for hypothesis 1 + 2) as well as the model fits and the relative impact of each mechanism of resistance on the absolute number of resistant cells. The model fit for hypothesis 2 alone was poor so was not considered. The contribution of sensitive cells mutating to become resistant during the study was estimated to be negligible, although this was with high relative standard error. The parameter estimates are given in Table 2.
Table 2.
Parameter estimates from resistance model fitted to the bioluminescence data, with relative standard errors from bootstrapping
| Parameters | Hypothesis 1 | Hypothesis 1 + 2 combined | ||
|---|---|---|---|---|
| Estimate (RSE%) | IIV CV% | Estimate (RSE%) | IIV CV% | |
| λ S [sensitive cell proliferation, × 106 (p/s)/day] | 0.108 (8.2) | 48.2 | 0.0992 (11.7) | 48.9 |
| λ R [resistant cell proliferation, × 106 (p/s)/day] | 0.0556 (49.1) | – | 0.0708 (49.3) | – |
| k R (conversion rate, 1/day) | – | – | 1.54 × 10−6 (139) | – |
| k D (cell death rate, 1/day) | 0.0139 (11.7) | 11.0 | 0.0132 (19.0) | 9.08 |
| Baseline [× 106 (p/s)] | 137 (19.6) | 245 | 177 (34.0) | 248 |
| Percentage sensitive at baseline (%) | 98.7 (9.3) | 48.4 | 99.6 (18.9) | 135 |
| Residual error (%) | 19.0 | 16.5 | ||
The proportion of the tumours estimated to be resistant to treatment over the study by dose level is shown in Fig. 4. In the control group, the proportion of resistant cells decreases over the study as sensitive cells were estimated to proliferate more quickly, consistent with previous findings [14, 15]. In the two-treated groups, the proportion of resistant cells increases over the study, as the number of sensitive cells is reduced by the treatment, while the resistant cells continue to proliferate. In the 15 mg/kg dose group by the end of the study, nearly the entire tumour is estimated to be resistant to treatment, explaining the observed regrowth.
Fig. 4.

Estimated proportion of cells sensitive (light) and resistant (dark) to treatment over the course of the study by dose
The visual predictive checks in Fig. 3b show that the model is able to describe the large variability in the data, which is mostly attributed to inter-individual variation at baseline. The resistance to treatment is well characterised by the model, including the description of the tumour regrowth observed in the 15 mg/kg dose group. In the control group, some tumour sizes are predicted to be higher than those observed due to the drop out of animals with the largest tumour burdens.
The estimated growth rates in the two mouse models were very similar, approximately 0.09 in the subcutaneous model (Table 1) and 0.11 in the brain metastasis model (Table 2). PK data showed similar concentrations were achieved in the brain as in plasma, showing AZD3759 can pass through the BBB, enabling comparison of dose–response between the animal models. The dose–response curves (Fig. 5) were estimated to be similar in magnitude between the two mouse models, although the shape differs due to the number of doses tested. These similarities suggest that despite the high level of variability observed in the brain metastasis models, when using appropriate modelling techniques it is possible to reach a reliable estimate of the dose–response.
Fig. 5.
Dose–response curves for the subcutaneous and brain metastasis mouse models
Discussion
The model proposed describes AZD3759 effectiveness in both subcutaneous and brain metastasis in mouse models. The preferred model based on AIC and model fit showed that the resistance to EGFR-inhibition was due to a small number of cells (approximately 1%) being resistant to treatment at baseline; while the contribution from cells mutating to become resistant during the study was negligible. Consequently, this model suggests that changes to dose level or dosing schedule may not help to overcome resistance in this case. If treatment is continued long enough there will be very few sensitive cells remaining, while the resistant cells will continue to proliferate at the same rate, resulting in all treated tumours ultimately ending up being the same volume, regardless of the dose administered.
The selected hypothesis would suggest that additional treatments which are effective against cells resistant to EGFR inhibitors need to be used in combination with EGFR-inhibition to avoid resistance to treatment; as has previously been suggested [14, 17]. However as these conclusions are based solely on hypothesis selection, further work is needed to reinforce these conclusions experimentally; especially given the highly variable data and the modest difference in AIC.
The bioluminescence data are highly variable which could in part be due to a number of issues around the imaging itself. Studies have found that the estimated tumour size from bioluminescence imaging does not correlate with true tumour volume [25, 26]. Measurements can be affected by the location of the tumour and the positioning of the animals during imaging [25, 27, 28], non-uniformity of luciferase expression across tumour cells, quenching of light emissions by brain tissue, skin and bone [29], as well as the ability of luciferase to diffuse through the blood–brain barrier [30]. However, the agreement of the model parameter estimates with those estimated using the less variable subcutaneous mouse models may suggest the estimates of dose–response are reliable. In the brain metastasis models, there were a small number of animals that dropped out of the study early due to large tumour burdens. This was investigated using a joint modelling approach to account for dropout [31], but the relatively small number of dropouts (10% of all animals) was found not to significantly affect the estimation of parameters in the model. However, this drop out could explain the over-estimation of the tumour volume in the control and 7.5 mg/kg dose groups in the visual predictive check in Fig. 3.
The two mouse models give very similar estimates of growth rate and dose–response despite differences in baseline and variability. Subcutaneous models are simpler and more convenient than the more complex brain metastasis models; and therefore in some cases it may be appropriate to use subcutaneous xenograft models to assess dose–response. However, it must first be shown that the treatment is crossing the blood–brain barrier, reaching the site of action, as was determined to be the case with AZD3759 [19].
Simple mathematical models were used to describe the growth of both sensitive and resistant populations of tumour cells, but it should be possible to use more complex models, for example, to describe the slowing of the growth rate as the tumour burden increases, if further data were available. Further work could be done to model combinations of treatment, potentially utilising the framework suggested for describing the combination of EGFR inhibition with a cytotoxic treatment, describing populations of cells resistant to one or both treatments [17].
Acknowledgements
This research was supported by the Biotechnology and Biological Sciences Research Council (Award number BB/L502583/1).
Conflict of interest
Author James W. T. Yates is employed by and owns shares in AstraZeneca. Authors Emma C. Martin and Leon Aarons declare they have no conflicts of interest.
Ethical approval
All applicable international, national, and/or institutional guidelines for the care and use of animals were followed.
Contributor Information
Emma C. Martin, Email: emma.martin@leicester.ac.uk
Leon Aarons, Email: leon.aarons@manchester.ac.uk.
James W. T. Yates, Email: james.yates@astrazeneca.com
References
- 1.Harari PM. Epidermal growth factor receptor inhibition strategies in oncology. Endocr Relat Cancer. 2004;11(4):689–708. doi: 10.1677/erc.1.00600. [DOI] [PubMed] [Google Scholar]
- 2.Dienstmann R, et al. Drug development to overcome resistance to EGFR inhibitors in lung and colorectal cancer. Mol Oncol. 2012;6(1):15–26. doi: 10.1016/j.molonc.2011.11.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Stewart EL, et al. Known and putative mechanisms of resistance to EGFR targeted therapies in NSCLC patients with EGFR mutations—a review. Transl Lung Cancer Res. 2015;4(1):67–81. doi: 10.3978/j.issn.2218-6751.2014.11.06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Yewale C, et al. Epidermal growth factor receptor targeting in cancer: a review of trends and strategies. Biomaterials. 2013;34(34):8690–8707. doi: 10.1016/j.biomaterials.2013.07.100. [DOI] [PubMed] [Google Scholar]
- 5.Morgillo F, et al. Resistance mechanisms of tumour cells to EGFR inhibitors. Clin Transl Oncol. 2009;11(5):270–275. doi: 10.1007/s12094-009-0354-6. [DOI] [PubMed] [Google Scholar]
- 6.Ohashi K, et al. Epidermal growth factor receptor tyrosine kinase inhibitor-resistant disease. J Clin Oncol. 2013;31(8):1070–1080. doi: 10.1200/JCO.2012.43.3912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Huang L, Fu L. Mechanisms of resistance to EGFR tyrosine kinase inhibitors. Acta Pharm Sin B. 2015;5(5):390–401. doi: 10.1016/j.apsb.2015.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tetsu O, et al. Drug resistance to EGFR inhibitors in lung cancer. Chemotherapy. 2016;61(5):223–235. doi: 10.1159/000443368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Gainor JF, Shaw AT. Emerging paradigms in the development of resistance to tyrosine kinase inhibitors in lung cancer. J Clin Oncol. 2013;31(31):3987–3996. doi: 10.1200/JCO.2012.45.2029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Engelman JA, Janne PA. Mechanisms of acquired resistance to epidermal growth factor receptor tyrosine kinase inhibitors in non-small cell lung cancer. Clin Cancer Res. 2008;14(10):2895–2899. doi: 10.1158/1078-0432.CCR-07-2248. [DOI] [PubMed] [Google Scholar]
- 11.Han CH, Brastianos PK. Genetic characterization of brain metastases in the era of targeted therapy. Front Oncol. 2017;7:230. doi: 10.3389/fonc.2017.00230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hata AN, et al. Tumor cells can follow distinct evolutionary paths to become resistant to epidermal growth factor receptor inhibition. Nat Med. 2016;22(3):262–269. doi: 10.1038/nm.4040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sun X, Bao J, Shao Y. Mathematical modeling of therapy-induced cancer drug resistance: connecting cancer mechanisms to population survival rates. Sci Rep. 2016;6:22498. doi: 10.1038/srep22498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chong CR, Janne PA. The quest to overcome resistance to EGFR-targeted therapies in cancer. Nat Med. 2013;19(11):1389–1400. doi: 10.1038/nm.3388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chmielecki J, et al. Optimization of dosing for EGFR-mutant non-small cell lung cancer with evolutionary cancer modeling. Sci Transl Med. 2011;3(90):90ra59. doi: 10.1126/scitranslmed.3002356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Eigenmann MJ, et al. PKPD modeling of acquired resistance to anti-cancer drug treatment. J Pharmacokinet Pharmacodyn. 2017;44(6):617–630. doi: 10.1007/s10928-017-9553-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Terranova N, et al. Resistance development: a major piece in the jigsaw puzzle of tumor size modeling. CPT Pharmacometrics Syst Pharmacol. 2015;4(6):320–323. doi: 10.1002/psp4.45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Yang Z, et al. AZD3759, a BBB-penetrating EGFR inhibitor for the treatment of EGFR mutant NSCLC with CNS metastases. Sci Transl Med. 2016;8(368):368ra172. doi: 10.1126/scitranslmed.aag0976. [DOI] [PubMed] [Google Scholar]
- 19.Zeng Q, et al. Discovery and evaluation of clinical candidate AZD3759, a potent, oral active, central nervous system-penetrant, epidermal growth factor receptor tyrosine kinase inhibitor. J Med Chem. 2015;58(20):8200–8215. doi: 10.1021/acs.jmedchem.5b01073. [DOI] [PubMed] [Google Scholar]
- 20.Benzekry S, et al. Classical mathematical models for description and prediction of experimental tumor growth. PLoS Comput Biol. 2014;10(8):e1003800. doi: 10.1371/journal.pcbi.1003800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gerlee P. The model muddle: in search of tumor growth laws. Cancer Res. 2013;73(8):2407–2411. doi: 10.1158/0008-5472.CAN-12-4355. [DOI] [PubMed] [Google Scholar]
- 22.Yates JW, et al. Irreversible inhibition of EGFR: modeling the combined pharmacokinetic–pharmacodynamic relationship of osimertinib and its active metabolite AZ5104. Mol Cancer Ther. 2016;15(10):2378–2387. doi: 10.1158/1535-7163.MCT-16-0142. [DOI] [PubMed] [Google Scholar]
- 23.Beal S, et al. NONMEM user’s guides (1989–2009) Ellicott City, MD: Icon Development Solutions; 2009. [Google Scholar]
- 24.Kemper EM, et al. Development of luciferase tagged brain tumour models in mice for chemotherapy intervention studies. Eur J Cancer. 2006;42(18):3294–3303. doi: 10.1016/j.ejca.2006.07.013. [DOI] [PubMed] [Google Scholar]
- 25.Keyaerts M, et al. Dynamic bioluminescence imaging for quantitative tumour burden assessment using IV or IP administration of d-luciferin: effect on intensity, time kinetics and repeatability of photon emission. Eur J Nucl Med Mol Imaging. 2008;35(5):999–1007. doi: 10.1007/s00259-007-0664-2. [DOI] [PubMed] [Google Scholar]
- 26.El Hilali N, Rubio N, Blanco J. Noninvasive in vivo whole body luminescent analysis of luciferase labelled orthotopic prostate tumours. Eur J Cancer. 2004;40(18):2851–2858. doi: 10.1016/j.ejca.2004.09.010. [DOI] [PubMed] [Google Scholar]
- 27.Cui K, et al. A quantitative study of factors affecting in vivo bioluminescence imaging. Luminescence. 2008;23(5):292–295. doi: 10.1002/bio.1032. [DOI] [PubMed] [Google Scholar]
- 28.Sim H, et al. Pharmacokinetic modeling of tumor bioluminescence implicates efflux, and not influx, as the bigger hurdle in cancer drug therapy. Cancer Res. 2011;71(3):686–692. doi: 10.1158/0008-5472.CAN-10-2666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Klerk CP, et al. Validity of bioluminescence measurements for noninvasive in vivo imaging of tumor load in small animals. Biotechniques. 2007;43(1 Suppl):7–13. doi: 10.2144/000112515. [DOI] [PubMed] [Google Scholar]
- 30.Aswendt M, et al. Boosting bioluminescence neuroimaging: an optimized protocol for brain studies. PLoS One. 2013;8(2):e55662. doi: 10.1371/journal.pone.0055662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Martin EC, Aarons L, Yates JW. Accounting for dropout in xenografted tumour efficacy studies: integrated endpoint analysis, reduced bias and better use of animals. Cancer Chemother Pharmacol. 2016;78(1):131–141. doi: 10.1007/s00280-016-3059-x. [DOI] [PMC free article] [PubMed] [Google Scholar]