Theory and practice of using solvent paramagnetic relaxation enhancement to characterize protein conformational dynamics

Abstract

Paramagnetic relaxation enhancement (PRE) has been established as a powerful tool in NMR for investigating protein structure and dynamics. The PRE is usually measured with a paramagnetic probe covalently attached at a specific site of an otherwise diamagnetic protein. The present work provides the numerical formulation for probing protein structure and conformational dynamics based on the solvent PRE (sPRE) measurement, using two alternative approaches. An inert paramagnetic cosolute randomly collides with the protein, and the resulting sPRE manifests the relative solvent exposure of protein nuclei. To make the back-calculated sPRE values most consistent with the observed values, the protein structure is either refined against the sPRE, or an ensemble of conformers is selected from a pre-generated library using a Monte Carlo algorithm. The ensemble structure comprises either N conformers of equal occupancy, or two conformers with different relative populations. We demonstrate the sPRE method using GB1, a structurally rigid protein, and calmodulin, a protein comprising two domains and existing in open and closed states. The sPRE can be computed with a stand-alone program for rapid evaluation, or with the invocation of a module in the latest release of the structure calculation software Xplor-NIH. As a label-free method, the sPRE measurement can be readily integrated with other biophysical techniques. The current limitations of the sPRE method are also discussed, regarding accurate measurement and theoretical calculation, model selection and suitable timescale.

1. Background

A protein can dynamically adopt more than one structure in order to carry out its function. Solution NMR is particularly useful to visualize protein dynamics and to characterize protein ensemble structures. Among the different NMR methods, paramagnetic relaxation enhancement (PRE) is exquisitely sensitive to subtle changes of protein conformation. As such, the PRE has been widely used for visualizing protein transient structure and transient interactions [1–3]. The PRE, the enhancement of either transverse or longitudinal relaxation rates, depends on <r⁻⁶> distance between the paramagnetic probe and protein nuclei, which can be commonly described by the Solomon-Bloembergen-Morgan equation [4, 5]. To measure the PRE, a paramagnetic probe needs to be site-specifically conjugated to an engineered cysteine residue [6] or unnatural amino acid [7] in an otherwise diamagnetic protein. The paramagnetic probe can also be installed with the insertion of a metal binding motif at protein termini or inside the protein [8–10]. However, the introduction of a paramagnetic probe may inadvertently perturb the protein structure and function.

Without covalent labeling, the PRE data can be obtained with the addition of a paramagnetic cosolute. This method is called solvent PRE or short as sPRE. It manifests the relative accessibility of protein nuclei to the paramagnetic probe added. The sPRE method has been used to study folded proteins [11], intrinsically disordered proteins [12], membrane proteins [13] and protein complexes [14, 15]. A number of paramagnetic small molecules have been used for the sPRE measurement, including Gd-DTPA-BMA [16], oxygen [17] and Fe(DO₃A) [12]. Among them, Gd-DTPA-BMA, otherwise known as a contrasting agent for magnetic imaging [18], is commonly used [19]. However, this probe leaves one coordination site of Gd³⁺ open for water (Fig. 1A). Owing to the exchange with relaxation enhanced water molecules, labile protons in the protein can experience unusually large sPRE values [11, 20].

Fig. 1. Structure of the three paramagnetic cosolute molecules.

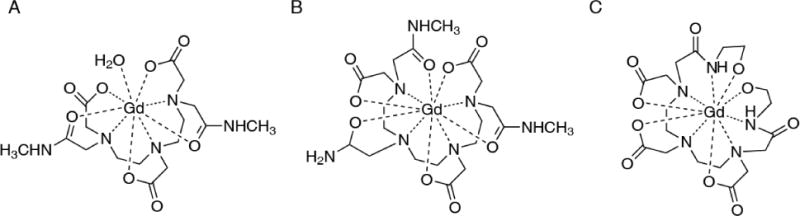
A) diethylenetriamine pentaacetate bismethylamide gadolinium chelate (Gd(III)-DTPA-BMA). B) triethylenetetraamine hexaacetate trimethylamide gadolinium chelate (Gd(III)-TTHA-TMA), which provides full coordination to Gd³⁺ and eliminates the need for an inner-sphere water. C) diethylenetriamine pentacetate bishydroxyethylamide gadolinium chelate (Gd(III)-DTPA-BEA), which is similar to compound B but less hydrophobic.

To eliminate the water exchange problem, we have previously designed and synthesized a chelator TTHA-TMA [20]. This chelator has 10 coordination sites for Gd³⁺, and requires no inner-sphere water (Fig. 1B). The absence of exchange simplifies the theoretical calculation of sPRE values [21, 22]. If perfectly inert, the cosolute molecule should just randomly collide with the protein, with the sPRE value indicative of the relative depth of protein nuclei and dictated by Solomon-Bloembergen-Morgan equation. More importantly, accurately measured sPRE data allowed us to evaluate whether the protein resides in a single structure or dynamically fluctuates among multiple conformations [23].

2. Assessing protein structure and dynamics based on the sPRE measurement

The experimental sPRE data can be assessed against the numerical values calculated from a particular structure, which can be the structure experimentally determined or generated from MD simulations. Alternatively, the experimental sPRE restraints can be used as an energy function, and force the back-calculated sPRE values of the resulting structure to be as consistent as possible, while the structure should also satisfy other types of experimental restraints at the same time.

2.1 Computation of theoretical sPRE values based on protein structure

In the past, theoretical sPRE values were often approximated when probing protein structure. Madl et al. used a set of pseudo-molecules to represent the paramagnetic cosolute near the protein surface, and converted the sPRE data to NOE distance restraints between nuclei with the largest sPRE values and those pseudo-molecules [11]. Wang et al. defined a solvent accessibly metric S_accz, which follows an <r⁻²> distance relationship between a protein nucleus and neighboring heavy atoms within a certain cutoff. The authors found that the S_acc term is about linearly related to ratio of peak intensities in the paramagnetic spectrum (with the cosolute added) vs. the diamagnetic control (without the cosolute) [24]. However, the intensity ratio is not a simple function of the sPRE, and can be affected by incomplete longitudinal recovery [25]. Moreover, the slope and intercept values for the linear function between S_acc and intensity ratio vary for each protein, and can only be determined through a grid search process.

The sPRE value can also be computed using a lattice model based on the Solomon-Bloembergen-Morgan equation with volume integration [16, 20, 26, 27]. Here we construct a cubic lattice around a protein structure with certain spacing between lattice points. A 4-Å radius is given to the paramagnetic cosolute of Gd-TTHA-TMA (Fig. 1B). With van der Waals radii padded, lattice points overlapping with the protein are assigned with 0, and the corresponding sPRE contributions are excluded. Thus the sPRE value for a protein nucleus is defined as

$${\mathrm{\Gamma }}_2={{\displaystyle \sum }}_{n}k\cdot r^{-6}$$ (1)

Here the r is the distance between a nucleus and any allowed lattice point within a distance cutoff (we use 40 Å), and the Γ₂ is the calculated sPRE value summed over all allowed lattice points around the protein. A universal scaling factor k is assumed, which is a function of the constants in the Solomon-Bloembergen-Morgan equation, and is also related to the experimental conditions like the concentration of paramagnetic cosolute, temperature, solvent viscosity etc.

The calculated sPRE values also depend on the spacing between lattice points. This is because the volume integral approach uses a discrete model as an approximation, while in reality he cosolute is continuously distributed around the protein. We calculated the sPRE transverse relaxation enhancement Γ₂ values for the backbone amide protons of GB1, the first globular domain of immunoglobulin protein G [28]. With a lattice spacing of 1.0 Å, the sPRE value is over-estimated for residue A23, the first residue in a helix. Finer lattice, like 0.5 Å and 0.1 Å, does produce sPRE values agreeing better with the observed values (Fig. 2A), albeit at a higher computation cost. For GB1, on a single Intel Xeon CPU E5-2670 v3 processor, it takes ~1 s with 1-Å spacing, ~2.7 s with 0.5 Å spacing, and close to 600 s with 0.1 Å spacing. As a compromise, we use a spacing of 0.5 Å between lattice points.

Fig. 2. Methods for evaluating theoretical sPRE.

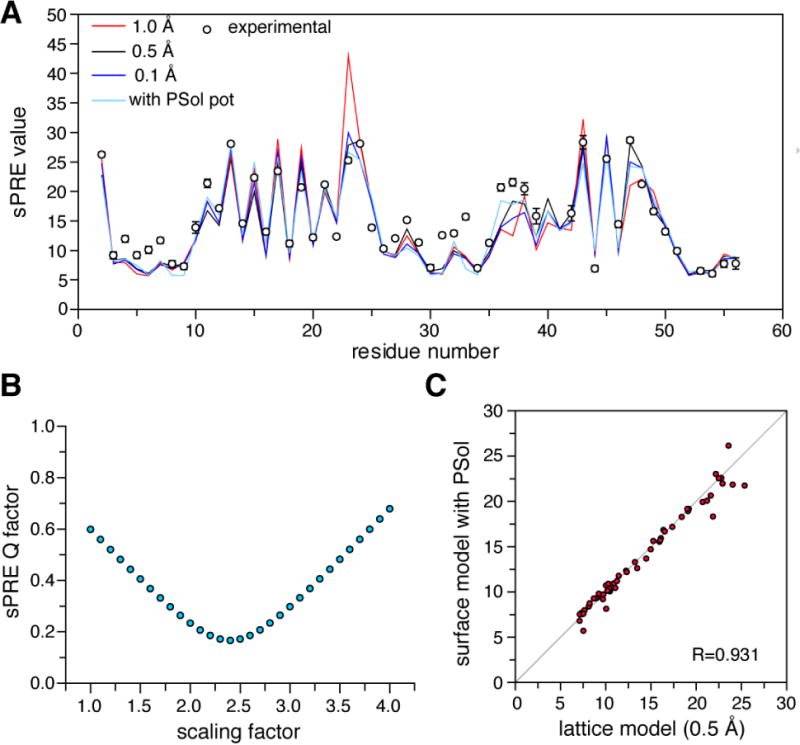
(A) For protein GB1 (PDB code 2GB1), the theoretical sPRE values for protein backbone amide protons can be calculated with lattice point model of different spacing or with surface integral model. Comparing to the experimental data, the correlation coefficient R is 0.866 for 1.0-Å spacing, 0.931 for 0.5-Å spacing, 0.917 for 0.1-Å spacing, and 0.927 for the values calculated with the PSol module in Xplor-NIH. (B) Evaluation of sPRE Q-factor by scaling the calculated sPRE values. The Q-factor can be as low as 0.16 for values calculated with lattice point model with 0.5 Å spacing. (C) The values calculated with the two alternative approaches are highly consistent. The experimental data was collected with 2 mM Gd³⁺-TTHA-TMA, and the error bars stand for 1 standard deviation in the measurement.

The correlation coefficient R is preferred for assessing the agreement between the calculated and observed sPRE values, as the calculation only gives arbitrary values. To plot the sPRE profile by residue or to calculate the sPRE Q-factor, we scale the calculated values to match the observed values. This can be done by normalizing the sPRE value for the residue that is deepest buried and therefore has smallest sPRE value. Alternatively, the sPRE Q-factor can be plotted against the scaling factor to identify the lowest point (Fig. 2B).

The stand-alone program to calculate the theoretical sPRE values from a given PDB structure is freely available at http://www.tanglab.org/resources/programs. In addition to backbone amide, the sPRE values can also be calculated for other types of nuclei such as backbone C’ and selectively labeled side chain methyl groups using the same program.

2.2 Sampling of protein conformational space

Owing to protein dynamics, the sPRE values calculated from a single known structure may not agree with the observed sPRE values. Considering possible inaccuracy of sPRE measurement and imperfection of the algorithms for calculating theoretical sPRE, we believe a correlation coefficient R of below 0.8 warrants further investigation. In addition, the discrepancy in the sPRE is likely localized and can be mapped to adjacent residues. Therefore, sequentially continuous or spatially contiguous residues with large sPRE discrepancy provide additional justifications.

We use molecular dynamics (MD) simulations to generate a large number of possible conformers that in theory cover the full extent of protein conformational space. The MD simulations performed for the protein of interest can afford protein alternative conformations with atomic details. With the use of GPU-accelerated computing, MD simulations can now routinely reach μs-ms timescale and hence a large conformational space. In addition, algorithms have been designed to speed up the simulation, such as accelerated sampling [29], elastic network model based sampling [30], and collective motions accelerating methods [31]. Further acceleration of the conformational sampling is possible with the use of coarse-grained model [32]. However, the protein side chains and other atomic details have to be fleshed out after each simulation run.

For a larger protein system, the MD simulation timescale attainable with the same computational power is shorter. Thus, it is possible that the conformational space of the subject protein is not fully sampled. To overcome this, for example, an empirical approach can be taken that efficiently randomize backbone dihedral angles for certain regions of the protein [33]. This approach is particularly useful when the protein comprises multiple domains that are connected by flexible linkers. We use Xplor-NIH [34] to generate protein alternative conformations—each domain is grouped as a rigid body, and the linkers are given full torsion angle freedom. The conformers generated by Xplor-NIH are further subjected to all-atom MD simulations. In this way, a wider range of protein conformational space can be covered. This hybrid approach enables efficient sampling across energy barriers, and the collection of all possible conformers provides the basis for structural analysis against experimental data, in this case sPRE Γ₂ values collected for protein amide protons. Note that the sampling process does not consider the thermodynamic or kinetic properties of these conformers, and therefore many of the generated conformers are not physically meaningful, which warrants further selection and reweighting of these conformers.

2.3 Identifying the ensemble structure from the sPRE data

The sPRE data allow one to assess the protein structure and dynamics, and to select one or more conformers from a pre-generated library. Using the lattice model, we first compute the theoretical sPRE values for each possible conformer. In this way, a library of conformers can be converted to a library of sPRE profiles. We use a Monte Carlo (MC) simulated annealing method to identify an N-membered ensemble (N can be as few as 1), of which the averaged sPRE values should be most consistent with experimental sPRE values. At a starting pseudo-temperature (t = 10), an N-membered ensemble of sPRE profiles is randomly selected to generate an initial structure with a correlation coefficient R. The sPRE profile for any one of the conformers in the ensemble is replaced by another sPRE profile from the pool if the R for the resulting ensemble is higher; otherwise accept with a probability P. The replacement probability P is defined as exp((R_i+1−R_i)/t), in which i is the replacement step starting from 1 to 10,000 MC steps at each temperature t. The temperature is gradually lowered, with t_j+1 = 0.9 * t_j for each temperature step j and for a total of 1,000 temperature steps. To assess the robustness of the method and the convergence of the ensemble structure, the MC simulated annealing is repeated 100 times, each from a randomly selected N-membered ensemble.

For a protein system under investigation, the number of conformers in the ensemble is gradually increased from 1 to N, and the correlation between the average of N-membered ensemble and experimental data is assessed until the correlation coefficient R flattens. Thus we select the ensemble structure with the minimum number of conformers right before the inflection point in the correlation coefficient. A workflow of the selection process is shown in Fig. 3. For the N-membered ensemble, the identification of structurally similar conformers means higher occupancy for this particular conformational state. For a simplified 2-state model, the ensemble structure can be identified with the selection against a binary combination of sPRE libraries, with the sPRE values pre-weighted by the relative populations.

Fig. 3. Flowchart for visualizing protein structure and dynamics using the sPRE.

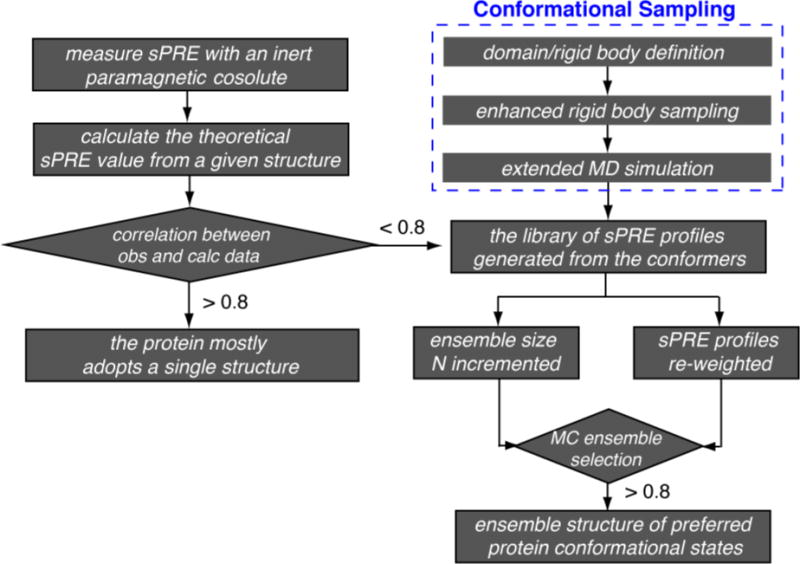
Protein structure can be directly refined, or selected from a library of conformers. Evaluation of the agreement between the observed and calculated sPRE values are based on correlation coefficient R at a certain cutoff.

To evaluate the performance of this MC-based selection method, we synthesize the sPRE data that are averaged from randomly selected N-membered ensemble (reference structure) from the pool. The conformer pool is generated from extended MD simulation trajectories of apo adenylate kinase and comprises 100,000 conformers [23]. MC simulated annealing is performed to identify the ensemble (working structure) of which the calculated sPRE values are most consistent with the synthesized sPRE values. When N < 5, the same set of conformers can always be found and are identical to the reference ensemble, affording an R of 1. When N ≥ 5, similar conformers may be nondiscriminatorily selected from the pool and replace conformers in the reference structure, affording an R of <1. When the number of conformers in the working ensemble is fewer than the size of reference ensemble, the correlation coefficient R is relatively poor (Fig. 4, above the diagonal), which justifies the introduction of one or more additional conformer. On the other hand, if the ensemble size of the working structure is larger than the size of the reference structure, the correlation coefficient R is also low (Fig. 4, below the diagonal), owing to the change of relative populations of the constituting conformational states.

Fig. 4. Evaluation of the robustness of the Monte Carlo ensemble selection algorithm.

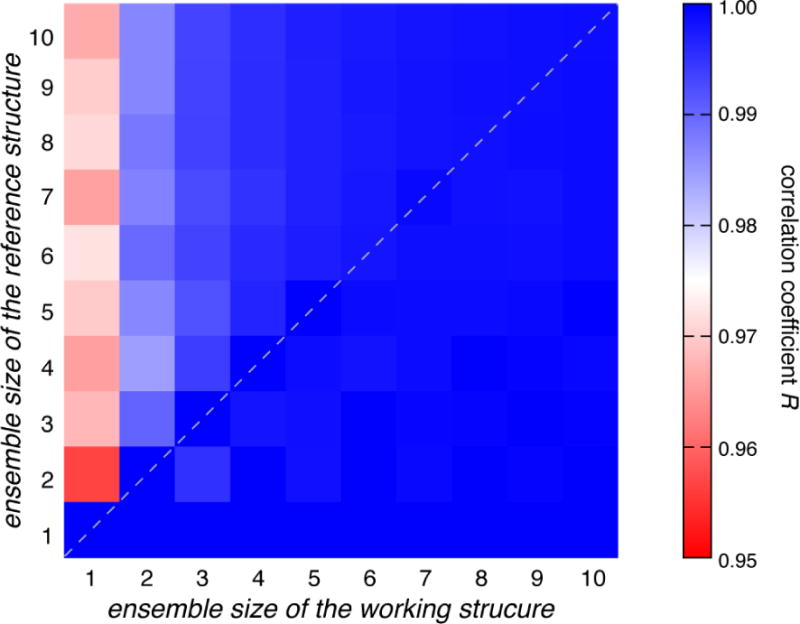
Different number of conformers (from 1 to 10) was selected from a sPRE library of apo AdK protein, derived from a pool of many different conformers, to construct a reference ensemble. The same set of conformers can be repeatedly identified in the working ensemble using our selection algorithm, affording a perfect correlation (dashed diagonal line).

Together, the MC selection algorithm permits efficient identification of an optimal ensemble structure based on the sPRE data with excellent convergence and robustness. The program is freely available at http://www.tanglab.org/resources/programs, which may also be used to identify the best combination of conformers based on other type of experimental input.

3. Direct refinement against the sPRE restraints

A second approach is to use a structure calculation program that makes the back-calculated sPRE of the target structure closest to the experimental values. This would addresses the possibility that the sampling of protein conformational space is not large enough, as our program can only identify conformers that are already in the pool. A PSolPot term has been introduced in the Xplor-NIH structure calculation program (release 2.46 or later), which allows the direct structure refinement against the sPRE data. In this term, we represent the sum expression for sPRE in Eq. 1 as volume integral

$${\mathrm{\Gamma }}_2={{\displaystyle \int }}_{\mathit{Ve}}\mathit{dvk}\prime r^{-6}$$ (2)

in which the integral is over all protein-excluded space that can be occupied by the paramagnetic cosolute, the distance r is taken from volume element dv to the nucleus of interest, and k′ is a constant pre-factor and is similar to the definition in Eq. 1. Through the use of the divergence theorem in vector calculus, the volume integral that a paramagnetic cosolute occupies can be converted to an integral over the cosolute-excluded molecular surface of the protein. The conversion assumes that the paramagnetic cosolute closest to protein makes the largest contribution to the observed sPRE. This makes sense as the transient adduct of cosolute-protein should have the largest correlation time τ_c, while the cosolute diffuse in and out the immediate vicinity of the protein, i.e. a cosolute-excluded surface. The surface integral is expressed as

$${\mathrm{\Gamma }}_2=-k\prime /3{{\displaystyle \int }}_{S}ds\mathbf{n}\cdot \mathbf{r}/{|\mathbf{r}|}^6$$ (3)

where n is the outward pointing normal of the surface at a surface element ds, and r is the vector q_s − q (q_s is the position on the surface at ds and q the position of the nucleus of interest). We represent the cosolute-excluded surface as a tessellation composed of triangular patches that can be efficiently generated [35]. In this way, the surface integral is replaced by a sum over triangle vertices:

$${\mathrm{\Gamma }}_2\approx -k\prime /9\sum _i{a}_i{\mathbf{n}}_i\cdot {\mathbf{r}}_i/|{\mathbf{r}}_i{|}^6,$$ (4)

Where q_i and n_i are the positions and normal at each vertex, a_i is the area of the associated triangle and r_i = q_i – q. In this surface representation, each triangle is associated with a particular atom, and therefore the gradient of a surface triangle vertex position is that of its associated atom to first approximation.

Covering the cosolute-excluded protein surface with tessellation, the surface integral approach does not have the problem encountered by the first approach employing raw atom-grid distances with 0 or 1 contribution from each grid point. Indeed, for protein GB1, the calculated sPRE values using the Xplor-NIH PSolPot module agree well with the experimental values (Fig. 2A). Importantly, sPRE values calculated with surface integral are highly correlated to the values calculated with the lattice model of volume integral; for GB1 the correlation coefficient between the two sets of calculated values reaches the highest value with 0.5 Å for the spacing between lattice points (Fig. 2C). In addition, in Xplor-NIH calculation, the PSolPot term can be used in conjunction with other types of energy terms. An example definition of the PSolPot term in an Xplor-NIH script is shown below:

• from psolPotTools import create_PSolPot

• psol = create_PSolPot("psol",file='./spre.tbl')

• psol.setRmin(0.1)

• psol.setThreshold(0)

• psol.setProbeRadius(4.0)

• psol.setTargetType("correlation")

Here R_min is the smallest allowed value of r_i in Eq. 4, and ProbeRadius is the radius of the paramagnetic cosolute molecule (set at 4 Å). As discussed in Section 2, a correlation-based energy function is used; when the correlation between back-calculated and experimental values is above a certain value (defined as the threshold), the restraint is considered violated and reported in the output file. The final correlation coefficient R as well as sPRE Q-factor (after proper scaling of the back-calculated values, e.g. Fig. 2B) is given in the header of the output PDB file. An example Xplor-NIH script is deposited in the Mendeley Data, and can also be downloaded from (http://www.tanglab.org/resources/scripts).

4. Examples of probing protein structure and dynamics from the sPRE data

We have previously used the Monte-Carlo selection method to identify an N=2 ensemble structure of apo adenylate kinase that comprises a fully open conformer and a partially closed conformer [23]. Building upon our previous work, we will present here how to directly refine protein structure and to characterize protein dynamics for two other proteins from the experimental sPRE data.

4.1 Structure characterization for a rigid protein

GB1 is a 56-residue stably folded protein and is fairly rigid with little dynamics [28]. The experimental sPRE values are taken from our previous work [20]. The protein is heated up to 3000 and gradually cooled to 25 °C. The PsolPot energy term is incorporated to refine the structure of GB1 with the probe radius set to 4.0 Å and the spin quantum number is set to 3.5. TALOS+-derived backbone dihedral angle restraints [36], a knowledge-based database term [37], a weak radius-of-gyration term [38], and covalent and nonbonded terms are also incorporated during the refinement.

With the incorporation of the sPRE term, the convergence of GB1 structure refinement is improved by more than three-fold. When the GB1 structure is refined with only the dihedral angle restraints, the r.m.s deviation for backbone heavy atoms is 5.14±1.79 Å (Fig. 5A). With the PsolPot term incorporated, the backbone r.m.s. deviation is improved to 1.67±0.34 Å (Fig. 5B). Importantly, the resulting structure is similar to the structure refined with extensive NOE restraints [28], with a backbone r.m.s. difference of 2.05±0.66 Å (Fig. 5C). Accordingly, the correlation coefficient between the observed and calculated sPRE values reaches 0.86 (Fig. 5D).

Fig. 5. Protein structure refinement against sPRE restraints.

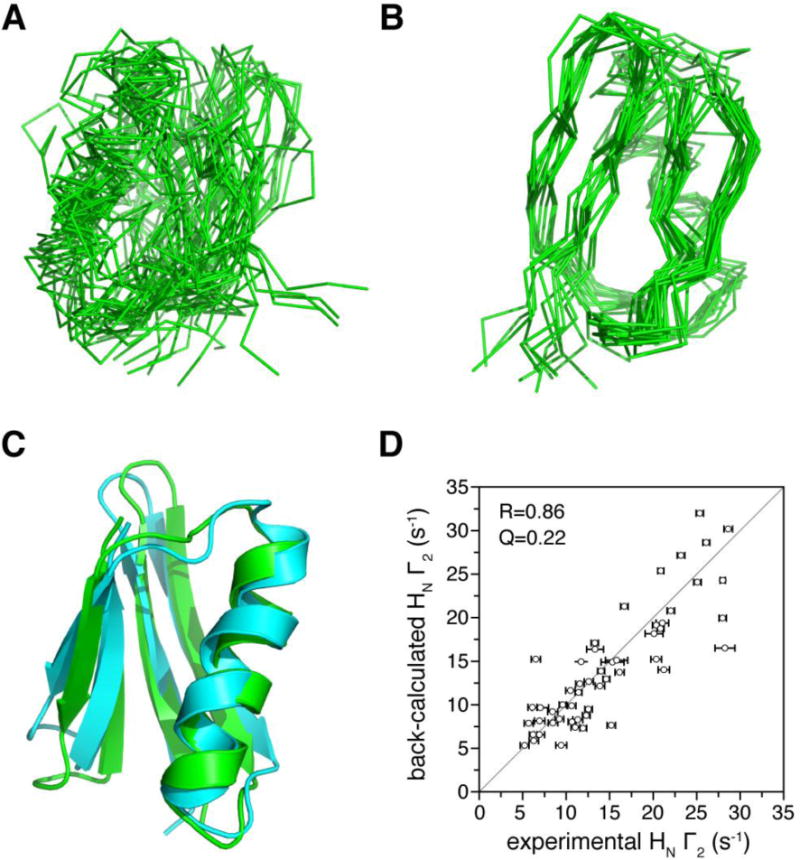
A) Superposition of 20 lowest-energy structures for GB1 protein refined with only dihedral angle restraints. The r.m.s. deviation for backbone heavy atoms is 5.14±1.79 Å. B) Superposition of 20 lowest energy structures with the sPRE restraints using the sPRE PsolPot term incorporated. The r.m.s. deviation for backbone heavy atoms is now improved to 1.67±0.34 Å. C) Comparison between the structure refined with PsolPot term (cyan) and the NMR structure previously determined (PDB code 2GB1, green). D) Correlation between back-calculated sPRE values for the GB1 structure in panel C and the observed values. The error bar in the x-axis is 1 standard deviation in sPRE measurement uncertainty. The correlation coefficient R is 0.86, and the sPRE Q-factor can be as low as 0.22 after appropriate scaling of the calculated values.

The NBtarget is the empirical term that had been included in Xplor-NIH for assessing the solvent accessibly S_acc of protein nuclei based on the sPRE data [24]. The term requires the optimization of the slope and intercept for the linear function between S_acc and intensity ratio. In our hands, the incorporation of the NBtarget term does not lead to an improvement in structure convergence: the resulting structure has an r.m.s. deviation of 5.53±0.89 Å for backbone heavy atoms, and has an r.m.s. difference of 8.91±0.88 Å from the previously determined structure. In comparison, the PSolPot term requires no fitting parameters and is less empirical. Thus for a rigid protein with no large conformational heterogeneity, the PsolPot term in Xplor-NIH allows direct refinement against the sPRE data and improves both precision and accuracy of the structures calculated.

4.2 Visualization of protein dynamic domain movement

A protein can comprise several domains and the relative movement between the domains is often essential for protein function. Here we use ligand-free Ca²⁺-loaded calmodulin (Ca²⁺-CaM) as an example to illustrate how to visualize large-scale protein dynamics from the analysis of the sPRE data. Ca²⁺-CaM consists of an N-terminal domain and a C-terminal domain. When binding to its cognate ligand, the two domains undergo a large rotating/twisting movement, as Ca²⁺-CaM switches from an open to a closed conformation [39].

We determined sPRE Γ₂ values for backbone amide protons of ligand-free Ca²⁺-CaM in the presence 2 mM and 4 mM paramagnetic cosolute of Gd³⁺-TTHA-TMA [20] using the standard pulse program [25]. The sPRE data collected at two cosolute concentrations differ by a scaling factor of 2 and are highly correlated (Fig. 6A), indicating that the cosolute is likely randomly distributing around the protein and has no specific interactions with the protein. On the other hand, the sPRE values calculated from the known open structure of Ca²⁺-CaM [40] does not fully agree well with the observed sPRE data, with the overall correlation coefficient R of only 0.71 (Fig. 6B). When we compare the calculated and observed sPRE values residue-by-residue, it becomes clear that the linker residues between the two domains have the largest discrepancy (Fig. 6C). In comparison, the observed and calculated sPRE values agree much better for the NTD (residues 6-72) and CTD (residues 88-145) residues. Thus we are confident to treat each domain as a rigid body during the initial search of the conformational space.

Fig. 6. Characterization of protein dynamic domain movement based on sPRE.

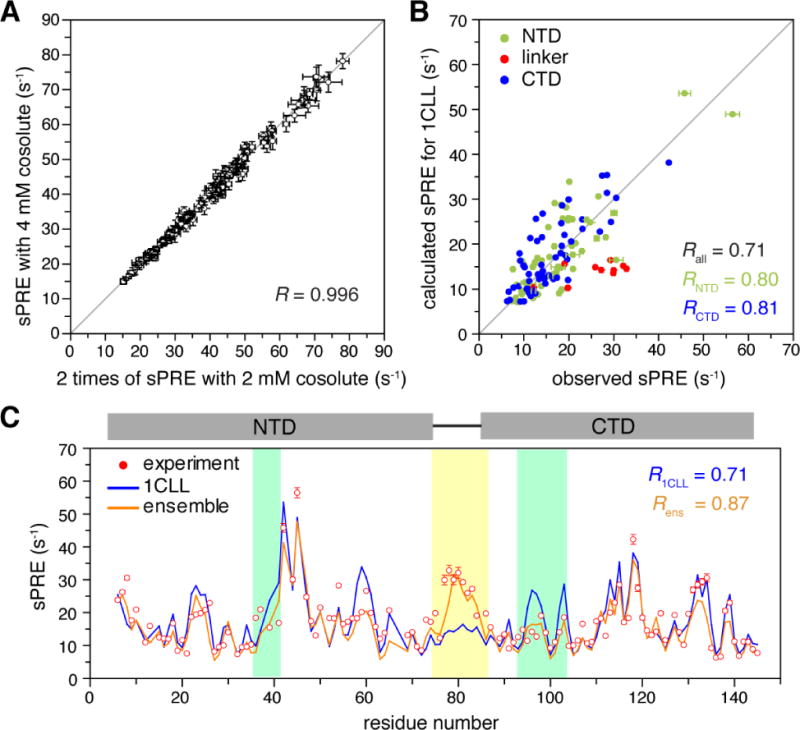
A) Correlation between the sPRE collected for ligand-free Ca²⁺-CaM in the presence of 2 mM and 4 mM paramagnetic cosolute, Gd³⁺-TTHA-TMA. PRE values and errors are both multiplied by 2 for the 2 mM dataset. B) Correlation between observed and calculated sPRE values based on the open structure of the protein (PDB code 1CLL). The sPRE values are colored by NTD (residues 1-74), linker region (residues 75-86), and CTD (residues 87-148). C) Comparison of the observed sPRE profile (red dots) and back-calculated sPRE profiles for the known crystal structure in the open conformation (blue line) and the ensemble structure identified in this study (orange line). Residues with large improvement in the agreement between observed and calculated sPRE values are color-shaded. The error bars stand for 1 standard deviation in sPRE measurement uncertainty.

To probe the dynamics of ligand-free Ca²⁺-CaM based on the sPRE data, we first generate the conformer library of the protein. To sample the conformational space more efficiently and exhaustively, we randomize the relative orientation between NTD and CTD using Xplor-NIH, with full torsion angle freedom given to the linker residues. Starting from these randomized structures of Ca²⁺-CaM, we perform MD simulations, which can stabilize these structures and further explore protein conformational space. Most of the conformers sampled in this way are closed or partially closed with the central helix bent or disappeared. We also perform MD simulation starting from the known open structure of Ca²⁺-CaM [40], which affords mostly open conformers. All these conformers obtained from Xplor-NIH randomization and MD simulation are converted to theoretical sPRE profiles.

To fully account for the sPRE data, we select an ensemble structure consisting of two conformers from the pre-generated library. Since the two conformers are unlikely equally populated, we multiply a pre-factor to the theoretical PRE values, and the calculated sPRE value is thus the population-weighted average of the two, ⟨sPRE⟩=Pa * sPRE_a + (1 − P_a) * sPRE_b. This is a variation from our previous approach that simply increments the number of conformers and uses structurally identical and similar conformers in lieu of occupancy. We vary the relative percentages for the two conformers from 1% to 99% in 1% increments, and the resulting ensemble-averaged sPRE values are assessed against the observed sPRE values. The MC selection process repeatedly identify an open conformer and a closed conformer from the library (Fig. 7A–B); at 55% for the open state and 45% for the closed state, the best agreement between the observed and calculated sPRE values can be achieved, affording a correlation coefficient R of 0.88.

Fig. 7. A two-conformer ensemble structure identified for ligand-free Ca²⁺-CaM.

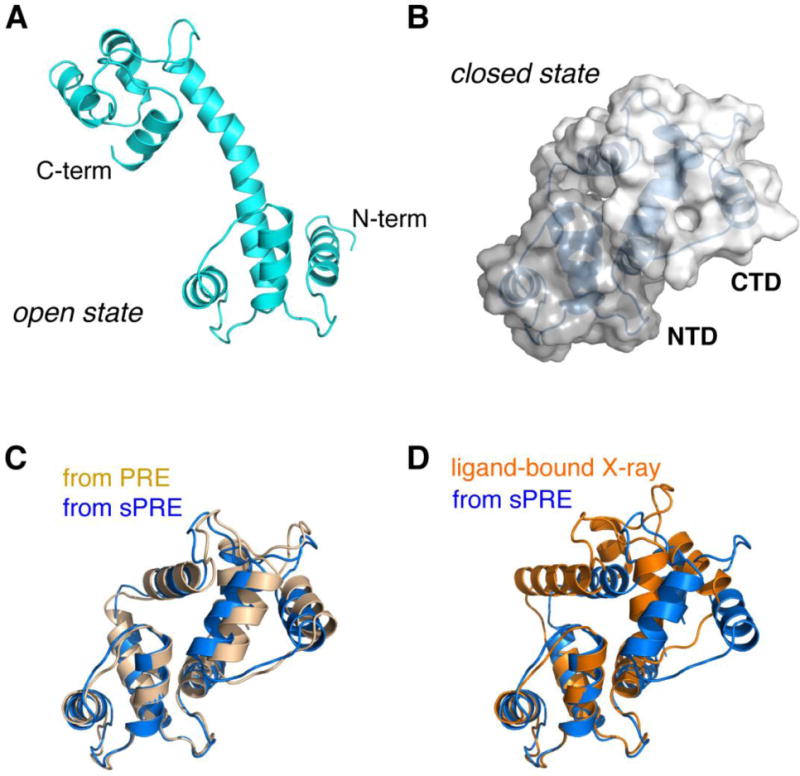
A) The open state selected from MD library with a population of 60%. B) The close state selected from MD library with a population of 40%. The two domains, with the NTD and CTD colored in different shades of gray, bury solvent accessible surface area of ~1255 Ų, while at the same time, the linker residues improve their solvent exposure at one side of the protein. C) Comparison of the closed-state structure identified based on the sPRE data (colored blue) and previously determined based on the PRE data with a nitroxide probe covalently attached at S17C site (colored light orange). The backbone r.m.s. difference between the two structures is as low as 1.50 Å. D) Comparison of the closed-state structure based on the sPRE (marine) and the crystal structure of the ligand-bound Ca²⁺-CaM (PDB code 1CDL, colored orange). The backbone r.m.s. difference between the two structures is as low as 3.50 Å.

The back-calculated sPRE values can account for the unusually large sPRE values for the linker residues. Upon domain closure, the linker residues lose helicity and increase their exposure to the paramagnetic cosolute. In addition, the ensemble structure can account for the small but noticeable sPRE discrepancy for residues 37-42 in the NTD and residues 93-103 in the CTD (Fig. 6C). The observed sPRE values for these residues are smaller than the calculated values for the open structure, which is attributed to closing between the two domains and the burial of the interfacial residues (Fig. 7B). As such, the PRE data for the interfaces on the NTD and CTD cross-validate each other. In addition, the closed-state structure of Ca²⁺-CaM obtained based on the sPRE data is similar to the closed-state structure previously determined based on the PRE data with a covalently conjugated paramagnetic probe [41] (Fig. 7C), and is also similar to the structure of ligand-bound Ca²⁺-CaM (Fig. 7D).

5. Further development of the sPRE method

5.1 Prospect for wider application

We have illustrated here that the sPRE measured in the presence of a newly developed paramagnetic cosolute can allow the characterization of protein structure and the visualization of protein dynamics. To identify the structure or an ensemble of structures that can best account for the sPRE data, we either select the structure from a pre-generated conformer library or directly refine against the sPRE using a newly installed module in Xplor-NIH, the popular structure refinement software. The biggest advantage for the sPRE method is that it is label-free, thus without the need for mutation and conjugation as for the established PRE method. Thus, the sPRE method can be readily integrated with other label-free methods, such as small angle scattering (SAS) and cross-linking coupled with mass spectroscopy (CXMS) [42]. The integration would also allow cross-validation between different types of experimental inputs. As such, the sPRE method may find its applications for probing the structure and dynamics of a variety of interesting biological macromolecules, including proteins, nucleic acids and their complexes.

5.2 Limitations and challenges

We have shown here that the sPRE method can be used to visualize protein structure and dynamics. However, the output structure can be prone to several sources of errors, which can be alleviated by fully addressing these questions. (1) Can the sPRE be measured accurately, free from artifact? (2) Can the sPRE values be calculated accurately and efficiently for each given structure? (3) Can the conformational space be sufficiently sampled, to be selected against the experimental sPRE data? (4) What is the resolution of sPRE method in discerning the amplitude or range of protein dynamics? (5) What is time-scale of the protein dynamics that can be visualized by the sPRE method?

For the first question, a perfectly inert paramagnetic cosolute should randomly collide with the subject protein. Though we have modified the paramagnetic cosolute to rid of water exchange problem, it may still occur, for some protein, that the cosolute is unevenly distributed. The stickiness can be manifested by disproportionally large sPRE values for certain residues of the protein, when the data are collected at multiple concentrations of the paramagnetic cosolute. To address the issue, we have designed and synthesized a third-generation paramagnetic cosolute with the molecule decorated with hydroxyl groups instead of methyl groups (Fig. 1C), which should decrease hydrophobic interactions between the cosolute and the protein.

This brings to the second question—how can the sPRE be accurately predicted if the cosolute is not fully inert? For the calculation with the volume integral approach, the cosolute is discretely positioned, and the paramagnetic effect for a protein nucleus is summed up over all protein-excluded lattice points within a cutoff. Thus the relaxation effect from translational diffusion of the cosolute [21] does not have to be considered. The surface integral approach gives similar prediction for the sPRE values as the volume integral approach. Both methods assume a constant pre-factor, and hence a constant correlation time for each transient protein-cosolute adduct, which may not hold if protein-cosolute encounter is not fully random. Indeed, Gd³⁺-TTHA-TMA likely has biased preference for a hydrophobic patch on GB1 encompassing residues Leu12 and Tyr33, which can account for the slightly higher experimental sPRE values for the adjacent residues than the calculated values and an imperfect correlation coefficient (Fig. 2A). The population for the closed state of ligand-free Ca²⁺-CaM has been previously estimated at < 5% [41], much lower than what we have determined here. It is thus possible that the paramagnetic cosolute may have slightly higher preference for certain regions of Ca²⁺-CaM, and fortuitously amplify the structural information for the closed state. In the future, extended MD simulations in the presence of the cosolute should allow the discernment of different residence times of the cosolute on the protein. This is conceptually similar to what has been done for the PRE calculation of an unfolded protein with a covalently linked paramagnetic probe [43]. It should be noted that with a sea of cosolute diffusing around the protein, the computational cost for explicit MD simulation of the sPRE would be extremely high.

Exhaustive sampling of the conformational space can be challenging for a protein even without the explicit paramagnetic cosolute. For small proteins, all-atom MD simulations may suffice. For large systems, some prior knowledge is required to define rigid bodies and to simply the calculation. Xplor-NIH and other software [33] can randomize torsional angles for a set of residues, as long as permitted by van der Waals and preferred by known high-resolution structures. The randomization procedure expands the search of conformational space, and subsequent MD simulations can generate more physically realistic conformers. As is difficult to know whether the sampling is truly sufficient, direct refinement against the sPRE data offers an alternative approach, and the structure identified from the sPRE can be cross-validated by other types of experimental data.

For the PRE measured with a covalently linked paramagnetic probe, the PRE value can be as large as several thousand s⁻¹, with the largest and smallest PRE values differing by >1000 fold. As a result, the PRE is highly sensitive to subtle protein conformational fluctuation [44]. In comparison, the overall magnitude of sPRE is smaller, the largest (for surface exposed residue) and smallest (for buried residue) sPRE values differ only by ~10 fold. As a result, even for our synthesized sPRE data, the sPRE method may only identify protein structure with the ensemble size no larger than 5 (Fig. 4). Therefore, it is best to use the sPRE method to characterize dynamic domain movement that accompanies large changes in sPRE. For Ockham’s razor, it is also better to first use a simple two-state exchange model, while varying the occupancies of the two constituting states in the ensemble.

Regarding the 5^th question postulated above, the sPRE is sensitive to protein dynamics as slow as tens of millisecond timescale. This also has to do with the overall magnitude of the sPRE, as we have previously shown from theoretical simulation [23]. Towards the other end of the dynamics timescale, both volume integral and surface integral approaches may no longer approximate the sPRE value well, if the protein conformation fluctuates at ps-ns timescale. This is because the calculation assumes the cosolute is distributed with respect to a rigid snapshot of the protein. However, the diffusion of cosolute takes time—depending on temperature and solvent viscosity, a small molecule has a translational diffusion coefficient at the order of 10⁻¹⁰ m²/s, and travels a few Å in one nanosecond, which may be comparable to some side-chain or loop motion in amplitude. Thus rotational modulation of dipole-dipole interactions between cosolute and protein nuclei may have to be considered, for more accurate calculation of the sPRE. Together, further development in the sPRE method, especially in the computational aspects, shall make this NMR method more insightful in characterizing protein structure and dynamics.

Highlights.

• Paramagnetic relaxation enhancement (PRE) for a protein can be measured label-free

• A new paramagnetic cosolute allows more accurate measurement of solvent PRE (sPRE)

• The sPRE can be calculated with volume or surface integral algorithms

• Incorporation of sPRE data improve precision and accuracy of structure refinement

• The sPRE identifies protein ensemble structure of preferred conformational states