Revisiting isotonic phase I design in the era of model-assisted dose-finding

Abstract

Background/aims:

In the conduct of phase I trials, the limited use of innovative model-based designs in practice has led to an introduction of a class of “model-assisted” designs with the aim of effectively balancing the trade-off between design simplicity and performance. Prior to the recent surge of these designs, methods that allocated patients to doses based on isotonic toxicity probability estimates were proposed. Like model-assisted methods, isotonic designs allow investigators to avoid difficulties associated with pre-trial parametric specifications of model-based designs. The aim of this work is to take a fresh look at an isotonic design in light of the current landscape of model-assisted methods.

Methods:

The isotonic phase I method of Conaway, Dunbar and Peddada was proposed in 2004 and has been regarded primarily as a design for dose-finding in drug combinations. It has largely been overlooked in the single-agent setting. Given its strong simulation performance in application to more complex dose-finding problems, such as drug combinations and patient heterogeneity, as well as the recent development of user-friendly software to accompany the method, we take a fresh look at this design and compare it to a current model-assisted method. We generated operating characteristics of the Conaway-Dunbar-Peddada method using a new web application developed for simulating and implementing the design, and compared it to the recently proposed Keyboard design that is based on toxicity probability intervals.

Results:

The Conaway-Dunbar-Peddada method has better performance in terms of accuracy of dose recommendation and safety in patient allocation in seventeen of twenty scenarios considered. The Conaway-Dunbar-Peddada method also allocated fewer patients to doses above the maximum tolerated dose than the Keyboard method in many of scenarios studied. Overall, the performance of the Conaway-Dunbar-Peddada method is strong when compared to the Keyboard method, making it a viable simple alternative to the model-assisted methods developed in recent years.

Conclusion:

The Conaway-Dunbar-Peddada method does not rely on the specification and fitting of a parametric model for the entire dose-toxicity curve to estimate toxicity probabilities as other model-based designs do. It relies on a similar set of pre-trial specifications to toxicity probability interval-based methods, yet, unlike model-assisted methods, it is able to borrow information across all dose levels, increasing its efficiency. We hope this concise study of the Conaway-Dunbar-Peddada method, and the availability of user-friendly software, will augment its use in practice.

Introduction

In clinical practice, implementation of novel dose-finding designs has been limited, with simple traditional or modified 3+3 designs remaining in frequent use.¹ Recent surveys have been conducted to attempt to pinpoint the most common barriers to implementation of novel designs in early-phase trials.^2,3 Two of the most prominent obstacles identified by both surveys were lack of suitable expertise or training on the use of novel designs and lack of available software. Related to these two obstacles, Jaki² reports that the length of time needed to properly design the study, partially due to the statistician’s late involvement, is insufficient. With limited time, expertise and software, it is difficult to conduct a thorough evaluation of a design’s operating characteristics through extensive simulation studies. Even with adequate expertise, there is often limited time to develop code and run simulation studies to provide review entities with sufficient information to adequately evaluate the study design. Published implementation recommendations^4,5 have attempted to facilitate the process of novel design application, and timelier reporting of use in real ongoing trials has attempted to increase the awareness of methodology acceptance.^6–8

Additional efforts to mitigate implementation barriers have been made through the recent development of a new class of “model-assisted” designs. These methods were developed with the aim of effectively balancing the trade-off between simplicity and performance, and have been receiving increased attention with clinical audiences.^9–11 Model-assisted designs combine the flexible use of a model for determination of the maximum tolerated dose (MTD) with a prespecified set of escalation and de-escalation rules similar to that of the 3+3. Allocation decisions during the trial conduct are guided by a model using only data observed “locally” at the current dose level, while MTD assessment is based on data from all dose levels and the fitting of a model. The performance of these designs has been shown to be superior to the 3+3, yet inferior to model-based designs, across a broad range of scenarios.¹² Model-assisted designs are all special cases of semi-parametric dose-finding methods¹³ in that they are less reliant on the pre-trial parametric specifications associated with model-based designs. Furthermore, these designs are all are accompanied by user-friendly software, potentially easing the burden of the design stage for statisticians who lack adequate expertise or access to training in the area of novel early-phase trial design. However, motivation for the choice of trial design should not be limited to the existence of easy-to-use software. It is important to choose a design that balances good operating characteristics with the ability to be efficiently implemented in clinical practice. Another method belonging to the semi-parametric class is the isotonic method of Conaway, Dunbar, and Peddada.¹⁴ It was implemented in a Phase I trial investigating induction therapy with VALCADE and Vorinostat in patients with surgically resectable non-small cell lung cancer.¹⁵ The main reason why the Conaway-Dunbar-Peddada method has not been used in more real trials is the lack of available software needed to implement it. The aim of this short communication is to revisit the operating characteristics of Conaway-Dunbar-Peddada method in the single-agent setting in light of the recent uptake in model-assisted methods, and to describe the development of a new web application for simulating and implementing the method.

Methods

Several motivating factors lead us to reexamine the operating characteristics of the Conaway-Dunbar-Peddada method in single-agents: (1) the aforementioned growing need for available methods that balance simplicity and performance, (2) favorable operating characteristics displayed in recent simulation studies in more complex dose-finding problems,^16–20 and (3) new user-friendly software for simulating and implementing the method. The details of the Conaway-Dunbar-Peddada method are provided elsewhere,¹³ so we only briefly recall them here.

Estimation

The Conaway-Dunbar-Peddada method uses dose-limiting toxicity (DLT) probability estimates based on isotonic regression²¹ for each of I dose levels being studied. At any point in the trial, the DLT response data for dose d_i, i = 1, …, I is of the form Y ={y_i: i = 1, …, I} with y_i equal to the number of observed DLTs from patients treated with dose d_i. Let A denote the set of doses that have been tried thus far in the trial, A = {d_i: n_i > 0}, where n_i denotes the number of patients evaluated for DLTs on each dose. Prior information for the DLT probabilities π_i is expressed through a distribution of the form π_i~Beta(α_i, β_i). Based on the expected value of π_i and a 95% upper limit u_i on the DLT probability, the equations

$$\begin{array}{ccc}𝔼\text{(}{\pi }_i)=\frac{{\alpha }_i}{{\alpha }_i+{\beta }_i}& \text{and}& \text{Pr(}{\pi }_i\le u_i)=0.95,\end{array}$$

are solved to obtain prior specifications for α_i and β_i. In the absence of prior information, a practical prior specification can be acquired by setting the prior mean equal to the target DLT rate θ, and setting the 95% upper limit u_i equal to 2 × θ at each dose level. This prior specification is recommended to avoid the problem of rigidity²² in which allocation can become confined to a sub-optimal dose level regardless of the ensuing observed data. Using the Beta(α_i, β_i) prior at each dose, the updated DLT probabilities, calculated only for d_i ∈ A, are given by

$${\widehat{\pi }}_i=\frac{y_i+{\alpha }_i}{n_i+{\alpha }_i+{\beta }_i}$$

To impose monotonicity with respect to the dose-toxicity relationship and borrow information across dose levels, we apply isotonic regression to the ${\widehat{\pi }}_i$ using the pool adjacent violators algorithm,²¹ denoting the resulting estimates by ${\tilde{\pi }}_i$. This algorithm replaces adjacent estimates that violate the monotonicity assumption with their weighted average, where the weights are the current sample size at each dose level.

Allocation

1. Assign the first patient cohort to the lowest dose. In some studies, an alternative dose, such as the second lowest dose, may be assigned to the first cohort.

2. For all d_i ∈ A, compute the loss $L_i({\tilde{\pi }}_i,\theta )=|{\tilde{\pi }}_i-\theta |$ associated with each dose.

3. Let $l_{min}={\text{min}}_{d_{{}_i}\in A}{L}_i({\tilde{\pi }}_i,\theta )$, and let T be the set of doses with losses equal to the minimum observed loss so that $T=\{d_i:L_i({\tilde{\pi }}_i,\theta )=l_{min}\}$.

4. If T contains more than one dose, then we choose from among them according to the rules:

   1. If ${\tilde{\pi }}_t>\theta \forall t\in T$, the suggested dose is the lowest dose in T.
   2. If ${\tilde{\pi }}_t\le \theta$ for at least one t ∈ T, the suggested dose is the highest dose in T with ${\tilde{\pi }}_t\le \theta$.

5. If the suggested dose level has an estimated DLT probability that is less than the target, then the next highest dose level will be chosen if it has not yet been tried.

6. Stop the trial for safety if the Pr(π₁ > θ| data) > 0.95, computed from the posterior distribution of π₁.

7. Otherwise, the MTD is defined as a tried dose level with an estimated DLT probability closest to the target DLT rate after a pre-defined sample size has been exhausted or a stopping rule has been triggered.

Results

We conducted computer simulation studies to evaluate the operating characteristics of the Conaway-Dunbar-Peddada method for single-agents. We compare the operating characteristics of the method to the Keyboard design of Yan et al.⁹ using the settings and scenarios provided in their paper. The authors conclude that the Keyboard method has very similar performance to the Bayesian optimal interval method,¹¹ both of which have superior performance to modified toxicity probability interval method¹⁰ and the 3+3. Consequently, for the sake of brevity, we chose to only include Keyboard in our comparison.

For each of the scenarios in Table 1, we simulated trials investigating five dose levels with each trial exhausting a maximum sample size of 30 patients in cohorts of size 1. We evaluated the operating characteristics of each method for target DLT rates of 20% and 30%, examining 10 assumed DLT probability scenarios for each target rate. For a target DLT rate of 20%, we used a Beta(2.6, 10.4) prior at each dose level, and for a target DLT rate of 30% we used a Beta(2.1, 4.8) prior at each dose level for the Conaway-Dunbar-Peddada method. In each scenario, 10,000 trials were simulated and the performance compared in terms of (1) the percentage of correct selection, defined as the percentage of times the MTD is correctly identified, (2) the average number of patients treated at the MTD, and (3) the average number of patients treated above the MTD. To generate the results for the Keyboard design, we used the available web application at www.trialdesign.org. For the Conaway-Dunbar-Peddada method, we generated results using the new web application available at https://uvatrapps.shinyapps.io/cdpsingle/ with the specifications above and a random seed of 34.

Table 1.

Ten true DLT probability scenarios for target DLT rates of 0.20 and 0.30. Boldface denotes the maximum tolerated dose (MTD).

Scenario	Dose level
	1	2	3	4	5
	Target DLT rate = 0.20
1	0.20	0.26	0.40	0.45	0.46
2	0.20	0.29	0.35	0.50	0.58
3	0.10	0.20	0.25	0.35	0.40
4	0.08	0.20	0.30	0.45	0.65
5	0.04	0.06	0.20	0.32	0.50
6	0.01	0.10	0.20	0.26	0.35
7	0.05	0.06	0.07	0.20	0.31
8	0.02	0.04	0.10	0.20	0.25
9	0.01	0.02	0.07	0.08	0.20
10	0.01	0.02	0.03	0.04	0.20
	Target DLT rate = 0.30
1	0.30	0.36	0.42	0.45	0.46
2	0.30	0.40	0.55	0.60	0.70
3	0.08	0.30	0.38	0.42	0.52
4	0.13	0.30	0.42	0.50	0.80
5	0.04	0.07	0.30	0.35	0.42
6	0.01	0.12	0.30	0.41	0.55
7	0.06	0.07	0.12	0.30	0.40
8	0.02	0.05	0.16	0.30	0.36
9	0.01	0.02	0.04	0.06	0.30
10	0.06	0.07	0.08	0.12	0.30

The results are reported in Figures 1 and 2. In general, Figure 1 illustrates that the Conaway-Dunbar-Peddada method has better performance than the Keyboard method in terms of correctly identifying the MTD. The Conaway-Dunbar-Peddada method has a higher percentage of correct selection in 8 of the 10 scenarios when the target rate is 20%, with gains as high as 16% in Scenario 2 (62% vs. 46%). These findings are consistent with those for a target rate of 30%, in which case the Conaway-Dunbar-Peddada method has a higher percentage of correct selection in 9 of 10 scenarios. With regards to allocating patients to the true MTD, Figure 2 (top) demonstrates superior performance for the Conaway-Dunbar-Peddada method for the same scenarios that reported a higher percentage of correct selection for both target DLT rate values. Finally, in terms of the number of patients allocated to doses above the MTD, the Conaway-Dunbar-Peddada method tends to do so less frequently than the Keyboard design (Figure 2 bottom). The first two scenarios for each target rate saw the Conaway-Dunbar-Peddada method allocate a slightly higher number of patients to doses above the MTD, but the subsequent six scenarios for each target rate reported that the Conaway-Dunbar-Peddada method is allocating less patients to doses above the MTD when compared to the Keyboard design. Note the final two scenarios for each target rate have no dose levels above the MTD, so the numbers are zero for each method. Overall, the performance of the Conaway-Dunbar-Peddada method is strong when compared to the Keyboard design, making it a viable simple alternative to the model-assisted methods developed in recent years.

Figure 1.

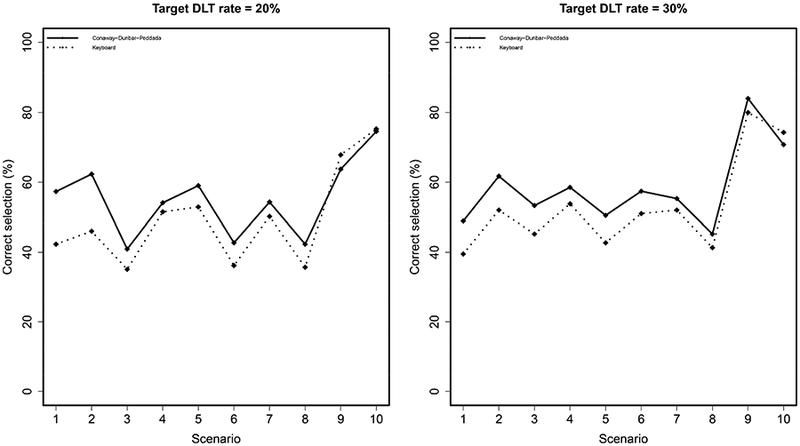
Percentage of correct MTD selection under the Keyboard and Conaway-Dunbar-Peddada designs. A higher value indicates better performance.

Figure 2.

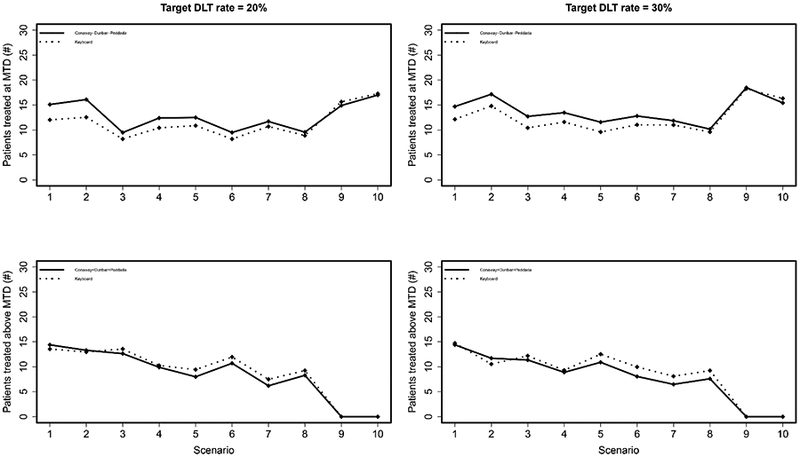
Top: Average number of patients treated at the MTD under the Keyboard and Conaway-Dunbar-Peddada designs. A higher value indicates better performance. Bottom: Average number of patients treated above the MTD under the Keyboard and Conaway-Dunbar-Peddada designs. A lower value indicates better performance.

Conclusions

In this brief communication, we have provided a fresh look at the Conaway-Dunbar-Peddada method within the context of a recently developed class of phase I methods termed model-assisted designs. The Conaway-Dunbar-Peddada method is a simple method that avoids some of the specification challenges associated with model-based designs, and the results in Figures 1 and 2 demonstrate its ability to be more accurate and safe than model-assisted methods that are guided by “local” behavior around the current dose level. We have developed a new web application that can generate simulated operating characteristics for the study design phase of the Conaway-Dunbar-Peddada method. The web application also has an implementation component for study conduct which can sequentially provide the next dose recommendation for each new accrual based on the current data. At the conclusion of the study, it can be used to estimate the MTD. In developing the web application, we have incorporated a safety stopping rule that did not appear in the original paper, as well as recommended a default prior distribution for the method that yields robust operating characteristics across a broad range of scenarios.

One advantage of the modified toxicity probability interval, the Bayesian optimal interval, and the Keyboard designs are their ability to output pre-tabulated escalation and de-escalation decision rules, similar to a 3+3 design. This is because these methods rely on decision-making based on observing what happens at the current level only. The Conaway-Dunbar-Peddada method adaptively borrows information across tried dose levels, making it difficult to output every possible decision prior to the beginning of the study. However, the web tool can easily be used to output the DLT probability estimates and dose recommendation given any particular set of outcomes, giving investigators a way of assessing the design’s behavior based on accumulated data. Another advantage for methods that sequentially borrow information across dose levels are their ability to accommodate revisions to data errors.²³ Subsequent allocations can proceed based on estimation from corrected data across all dose levels. This would be more challenging for local methods if the error occurs at a level far from that at which the study is currently experimenting. The web tool requires no programming knowledge, and it is free to access on any device with an internet browser. We hope this article will bring increased attention to the Conaway-Dunbar-Peddada method, and facilitate its use in single-agent dose finding.