Design of non-inferiority randomized trials using the difference in Restricted Mean Survival Times

Abstract

Background/Aims:

Non-inferiority trials with time-to-event outcomes are becoming increasingly common. Designing non-inferiority trials is challenging, in particular, they require very large sample sizes. We hypothesized that the difference in restricted mean survival time, an alternative to the hazard ratio, could lead to smaller required sample sizes.

Methods:

We show how to convert a margin for the hazard ratio into a margin for the difference in restricted mean survival time and how to calculate the required sample size under a Weibull survival distribution. We systematically selected non-inferiority trials published between 2013 and 2016 in 7 major journals. Based on the protocol and article of each trial, we determined the clinically relevant time horizon of interest. We reconstructed individual patient data for the primary outcome and fit a Weibull distribution to the comparator arm. We converted the margin for the hazard ratio into the margin for the difference in restricted mean survival time. We tested for non-inferiority using the difference in restricted mean survival time and hazard ratio. We determined the required sample size based on both measures, using the type I error risk and power from the original trial design.

Results:

We included 35 trials. We found evidence of non-proportional hazards in 5 (14%) trials. The hazard ratio and the difference in restricted mean survival time were consistent regarding non-inferiority testing, except in one trial where the difference in restricted mean survival time led to evidence of non-inferiority while the hazard ratio did not. The median hazard ratio margin was 1.43 (Q1-Q3, 1.29–1.75). The median of the corresponding margins for the difference in restricted mean survival time was −21 days (Q1-Q3, −36 to −8) for a median time horizon of 2.0 years (Q1-Q3, 1–3 years). The required sample size according to the difference in restricted mean survival time was smaller in 71% of trials, with a median relative decrease of 8.5% (Q1-Q3, 0.4%−38.0%). Across all 35 trials, about 25,000 participants would have be spared from enrollment using the difference in restricted mean survival time compared to hazard ratio for trial design.

Conclusions:

The margins for the hazard ratio may seem large but translate to relatively small differences in restricted mean survival time. The difference in restricted mean survival time offers meaningful interpretation and can result in considerable reductions in sample size. Restricted mean survival time-based measures should be considered more widely in the design and analysis of non-inferiority trials with time-to-event outcomes.

Introduction

Non-inferiority trials have grown increasingly common, in particular in cancer and cardiovascular diseases.^{1, 2} The design, conduct, and interpretation of non-inferiority trials present major challenges.^3–6 One issue of paramount importance is sizing the trial. Non-inferiority trials generally require smaller sample sizes compared to active-control superiority trials. However, they often require considerably larger sample sizes compared to placebo-controlled trials.^{7, 8}

The issue of sizing a non-inferiority trial is intrinsically linked to the choice of a clinically meaningful margin.⁶ Choosing a larger, less conservative margin will increase the chance of successfully demonstrating non-inferiority for a given sample size. Trialists may then juggle with the margin to achieve a feasible sample size using plausible assumptions.^9–11 This possibility has led to concerns over the use of lenient margins.^12–15

In this context, the design and analysis of non-inferiority trials with time-to-event outcomes commonly rely on the hazard ratio (HR) as a measure of treatment effect.¹⁶ However, HRs say little about the absolute effect of treatment with respect to the cumulative risk or time scale.¹⁷ Furthermore, if the proportional hazards assumption is violated, using the single HR averaged over the duration of the trial’s follow-up could lead to a non-inferiority conclusion while the rate of event truly differs between the two groups over time, for example early on after randomization.¹⁸ In addition, the conclusion may change with the follow-up duration.

As an alternative, the difference or ratio of restricted mean survival times (RMST) can be used for time-to-event outcome comparisons. The RMST captures the expected survival time for a patient followed up to a pre-specified, clinically relevant time horizon. The RMST does not rely on the proportional hazard assumption. Therefore, non-inferiority inference with RMST-based measures is unaffected by violation of this assumption. However, the RMST relies on a pre-specified time horizon.¹⁹

Recent works have highlighted the application of RMST for the design and analysis of trials.^19–23 In Figure 1, we use the PARTNER 2 trial to illustrate how the difference in RMST can be used to analyze a non-inferiority trial. Furthermore, Wei and colleagues have suggested that using the RMST in non-inferiority trials may result in decreased sample sizes while maintaining an adequate level of power.^24–26 We aimed to investigate if designing a non-inferiority trial using an RMST-based measure could lead to a smaller required sample size, as compared to a trial designed using the HR. Previous work has described how to determine a reasonable hazard ratio margin.^{3, 16, 27, 28} In the next section, we show how to convert a margin for the HR into a margin for the difference in RMST and how to calculate the required sample size under a Weibull survival distribution. To illustrate this approach with realistic survival distributions, we then re-designed a sample of recently published non-inferiority randomized controlled trials (RCT) and compared the required sample sizes when using the difference in RMST and the HR, while maintaining constancy of all other parameters.

Figure 1.

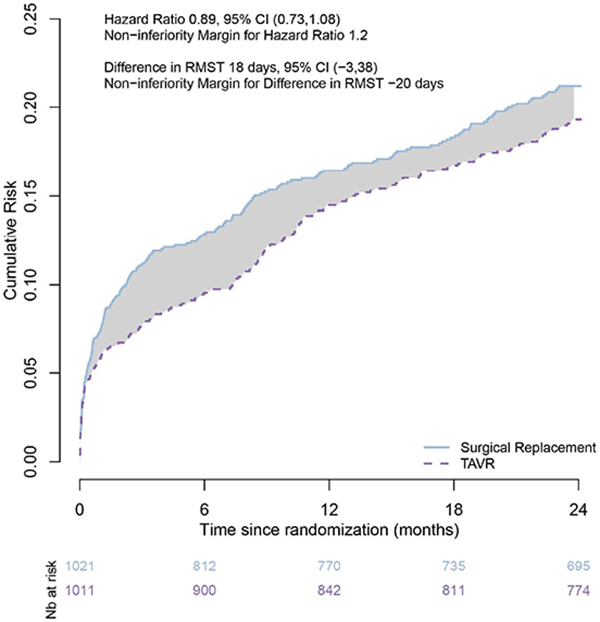
Estimated cumulative risk curves in the PARTNER 2 non-inferiority trial.

The PARTNER 2 trial tested for the non-inferiority of trans catheter aortic valve replacement (TAVR) against surgical replacement in intermediate-risk patients with severe aortic stenosis. The primary endpoint was death from any cause or disabling stroke at 2 years. The upper bound of the 95%CI for the HR fell below the non-inferiority margin, leading to a conclusion of non-inferiority. In each group, the RMST measures the average number of months alive and free of disabling stroke over 2 years. The difference in RMST (the area between the curves) measures the difference in 2-year life-expectancy associated with TAVR as compared to surgical replacement, a gain of 18 days over 2 years. The lower bound of the 95%CI for the difference in RMST fell above the respective non-inferiority margin, resulting in a consistent conclusion of non-inferiority.

Methods

Power analysis with the RMST for non-inferiority trials under the Weibull model

The RMST is the area under the survival function of event time T, S(t) = P(T > t), up to time horizon τ We estimate the RMST by integrating the Kaplan Meier estimator, $\widehat{\mu }={\displaystyle {\int }_0^{\tau }\widehat{S}}(t)dt$ The associated variance is ${\widehat{\sigma }}_{\mu }^2={\displaystyle {\sum }_{i=1}^D{\left[{\displaystyle {\int }_{t_i}^{\tau }\widehat{S}(t)dt}\right]}^2\frac{d_i}{Y_i(Y_i-d_i)}},$ where t_i denotes the event times, d_i and Y_i the number of events and number at risk at t_i, respectively. We estimate Δ, the difference in RMST by $\widehat{\Delta }={\widehat{\mu }}_E-{\widehat{\mu }}_C$. The associated (1 - α) % confidence interval is $\widehat{\Delta }\pm Z_{1-\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\sqrt{{\widehat{\sigma }}_{{\mu }_E}^2+{\widehat{\sigma }}_{{\mu }_{C^{.}}}^2}$ The null hypothesis for a non-inferiority trial is H₀: Δ ≤ Δ_m VS.H₁ Δ > Δ_m where Δ_m is the non-inferiority margin for the difference in RMST (Appendix Figure 1 in the online Supplementary Material). We reject the null hypothesis if $\widehat{\Delta }-Z_{1-\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\sqrt{{\widehat{\sigma }}_{{\mu }_E}^2+{\widehat{\sigma }}_{{\mu }_{{}_C}}^2}>{\Delta }_m$.

We calculate the required sample size under the assumption that the pattern of event times follows a Weibull distribution. We assume that the shape and scale parameters in the comparator group, ν_c and λ_c, respectively, are known. In addition, we assume that θ_m, the non-inferiority margin for the HR and τ, a clinically relevant time horizon are set.

Conversion of the non-interiority margin for the HR to the margin for the difference in RMST.

Under the Weibull model, we first convert the non-inferiority margin for the HR, θ_m, to the equivalent margin for the difference in RMST, Δ_m. The RMST in the comparator group at time τ is $RMS{T}_c={\displaystyle {\int }_0^{\tau }{S}_c}(t)dt={\displaystyle {\int }_0^{\tau }\exp }\left(-{\left(\frac{t}{{\lambda }_c}\right)}^{v_C}\right)dt$.

Under the assumption of proportional hazards, the Weibull shape parameter is set equal for the experimental and comparator groups. At the non-inferiority margin, it is known that $S_E\left(t\right)=S_c{\left(t\right)}^{{\theta }_m}$. The margin for the hazard ratio reduces to ${\theta }_m={\left(\frac{{\lambda }_c}{{\lambda }_E}\right)}^{v_c}$. Thus, the scale parameter for the experimental group is ${\lambda }_E={\lambda }_c\exp \left(-\frac{\log \left({\theta }_m\right)}{v_c}\right)$.

Therefore, the margin for the difference in RMST at time τ is

$$\begin{gathered} {\Delta }_m={\displaystyle \underset{0}{\overset{\tau }{\int }}\text{exp}}\left(-{\left(\frac{t}{{\lambda }_c\left(\frac{-\text{log}{\theta }_m}{v_c}\right)}\right)}^{v_c}\right)dt-{\displaystyle \underset{0}{\overset{\tau }{\int }}\exp \left(-{\left(\frac{t}{{\lambda }_c}\right)}^{v_c}\right)}dt= \\ {\displaystyle \underset{0}{\overset{\tau }{\int }}\exp \left(-{\theta }_m{\left(\frac{t}{{\lambda }_c}\right)}^{v_c}\right)}dt-{\displaystyle \underset{0}{\overset{\tau }{\int }}\exp \left(-{\left(\frac{t}{{\lambda }_c}\right)}^{v_c}\right)}dt \end{gathered}$$

Similarly, the margin for the ratio of RMST at time τ is given by the ratio of the two component integrals above. Note that if a non-inferiority margin is initially set for the absolute risk difference, ω_m one can convert it to the margin for the HR by ${\theta }_m=\raisebox{1ex}{$\text{log}\left({\omega }_m+S_c\left(t\right)\right)$}\!\left/ \!\raisebox{-1ex}{$\text{log}{S}_C(t)$}\right.$ and then derive the margin for the difference or ratio of RMST.

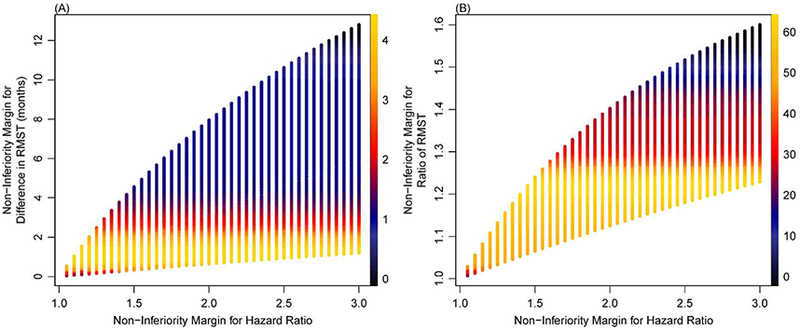
We first explored the correspondence between the non-inferiority margins for the HR and the difference and ratio of RMST for 5 specific Weibull distributions parameterized for a range of cumulative risks of event at 3 years (Appendix Figures 2–3 in the online Supplementary Material). Margins for the HR ranging up to 3.0 correspond to relatively smaller margins for the RMST-based measures, up to 10 months for the difference in RMST and up to 1.35 for the ratio of RMST. In addition, for a given margin for the HR, the margin for the difference in RMST gets closer to the null as the cumulative risk of event increases. Finally, the margin for the difference in RMST gets closer to the null as the time horizon decreases.

We then examined the correspondence between non-inferiority margins for the HR and the RMST-based measures across 3,358 Weibull survival distributions each explored at up to 3 time horizons for a total of 317,720 combinations (Appendix Figure 4 in the online Supplementary Material). Figure 2 (A) shows that for the full range of HRs from 1.0 to 3.0, 50% of difference in RMST margins are less than 3 months for a time horizon of 3 years. Analogously, Figure 2 (B) indicates that for the full range of HR margins, 65% of the ratio of RMST margins fall below 1.25.

Figure 2.

Density plots for margin equivalence across 3,358 Weibull distributions.

Each point corresponds to one of 3,358 unique Weibull distributions evaluated at up to 3 time horizons across the range of hazard ratio margins from 1.05 to 3.00, totaling 317,720 unique combinations. We describe the Weibull distribution parameters and time horizons in Appendix Figure 4.

Sample size calculation for the margin for the difference in RMST.

We determine the required sample size based on a sequential simulation approach. We set a Weibull distribution, non-inferiority margin, time horizon, power, type I error risk. We also set the allocation ratio and accrual rate and period. We initially simulate 20,000 RCTs of sample size 100. We generated event times in both groups according to the set Weibull model. For each simulated RCT, we conclude non-inferiority if the lower bound of the confidence interval for the difference in RMST is above the non-inferiority margin (and if the upper bound of the confidence interval for the HR is below the non-inferiority margin; Appendix Figure 1 in the online Supplementary Material). We determine the power as the proportion of simulated RCTs in which we conclude non-inferiority. Generating 20,000 RCTs ensures precision on the calculated power to within 1%. The process continues sequentially by increasing the sample size by increments of 10 until the computed power exceeds the desired level of power for the trial.

We examined how varying sample size, non-inferiority margin, and cumulative risk influences power. We found that power was larger with the difference in RMST as compared to the HR across sample sizes and margins (Figure 3). The difference in RMST yielded a higher power than the HR for 3-year cumulative risks lower than 65% (Appendix Figure 5 in the online Supplementary Material). Finally, we examined how one could size a trial based on the HR margin but use a margin for the difference in RMST closer to the null (Appendix Table 1 in the online Supplementary Material).

Figure 3.

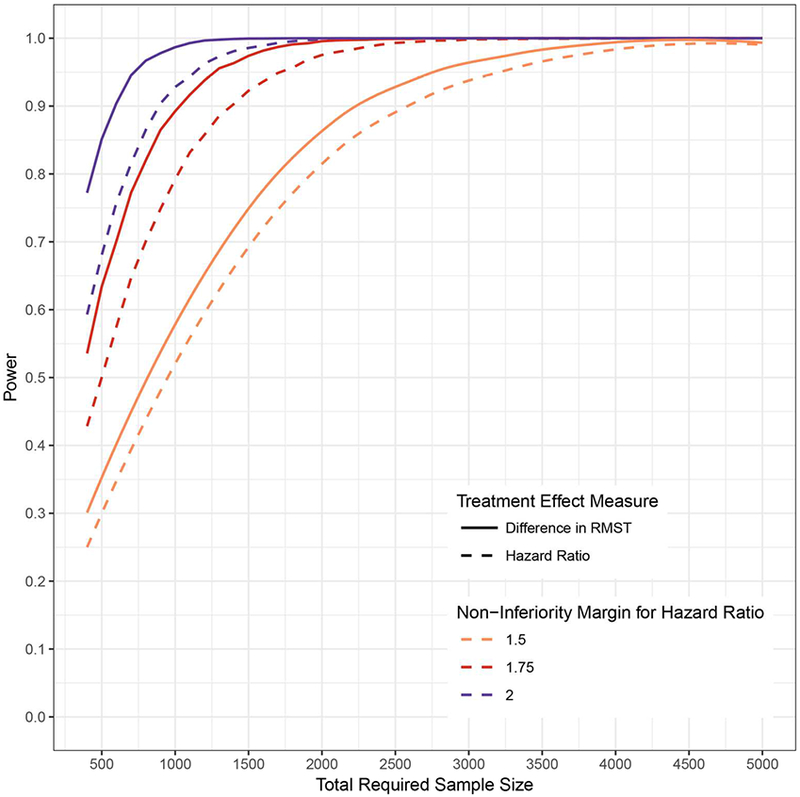
Power based on the HR and difference in RMST by varying sample sizes and non-inferiority margins.

We calculated power for three non-inferiority margins and sample sizes ranging from 450 to 5000. The underlying distribution is a Weibull with shape parameter 0.9 and scale parameter 36.56. The accrual period is one year with a total trial duration of 4 years and time horizon of 3 years. The allocation ratio is 1:1 and one-sided alpha of 0.025. For margins for the hazard ratio of 1.5, 1.75, and 2.0, the equivalent margins for the difference in RMST were −28 days, −41 days, and −55 days, respectively.

Reanalysis and redesign of published non-inferiority trials

Selection of trials.

We selected non-inferiority RCTs published between 2013 and 2016 in the New England Journal of Medicine, Lancet, JAMA, JAMA Internal Medicine, PLoS Medicine, Annals of Internal Medicine, and BMJ (Appendix Text 1 in the online Supplementary Material). We included non-inferiority RCTs with exactly two intervention groups, a primary time-to-event outcome graphically represented with Kaplan-Meier curves. We excluded RCTs with non-comparative designs, and any secondary, subgroup, or follow up analyses.

Data extraction.

For each RCT, we accessed the article and protocol. We extracted the statistical power, type I error risk, and the non-inferiority margin under which the trial was designed. We noted the randomization ratio and extracted the start and end dates of enrollment to calculate the accrual rate. We noted whether the protocol included plans to assess the proportional hazards assumption and whether the article described this assessment. We extracted data independently and in duplicate; we discussed discrepancies to reach consensus.

Reconstruction of individual participant data.

For each RCT and respective primary endpoint, we reconstructed the individual patient data from each randomization group. We first extracted the time and survival probability coordinates from the Kaplan-Meier curves using the DigitizeIt software (http://www.digitizeit.de/). We used these coordinates, the total numbers of events, and the numbers of participants at risk to determine individual event times and event indicators.²⁹ We assessed the accuracy and reproducibility of the data reconstruction process and found both to be high (Appendix Text 2 and Appendix Table 2 in the online Supplementary Material).

Clinically relevant time point of interest.

For each trial, we identified the clinically relevant time point for measuring the primary outcome.^30–32 We defined it as the time point used for sample size calculation, as reported in the protocol or the article. In 6 cases, this value was not clear, and we chose a time point based on the reported analyses and reverse Kaplan-Meier curves to quantify follow-up.³³ The specific measurement time point and justification for each trial are reported in Appendix Table 3 in the online Supplementary Material.

For each trial, we censored the reconstructed dataset at the clinically relevant time point. We fit a Weibull distribution to the comparator group. We used this distribution to characterize the observed pattern of primary endpoint times in both the comparator and intervention groups.

Reanalysis of reconstructed data.

Firstly, we tested the assumption of proportional hazards with a Grambsch-Therneau test at a significance level of 0.10. Secondly, we tested non-inferiority based on both the HR and difference in RMST with respect to the α level extracted from the article.³⁴ The margin for the difference in RMST was calculated to correspond to the HR margin using the event distribution observed in the comparator group.³⁵ Finally, we compared the conclusions drawn from the non-inferiority testing based on the difference in RMST and the HR, for equivalent margins, across all trials.

Redesign of trials.

We redesigned the trials using the respective clinically relevant time points of interest. We compared the magnitude of the HR margin against that of the RMST difference margin, which was calculated to correspond to the HR margin and expressed as number of days. We also considered the RMST difference margin as a percentage of the RMST in the control group and as a percentage of the time horizon.

We used the reconstructed data for each trial for the purpose of obtaining the fitted Weibull parameters. Using these parameter values, we redesigned each trial to determine the sample size required to achieve the original target power based on the HR and the difference in RMST, respectively. We assumed that the observed pattern of event times in the comparator group was the true model for the event times in both randomization groups. We determined the required sample size by using the values for α, power, accrual rate, and randomization ratio extracted for each trial. In a sensitivity analysis, we used a one-sided α level of 0.025 and power of 80% for all trials.

We determined the required sample size using the simulation method described in the previous section. We compared the required sample sizes based on the HR and the difference in RMST across all re-designed trials. We also compared the relative difference in required sample sizes based on the HR and the difference in RMST with the cumulative risk of endpoint in the comparator group at the clinically relevant time point.

Reproducibility.

The full set of reconstructed trial data are available on GitHub along with our sample size calculation function (github.com/iweir/powerRMST). We executed all analyses with R version 3.2.3 (R Development Core Team, Vienna, Austria).

Results

Characteristics of selected trials and clinically relevant time points

We selected 35 non-inferiority trials (Appendix Text 3 in the online Supplementary Material). The primary reasons for exclusion were non time-to-event outcomes and multiple armed designs (Appendix Figure 6 in the online Supplementary Material). All-cause mortality was the primary outcome in 6 trials, and arrhythmic death in 1 trial; 19 additional trials used a primary composite outcome, which included all-cause or cardiovascular death; in the 9 other trials, the primary outcome was time to a non-fatal event. The median number of randomized patients was 1905 (Table 1). Overall, 29 (83%) trials found the intervention of interest non-inferior to a comparator, 2 of which further established superiority. The extracted effect measures, conclusions, and whether the analysis was adjusted are described in Appendix Table 2 in the online Supplementary Material. The time horizons ranged from 6 months to 9 years, with a median of 2 years.

Table 1.

Characteristics of selected non-inferiority trials

Feature		N=35 trials
Journal
New England Journal of Medicine	24a	(68.6)
Lancet	7	(20.0)
JAMA	4	(11.4)
Funding Source
Industry	23	(65.7)
Non-Industry	6	(17.1)
Both	6	(17.1)
Clinical Condition
Asthma	3	(8.6)
Cancer	10	(28.6)
Chronic Obstructive Pulmonary Disease	3	(8.6)
Cardiovascular Disease	12	(34.3)
Diabetes	4	(11.4)
HIV	1	(2.9)
Infectious Disease	1	(2.9)
Obesity	1	(2.9)
Intervention
Pharmacological	24	(68.6)
Non-pharmacological	10	(28.6)
Both	1	(2.9)
Randomization Ratio
1:1	33	(94.3)
1:2	1	(2.9)
1:3	1	(2.9)
Analysis
Intention-To-Treat	26	(74)
Modified Intention-To-Treat	5	(14)
Per Protocol	4	(11)
Assessment of Proportional Hazards
No mention	16	(46)
In protocol only	12	(34)
In article only	7	(20)
In protocol and article	0	(0)
Trial Stopped Early	6	(17.1)
Slow Enrollment	3	(8.6)
Non-Inferiority Established Early	2	(5.7)
Premature Release of Interim Data	1	(2.9)
Number of Randomized Patients, median (Q1-Q3)	1905	(733, 3330)

^aData are numbers (percentages) unless stated otherwise

Reanalysis of reconstructed data

The reconstructed Kaplan-Meier curves are included in Appendix Figure 7 in the online Supplementary Material. Reanalyzing these data, we found evidence of non-proportional hazards in 5 (14%) trials. The hazard plots show when the hazards differed for these trials (Appendix Figure 8 in the online Supplementary Material). Only 12 trials reported plans to assess proportional hazards in the study protocol and of these trials, none reported results in the article. Moreover, 7 trials reported an assessment of proportional hazards in the article without any mention in the protocol. The verbatim phrases regarding proportional hazards are shown in Appendix Table 4 in the online Supplementary Material. Among the 5 trials for which we found evidence of non-proportional hazards, 3 did not mention any assessment, 1 planned an assessment in the protocol, and 1 reported having met the assumption in the article.

Based on our reanalysis, we found evidence of non-inferiority in 28 (80%) trials when using the HR as a treatment effect measure. Using the margin on the difference in RMST calculated to correspond to the HR margin, we reached a non-inferiority conclusion for 29 (83%) trials. This conclusion was consistent between the two effect measures in 28 trials while in 1 trial, we found evidence of non-inferiority using the difference in RMST but not when using the HR.

When analyzing the reconstructed data for this trial, we found a HR of 1.63, 95% confidence interval from 0.94 to 2.82, compared against a margin of 2.47, suggesting that non-inferiority was not shown. Using the difference in RMST however, we found an effect estimate of −16.8 days, 95% confidence interval from −38.72 to 5.48, compared against a margin of −40.2 days, leading to a conclusion of non-inferiority. This difference in RMST means that the experimental intervention would decrease the average event-free survival time over 2 years by 16.8 days compared to the comparator intervention.

Redesign of trials

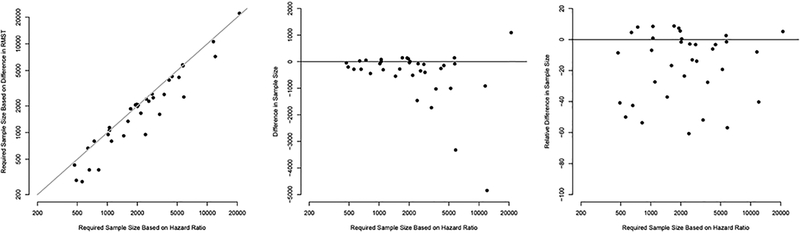
Figure 4 and Appendix Table 5 in the online Supplementary Material show the non-inferiority margins for the HR and difference in RMST across the 35 trials. The HR margins ranged from 1.15 to 2.85 with a median of 1.49 (Q1-Q3, 1.29–1.87). The HR margin was ≥ 2 in nine trials (26%). When converting the HR margins to the time scale, the median margin for the difference in RMST was −21 days (Q1-Q3, −36, −8). When standardizing according to the RMST in the control group, the median margin was −3.5% (−6.5, −1.9). Non-inferiority would be claimed if the mean survival time in the experimental group was no less than 96.5% of the mean survival in the comparator group. When expressed as a percentage of the time horizon, the median margin was −3.2% (−4.8, 1.9) (Appendix Figure 9 in the online Supplementary Material). For the 7 trials in which the HR margin was ≥ 2, the converted margins on the RMST scale ranged from −140 days to −0.6 days (median −7.0 days) and from −8.4% to −0.3% (median −1.3%) when standardized according to the RMST in the control group. Across the 35 non-inferiority trials, there were 11 combination settings of type I error risk α and power. The most frequent was a one-sided α level of 0.025, or equivalently a two-sided α level of 0.05, with a power of 80% in 11 (31%) trials (Appendix Table 6 in the online Supplementary Material). Moreover, 10 (29%) trials used a two-sided α equivalent or greater than 0.05. The results of the sample size calculations in each RCT are shown in Figure 5. The required sample size ranged from 430 to 26,210 (median 2600) when calculated for the HR and from 280 to 27,350 (median 1990) when calculated for the RMST difference. If we were to redesign the 35 trials using the difference in RMST as the effect measure rather than the HR, we would see a smaller required sample size in 25 (71%) of the trials. In total, we would spare 24,790 people from enrollment by using the RMST difference instead of the HR (131,690 vs. 156,480). This is equivalent to a median absolute decrease of 195 (Q1-Q3, 22.5–517.5) participants or a median relative decrease of 8.5% (0.37%−38%) in required sample size across all trials. Appendix Figure 10 in the online Supplementary Material shows that the decrease in required sample size was mostly observed when the risk of event in the comparator group was low. In the sensitivity analysis with a one-sided α level of 0.025 and power 80% to design all trials, the median relative decrease was 10.8% (0.02% 38.5%) (Appendix Figure 11 in the online Supplementary Material).

Figure 4.

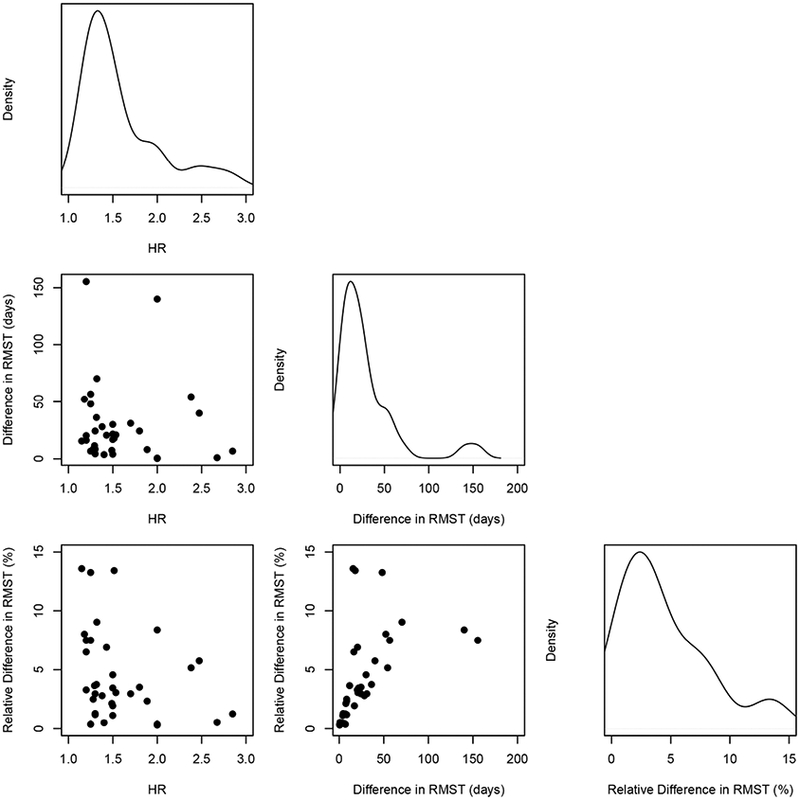
Comparisons of the non-inferiority margins for the HR and for the difference in Restricted Mean Survival Times corresponding to the 35 trials.

Plots in the main diagonal show the density distribution of the margins corresponding to the 35 trials. Scatter plots below the diagonal display margins for the HR against margins for the difference in Restricted Mean Survival Times. The relative difference in RMST is expressed as a percentage of the RMST in the comparator group.

Figure 5.

Comparison of the required sample sizes calculated for the HR and for the difference in Restricted Mean Survival Times corresponding to the 35 trials.

Plot A shows a direct comparison of the required sample size under the HR versus that under the difference RMST corresponding to the 35 trials. In Plot B, we compare the required sample size under the HR to the absolute difference (sample size under RMST minus sample size under HR). Plot C compares the required sample size under the HR to the relative difference in required sample sizes ((RMST – HR) / HR).

Discussion

In a re-analysis of 35 non-inferiority trials, we found that the difference in RMST gave consistent results as compared to the HR with respect to non-inferiority testing, except in 1 case where the difference in RMST showed evidence of non-inferiority while the HR did not. Second, we found evidence of non-proportional hazards in 14% of trials, while there were deficiencies in the reporting of plans and results of non-proportional hazard assessments. Third, non-inferiority HR margins were large but the equivalent margins for the difference in RMST were relatively small. Finally, we found that using RMST, as compared to HR as an effect measure, led to a reduction in required sample size by a median of 8.5%.

Previous works have focused mainly on the use of the HR.^{16, 34, 36–38} Absolute measures may exhibit interactions and thus are less likely to be generalizable to populations with a different risk profile.³⁹ However, absolute effects, not relative effects, are what matter for decision making.^{40, 41} Interpreting the non-inferiority margin and treatment effect expressed as HRs can be challenging because HRs say little about absolute effects.^42–44 Across the 35 trials, we observed large variability in the non-inferiority HR margins, consistent with previous findings.⁴⁵ This variation may reflect the arbitrary nature of the choice of margin, but HR margins also differ due to variability in the comparator event risk across diverse medical conditions.⁴⁶ In particular, small cumulative event risks are likely to result in large HR margins. Another challenge is that HRs rely heavily on the proportional hazards assumption. In previous work, we also found evidence of non proportionality in 13 (24%) out of 54 cancer trials.²⁰ This issue appears to be neglected, as reflected by the small proportion of non-inferiority trial protocols that mentioned plans to assess proportional hazards. While using the RMST circumvents these issues, we acknowledge that it may also have limitations. One caveat is the need to choose a specific time horizon and the inference may not be the same at different time points.¹⁹ In our framework, we considered that a clinically relevant time horizon would be pre specified and that one would perform the analysis at this horizon. Royston and Parmar suggested determining the time horizon for the design that minimizes the required sample size given the remaining parameters. In addition, they suggested determining a time horizon for the final analysis that maximizes power.¹⁹ Another caveat is that, considering our findings, designing a non-inferiority trial with the RMST could imply that one makes decisions based on fewer events as compared to designing with the hazard ratio.

Our sample size calculations relied on the use of a simulation based approach. To our best knowledge, there is no closed form formula for sample size determination based on the RMST. Uno and colleagues previously illustrated this simulation-based approach.²⁴ Royston and Parmar described another simulation-based approach for sample size determination.¹⁹ Tian et al. have derived a formula for the asymptotic relative efficiency for the hazard ratio and difference in RMST for a superiority trial.⁴⁷

When designing a superiority trial, simulation studies have shown that the HR and the difference in RMST give similar sample size requirements under the assumption of proportional hazards, but RMST-based sample sizes can be markedly reduced under non-proportional hazards.^{19, 47} A potential explanation for the reduction in required sample size is that the precision of the HR is driven by the number of events, with little weight given to length of follow-up or sample size. Thus, precision on the HR will be poor when the number of events is small. In contrast, the difference in RMST does not suffer from this limitation, and we observed relative decreases in the required sample size when the risk in the control group was low.

Our analysis has limitations. Firstly, we used reconstructed data for all analyses. We assessed the reliability of the reconstruction process and we found a high degree of accuracy, as in previous works.^{20, 29} Most importantly, we show how the reconstructed data allowed us to determine an approximation of the pattern of event times from the comparator group to inform the sample size calculation. In practice, trialists could use this approach by using a previously randomized trial that assessed the intervention used as a comparator in the non-inferiority trial to be designed.

Secondly, our findings are not intended to be compared to the original sample size calculations or conclusions. In fact, we calculated the sample size under the pattern of event times observed in the control group. We did not account for interim analyses. It would lead to increased sample sizes, but would affect both effect measures therefore resulting in a consistent pattern of results. In addition, interim analyses affected the original conclusions. For example, assessing non-inferiority was not possible in the NBCVOT trial because of the premature release of interim data. Finally, we have not examined the motivation for the original margins. Previous works have shown that many trial reports fail to provide any justification for the margin.^48–51

In conclusion, the difference in RMST deserves greater attention, as an essential adjunct to other measures of treatment effect in trials with time-to-event outcomes. In this empirical investigation, we have shown how designing non-inferiority trials with the difference in RMST gives insight into the non-inferiority margin and could lead to much smaller required sample size.