Abstract
The effect of the drying conditions on the retention quality for dried chicory roots (Cichorium intibyus L.) was investigated. Cubes of chicory roots were dried using hot air and vacuum dryers at 60 and 80 °C. Two different air velocities (0.2 and 0.7 m/s) were used in the hot air dryer, and two vacuum pressures (25 and 50 mmHg absolute) were set in the vacuum chamber. An exhaustive three dimensional mathematical model to describe mass transfer during drying of chicory roots of 1 cm of side was presented considering a polynomial functionality for the contraction kinetics. Experimental data obtained at laboratory scale were used to validate the proposed model showing good agreement between the experimental and estimated moisture profiles for both drying procedures. Moisture diffusivity was found to increase with the air drying temperature, velocity and vacuum pressure depending on the drying method. However, higher moisture diffusivity coefficients and lower activation energy values were obtained for the vacuum drying method. Samples dried using the vacuum drier at 60 °C and 25 mmHg presented better retention quality attributes, i.e., better rehydration, lower shrinkage and higher total phenolic content. The proposed mathematical model was able to satisfactorily predict the described behavior.
Keywords: 3-D, Drying, Chicory roots, First-principles modeling, Effective moisture diffusivity, Physicochemical properties
Introduction
Chicory root (Cichorium intibyus L.) is a potentially beneficial product that possesses many advantages due to its composition. This root contains several antioxidant compounds, mainly polyphenols and inulin that have been identified as functional ingredients, being applied in the pharmaceutical and food industries for the production of medicines or functional foods (Oliveira 2005).
Both antioxidant or inulin extraction processes require a previous drying stage to achieve availability for the industrial processing because chicory roots are highly perishable. Hot-air or conventional drying is a traditional drying method, which is a relatively simple and cost-efficient operating procedure. However, it has several disadvantages regarding the quality of the obtained dried product, such as darkening, shrinkage, lower antioxidant content, among others (Lee and Zuo 2013). Vacuum drying is an alternative method for processing heat sensitive products, like vegetables and fruits (Ah-Hen et al. 2012), that can also improve quality aspects of dried products compared to conventional drying (Lee and Zuo 2013).
For the process design task, detailed models involving heat and mass transfer balances are required to analyze at least moisture and shrinkage profiles resulting from the adopted operative conditions. To build such a model, it is important to use an optimization environment, where an adequate set of experimental runs must be available for model parameter determination and validation purposes.
This kind of model is the basis for drying unit design. If the drying operation is the design goal, quality and cost target functions must be simultaneously considered subjected to the heat and mass transfer balances as well as kinetics functionalities. In this work, the first type of model is implemented and described. In further works, the model will be extended for the design of optimal drying units and the determination of optimal operative strategies.
Drying operation involves several heat and mass transfer mechanisms, which depend on the drying method. Non-steady heat conduction within the product is considered in general with different boundary conditions according to the drying equipment and its operative parameters, such as convective or irradiative transfer or equilibrium conditions among others (Ruiz-Lopez et al. 2012). However, water diffusion within the sample is the major factor for the mass transfer balance, which is regularly well represented by the Fick’s second law, being the analytical solution of the diffusion equation reported in several works (Hacihafizoglu et al. 2008; Pereira da Silva et al. 2014).
Meanwhile, many authors prefer to consider the evaluation of different thin layer models (Exponential, Generalized Exponential, Page, Logarithmic, Parabolic, among others) for the estimation of the kinetics drying parameters for different drying methods and products (Lee and Zuo 2013; Murthy and Manohar 2014; Afolabi et al. 2015), obtaining diverse results of the best fit according to the scenario under evaluation. Thin layer models are obtained from simplification or modification of the Fick’s second law solution. In general, the solutions depend on the experimental conditions with low leverage on the drying process (Sahari and Driscoll 2013). Other disadvantage of this kind of models is that they can only be applied to the drying process of one-layer sample particles or slices and that no shrinkage is assumed.
Rigorous and detailed modeling is a difficult task due to the complexity of the underlying mechanisms and the procurement of reliable experimental data. Models based on first principles have the advantage that multidimensional geometries for diverse food shapes can be solved in the context of diverse unit operations, addressing realistic boundary conditions and other equations describing the process equipment plus other technological constraints, like shrinkage phenomena in the case of drying. Usually, these models consist of a set algebraic and partial and ordinary differential equations, resulting in non-linear problems.
The goal of this work is to describe hot air and vacuum drying processes using a first-principles based model to precisely quantify the influence of the operating conditions (temperature, air velocity, vacuum pressure) on process optimization. Then, a complete three-dimensional model for mass transfer balances considering variable shrinkage profile as a function of the moisture content is proposed for both hot-air and vacuum drying of chicory root cubes. In addition, different quality attributes are evaluated for different experimental runs of both drying techniques to evaluate how the drying method and the operating conditions (temperature, air velocity, vacuum pressure) affect the drying kinetics, shrinkage and quality aspects of the dried samples.
Materials and methods
Raw material and sample preparation
Fresh chicory roots (Cichorium intybus L.) were provided by a nearby farmer to the city of Rosario, Santa Fe, Argentina. These roots were washed with an aqueous solution of neutral detergent (Prol Det, Prolimp) and rinsed with tap water three times. Samples of approximately 700 g were cut into cubes with length of 1 cm using a special cutting tool.
Drying experiments
Drying experiments were conducted using a forced convection laboratory dryer (Tecno Dalvo, Model CHC/F/I, Argentina) at temperatures of 60 and 80 °C and air velocities of 0.2 and 0.7 m/s, considering the values reported by Figueira et al. (2004), who obtained suitable results in the drying process of chicory roots at different temperatures. In addition, a vacuum dryer (ORL, Argentina) was used at the same temperatures and two different vacuum pressures, 25 and 50 mmHg absolute. Drying experiments were done in duplicate.
In order to compute the moisture content, the total weight of the partially dehydrated products was recorded at time intervals using a digital balance with an accuracy of ± 0.01 g until no mass change of the samples was observed. Three control samples were used to track changes in the cube dimensions, which were measured with a Vernier.
Rehydration evaluation
Rehydration ratio (RR) was used to measure the water absorption ability of dried samples. RR was calculated as the ratio between rehydrated and dried sample weights, according to Eq. (1).
| 1 |
RR was determined by immersing a wire mesh with 1 g of dried chicory root cubes in 50 ml of distilled water at 30 and 100 °C temperatures. The water was drained and the samples weighed every 5 min during 15 min, and then every 15 min until constant weight for the samples at and 30 °C and every 1 min for those at 100 °C. Measurements were done in triplicate.
Non-enzymatic browning index determination
Non enzymatic browning compounds solubilized in the rehydration water during the rehydration evaluation was first clarified by centrifugation at 3200×g for 10 min. The supernatant was diluted with an equal volume of ethanol at 95% v/v and centrifuged again at the same conditions. Then, the browning index (BI) was determined in the clear extracts using a spectrophotometer (UV-1800, Shimatzu, Japan) at a wavelength of 420 nm. BI was also determined for fresh samples. Measurements were done in triplicate.
Extraction of phenolic compounds
Extraction of total phenolic compounds were carried out for all the dried samples. Each dried sample was grounded in a domestic mill. The powdered samples were sieved to separate particles passing an ASTM 40 sieve using a Ro-Tap sieve shaker (Tyler, US). In all the extraction runs, 20 g of dried chicory root flour were extracted using 600 ml of a hydro-alcoholic mixture of ethanol (50–50%) in a batch extractor using an agitation propeller at 150 rpm for 90 min at 50 °C. Then, the extract was separated for further determinations.
Determination of total phenolic content
Diverse spectrophotometric methods have been developed for the quantification of phenolic compounds in a vegetable matrix. These methods use different analytes (catechine, gallic acid, quercetin, vanillin, caffeic acid, ferulic acid, Trolox, ascorbic acid, and ferrous sulfate, among others) to reproduce and estimate phenolic compounds content. Spectrophotometric methods like Folin–Ciocalteu, Prussian blue and o-phenanthroline have been implemented for total phenolic compounds in vegetables (Escarpa and Gonzalez 2001; González et al. 2003). Swain and Goldstein (1964) revised several spectrophotometric methods in diverse vegetables and recommended the Folin–Ciocalteu method as the most suitable for total phenolic quantification. After that, this technique has been successfully implemented in diverse works (Milala et al. 2009; Rohman et al. 2010; Shad et al. 2013).
Then, the Folin–Ciocalteu method proposed by Boroski et al. (2015), with some modifications, was here used to determine the phenolic compounds in the hydro-alcoholic chicory root extract samples. A 250 µl portion of sample was mixed with 250 µl of Folin–Ciocalteu’s reagent. After 3 min, 500 µl of saturated Na2CO3 (20%) was added to the mixture. The reaction was maintained in the dark for 120 min and its absorbance was measured at a wavelength of 725 nm relative to a blank. The calibration curve was obtained with a gallic acid solution as a reference standard (R2 = 0.998) and total phenolic content was expressed as mean ± the standard deviation of gallic acid equivalent (GAE) per 100 g of sample (mg/100 g). Measurements were done in triplicate.
Determination of DPPH radical scavenging activity
Free radical scavenging activity of the samples was determined using the 2,2-diphenyl-1-picrylhydrazil (DPPH) method described by Shimada et al. (1992). An aliquot of 1 ml of the hydroalcoholic extract was added to 5 ml of ethanolic solution of DPPH radical (0.1 mM). The mixture was stirred with a vortex for 30 s and left to rest at room temperature for 50 min. The absorbance was measured at a wavelength of 517 nm, using a spectrophotometer (UV-1800, Shimatdzu, Japan). The control sample was prepared without adding extract. All samples were analyzed in triplicates and results are presented as the average value ± the standard deviation. The DPPH scavenging activity was determined by Eq. (2).
| 2 |
Statistical analysis
The data was subjected to analysis of variance (ANOVA) and Duncan’s New Multiple Range test at a confidence level of p = 0.05 using the SPSS Statistical Analysis Program for Windows (SPSS Inc., Chicago, IL, USA).
Mathematical model
Assumptions
The equation system detailed in the next section is developed under the assumptions here detailed for both hot- air and vacuum drying methods. It is considered that the cubes of chicory roots initially have homogenous structures, i.e. initial composition and moisture content are uniform in the whole matrix. Cubes have initial side length of 1 cm. Shrinkage occurs on the six sides of cubes, but their shape does not change during drying. Drying takes place t every side of the cubes because a stainless steel mesh tray is used within both chambers. In addition, the air flow rate is large enough for the drying conditions (humidity, temperature) to be kept constant throughout the material. The diffusion process is the dominant mass transfer mechanism. The water diffuses to the surface of each particle according to Fick´s second law. Heat generation inside the material and radiation effects are negligible.
These assumptions are reliable with some characteristics of the real dryer to be designed. In fact, it is assumed, for example, perfect mixed air inside the dryer chamber and invariant air flux characteristics, which have critical influence on the real drying performance. The temperature dependence of the thermophysical properties in conjunction with the heat transfer model will be addressed in future works.
Mass transfer model
The Fick’s second law to describe the diffusion of moisture within each chicory root cube is applied in three dimensions, given by Eq. (3).
| 3 |
where HS is the food moisture content at each instant of time; t is the drying time and L is the characteristic length of the sample (semi-thickness). ρs is the food density and Deff is the effective diffusivity coefficient of the moisture content.
The initial and boundary conditions given by Eqs. (4–6b), are adopted to solve Eq. (3).
| 4 |
| 5 |
| 6a |
| 6b |
Equation (6a) states that a convective mass transfer mechanism is considered from the product surface to the bulk air for the hot-air drying method, where k and HSeq, are the external mass transfer coefficient and the equilibrium moisture content of the dried solid, respectively.
Equation (6b) assumes that the moisture content in the cube surface is equal to the equilibrium moisture content at the atmospheric condition of the vacuum dryer. Moisture from the product could be completely removed due to the fact that the drying temperatures used in the experiments (60 and 80 °C) are much higher than the boiling point of pure water at the applied vacuum, since the pressures that prevail inside the vacuum dryer, 25 and 50 mmHg absolute, correspond to a saturation temperature of 25.86 and 37.18 °C, respectively.
The mass transfer coefficient, k, used in Eq. (6a), is determined using the Sherwood number, Sh, calculated from the dimensionless Eq. (7) reported by Mills (1995) in conjunction with Eqs. (8–13).
| 7 |
| 8 |
| 9 |
| 10 |
| 11 |
| 12 |
| 13 |
where Ma is the air molecular weight (kg/mol), Ga is the mass flow rate of air (kg/m2 s), Ra is the universal gas constant (8.3144 × 10−3 kJ/K mol) and Pa is the air pressure (0.101325 × 10−9 kJ/m3) (Geankoplis 1998). The diffusion coefficients of water vapor, Dwa, at 60 and 80 °C, are 3.09 × 10−5 and 3.43 × 10−5 m2/s, respectively (Pakowski et al. 1991).
In this model, the effective diffusivity is expressed using an Arrhenius-type relationship considering the temperature effect over the drying process for both drying methods:
| 14 |
where Deff is the moisture diffusivity in m2/s; D0 is the Arrhenius factor m2/s; R represents the universal gas constant, Ta is the absolute air drying temperature in K and Ea is the activation energy of the moisture diffusion in kJ/mol, which is the energy barrier that must be overcome to start the moisture diffusion.
The estimation of the average moisture content at each instant of time in the chicory root cubes is obtained by integrating local moisture content over volume. Specifically, the average moisture content is expressed as stated in Eq. (15), which can be solved by means of Trapezius’s rule.
| 15 |
A polynomial contraction kinetic is proposed to describe the shrinkage process as a function of the moisture content, according to Eq. (16).
| 16 |
where a, b and c are constants obtained by fitting the equation to the experimental results obtained at the different drying conditions for conventional and vacuum drying.
Objective function and solution strategy for model parameter estimation
The objective function based on the minimization of the sum of squared errors (SSE) between the experimental and predicted data points of moisture content is implemented according to Eq. (17) to evaluate model parameters and the goodness of the fit. In addition, the r-square (R2) is calculated.
| 17 |
where HSexp is the experimental moisture ratio, HScalc the calculated moisture ratio and N the number of data values.
The proposed non-linear programming model is implemented in GAMS (General Algebraic Modeling System) and solved using CONOPT (Singh and Heldman 1993), an algorithm based on the reduced gradient method. For the implementation, Eqs. (3, 5, 6b) are discretized using the central finite difference method (CFDM) and the implicit method. This scheme, which has first-order accuracy in time and second-order accuracy in space, is unconditionally stable and convergent. Equations (18–19) define the spatial and temporal variations, respectively, with M = 9 and N = 32. The values of M and N have been previously proved and ensure the stability of the solution with a low computational demand.
| 18 |
| 19 |
The solution of the minimization problem is achieved only using correlations reported in the literature to predict mass transfer coefficients in order to reduce the model degrees of freedom and facilitate the resolution of the NLP model. The resulting models involve 893 variables and 864 constraints, and 817 variables and 787 constraints for conventional and vacuum drying models, respectively.
Results and discussion
As mentioned, this work is the first step of a model-based optimization project of a full-scale facility to manufacture chicory root flour with antioxidant properties. The mathematical model here presented (for hot-air and vacuum drying) involves algebraic and partial differential equations to describe moisture diffusion process, Eqs. (3–15), which contains specific parameters that must be estimated. This is achieved by the minimization of the sum of squared errors (SSE) among the experimental and model-estimated moisture profiles, stated in Eq. (17), simultaneously taking into account the shrinkage kinetics represented by Eq. (16). So, the objective is to estimate the mass transfer model parameters associated to the drying kinetics (diffusion coefficients and activation energies) and the shrinkage kinetics. The optimal estimated parameters are reported in Table 1 with the corresponding SSE and R2 values. The model’s goodness-of-fit is also evaluated by the analysis of the drying and shrinkage profiles presented in Figs. 1 and 2, as discussed in the following sections.
Table 1.
Adjustment data
| Conventional drying | Drying kinetics | Shrinkage kinetics | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| T (°C) | v (m/s) | D0 (m2/s) | Ea (kJ/mol) | Deff (m2/s) | SSE | R2 | a | b | c | R2 |
| 60 | 0.2 | 0.529e−10 | 27.517 | 2.553e−10a | 0.002 | 0.997 | − 0.0227 | 0.3168 | 0.1233 | 0.9983 |
| 0.7 | 0.410e−10 | 26.535 | 2.825e−10b | 0.002 | 0.997 | − 0.0478 | 0.4411 | 0.0632 | 0.9951 | |
| 80 | 0.2 | 0.275e−10 | 25.990 | 3.928e−10c | 0.009 | 0.992 | − 0.0428 | 0.3954 | 0.2693 | 0.9882 |
| 0.7 | 0.185e−10 | 24.580 | 4.280e−10d | 0.001 | 0.999 | − 0.0698 | 0.4661 | 0.2060 | 0.9296 | |
| Vacuum drying | Drying kinetics | Shrinkage kinetics | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| T (°C) | D0 (m2/s) | Ea (kJ/mol) | Deff (m2/s) | SSE | R2 | a | b | c | R2 | |
| 60 | 25 | 0.260e−10 | 23.523 | 5.319e−10a | 0.001 | 0.999 | − 0.0826 | 0.3900 | 0.5417 | 0.9222 |
| 50 | 0.180e−10 | 22.435 | 5.459e−10b | 0.002 | 0.999 | − 0.0667 | 0.3625 | 0.5108 | 0.9313 | |
| 80 | 25 | 0.162e−10 | 21.963 | 9.159e−10c | 0.002 | 0.998 | − 0.0723 | 0.4136 | 0.3993 | 0.9049 |
| 50 | 0.103e−10 | 20.448 | 9.746e−10d | 0.002 | 0.999 | − 0.0243 | 0.2538 | 0.3925 | 0.9563 | |
Different letters in the same column indicate that values are significantly different (p value < 0.05)
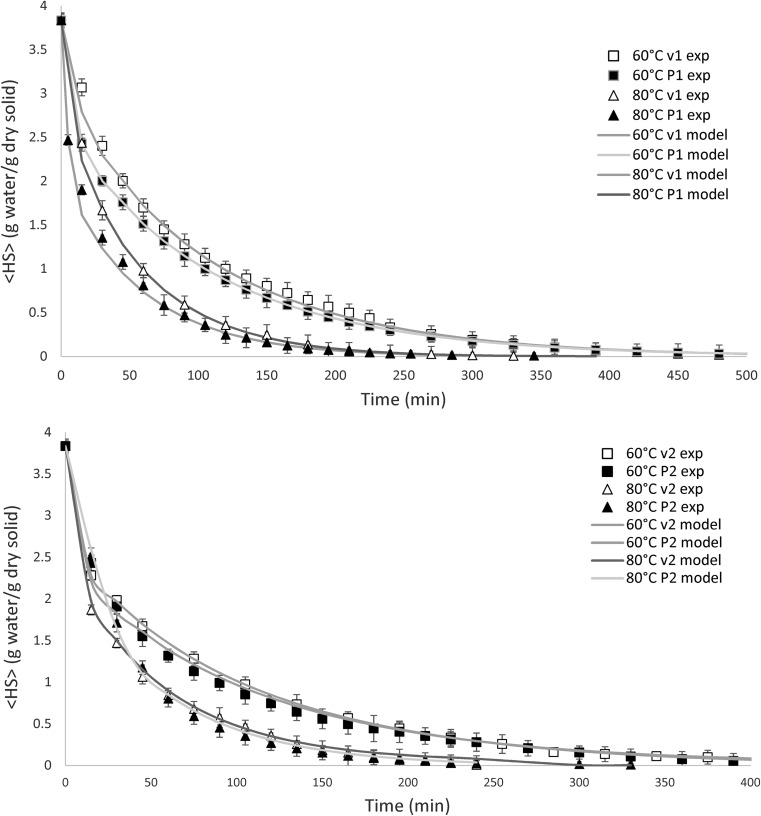
Fig. 1.
Moisture content variation during drying time for chicory root cubes at different operating conditions for conventional and vacuum drying (v1 = 0.2 m/s; v2 = 0.7 m/s; P1 = 25 mmHg absolute; P2 = 50 mmHg absolute)
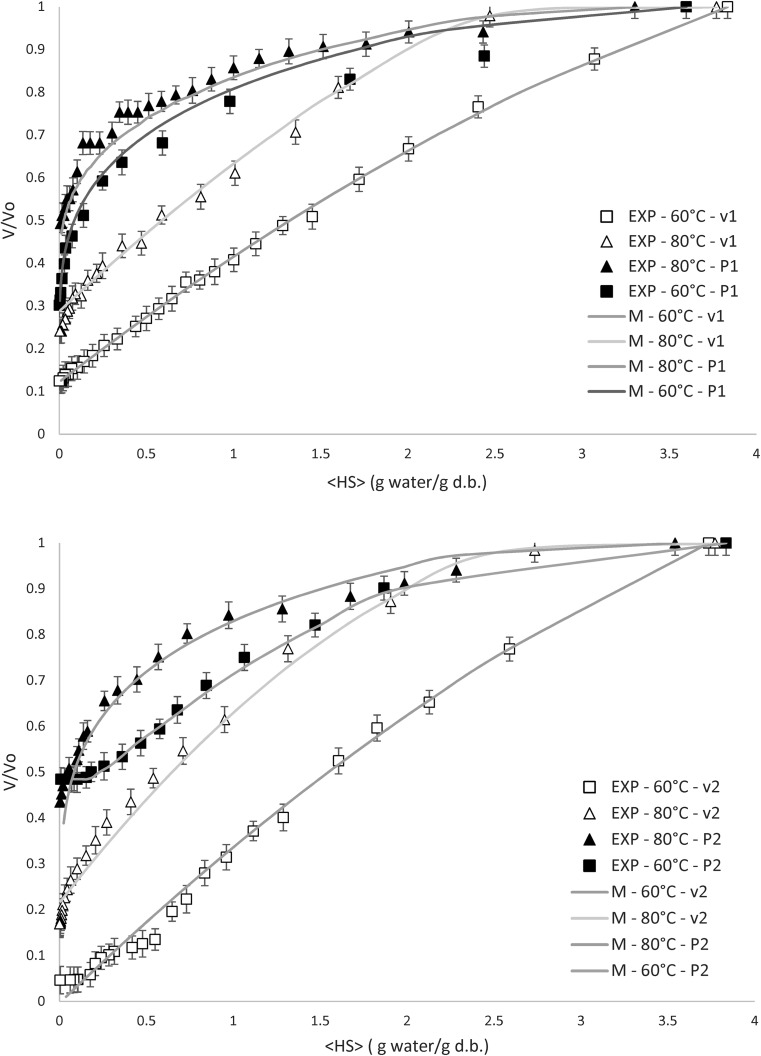
Fig. 2.
Experimental and calculated shrinkage profiles for chicory roots under hot-air and vacuum drying (v1 = 0.2 m/s; v2 = 0.7 m/s; P1 = 25 mmHg absolute; P2 = 50 mmHg absolute)
Drying kinetics
Initial moisture content of chicory roots is evaluated as 3.840 ± 0.021 kg/kg product. Figure 1 shows the experimental and predicted profiles of the mean moisture content for experimental temperatures, air velocities and pressures depending on the used drying method (conventional or vacuum, respectively). The graphics are grouped according to the level of air velocity and vacuum pressure (lower values of air velocity and vacuum pressure and the upper ones). It is observed that the proposed model, which takes into consideration shrinkage kinetics, accurately describes the drying kinetics for all the experiments. The results are consistent and show that the vacuum drying at any temperature is slightly faster at the beginning of the drying process than the drying under atmospheric pressure.
From Fig. 1, it can be also observed shorter drying times and higher drying rates are achieved at higher air temperature. Half of time is required to reach equilibrium moisture in the vacuum drier at 80 °C and 50 mmHg absolute, compared to the required time in the experiment using the conventional drier at 60 °C and 0.2 m/s.
In the vacuum drying process, as temperature increased, vapor pressure inside the sample also increased. Therefore, the pressure gradient between the surface and inner side of the sample is greater resulting in a higher drying rate and consequently lesser drying time (Mitra et al. 2011). The same drying tendency was reported for the increment of the air temperature by keeping the vacuum pressure constant for the drying of gooseberry flakes (Methakhup et al. 2005), pumpkin slabs (Arévalo-Pinedo and Murr 2006), and onion slices (Mitra et al. 2011). The thermodynamic behavior resulting from the increment of the inner vapor pressure driving force is similar for different food matrix, resulting in similar drying performances.
As shown in Fig. 1, the moisture variation considering both drying temperatures, 60 °C and 80 °C, under either atmospheric or vacuum pressures, exhibit similar tendencies during the second part of the drying process. Under vacuum conditions, the drying rate during the first period is high, and the cube sides suffer hardening, which could increase the moisture diffusion process resistance; therefore, the drying rate is slower in the last period because of the lower driving force. Similar results were evidenced by others authors (Corzo et al. 2008; Ah-hen et al. 2012).
Effect of drying method and conditions on activation energy and effective diffusivities
Table 1 presents the values of D0, Ea and Deff for each experiment. The results present high values of R2 and low values of error of prediction, evidencing an aceptable goodness-of-fit. The analysis of the prediction bands (not shown) evidence a range between ± 0.2 and ± 0.6 g water/g d.b. of deviation as the region where 95% of the experimental data points are expected to be, whereas it is here observed that all obtained observations fall within.
Water diffusion coefficient increases with the increment of drying air temperature for both drying methods. As expected, the use of higher drying temperatures promotes a higher water mobility in food systems from the interior to the surface (Ruiz-Lopez et al. 2012), and thus increases the effective diffusivity of mass transfer, despite the fact that temperatures higher than 80 °C are not appropriate due to the thermal degradation of antioxidant components. Furthermore, the effective diffusivity increases as air-drying velocity increases. In addition, the air velocity has evidenced a significant influence on the diffusion coefficient for both drying temperatures during conventional drying. Also, the influence of the pressure on the drying process affects the effective diffusivity coefficients. The drying time is reduced by decreasing the drying pressure.
Comparing both drying methods, the effective diffusivity for vacuum drying is higher at the same temperature than for the conventional drying method. The main difference between both drying techniques is the partial vapor pressure, which is lower during vacuum drying; therefore, the remnant liquid water reaches its boiling point and it is vaporized, explaining the higher moisture transfer rate.
Similar values of effective diffusivity coefficients for comparable conditions were obtained by different authors using other fruit and vegetables matrix (Jaya and Das 2003; Mitra et al. 2011; Lee and Zuo 2013).
During drying, the activation energy is considered as the energy barrier that must be overcome to initiate the moisture diffusion (Babalis and Belessiotis 2004). Lower values were obtained for vacuum drying, although differences are not so high as the values reported for other authors (Jaya and Das 2003; Ah-Hen et al. 2012).
Shrinkage kinetics
Experimental and predicted contraction data obtained during both drying methods as a function of the average moisture content at different conditions are plotted in Fig. 2. The ratio between the sample volume being dried and the initial volume (V/V0) is the parameter used for describing the shrinkage process. The effect of moisture content on the shrinkage is well fitted (R2 > 0.90) by a quadratic model, according to Eq. (16). The obtained coefficients for Eq. (16) are presented in Table 1. It is observed in Fig. 2 that the lower the moisture content, the higher the shrinkage for all the drying experiments. The size reduction under atmospheric pressure is considerable higher when compared with samples dried under vacuum.
In Fig. 2, it is also observed that the degree of shrinkage of chicory roots during low temperature drying is greater than at high temperature drying, for the same vacuum pressure or air velocity, due to surface hardening at higher temperatures which restrains the size reduction.
During convective drying the sample structure collapses because of the moisture loss, whereas vacuum expands air and water vapor contained in the food. The cube shape is maintained but a porous internal structure is generated providing a large area-to-volume ratio appropriated for the mass transfer (Jaya and Das 2003). Therefore, lower cube contraction is verified at higher vacuum pressure.
A pressure unbalance is created between the sample inner and the external chamber pressure. This pressure difference is responsible of the sample contracting stresses that causes the shrinkage. In vacuum drying, this pressure unbalance is lower because of the reduction of the air pressure, hence, the shrinkage process is relatively lower (Wu et al. 2007).
Influence of the drying experiments on quality aspects
Rehydration
Rehydration is an important attribute to evaluate dried foodstuffs. The RR is directly related to the drying method. Different physical and chemical changes are observed depending on the drying treatment (Noshad et al. 2012). The rehydration curves of chicory roots samples dried at different conditions are shown in Fig. 3, which exhibit an asymptotic value for all drying conditions that corresponds to the saturation level.
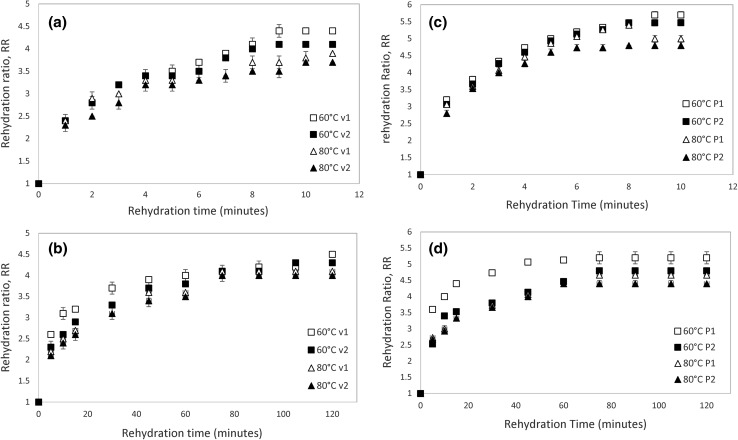
Fig. 3.
Weight gain on rehydration as a function of the rehydration temperature and time for both drying methods. a Rehydration curve at 100 °C for hot-air dried samples. b Rehydration curve at 30 °C for hot-air dried samples. c Rehydration curve at 100 °C for vacuum dried samples. d Rehydration curve at 30 °C for vacuum dried samples (v1 = 0.2 m/s; v2 = 0.7 m/s; P1 = 25 mmHg absolute; P2 = 50 mmHg absolute)
The rehydration ratio is higher for the vacuum dried samples in comparison to air dried ones. Vacuum drying creates a porous structure with very less shrinkage than those obtained by air drying, thereby providing better rehydration characteristics in agreement with the results reported in the shrinkage’s section.
Higher RR are evidenced for lower air drying temperature, velocity and absolute pressure depending on the drying procedure. It is observed that a more severe drying treatment (higher air temperature and velocity or pressure) affects the RR because the dried samples uptake less water due to the stronger surface case hardening associated with less contraction and broken cells, as is shown in Fig. 2. These results are in agreement with those obtained by Giri and Prasad (2007) and Apati et al. (2010).
Non-enzymatic browning
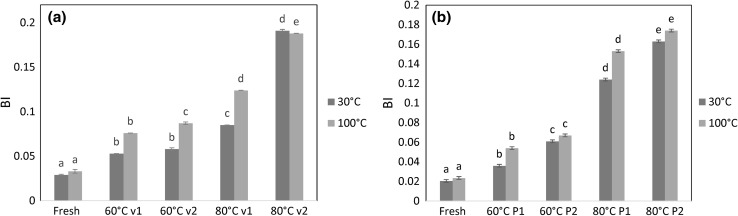
Browning is another important quality attribute for dried products. Figure 4 shows the BI for each drying treatment and rehydration evaluation at 30 and 100 °C. It is shown that higher drying temperatures and velocities or absolute pressures, depending on the drying method, significantly accelerate deterioration of samples color because of non-enzymatic browning reactions (Xiao et al. 2014). Drying temperature of 80 °C or higher generates accumulation of melanoidins derived from Maillard reactions (Miranda et al. 2009). The results clearly evidence how BI increases with the air temperature and velocity or air pressure, while BI is not influenced by the rehydration treatment because it is only affected by the drying conditions. However, slight difference in the BI is detected comparing both drying methods. Even though, for vacuum drying, the BI is lower than the one obtained at atmospheric pressure and the same drying temperature. Arévalo-Pinedo and Murr (2006) explained that the vacuum state helps to inhibit Maillard browning reaction due to its contribution to oxygen isolation.
Fig. 4.
Effect of Browning index for the different drying treatments. Different letters in the same column indicate that values are significantly different (p value < 0.05) (v1 = 0.2 m/s; v2 = 0.7 m/s; P1 = 25 mmHg absolute; P2 = 50 mmHg absolute)
Total phenolic content
Phenolic compounds or polyphenols are important metabolites present in plants, vegetables and some fruits. Many of them possess high levels of antioxidant activity, avoiding decomposition of hydroperoxides into free radicals due to the presence of high activity as hydrogen or electron donor (Dzharova et al. 2016).
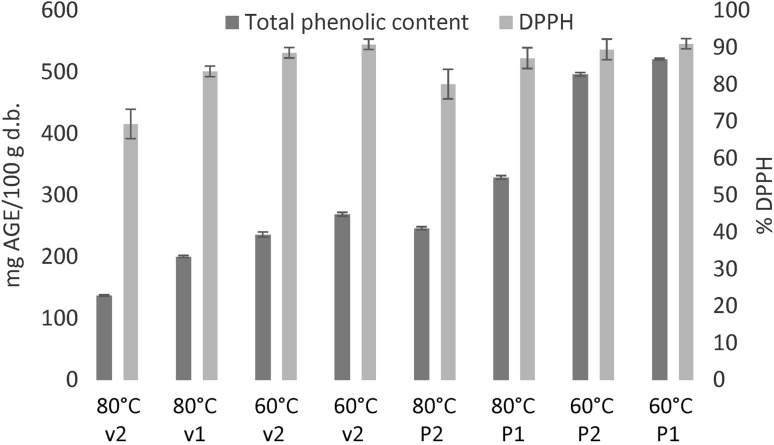
In this work, the total phenolic content of the dried samples is examined using a well proven extraction technique (Shad et al. 2013). The results are presented in Fig. 5. After 90 min of extraction, the total phenolic contents varied within 137.4–269.3 and 246.5–521.2 mg GAE/100 g d.b. for conventional and vacuum drying, respectively, using gallic acid as standard. Higher content of polyphenols is obtained using the vacuum drying samples, while also higher content is achieved at a lower drying temperature of 60 °C. These results are consistent with other values reported in the literature (Wang et al. 2003; Shad et al. 2013). It is also proved that higher drying temperatures affect the sample composition due to thermal damage.
Fig. 5.
Total phenolic content for extraction at 50 °C using solvent mixture of ethanol: water (50:50 v/v) and DPPH radical scavenging capacity values for all dried samples (v1 = 0.2 m/s; v2 = 0.7 m/s; P1 = 25 mmHg absolute; P2 = 50 mmHg absolute)
DPPH radical scavenging capacity values presented in Fig. 5 show that the dried samples retain good reducing power due to not only to the phenolic content, but also because the generation of Maillard derived melanoidins that have antioxidant activity and enhance the antioxidant capacity at air drying temperatures of 80 °C or higher (Miranda et al. 2009). Therefore, DPPH values do not have the same tendency then the phenolic content.
Conclusion
In this work, experimental runs for drying of chicory root cubes by hot-air and vacuum mechanisms at different operating conditions are reported and thoroughly analyzed. Then, a complete mathematical model to describe the mass transfer mechanism for both methods is developed using first principles equations through DAEs and semi-empirical correlations.
SSE and R2 show that the proposed model satisfactorily predicts the drying and shrinkage kinetics, while computing the effective moisture diffusion coefficients.
Samples dried using the vacuum dryer at 60 °C and 25 mmHg absolute pressure presented better rehydration, lower shrinkage and higher total phenolic content.
Acknowledgments
The authors kindly acknowledge the financial support of the Universidad Tecnológica Nacional (UTN) and the Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET) of Argentina.
List of symbols
- a, b, c
Parameters of the shrinkage’s equation
- BI
Browning index (abs kg of dry matter−1)
- D0
Arrhenius factor (m2/s)
- Deff
Effective diffusion coefficient (m2/s)
- Deq
Equivalent diameter (m)
- Dwa
Diffusion coefficient of water vapor (m2/s)
- Ea
Activation energy for the moisture diffusion (KJ/mol)
- G
Mass flow rate (kg/m2 s)
- HS
Food moisture content (kg of water kg of dry matter−1)
Average food moisture content (kg of water kg of dry matter−1)
- k
Mass transfer coefficient (m/s)
- L
Characteristic length, sample semi-thickness (m)
- M
Number of spatial discretization points
- MW
Molecular weight (kg/mol)
- N
Number of temporal discretization points
- P
Pressure (KJ/m3)
- R
Universal gas constant (KJ/°C mol)
- RR
Rehydration ratio (kg absorbed water kg of dry matter−1)
- SSE
Sum square error
- T
Temperature (°C)
- t
Drying time (min)
- x, y, z
Coordinate axes/directions
- v
Velocity (m/s)
- V
Volume (m3)
Dimensionless groups
- Re
Reynolds number
- Sc
Schmidt number
- Sh
Sherwood number
Greek symbols
- ΔL
Space grid with (m)
- Δt
Temporal grid with (s)
- µ
Viscosity (kg/m s)
- ρ
Density (dry basis) (kg/m)
Subscripts
- a
Air
- eq
Equilibrium
- f
At final time
- o
At initial condition
- s
Food
References
- Afolabi TJ, Tunde-Akintunde TY, Adeyanju JA. Mathematical modeling of drying kinetics of untreated and pretreated cocoyam slices. J Food Sci Technol. 2015;52(5):2731–2740. doi: 10.1007/s13197-014-1365-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ah-Hen K, Zambra CE, Aguëro JE, Vega-Gálvez A, Lemus-Mondaca R. Moisture diffusivity coefficient and convective drying modelling of murta (Ugni molinae Turcz): influence of temperature and vacuum on drying kinetics. Food Bioprocess Technol. 2012;6(4):919–930. doi: 10.1007/s11947-011-0758-5. [DOI] [Google Scholar]
- Apati GP, Furlan SA, Laurindo JB. Drying and rehydration of oyster mushroom. Braz Arch Biol Technol. 2010;53(4):945–952. doi: 10.1590/S1516-89132010000400025. [DOI] [Google Scholar]
- Arévalo-Pinedo A, Murr FEM. Kinetics of vacuum drying of pumpkin (Cucurbita maxima): modeling with shrinkage. J Food Eng. 2006;76(4):562–567. doi: 10.1016/j.jfoodeng.2005.06.003. [DOI] [Google Scholar]
- Babalis SJ, Belessiotis VG. Influence of the drying conditions on the drying constants and moisture diffusivity during the thin-layer drying of figs. J Food Eng. 2004;65:449–458. doi: 10.1016/j.jfoodeng.2004.02.005. [DOI] [Google Scholar]
- Boroski M, Visentainer JV, Cottica SM, Rodrigues de Morais D (2015) Antioxidantes, príncipios e métodos analíticos. Curitiba, Brazil
- Corzo O, Bracho N, Alvarez C. Water effective diffusion coefficient of mango slices at different maturity stages during drying. J Food Eng. 2008;87(4):479–484. doi: 10.1016/j.jfoodeng.2007.12.025. [DOI] [Google Scholar]
- Dzharova VV, Mishrab AP, Shariatic MA, Atanassovad MS, Plygun S. Phytochemical contents in solid–liquid extraction of aqueous alcoholic extract of chicory (Cichorium intybus L.) leaves. Foods Raw Mat. 2016;4(2):32–37. doi: 10.21179/2308-4057-2016-2-32-37. [DOI] [Google Scholar]
- Escarpa A, Gonzalez MC. An overview of analytical chemistry of phenolic compounds in foods. Crit Rev Anal Chem. 2001;31(2):57–139. doi: 10.1080/20014091076695. [DOI] [Google Scholar]
- Figueira GM, Park KJ, Brod FPR, Honório SL. Evaluation of desorption isotherms, drying rates and inulin concentration of chicory roots (Cichorium intybus L.) with and without enzymatic inactivation. J Food Eng. 2004;63:273–280. doi: 10.1016/j.jfoodeng.2003.06.001. [DOI] [Google Scholar]
- Geankoplis CJ. Transport processes and unit operations. México: Compañia Editorial Continental; 1998. [Google Scholar]
- Giri SK, Prasad S. Drying kinetics and rehydration characteristics of microwave-vacuum and convective hot-air dried mushrooms. J Food Eng. 2007;78(2):512–521. doi: 10.1016/j.jfoodeng.2005.10.021. [DOI] [Google Scholar]
- González M, Guzmán B, Rudyk R, Romano E, Molina MAA. Spectrophotometric determination of phenolic compounds in propolis. Lat Am J Pharm. 2003;22(3):243–248. [Google Scholar]
- Hacihafizoglu O, Cihan A, Kahveci K, Lima AGB. A liquid diffusion model for thin-layer drying of rough rice. Eur Food Res Technol. 2008;226(4):787–793. doi: 10.1007/s00217-007-0593-0. [DOI] [Google Scholar]
- Jaya S, Das PH. A vacuum drying model for mango pulp. Drying Technol. 2003;21(7):1215–1234. doi: 10.1081/DRT-120023177. [DOI] [Google Scholar]
- Lee JH, Zuo L. Mathematical modeling on vacuum drying of Zizyphus jujube miller slices. J Food Sci Technol. 2013;50(1):115–121. doi: 10.1007/s13197-011-0312-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Methakhup S, Chiewchan N, Devahastin S. Effects of drying methods and conditions on drying kinetics and quality of Indian gooseberry flake. LWT – Food Sci Technol. 2005;38(6):579–587. doi: 10.1016/j.lwt.2004.08.012. [DOI] [Google Scholar]
- Milala J, Grzelak K, Król B, Juśkiewicz J, Zduńczyk Z. Composition and properties of chicory extracts rich in fructans and polyphenols. Pol J Food Nutr Sci. 2009;59(1):35–43. [Google Scholar]
- Mills AF. Basic heat and mass transfer. Massachusetts, Irwin: Prentice Hall, Inc.; 1995. [Google Scholar]
- Miranda M, Maureira H, Rodriguez K, Vega-Galvez A. Influence of temperature on the drying kinetics, physicochemical properties, and antioxidant capacity of aloe vera (Aloe Barbadensis Miller) gel. J Food Eng. 2009;91:297–304. doi: 10.1016/j.jfoodeng.2008.09.007. [DOI] [Google Scholar]
- Mitra SL, Shrivastava P, Srinivasa R. Process optimization of vacuum drying of onion slices. Czech J Food Sci. 2011;29:586–594. doi: 10.17221/162/2010-CJFS. [DOI] [Google Scholar]
- Murthy TPK, Manohar B. Hot air drying characteristics of mango ginger: prediction of drying kinetics by mathematical modeling and artificial neural network. J Food Sci Technol. 2014;51(12):3712–3721. doi: 10.1007/s13197-013-0941-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noshad M, Mohebbi M, Shahidi F, Mortazavi SA. Kinetic modeling of rehydration in air-dried quinces pretreated with osmotic dehydration and ultrasonic. J Food Process Preserv. 2012;36(5):383–392. doi: 10.1111/j.1745-4549.2011.00593.x. [DOI] [Google Scholar]
- Oliveira R (2005) Effect of chicory roots of drying in obtaining inulin. Ph.D. thesis. Campinas University UNICAMP, Campinas, San Pablo, Brazil
- Pakowski Z, Bartczak Z, Strumillo C, Stenstrom S. Evaluation of equations approximating thermodynamic and transport properties of water, steam and air for use in cad of drying processes. Drying Technol. 1991;9:753–773. doi: 10.1080/07373939108916708. [DOI] [Google Scholar]
- Pereira da Silva W, Silva C, Palmeira Gomes J. Comparison of boundary conditions to describe drying of turmeric (Curcuma longa) rhizomes using diffusion models. J Food Sci Technol. 2014;51(11):3181–3189. doi: 10.1007/s13197-012-0813-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rohman A, Riyanto S, Yuniarti N, Saputra WR, Utami R, Mulatsih W. Antioxidant activity, total phenolic, and total flavaonoid of extracts and fractions of red fruit (Pandanus conoideus Lam) Int Food Res J. 2010;17:97–106. [Google Scholar]
- Ruiz-Lopez II, Ruiz-Espinosa H, Arellanes-Lozada P, Bárcenas-Pozos ME, García-Alvarado MA. Analytical model for variable moisture diffusivity estimation and drying simulation of shrinkable food products. J Food Eng. 2012;108:427–435. doi: 10.1016/j.jfoodeng.2011.08.025. [DOI] [Google Scholar]
- Sahari Y, Driscoll RH (2013) Thin layer drying of agricultural products: a review. In: 3rd Malaysian postgraduate conference (MPC2013), pp 8–21
- Shad MA, Nawaz H, Rehman T, Ikram N. Determination of some biochemicals, phytochemicals and antioxidant properties of different parts of Cichorium intybus L.: a comparative study. J Anim Plant Sci. 2013;23(4):1060–1066. [Google Scholar]
- Shimada K, Fujikawa K, Yahara TN. Antioxidant properties of xhantan on the antioxidant of soybean oil in cyclodextrin. J Agric Food Chem. 1992;40:945–948. doi: 10.1021/jf00018a005. [DOI] [Google Scholar]
- Singh RP, Heldman DR. Introduction to food engineering. 2. San Diego, USA: Academic Press; 1993. [Google Scholar]
- Swain T, Goldstein JL. The quantitative analysis of phenolic compounds. In: Pridham JB, editor. Methods in polyphenol chemistry. Oxford: Pergamon Press; 1964. pp. 131–146. [Google Scholar]
- Wang M, Simon JE, Aviles JF, Zheng QY, Tadmor Y. Analysis of antioxidative phenolic compounds in artichoke. J Agric Food Chem. 2003;51:601–608. doi: 10.1021/jf020792b. [DOI] [PubMed] [Google Scholar]
- Wu L, Orikas T, Ogawa Y, Tagawa T. Vacuum drying characteristics of eggplants. J Food Eng. 2007;83(3):422–429. doi: 10.1016/j.jfoodeng.2007.03.030. [DOI] [Google Scholar]
- Xiao HW, Law C, Sun DW, Gao ZJ. Color change kinetics of American ginseng (Panax quinquefolium) slices during air impingement drying. Drying Technol. 2014;32:418–427. doi: 10.1080/07373937.2013.834928. [DOI] [Google Scholar]